Interrelationship between viscosity and electrical properties for edible oils

Abstract

Electrical properties of edible oil depend upon its total polar component, temperature and the frequency of the applied voltage. Dielectric constant, dielectric loss tangent and electrical conductivity were measured for cottonseed (Gossypium sp.), ground nut (Apios americana), mustard (Brasicca compestriss) and sun flower (Helianthus annuus) oils in the temperature range of 20 to 100°C so as to assess the potential of their applicability for assessing the quality of oils. Viscosity of the oils is an other important physical property associated with their processing and quality control. Viscosity of these oils was experimentally measured. The correlation of viscosity with dielectric loss tangent and viscosity with electrical conductivity were tested. The best correlating relations along with correlation constants, valid for the temperature range of 20–100°C are presented. The regression equation developed relating viscosity with loss tangent and electrical conductivity had high correlation coefficient (R² > 0.96) for all the four oils within temperature range of 20–100°C.

Introduction

A series of complex changes and reactions produce numerous decomposition products during the deep frying of fat. Assessment of frying fats has been a subject of study as it is important to have simple objective methods for assessing their quality. . In 1973, one of the first attempts was made to define deteriorated frying oil by German Society of Fat Research (Kurzbericht Zum 1973). Presently, total polar component (TPC) value of oils has been accepted as the most reliable parameter for assessing the condition of frying fats. The column chromatography has been recommended as the standard laboratory method for measuring TPC values of oils. The prescribed chromatography procedure for TPC determination besides, being time consuming has another drawback, as it requires considerable skill. Therefore, attempts have been made to assess the quality of the oil based on easily measurable physical properties. Viscosity, refractive index, optical absorption etc have been used to assess the quality of oils. Al-Kahtani (1991) found a linear relation between TPC values and viscosity for oils. (Pace et al. 1968; Risman and Bengtsson 1971; El-Shami et al. 1992) have suggested that electrical properties may be used as indicators of condition and quality of edible oils.

Dielectric constant, dielectric loss tangent and dc electrical conductivity of edible oils can be of interest in this regard. The dielectric constant of a material is a measure of its polarizability and its dielectric loss tangent is related to the loss of power when the material is subjected to an alternating voltage (Tareev 1979). Usually the dielectric loss tangent are small, therefore these are presented as percentage. Further, the dielectric constant and dielectric loss tangent of a material depend upon the frequency of the applied ac voltage. The dc electrical conductivity and dielectric loss tangent are manifestations of the motion of polar molecules in a viscous media under an applied potential. Knowledge of these electrical properties of oils is essential to assess the potential of their applicability in determining the quality of oil. Fritsch (1981) has observed that the change in the dielectric constant of oils provided the simplest method for assessing their deterioration. Augustin et al. (1987) have reported existence of highly significant correlation between the dielectric constant of oil and the polar components present in it. Further, the dielectric constant of different fresh fats has been found to be different. Both of these observations regarding dielectric constant of oils are manifestations of behavior of polar molecules in a viscous media. Kaufmann et al. (2001) compared the performance of High Performance Liquid Chromatography (HPLC) method for the determination of polar compound in used frying oils/fats with chromatographic technique and dielectric constant measurement. The various studies undertaken so far have remained confined to their dielectric constant at high frequencies.

Viscosity of oils is another physical property of paramount importance. Its knowledge is necessary for the designing and operation of the processing equipment. Conventional techniques for measuring viscosity, besides, being time consuming suffer from inherent shortcomings attribu to the handling of measuring equipment. There is a need to evolve cheap and accurate indirect techniques for on line determination of viscosity, which are rapid, reliable and employable during the processing of oils (Sadat and Khan 2007). The viscosity of an oil is dependent upon its TPC value and so are its electrical properties, therefore, it seems plausible that the viscosity of oil can be estimated from its electrical properties. The advantage of knowing such a relation would enable to determine the viscosity of oil by measuring only its electrical properties. In the present study viscosity, dielectric constant, electrical conductivity and dielectric loss tangent of four edible oils have been experimentally measured as a function of temperature. The correlation relations between viscosity and dielectric loss tangent and electrical conductivity were determined.

Materials and methods

Four commonly consumed edible oils e.g. cottonseed (Gossypium sp), groundnut (Apios americana), mustard (Brasicca compestriss) and sunflower (Helianthus annuus) were selected for this study. Commercially available cottonseed and groundnut oils were bought from the market without preference for any brand. Mustard and sunflower oils were freshly extracted from the seeds of gobi sarson and PSFH–67 varieties, respectively. The viscosity of these oils was measured using Brookfield Dial Reading Viscometer (Model LVT, Brookfield Engg. Laboratories INC. Stoughton, MA-02072, USA) at 60 rpm employing the largest spindle (#40). The oil samples were maintained at various constant temperatures between 20 and 100°C in a thermally controlled water bath.

A three terminal test cell for oils supplied by M/s Sivananda Electronics, Devlali, Maharastra, India was used for measuring dielectric constant, dielectric loss tangent and electrical resistivity of edible oils. The test cell confirmed to the measuring standards prescribed by Bureau of Indian Standards (IS 6103 1971), New Delhi regarding measurements of electrical resistivity of insulating oils. The test cell had stainless steel electrodes with terminals separated by teflon rings. For ensuring accuracy of measurements a guard terminal shielded the measuring electrodes. The test cell was housed in a specially designed heating chamber. The heating chamber produced a uniform heating with the desired temperature obtainable in less than 20 min as per the recommendations of Bureau of Indian Standards (IS 6262 1971). The temperature was sensed by a solid state sensing probe attached to a digital panel calibrated to indicate the temperature of the oils in Celsius. Oil Loss Angle meter (MLO-ID) capable of measuring up to 199.9% was used to measure the dielectric loss tangent (in percentage) and dielectric constant for all oils. The measurements were made at 500 V and 50 Hz. The dc electrical conductivity was determined experimentally by employing 500 V DC. The sensitivity of power supply used in the measurements of conductivity was in accordance with BIS recommendations (IS 6103 1971). As prescribed by BIS in paragraph 8.3 of IS 6103 1971, the cell constant was calculated yielding its value to be 734.5. The electrical conductivity was measured by using Millions Megohm meter (LS-3D, Sivananda Electronics, Devlali, India). The measurements were made on five replicates in respect of every physical quantity reported herein.

When a dielectric is subjected to an alternating electric field, the induced polarization also varies periodically with time. In general, the polarization may lag behind in phase relative to the applied electric field. The dielectric constant (ε*) then becomes a complex quantity ε* (=ε′ - j ε′′), where ε′ is real dielectric constant, ε′′ is imaginary part of dielectric constant ε′′ and j is unit vector. Both ε′ and ε′′ (also called dielectric loss) are frequency dependent. The imaginary part of dielectric constant (ε′′) is a measure of the energy dissipation in the medium. The relaxation of the polarization is accounted through relaxation time (τ). The relaxation time depends upon the temperature, the chemical composition and the physical state of the material. The relaxation process of dipoles has been treated as analogous to a chemical rate process. In the simplest model, when the motion of the dipole moment of the polar molecule in the dielectric is considered to take place through discrete orientations, the relaxation time obeys an Arrhenious like equation, involving activation energy for relaxation to take place. The thermal fluctuations provide the require activation energy for the relaxation process (Flugge 1956). In non-equilibrium statistical mechanics, the viscosity of the system appears naturally as a measure of dissipation of energy through the fluctuation-dissipation theorem (Zwanzig 2001). The viscosity of a liquid can also be described through the theory of rate process. The activation energies for the molecular dipole moment orientations and viscous flow need not to be same. A combination of these two physical phenomena provided that for a simple system, the logarithms of relaxation times and of viscosity should vary linearly with inverse temperature. Therefore, it is possible to obtain a relation between dielectric relaxation time and co-efficient of viscosity of liquid through the elimination of temperature. The existence of such an inter-relationship between the dielectric relaxation time and viscosity is not surprising because both of the processes are related to the dissipation of different forms of energy.

The edible oils are mixtures of several polar molecules which render the system very complex. The system composed of mixtures of dipoles can never be adequately represented through a single relaxation time. Rather, for such systems a distribution of relaxation times may adequately account their dielectric behavior. The oils may be having non-Newtonian behavior by virtue of the interactions among its constituents. For complex systems the derivation of the inter-relationship between viscosity and dielectric parameters would not be easy. It is proposed, on the basis of the results of simple liquids, that for complex systems interrelationships between viscosity and dielectric constant exist. As an exploratory attempt based on this hypothesis the inter-relationship between viscosity and dielectric constant has been derived empirically.

The ε′′(ω), in the low frequencies range i.e. ω << τ −¹, is proportional to the frequency, where ω is angular frequency and the rate of heating is proportional to ω ² . Further, ε′′(ω) has appreciable variation in the low frequency region, while ε ′ practically remains unchanged in this region.

Results and discussion

The viscosity of all the oils decreased with an increase in temperature (Table 1). The decrease in viscosity of oil as its temperature increased is an expected behavior. The dependence of viscosity of a fluid on temperature is a manifestation of its cohesive and thermal energies behavior. With a rise in temperature, the attraction between the polar molecules decreased while their thermal energies increased thereby the viscosity of oil decreased. The variation of viscosity with temperature could be well represented for all the oils by the equation

where η is the viscosity, A and B are constants and T is the temperature in Kelvin. The above equation has good correlation coefficient for all the oils with value of R² greater than 0.995.

Table 1.

Variation of viscosity and dc electrical conductivity of edible oils with temperature

Temp. °C	Viscosity (centi poise)				Electrical conductivity ×10−13 (Scm−1)
	C	G	M	S	C	G	M	S
20	77.0 ± 1.73	48.0 ± 0.00	71.0 ± 1.00	64.0 ± 2.63	4 ± 0.2	12 ± 0.1	54 ± 3.4	91 ± 3.0
40	36.5 ± 0.51	26.5 ± 1.31	37.5 ± 0.52	31.5 ± 1.00	18 ± 1.2	26 ± 0.1	170 ± 11.0	194 ± 1.91
60	19.5 ± 1.35	15.0 ± 1.67	25.0 ± 2.59	17.5 ± 0.50	62 ± 5.2	60 ± 1.3	504 ± 19.0	378 ± 10.5
80	14.5 ± 1.57	10.5 ± 1.52	16.0 ± 3.62	11.5 ± 2.23	92 ± 0.0	136 ± 0.0	756 ± 26.0	524 ± 41.8
100	10.0 ± 1.00	8.0 ± 2.36	13.0 ± 3.51	9.0 ± 2.60	121 ± 0.0	206 ± 0.0	908 ± 0.0	716 ± 0.0

C- cottonseed, G-groundnut, M- mustard, S-sunflower

The dc electrical conductivity of all the oils increased manifold with a rise in temperature as evident from its data. The decrease in viscosity of oil and increased mobility of polar molecules as the temperature increased, are responsible for increase in electrical conductivity of oil. The temperature dependence of electrical conductivity was well reproduced by quadratic relation

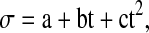where σ is electricity conductivity a, b and c being constants and t is temperature in Celsius. The values of these coefficients (R²) for all the oils are given in Table 1.

The dielectric constant values for all the four edible oils remained constant (Table 2). The values of A and B for all the oils are given in Table 3. These results cannot be compared with the results reported by Pace et al. (1968) due to the vast differences between the frequencies of applied alternating electric fields. The dielectric loss tangent (in percentage) increased manifold with an increase of temperature for all the oils (Table 2). The temperature dependence of loss tangent can be considered as; a rise in temperature and the resulting decrease in viscosity produced a double effect on the amount of power losses. On one hand, the degree of dipole orientation increased, while on the other hand, there was a reduction in the energy required to overcome the resistance of the less viscous medium when the dipole rotated through a unit angle. The first factor increased tanδ values and the second diminished it. For all the oils the dielectric loss tangent dependence on temperature was well represented by the quadratic equation,

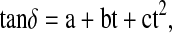where tanδ is the dielectric loss tangent, a, b and c are constants with t being the temperature of the oil in Celsius. The above equation has correlation coefficient greater than 0.992 for all the oils. The values of various constants for all the oils are given in Table 4. The dc electrical conductivity of all the oils increased manifold with a rise in temperature as evident from its data. The decrease in viscosity of oil and increased mobility of polar molecules as the temperature increased, are responsible for increase in electrical conductivity of oil. The temperature dependence of electrical conductivity was well reproduced by quadratic relation

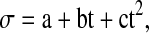where σ is electricity conductivity a, b and c being constants and t is temperature in Celsius. The values of these coefficients (R²) for all the oils are given in Table 5.

Table 2.

Variation of dielectric constant and dielectric loss tangent of edible oils with temperature

Temp. °C	Dielectric Constant at 50 Hza				Dielectric loss tangent in %
	C	G	M	S	C	G	M	S
20	2.8	2.7	2.9	2.9	0.5 ± 0.00	1.5 ± 0.00	18.8 ± 0.27	14.2 ± 0.11
40	2.8	2.7	2.9	2.9	2.6 ± 0.16	2.9 ± 0.17	38.5 ± 0.53	27.4 ± 0.25
60	2.8	2.7	2.9	2.9	4.7 ± 0.10	5.6 ± 0.00	56.4 ± 0.21	39.2 ± 0.37
80	2.9	2.7	2.9	2.9	6.7 ± 0.37	10.8 ± 0.12	71.1 ± 0.24	54.4 ± 0.41
100	3.0	2.9	3.0	3.0	11.0 ± 0.23	15.2 ± 0.21	83.5 ± 0.23	72.0 ± 0.35

C- cottonseed, G-groundnut, M- mustard, S-sunflower

^a The instrument used for this study had least count of 0.1. The increase in dielectric constant was not distinctly visible within this temperature range. The change in dielectric constant was mostly confined to second or third decimal place was also reported Pace et al. 1968

Table 3.

Constants and regression coefficients for regression equation between viscosity and temperature in range of 20–100°C

Oils	A	B × 10−6	R2**
Cotton	1.4567	99.024	0.996
Ground seed	1.4094	88.872	0.998
Mustard	2.5070	83.759	0.997
Sunflower	1.2999	97.555	0.997

^** p ≤ 0.01

Table 4.

Constants and statistical coefficients for loss tangent equation 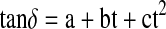in the temperature range of 20–100°C

Oils	a	b	c	R2**	Std error
Cotton seed	0.251	0.032	0.0008	0.993	0.333
Ground nut	1.075	0.018	0.0016	0.995	0.399
Mustard oil	4.178	1.207	0.0033	0.999	0.208
Sunflower	5.094	0.460	0.0020	0.997	1.165

^** p ≤ 0.01

Table 5.

Constants and statistical coefficients for electrical conductivity equation 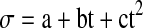in the temperature range of 20–100°C

Oils	a×1010	b×1010	c×1013	R2**	Standard error
Cotton seed	2.464	0.1002	0.495	0.975	8.600
Ground nut	1.948	0.0978	2.857	0.995	5.667
Mustard oil	24.291	1.2399	0.316	0.981	53.300
Sunflower	1.998	0.0045	2.914	0.997	13.382

^** p ≤ 0.01

The experimentally observed data brought forth that for cotton seed and groundnut oil the values of tangent loss and electrical conductivity differed at least by an order of magnitude when compared with the corresponding values for mustard and sunflower oils. This difference may be due to the non-existence of the waxes in the processed cottonseed and groundnut oils, while the waxes were present in the freshly extracted mustard and sunflower oils. Further, from the data it was observed that around certain temperatures the values of the loss tangent and electrical conductivity deviated from smooth dependence by having a sudden increase. This is not an unexpected behavior as such behavior was also observed by Pace et al (1968) and they have attributed these deviations especially for loss tangent to the heterogeneity of oils. Both, the dielectric loss tangent and dc electrical conductivity besides being inherently dependent upon TPC values of oil have exhibited manifold increase in their values as the temperature of the oil increased. This behavior renders these electrical properties suitable for their adoption in estimating the quality of oils.

The viscosity and loss tangent have opposite temperature dependence. A regression relation between these two quantities was developed. In the temperature range of 20 to 100°C, the relation which adequately provided the regression between viscosity,η and dielectric loss tangent tanδ, being

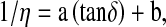where a and b are oil specific constants. The performance of the proposed regression relation is given in Table 6. The above equation correlated well with the experimental data with the value of R² being 0.993 for cotton seed, 0.992 for sunflower, 0.981 for groundnut and 0.968 for mustard oil.

Table 6.

Constants and statistical parameters (R² and standard error) for regression equation relating viscosity and loss tangent in the temperature range of 20–100°C

Oils	A	B	R2**	Standard error
Cotton seed	0.0085	0.0088	0.993	0.0038
Ground nut	0.0073	0.0164	0.981	0.0067
Mustard oil	0.00098	−0.0087	0.968	0.0053
Sunflower	0.0017	−0.0108	0.992	0.0039

^** p ≤ 0.01

The linear regression equation was developed relating the viscosity,η with the dc electrical conductivity, σ

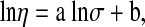where a and b are oil specific constants. This relation was found to be well obeyed by all the oils. The value of R² for sunflower was highest (0.998) and was lowest for mustard oil (0.970). The value of constants , R² and standard error is given in Table 7. SPSS package was used for the statistical analysis of the experimental data and establish the equations of regression between viscosity, loss tangent, electrical conductivity and temperature; viscosity and loss tangent and viscosity and electrical conductivity. The values of R² are significant at 1% level of significance for the various regression equations.

Table 7.

Constants and statistical parameters (R² and standard error) for regression equation relating viscosity and electrical conductivity in the temperature range of 20–100°C

Oils	a	b	R2**	Standard error
Cotton seed	−0.5662	−11.764	0.981	0.1306
Ground nut	−0.6159	−13.105	0.991	0.08263
Mustard oil	−0.5672	−10.424	0.970	0.13559
Sunflower	−0.9524	−20.195	0.998	0.04434

^** p ≤ 0.01

It is evident from the graphs (Fig 1) that the regression between viscosity and temperature is excellent. Further, the estimated values of viscosity obtained from the dielectric loss tangent and dc electrical conductivity values through the proposed regressions equations are reasonably close to the corresponding experimental values for all the oils. The agreement between the two sets of values improved as the temperature of the oil increased. Both of these regression equations suggest that the viscosity of edible oil can be accurately estimated from its electrical properties e.g. electrical conductivity or dielectric loss tangent.

Fig. 1.

Variation of viscosity of different oils with temperature. Points represent experimental values. Continuous line is regression between the viscosity and temperature. Dashed and dotted lines are of loss tangent and dc conductivity regression, respectively

Conclusion

Electrical properties provide opportunities for non-destructive sensing of quality characteristics in food products where those quality characteristics can be well correlated with the electrical properties. If good correlation exists, these properties can be sensed with appropriately designed instruments which can be calibrated to provide the desired information about the quality of the product. The regression equation developed relating viscosity with loss tangent had high correlation coefficient (R² > 0.96) for all the four oils within temperature range of 20–100°C. The predicted values were more consistent with experimental values in temperature range 40–100°C. The regression equation developed relating viscosity with electrical conductivity had also high correlation coefficient (R² > 0.98) within temperature range of 20–100°C.