The Nature of the Intramolecular Charge Transfer State in Peridinin

Abstract

Experimental and theoretical evidence is presented that supports the theory that the intramolecular charge transfer (ICT) state of peridinin is an evolved state formed via excited-state bond-order reversal and solvent reorganization in polar media. The ICT state evolves in <100 fs and is characterized by a large dipole moment (∼35 D). The charge transfer character involves a shift of electron density within the polyene chain, and it does not involve participation of molecular orbitals localized in either of the β-rings. Charge is moved from the allenic side of the polyene into the furanic ring region and is accompanied by bond-order reversal in the central portion of the polyene chain. The electronic properties of the ICT state are generated via mixing of the “1¹B_u⁺” ionic state and the lowest-lying “2¹A_g^–” covalent state. The resulting ICT state is primarily ¹B_u⁺-like in character and exhibits not only a large oscillator strength but an unusually large doubly excited character. In most solvents, two populations exist in equilibrium, one with a lowest-lying ICT ionic state and a second with a lowest-lying “2¹A_g^–” covalent state. The two populations are separated by a small barrier associated with solvent relaxation and cavity formation.

Introduction

Photosynthetic organisms exist at the base of the trophic pyramid, and they produce the energy and nutrients required to support higher organisms via the conversion of solar energy into chemical energy (1). The photosynthetic marine dinoflagellate Amphidinium carterae utilizes a water-soluble complex, peridinin-chlorophyll-a protein (PCP), for light harvesting (2). The PCP complex contains the highly substituted carotenoid, peridinin, and chlorophyll-a (Chl-a) in a stoichiometric ratio of 4:1 (2). This carotenoid absorbs solar energy in the blue-green region of the visible spectrum (∼470–550 nm) and transfers energy to Chl-a with high efficiency (∼95%) (3–7). Peridinin contains a relatively short C-37 backbone comprised of an allene moiety and a furanic ring (often referred to as a lactone ring), which are conjugated with the π-electron system, in addition to an ester group located on one β-ring and an epoxy group on the opposite β-ring (Fig. 1) (8,9).

Figure 1.

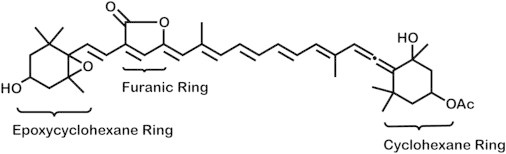
Molecular structure of peridinin.

The properties of the low-lying singlet-state manifold are often analyzed by using symmetry labels that reflect the C_2h symmetry origins of the parent linear polyene. To uphold the rigorous nature of symmetry labels, it is common in the polyene literature to use quotations to represent inexact descriptors (i.e., “¹A_g⁻” refers to an ¹A_g⁻-like state), and this convention is followed in the text hereafter. Accordingly, the S₀, S₁, and S₂ states of carotenoids usually exhibit behavior characteristic of “1¹A_g^–,” “2¹A_g^–,” and “1¹B_u⁺” symmetries, respectively (10,11). Thus, a transition from 1¹A_g⁻ to 2¹A_g^– is forbidden, and direct observation requires either two-photon methods or fluorescence spectroscopy (12). The absorption of peridinin and all carotenoids in the blue-green region of the visible spectrum is due to the strongly allowed S₀ → S₂ (“1¹A_g^–” → “1¹B_u⁺”) transition. From studies on peridinin in a range of polar to nonpolar solvents, the dynamic spectroscopic properties of peridinin and the lifetime of the lowest excited singlet state have been shown to display a strong dependence on solvent polarity (13). This solvent-dependent behavior of peridinin was initially reported by Bautista et al. (13) and was attributed to the formation of an intramolecular charge transfer (ICT) state (13–15).

The characteristics and biological relevance of the ICT state of peridinin have been investigated using both experimental and theoretical methods (16–18). Investigations using steady-state and fast-transient absorption spectroscopy have suggested that solvent and protein polarity plays an integral role in the formation of the ICT state and the resulting energy transfer within the PCP complex (15,16,19). In nonpolar solvents, the relaxation pathway from S₂ has a lifetime of ∼160 ps, whereas polar solvents elicit an excited-state lifetime of ∼10 ps, which is facilitated by the low-lying ICT state (13,19). The ICT state, which is the lowest excited singlet state in polar environments, is thought to enhance the efficiency of the energy-transfer channel in the polar binding sites of peridinin in the PCP complex (14,20). Nonlinear polarization spectroscopy in the frequency domain has suggested that the ICT state is isoenergetic or slightly above the Q_y state of Chl-a, which leads to efficient electronic energy transfer between the chromophores in the PCP complex (14,21). The mechanism of energy transfer is facilitated by formation of the ICT state, which strongly enhances the weak transition dipole moment that is characteristic of the S₁ state and leads to stronger electronic coupling with Chl-a (14). Several studies of carotenoids further suggest that ∼25% of the excitation energy is transferred directly from S₂ to the Q_x state of Chl-a (4,18,21,22).

Several models have been proposed to explain the structural origin of the peridinin ICT-state dynamics in solution and the role that the peridinin ICT state plays in energy transfer between peridinin and Chl-a in the PCP complex. Previous experimental and theoretical observations of this interaction suggest that either 1), the ICT state is an electronic state that is distinct from S₁ (S₁ + ICT) (9,13,23,24), 2), the ICT state and the S₁ state are coherently mixed (S₁/ICT) (15,22), or 3), the ICT state is simply the S₁ state with a large intrinsic dipole moment (S₁(ICT)) (12).

There are numerous theoretical models of the ICT state. A screened (INDO/S) study suggested that the ICT state is induced via an electron density shift from the lactone ring into the polyene chain (13). Alternative models proposed that dispersive interactions exist between the transition dipole moment and the solvent environment (20). Others suggest that the carbonyl group of the lactone ring forms hydrogen bonds with the solvent, and the resulting interaction induces the ICT state (25,26). Carotenoids containing a carbonyl group in conjugation with the π-electron system of the carbon-carbon chain exhibit similar solvent-dependent lifetimes, with C-33 peridinin showing the most pronounced effect (15–18,27). In addition, examination of peridinin and allene-modified analogs by Stark absorption spectroscopy suggests that the allene group in peridinin plays a role as the electron donor in the charge-transfer process after photoexcitation (28). Premvardhan et al. (20) suggested the possibility that the ICT state may be a relaxed “1¹B_u⁺” state based on a Stark-effect analysis showing that this state has a very large dipole moment.

Calculations that employed time-dependent density functional theory (TD-DFT) (29,30) have proposed the S₁ + ICT model (24,31). Using TD-DFT methods under the Tamm-Dancoff approximation (32), Vaswani et al. (24) predict that the ICT state is distinct from the “2¹A_g⁻” (S₁) and “1¹B_u⁺” (S₂) symmetries observed in adjacent excited states and is characterized by the transfer of electron density from the epoxycyclohexane and furanic rings to a virtual orbital in the polyene chain (see Fig. 2). However, the use of TD-DFT has recently been shown to incorrectly describe charge-transfer states in many highly polar molecules (33).

Figure 2.

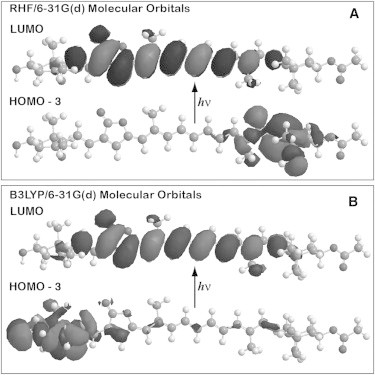
Two potential charge-transfer excitations in peridinin involving a molecular orbital (HOMO – 3) localized in the cyclohexane ring (A) and a molecular orbital (HOMO – 3) localized in the epoxycyclohexane ring (B). The model shown in B represents the ICT event as proposed by Vaswani et al. (24).

Theoretical studies by Shima et al. (12) investigated the photochemical properties of peridinin and the ICT state using modified neglect of differential overlap (MNDO) methods with partial single- and double-configuration interaction (MNDO-PSDCI) (34) and predicted that the ICT state is the solvent-stabilized “2¹A_g⁻” state. In this S₁(ICT) model, the ICT state was assigned as the lowest-lying “2¹A_g⁻” excited state after solvent reorganization, suggesting that a polar solvent environment increases the oscillator strength of the lowest-lying “2¹A_g⁻” excited state via coupling of this state to the second excited, strongly allowed “1¹B_u⁺” state.

In this article, we have used experiment and theory to show that the ICT state is an evolved excited state that is formed via solvent-induced mixing of the highly polar excited singlet states. We have examined the formation of the ICT state in peridinin by measuring the excited-state spectra and kinetics in solvents having various polarities. The model presented here differs from previous models of the ICT state in that it requires relaxation of the excited-state manifold for the ICT state to be formed. We argue that the ICT state cannot be properly described using molecular orbitals generated for the ground-state (Franck-Condon) conformation.

Materials and Methods

Sample Preparation

Peridinin was extracted from thylakoid membranes of Amphidinium carterae as previously described (35) and purified on a Millipore (Billerica, MA) Waters 600E high-performance liquid chromatograph (HPLC) equipped with a photodiode array detector and a YMC-Carotenoid C₃₀ column. The pigment was eluted using an isocratic mobile phase consisting of acetonitrile/methanol/water (87:10:3, v/v/v). Upon elution from the HPLC, peridinin was collected, dried under nitrogen gas, and stored at −80°C until ready for spectroscopic studies.

Spectroscopic methods

Peridinin was dissolved in solvents of different polarities and adjusted to an optical density between 0.3 and 0.5 at the excitation wavelength in a 2-mm-pathlength cuvette. Transient absorption spectra were recorded using a femtosecond spectrometer system based on an amplified Ti:Sapphire laser described in a previous work (36). Pump pulses were obtained from an optical parametric amplifier OPA-800C (Spectra-Physics, Santa Clara, CA) and a Type II barium borate crystal that produced a pump beam tunable to 485 nm. The pump laser has a temporal pulse width of ∼100 fs. Probe pulses were derived from a white-light continuum generated by a 3-mm sapphire plate inside the Ultrafast spectrometer system (Sarasota, FL). Pump and probe pulses were overlapped at the sample at the magic-angle (54.7°) polarization. A charge-coupled detector (S2000) with a 2048-pixel array was used for detection. The sample was continuously stirred with a magnetic microstirrer during transient absorption measurements. Steady-state absorption spectra were taken before and after laser excitation to confirm the integrity of the sample. Light-scattering effects were removed by subtraction and the spectral profiles were chirp-corrected using Surface Xplorer Pro (Ultrafast Systems) 1.0.6 software.

Theoretical methods

Ground-state geometries were generated using B3LYP/6-31G(d) methods. Excited-state geometries were generated using single-configuration-interaction (CIS) methods, which provided stable results for both vacuum and solvent calculations (37). The effect of the solvent environment was simulated using the polarizable continuum model (PCM) (38–40), as implemented in Gaussian 09 (41). We found that a combination of CIS and PCM methods provided the most reliable method of generating excited-state geometries in a solvent environment (38–40). Unless stated otherwise, we used an active space consisting of the eight highest-energy filled orbitals and the eight lowest-energy virtual orbitals when optimizing the excited singlet states.

Spectroscopic properties were calculated using MNDO-PSDCI (12,34,42), symmetry-adapted-cluster-configuration-interaction (SAC-CI) (43–47), and equation-of-motion-coupled-cluster-singles-and-doubles (EOM-CCSD) (48–50) methods. The MNDO-PSDCI methods are semiempirical and have been used successfully to study carotenoids (18,51,52), as well as peridinin (12). The SAC-CI methods are very efficient and are optimal for calculating the dipolar properties of the excited states (43–47). However, these methods often do not properly order the covalent and ionic states in polyenes, and must be used with caution (17,53). The EOM-CCSD methods are relatively new and provide the most accurate transition energies and oscillator strengths (48–50). These methods also work well in conjunction with PCM solvent effects (38). All Hartree-Fock calculations were carried out using a D95 double-zeta basis set (54).

A majority of our calculations were carried out on the model chromophore shown in Fig. 3. This chromophore includes the entire central polyene portion, but replaces the cyclohexane and epoxycyclohexane rings with a methyl group and an allenic CH₂ group, respectively. The resulting model polyene has C_s symmetry, and this symmetry, in combination with the smaller size, allows high-quality calculations to be carried out with computational efficiency, with the inclusion of state-specific solvation. Because a majority of the photophysical properties of peridinin are determined by the polyene portion, the use of a model chromophore is appropriate. From preliminary calculations on the chromophore, it is noted that the rings do not have an impact on the atomic charges other than a minor one on the charges of the end polyene atoms, 1 and 16. The total dipole moment is changed in magnitude and direction, but the local charges relevant to solvation of the polyene portion remain largely the same. The difference in the dipole-moment direction is due primarily to the orientation of the acetate group on the cyclohexane ring. The two rings do enhance solvent mixing, but as we demonstrate below, calculations on the full chromophore versus the truncated chromophore generate nearly identical excited-state properties. Our structural model of peridinin is very similar to that proposed by Bovi et al. (25) in a theoretical study of peridinin. The only difference is that we have included the methyl group on atom 14.

Figure 3.

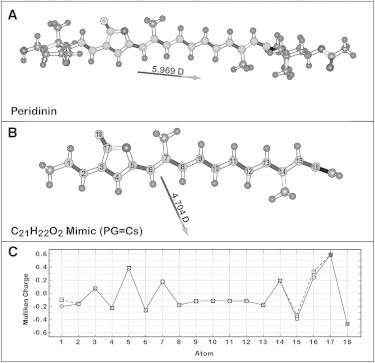
Comparison of the full (A) and C_s-model compound (B) versions for which calculations are carried out in this study. Both structures were minimized using B3LYP/6-31G(d) methods, and the polyene system is marked using light gray atoms. (C) The Mulliken atomic charges are compared to those in this study, where the full-chromophore charges are indicated by circles and the charges on the model compound structure by squares. Note that atoms C17 and O18 form the carbonyl group of the furanic (lactone) ring.

The vacuum transition energies calculated for the full chromophore and the model chromophore are compared in Fig. 4 and are based on semiempirical MNDO-PSDCI methods and EOM-CCSD procedures. Note that the level ordering of the lowest four excited singlet states is invariant to the method and the inclusion of the two rings. The main impact of the rings is to mix the lowest two excited states. This mixing is similar to that induced by solvent effects, as explored in more detail below. Although the MNDO-PSDCI calculations predict that the lowest-lying “2¹A_g^–” excited state has a significant dipole moment, and was assigned by Shima et al. (12) to represent the ICT state, it does not have sufficient dipolar properties or energy to reproduce the experimental observations regarding the ICT state (see below). Thus, none of the four lowest-lying states calculated by these Hartree-Fock CI methods has the full characteristics of an ICT state. We seek alternative models in this work.

Figure 4.

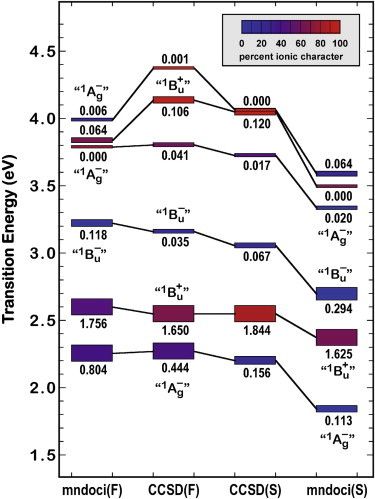
Comparison of the excited-singlet-state level ordering as calculated by semiempirical MNDO-PSDCI (mndoci) and EOM-CCSD (CCSD) coupled-cluster methods for the full chromophore (F) and the model chromophore (S) in vacuum. Note that the level ordering of the lowest four excited singlet states is invariant to the method and the complexity of the chromophore model. These levels are calculated based on the ground state geometry, and should correlate with the Franck-Condon maxima of the electronic spectra. The transition energies calculated for the second excited “1¹B_u⁺” state correlate reasonably well with the observed Franck-Condon maxima in hexane (2.72 eV (12)). The ionic versus covalent character of the states is indicated by color based on the scheme shown at upper right. The oscillator strength for excitation from the ground state is given directly above or below the state rectangle. The lowest excited singlet state generated by the MNDOCI calculations was assigned as the ICT state by Shima et al. (12).

Results and Discussion

This study combines experiment and theory to better understand the nature of the ICT state in peridinin. We demonstrate that the ICT state in peridinin is an evolved state that is formed via bond-order reversal induced by the interaction of the highly polar excited singlet states with a polar solvent environment. We begin our analysis by presenting time-resolved pump-probe spectroscopic experiments on this manifold of states as a function of solvent environment. We then present theoretical calculations that address the nature of the ICT state.

Pump-probe transient absorption experiments on peridinin in solution

The transient-absorption (TA) spectra of peridinin in various solvents are presented in Fig. 5. There have been a number of previous studies of peridinin using TA spectroscopy (15,23,27). This study explores the early-time transient behavior as a function of solvent environment and uses our theoretical model to describe population dynamics. These spectra were recorded by pumping at 485 nm directly into the strongly allowed “1¹B_u⁺” state.

Figure 5.

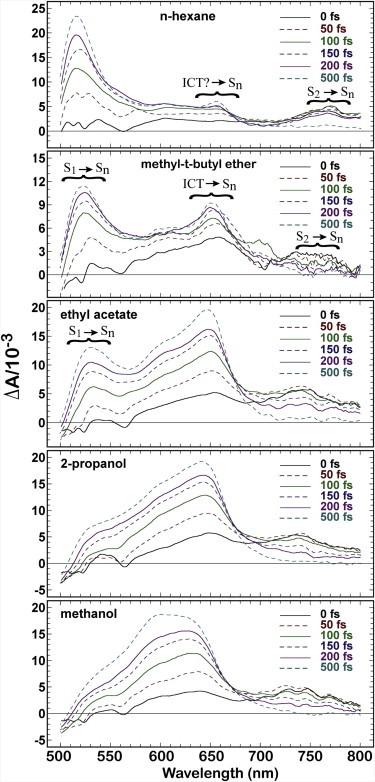
Transient absorption spectra of peridinin at ambient temperature taken at different time delays after excitation at 485 nm in n-hexane (upper), methyl-t-butyl ether, ethyl acetate, 2-propanol and methanol (lower). The different time delays are represented by lines of different type and color, as shown at the right. The band assignments are based on literature studies, as discussed in the text, where S₁ is the lowest-lying “2¹A_g^–” covalent state, S₂ is the strongly allowed “1¹B_u⁺” state, and S_n is a generic higher excited singlet state. The unexpected observation of an ICT state in hexane is discussed at the end of the article.

There are three band systems observed in the TA spectra of Fig. 5, and previous studies on peridinin and related carotenoids provide definitive assignments of the electronic transitions responsible for these bands (15,23,27,55–57). The individual band systems are marked in Fig. 5. Two features are worth noting at the outset. First, the ICT state starts to form within 100 fs, which corresponds to the temporal resolution of our experiments. This places important constraints on the model of the ICT state, as this observation rules out any major structural changes. Second, the ICT state appears to form even in hexane, although our calculations indicate that this state is not a true ICT state, because it does not exhibit a large change in dipole moment (see below). A more detailed discussion of the TA spectra is presented below. It is convenient to introduce our model of the ICT state before the full discussion, as we use our model to deconvolute the excited-state population dynamics. Analysis of the population dynamics provides important insight into the nature of the ICT state.

Modeling of the ICT state

All previously developed models of the ICT state use wavefunctions calculated for the ground-state geometry. This approach has a long and distinguished history and is known to work well in describing the excited-state manifolds of many polar and nonpolar polyenes and carotenoids (58–60). However, these Franck-Condon based models fail to explain the unique properties of the ICT state.

We explore here an alternative approach based on an evolved excited-state manifold. We generated relaxed excited-state species using two methods. The most efficient method uses CIS procedures and an active space of the eight highest-energy filled orbitals and the eight lowest-energy virtual orbitals. Test calculations in which this 8 × 8 active space was restricted to the π system produced nearly identical results but often failed because of molecular orbital-level migration. We also used SAC-CI optimization with high levels of double-configuration interactions, but these calculations were extremely CPU expensive, converged poorly when PCM methods were included, and yielded only modest improvements in the final energy of stabilization. We selected the simple CIS (8 × 8) optimization coupled with PCM state-specific solvation for our full series of solvent calculations. The results are shown in Fig. 6, where the transition energies and oscillator strengths are calculated using EOM-CCSD methods and a 16 × 16 active space. Properties were calculated relative to the third-order Møller-Plesset (MP3) (7,61) ground state.

Figure 6.

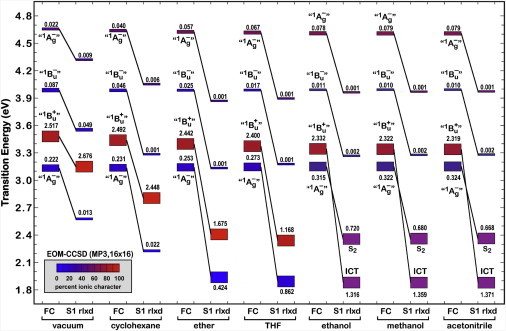
Effect of solvent environment on the lowest excited Franck-Condon (FC) and relaxed (S1 rlxd) singlet states of the model chromophore of peridinin based on EOM-CCSD procedures. Transition energies are relative to the MP3 ground state. Solvent polarity increases from left to right, but the leftmost pair is for vacuum conditions.

These calculations provide insight into the remarkable impact of solvent environment on the lifetime of the lowest excited singlet state, which is the fluorescing state of peridinin. The fluorescence lifetime should correlate with oscillator strength, as determined by the equation

$${\tau }_f\left(s\right)\approx \frac{1.5{\Phi }_f}{n{f}_{nm}{\left[{\tilde{\nu }}_{nm}\left({\text{cm}}^{-1}\right)\right]}^2},$$ (1)

where Φ_f is the fluorescence quantum yield, n is the refractive index of the solvent, ${\tilde{\nu }}_{nm}\left({\text{cm}}^{-1}\right)$ is the wavenumber of the transition, and f_nm is the oscillator strength of the transition (59). Unfortunately, we do not have accurate values for the quantum yield as a function of solvent environment, which precludes plotting the righthand side versus lifetime. If we simply plot lifetime versus oscillator strength, we obtain the graph shown in Fig. 7. The observed trend supports the notion that increased solvent polarity enhances the formation of the ICT state, which exhibits not only a large oscillator strength but also enhanced coupling to the ground state via internal conversion.

Figure 7.

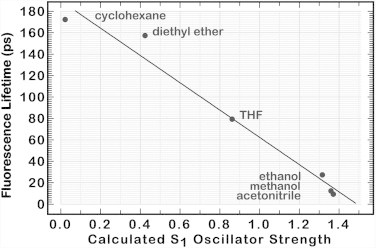
Observed fluorescence lifetime of peridinin plotted versus calculated oscillator strength of the first excited singlet state for selected solvents. Oscillator strength data are from Fig. 6. Fluorescence-lifetime data are from Table 3 of Frank et al. (16). The approximate linear relationship is fortuitous, as Eq. 1 would predict a more quadratic relationship. However, the trend is in the correct direction, illustrating the realistic nature of the course features of our model.

We explored the dipolar properties of the ICT state using SAC-CI methods, which can calculate the dipole moment and oscillator strength in a basis set of full single- and extensive double-configuration interaction. The results for the ground state and lowest three excited singlet states are shown in Fig. 8, with configurations on the left based on the ground-state geometry and those on the right based on the relaxed first excited-singlet-state geometry. Both minimizations were carried out in methanol solvent using PCM methods (see Theoretical methods). We note that the SAC-CI methods often fail to predict the correct level ordering, and the EOM-CCSD methods are more accurate (Fig. 6). However, the SAC-CI methods are preferred when calculating the dipolar properties of individual excited states. In this case, the SAC-CI and EOM-CCSD calculations are in good agreement for the level ordering in the excited-singlet-state minimized manifold (ICT Set), which is the principal topic of this study.

Figure 8.

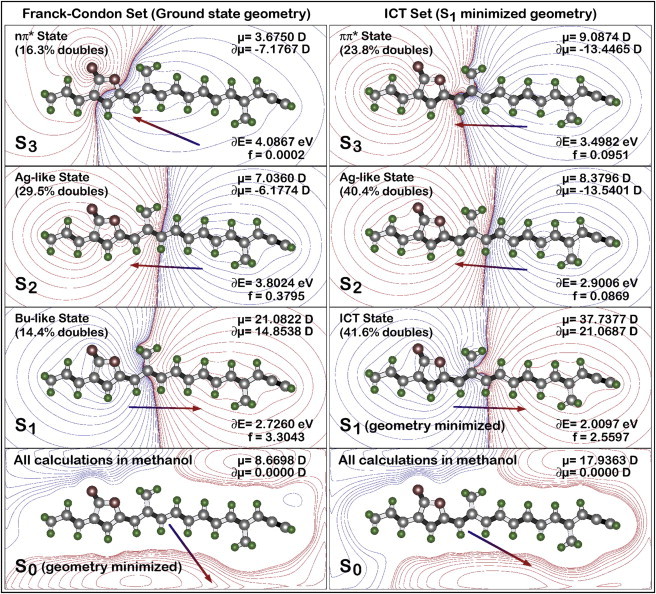
Electrostatic properties of the ground and first three excited singlet states of the equilibrium ground state (left; Franck-Condon) and S₁/ICT minimized (right) geometries of the peridinin model compound in methanol. The contours in the S₀ panels display the charge distribution in the ground state, with red representing regions of net positive charge and blue representing regions of net negative charge. The contours for S₁, S₂, and S₃ (upper three rows) show the charge shifts that accompany excitation into the respective excited states. Red contours now represent regions of increased positive charge and blue contours represent regions of increased negative charge after excitation. Properties are based on level-three SAC-CI methods, and the configuration interaction included 3606 singles and ∼890,000 doubles. The dipole-moment changes (δm) are relative to the ground-state dipole moment and are evaluated in terms of vector differences (see text). The oscillator strengths (f) are for electronic transitions from the ground state. The arrows show the directions, but not the magnitudes, of the dipole moments or dipole-moment changes. The character of the S₃ states differs for the two geometries (nπ^∗ for ground state geometry (left), ππ^∗ for S₁ minimized geometry (right)). The level ordering from the SAC-CI and EOM-CCSD (Fig. 6) is different (see Theoretical methods).

As shown in Fig. 8, relaxation of the S₁ excited singlet state yields a lowest excited singlet state with unusual properties, including a dipole moment of 37.7 D and a large oscillator strength coupled with an unusually high configurational contribution from double excitations. The dipole-moment changes (δμ) are relative to the ground-state dipole moment and are calculated based on a difference vector, not a difference of the total dipole moments. For example, for the ICT state (Fig. 8, right, S₁), the value of 21.07 D is calculated as follows:

$${\mu }_0=\left\{{\mu }_0^{\left(x\right)},{\mu }_0^{\left(y\right)},{\mu }_0^{\left(z\right)}\right\}=\left[15.96D,8.18D,0.0D\right]$$

$${\mu }_{ICT}=\left\{{\mu }_{ICT}^{\left(x\right)},{\mu }_{ICT}^{\left(y\right)},{\mu }_{ICT}^{\left(z\right)}\right\}=\left\{37.01D,7.36D,0.0\right\}$$

$$\delta \mu =S^{\pm }{\left[{\left({\mu }_{ICT}^{\left(x\right)}-{\mu }_0^{\left(x\right)}\right)}^2+{\left({\mu }_{ICT}^{\left(y\right)}-{\mu }_0^{\left(y\right)}\right)}^2+{\left({\mu }_{ICT}^{\left(z\right)}-{\mu }_0^{\left(z\right)}\right)}^2\right]}^{\frac{1}{2}}$$

$$\delta \mu =21.07D,$$

where the sign term, S^±, is determined based on the relative direction of the ground- and excited-state dipole moments. If the vector representing the dipole-moment change has a direction within ±90° of the ground-state dipole-moment vector, the sign is positive; otherwise, it is negative. The magnitude is calculated, and the resulting sign serves as a qualitative descriptor.

The unusual properties of the ICT state are principally derived from the unique combination of a large dipole moment and large doubly excited configurational character. Normally, covalent states (with electrons more evenly distributed yielding less charge separation) have the largest doubly excited character and ionic states (with electrons more localized in various regions) have the largest dipole moments. This simple notion is indeed observed for the Franck-Condon excited-state systems (Fig. 8, left column). However, when the characteristics are calculated for the geometry minimized for the lowest excited singlet state, we generate the unique characteristics described above. The doubly excited configurations serve to stabilize the bond-order reversal and contribute in a significant way to the lowering of the excited-state energy. Simply stated, the low energy of the ICT state derives in large part from the importance of doubles to the configurational description. However, the ICT state is very ionic in character and is therefore best described as a “¹B_u⁺” state. The second excited state in this manifold is best described as a “¹A_g^–” state. It has a relatively small dipole moment (in comparison to the ground and ICT states), and is primarily covalent in character. It also has relatively high double-configuration interaction character, which is characteristic of “¹A_g^–” states.

Fig. 9 provides a useful perspective on the role played by solvent in the creation and stabilization of the ICT state. The dipole-moment vectors in the ground and first excited singlet states are pointed in the same relative directions in the ground-state optimized calculations (Fig. 8, left). This observation indicates that solvent organization in the ground state will be such that it will also stabilize the first excited singlet state. This observation is true regardless of the calculated level ordering. If the lowest excited singlet state is calculated to be the “2¹A_g^–” state, as predicted by MNDO-PSDCI calculations, the dipole-moment vectors are almost identical in directionality to those shown in Fig. 8 (see discussion in Shima et al. (12)).

Figure 9.

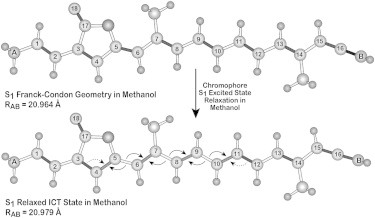
Ground- and excited-state geometries of the peridinin model compounds in methanol (see text). Arrows indicate bond-order reversal, and bonds that are strengthened (shortened) in the ICT state are marked with the arrows. The total length of the chromophore is represented by R_AB, and increases by ∼0.01 Å upon population of the ICT state relative to the Franck-Condon (ground-state) geometry. Both ground- and excited-state geometries are planar (except for hydrogen atoms), and dihedral distortions along the polyene chain were tested and found to be energetically unfavorable.

Structural characteristics of the ICT state

The bond-order reversal that accompanies formation of the ICT state is schematically shown in Fig. 9. The bond lengths and bond angles, as well as the Cartesian and internal coordinates, are presented in Figs. S2 and S3 and Tables S1–S4 in the Supporting Material. The bond-order reversal occurs primarily in the central region of the polyene chain. To a first approximation, the ground-state bonding pattern,

$$\text{C}4-\text{C}5=\text{C}6-\text{C}7=\text{C}8-\text{C}9=\text{C}10-\text{C}11=\text{C}12,$$

rearranges in the relaxed excited singlet state to the pattern

$$\text{C}4=\text{C}5-\text{C}6=\text{C}7-\text{C}8=\text{C}9-\text{C}10=\text{C}11-\text{C}12.$$

Thus, the bonding patterns shift to the left in Fig. 9, toward the furanic (lactone) ring, placing more bonding electron density in the furanic region and less bonding electron density in the allenic region. The central methyl group next to the furanic ring is the null center point of the charge shift. The charge migration increases the electron density in a region of the polyene, which is already electron-rich in the ground state, and as a result, excitation into the ICT state enhances the dipole moment of the molecule without significantly altering the direction (Fig. 8, right, ICT State). Thus, the bond-order reversal and charge shifts of the ICT state are both characterized by the transfer of bonding electron density toward the furanic ring. Polar solvent enhances this process because the dipole moment and charge distribution in the ground state are very similar to those in the ICT state.

Population dynamics in the excited-state manifold of peridinin

We can now combine our theoretical models of excited-state manifolds with the spectra of Fig. 5 to examine the population dynamics of the excited-state manifold. We assume that the population of an excited singlet state is given by the integral of the TA signal of the vibronic band divided by the oscillator strength of the transition responsible for the band. We assigned the oscillator strengths using MNDO-PSDCI theory, because this theory is the only one that provides such information while simultaneously reproducing the level ordering predicted by the more accurate EOM-CCSD methods (see Theoretical methods and Fig. 4). The relative populations of the various states are calculated from the absorbance changes (see Fig. 5) as follows:

$${\left[2^1{\text{A}}_g^{-}\right]}_{rel}=\underset{{\tilde{\nu }}_1}{\overset{{\tilde{\nu }}_2}{\int }}\frac{\Delta \text{A}\left(\tilde{\nu }\right)}{f}d\tilde{\nu }=\underset{19,200-\Delta \tilde{\nu }}{\overset{19,200+\Delta \tilde{\nu }}{\int }}\frac{\Delta \text{A}\left(\tilde{\nu }\right)}{0.84}d\tilde{\nu }$$ (2)

$${\left[1^1{\text{B}}_u^{+}\right]}_{rel}=\underset{{\tilde{\nu }}_1}{\overset{{\tilde{\nu }}_2}{\int }}\frac{\Delta \text{A}\left(\tilde{\nu }\right)}{f}d\tilde{\nu }=\underset{13,000-\Delta \tilde{\nu }}{\overset{13,000+\Delta \tilde{\nu }}{\int }}\frac{\Delta \text{A}\left(\tilde{\nu }\right)}{0.92}d\tilde{\nu }$$ (3)

$${\left[\text{ICT}\right]}_{rel}=\underset{{\tilde{\nu }}_1}{\overset{{\tilde{\nu }}_2}{\int }}\frac{\Delta \text{A}\left(\tilde{\nu }\right)}{f}d\tilde{\nu }=\underset{15,600-\Delta \tilde{\nu }}{\overset{15,600+\Delta \tilde{\nu }}{\int }}\frac{\Delta \text{A}\left(\tilde{\nu }\right)}{0.39}d\tilde{\nu },$$ (4)

where the symmetry labels are approximate, and the integration limits are in wavenumbers and are carried out using an identical integration window of $\Delta \tilde{\nu }$ of 500 cm⁻¹. The choice of a 500-cm⁻¹ integration window was determined, by trial and error, to minimize noise while providing good selectivity. All integrations must use the same window to permit quantitative comparisons. The band centers are selected to best capture the target states (Fig. 5 and Fig. S1).

The resulting population dynamics are shown in Fig. 10. These results support the notion that there is a dynamic equilibrium between the “2¹A_g^–” state and the ICT state because the concentration ratio remains nearly constant during the entire time, regardless of solvent. As solvent polarity increases, the ratio [ICT]/[“2¹A_g^–”] increases. The fact that a small amount of the ICT state is observed in hexane is due to the formation of a relaxed “2¹A_g^–” state, which has many of the bond-order reversal properties of the ICT state but a smaller excited-state dipole moment. This relaxed state is calculated to have a TA band similar to that of the ICT state but slightly red-shifted (see Fig. S7). We refer to this state as a pre-ICT state, and do not support the notion that the ICT state is formed in any significant quantity in nonpolar solvents.

Figure 10.

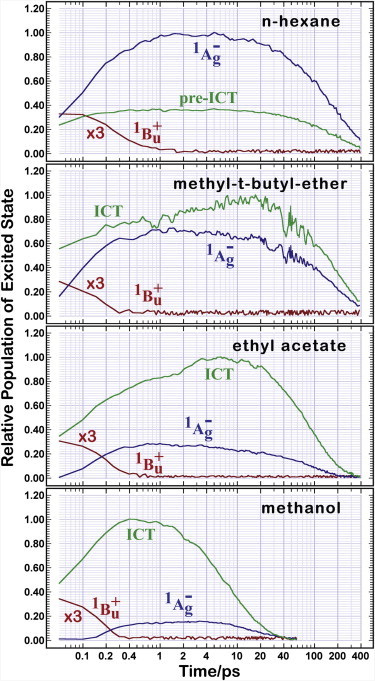
Relative population of the excited states in peridinin as a function of time in various solvents. The populations are based on an analysis of the transient absorption spectra (Fig. 5) and adjusted for oscillator strength (see text). Note that the horizontal time axis is logarithmic.

In Fig. 11, our model of the ICT state is compared to models in the literature. We refer to our model as (S₁ + S₂)/ICT to emphasize that the ICT state is formed via mixing of the S₁ and S₂ excited singlet states. In that regard, when the ICT state is formed, an S₂ excited singlet state is also formed, with properties quite different from those of the normal S₂ (“¹B_u⁺”) state. In principle, this state could be observed in the TA spectra (a strong band at ∼780 nm is predicted (Fig. S6 C)), but no such transition was observed. We conclude that this state is never populated, because it is only present when the lower-lying ICT state is formed, and Boltzmann statistics would not favor an observable thermal population.

Figure 11.

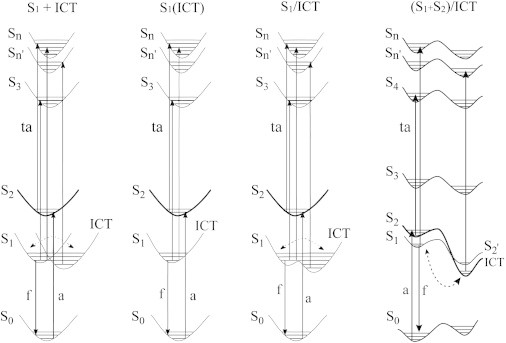
Schematic diagrams of the various literature models of the ICT state, where S₁ is the lowest-lying “2¹A_g^–” covalent state, S₂ is the strongly allowed “1¹B_u⁺” state, and S_n and S_n’ are generic higher excited singlet states. The thickness of the potential surfaces reflects the oscillator strength for absorption (a) from the ground state. Fluorescence (f) is only observed from the S₁ state. In most of the models, the ICT state is in equilibrium with the S₁ state, as shown by the dual arrows connected with the dotted line. Our model is shown at the right, with energy surfaces appropriate for a highly polar solvent such as methanol. In our model, the ICT state is formed via mixing of the S₁ and S₂ states (see text), which generates an ICT state with a large oscillator strength, bond-order reversal in the polyene chromophore, and a high degree of doubly excited character.

Our proposed role of solvent-induced S₁ + S₂ mixing in the creation of the ICT state is new, to our knowledge, but S₁ + S₂ mixing has been proposed before as a mechanism for enhancing the coupling of the low-lying manifold of carotenoid excited states to chlorophylls (62,63). Protein environment can facilitate formation of the ICT state as a mechanism for enhancing energy transfer in peridinin-containing proteins. It is noted that the various peridinin binding sites induce varying amounts of coupling and in some cases even invert the level ordering of the lowest-lying singlet states (12,24,64). Furthermore, the protein binding sites can induce dihedral distortions along the polyene chain, which, depending on their location, can also enhance S₁ + S₂ mixing (12,62,63,65). Our study suggests that the ICT state will be formed even in planar systems, provided the solvent environment can accommodate the large dipole moment that is created via excited-state relaxation and bond-order reversal.

Recently, the TA spectra were measured for a pair of peridinin chromophores modified such that the furanic ring was shifted two and four carbon atoms toward the cyclohexane ring (66). The theoretical procedures described here generated descriptions of the photophysical properties of these molecules that are in good agreement with experiment and correctly predicted that if the furanic ring is shifted four atoms toward the center of the polyene chain, no ICT state is formed (66). These results provide support not only for our methods and procedures, but also for our model of the ICT state as a solvent-induced, evolved excited-state species.

Conclusions

• 1.The ICT state of peridinin is an evolved state formed via bond-order reversal in the excited-state manifold and configurational mixing of the lowest two excited singlet states. This state is in equilibrium with the “2¹A_g⁻” (S₁) and “1¹B_u⁺” (S₂).
• 2.The ICT state is characterized by an enhanced dipole moment, calculated to be on the order of 30–40 D, and thus requires a polar solvent for stabilization.
• 3.The charge-transfer character of the ICT state involves the motion of electron density from within the polyene portion, and does not involve participation by either of the β-rings. Charge is moved from the allenic side of the polyene into the furanic ring region, and is accompanied by bond-order reversal in the central portion of the polyene chain. High-level molecular orbital calculations on the full chromophore (Fig. 3 and Fig. S4) do not reveal any significant participation of the β-rings in the four lowest-lying electronic states.
• 4.The electronic properties of the ICT state are characterized by polar-solvent-induced mixing of the “1¹B_u⁺” ionic state and the lowest-lying “2¹A_g^–” covalent state. Thus, the ICT state gains the oscillator strength characteristics of a “1¹B_u⁺” state but has the doubly-excited-character trait of a “2¹A_g^–” state. However, in terms of most properties, the ICT state is ¹B_u⁺-like in character.
• 5.Although solvents of medium polarity will create an ensemble mixture containing a large portion of ICT states, a small portion of molecules in the ensemble retain lowest-lying “2¹A_g^–” states. The two populations are separated by a small barrier, although the forward barrier (to the ICT state) may be very small in highly polar solvents such as methanol or acetonitrile.