Theory and Simulations of Adhesion Receptor Dimerization on Membrane Surfaces

Abstract

The equilibrium constants of trans and cis dimerization of membrane bound (2D) and freely moving (3D) adhesion receptors are expressed and compared using elementary statistical-thermodynamics. Both processes are mediated by the binding of extracellular subdomains whose range of motion in the 2D environment is reduced upon dimerization, defining a thin reaction shell where dimer formation and dissociation take place. We show that the ratio between the 2D and 3D equilibrium constants can be expressed as a product of individual factors describing, respectively, the spatial ranges of motions of the adhesive domains, and their rotational freedom within the reaction shell. The results predicted by the theory are compared to those obtained from a novel, to our knowledge, dynamical simulations methodology, whereby pairs of receptors perform realistic translational, internal, and rotational motions in 2D and 3D. We use cadherins as our model system. The theory and simulations explain how the strength of cis and trans interactions of adhesive receptors are affected both by their presence in the constrained intermembrane space and by the 2D environment of membrane surfaces. Our work provides fundamental insights as to the mechanism of lateral clustering of adhesion receptors after cell-cell contact and, more generally, to the formation of lateral microclusters of proteins on cell surfaces.

Introduction

The three-dimensional structures of the extracellular domains of many adhesion receptors have been determined in atomic detail (1–6), thus enabling a detailed description of the molecular basis of crucial events in cell-cell adhesion. However, there have been only limited theoretical and computational atomic-level studies of protein-protein interactions on membrane surfaces, in part due to the complexity of the systems involved. Adhesion receptors translate and rotate in the two-dimensional (2D) environment of a cell surface and can interact in cis with molecules on the same surface and in trans with molecules on apposed cell surfaces. In addition, many adhesion processes involve the clustering of proteins into complex supramolecular assemblies (7–10), a phenomenon that is not normally treated by standard molecular simulations.

Given the significant extent of structural characterization of adhesion receptors and their assemblies, a complementary development in theoretical and simulation methodologies can play an important role in the understanding of cell-cell adhesion processes. While there have been numerous studies of protein-protein interactions in three-dimensional (3D) solution, the physical and energetic constraints introduced by the confined 2D environment on membrane-bound proteins are far less understood (11). We recently reported a heuristic theory (12) relating K_d values measured in 3D solution ($K_d^{\left(3D\right)}$) to those appropriate to the 2D environment of a membrane surface ($K_d^{\left(2D\right)}$). The crucial parameters of the theory depend on structural properties of the protein, specifically the motion of the binding site with respect to the intermembrane normal axis and the rotational freedom of the binding domains. These variables can be obtained from simulations of individual molecules, as was done for monomers and cis and trans dimers of E- and N-cadherin (12).

In this work, we present a rigorous statistical thermodynamic expression for the ratio $K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$, and carefully define the molecular and intercellular parameters that relate the two K_d values. The factors that determine trans and cis binding affinities are discussed in detail and are shown to include spatial and angular factors that have a clear physical meaning. Inherent to the theory are a number of simplifying approximations. To both validate the theory and as a step toward providing a detailed description of adhesion processes, we present a new, to our knowledge, simulation methodology that specifically calculates binding free energies for receptor dimerization in 3D and 2D environments. The very good agreement between the ratios of K_d values obtained from the theory (utilizing simulations of individual molecules) and those derived from direct simulations of the dimerization process between interacting mobile receptors indicates that our approach is robust, and that it can be used to describe essential features of cis and trans dimerization processes on cell surfaces.

Based on our results we discuss how dimerization affinities are affected by molecular structure, flexibility, and the proximity of the interacting domains to the membrane surface, and comment on the role of membrane elasticity. Further, our work provides estimates of cis and trans $K_d^{\left(2D\right)}$ values for molecules with different $K_d^{\left(3D\right)}$ values and different structural and dynamic properties, thus offering a basis for the structure-based interpretation of experimental observations on association/dissociation phenomena on membrane surfaces. Finally, the novel, to our knowledge, simulation methodology we introduce can be applied to cell-surface receptors other than cadherins (13) — the specific focus of this article. We note in this regard that cadherins assemble into ordered structures (adherens junctions) in the complete absence of cytoplasmic interactions in a cooperative process involving both extracellular trans and cis interactions (2,9,12,13). However, cadherin function, as well as that of essentially all cell-surface molecules, involves interactions with other proteins, both inside and outside the cell, that are influenced by the restrictions arising from the quasi-2D environment provided by a membrane surface. For this reason, we believe that the methods and concepts introduced in this work are of quite general applicability.

Theory

In this section, we outline the basic statistical thermodynamic treatment that relates the equilibrium constants of the dissociation-association reaction

$$AB\rightleftarrows A+B$$ (1)

between membrane bound receptors (Fig. 1), and the corresponding reaction in bulk 3D solution (details can be found in the Supporting Material). We focus primarily on the formation of trans dimers but will extend the treatment to cis interactions as well. Receptor adhesion in trans is mediated by the interaction between two subdomains (labeled a and b in Fig. 1). In the case of cadherins, these adhesive subdomains are located at the outermost (EC1) repeats of the receptors’ ectodomains, and the binding is mediated by the swapping of the two N-terminal β-strands of a and b (2,13). In Fig. 1, for the sake of simplicity, the ectodomains are depicted as stems with the trans binding units at their tips. Cis dimerization is mediated by a second interface (schematically illustrated by the double arrows in Fig. 1), which in the case of cadherins involves an interaction between the EC1 repeat of one receptor and the linker region connecting EC2 and EC3 of a second receptor (2,13).

Figure 1.

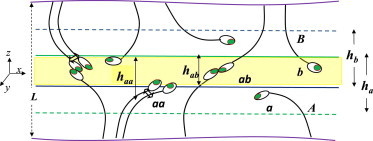
Schematic description of the 2D system. Adhesion is mediated by trans dimers, bound via their adhesive domains a and b (darker dots) that form the adhesive pair ab. Monomers on the same membrane can interact via their cis interface aa (schematized by double arrows). The values h_a, h_b, h_ab, and h_aa are the ranges of motion along the membrane normal of the corresponding species. (Highlighted region) Reaction shell, which is accessible to both a and b.

Trans dimer formation

Assuming ideal solution behavior, the equilibrium constant of the trans binding reaction in the 2D environment is given by

$$K_d^{\left(2D\right)}=\frac{{\sigma }_A{\sigma }_B}{{\sigma }_{AB}}=\frac{q_A{q}_B}{q_{AB}}{e}^{-\frac{\Delta E_0^{\left(2D\right)}}{kT}},$$ (2)

where σ_A = N_A/W, σ_B = N_B/W, and σ_AB = N_AB/W are the surface densities of A and B monomers and AB dimers, respectively. The N_I (I = A, B, AB) values denote the numbers of molecules in the contact region of area W, and q_I is the partition function, per unit area, of a single molecule I, calculated using energy levels measured relative to its ground state energy, $E_{0,I}^{\left(2D\right)}$ (14). Thus $\Delta E_0^{\left(2D\right)}=E_{0,A}^{\left(2D\right)}+E_{0,B}^{\left(2D\right)}-E_{0,AB}^{\left(2D\right)}\left(\Delta E_0^{\left(2D\right)}>0\right)$ is the dissociation energy of the dimer, where k is the Boltzmann’s constant, and T is the temperature.

Binding free energies (ΔG₀ = −kT ln K_d) are generally inferred from equilibrium measurements of reaction 1 in bulk 3D solution, whose equilibrium constant is given by

$$K_d^{\left(3D\right)}=\frac{{\rho }_A{\rho }_B}{{\rho }_{AB}}=\frac{z_A{z}_B}{z_{AB}}{e}^{-\frac{\Delta E_0^{\left(3D\right)}}{kT}}.$$ (3)

Here ρ_I = N_I/V is the 3D (number) density of I = A, B, AB within the solution volume V, and z_I is the molecular partition function of species I, per unit volume. We assume that the binding energies in the 2D and 3D environments are equal, because we are considering the same protein-protein interface in both cases, so we set $\Delta E_0^{\left(2D\right)}=\Delta E_0^{\left(3D\right)}\equiv \Delta E_0$.

The first important factor distinguishing the trans binding reaction in 2D from its 3D analog is that a and b, the adhesive subdomains of A and B, occupy different, and only partially overlapping, regions of the intermembrane space. As illustrated in Fig. 1, trans dimers can only be formed within the reaction shell—the overlap region where both a and b can be found. More explicitly, if h_a, h_b, and h_ab denote, respectively, the ranges of motion of a, b, and their dimer ab, along the membranes’ normal (the z axis in Fig. 1), then h_ab is, by definition, the thickness of the reaction shell. The magnitudes of h_a, h_b, and h_ab are dictated by the combined effect of two types of molecular motions: overall rotations of the ectodomain, and internal structural fluctuations of the ectodomain backbone. Note that only those monomeric receptors whose adhesive subdomains are present within the reaction shell are potentially reactive. In the Supporting Material, we show that this implies

$$K_d^{\left(2D\right)}=\frac{h_a{h}_b}{h_{ab}}{\tilde{K}}_d^{\left(3D\right)},$$ (4)

where ${\tilde{K}}_d^{\left(3D\right)}$ represents the 3D equilibrium constant of the reaction $ab\rightleftarrows a+b$ between the adhesive subdomains in the quasi-3D volume of the reaction shell, V_ab = Wh_ab. That is, ${\tilde{K}}_d^{\left(3D\right)}=\left({\tilde{\rho }}_a{\tilde{\rho }}_b/{\tilde{\rho }}_{ab}\right)$, with ${\tilde{\rho }}_i={\tilde{\sigma }}_I/h_{ab}$ denoting the equilibrium 3D densities of a, b, and ab in the reaction shell. We note, however, that ${\tilde{K}}_d^{\left(3D\right)}$ this is not an ordinary 3D constant because the motions, primarily the rotations, of the adhesive subdomains a, b, and ab are constrained by their being connected to the rest of the ectodomain, as opposed to the case of freely rotating receptors in bulk 3D solution. In the Supporting Material, we elaborate on this point and argue that ${\tilde{K}}_d^{\left(3D\right)}/K_d^{\left(3D\right)}=\left(\Delta {\omega }_a\Delta {\omega }_b/\Delta {\omega }_{ab}\right)/8{\pi }^2$, where $K_d^{\left(3D\right)}$ is the 3D equilibrium constant in bulk solution and Δω_i (i = a, b, ab) are the rotational ranges of motion (phase space volume) of the binding subdomains of reactive receptors within the reaction shell. For freely rotating receptors in 3D, Δω ≡ 8π². Substituting this result into Eq. 4, we find that $\lambda =K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$, the ratio between the 2D and 3D dimerization constants, can be expressed as a product of a spatial factor containing the ranges of motion of a, b, and ab, and a rotational factor involving their angular ranges of motion,

$$\lambda =\frac{K_d^{\left(2D\right)}}{K_d^{\left(3D\right)}}=\frac{h_a{h}_b}{h_{ab}}\frac{\Delta {\omega }_a\Delta {\omega }_b}{8{\pi }^2\Delta {\omega }_{ab}},$$ (5)

a result that we have previously derived based on heuristic arguments (12), but with Δω_i calculated for all receptors, whether reactive or not. (In Eq. 5, the Δω_i values involve only those receptors whose adhesive domains reside within the reaction shell.)

In addition to providing the appropriate conversion unit (i.e., length) between the 2D and 3D constants, we note that (for a given $K_d^{\left(3D\right)}$) smaller λ means smaller $K_d^{\left(2D\right)}$, and hence enhanced dimerization affinity in 2D. We may thus refer to λ as the equivalent thickness of the reaction shell. Insights into the origin and significance of λ can be gained by further decomposition of Eq. 5 in the form

$$\lambda =L\left(\frac{h_{ab}}{L}\right)\left[\left(\frac{h_a}{h_{ab}}\right)\left(\frac{h_b}{h_{ab}}\right)\right]\left(\frac{\Delta {\omega }_{ab}}{8{\pi }^2}\right)\left[\left(\frac{\Delta {\omega }_a}{\Delta {\omega }_{ab}}\right)\left(\frac{\Delta {\omega }_b}{\Delta {\omega }_{ab}}\right)\right],$$ (6)

where all the factors except the first (L, the thickness of the intermembrane gap) are dimensionless. We consider two special cases and then a realistic one:

• 1.In the limit where the adhesive subdomains of all species (a, b, and ab) can freely translate and rotate anywhere within the entire intermembrane space (so that h_a = h_b = h_ab = L, and Δω_a = Δω_b = Δω_ab = 8π²), this volume is equivalent to that of an ordinary 3D solution, and λ = L is simply the numerical-dimensional conversion factor relating the 3D and 2D dissociation constants.
• 2.If all of the adhesive subdomains a, b, and ab are present and can freely rotate (i.e., Δω_a = Δω_b = Δω_ab = 8π²) and translate (i.e., h_a = h_b = h_ab) within the same narrow shell, then λ = h_ab is simply the thickness of the reaction slab, similar to Bell’s original model (15,16).
• 3.Realistically, dimer formation will add restrictions to molecular motions so that, in general, h_a < h_ab, h_b < h_ab. Thus, the two spatial factors in the square brackets in Eq. 6 tend to increase the effective thickness of the reaction shell (λ) beyond its physical size (h_ab), effectively lowering the dimerization affinity. The qualitative effects of the angular factor on λ are more complicated. In general, due to restricted rotational motion in 2D relative to 3D, (Δω_ab/8π²) < 1. On the other hand, restrictions in motion due to dimerization result in (Δω_a/Δω_ab)(Δω_b/Δω_ab) > 1. The combined effect depends on the details of the system involved but in the next section we show that, for the case of cadherins, Δω_aΔω_b/8π²Δω_ab < 1, revealing that the limited rotational freedom of the monomers in the 2D system favors dimer formation.

Cis dimer formation

By a straightforward extension, Eq. 5 can be applied to describe other association processes. Thus, for instance, the ratio between the 2D and 3D equilibrium constants of cis dimerization of two receptors of type A, ($AA\left(cis\right)\rightleftarrows A+A$), is obtained by replacing every subscript b by a, yielding (see Fig. 1)

$${\lambda }_{cis}=\frac{K_{d,cis}^{\left(2D\right)}}{K_{d,cis}^{\left(3D\right)}}=\frac{h_a^2}{h_{ab}}\frac{\Delta {\omega }_a^2}{8{\pi }^2\Delta {\omega }_{aa}}.$$ (7)

Analogously, we can extend Eq. 6 to estimate the equilibrium constants corresponding to cis dimerization of a monomer and a trans dimer, or two trans dimers, etc.

Simulation Methodology

Dynamic and individual MC simulations

The Monte Carlo (MC) simulation algorithm described in this section uses realistic structural and dynamical representations of receptor conformations to enable a direct determination of $K_d^{\left(2D\right)}$ and $K_d^{\left(3D\right)}$ and hence of their ratio, $\lambda =K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$. We refer to these calculations as dynamical-MC (DMC) simulations. To compare their results to the theoretical predictions of Eq. 5, the h_i and Δω_i appearing in Eq. 5 are evaluated by separately sampling monomer and dimer configurations from those encountered in the course of the DMC simulations. This is equivalent to simulating the motion of isolated, translationally immobile yet structurally flexible receptors, yielding similar information to that obtained in our previous work (12). We refer to these calculations as IMC simulations (I for individual or isolated receptors).

Deriving 2D and 3D equilibrium constants from simulations

At low densities, the equilibrium concentrations of monomers and dimers can be obtained from DMC simulations of a system containing just two interacting receptors. Fig. 2 outlines our overall approach. Monomers translate, rotate, and undergo structural fluctuations, and upon encounter may form a dimer, which also translates and rotates and eventually dissociates, with probabilities that depend on the binding energy, following the usual Metropolis procedure. The equilibrium concentrations are determined by the relative frequencies of finding the pair of receptors bound or dissociated. Fig. 2 a describes the simulations in 3D. At time zero, the monomers are not in contact but occasionally a dimer is formed and the energy of the system decreases by an amount equal to the binding energy. The dimer can then dissociate with a corresponding increase in the energy of the system, and the simulation continues. Fig. 2 b shows the same behavior in a constrained 2D environment. Note that the dimerization energy is the same in both cases. The equilibrium constants (and hence the dimerization free energies) are determined by the time intervals, τ_AB and τ_A+B, which denote the sum of time intervals that the pair of receptors in the simulation box is bound or dissociated, respectively. Provided the total simulation time, τ = τ_AB and τ_A+B, is long enough, then τ_A+B/τ is the probability of finding receptors A and B in their unbound state, and τ_AB/τ = 1 − τ_A+B/τ is the probability of finding them dimerized. Specifically, ρ_A/ρ_AB = ρ_β/ρ_AB = τ_A+B/τ_AB and σ_A/σ_AB = σ_β/σ_AB = τ_A+B/τ_AB, in the 3D and 2D systems, respectively. The Supporting Material includes a movie describing the association of two monomers into a trans dimer.

Figure 2.

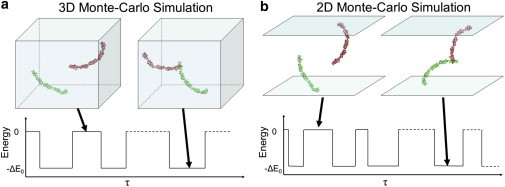
Schematic illustration of the simulation boxes used to calculate trans dimer binding affinities of freely translating and rotating receptors in 3D (a) and 2D (b). (Lower traces) Temporal fluctuations determining the dynamical equilibrium between monomer and dimer states; τ is the simulation time.

Simulation conditions and parameters

In the 3D system (Fig. 2 a) the two receptors were placed in a cubic box of volume V = L_x L_yL_z = (20 nm)³ = 8000 nm³, with periodic boundary conditions in all directions. The 2D simulation box consists of two parallel membranes of area W = L_xL_y = (50 nm)² = 2500 nm², separated from each other by a distance L_z ≡ L = 24 nm (corresponding to one layer of trans dimers in the crystalline state (2)), using periodic boundary conditions in the x and y directions. The two bow-like monomers comprising a trans dimer are embedded in different (nearly orthogonal) planes. Their end-to-end vectors are tilted by ∼40° relative to the membrane normal. The dimensions of the 2D and 3D boxes are not much larger than the maximal length of a monomer (∼20 nm) or a trans dimer (∼38 nm), yet considerably larger than the dimensions (∼4 nm) of the adhesive (EC1) subdomain of cadherins (2).

As in our previous work, a full C_α representation is used to model the structure and conformational dynamics of the cadherin receptors. Structural fluctuations (such as bending or twisting) around the average structure of the cadherin ectodomain are accounted for by the normal mode motions (17–19) of the hinge domains that link adjacent EC repeats (12). In addition, and crucially so in the DMC simulations, the receptors are allowed to perform both translational and rotational motions, in both the 3D and 2D systems. In the 2D system, lateral translation of monomers is mediated by EC5 diffusion parallel to the membrane plane. Dimer translation involves concerted movement of the two EC5 ends, allowing for small changes in their relative position and distance, provided they keep the dimer intact. Monomers undergo rotational motions, subject to the assumed flexibility of the EC5 subdomain with respect to the membrane surface. The EC5 domains of the monomers comprising a trans dimer are allowed the same range of rotation angles as in their free state; however, due to the additional constraints implied by the binding interface of their EC1 domains, the actual range of their EC5 rotations is far more restricted than those of the free monomers.

In both the 2D and 3D systems, a stable trans dimer is defined by the requirement that the root-mean square deviation (RMSD) of the C_α values comprising the pair of EC1(A)-EC1(B) domains is <6 Å, with respect to the known crystal structure. This criterion was established based on MD simulations of individual trans dimers as discussed previously in Wu et al. (12). When this condition is met, the dimer is assigned the binding energy ΔE₀. Two- and three-dimensional simulations were carried out for ΔE₀ between 5 and 10 kT at 1 kT intervals. In the 3D simulations, the two monomers perform independent movements, consisting of a sequence of random translational moves, followed by random rotations, and internal conformational changes. If the centers of mass of EC1(A) and EC1(B) happen to be close to each other (specifically, <50 Å apart), the RMSD of the EC1(A)-EC1(B) pair is calculated and if it is less than the 6 Å cutoff, a trans dimer is assumed to form, stabilized by ΔE₀. Otherwise, the monomers continue their random motions. Once a dimer is formed, it is also allowed to translate and rotate, as well as to undergo internal conformational changes of its constituent monomers. If the independent conformational changes of the monomers result in an RMSD of the EC1(A)-EC1(B) pair larger than 6 Å, i.e., a dissociated dimer, the move is accepted with the Metropolis probability exp(−ΔE₀/kT), and so on (20). The same procedure is used in the 2D simulations, augmented by the restrictions on EC5 motion. Separate 2D simulations were carried out for five different values of ΔΩ = Δ(cosΘ)ΔΦΔΨ, the range of angular motion of the membrane-anchored subdomain (EC5), and hence also of the entire ectodomain. Specifically, ΔΘ is used to define the range of polar angles available to the long axis of EC5 around its equilibrium (crystal structure) orientation (Θ₀ ≈ 20°) relative to the z axis. The angle Φ is the between the projection of the EC5 axis on the x,y (membrane) plane and the x axis, and Ψ is the angle of rotation of EC5 around its own long axis (resulting in rotation of the plane containing the bow-like ectodomain). The azimuthal angle of the membrane bound receptors is not restricted, so that 0 ≤ Φ ≤ 2π. Larger ΔΩ values imply larger values of all the h_i values (h_a and h_b are always larger than h_ab). Note, however, that significant contributions to all h_i values arise also from structural fluctuations associated with normal mode vibrations in the linker regions between adjacent EC repeats. Thus, the h_i values are nonzero even when no EC5 rotations are allowed (ΔΘ = ΔΨ = 0°). Simulations were carried out for five different values of ΔΩ; that is, ΔΘ = ΔΨ = 0°, 5°, 10°, 30°, and 60°, with no restrictions on Φ. EC5 orientations were uniformly sampled within the specified ranges of Θ and Ψ, discarding conformations which cross the membrane surface.

Results

We carried out DMC simulations of $K_d^{\left(3D\right)}$ and $K_d^{\left(2D\right)}$ that correspond to cadherin trans dimerization, for several different choices of the binding energies (ΔE₀), and different extents of angular flexibility of the membrane bound receptors (ΔΩ, as defined above). For each case, we calculated the ratio $\lambda =K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$ obtained from the DMC simulations, and compared it to the theoretical value derived from Eq. 5, with molecular parameters evaluated using IMC simulations. Because λ has a nanometer scale, we find it convenient to express the surface (2D) concentrations, σ, and thus $K_d^{\left(2D\right)}$, in units of nm⁻² (i.e., molecules/nm²) or μm⁻², and the 3D concentrations, ρ, and correspondingly $K_d^{\left(3D\right)}$, in units of nm⁻³ or μm⁻³. Note that the relationship between $K_d^{\left(3D\right)}$ and the corresponding constant in molar units, $K_{d,C}^{\left(3D\right)}$, follows simply from the identity 1 nm⁻³ = 10⁹ μm⁻³ = 1.67 M, yielding $K_d^{\left(3D\right)}=1.67K_{d,C}^{\left(3D\right)}$ (for $K_d^{\left(3D\right)}$ expressed in nm⁻³). The corresponding binding free energies, $\Delta G_0^{\left(3D\right)}=-kT\text{ln}{K}_d^{\left(3D\right)}$ and $\Delta G_{0,C}^{\left(3D\right)}=-kT\text{ln}{K}_{d,C}^{\left(3D\right)}$, differ by $\Delta G_0^{\left(3D\right)}=\Delta G_{0,C}^{\left(3D\right)}-0.51kT$.

3D dimerization constants and affinities

From the 3D DMC simulations we derived $K_d^{\left(3D\right)}\left(trans\right)$ for ΔE₀ = 5,…,10 kT. The corresponding binding free energies, $\Delta G_0^{\left(3D\right)}/kT=-\text{ln}{K}_d^{\left(3D\right)}$, are shown in Fig. 3. The linear increase of $\Delta G_0^{\left(3D\right)}$ with ΔE₀ (with slope 1) reveals that the entropic component of the binding affinity, $T\Delta S_0^{\left(3D\right)}=\Delta E_0-\Delta G_0^{\left(3D\right)}\approx 3.5kT$, is a constant, independent of the binding energy. Moreover, $T\Delta S_0^{\left(3D\right)}>0$, indicating that dimer dissociation is favored on entropic grounds. Note that $\Delta S_0^{\left(3D\right)}$ (as well as $\Delta S_0^{\left(2D\right)}$ below) correspond to entropy changes associated solely with the nontranslational degrees of freedom (i.e., internal vibrations and rotations as well as overall rotations) of the receptors (21) (e.g., Ben-Shaul and Gelbart (22), and see the Supporting Material).

Figure 3.

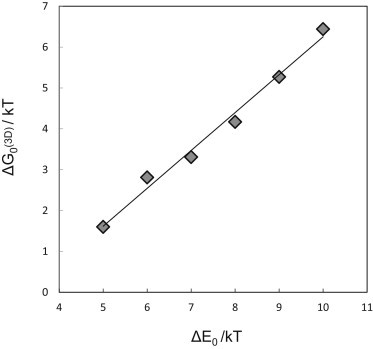
The binding free energy in 3D as a function of the adhesion energy. The linear dependence, with unit slope, indicates that $\Delta S_0^{\left(3D\right)}=(\Delta E_0-\Delta G_0^{\left(3D\right)})/T\approx 3.5k$ is independent of the binding energy.

2D dimerization constants and affinities

Binding affinities of membrane bound receptors, $\Delta G_0^{\left(2D\right)}/kT=-\text{ln}{K}_d^{\left(2D\right)}$, were derived from DMC simulations for the same six values of ΔE₀ used in the 3D simulations. For every value of ΔE₀, simulations were performed for the abovementioned values of ΔΩ (ΔΘ = ΔΨ = 0°, 5°, 10°, 30°, and 60°, with no restriction on Φ). The results are shown in Fig. 4. Although in this case the numerical errors are slightly larger than in Fig. 3, it is again apparent that $\Delta G_0^{\left(2D\right)}$ increases linearly with ΔE₀ in all cases considered, and the slope is again 1. Thus, as in 3D, $\Delta S_0^{\left(2D\right)}$ is a constant, independent of ΔE₀. We note, however, that $\Delta S_0^{\left(2D\right)}$ depends on ΔΩ: a larger ΔΩ implies greater rotational-conformational freedom (hence entropy) of the receptors, which is primarily pronounced in their unbound monomeric state. This increase is somewhat implicit in Fig. 4, but can be clearly seen in Fig. 5, where we note that $\Delta S_0^{\left(2D\right)}$ increases from ∼2 k to ∼4 k as ΔΩ increases from 0° to 60°. These values are comparable in magnitude to the 3D entropy change of $\Delta S_0^{\left(3D\right)}\approx 3.5k$, yet it should be noted that unlike in the 3D system, where the major contribution to $\Delta S_0^{\left(3D\right)}$ arises from the overall rotations of the receptors, the major (positive) contribution to $\Delta S_0^{\left(2D\right)}$ results from the spatial factor ($\Delta S_{0,sp}^{\left(2D\right)}=k\text{ln}\left[\right(h_a/h_{ab}\left)\right(h_b/h_{ab}\left)\right]$), which has no 3D counterpart. The angular contribution to $\Delta S_0^{\left(2D\right)}$ is rather small compared to the 3D case, reflecting the fact that, in general, $\Delta {\omega }_a\Delta {\omega }_b/8{\pi }^2\Delta {\omega }_{ab}<1$.

Figure 4.

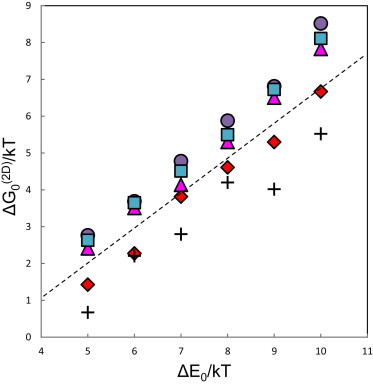
The binding free energy of a cadherin trans dimer in 2D as a function of the adhesion energy, for five different values of the angular range, ΔΩ, available to the membrane bound (EC5) subdomain. (Specifically, ΔΩ refers to ΔΘ = ΔΨ, while in all cases ΔΦ = 2π.) (Circles, squares, triangles, diamonds, crosses) ΔΩ = 0°, 5°, 10°, 30°, and 60°, respectively. (Straight dashed line) Guide to the eye. Its slope is 1, indicating that in all five cases the dissociation entropy in reaction 1, $\Delta S_0^{\left(2D\right)}=(\Delta E_0-\Delta G_0^{\left(2D\right)})/T$, is independent of the binding energy. As expected, $\Delta S_0^{\left(2D\right)}$ increases with ΔΩ.

Figure 5.

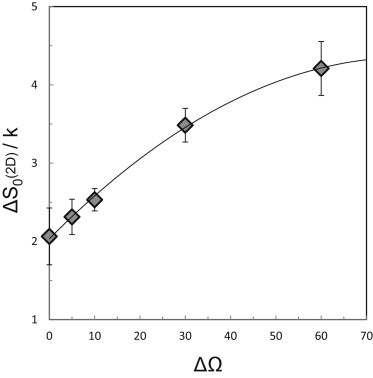
The standard 2D entropy change of cadherin dimer dissociation (reaction 1) in 2D, as a function of the angular allowance ΔΩ (see legend to Fig. 4).

The ratio $K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$: comparing simulation to theory

In Fig. 6 we show the values obtained for $\lambda =K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$ from the DMC simulations, and compare them to those predicted by Eq. 5 using spatial and angular ranges of motions obtained from IMC simulations. The agreement between the two approaches is very good. As expected, the results in Fig. 6 reveal that λ gets larger as the flexibility (ΔΩ) of the receptor’s ectodomain increases, and that in all cases it is considerably smaller than the intermembrane distance (L = 24 nm). Less obvious is the fact that in all cases considered, λ is still significantly smaller than $h_{ab}$, indicating that the angular factor in Eq. 6 favors trans dimer formation to the extent that it overcompensates the effect of the spatial factor, which disfavors this process. (Specifically, we found λ ≈ 0.25, 0.30, 0.38, 0.99, and 2.17 nm as compared to h_ab ≈ 1.5, 1.5, 2.5, 5.0, and 6.0 nm, for ΔΩ = 0°, 5°, 10°, 30°, and 60°, respectively.)

Figure 6.

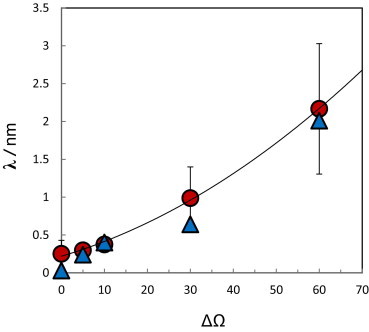
The ratio between the equilibrium constants of reaction 1 in the 2D and 3D environment, $\lambda =K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$, as a function of the angular allowance ΔΩ. (Circles) Results of the dynamic Monte Carlo simulations. (Triangles) Results obtained using Eq. 5, with molecular parameters (h_i, Δω_i) derived from the IMC simulations of structural fluctuations of immobile receptors.

Discussion

In the Theory section and in the Supporting Material we presented the basic statistical-thermodynamic principles underlying the formation of trans dimers, and outlined the extension of these notions to cis interactions between receptors that diffuse on the same membrane. These ideas were then corroborated based on detailed Monte Carlo simulations modeling the trans interaction between cadherin receptors. The theory and simulation methodology presented in this work are directly applicable to other membrane-bound receptors. The molecular parameters appearing in Eqs. 5 and 6 can be obtained using our simulation methodology or estimated based on the properties of the particular system of interest. We note, however, that many cell surface receptors are composed of strings of immunoglobulin-like domains and that the results obtained in this work offer first-order approximations of λ for many of these proteins. Obviously, the expectation is that λ will increase as the number of extracellular domains increases and as the linkers between them become more flexible. Below we summarize key results of our analysis and discuss factors that are relevant to cell-surface proteins in general.

Relating 2D to 3D trans interactions

Equation 5, which represents the ratio between the 2D and 3D dimerization constants as a product of spatial and angular components, offers a clear picture of the factors that determine dimerization affinities in the intercellular space. The subsequent factorization in Eq. 6 provides additional insights into this scheme, as exemplified by the special cases discussed above. Two of the factors in this equation, h_ab/L and Δω_ab/8π², which account for the spatial and angular confinements of the adhesive subdomains, are present in all systems. Both of these factors tend to reduce $\lambda =K_d^{\left(2D\right)}/K_d^{\left(3D\right)}$ and thus favor the adhesion affinity in 2D relative to the 3D environment. On the other hand, the two factors in square brackets in Eq. 6, reflecting the spatial and angular entropy losses upon dimerization, depend more sensitively on the structural-dynamical properties of the adhesive receptors involved. Thus, for example, relatively long and semiflexible receptors such as cadherins are likely to suffer greater entropy losses upon dimerization than shorter and less flexible proteins such as T-cell receptors.

Relating 2D to 3D cis interactions

Although this article has focused on trans interactions, the same theoretical and qualitative principles come into play when cis interaction is involved. One basic difference, of course, is that cis interactions do not depend on intermembrane spacing and, in principle, can take place between any two cell surface proteins. It is thus important to estimate the relevant dissociation constants, $K_{d,cis}^{\left(2D\right)}$. For the specific case of cadherin monomers, cis dimerization affinities are quite weak, $K_{d,cis}^{\left(3D\right)}\ge 1\text{mM}$. Using an expression similar to Eq. 7, we showed that this value translates to $K_{d,cis}^{\left(2D\right)}\le 500\mu {\text{m}}^{-2}$, suggesting that cadherins tend not to dimerize in 2D. The weak binding affinity is due in part to the weak cis binding energy, but also to the considerable configurational entropy loss of the monomers upon dimerization (see Eq. 7). Notably, however, the cis binding affinity increases dramatically when one of the monomers is already engaged in a trans dimer, because a substantial portion of the cis dimerization entropy penalty has already been paid when the trans dimer was formed. The effect is even more pronounced when two trans dimers interact in cis.

It is also important to consider the possibility that cis interactions will occur on their own, even when the 3D affinities are weak. If, for example, unlike in cadherins, the cis binding interface is located on membrane proximal domains (23), one expects lower entropy losses upon dimerization because fewer interdomain linkers are rigidified by dimerization. Indeed, using Eq. 7 we estimated the hypothetical cis dimerization affinities of two cadherins mediated by either their EC4, EC3, or EC2 interfaces, and found that $K_{d,cis}^{\left(2D\right)}$ decreases dramatically, from the value mentioned above of ∼500 μm⁻² for EC1-EC1 mediated dimerization to ∼25 μm⁻² for EC4-EC4 adhesion. The latter case corresponds to a binding affinity of ∼9 kT, which is strong enough to induce substantial lateral aggregation (24). We speculate that at least in some cases, glycosylation of membrane proximal domains may play a role in preventing lateral receptor aggregation.

Clustering of adhesion receptors

The formation of intercellular trans dimers is often followed by their clustering in cell-cell contact regions (1,25,26). Different theoretical approaches were suggested to account for this phenomenon, including models invoking cis/trans coupling, segregation of long and short receptors, and membrane fluctuations effects (27–29). In a previous study (24) we presented a lattice model whereby cooperative cis/trans interactions among cadherin receptors lead to a 2D phase transition resulting in the formation of a condensed 2D junction phase (e.g., an adherens junction), composed (mostly) of trans dimers.

We also showed that the formation of ordered junctions is greatly enhanced, especially at low expression levels, through the diffusion trap mechanism (see, e.g., Perez et al. (30)), as schematically illustrated in Fig. 7. In this mechanism, once a stable adhesive region between two cells is nucleated (e.g., after initial contact between two curved cell surfaces or protrusions), it serves as a trap, attracting additional monomers that migrate into this region, thus forming additional trans dimers. The dimer binding energy compensates for the reduced translational entropy of the receptors in the crowded trap environment. If long molecules whose size is incompatible with the preferred intermembrane distance were initially present in the contact zone, they can diffuse away from this region, thereby enjoying greater configurational entropy. In addition, membrane regions around the trap can more freely undergo elastic curvature fluctuations, providing an additional potential driving force for receptor clustering (29,31,32).

Figure 7.

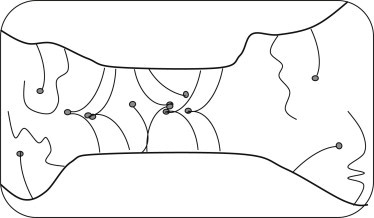
Receptor clustering in the diffusion trap. Membrane regions around the contact region can distance from each other if the receptors cluster, thus gaining curvature undulation entropy.

Molecules such as cadherins and ephrins form ordered junctions in cell-cell contact zones due to well-defined interprotein cis interfaces, but it is not clear that this is the general case. In other systems, comparable 2D lattices have yet to be identified, although ordered one-dimensional arrays are frequently observed (1). However, even in the absence of lateral interactions, the diffusion trap mechanism (30) will lead to a buildup of density in the contact zone (33,34). In such cases, the clusters observed experimentally are likely to be disordered (liquid-like) (35), yet much remains to be done before this issue is resolved.

Membrane fluctuations

Our model of the intercell contact region, as consisting of two plane parallel membranes at a fixed distance from each other, is obviously approximate, because it totally ignores the possible effects of fluctuations in intermembrane distance as a result of intrinsic membrane curvature fluctuations or cytoplasmic events that can influence this distance. This picture is applicable to locally flat contact regions where receptor density is relatively high, of the kind associated with the diffusion trap mentioned above. An order-of-magnitude estimate of membrane curvature effects in such regions can be obtained based on the premise that intact trans dimers dictate a well-defined intermembrane distance.

The average amplitude of the height fluctuations presented by a membrane undergoing random thermal undulations is given by ${\langle u^2\rangle }^{1/2}=cl{\left(kT/\kappa \right)}^{1/2}$ (4,30,36), where c ≈ 0.1 is a dimensionless numerical constant, κ is the bending modulus of the membrane (37), and l² is the area of a fluctuating membrane patch whose edges are kept stationary. If trans dimers can be regarded as membrane pinning points, then for a typical bending rigidity of a biological cell membranes with, e.g., κ = 400 kT (38), we find, assuming an interreceptor distance of 50 nm (appropriate to relatively high cell surface expression levels), that ${\langle u^2\rangle }^{1/2}\approx 0.2\text{nm}$. This value is much smaller than the assumed intermembrane separation, L = 24 nm, considerably smaller than the ranges of motion of the cadherin monomers (h_a,h_b) and even smaller than the range of motion of the dimer interface (h_ab). The actual value of ${\langle u^2\rangle }^{1/2}$ may be higher, owing to the fact that isolated trans dimers are not entirely rigid and may tolerate small changes in the intermembrane distance. In any case, this simple estimate suggests that membrane fluctuations in crowded contact regions are likely to be small. Nevertheless, we note that local membrane fluctuations can be incorporated approximately in the theoretical framework, by adding their contributions to the monomers' ranges of motion (h_a,h_b); their effect on dimer fluctuations is expected to be smaller. However, extensions and ramifications of this kind for specific systems are warranted and instructive only when the dynamical and structural aspects of the relevant adhesive receptors and the membranes to which they are bound are realistically represented.