Conformational States of Melittin at a Bilayer Interface

Abstract

The distribution of peptide conformations in the membrane interface is central to partitioning energetics. Molecular-dynamics simulations enable characterization of in-membrane structural dynamics. Here, we describe melittin partitioning into dioleoylphosphatidylcholine lipids using CHARMM and OPLS force fields. Although the OPLS simulation failed to reproduce experimental results, the CHARMM simulation reported was consistent with experiments. The CHARMM simulation showed melittin to be represented by a narrow distribution of folding states in the membrane interface.

Unstructured peptides fold into the membrane interface because partitioned hydrogen-bonded peptide bonds are energetically favorable compared to free peptide bonds (1–3). This folding process is central to the mechanisms of antimicrobial and cell-penetrating peptides, as well as to lipid interactions and stabilities of larger membrane proteins (4). The energetics of peptide partitioning into membrane interfaces can be described by a thermodynamic cycle (Fig. 1). State A is a theoretical state representing the fully unfolded peptide in water, B is the unfolded peptide in the membrane interface, C is the peptide in water, and D is the folded peptide in the membrane. The population of peptides in solution (State C) is best described as an ensemble of folded and unfolded conformations, whereas the population of peptides in State D generally is assumed to have a single, well-defined helicity, as shown in Fig. 1 A (5). Given that, in principle, folding in solution and in the membrane interface should follow the same basic rules, peptides in state D could reasonably be assumed to also be an ensemble. A fundamental question (5) is therefore whether peptides in state D can be correctly described as having a single helicity. Because differentiating an ensemble of conformations and a single conformation may be an impossible experimental task (5), molecular-dynamics (MD) simulations provide a unique high-resolution view of the phenomenon.

Figure 1.

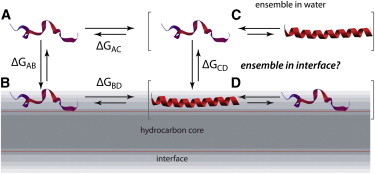
Thermodynamic cycles for peptide partitioning into a membrane interface. States A and B correspond to the fully unfolded peptide in solution and membrane interface, respectively. The folded peptide in solution is best described as an ensemble of unfolded and folded conformations (State C). State D is generally assumed to be one of peptides with a narrow range of conformations, but the state could actually be an ensemble of states as in the case of State C.

Melittin is a 26-residue, amphipathic peptide that partitions strongly into membrane interfaces and therefore has become a model system for describing folding energetics (3,6–8). Here, we describe the structural dynamics of melittin in a dioleoylphosphatidylcholine (DOPC) bilayer by means of two extensive MD simulations using two different force fields.

We extended a 12-ns equilibrated melittin-DOPC system (9) by 17 μs using the Anton specialized hardware (10) with the CHARMM22/36 protein/lipid force field and CMAP correction (11,12) (see Fig. S1 and Fig. S2 in the Supporting Material). To explore force-field effects, a similar system was simulated for 2 μs using the OPLS force field (13) (see Methods in the Supporting Material). In agreement with x-ray diffraction measurements on melittin in DOPC multilayers (14), melittin partitioned spontaneously into the lipid headgroups at a position below the phosphate groups at similar depth as glycerol/carbonyl groups (Fig. 2).

Figure 2.

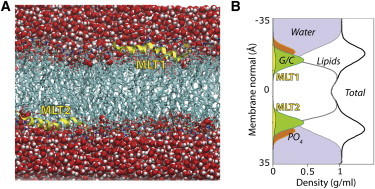
Melittin partitioned into the polar headgroup region of the lipid bilayer. (A) Snapshot of the simulation cell showing two melittin molecules (MLT1 and MLT2, in yellow) at the lipid-water interface. (B) Density cross-section of the simulation cell extracted from the 17-μs simulation. The peptides are typically located below the lipid phosphate (PO4) groups, in a similar depth as the glycerol/carbonyl (G/C) groups.

To describe the secondary structure for each residue, we defined helicity by backbone dihedral angles (φ, ψ) within 30° from the ideal α-helical values (–57°, –47°). The per-residue helicity in the CHARMM simulation displays excellent agreement with amide exchange rates from NMR measurements that show a proline residue to separate two helical segments, which are unfolded below Ala⁵ and above Arg²² (15) (Fig. 3 A). In contrast, the OPLS simulation failed to reproduce the per-residue helicity except for a short central segment (see Fig. S3).

Figure 3.

Helicity and conformational distribution of melittin as determined via MD simulation. (A) Helicity per residue for MLT1 and MLT2. (B) Corresponding evolution of the helicity. (C) Conformational distributions over the entire 17-μs simulation.

Circular dichroism experiments typically report an average helicity of ∼70% for melittin at membrane interfaces (3,6,16,17), but other methods yield average helicities as high as 85% (15,18). Our CHARMM simulations are generally consistent with the experimental results, especially amide-exchange measurements (15); melittin helicity averaged to 78% for MLT1, whereas MLT2 transitioned from 75% to 89% helicity at t ≈ 8 μs, with an overall average helicity of 82% (Fig. 3 B). However, in the OPLS simulation, melittin steadily unfolds over the first 1.3 μs, after which the peptide remains only partly folded, with an average helicity of 33% (see Fig. S3). Similar force-field-related differences in peptide helicity were recently reported, albeit at shorter timescales (19). Although suitable NMR data are not presently available, we have computed NMR quadrupolar splittings for future reference (see Fig. S4).

To answer the question asked in this article—whether the conformational space of folded melittin in the membrane interface can be described by a narrow distribution—the helicity distributions for the equilibrated trajectories are shown in Fig. 3 C. Whereas MLT1 in the CHARMM simulation produces a single, narrow distribution of the helicity, MLT2 has a bimodal distribution as a consequence of the folding event at t ≈ 8 μs (Fig. 3 C). We note that CHARMM force fields have a propensity for helix-formation and this transition might therefore be an artifact. We performed a cluster analysis to describe the structure of the peptide in the membrane interface. The four most populated conformations in the CHARMM simulation are shown in Fig. 4. The dominant conformation for both peptides was a helix kinked at G12 and unfolded at the last 5–6 residues of the C-terminus. The folding transition of MLT2 into a complete helix is visible by the 48% occupancy of a fully folded helix.

Figure 4.

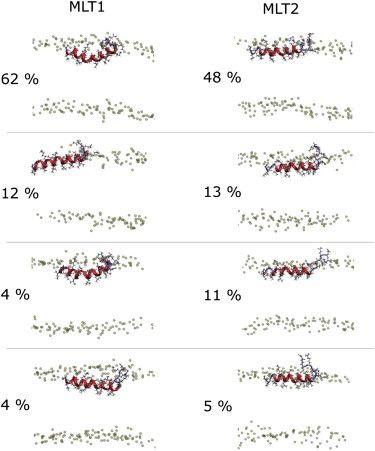
Conformational clusters of the two melittin peptides (MLT1 and MLT2) from the 17-μs CHARMM simulation in DOPC. Clustering is based on Cα-RMSD with a cutoff criterion of 2 Å.

We conclude that the general assumption when calculating folding energetics holds: Folded melittin partitioned into membrane interfaces can be described by a narrow distribution of conformations. Furthermore, extended (several microsecond) simulations are needed to differentiate force-field effects. Although the CHARMM and OPLS simulations would seem to agree for the first few hundred nanoseconds, the structural conclusions differ drastically with longer trajectories, with CHARMM parameters being more consistent with experiments. However, as implied by the difference in substate distributions between MLT1 and MLT2, 17 μs might not be sufficient to observe the fully equilibrated partitioning process. The abrupt change in MLT2 might indicate that the helicity will increase to greater than experimentally observed in a sufficiently long simulation. On the other hand, it could be nothing more than a transient fluctuation. Increased sampling will provide further indicators of convergence of the helix partitioning process.