Nanoscale Measurement of the Dielectric Constant of Supported Lipid Bilayers in Aqueous Solutions with Electrostatic Force Microscopy

Abstract

We present what is, to our knowledge, the first experimental demonstration of dielectric constant measurement and quantification of supported lipid bilayers in electrolyte solutions with nanoscale spatial resolution. The dielectric constant was quantitatively reconstructed with finite element calculations by combining thickness information and local polarization forces which were measured using an electrostatic force microscope adapted to work in a liquid environment. Measurements of submicrometric dipalmitoylphosphatidylcholine lipid bilayer patches gave dielectric constants of ε_r ∼ 3, which are higher than the values typically reported for the hydrophobic part of lipid membranes (ε_r ∼ 2) and suggest a large contribution of the polar headgroup region to the dielectric response of the lipid bilayer. This work opens apparently new possibilities in the study of biomembrane electrostatics and other bioelectric phenomena.

Introduction

The dielectric constant of biomembranes is an important parameter in cell electrophysiology, because it ultimately determines phenomena such as the membrane permeability to ions, membrane potential formation, or the action potential propagation velocity (1–4). Furthermore, it also determines the cell’s response to externally applied electrical fields employed by bioelectrical techniques, such as dielectrophoresis (5), impedance spectroscopy (6), or electroporation (7). Finally, it gives information about the membrane-liquid interfacial properties, particularly those relating to the hydration of the membrane surface, which plays an important role in phenomena such as lipid bilayer fusion (8) or in the correct insertion, folding, and function of membrane proteins.

A number of techniques have been developed to provide a quantitative estimation of this important membrane physical parameter. Some of the most commonly used are: impedance spectroscopy (6,9), environment-sensitive fluorescent microscopy (10,11), and electron paramagnetic resonance (12,13). However, to date, none of these has been able to quantify the dielectric constant of biomembranes with nanometric (lateral) spatial resolution. Achieving nanoscale spatial resolution is challenging due to different factors depending on the technique considered. For instance, in the case of impedance spectroscopic techniques, the large stray contributions when shrinking the area of the measuring electrodes and the complex frequency response of the membrane-liquid interface constitute the most important challenges. However, reaching nanometric spatial resolution is essential for a better understanding of bioelectric phenomena in biomembranes, as they show a two-dimensional heterogeneous fluid structure with small domains whose dimensions lie on the order of 10–100 nm (e.g., lipid rafts) (14–16).

In recent years, some efforts have focused on increasing the spatial resolution of electric measuring techniques for biomembranes, mostly using a scanning probe microscopy approach. For instance, membrane surface charges and membrane dipole potentials have been probed at the nanoscale with AFM measurements in liquid (17,18). However, the static nature of these measurements makes a precise quantification of the membrane dielectric constant difficult, because both charges and membrane dielectric polarization influence the measured electrostatic forces. Dielectric properties of membranes were probed by nanoscale dielectrophoretic force microscopy and spectroscopy (19); however, it was not possible to estimate the dielectric constant with sufficient accuracy because dielectric contributions were convoluted with topographic effects. On the other hand, the dielectric constant of biomembranes was precisely measured and quantified at the nanoscale by scanning capacitance microscopy (20) and electrostatic force microscopy (21). However, these measurements were performed in air on dried biomembranes due to difficulties in applying these techniques in a liquid environment. In summary, no technique has succeeded in quantifying the dielectric constant of biomembranes with nanoscale spatial resolution and in electrolyte solutions without ambiguities in data interpretation.

In this article, we take advantage of very recent developments in the implementation of dynamic electrostatic force microscopy in liquid (22) to quantify the dielectric constant of supported lipid bilayers in electrolyte solutions with nanoscale lateral spatial resolution. The results reveal the prominent role played by the headgroup region in the dielectric response of the lipid bilayer, and show the great potential of this approach.

Materials and Methods

Dynamic electrostatic force microscopy in liquids

Local electric force measurements were obtained with an electrostatic force microscope adapted to measure under liquid and able to detect forces in the MHz frequency range. In this frequency range, the ionic-dependent electric force acting on the probe becomes localized to the tip apex and enables the recording of local dielectric properties of materials, as has been demonstrated elsewhere (22). Electrostatic forces in the MHz range are detected by using a heterodyne detection system in which the dc bending induced by the high-frequency applied signal is modulated by a low-frequency signal in the 10-kHz range as shown in Fig. 1 and further detailed in Gramse et al. (22). All measurements were performed under electrolyte solution with a commercial AFM (Nanotec Electrónica, Madrid, Spain), customized with a homemade liquid cell, using solid platinum tips (Rocky Mountain Nanotechnology, Salt Lake City, UT) with a spring constant of k ∼ 0.3 N/m. High-frequency ac voltages (80 MHz) were applied with a model No. 33250A external waveform generator (Agilent Technologies, Santa Clara, CA) in amplitude modulation mode, with the low-frequency (2 kHz) modulation signal being provided by an external eLockIn 204/2 (Anfatec Instruments, Oelsnitz, Germany). Initially, topographic images were acquired in conventional dynamic mode, then dielectric images were acquired with the tip scanning at a constant height (z ∼50–80 nm) above the sample topography. This separation was chosen to avoid both electric double layer interactions (the Debye length is typically 10 nm in 1 mM monovalent electrolyte solutions) and any possible lipid bilayer damage. The dynamic nature of the electric measurement makes the recorded signal insensitive to static charges, allowing unambiguous determination of the dielectric properties. All the forces are presented as an effective capacitance gradient, defined as

$$C^{\prime }\left(z\right)=\frac{4\left|F_{\text{elec},f_{\mathrm{mod}}}\right|}{v_0^2},$$

where $\left|F_{\text{elec},f_{\mathrm{mod}}}\right|$ is the amplitude of the modulated electric force measured at the first harmonic and v₀ is the voltage amplitude.

Figure 1.

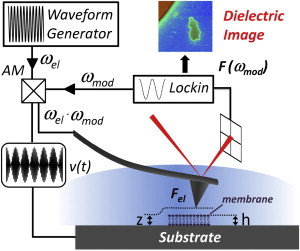
Electrostatic force microscopy setup for measuring local dielectric properties of materials in electrolyte solution. An amplitude-modulated ac-potential with frequency ω_el (>MHz) and modulation frequency ω_mod (<10 kHz) is applied between a conductive tip and a substrate in an electrolyte solution. An external lock-in amplifier detects the modulated bending of the cantilever. The cantilever bending depends, among other factors, on the local dielectric properties of the sample, which we mapped by scanning with the tip at a constant separation, z, from the sample and the substrate.

Lipid bilayer formation

As a representative example of a lipid bilayer we considered DPPC (1,2-dipalmitoyl-sn-glycero-3-phosphocholine) single bilayers. Phosphatidylcholines are the main components of eukaryotic cell membranes (23), and DPPC is one of the most widely used phosphatidylcholines in membrane models. DPPC bilayer patches were formed by liposome fusion on a SiO₂/Si⁺⁺ microstructured substrate (20-nm-thick SiO₂ stripes on a highly doped silicon substrate purchased from AMO GmbH (Aachen, Germany). The SiO₂/Si⁺⁺ substrate was used here to allow a proper in situ calibration of the tip on the doped Si⁺⁺ substrate, and to validate the dielectric measurements on the test SiO₂ structures, as further detailed below. The supported DPPC planar bilayers were prepared by vesicle fusion. Concentration, temperature, and time of deposition were adjusted to obtain lipid bilayers partially covering the substrate surface. DPPC, specified as ≥99% pure, chloroform and methanol, HPLC grade, were purchased from Sigma Aldrich (St. Louis, MO). High purity water (18.2 MΩ cm) used in this study was obtained with a MilliQ water purification system (Millipore, Billerica, MA). DPPC was obtained in powder form and used without further purification. DPPC was first dissolved in chloroform-methanol (3:1) (v/v) solution to a final lipid concentration of 1 mg/mL, then the solvent was evaporated under a nitrogen stream with constant rotation of the vial. The vial was kept at vacuum overnight to ensure the absence of organic solvent traces. The dry lipid was then resuspended in distilled water at ∼45°C to its final concentration of 0.1 mg/mL. The solution was finally sonicated for 10 min. The sonicated vesicles were stored at 4°C and used within 2–3 days, and were always protected from light. Vesicle suspensions were incubated at 45°C for 5 min and used immediately. A droplet of 100 μL of the vesicle suspension was added to the substrate at room temperature (25°C) and incubated for 12 min, allowing deposition of the vesicles and the formation of a lipid bilayer only partially covering the surface. After that, the substrate was rinsed twice with water to remove the excess vesicles in suspension. Finally, water was substituted by an electrolyte solution of KClO₄ (99.99% purity, Sigma Aldrich) with a concentration 1 mM. KClO₄ was selected because it is well known not to interact with noble metals such as the platinum of which the tip is made. In addition, we did not observe any obvious effect on the topography of the DPPC lipid bilayers associated to the presence of this salt.

Finite element numerical calculations

For the quantitative interpretation of the experiments, we compared the measured forces to forces calculated with a finite-element model of the AFM tip in close proximity to the membrane. To obtain the electrostatic force acting on a specific tip geometry, the equation

$$\nabla \left(\left(\sigma +i\omega {\epsilon }_r{\epsilon }_0\right)\nabla V\right)=0$$ (1)

was solved using the electrostatic AC/DC module of the COMSOL Multiphysics 4.0 simulation environment (Comsol Multiphysics, Burlington, MA). In Eq. 1, V is the phasor voltage, σ the local conductivity, ε_r the local dielectric constant, and i = √−1. All simulations were carried out in a two-dimensional axisymmetric geometry (electric quasistatics, meridional electric currents). The geometry was defined as shown in Fig. 2 with the following tip parameters: tip radius, R; cone angle, θ; and cone height H. The membrane is defined by its thickness, h; radius, l; and dielectric constant ε_r,mem (we assume no membrane conductivity, expressed as σ_mem = 0). The membrane dielectric constant should be taken as an equivalent dielectric constant, i.e., the dielectric constant that a homogeneous material would have to give the same external electric field as the membrane in response to the applied external electric field. For nonhomogeneous materials in the vertical direction, like a lipid bilayer, and for the electric fields created by a sharp metallic tip, it can be shown, by means of finite element numerical simulations of stacked structures, that such an equivalent dielectric constant can be defined and that it is an intrinsic property of the material as long as its thickness is below tens of nanometers (data not shown). Note that the membrane patch is modeled as a disk because we are working in an axisymmetric two-dimensional geometry. To account for the native oxide on the highly doped silicon substrate, we added a distributed capacitance, C_native, on top of the conducting substrate that was set to ground. The solution medium is defined by its dielectric constant ε_r,sol and its conductivity σ_sol = Λ c, where c is the electrolyte concentration and Λ is the molar conductivity. While the domain containing the solution is enclosed by outer boundary conditions corresponding to electric insulation (n⋅J = 0, where n is the normal vector to the boundary and J is the electric flux), finite-size effects were mitigated by a coordinate transform using the infinite-elements option in COMSOL Multiphysics. The geometry was meshed with extra refinement about the tip and the sample surface. The Maxwell stress tensor was integrated over the whole tip surface to obtain the tip force.

Figure 2.

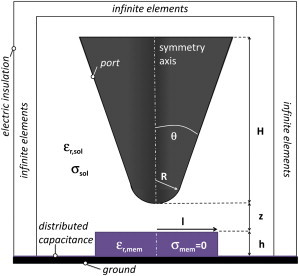
Schematic representation of the numerically simulated model (not to scale). The AFM-tip is defined by its apex radius, R; cone angle, θ; and cone height, H. The sample is defined by its thickness, h; radius, l; and dielectric constant, ε_r,mem. A distributed capacitance was added on the conducting substrate. Tip and sample are surrounded by a solution defined by its dielectric constant ε_r,sol and conductivity σ_sol. A coordinate transform maps the outer boundary to infinity.

Quantification of the dielectric constant of the membranes

The dielectric constant of the DPPC bilayers was quantified from force-distance curves using a modification of the method we developed for a dry environment (20,21,24–26) and recently applied to thin oxide films in electrolyte solutions (22). For a given high frequency (f = 80 MHz in this case) and given electric properties of the liquid (ε_r,sol = 78 and σ_sol = Λ c, with Λ = 13.3 S m⁻¹ mol⁻¹), approach curves were numerically calculated and compared to the experimental curves measured on the sample using the fitting procedure also detailed in Gramse et al. (22). For convenience, simulations were carried out for an extensive set of parameters (R = 25–125 nm; θ = 10−30°; C_native = 0.5–3.5 μF/cm²; h = 5–20 nm; l = 750–1500 nm; z = 10–1000 nm; and ε_r,mem = 2–10) and the data were interpolated using the software Mathematica 7 (Wolfram Research, Champaign, IL) to finally obtain a fitting function which we fitted to experimental data. Simulation data for h = 0 (no membrane) were first fitted to approach curves on the Si⁺⁺ substrates to obtain the probe geometry (R and θ) and the native oxide capacitance (C_native). Simulations using this probe geometry (R, θ, C_native) and the known (measured) sample geometry (h = 5 nm, l = 750 nm) were then fitted to approach curves taken onto DPPC bilayer patches, with the dielectric constant of the bilayer, ε_r,mem, as a single fitting parameter. The procedure was validated in situ by repeating the same procedure with approach curves taken on a nearby SiO₂ stripe, and verifying that one obtains the expected value for this material (ε_r,SiO2 ∼ 4). To exclude any modification or contamination of the tip with DPPC, the approach curves onto the DPPC bilayers were carried out after acquiring images and the approach curves onto the clean Si⁺⁺ and SiO₂.

Results and Discussion

Fig. 3 shows the topography (a) and phase (b) images of a single DPPC bilayer adsorbed onto the SiO₂/Si⁺⁺ substrate in an aqueous solution with an electrolyte concentration of 1 mM. The images show that the DPPC lipid bilayer partially covers the Si⁺⁺ substrate and the SiO₂ stripes, with a total surface coverage of ∼20%. The measured lipid bilayer thickness was ∼5 nm, in good agreement with values reported in the literature for DPPC (27,28). We note the occasional presence of double bilayers and of small isolated bilayer patches with dimensions in the micrometer-to-hundred-nanometers range, more clearly observed in the phase image as small spots (Fig. 3 b). The corresponding dielectric image, represented by the capacitance gradient variation, ΔC′(z), as obtained from the measured force, is shown in Fig. 3 c. It was measured in a dual-pass method retracing the topography image at a lift height of z = 80 nm, and at frequency f = 80 MHz. The dielectric image clearly resolves the 5-nm-thick lipid bilayer on the Si⁺⁺ substrate and, with inferior resolution, on the SiO₂ stripe as well. This is also shown in Fig. 3 d, in which we give the corresponding profiles taken along the lines in Fig. 3, a–c. Note that capacitance gradient variations are ∼0−5 aF/nm, which correspond to electric force variation in the range of 0−80 pN. Remarkably, double lipid bilayers (10-nm thick, marked with an arrow in Fig. 3 c) can be distinguished in the dielectric image.

Figure 3.

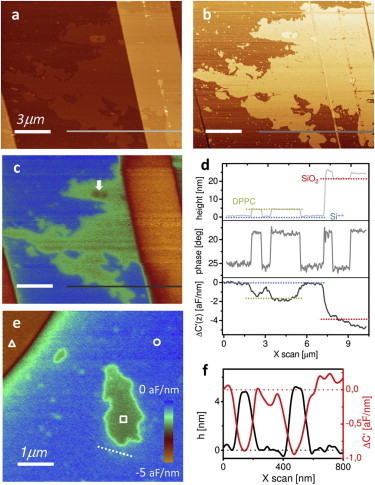
Dielectric constant measurement of DPPC patches adsorbed onto SiO₂/Si⁺⁺ microstructures. (a) Topography, (b) phase, and (c) dielectric images (the capacitive gradient, variation, ΔC′(z)) for a large scan area. The dielectric image was obtained in lift mode at z = 80 nm above the sample with an applied voltage of frequency f = 80 MHz and v₀ = 0.25 V amplitude. (d) Profiles of topography, phase and dielectric images. Note that ΔC′(X = 0) is set to zero. (e) Zoomed-in dielectric image of isolated lipid bilayer patches next to the SiO₂ structure, acquired at z = 50 nm. (f) Topographic and dielectric profiles of two closely spaced ∼100-nm bilayer patches (taken along the dashed light-gray line in panel e).

Fig. 3 e shows a zoomed-in dielectric image containing isolated DPPC patches next to a bare SiO₂ stripe taken at a closer distance (z = 50 nm). The dimensions of the patches in this image range from micrometers down to ∼100 nm; the latter are seen as small light spots on the substrate. Fig. 3 f shows the topographic and dielectric profiles taken across two of these small patches (dashed line in Fig. 3 e). These profiles show the good spatial resolution of the dielectric image which resolves closely spaced membrane patches of only ∼100 nm in diameter. These results demonstrate that electrostatic force microscopy can image the dielectric properties of single bilayer membranes in liquid with spatial resolution down to ∼100 nm; as of this writing, this is not believed achievable with any other dielectric membrane measuring technique.

Fig. 4 shows capacitive gradient-distance curves measured on the Si⁺⁺ substrate, the SiO₂ stripe, and a DPPC patch, in the locations marked with symbols (○, ▵, and □, respectively) in Fig. 3 e. All data are presented with ΔC′(z = 1000 nm) set to zero. The electric force sensed by the tip shows a clear increase as the sample is approached, showing a distinct behavior for the three different materials considered. The highest electric forces correspond to the Si⁺⁺ substrate and are due to its almost metallic nature, which is a consequence of its high doping level. The curves on the DPPC patch and on the SiO₂ stripe show smaller forces than the one on the Si⁺⁺, indicating their insulating natures. Although the forces on the DPPC patch appear larger than on the SiO₂ stripe this should not be taken as an indication of a larger dielectric constant for DPPC, because the forces depend on both the dielectric constant of the material and its thickness (DPPC ∼5 nm; SiO₂ ∼20 nm).

Figure 4.

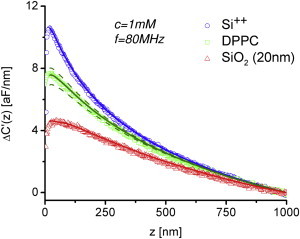
Experimental capacitance gradient approach curves (symbols) measured onto the Si⁺⁺ substrate (circles), the SiO₂ stripe (triangles), and the DPPC patch (squares) at the locations indicated by symbols in Fig. 3e. The applied voltage was v₀ = 0.25 V, the frequency f = 80 MHz, and the concentration 1 mM. (Solid lines) Finite element numerical simulations of the tip-sample system with dielectric constants ε_r,_SiO2 = 4 and ε_r,_DPPC = 3.2, for SiO₂ and DPPC, respectively. In the calculations we used a tip radius R = 45 nm, a cone angle θ = 15°, and a native oxide capacitance C_native = 0.71 μF/cm² obtained by fitting the numerical calculations to the force curve on the Si⁺⁺ substrate (solid line). (Dashed lines) Simulations for ε_r,_DPPC = 2.2 and 4.2. Additional model parameters used in the numerical calculations: oxide/lipid heights and radii: h_SiO2 = 20 nm; l_SiO2 = 1.5 μm; h_DPPC = 5 nm; l_DPPC = 0.75 μm; and cone height H = 10 μm. The data are presented with ΔC′(z = 1000 nm) set to zero.

The probe geometry (R = 45 nm, cone angle θ = 15°) and the native oxide capacitance C_native = 0.71 μF/cm² were extracted by fitting the curve measured on the Si⁺⁺ substrate. These parameters, together with the measured thicknesses, were used to fit the curves on the DPPC bilayer and the SiO₂ stripe, with the dielectric constant as the single fitting parameter. The best fit to the experimental curves gave ε_r,DPPC = 3.2 ± 0.1 and ε_r,SiO2 = 4 ± 0.2, respectively (errors are from the fitting routine with ε_r as parameter, confidence level 95%). The value obtained for the SiO₂ stripe is in excellent agreement with the value reported for this material and supports the reliability of the procedure. The sensitivity of the procedure on the dielectric constant of the DPPC bilayer is further illustrated by the dashed lines in Fig. 4, which correspond to values of ε_r,DPPC = 4.2 and 2.2 and clearly lie outside of the experimental error. These results demonstrate the capability of the proposed methodology to sensitively quantify the dielectric constant of lipid bilayers at the nanoscale in electrolyte solutions.

The dielectric constant obtained for the DPPC bilayer (ε_r,DPPC ∼ 3.2) is larger than the value usually quoted for the hydrophobic part of lipid bilayers (ε_r ∼ 2) (29). This suggests that the interfacial polar headgroup region contributes significantly to the measured dielectric response. We note that at the high frequencies (80 MHz) it is unlikely that this contribution could be attributed to ionic space charges formed close to the membrane. Therefore, this contribution should be associated to the polarization properties of the bilayer region itself. A rough estimation of the dielectric constant of this interfacial polar region can be obtained from the well-known relation

$$\frac{h}{{\epsilon }_{r,\text{DPPC}}}=\frac{h_{\text{polar}}}{{\epsilon }_{r,\text{polar}}}+\frac{h_{\text{core}}}{{\epsilon }_{r,\text{core}}},$$ (2)

where h_polar and h_core are the total thicknesses of the polar and hydrophobic regions (including both leaflets), and ε_r,polar and ε_r,core their respective dielectric constants. By using the measured values for the membrane thickness and dielectric constant, and assuming thicknesses of h_polar = 2 nm, h_core = 3 nm, and a dielectric constant ε_r,core = 2, one obtains a value of ε_r,polar ∼ 30 for the dielectric constant of the polar region. This value is only a rough estimation as it is highly sensitive to the thicknesses assigned to the hydrophobic and polar regions, but in all reasonable cases, it is much larger than the dielectric constant of the hydrophobic part of the membrane. Studies using other dielectric-sensitive techniques have reported similarly large polarization responses from the interfacial region of lipid bilayers (8–13), but such measurements have never before been reported from a nanoscale measurement. Molecular-dynamic simulations of the dielectric properties of DPPC bilayers provide an explanation for the large dielectric constant value of the polar interfacial region (30). The simulations report an appreciable presence of water in the superficial region of the membrane. This was also experimentally observed by Fukama (31), and relatively large dipoles formed by the choline and phosphate groups, both of which could contribute to a large dielectric constant value, even when reduced dipole orientation capabilities exist due to the high measuring frequencies considered. An aspect of our measurements that needs to be considered during interpretation is that the dielectric constant measured corresponds to polarization phenomena occurring in the MHz range. In this frequency range the dielectric constant is sensitive to electronic polarization of the material and to dipolar polarization of small molecules free to follow the ac electric field applied (e.g., water molecules). Therefore, static or quasistatic effects associated to surface charges, pH, or ionic strength of the solution are likely to not affect the measured results, as long as the measuring distance is larger than the interfacial membrane electrolyte layer. On the contrary, the phase of the lipid bilayer, which determines the packing density and mobility of the lipids, could, in principle, affect the measured dielectric constant to a relatively small extent. To address this effect, one should improve the sensitivity of the measuring technique and consider experimental setups enabling phase transition or phase state control (e.g., temperature control).

We note that the results reported here do not represent the absolute limit of the technique. For example, extending the frequency range to higher values would allow measurements to be performed at higher concentrations, such as physiological conditions (∼0.1 M), although frequencies in the microwave range can become necessary. It should also be possible to take the experimental data at smaller tip-sample distances and employ force gradient detection to increase both the spatial resolution and the dielectric sensitivity of the technique. However, at very close tip-samples distances, the theoretical models have to be improved to also take into account the overlapping of surface double-layers or other interfacial electric phenomena.

Conclusions

We have shown that the dielectric properties of single lipid bilayers can be quantified and imaged at the nanoscale and in electrolyte solutions with an electrostatic force microscope adapted to work in liquid. The results obtained on DPPC bilayer patches give an effective dielectric constant ε_r,DPPC ∼ 3.2, which is larger than the value typically reported in the literature (∼2)—suggesting a large contribution of the polar headgroup region to the dielectric properties of the bilayers. These results open a number of possibilities in fields such as membrane electrostatics and electrophysiology in which nanoscale dielectric information could provide new insights.