Interaction of temporal and ordinal representations in movement sequences

Abstract

The production of movement sequences requires an accurate control of muscle activation in time. How does the nervous system encode the precise timing of these movements? One possibility is that the timing of movements (temporal sequence) is an emergent property of the dynamic state of the nervous system and therefore intimately linked to a representation of the sequence of muscle commands (ordinal sequence). Alternatively, timing may be represented independently of the motor effectors and would be transferable to a new ordinal sequence. Some studies have found that a learned temporal sequence cannot be transferred to a new ordinal sequence, thus arguing for an integrated representation. Others have observed temporal transfer across movement sequences and have advocated an independent representation of temporal information. Using a modified serial reaction time task, we tested alternative models of the representation of temporal structure and the interaction between the output of separate ordinal and temporal sequence representations. Temporal transfer depended on whether a novel ordinal sequence was fixed within each test block. Our results confirm the presence of an independent representation of temporal structure and advocate a nonlinear multiplicative neural interaction of temporal and ordinal signals in the production of movements.

skilled motor behaviors require precisely timed patterns of muscle activation. Pianists coordinate finger and arm movements to achieve a desired rhythm, loudness, and pitch. In our daily life, we coordinate articulatory effectors to produce speech or different body parts while performing sports activities such as swimming. How does the nervous system store such skilled movement sequences?

One possibility is that the next movement in a sequence is issued depending on the current state estimate of the body (Diedrichsen et al. 2010), e.g., a specific configuration of the limbs. Timing would therefore be inseparable from the movements performed, an emergent property of the state of the system, not represented by a dedicated mechanism (Shin and Ivry 2002; Spencer et al. 2009; Conditt and Mussa-Ivaldi 1999). Evidence for this comes from serial reaction time tasks (SRTT), in which participants respond with movements (typically finger movements) to instructive visual cues presented according to a specific sequence. The difference in response times between sequential and random phases (Robertson 2007) indicates learning of the sequence of digit movements (here referred to in short as order). Several studies have shown that the temporal structure (timing) of a trained finger sequence cannot be transferred to a new or random order of movements (Shin and Ivry 2002; O'Reilly et al. 2008). This would argue that the temporal and ordinal structure of sequential movements is indeed stored as an integrated (combined) representation of these parameters.

Alternatively, timing may be stored independently of the order of the movements that it was combined with during training. The defining criterion for an independent (as opposed to a combined) temporal representation is that trained timing can produce performance advantages in the context of a new ordinal sequence of movements. Such training-related transfer effects have been observed and in noncued sequence production tasks (Ullen and Bengtsson 2003). Here participants were able to learn and transfer trained timing to a new sequence of key presses. The new movement sequence, with which the trained timing was tested, became quickly familiar, since subjects pressed just one key or produced the same sequence repeatedly. These results suggests that the nervous system stores a temporal representation independently of movement order and can, under certain circumstances, transfer this temporal representation to novel sequences of motor commands.

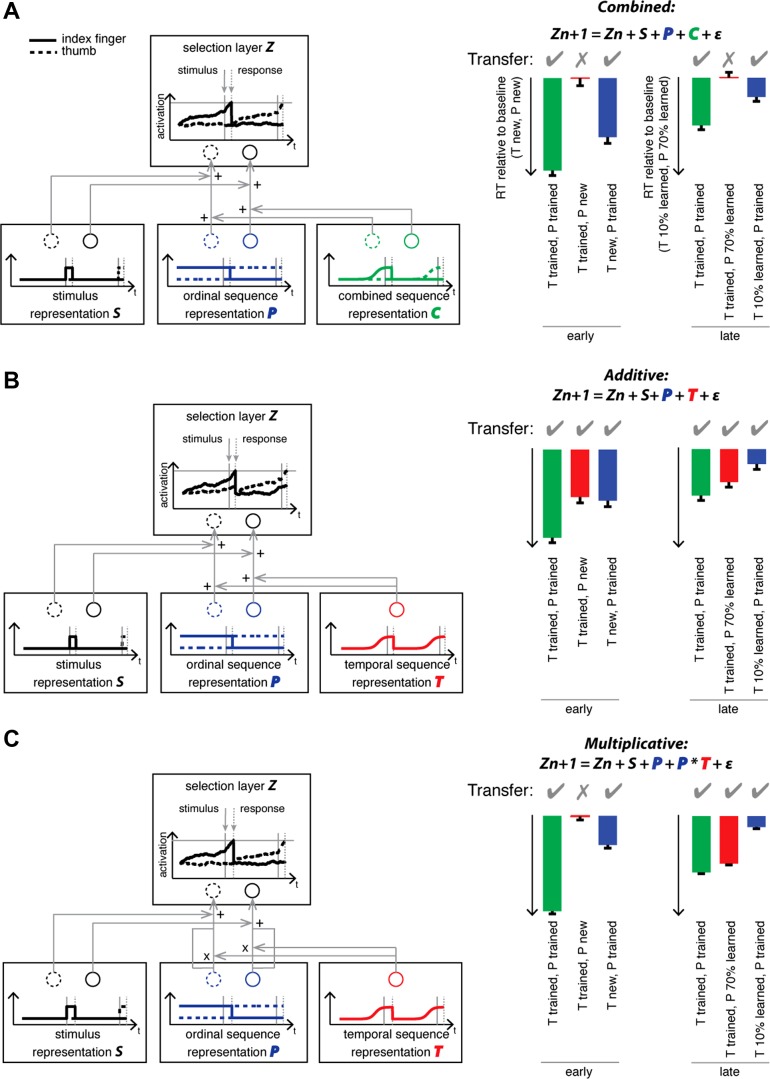
How can then the failure to find evidence for independent temporal representation in some SRTT tasks be explained? Here we address this question by examining how independent ordinal and temporal representations interact during movement production. The three possible types of interactions can be illustrated using a drift-diffusion model of sequential action selection (Ratcliff 1978; Ratcliff and McKoon 2007) (Fig. 1; for details, cf. materials and methods). The output stage of the model is a selection layer with one unit for each finger (Z). Once a unit reaches a fixed threshold, the corresponding finger response is executed.

Fig. 1.

Alternative hypotheses of the interaction between ordinal and temporal representations in a timed serial reaction time task (SRTT) and its implications for transfer of the trained temporal sequence. At the beginning of learning, the motor commands are exclusively triggered by a sequence of cues (illustrated for index followed by thumb) through a learned stimulus-response association S (imperative cue: finger mapping). This layer triggers activity in the corresponding unit of the selection layer Z, which in turn issues a correct response when the activation reaches threshold. With learning, the motor system acquires a representation of the ordinal sequence of finger movements P that predicts the next response in form of a tonic preactivation of the effector, which is sent to the corresponding unit in the selection layer. A: combined model: Furthermore, the nervous system is hypothesized to acquire a combined sequence representation C, which contains a more precisely timed ordinal representation, that phasically increases the predicted unit just before the expected times of cue onset (left). Since the timing of movements is bound to the learned order of movements, no transfer [reaction time (RT) advantage to baseline] of temporal structure can occur when the latter is tested with a new ordinal structure (right). B: additive model: an independent representation of the temporal sequence is acquired that sends phasic signals to all the units just before the expected times of cue onset (left). Temporal structure would be transferrable to a new order of movements (right) even when the ordinal structure with which it is recombined is completely unknown. C: multiplicative model: An independent representation of temporal structure is acquired, that is integrated with the ordinal signal multiplicatively, before it is propagated to the selection layer. Transfer can only occur once the ordinal structure with which it is paired is partly learned (right, late transfer phase), because the temporal representation can only take effect on preactivated units.

At the beginning of SRTT learning, the activity of the selection units is driven solely by the stimulus representation S (reactive responses). However, behavioral and neurophysiological findings suggest that with learning of movement sequences an ordinal representation P of the sequence is formed (Shima and Tanji 1998; Shin and Ivry 2003; Ullen and Bengtsson 2003; O'Reilly et al. 2008). Because this ordinal representation can be learned independent of the temporal structure, it is modeled here by tonically preactivating the next expected unit, as soon as the preceding response is made, e.g., first the index finger, then the thumb, etc. When the signal from the stimulus representation is added to the selection layer, the corresponding unit is already closer to threshold, which leads to faster reaction times (RTs) than before learning.

Associating a specific movement order to a specific temporal structure has been shown to produce RT advantages compared with a movement order with a changing temporal structure (Shin and Ivry 2002; O'Reilly et al. 2008). For learning of temporal structure, we consider three possible architectures. One possibility is that a temporal representation T may be stored together with a particular ordinal structure, effectively amounting to another more precisely timed ordinal representation (combined representation, Fig. 1A). In addition to tonically preactivating the next expected unit, it would phasically boost the next unit at an expected point of cue onset leading to faster RT on top of a merely ordinal representation. The timing of movements would consequently be bound to that specific order of movements.

Alternatively, a representation of temporal structure may be formed that is independent of the movements with which it is performed. Such a representation would send phasic signals to all the units to boost motor activity, just before the expected time of cue onset. Consequently, the temporal structure would be transferrable to a new order of movements. This independent temporal representation may influence the selection layer in two ways: In the additive model (Fig. 1B), the activation would combine linearly with the activation coming from the ordinal layer. As a consequence, the independent temporal representation would lead to performance advantages even if the ordinal signal were at zero (no ordinal prediction), since the temporal signal is added to all units and therefore facilitates all responses. In contrast, if the temporal signal combines with the ordinal signal multiplicatively (Fig. 1C), then it would lead only to performance advantages once the new ordinal representation has been formed, since the temporal signal boosts only units that are preactivated by the ordinal representation.

We designed a modified SRTT to identify the type of interaction between temporal and ordinal representations during movement production. Subjects were trained on a particular combination of temporal and ordinal sequence of finger presses by reacting to digits presented on the screen. In the test phase, we tested transfer of learning by recombining the trained temporal and ordinal sequence with a new ordinal and temporal sequence, respectively (Fig. 2B), and measuring the RT advantage compared with a baseline condition that has a new temporal and ordinal structure. Importantly, we introduced conditions in which the test phase allows for learning of the new dimensions through repetition of the sequence (“early phase”: trials 1–3; “late phase”: trials 8–10 of each test block). If ordinal and temporal sequences were completely integrated (combined representation), we should see no transfer, neither in the early phase nor in the later phase when the new order has become familiar (Fig. 1A, right). Alternatively, if the temporal sequence representation were independent of the ordinal representation and interacted additively with the latter, temporal transfer should be observed immediately in the early transfer phase (Fig. 1B). Finally, if ordinal and temporal sequence representations interacted multiplicatively, we should find transfer of order but no transfer of timing in the early phase. Temporal transfer should emerge towards the late phase once the new ordinal structure has become familiar through repetition (Fig. 1C, experiment 1). Likewise, it should not be manifest in conditions in which the order of finger presses is random on every trial, since learning of the new sequence is not possible (experiment 2).

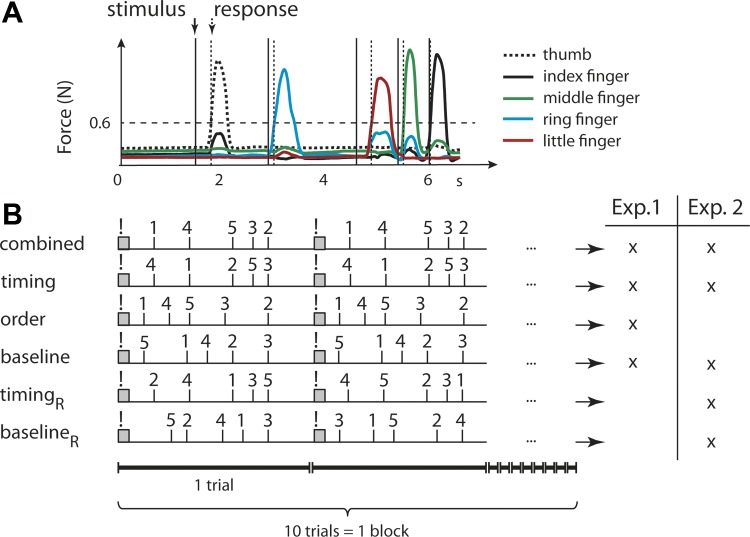
Fig. 2.

Task design. A: subjects performed a SRTT by producing a force press with the selected finger of the right hand as fast and accurately as possible after a visual presentation of an imperative stimulus (e.g., “4” ring finger). Cues were separated by a specific sequence of inter-stimulus-intervals. Reaction time was defined as force exceeding 0.6 N both for online feedback and data analysis. B: after training (200 trials) on the combination of a specific sequence of finger presses and temporal intervals, participants were tested on different condition in blocks of 10 trials each. In experiment 1, subjects were tested on the trained sequence (combined), on the trained temporal sequence combined with a new ordinal sequence (timing), on the trained ordinal sequence combined with a new temporal sequence (order), as well as on new ordinal and temporal sequence (baseline). In all these conditions, the sequence stayed the same for a block of 10 trials. In experiment 2 subjects were also tested on the trained temporal sequence combined with a random finger order (timing_R) and on a random temporal sequence combined with a random ordinal sequence (baseline_R). The order condition was not tested in the latter.

MATERIALS AND METHODS

Subjects.

Sixteen neurologically healthy volunteers (8 female, mean age: 25, SD: 3.1) participated in experiment 1 and 15 in experiment 2 (7 female, mean age: 21.8, SD: 1.5). There was no overlap in subjects between the two experiments. All subjects were right-handed according to the Edinburgh Inventory of Manual Preference (Oldfield 1971). None of them were professional musicians. All subjects were naïve concerning the hypothesis of this study. The University College London Ethics Committee approved experimental and consent procedures.

Stimuli and task.

We implemented a modified version of the SRTT (Nissen and Bullemer 1987; Penhune and Steele 2012). Subjects were seated in front of a computer screen with the five fingers of their right hand placed on a keyboard. Each key had a small groove into which a fingertip could be placed. The transducer underneath each key measured the force of individual fingers. An individually adjustable chin rest was provided for comfort. Subjects were presented with a sequence of white digits (1–5) in the middle of a black screen. The digits 1, 2, 3, 4, and 5 instructed to press the thumb, index, middle, ring, and little finger of the right hand, respectively. They were instructed to perform the task as fast and accurately as possible. Each trial started with a warning cue (“!”; duration: 400 ms). It was followed by a sequence of five digits that was timed according to a sequence of five possible interstimulus interval (ISI) values (600, 800, 1,000, 1,400, and 1,700 ms). The first ISI commenced when the warning cue disappeared. Digits remained on the screen until the onset of the next digit or for 600 ms after the last digit, respectively. In contrast to a classical SRTT, each trial consisted only of one sequence cycle, starting with the warning cue. The trial duration was 6.5 s, and the ISI was 7.3 s (0.8-s gap between trials). Subjects received feedback on their performance throughout the experiment as follows: if the subjects pressed the correct button within the limits of 50 ms before the onset of the current and 50 ms before the onset of the next digit, that digit turned green. If the response was too early, the next digit appeared in yellow. If the response was too late, the digit turned turquoise. If the finger press was incorrect, the digit turned red. Subjects received a point only when all digits in a sequence turned green, i.e., when they pressed the right finger at the right moment.

Movements were instructed by sequences with a particular combination of digit order and timing (ISI sequence). Digit runs or triplets (e.g., 2–3–4) were excluded from the pool of possible sequences. Identical triplets across sequences were prohibited. The sequences for each subject were randomly generated according to these criteria.

Both experiments 1 and 2 consisted of training and subsequent test phase. The training phase consisted of 20 blocks with 10 trials each. During this phase, the subjects were trained to produce a sequence of finger presses (here simply referred to as order), in combination with a particular sequence of ISIs (here referred to as timing; cf. Fig. 2). Subjects were not informed of the separation between training and test phase. However, most subjects reported that they noticed changes to the order and timing of the sequences in the experiment. When asked whether they noticed anything particular about the sequences right after the completion of the experiment, 12 of 16 subjects in experiment 1 reported that a sequence has been repeated at the beginning of the experiment, with 8 subjects specifically pointing out that the finger order was changed and 8 subjects pointing out that the timing changed occasionally. 11 of 15 subjects in experiment 2 reported that a sequence has been repeated in the training phase, with 5 subjects specifically pointing out that the finger order changed and 5 subjects pointing out that the timing changed occasionally.

Experiment 1 served to quantify transfer of the learned temporal sequence, and the learned ordinal sequence. Therefore, the test phase of experiment 1 consisted of 12 blocks of 10 trials, with three blocks in each of the four conditions: In the combined condition, subjects produced the trained sequence, using the same order and timing (Fig. 2). In the timing condition, the cues appeared with the same temporal intervals but indicated a different order of finger presses. The new order was different in each of the three timing blocks but was repeated across the ten trials of each block. In the order condition, the same sequence of finger presses as the training phase was cued but in combination with a new sequence of ISIs. The new temporal sequence was different in each of the three order blocks but did not change across the ten trials of each block. Finally, the baseline condition cued a sequence of finger presses and ISIs that was different from any other trained or tested condition. Again, the novel combination of finger and temporal sequence was different in each of the three baseline blocks but was repeated across the ten trials of each block. This condition served as an individual baseline to estimate the transfer of a combined, timing, and order representation. The condition with which the test phase started was counterbalanced across 16 subjects as follows: 1, 2, 3, 4; 2, 3, 4, 1; 3, 4, 1, 2; 4, 1, 2, 3 (1, combined; 2, timing; 3, order; 4, baseline).

Experiment 2 served to contrast two temporal transfer conditions, in which the trained temporal sequence was paired with a new finger sequence that either was or was not repeated across trials in a test block. Training was the same as in experiment 1. After the training phase subjects were tested on five conditions, with three blocks in each condition. Accordingly, the test phase in experiment 2 consisted of 15 blocks. The condition with which the test phase started was counterbalanced across subjects. The five conditions were as follows: The combined, timing, and baseline conditions were the same as in experiment 1. Here the respective sequence was repeated across all 10 trials of each block (cf. above). Importantly, we also introduced a condition with fixed timing and random order (timing_R). Here the order changed on every single trial, rather than on every block. As a baseline for this condition, we also tested a condition in which both timing and order were random on each trial (baseline_R). Each new repeated or random sequence contained an ordinal or temporal sequence that subjects did not encounter before. The condition with which the test phase started was counterbalanced across 15 subjects as follows: 1, 2, 3, 4, 5; 2, 3, 4, 5, 1; 3, 4, 5, 1, 2; 4, 5, 1, 2, 3; 5, 1, 2, 3, 4 (1, combined; 2, timing; 3, baseline; 4, timing_R; 5, baseline_R).

Data analysis.

Data analysis and simulations were conducted using Matlab (The Mathworks). RTs for each response were defined as time at which the force of a finger exceeded 0.6 N. Only correct responses were considered. Also, responses that occurred >100 ms before stimulus onset or >600 ms after stimulus onset were considered as errors and excluded from further analysis. For each trial, we averaged the RT for all correct responses. We then used the median RT for each individual and condition in the group analysis.

Preplanned one-tailed paired-samples t-tests were calculated to assess RT savings (decreases) of the different conditions with respect to baseline. Bonferroni corrections were applied to adjust the P level for multiple comparisons. Overall differences of combined, timing, and order against baseline conditions were corrected for three comparisons (p = p_uncorrected * 3). Early and late test phase differences of these conditions against baseline were corrected for six comparisons (p = p_uncorrected * 6), respectively. A repeated-measures ANOVA was calculated in SPSS Statistics (Version 20) to test for an interaction between condition (timing and order transfer) and test phase (early and late).

In addition, error rates (%correct trials) in early and late test phases were calculated to evaluate the possibility that RT differences amount to different speed-accuracy strategies.

Drift-diffusion model.

Activity in the five units of the selection layer Z corresponding to fingers was modeled for each stimulus-response event in time steps of 1 ms (as an example only thumb and index finger activity is displayed in Fig. 1). Each unit received input from the visual signal (S), the ordinal (P), and either the temporal (T) or the combined (C) representation, depending on the model. The integration of these inputs determined the rate at which the unit approached the response threshold (100 arbitrary units). When one of the two finger units of the selection layer Z reached threshold, a response was triggered and the model was reset. The corresponding time point n relative to stimulus onset was defined as RT.

We compared three models of interaction between the temporal and ordinal representations. Note that the purpose of the model was to illustrate the qualitative differences in the predicted transfer and that these qualitative predictions are stable over a wide range of parameter setting. In the combined model (Fig. 1A), the temporal tuning was linked to a specific ordinal sequence. Each unit in the selection layer was updated as Z_n+1 = a * Z_n + S + b * P + b * C + ε.

In the additive model (Fig. 1B), the temporal representation was separate from the ordinal sequence and each unit was updated as Z_n+1 = a * Z_n + S + b * P + b * T + ε. Finally, in the multiplicative model (Fig. 1C), each unit was updated as Z_n+1 = a * Z_n + S + b * P + (P * T) + ε. Note that the ordinal sequence representation (sequence of finger presses) P was added to the activity in the selection layer in all three models based on previous findings that consistently show a representation of movement to be independent of the timing with which it is produced (cf. Introduction).

In all three models, the visual stimulus (S) was modeled as a step response, increasing from 0 to 1 on the cued finger at time step n = 500 ms. The ε was the Gaussian noise centered at 0 with constant variance σ² = 1. The ordinal representation provided predictive input specific to the anticipated finger, a step response increasing from 0 to 1 right after the completion of the previous response. Therefore, the ordinal input was tonic and did not contain a temporal representation. In contrast, the combined and the temporal representation increased linearly from 0 to 1 starting 100 ms before the stimulus onset to stimulus onset (phasic activation). In the combined representation, the output was specific to the upcoming finger in the trained sequence (Fig. 1A). In contrast, in the temporal representation, the output was unspecific to the finger and was sent to all fingers (Fig. 1, B and C). The forgetting rate a of Z was set to 0.99. The weights of the ordinal, the temporal, and the combined representations (b) were set at 0.1. These modulated the rate with which the activity in the selection layer approached the threshold.

The predicted RT (time point n at which activity reaches threshold) is plotted in corresponding bar graphs for 100 iterations of each stimulus-response event (Fig. 1, A–C, right), respectively. We considered the prediction of each model regarding savings in RT relative to a baseline condition (timing and order new) for conditions in which either timing, order, or both is preserved. The left part of the bar diagram (early transfer) predicts immediate transfer when the new dimension is introduced. The right part of the bar diagram (late transfer) predicts late transfer, once the new dimension has become more familiar after a few repeated executions of the test sequence.

The transfer of timing in the multiplicative model requires short-term learning of the new order to occur after a few repetitions. Previous findings suggest that a sequence of nine key presses can be learned within a couple of trials and faster than the temporal sequence (Ullén and Bengtsson 2003). In all three models, we therefore assumed that the ordinal representation was learned to 70%, whereas the temporal and combined representations were learned to 10% in the late phase. Since the new ordinal representation is acquired to 70% in the baseline, too, the RT savings of the order condition relative to baseline (new order, new timing) were predicted to decrease in the late transfer phase across the three alternative models.

RESULTS

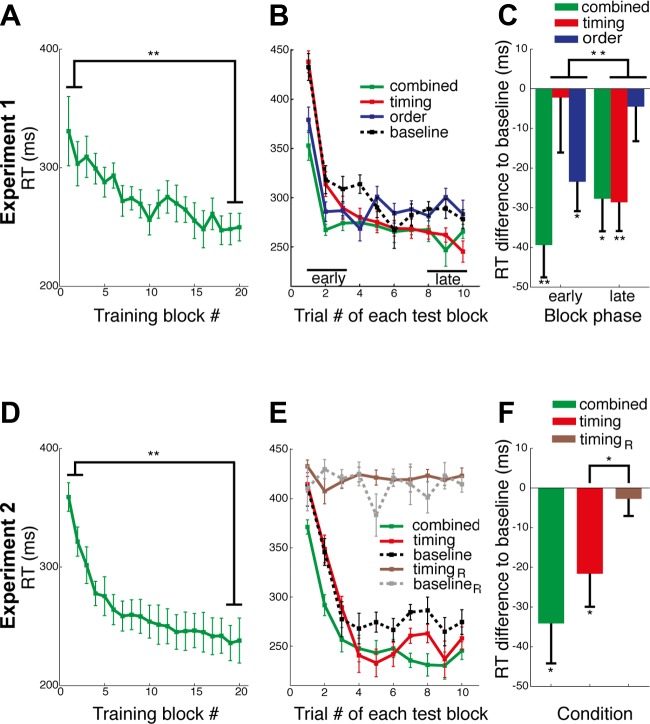
The RTs of the participants in the training phase of our experiments indicate that subjects learned the task and started to anticipate the correct finger at the correct time. To examine the effect of training, we tested the difference between the first two and the last two blocks of the training phase. In experiment 1 (Fig. 3A), subjects' RT significantly decreased from 310 ms (SE = 20) to 251 ms (SE = 11) [t(15) = 2.84, P = 0.006]. In experiment 2 (Fig. 3D), RT significantly decreased from 332 ms (SE = 11) to 240 ms (SE = 16) [t(14) = 5.14, P < 0.001]. At the end of training a substantial portion of the RTs were faster than 200 ms, indicating stimulus anticipation (Hick 1952).

Fig. 3.

RT results: reaction time decreased from the beginning to the end of training by around 100 ms in both experiments (A and D). Within each test block RT decreased when order and timing was repeated across trials (B and E) but remained on the same level when order or both timing and order were random (E). A significant decrease from baseline appeared in the timing condition, in particular in the late phase, after the test sequence has been repeated across each block (C and F). This decrease could not be observed when finger order changed on every trial (F). Error bars denote SE. *P < 0.05, **P < 0.01.

To evaluate whether subject acquired sequence specific knowledge through training, we compared the RT of the combined (timing and order trained) and the baseline (timing and order not trained) conditions. In experiment 1, the overall difference between combined (273 ms, SE = 10) and baseline (298 ms, SE = 12) was significant [t(15) = −4.512, P < 0.001, Bonferroni corrected]. This result could be replicated in experiment 2, in which combined (252 ms, SE = 17) had a significantly lower RT than baseline condition (286 ms, SE = 11) [t(14) = −3.392, P = 0.012, Bonferroni corrected; Fig. 3F]. This confirmed that subjects acquired knowledge of the trained sequence.

All three models predicted that the trained order of finger presses would be transferred to a new timing. In contrast, the models make divergent predictions regarding the transfer of timing. The combined model (Fig. 1A) predicts that timing transfer would not occur, since the temporal representation is bound to the specific sequence of finger presses with which it is learned (combined representation). In contrast, the additive model (Fig. 1B) predicts that the transfer of timing to a new order of finger presses will occur immediately, even though the order is not learned, and would persist in the late phase once the new order is acquired. Finally, the multiplicative model predicts that the timing would not be transferred when the order of finger presses is new but will emerge once the order of finger presses has become familiar.

Immediately at the beginning of each test block (trials 1–3), the timing condition showed only a benefit of 2 ms compared with baseline, where both timing and order were new but fixed throughout the respective block. In contrast, the condition with trained order and new temporal structure revealed a benefit of 23 ms compared with baseline [t(14) = −3.155, P = 0.018, Bonferroni corrected] relative to baseline. However, at the end of each test block (trials 8–10), this relationship reversed: the timing was 29 ms lower than the respective baseline [t(14) = −3.956, P = 0.006, Bonferroni corrected], whereas order exhibited only a nonsignificant decrease of 5 ms (Fig. 3, B and C). Transfer was computed by subtracting the individual baseline from the timing and order conditions, respectively. A repeated-measures ANOVA with the factors transfer (timing transfer, order transfer) by test phase (early: trials 1–3, late: trials 8–10) confirmed a significant interaction between the two factors [F(1,15) = 10.14, P = 0.006; Fig. 3C]. This result corroborated our hypothesis that in contrast to finger order the transfer of timing emerges only at a later stage, when the repetition of the new order allows the subjects to recombine the old timing with a new order.

These results also indicate that the ordinal sequence of movements is learned more quickly than the temporal sequence; indeed so quickly that it was completely learned within each block of 10 trials. On trials 8–10 of each block, the order condition was not significantly different from baseline [t(15) = −0.517, P = 0.306, one-tailed, uncorrected], and the temporal condition was not significantly different from the combination condition [t(15) = −0.119, P > 0.453, one-tailed, uncorrected, Fig. 3C]. This fast ordinal learning may be explained by the fact that the stimuli in the current task explicitly instructed the effectors by digits, thereby facilitating a conscious verbal strategy for the ordinal sequence as opposed to the temporal sequence. Indeed, subjects' reports indicate that they tended to be more aware of the ordinal as opposed to the temporal sequence during the task (Wilcoxon signed-rank test: Z = −1.89; P = 0.06; mean ordinal awareness: 1.68; and mean temporal awareness: 1.94; on a Likert scale of 1 always aware to 5 never aware). Nevertheless, the temporal structure of the sequences was equally task relevant, since subjects did not gain points if the pressed the corresponding finger to late or too early (cf. materials and methods).

In experiment 2, we attempted to replicate these findings, while simultaneously contrasting these within the same participants to the condition used by Shin and Ivry (2002) and O'Reilly et al. (2008), in which learned temporal structure was paired with a (pseudo)random sequence of finger presses. To replicate these results in our paradigm, we tested for transfer of learned timing to a pseudorandom order. We compared a baseline condition in which both timing and order were random on each trial (baseline_R) to a condition with trained timing and random order on each trial (timing_R). We also replicated the baseline condition, in which both timing and order were new but fixed across the test block, and the timing condition with trained timing and fixed new order from experiment 1.

As can be seen from Fig. 3F, the overall RTs in the timing condition were significantly different from baseline [t(14) = −2.592, P = 0.033, Bonferroni corrected], with a decrease in mean RT emerging in the second part of each test block (Fig. 3E). This replicated our results from experiment 1. In contrast, there was no significant difference between the timing_R and baseline_R conditions [t(14) = −0.64, P = 0.798, Bonferroni corrected], replicating the lack of significant RT costs associated with a random probe in the timing conditions (Shin and Ivry 2002; O'Reilly et al. 2008). Importantly, the transfer of the learned temporal structure in the timing condition (22 ms, SE = 8) was significantly stronger than the transfer in the timing_R condition (3 ms, SE = 4) [t(14) = −2.603, P = 0.01; Fig. 3F]. This finding again shows that an independent representation of timing can only be revealed when the trained temporal sequence is recombined with a new, stable, ordinal sequence.

DISCUSSION

To address divergent findings with regard to the representation of temporal structure in movement sequences, we hypothesized three alternative models regarding the representation of timing and the interaction of timing and order. The combined model hypothesized that temporal structure is bound to the ordinal structure of movements (finger sequence) with which it was acquired and when decoupled from this ordinal structure shows no savings relative to an untrained sequence. This model would be in accordance with previous SRTT studies (Shin and Ivry 2002; O'Reilly et al. 2008). In contrast, the additive model hypothesized that the temporal structure is represented independently of the ordinal structure of finger movements, increasing all eligible movement signals at specific points in time. Accordingly, a known temporal structure is expected to produce performance advantages even when paired with a new sequence of finger movements. Finally, a multiplicative model hypothesized that the nervous system acquires an effector-independent representation of temporal structure, but in contrast to the additive model its signals interact multiplicatively with the signals originating from the ordinal representation. Accordingly, timing signals from the temporal representation modulate only the expected ordinal structure and performance advantages of a trained temporal structure can only occur once the new ordinal structure becomes familiar but not when it is unknown.

We conducted two experiments in which we used a temporally structured serial reaction time task with visually cued responses. Our results offer strong support for the multiplicative model (Figs. 1C and 3). Towards the end of each test block (late transfer phase) that consisted of 10 sequence repetitions, shorter reaction times RT occurred when subjects produced a new order of finger movements with a timing that was previously trained, compared with a baseline in which both timing and order were new (experiments 1 and 2). In contrast, when the order changed on each trial and test block, the previously trained timing did not show any performance advantages (experiment 2). The latent temporal representation could be revealed because of the fast learning rate for the ordinal representation, which is in line with previous findings demonstrating that subjects learn order faster than timing (Ullén and Bengtsson 2003).

The RT findings did not amount to a change in strategy such as slowing down responses to be more accurate in the early phase or speeding up in the late phase while sacrificing fidelity in finger order of each timing test block. On the contrary, the error rate paralleled the RT results (Fig. 4): subjects made more errors in the early as opposed to the late phase of each timing test block in both experiments. This suggests that the reported RT findings reflect a true temporal transfer effect.

Fig. 4.

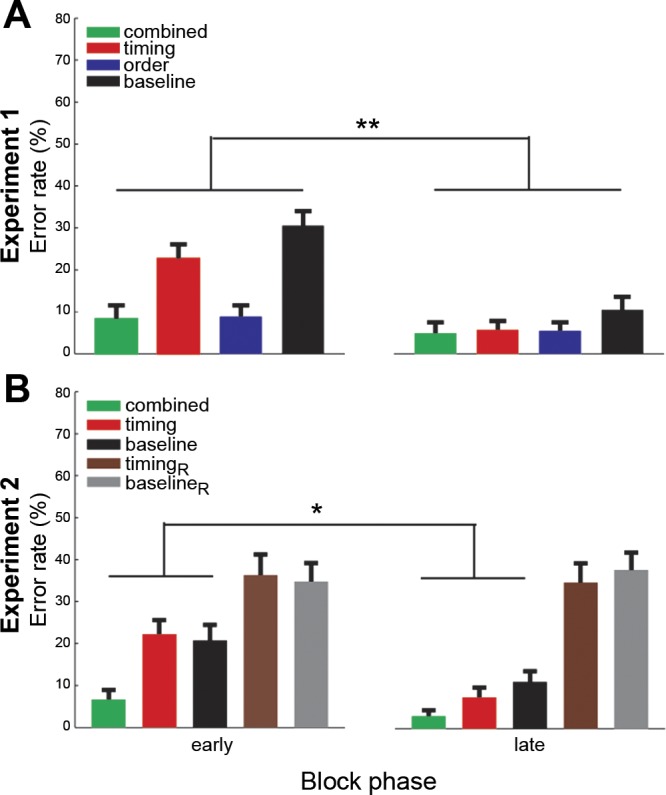
Error rate (%correct trials) in early and late phases of experiments 1 (A) and 2 (B) across subjects paralleled RT results. The error rate significantly decreased in the late compared with the early phases of experiment 1 [t(15) = 2.905, P = 0.005] and experiment 2 [t(14) = 2.092, P = 0.028]. This suggests that the reported RT findings do not amount to a change in strategy, slowing down responses to be more accurate in the early phase or speeding up in the late phase sacrificing fidelity in finger order, but reflect a learning-related transfer effect. *P < 0.05, **P < 0.01.

Our findings reconcile contradictory results from previous studies (Salidis 2001; Shin and Ivry 2002; Ullén and Bengtsson 2003; O'Reilly et al. 2008; Gobel et al. 2011) regarding the representation of timing in sequential finger movements. O'Reilly et al. (2008) specifically showed that the cost of changing the order was as high as changing both order and timing. We confirmed this result but could show that performance advantages emerge compared with baseline (where both timing and order changed) once subjects become familiar with the sequence of movements they have to perform. This demonstrates that the nervous system can acquire a temporal representation in a reaction time task and transfer it across different sequences of muscle commands, unlike previously suggested (Shin and Ivry 2002; O'Reilly et al. 2008). Notably, the above studies have also demonstrated that temporal learning does not occur unless timing is associated with a specific order in the first place. Indeed, the transfer in our study occurred after training of a temporal sequence in combination with a fixed finger order. Taken together, this suggests that the transferable temporal representation can only be acquired when initially linked to a specific movement order.

The current design differs from the SRTT in previous studies (Salidis 2001; Shin and Ivry 2002; O'Reilly et al. 2008) insofar as it employs shorter sequences and only one cycle of each sequence per trial. It is likely that this design led to more awareness of the ordinal and temporal structure than traditional SRTT designs. While our postexperimental questionnaire rating indeed suggests awareness of the ordinal and temporal sequential structure, within the same paradigm we were able to replicate both transfer and failure of transfer of temporal structure, as found with the more traditional SRTT tasks (Shin and Ivry 2002; O'Reilly et al. 2008). We therefore expect that our findings will generalize to more implicit versions of the task.

Our model assumes that with training of a finger sequence an ordinal representation of the sequence emerges, which tonically preactivates the next movement in the selection layer prior to the imperative cue. Electrophysiological measurements in the (pre)supplementary motor area (SMA) and the premotor cortex in monkeys have shown that after movement sequence training different neurons can become tuned to movement transitions or whole sequences (Mushiake et al. 1991; Shima and Tanji 2000). Activity in these neurons is upregulated during each interval between movements of a specific movement transition or preceding a specific movement sequence, respectively. This tonic preparation is in line with the neuronal activity increase reported in direction-selective premotor (but not primary motor) cortex during preparatory movement selection (Cisek and Kalaska 2005). Since the foreperiod varied randomly across trials (within a certain time range) in this study, this increase is likely to be driven by movement preparation alone.

Our results support the hypothesis that the nervous system also acquires an independent temporal representation of the trained sequence, which phasically boosts the tonic signals emitted from the ordinal representation at the predicted time of the visual cue. Neuroimaging studies have reported regions that may be associated with temporal sequence representation in movements (Ramnani and Passingham 2001; Bengtsson et al. 2004), i.e., premotor areas, superior temporal gyrus, and parts of the cerebellum. While there is no neurophysiological data on the production of timed finger sequences, direct stimulation of the circuitries enabling eye-blink conditioning tasks suggests that individual Purkinje cells can be trained to respond with temporal profiles adapted to a specific ISI between conditioned responses (Jirenhed and Hesslow 2011a,b). Towards the end of conditioning, Purkinje cells exhibit a decrease of simple spike activity in anticipation of the air-puff leading to an accurately timed response. However, it is not known whether Purkinje cells, similarly to cortical cells in the pre-SMA/SMA, can also code for certain transitions or whole sequences of temporal intervals or whether interval-specific coding can be utilized across effectors.

In our model, the temporal representation was specified as a phasic increase of activity briefly before the anticipated onset of the cue modulating the drift rate of the selection layer. Alternative ways may be employed to model the temporal representation. Instead of phasic increases suggested in our model, temporal information could be an amplitude-modulated version of the tonic ordinal representation with higher amplitude for shorter intervals between two movements. Crucially, however, adjusting the drift rate based on the position in the sequence would also imply that the nervous system has a representation of the temporal structure.

The multiplicative model can also be applied to studies of choice reaction time tasks. Of particular interest here are TMS studies. TMS can be taken to probe the excitability of units in the selection layer, since TMS pulses are delivered over motor regions with connections to the periphery via the corticospinal tract. Mars et al. (2007) and Van Den Hurk et al. (2007) demonstrated that knowledge about the effector can decrease RT and increase cortico-spinal excitability of the respective effector in the preparation phase (foreperiod). Since the duration of the foreperiod was random and the preparatory increase in excitability was prolonged, this effect reflects effector-specific preparation rather than temporal preparation, although the likelihood of target occurrence (hazard rate of elapsed time) may also play a role (Nobre et al. 2007).

In contrast, when the timing is known due to a fixed foreperiod, suppression of cortico-spinal excitability has been reported specifically for the precued effector (Touge et al. 1998; Davranche et al. 2007; Duque and Ivry 2009; Duque et al. 2012). The suppression becomes more prominent with proximity to the expected imperative cue, then turning into selective facilitation at imperative cue onset. Such a time-dependent modulation has been associated with faster RT, and it is likely to be related to temporal preparation to ensure that the response does occur at the correct point in time. Although our model does not assume that the temporal representation can provide inhibitory input to the selection layer, our hypothesis of a multiplicative interaction between temporal and ordinal signals is congruent with the finding that the inhibitory effects are especially pronounced for the precued effector.

Our findings did fail to show immediate transfer (early test phase) of the temporal sequence when a novel finger movement sequence is cued. This result appears at odds with the foreperiod effect observed in a choice-RT task (Bertelson and Boons 1960). This study has shown reaction times for fixed foreperiods even though the cued effector is not known during the foreperiod. As only two fingers have been task-relevant in the latter study, it is possible that both are activated to an equal extent and modulated similarly by the temporal signal in the expected fixed period condition. Both additive and a multiplicative integration of effector and timing interaction could explain this behavior and future studies should address whether the number of relevant effectors, as well as their sequential organization in time, modulate the interaction between temporal and effector representations.

Nonlinear multiplicative interaction between different representation is a common computational tool in the nervous system, such as during sensorimotor transformations in parietal neurons (Andersen et al. 1985; Pouget and Sejnowski 1997), auditory space localization in the subcortical auditory pathway (Peña and Konishi 2004), or the integration of multisensory input (Huston and Krapp 2009). On the level of a single neuron, multiplicative neural interaction may be achieved by a clustering of synapses at the dendritic tree (Koch and Segev 2000). Accordingly, if synapses cluster together on neighboring dendritic patches, they can cooperate in activating the local excitable dendritic channels, thereby elevating the firing probability of the respective neuron. Alternatively, a multiplicative interaction of timing and finger order could arise from neural units with linear summation of the input combined with an output nonlinearity (Dayan and Abbott 2001). Future studies should address how the nervous system represents and integrates temporal and ordinal sequential information for skilled movement.

In conclusion, our behavioral results reveal that sequential movement timing is represented independently of the sequence of muscle commands but modulates the motor output in a nonlinear multiplicative fashion.

GRANTS

This work was supported by the Marie Curie Initial Training Network “Cerebellar-cortical control: cells, circuits, computation, and clinic” and the Sir Henry Wellcome Postdoctoral Fellowship (098881/Z/12/Z).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: K.K. and J.D. conception and design of research; K.K. and A.S. performed experiments; K.K. and A.S. analyzed data; K.K., A.S., and J.D. interpreted results of experiments; K.K. prepared figures; K.K. drafted manuscript; K.K., A.S., and J.D. edited and revised manuscript; K.K., A.S., and J.D. approved final version of manuscript.