A method to find palindromes in nucleic acid sequences

Abstract

Various types of sequences in the human genome are known to play important roles in different aspects of genomic functioning. Among these sequences, palindromic nucleic acid sequences are one such type that have been studied in detail and found to influence a wide variety of genomic characteristics. For a nucleotide sequence to be considered as a palindrome, its complementary strand must read the same in the opposite direction. For example, both the strands i.e the strand going from 5' to 3' and its complementary strand from 3' to 5' must be complementary. A typical nucleotide palindromic sequence would be TATA (5' to 3') and its complimentary sequence from 3' to 5' would be ATAT. Thus, a new method has been developed using dynamic programming to fetch the palindromic nucleic acid sequences. The new method uses less memory and thereby it increases the overall speed and efficiency. The proposed method has been tested using the bacterial (3891 KB bases) and human chromosomal sequences (Chr-18: 74366 kb and Chr-Y: 25554 kb) and the computation time for finding the palindromic sequences is in milli seconds.

Background

A palindrome, in the literary sense, refers to a word or a phrase that reads the same in both directions, i.e when it is read in forward and reverse. One of the oldest palindromes known is the phrase “Sator arepo tenet opera rotas” which can roughly be translated to “The farmer uses a plough for his work” [1]. In the biological sense, however, a palindromic sequence is viewed in a slightly different manner. A palindromic sequence in a protein would be similar to one found in the English language, as the palindromic protein sequence would read the same in both directions. For example, AMMA is a typical palindrome in a protein sequence. However, categorizing a palindrome in a nucleic acid sequence (either DNA or RNA) is slightly different. In this case, both the strands i.e the strand going from 5' to 3' and its complementary strand from 3' to 5' must be checked for complementarity. For a nucleotide sequence to be considered as a palindrome, its complementary strand must read the same in the opposite direction [2]. For example, the sequence 5'-CGATCG-3' is considered a palindrome since its reverse complement 3'-GCTAGC-5' reads the same.

Palindromes can be exact or approximate. An exact palindrome is one in which there is no asymmetry in the centre or mismatch in any part of the sequence, such that its reverse compliment reads the same as the original sequence itself [3]. Inverted repeats are close cousins of palindromes. In inverted repeats a ‘spacer’ sequence, which is just a random stretch of nucleotides, exists in the middle of the palindromic sequence. As such, the sequence cannot be considered as a palindrome in the exact sense [4]. The importance of detecting such inverted repeats in both protein as well as nucleotide sequences and the methods used for the same has been elucidated before [5–7].

One important criterion to be taken into account while detecting palindromes in nucleic acid sequences is the fact that DNA palindromes are sometimes approximate i.e they contain spacers [8]. Evidence has shown that palindromes both with and without spacers have an influence on the evolutionary history of a protein. Apart from this, the presence of a large number of palindromes in the Y-chromosome is also an important characteristic that must be taken into consideration. Certain palindromes in the Y-chromosome have also been linked to sex-disorders [8]. Thus, an algorithm has been developed for the identification of these palindromes.

In a nucleic acid sequence, an exact palindrome is essentially even in length. This is because the middle base in a palindrome of odd length cannot be the same as its complement [9]. The proposed method locates all palindromic sequences that are present in a given nucleotide based on queries given by the user. A selection control statement in the form of a switch-case is used as the main basis for the user to give his or her preference. A generic flow chart is illustrated with an example (Figure 1). The subsequent section elucidates the approach taken by this algorithm.

Figure 1.

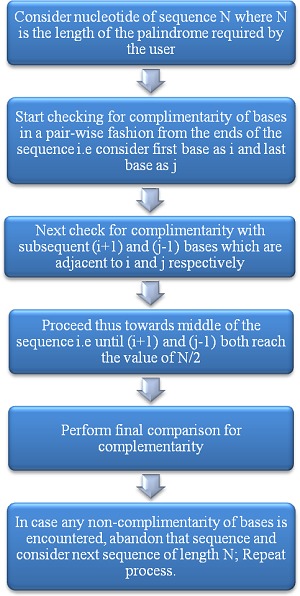
Representation of the method by which the proposed algorithm traverses a palindromic sequence.

Methodology

The linear time algorithmic approach has been used to identify the palindromes among the given nucleotide sequences. This approach will traverse the string from left to right and will find only exact palindromes and not palindromes that contain any mismatches in their sequence. The memory allocation is dynamic and four arguments are needed to be given as input while running this method.

Initially, the first argument given as input is the nucleotide sequence which is stored in FASTA format as a text file. The second argument refers to the length of the palindrome required by the user. A control statement in the form of a switch-case is used to enter the choices. This is indicated by the numbers 1 to 4. The first choice given by number 1 indicates that the user requires a palindromic sequence greater than or equal to a certain length. The length is then given as the fourth argument. The second choice denoted by number 2 signifies a request for a palindromic sequence lesser than or equal to a certain length which is again input as the 3rd argument. Choice 3 denotes a user request for a palindromic sequence that is between two lengths given as the 3rd and 4th arguments for lower and upper limit, respectively. In all the switch-case choices from 1 to 3, the 4th argument is given as zero. These options serve to enhance the flexibility of the algorithm.

Initial Scanning process:

For example, consider the sequence “S” (S=GAATTCXXXXCTTAAG) which has two palindromes from 1 to 6 and 11 to 16, respectively (Figure 1). Though the two sequences appear to be linear palindromes of each other, they are considered as two separate palindromic hits. During the initial scanning process, each nucleotide position is used as a starting point [i] and adjacent left and right side bases are checked for complementarity. For example, the scanning var [i] is at position 3 ‘A’ in the example sequence S, the loop iterates var [j] from 3 to 1 and var [k] from 4 to end of the sequence. Thus, we find the positions 3,4;2,5;1,6 are complementary (i.e GAATTC) and assign a var [flag] to 1, for future reference. The loop ends when a mismatch occurs. In this case, when the loop ends, the vars [j] and [k] hold the values 1 and 6, respectively. Furthermore, these values are stored in two separate vectors [startPOS] and [endPOS].

Identifying the maximum and minimum positions:

As mentioned above, when the var [flag] is equal to 1, the values of [j] and [k] are stored in vectors. From these vectors, the minimum and maximum values are identified and are assigned as previous start and end, respectively. After the first repeat region “GAATTC” is found, the previous start and end variables hold 1 and 6 respectively.

Finding new palindromes and printing the last one:

While finding new palindromes, the function prints the details of the previous one only if a new palindrome is identified lateron. In this case, the sequence “GAATTC” is a first hit. So, it will skip the condition that checks if the current j and k positions are different from the previous [startPOS] and [endPOS] values. However, when the second palindrome “CTTAAG” is encountered, the details of the previous sequence “GAATTC” will be printed. By that time, the values of j and k will be 11 and 16, and the values of the previous start and end will be 1 and 6. Here, the printing of the last palindrome becomes a problem; this has been fixed by using a type of basic sort function. This function will also be used when the input sequence contains only one palindrome. Here, the entire length of the input sequence [n] is scanned and checked to see if it is greater than the minimum length of the palindrome. If such be the case, the palindrome details are printed. So it would in effect run on quadratic-time.

Implementation:

The algorithm has been tested vigorously using platforms Windows 2000/XP and on Linux. The performance of the algorithm might vary to a minimal extent based on the configurations of the system it is run on. The algorithm was written and compiled using C++.

Results and Discussion

Case Study 1:

The efficiency of the proposed method is tested by using the genome of the bacterium Bacillus amyloliquefaciens which contains 3,918,589 bases and is 3.8MB in size. This bacterium is a gram positive, rod-shaped bacterium whose genome has a low G+C content. It contains the popular restriction endonuclease BamH1 which cleaves at a palindromic recognition site, GGATCC. In order to find out how many times this recognition site occurred in the genome of B. amyloliquefaciens, a query is given to search for palindromes between and including four and twenty bases in length. This was done so as to include the palindromic sequences where this recognition site was present as a substring. The upper limit of twenty was used since this recognition motif was not present in palindromes of length greater than twenty. The output obtained gives the starting and ending positions of the palindromic sequences. This is followed by the sequence itself. Finally, the length of the sequence is listed. The results obtained were analyzed and it is found that a total of 222,722 palindromes are present in the genome of B. amyloliquefaciens. Out of these, the palindromic recognition sequence is present 252 times. This was in concordance with the number of times this motif was present in the original FASTA sequence. This query took approximately 0.575 seconds real time to complete.

Case Study 2:

After removing low-complexity regions, the Y chromosome (human) sequence is found to be of size 25.0 MB and has a total of 25,653,966 bases. In order to obtain all possible palindromes in the Y chromosome, palindromes of size four and greater are queried since palindromes of length 3 or less are not biologically relevance in this context. From the output obtained, it is observed that the maximum palindrome in this chromosome is 86 bases long and resembles a tandem repeat consisting of A's and T's. There are two such palindromes present in the overall chromosome sequence. Apart from this, there are other large palindromes which also have AT repeats. These include two palindromes of length 62 and four of length 56. There are a total of 1979 palindromes which are similar to AT-rich tandem repeats.

Essentially, the longest exact palindromes in the Y chromosome are all found to be AT-rich repeats. The question then arises as to why the Y chromosome has such huge, seemingly meaningless palindromes. The answer lies in the Y 's quest for survival. The X chromosome has the ability to exchange genetic material with another X chromosome, thereby giving it the opportunity to correct any errors. However, the Y chromosome cannot engage in this kind of an exchange. Therefore, it adopts another mechanism for ensuring genetic robustness. A region on the Y chromosome called MSY (Male Specific Region) is responsible for coding for male characteristics. It was found that around 30% of the MSY regions showed greater than 99.9% similarity. This was attributed to a phenomenon called Y-Y gene conversion in which sequence information was exchanged between the different regions of the Y chromosome. These palindromes form a cruciform type structure, by which the genes contained in different parts of the palindrome come into contact and the Y chromosome is able to compare and check the genes for errors [10, 11]. As expected, most of the genes in the MSY, which are testis specific, are contained within 8 massive palindromes [10]. The output for the above given query was generated in 6.374 seconds real-time.

Case Study 3:

In human chromosome number 18 the low-complexity regions and interspersed repeats were removed from the sequence after which the sequence had a size of 72.6MB. This sequence was queried for all palindromes of size four and greater in order to find the decanucloetide regulatory motif TCTCGCGAGA. This motif is found in the HNRNKP (heterogenous nuclear ribonucleoproteins or hnRNPs) promoter protein and greatly enhances its activity. HNRNPK is an abundant protein factor found in the nucleus, cytoplasm, mitochondria and plasma membrane and co-ordinates several biological processes ranging from telomere biogenesis to DNA repair [10]. From the entire bacterial sequence, 70,674 palindromes of length 10 are obtained. Upon further analysis of these deca-palindromes, it was found that the regulatory motif occurred four times.

This is in concordance with the number of times this motif is found in the original sequence by in-vitro studies. HNRNPK is found in elevated levels in cancer cells and is believed to play a role in carcinogenesis. The proposed algorithm could be used to detect the location of this motif in the promoter sequence without having to worry about the issues that accompany in vitro studies. Further, the information obtained could be used while devising anti-cancer therapies. The output for the above mentioned query was generated in 8.157 seconds real-time.

Conclusion

The proposed method locates all palindromic sequences present in a given nucleotide sequence. Dynamic allocation of memory by using dynamic arrays increases the overall speed of the program as there is no large and cumbersome memory that needs to be managed. The program uses only the memory it needs to store the palindromes. This improves the overall efficiency and makes the algorithm more robust.

The source code of the algorithm may be obtained upon request to Prof. K. Sekar (sekar@physics.iisc.ernet.in and sekar@serc.iisc.ernet.in). The users are requested to cite this article whenever the algorithm or its implementation is used.

Conflict of interest

The authors declare that there is no conflict of interest.

Figure 2.

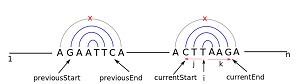
Schematic representation of the method by which the program identifies palindromes. Here [i] refers to the initial starting position. The variables [j] and [k] denote adjacent positions to the left and right respectively. currentStart and currentEnd refer to the current positions from where the search is starting. previousStart and previousEnd denote the starting and ending positions of the previous palindromic repeat.