An information-theoretic derivation of min-cut based clustering

Abstract

Min-cut clustering, based on minimizing one of two heuristic cost-functions proposed by Shi and Malik nearly a decade ago, has spawned tremendous research, both analytic and algorithmic, in the graph partitioning and image segmentation communities over the last decade. It is however unclear if these heuristics can be derived from a more general principle facilitating generalization to new problem settings. Motivated by an existing graph partitioning framework, we derive relationships between optimizing relevance information, as defined in the Information Bottleneck method, and the regularized cut in a K-partitioned graph. For fast-mixing graphs, we show that the cost functions introduced by Shi and Malik can be well approximated as the rate of loss of predictive information about the location of random walkers on the graph. For graphs drawn from a generative model designed to describe community structure, the optimal information-theoretic partition and the optimal min-cut partition are shown to be the same with high probability.

1 Introduction

MIN-CUT based graph partitioning has been used successfully to find clusters in networks, with applications in image segmentation as well as clustering biological and sociological networks. The central idea is to develop fast and efficient algorithms that optimally cut the edges between graph nodes, resulting in a separation of graph nodes into clusters. Particularly, since Shi and Malik successfully showed [1] that the average cut and the normalized cut (defined below) were useful heuristics to be optimized, there has been tremendous research in constructing the best normalized-cut-based cost function in the image segmentation community.

Additionally, several insightful works have focused on providing an interpretation and a justification for min-cut based clustering, within the framework of graph diffusion. Meila et al. [2] showed rigorous connections between normalized min-cut based clustering and the lumpability of the Markov chains underlying the corresponding discrete-diffusion operator. More recently, Lafon et al. [3] and Nadler et al. [4] showed the close relationship between the problem of spectral clustering and that of learning locality-preserving embeddings of data, using diffusion maps.

The Information Bottleneck (IB) method [5], [6] is a clustering technique, based on rate-distortion theory [7], that has been successfully applied in a wide variety of contexts including clustering word documents and gene-expression profiles [8]. The IB method is also capable of learning clusters in graphs and has been used successfully for synthetic and natural networks [9]. In the hard clustering case, given the diffusive probability distribution over a graph, IB optimally assigns probability distributions, associated with nodes, into distinct groups. These assignment rules define a separation of the graph nodes into clusters.

We here illustrate how minimizing the two cut-based heuristics introduced by Shi and Malik can be well-approximated by the rate of loss of relevance information, defined in the IB method applied to clustering graphs. To establish these relations, we must first define the graphs to be partitioned; we assume hard-clustering and the cluster cardinality to be K. We show, numerically, that maximizing mutual information and minimizing regularized cut amount to the same partition with high probability, for more modular 32-node graphs, where modularity is defined by the probability of inter-cluster edge connections in the Stochastic Block Model for graphs (See NUMERICAL EXPERIMENTS). We also show that the optimization goal of maximizing relevance information is equivalent to minimizing the regularized cut for 16-node graphs.¹

2 The Min-Cut Problem

Following [10], for an undirected, unweighted graph $\mathcal{G}=\left(V,E\right)$ with n nodes and m edges, represented² by its adjacency matrix A := {A_xy = 1 ⇔ x ~ y}, we define for two not necessarily disjoint sets of nodes V₊, V₋ ⊆ V, the association

$$W({\mathbf{V}}_{+},{\mathbf{V}}_{-})=\sum _{x\in {\mathbf{V}}_{+},y\in {\mathbf{V}}_{-}}{A}_{xy}$$ (2.1)

We define a bisection of V into V_± if V₊ ∪ V₋ = V and V₊ ∩ V₋ = ∅. For a bisection of V into V₊ and V₋, the `cut' is defined as c(V₊, V₋) = W (V₊, V₋). We also quantify the size of a set V₊ ⊆ V in terms of the number of nodes in the set V₊ or the number of edges with at least one node in the set V₊:

$$\begin{array}{cc}\hfill \omega \left({\mathbf{V}}_{+}\right)& =\sum _{x\in {\mathbf{V}}_{+}}1\hfill \\ \hfill \Omega \left({\mathbf{V}}_{+}\right)& =\sum _{x\in {\mathbf{V}}_{+}}{d}_x,\hfill \end{array}$$ (2.2)

where d_x is the degree of node x.

Shi and Malik [1] defined a pair of regularized cuts, for a bisection of V into V₊ and V₋; the average cut was defined as

$$\mathcal{A}=\frac{W({\mathbf{V}}_{+},{\mathbf{V}}_{-})}{\omega \left({\mathbf{V}}_{+}\right)}+\frac{W({\mathbf{V}}_{+},{\mathbf{V}}_{-})}{\omega \left({\mathbf{V}}_{-}\right)}$$ (2.3)

and the normalized cut was defined as

$$\mathcal{N}=\frac{W({\mathbf{V}}_{+},{\mathbf{V}}_{-})}{\Omega \left({\mathbf{V}}_{+}\right)}+\frac{W({\mathbf{V}}_{+},{\mathbf{V}}_{-})}{\Omega \left({\mathbf{V}}_{-}\right)}.$$ (2.4)

This definition can be generalized, for a K-partition of V into V₁, V₂, …, V_K [10], to

$$\mathcal{A}=\sum _j\frac{W({\mathbf{V}}_j,{\stackrel{‒}{V}}_j)}{\omega \left({\mathbf{V}}_j\right)}$$ (2.5)

$$\mathcal{N}=\sum _j\frac{W({\mathbf{V}}_j,{\stackrel{‒}{V}}_j)}{\Omega \left({\mathbf{V}}_j\right)}$$ (2.6)

where ${\stackrel{‒}{\mathbf{V}}}_j=\mathbf{V}{\mathbf{V}}_j$ .

For the graph $\mathcal{G}$, we can define the graph Laplacian Δ = D − A where D is a diagonal matrix of vertex degrees. For a bisection of V, we also define the partition indicator vector h [11]

$$h_x=\{\begin{array}{cc}+1\hfill & {\forall }_x\in {\mathbf{V}}_{+}\hfill \\ -1\hfill & {\forall }_x\in {\mathbf{V}}_{-}.\hfill \end{array}\phantom{\}}$$ (2.7)

Specifying two `prior' probability distributions over the set of nodes V : (i) p(x) ∝ 1 and (ii) p(x) ∝ d_x, we then define the average of h to be

$$\begin{array}{cc}\hfill \stackrel{‒}{h}& =\frac{{\Sigma }_{x\in \mathbf{V}}{h}_x}{n}\hfill \\ \hfill \langle \mathbf{h}\rangle & =\frac{{\Sigma }_{x\in \mathbf{V}}{d}_x{h}_x}{2m}.\hfill \end{array}$$ (2.8)

The cut, as defined by Fiedler [11], and the regularized cuts, as defined by Shi and Malik [1], can then be written in terms of h as (See Appendix A)

$$\begin{array}{cc}\hfill \mathcal{c}& =\frac{1}{4}{h}^T\text{Δ}\mathbf{h}\hfill \\ \hfill \mathcal{A}& =\frac{1}{n}\frac{h^T\text{Δ}\mathbf{h}}{1-{\mathbf{h}}^{-2}}\hfill \\ \hfill \mathcal{N}& =\frac{1}{2m}\frac{h^T\text{Δ}\mathbf{h}}{1-{\langle \mathbf{h}\rangle }^2}.\hfill \end{array}$$ (2.9)

More generally, for a K-partition, we define the partition indicator matrix Q as

$$Q_{zx}\equiv p(z\mid x)=1{\forall }_x\in z$$ (2.10)

where z ∈ {V₁, V₂, …, V_K and define P as a diagonal matrix of thew `prior' probability distribution over the nodes. The regularized cut can then be generalized as

$$\mathcal{C}=\sum _j\frac{{\left[\mathrm{Q}\text{Δ}{\mathrm{Q}}^{\mathbf{T}}\right]}_{jj}}{{\left[{\mathrm{QPQ}}^{\mathbf{T}}\right]}_{jj}}$$ (2.11)

where for $p\left(x\right)\propto 1,\mathcal{C}=\mathcal{A}$; and for $p\left(x\right)\propto d_x,\mathcal{C}=\mathcal{N}$.

Inferring the optimal h (or Q) however, has been shown to be an NP-hard combinatorial optimization problem [12].

3 Information Bottleneck

Rate-distortion theory, which provides the foundations for lossy data compression, formulates clustering in terms of a compression problem; it determines the code with minimum average length such that information can be transmitted without exceeding some specified distortion. Here, the model-complexity, or rate, is measured by the mutual information between the data and their representative codewords (average number of bits used to store a data point). Simpler models correspond to smaller rates but typically suffer from relatively high distortion. The distortion measure, which can be identified with loss functions, usually depends on the problem; in the simplest of cases, it is the variance of the difference between an example and its cluster representative.

The Information Bottleneck (IB) method [6] proposes the use of mutual information as a natural distortion measure. In this method, the data are compressed into clusters while maximizing the amount of information that the `cluster representation' preserves about some specified relevance variable.<sup>3</sup> For example, in clustering word documents, one could use the `topic' of a document as the relevance variable.

For a graph $\mathcal{G}$, let X be a random variable over graph nodes, Y be the relevance variable and Z be the random variable over clusters. Graph partitioning using the IB method [9] learns a probabilistic cluster assignment function p(z|x) which gives the probability that a given node x belongs to cluster z. The optimal p(z|x) minimizes the mutual information between X and Z, while minimizing the loss of predictive information between Z and Y . This complexity-fidelity trade-off can be expressed in terms of a functional to be minimized

$$\mathcal{F}\left[p(z\mid x)\right]=-I[Y;Z]+TI[X;Z]$$ (3.1)

where the temperature T parameterizes the relative importance of precision over complexity. As T → 0, we reach the `hard clustering' limit where each node is assigned with unit probability to one cluster (i.e. p(z|x) ∈ {0, 1}).

Graph clustering, as formulated in terms of the IB method, requires a joint distribution p(y, x) to be defined on the graph; we use the distribution given by continuous-time graph diffusion⁴ as it naturally captures topological information about the network [9]. The relevance variable Y then ranges over the nodes of the graph and is defined as the node at which a random walker ends at time t if the random walker starts at node x at time 0. For continuous-time diffusion, the conditional distribution p(y|x) is given as

$$G_{yx}^t=p(y\mid x)={\left[e^{-t\text{Δ}{\mathbf{P}}^{-1}}\right]}_{yx}$$ (3.2)

where Δ is the positive semi-definite graph Laplacian and P is a diagonal matrix of the prior distribution over the graph nodes, as described earlier. Note that the diagonal matrix P can be any prior distribution over the graph nodes. The characteristic diffusion time scale τ of the system is given by the inverse of the smallest non-zero eigenvalue of the diffusion operator exponent ΔP⁻¹ and characterizes the slowest decaying mode in the system. A more common convention for matrix operations in graph theory is to use left eigenvectors. However, since our analysis is within a probabilistic framework, we use right eigenvectors throughout this paper to conform to conventions used in probability theory (particularly with regard to conditional and marginal distributions).

To calculate the joint distribution p(y, x) from the conditional G^t, we must specify an initial or prior distribution⁵; we use the two different priors p(x), used in Eq. (2.8) to calculate $\stackrel{‒}{\mathbf{h}}$ and 〈h〉 : (i) p(x) ∝ 1 and (ii) p(x) ∝ d_x. Throughout this paper, time dependence needs to be considered only when the conditional distribution p(y|x) is replaced by the diffusion Green's function G; thus, time dependence will be explicitly denoted only once G is invoked.

4 Rate of Information Loss in Graph Diffusion

We analyze here the rate of loss of predictive information between the relevance variable Y and the cluster variable Z, during diffusion on a graph $\mathcal{G}$, after the graph nodes have been hard-partitioned into K clusters.

4.1 Well-mixed limit of graph diffusion

For a given partition Q of the graph, defined in Eq. (2.10), we approximate the mutual information I [Y ;Z] when diffusion on the graph reaches its well-mixed limit. We introduce the linear dependence η(y, z) such that

$$p(y,z)=p\left(y\right)p\left(z\right)(1+\eta ).$$ (4.1)

This implies 〈η〉_y = 〈η〉_z = 0 and 〈〈η〉_z〉_y = 〈η〉 where 〈〉 denote expectation over the joint distribution and 〈〉_y and 〈〉_z denote expection over the corresponding marginals.

In the well-mixed limit, we have |η| ⪡ 1. The predictive information (expressed in nats) can then be approximated as:

$$\begin{array}{cc}\hfill I[Y;Z]& =\langle \ln \frac{p(z,y)}{p\left(z\right)p\left(y\right)}\rangle \hfill \\ \hfill & ={\langle {\langle (1+\eta )\ln (1+\eta )\rangle }_y\rangle }_z\hfill \\ \hfill & \approx {\langle {\langle (1+\eta )(\eta -\frac{1}{2}{\eta }^2)\rangle }_y\rangle }_z\hfill \\ \hfill & \approx {\langle {\langle \eta +\frac{1}{2}{\eta }^2\rangle }_y\rangle }_z\hfill \\ \hfill & =\frac{1}{2}{\langle {\langle {\eta }^2\rangle }_y\rangle }_z\hfill \end{array}$$ (4.2)

$$\begin{array}{cc}\hfill & =\frac{1}{2}\sum _{y,z}p\left(y\right)p\left(z\right){\left(\frac{p(z,y)}{p\left(z\right)p\left(y\right)}-1\right)}^2\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{y,z}\frac{p{(y,z)}^2}{p\left(y\right)p\left(z\right)}-1\right)\equiv \iota .\hfill \end{array}$$ (4.3)

Here, we define ι as a first-order approximation to I [Y ;Z] in the well-mixed limit of graph diffusion. This quadratic approximation for I [Y ;Z] is known as the χ²-approximation.

Note that the joint and marginal distributions can also be related by the exponential dependence θ(y, z) defined by

$$p(y,z)=p\left(y\right)p\left(z\right)e^{\theta }.$$

Under this definition, the domain of the dependence is unbounded (i.e. $\theta \in \mathbb{R}$) and the mutual information is easily expressed as I [Y ;Z] = 〈θ〉. We also have

$$\sum _{i=1}^{\infty }\frac{{\langle {\theta }^i\rangle }_y}{i!}=\sum _{i=1}^{\infty }\frac{{\langle {\theta }^i\rangle }_z}{i!}=0.$$

However, in the well-mixed limit |θ| ⪡ 1, to first non-trivial order, θ ≈ η and the expression for I [Y ;Z] in terms of θ has the same form as Eq. (4.2).

We also have

$$\begin{array}{cc}\hfill \eta (y,z)& =\frac{p(z\mid y)}{p\left(z\right)}-1\hfill \\ \hfill & \le \frac{1}{p\left(z\right)}-1\hfill \\ \hfill & \le \underset{z}{\max }\left(\frac{1}{p\left(z\right)}\right)-1\hfill \\ \hfill \eta (y,z)& \le \underset{y}{\max }\left(\frac{1}{p\left(y\right)}\right)-1.\hfill \end{array}$$

$$\Rightarrow \eta (y,z)\le \min \left(\underset{z}{\max }\left(\frac{1}{p\left(z\right)}\right),\underset{y}{\max }\left(\frac{1}{p\left(y\right)}\right)\right)-1.$$ (4.4)

Thus, η(y, z) is bounded from below by −1 (by definition) and from above as shown in Eq. (4.4). However, θ(y, z) is unbounded and negatively divergent for short times. Since η is much better behaved than θ for short times, and for the sake of simplicity, we choose to use the linear dependence instead of the exponential dependence.

4.1.1 Well-mixed K-partitioned graph

As in the IB method, the Markov condition Z – X – Y allows us to make several simplifications for the conditional distributions and associated information theoretic measures. For a K-partition Q of the graph, we have

$$\begin{array}{cc}\hfill p(y,z)& =\sum _{x}p(x,y,z)\hfill \\ \hfill & =\sum _{x}p(z\mid y,x)p(y\mid x)p\left(x\right)\hfill \\ \hfill & =\sum _{x}p(z\mid x)p(y\mid x)p\left(x\right)\equiv {\mathbf{QPG}}^{t^{\mathbf{T}}}.\hfill \end{array}$$ (4.5)

$$\begin{array}{cc}\hfill p{(y,z)}^2& ={\left(\sum _{x}p(z\mid x)p(y\mid x)p\left(x\right)\right)}^2\hfill \\ \hfill & =\sum _{x,x\prime =1}^{n}p(z\mid x)p(y\mid x)p\left(x\right)p(z\mid x\prime )p(y\mid x\prime )p(x\prime )\hfill \\ \hfill & =\sum _{x,x\prime =1}^n{Q}_{zx}{G}_{yx}^t{P}_x{Q}_{zx\prime }{G}_{yx\prime }^t{P}_{x\prime }.\hfill \end{array}$$ (4.6)

$$\begin{array}{cc}\hfill p\left(z\right)& =\sum _{x}p(z\mid x)p\left(x\right)\hfill \\ \hfill & =\sum _x{Q}_{zx}{P}_x.\hfill \end{array}$$ (4.7)

Graph diffusion being a Markov process, we have ${\sum }_{y=1}^n{G}_{x^{\prime }y}^t{G}_{yx}^t=G_{x^{\prime }y}^{2t}$. Using this and Bayes rule $G_{yx}^t{P}_x=G_{xy}^t{P}_{y\prime }$, we have

$$\begin{array}{cc}\hfill \iota & =\frac{1}{2}\left(\sum _{y,z}\frac{{\Sigma }_{x,x\prime =1}^n{Q}_{zx}{G}_{yx}^t{P}_x{Q}_{zx\prime }{G}_{yx\prime }^t{P}_{x\prime }}{\left({\Sigma }_{x″}{Q}_{zx″}{P}_{x″}\right)P_y}-1\right)\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{y,z}\frac{{\Sigma }_{x,x\prime =1}^n{Q}_{zx}{Q}_{zx\prime }{P}_y{G}_{x\prime y}^t{G}_{yx}^t{P}_x}{\left({\Sigma }_{x″}{Q}_{zx″}{P}_{x″}\right)P_y}-1\right)\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{z=1}^K\frac{{\Sigma }_{x,x\prime =1}^n{Q}_{zx}{Q}_{zx\prime }\left({\Sigma }_{y=1}^n{G}_{x\prime y}^t{G}_{yx}^t\right)P_x}{\left({\Sigma }_{x″}{Q}_{zx″}{P}_{x″}\right)}-1\right)\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{z=1}^K\frac{{\Sigma }_{x,x\prime =1}^n{Q}_{zx}{Q}_{zx\prime }{G}_{x\prime x}^{2t}{P}_x}{\left({\Sigma }_{x″}{Q}_{zx″}{P}_{x″}\right)}-1\right).\hfill \end{array}$$ (4.8)

In the hard clustering case, Σ_xQ_zxP_x = p(z) = [QPQ^T]_zz and we have

$$\iota =\frac{1}{2}\left(\sum _{z=1}^K\frac{{\left[\mathbf{Q}\left({\mathbf{G}}^{2t}\mathbf{P}\right){\mathbf{Q}}^{\mathbf{T}}\right]}_{zz}}{{\left[\mathbf{Q}\mathbf{P}{\mathbf{Q}}^{\mathbf{T}}\right]}_{zz}}-1\right).$$ (4.9)

4.1.2 Well-mixed 2-partitioned graph

We can re-write ι as

$$\begin{array}{cc}\hfill \iota & =\frac{1}{2}{\langle {\langle {\eta }^2\rangle }_y\rangle }_z\hfill \\ \hfill & =\frac{1}{2}{\langle {\langle \frac{{(p(z\mid y)-p\left(z\right))}^2}{P{\left(z\right)}^2}\rangle }_z\rangle }_y.\hfill \end{array}$$ (4.10)

For a bisection h of the graph, z ∈ {+1, −1} and we have

$$p(z\mid x)=\frac{1}{2}(1\pm h_x)\equiv \frac{1}{2}(1+z{h}_x).$$ (4.11)

$$\begin{array}{cc}\hfill p(z\mid y)& =\frac{1}{p\left(y\right)}\sum _{x}p(z,y,x)\hfill \\ \hfill & =\frac{1}{p\left(y\right)}\sum _{x}p(z\mid x)p(y\mid x)p\left(x\right)\hfill \\ \hfill & =\frac{1}{2}\sum _x(1+z{h}_x)p(x\mid y)\hfill \\ \hfill & =\frac{1}{2}(1+z\langle \mathbf{h}\mid y\rangle ).\hfill \end{array}$$ (4.12)

$$\begin{array}{cc}\hfill p\left(z\right)& =\sum _{x}p(z,x)=\sum _{x}p(z\mid x)p\left(x\right)\hfill \\ \hfill & =\frac{1}{2}\sum _x(1+z{h}_x)p\left(x\right)\hfill \\ \hfill & =\frac{1}{2}(1+z\langle \mathbf{h}\rangle ).\hfill \end{array}$$ (4.13)

$$\begin{array}{cc}\hfill p(z\mid y)-p\left(z\right)& =\frac{1}{2}(1+z\langle \mathbf{h}\mid y\rangle )-\frac{1}{2}(1+z\langle \mathbf{h}\rangle )\hfill \\ \hfill & =\frac{1}{2}z(\langle \mathbf{h}\mid y\rangle -\langle \mathbf{h}\rangle ).\hfill \end{array}$$ (4.14)

We then have

$$\begin{array}{cc}\hfill {\langle \frac{{(p(z\mid y)-p\left(z\right))}^2}{p{\left(z\right)}^2}\rangle }_z& =\sum _{z=-1,1}\frac{\frac{1}{4}{(\langle \mathbf{h}\mid y\rangle -\langle \mathbf{h}\rangle )}^2}{\frac{1}{2}(1+z\langle \mathbf{h}\rangle )}\hfill \\ \hfill & =\frac{{(\langle \mathbf{h}\mid y\rangle -\langle \mathbf{h}\rangle )}^2}{2}\sum _{z=-1,1}\frac{1}{1+z\langle \mathbf{h}\rangle }\hfill \\ \hfill & =\frac{{(\langle \mathbf{h}\mid y\rangle -\langle \mathbf{h}\rangle )}^2}{1-{\langle \mathbf{h}\rangle }^2}.\hfill \end{array}$$ (4.15)

The mutual information I [Y ;Z] can then be approximated as

$$\begin{array}{cc}\hfill \iota & =\frac{1}{2}\frac{{\langle {(\langle \mathbf{h}\mid y\rangle -\langle \mathbf{h}\rangle )}^2\rangle }_y}{1-{\langle \mathbf{h}\rangle }^2}\hfill \\ \hfill & =\frac{1}{2}\frac{{\sigma }_y^2\left(\langle \mathbf{h}\mid y\rangle \right)}{1-{\langle \mathbf{h}\rangle }^2}.\hfill \end{array}$$ (4.16)

Using Bayes rule p(x|y)p(y) = p(y|x)p(x), we have

$$\langle \mathbf{h}\mid y\rangle =\sum _x{h}_{x}p(x\mid y)=\sum _x\frac{h_{x}p(y\mid x)p\left(x\right)}{p\left(y\right)}.$$ (4.17)

$$\begin{array}{cc}\hfill {\langle {\langle \mathbf{h}\mid y\rangle }^2\rangle }_y& =\sum _{y=1}^{n}p\left(y\right)\sum _{x,x\prime =1}^n{h}_x{h}_{x\prime }\frac{p(y\mid x)p\left(x\right)p(x\prime \mid y)}{p\left(y\right)}\hfill \\ \hfill & =\sum _{y=1}^n\sum _{x,x\prime =1}^n{h}_x{h}_{x\prime }p(x\prime \mid y)p(y\mid x)p\left(x\right).\hfill \end{array}$$ (4.18)

Again, graph diffusion being a Markov process,

$$\begin{array}{cc}\hfill {\langle {\langle \mathbf{h}\mid y\rangle }^2\rangle }_y& =\sum _{x,x\prime =1}^n{h}_x{h}_{x\prime }{p}^{2t}(x\prime \mid x)p\left(x\right)\hfill \\ \hfill & =\langle h_x{h}_{x\prime }\rangle 2t.\hfill \end{array}$$ (4.19)

Time dependence is explicitly denoted here to highlight the fact that diffusion on the graph is till time 2t. Substituting 〈h|y〉 in Eq. (4.16), we get

$$\begin{array}{cc}\hfill {\sigma }^2\left(\langle \mathbf{h}\mid y\rangle \right)& ={\langle {\langle \mathbf{h}\mid y\rangle }^2\rangle }_y-{\langle \mathbf{h}\rangle }^2\hfill \\ \hfill & ={\langle h_x{h}_{x\prime }\rangle }_{2t}-{\langle \mathbf{h}\rangle }^2.\hfill \end{array}$$ (4.20)

$$\iota =\frac{1}{2}\frac{{\langle h_x{h}_{x\prime }\rangle }_{2t}-{\langle \mathbf{h}\rangle }^2}{1-{\langle \mathbf{h}\rangle }^2}.$$ (4.21)

4.2 Fast-mixing graphs

When diffusion on a graph reaches its well-mixed limit in short times, we have G^2t ≈ I – 2tΔP⁻¹. Thus, for a K-partition of a graph

$$\begin{array}{cc}\hfill \mathbf{Q}\left({\mathbf{G}}^{2t}\mathbf{P}\right){\mathbf{Q}}^{\mathbf{T}}& \approx \mathbf{Q}(\mathbf{P}-2t\text{Δ}){\mathbf{Q}}^{\mathbf{T}}\hfill \\ \hfill & =\mathbf{Q}\mathbf{P}{\mathbf{Q}}^{\mathbf{T}}-2t\mathbf{Q}\text{Δ}{\mathbf{Q}}^{\mathbf{T}}.\hfill \end{array}$$ (4.22)

For bisections, the short-time approximation of 〈h_xh_x′〉2t can be written as

$$\begin{array}{cc}\hfill {\langle h_x{h}_{x\prime }\rangle }_{2t}& =\sum _{x,x\prime =1}^n{h}_{x\prime }{p}^{2t}(x\prime ,x)h_x\hfill \\ \hfill & ={\mathbf{h}}^{\mathbf{T}}{\mathbf{G}}^{2t}\mathbf{P}\mathbf{h}\hfill \\ \hfill & \approx {\mathbf{h}}^{\mathbf{T}}(I-2t\text{Δ}{\mathbf{P}}^{-1})\mathbf{Ph}\hfill \\ \hfill & ={\mathbf{h}}^{\mathbf{T}}\mathbf{Ph}-2t{\mathbf{h}}^{\mathbf{h}}\text{Δ}\mathbf{h}\hfill \\ \hfill & =1-2t{\mathbf{h}}^{\mathbf{h}}\text{Δ}\mathbf{h}.\hfill \end{array}$$ (4.23)

Note that this approximation to 〈h_xh_x′〉_2t makes no assumption about the choice of prior distribution P on the nodes of the graph. Furthermore, if the discrete-time diffusion operator is used instead, 〈h_xh_x′〉_2t does not approximate to h^TΔh in such a simple manner (See Appendix B).

For fast-mixing graphs, the long-time and short-time approximations for I [Y ;Z] and 〈h_xh_x′〉_2t, respectively, hold simultaneously.

$$\begin{array}{cc}\hfill & I[Y;Z]\left(t\right)\approx \iota \left(t\right)\approx \left(\frac{1}{2}-t\frac{{\mathbf{h}}^T\text{Δ}\mathbf{h}}{1-{\langle \mathbf{h}\rangle }^2}\right)\hfill \\ \hfill & \Rightarrow \frac{dI[Y;Z]}{dt}\approx \frac{d\iota }{dt}\propto \{\begin{array}{cc}\hfill \mathcal{A};\hfill & \hfill p\left(x\right)\propto 1\hfill \\ \hfill \mathcal{N};\hfill & \hfill p\left(x\right)\propto d_x\hfill \end{array}\phantom{\}}.\hfill \end{array}$$ (4.24)

We have shown analytically that, for fast mixing graphs, the heuristics introduced by Shi and Malik are proportional to the rate of loss of relevance information. The error incurred in the approximations I [Y ;Z] ≈ ι and 〈h_xh_x′〉_2t ≈ 1 – 2th^T Δh can be defined as

$${\epsilon }_0\left(t\right)=\mid \frac{{\langle h_x{h}_{x\prime }\rangle }_{2t}-(1-2t{\mathbf{h}}^{\mathbf{T}}\text{Δ}\mathbf{h})}{{\langle h_x{h}_{x\prime }\rangle }_{2t}}\mid$$ (4.25)

$${\epsilon }_1\left(t\right)=\mid \frac{I[Y;Z]\left(t\right)-\iota \left(t\right)}{I[Y;Z]\left(t\right)}\mid .$$ (4.26)

5 Numerical Experiments

The validity of the two approximations can be seen in a typical plot of ε₁(t) and ε₀(t) as a function of normalized diffusion time $\tilde{t}=t∕\tau$, for the two different choices of prior distributions over the nodes. ε1, as seen in Fig. 1, is often found to be non-monotonic and sometimes exhibits oscillations. This suggests defining ε_∞, a modified monotonic `ε₁':

$${\epsilon }_{\infty }\left(t\right)\equiv \underset{t^{\prime }\ge t}{\max }{\epsilon }_1\left(t^{\prime }\right).$$ (5.1)

ε∞(t) is the maximum of ε₁ over all time greater than or equal to t. We do not need to define a monotonic form for ε₀ since this error is always found to be monotonically increasing in time.

Fig. 1.

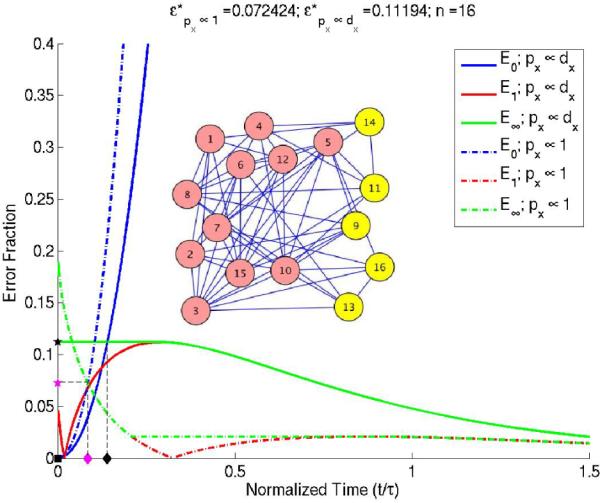
ε₁ and ε₀ vs normalized diffusion time for two choices of priors over the graph nodes. ε₁ (red) typically tends to have a non-monotonic behavior which motivates defining a monotonic ε_∝ (green). ★ – ε*, ▪ – ${\tilde{t}}_{-}^{\ast }$, ◆ – ${\tilde{t}}_{+}^{\ast }$. Black – p_x ∝ d_x, Magenta – p_x ∝ 1.

By fast-mixing graphs, we mean graphs which become well-mixed in short times, i.e. graphs for which both the long-time and short-time approximations hold simultaneously within a certain range of time ${\tilde{t}}_{-}^{\ast }\le \tilde{t}\le {\tilde{t}}_{+}^{\ast }$, as illustrated Fig. 1, where we define

$$\epsilon \left(t\right)=\max ({\epsilon }_{\infty }\left(t\right),{\epsilon }_0\left(t\right))$$ (5.2)

$${\epsilon }^{\ast }=\underset{t}{\min }\epsilon \left(t\right)$$ (5.3)

$${\tilde{t}}_{-}^{\ast }=\min \underset{\tilde{t}}{\left(\arg \min \epsilon \left(\tilde{t}\right)\right)}$$ (5.4)

$${\tilde{t}}_{+}^{\ast }=\min \underset{\tilde{t}}{\left(\arg \min \epsilon \left(\tilde{t}\right)\right)}.$$ (5.5)

ε(t) is the larger of the modified long- and short-time errors, ε_∞ and ε₀, at time t. ε* is the minimum of ε(t) over all time. For some graphs, the plot of ε(t) at its minimum might exhibit a plateau instead of a single point, as in Fig. 1 (for prior proportional to degree). t*₋ and t*₊ denote the left– and right– limits of this plateau. Note that the use of ε_∞ instead of ε₁ overestimates the value of ε*; the ε* calculated is an upper bound.

Graphs were drawn randomly from a Stochastic Block Model (SBM) distribution [14], with block cardinality 2, to analyze the distribution of ε*, ${\tilde{t}}_{-}^{\ast }$ and ${\tilde{t}}_{+}^{\ast }$. As is commonly done in community detection [15], for a graph of n nodes, the average degree per node is fixed at n/4 for graphs drawn from the SBM distribution: two nodes are connected with probability p₊ if they belong to the same block, but with probability p₋ < p₊, if they belong to different blocks. The two probabilities are, thus, constrained by the relation

$$p+\left(\frac{n}{2}-1\right)+p-\left(\frac{n}{2}\right)=\frac{n}{4}$$ (5.6)

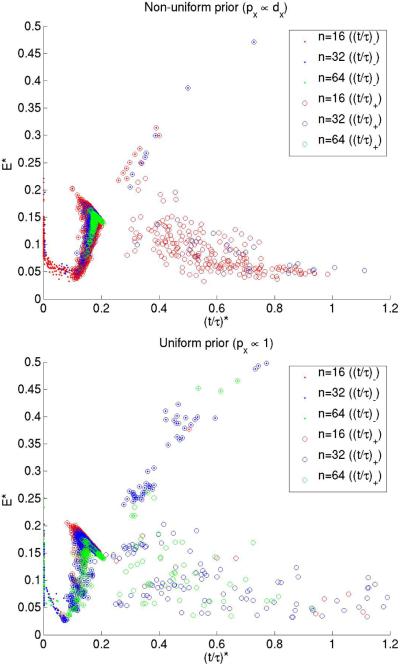
leaving only one free parameter p₋ that tunes the `modularity' of graphs in the distribution. Starting with a graph drawn from a distribution specified by a p₋ value and specifying an initial cluster assignment as given by the SBM distribution, we make local moves — adding or deleting an edge in the graph and/or reassigning a node's cluster label — and search exhaustively over this move-set for local minima of ε*. Fig. 2 compares the values of ε* and $\{{\tilde{t}}_{-}^{\ast },{\tilde{t}}_{+}^{\ast }\}$ for graphs obtained in this systematic search, starting with a graph drawn from a distribution with p₋ = 0.02 and n = {16, 32, 64}. We note that the scatter plots for graphs of different sizes collapse on one another when ε* is plotted against normalized time, confirming the Fiedler value 1/τ to be an appropriate characteristic diffusion time-scale as used in [9]. A plot of ε* against actual diffusion time shows that the scatter plots of graphs of different sizes no longer collapse (see Supplemental Material).

Fig. 2.

ε* vs ${\tilde{t}}^{\ast }$ for graphs of different sizes and different prior distributions over the graph nodes. In the above plot, ${\tilde{t}}_{-}^{\ast }$ and ${\tilde{t}}_{+}^{\ast }$ are represented by · and ο, respectively.

Having shown analytically that, for fast mixing graphs, the regularized mincut is approximately the rate of loss of relevance information, it would be instructive to compare the actual partitions that optimize these goals. Graphs of size n = 32 were drawn from the SBM distribution with p₋ = {0.1, 0.12, 0.14, 0.16}. Starting with an equal-sized partition specified by the model itself, we performed iterative coordinate descent to search (independently) for the partition that minimized the regularized cut (h_cut) and one that minimized the relevance information (h_inf(t)); i.e. we reassigned each node's cluster label and searched for the reassignment that gave the new lowest value for the cost function being optimized. Plots comparing the partitions h_inf(t) and h_cut, learnt by optimizing the two goals (averaged over 500 graphs drawn from each distribution), are shown in Fig. 3.

Fig. 3.

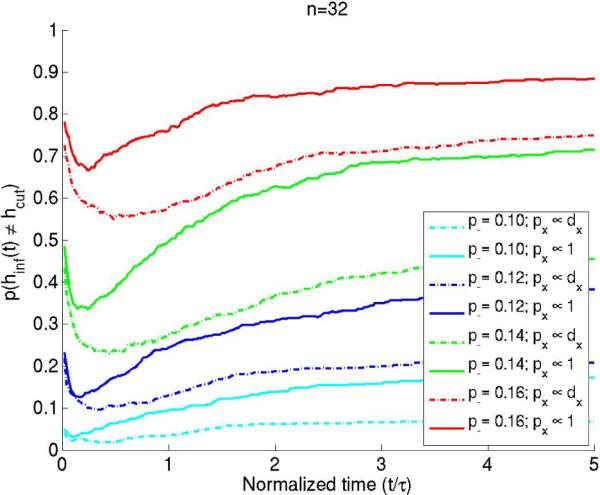
p(h_inf(t) ≠ h_cut) vs normalized diffusion time, averaged over 500 graphs drawn from a distribution parameterized by a given p_— value, is plotted for different graph distributions

6 Concluding Remarks

We have shown that the normalized cut and average cut, introduced by Shi and Malik as useful heuristics to be minimized when partitioning graphs, are well approximated by the rate of loss of predictive information for fast-mixing graphs. Deriving these cut-based cost functions from rate-distortion theory gives them a more principled setting, makes them interpretable, and facilitates generalization to appropriate cut-based cost functions in new problem settings. We have also shown (see Fig. 2) that the inverse Fiedler value is an appropriate normalization for diffusion time, justifying its use in [9] to capture long-time behaviors on the network.

Absent from this manuscript is a discussion of how not to overpartition a graph, i.e. a criterion for selecting K. It is hoped that by showing how these heuristics can be derived from a more general problem setting, lessons learnt by investigating stablilty, cross-validation or other approaches may benefit those using min-cut based approaches as well. Furthermore, a derivation of some rigorous bounds on the magnitude of the approximation errors, under some conditions, and analysis of algorithms used in rate-distortion theory and min-cut minimization are highly promising avenues for research.

Biographies

Anil Raj received his Bachelor of Technology in Aerospace Engineering from the Indian Institute of Technology Madras, Chennai, in 2005, his MS degree in Applied Physics and his MPhil degree in Applied Mathematics from Columbia University in the city of New York in 2006 and 2009, respectively. He is currently working toward his PhD degree under the supervision of Dr. Chris Wiggins. His research interests include information theory, graph theory, statistical learning theory and machine learning, and their application to problems in pattern recognition, data mining and computational biology.

Chris H. Wiggins received his PhD degree in physics from Princeton University in 1998. Between 1998 and 2001, he was an NSF Mathematical Sciences Foundation Postdoctoral Research Fellow at the Courant Institute, NYU. Since 2001, he has been a member of the Department of Applied Physics and Applied Mathematics of Columbia University in the city of New York, where he is currently an associate professor. His research interests include applications of machine learning, statistical inference, and information theory for the inference, analysis, and organization of biological networks. He is also affiliated with the Center for Computational Biology and Bioinformatics and the NanoMedicine Center for Mechanical Biology at Columbia University.

Appendix A Normalized and Average Cut

Using the definition of Δ, for any general vector f over the graph nodes, we have for symmetric A

$$\begin{array}{cc}\hfill f^T\text{Δ}\mathbf{f}& =f^T\mathrm{Df}-f^T\mathrm{Af}\hfill \\ \hfill & =\sum _x{d}_f{f}_x^2-\sum _{x,y=1}^n{f}_x{f}_y{A}_{xy}\hfill \\ \hfill & =\sum _x\left(\sum _{y=1}^n{A}_{xy}\right)f_x^2-\sum _{x,y=1}^n{f}_x{f}_y{A}_{xy}\hfill \\ \hfill & =\frac{1}{2}\left(\sum _{x,y=1}^n{f}_x^2{A}_{xy}-2\sum _{x,y=1}^n{f}_x{f}_y{A}_{xy}+\sum _{x,y=1}^n{f}_y^2{A}_{xy}\right)\hfill \\ \hfill & =\frac{1}{2}\sum _{x,y=1}^n{A}_{xy}{(f_x-f_y)}^2.\hfill \end{array}$$ (A.1)

When f = h, with h_x ∈ {−1, 1}, we have

$$\begin{array}{cc}\hfill h^T\text{Δ}\mathbf{h}& =\frac{1}{2}\sum _{h_x\times h_y=-1}4A_{xy}\hfill \\ \hfill & =4\times c.\hfill \end{array}$$ (A.2)

The factor $\frac{1}{2}$ disappears because summation over all nodes counts each adjacent pair of nodes twice.

Using the definitions of $\mathcal{A}$ and $\mathcal{N}$ , we have

$$\begin{array}{cc}\hfill \mathcal{A}& =c\times \left(\frac{1}{\sum _{h_x=+1}1}+\frac{1}{\sum _{h_y=-1}1}\right)\hfill \\ \hfill & =c\times \left(\frac{1}{{\Sigma }_x\left(\frac{1+h_x}{2}\right)}+\frac{1}{{\Sigma }_x\left(\frac{1-h_x}{2}\right)}\right)\hfill \\ \hfill & =2c\times \left(\frac{{\Sigma }_x(1-h_x+1+h_x)}{{\Sigma }_x(1+h_x){\Sigma }_x(1-h_x)}\right)\hfill \\ \hfill & =2c\times \left(\frac{2n}{(n+{\Sigma }_x{h}_x)(n-{\Sigma }_x{h}_x)}\right)\hfill \\ \hfill & =2c\times \left(\frac{2}{n(1+\stackrel{‒}{\mathbf{h}})(1-\stackrel{‒}{\mathbf{h}})}\right)\hfill \\ \hfill & =\frac{4}{n}\frac{c}{1-{\stackrel{‒}{\mathbf{h}}}^2}.\hfill \end{array}$$ (A.3)

$$\begin{array}{cc}\hfill \mathcal{N}& =c\times \left(\frac{1}{\sum _{h_x=+1}{d}_x}+\frac{1}{\sum _{h_x=-1}{d}_x}\right)\hfill \\ \hfill & =c\times \left(\frac{1}{{\Sigma }_x{d}_x\left(\frac{1+h_x}{2}\right)}+\frac{1}{{\Sigma }_x{d}_x\left(\frac{1-h_x}{2}\right)}\right)\hfill \\ \hfill & =2c\times \left(\frac{{\Sigma }_x{d}_x(1-h_x+1+h_x)}{{\Sigma }_x\left(d_x(1+h_x)\right){\Sigma }_x\left(d_x(1-h_x)\right)}\right)\hfill \\ \hfill & =2c\times \left(\frac{4m}{(2m+{\Sigma }_x{h}_x{d}_x)(2m-{\Sigma }_x{h}_x{d}_x)}\right)\hfill \\ \hfill & =2c\times \left(\frac{1}{m(1+\langle \mathbf{h}\rangle )(1-\langle \mathbf{h}\rangle )}\right)\hfill \\ \hfill & =\frac{2}{m}\frac{c}{1-{\langle \mathbf{h}\rangle }^2}.\hfill \end{array}$$ (A.4)

Appendix B Discrete Time Diffusion

For discrete-time diffusion, the conditional distribution p(y|x) is given as

$${\tilde{G}}_{yx}^s=p(y\mid x)={\left[{\left({\mathbf{AD}}^{-1}\right)}^s\right]}_{yx}$$ (B.1)

where D is the diagonal matrix of node degrees, A is the adjacency matrix and s is the number of time steps. For any s, substituting A = D − Δ and expanding the binomial gives

$$\begin{array}{cc}\hfill {\tilde{G}}^{2s}& ={(\mathbf{I}-\text{Δ}{\mathbf{D}}^{-1})}^{2s}\hfill \\ \hfill & =\mathbf{I}-2s\text{Δ}{\mathbf{D}}^{-1}+\sum _{j=2}^{2s}{(-1)}^j\left(\begin{array}{c}\hfill 2s\hfill \\ \hfill j\hfill \end{array}\right){\left(\text{Δ}{\mathbf{D}}^{-1}\right)}^j\hfill \end{array}$$ (B.2)

Thus, for p(x) ∝ d_x, the expression for 〈h_xh_x′〉_2s becomes

$$\begin{array}{cc}\hfill {\langle h_x{h}_{x^{\prime }}\rangle }_{2s}& =1-\frac{2s}{m}{h}^T\text{Δ}\mathbf{h}\hfill \\ \hfill & +\sum _{j=2}^{2s}\frac{{(-1)}^j}{m}\left(\begin{array}{c}\hfill 2s\hfill \\ \hfill j\hfill \end{array}\right)h^T\text{Δ}{\left({\mathbf{D}}^{-1}\text{Δ}\right)}^j\mathbf{h}\hfill \end{array}$$ (B.3)

From the above equation, we see that even when s = 1, unlike in the continuous-time diffusion case, 〈h_xh_x′〉_2s does not approximate as simply to the cut and ι does not approximate to the normalized or average cut.