Free-breathing 3D Cardiac MRI Using Iterative Image-Based Respiratory Motion Correction

Abstract

Respiratory motion compensation using diaphragmatic navigator (NAV) gating with a 5 mm gating window is conventionally used for free-breathing cardiac MRI. Due to the narrow gating window, scan efficiency is low resulting in long scan times, especially for patients with irregular breathing patterns. In this work, a new retrospective motion compensation algorithm is presented to reduce the scan time for free-breathing cardiac MRI that increasing the gating window to 15 mm without compromising image quality. The proposed algorithm iteratively corrects for respiratory-induced cardiac motion by optimizing the sharpness of the heart. To evaluate this technique, two coronary MRI datasets with 1.3 mm³ resolution were acquired from 11 healthy subjects (7 females, 25±9 years); one using a NAV with a 5 mm gating window acquired in 12.0±2.0 minutes and one with a 15 mm gating window acquired in 7.1±1.0 minutes. The images acquired with a 15 mm gating window were corrected using the proposed algorithm and compared to the uncorrected images acquired with the 5 mm and 15 mm gating windows. The image quality score, sharpness, and length of the three major coronary arteries were equivalent between the corrected images and the images acquired with a 5 mm gating window (p-value>0.05), while the scan time was reduced by a factor of 1.7.

INTRODUCTION

The noninvasive evaluation of coronary artery disease (CAD) is a major goal of coronary MRI. This is difficult to accomplish because the coronary arteries are in constant motion during the cardiac and respiratory cycles (1). To account for cardiac motion, k-space lines are sorted into multiple segments and each segment is acquired during the mid-diastolic rest period (2-4). Due to the small diameter of the coronary arteries, a high spatial resolution is required to visualize the stenosis in the vessels, thus resulting in extended scan times, which is beyond the duration of a single breath-hold. Therefore, coronary MRI is acquired during free-breathing with a respiratory motion compensation algorithm (5). Commonly, a diaphragmatic navigator (NAV) is used to measure the right hemi-diaphragmatic (RHD) displacement and to gate and correct the respiratory motion of the heart (6,7). Before the acquisition of each k-space segment, the location of the RHD is monitored by the NAV. If k-space lines are acquired when the RHD position is within a gating window placed around the respiratory end-expiration position, the k-space lines are accepted for image reconstruction. Otherwise, the k-space lines are rejected and reacquired in the next cardiac cycle. Although this accept/reject approach successfully minimizes the respiratory motion of the heart, it is hindered by low respiratory efficiency (defined as the percentage of k-space lines acquired within the gating window) that results from using a narrow gating window, particularly for subjects with irregular breathing patterns (8,9). During a long scan, drifts in respiratory motion can reduce the gating efficiency to zero and result in failure of the image acquisition (10,11).

Several methods have been proposed to increase the size of the gating window and thereby raise the gating efficiency. Larger gating windows with k-space weighting (12,13) and phase ordering (14,15) techniques as well as diminishing variance algorithm (16) have been shown to improve the image quality over the acceptance/rejection approach. However, the effectiveness of these techniques is based on the breathing pattern, and variations in respiration during a long scan can adversely impact the gating efficiency. Phase ordering with automatic window selection (17) and continuously adaptive windowing strategies (9,18) have been presented as robust methods to avoid scan prolongation resulting from respiratory drift. In these approaches, the respiratory pattern is divided into multiple windows, each with a corresponding bin, and it is assumed that the data acquired at each window maybe used in final image reconstruction. Ultimately, the final image is reconstructed from the bin with the highest number of acquired k-space lines.

Self-gating NAVs have also been proposed to estimate the respiratory motion of the heart directly from the acquired k-space lines rather than the RHD motion (19-23). This technique accounts for the respiratory motion of the heart along the superior-inferior (SI) direction, but, for a gating window greater than 7 mm, the motion of the heart along the anterior-posterior (AP) and right-left (RL) directions becomes important and must be considered in the motion compensation algorithm (24-27). Two- and three-dimensional NAVs have been proposed to correct for the motion of the heart along the SI, AP, and RL directions (23,28-31). Rigid and affine transformations have also been used to correct for the respiratory-induced heart motion. Fast low resolution 3D images of the heart are acquired at different respiratory locations and registered to compute rigid or affine transformations at those respiratory positions. The estimated transformations are then used to prospectively correct for the respiratory-induced heart motion in a high resolution 3D coronary MRI (32,33).

The binning strategy has also been used to correct for the respiratory-induced heart motion using an affine transformation (8,34). The respiratory pattern is divided into multiple bins and a 3D radial sample ordering is used to acquire k-space lines at different respiratory bins. Low resolution images generated from the k-space lines acquired in each bin are registered together to estimate the affine transformations used to correct the respiratory motion of the heart. Instead of affine transformation, non-rigid motion has also been used to model and correct for the respiratory motion of the heart (35-38). Nearly all of the above algorithms involve either acquiring auxiliary pulses before the acquisition of k-space segments to generate a low resolution image and to estimate and correct for the respiratory motion of the heart, or modifying the k-space sampling scheme from Cartesian to radial to generate the low resolution image from the acquired inner k-space lines and to correct for the respiratory motion.

In this study, we propose an alternative respiratory motion compensation technique for cardiac MR that yields near 100% gating efficiency. In this technique, similar to (8,34), the respiratory motion pattern was divided into multiple bins using a diaphragmatic NAV. The acquired k-space lines at each bin were then corrected for the respiratory motion of the heart using an iterative algorithm that optimizes the sharpness of the heart. Phantom and in-vivo experiments were performed to evaluate the performance of the proposed technique.

THEORY

Motion Detection, Estimation, and Correction

The proposed motion compensation algorithm consists of two parts: motion detection and estimation/correction. First, a diaphragmatic NAV is used to detect respiratory motion and segment the respiratory pattern into multiple bins to separate the k-space lines acquired at different respiratory positions. A set of 3D translation parameters that corrects the respiratory motion of the heart is assigned to each bin. The translation parameters are estimated by maximizing the sharpness of the heart in the final motion-corrected image using an iterative optimization algorithm.

A schematic diagram of the proposed motion compensation algorithm is shown in Figure 1. As illustrated, a diaphragmatic NAV measures the RHD position prior to k-space sampling. This RHD location is used to define the respiratory position for the acquired k-space lines.

Figure 1.

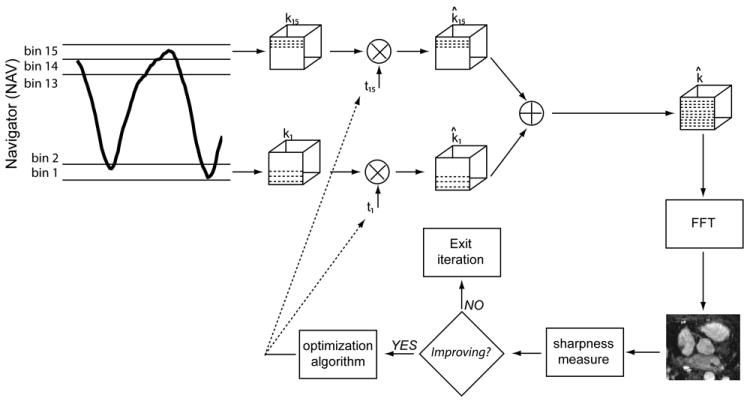
Schematic of the proposed motion compensation algorithm. The respiratory pattern measured by a diaphragmatic navigator (NAV) is divided into 15 bins to sort the k-space lines acquired at different states of respiratory cycle. A 3D translation parameter is assigned to each bin to correct the k-space segments acquired at that bin. The sharpness of the image reconstructed from the corrected k-space lines from all bins is measured and passed into an optimization algorithm to update the translation parameters such that the sharpness of the image is maximized. FFT = fast Fourier transform.

The respiratory cycle is divided into N = 15 bins where each bin represents a unique respiratory state. For example in Figure 1, bins 1 and 15 correspond to the end-expiratory and end-inspiratory states, respectively. An empty k-space matrix k_i(k_x, k_y, k_z) is created for each bin, where 1≤i≤N. k_i(k_x, k_y, k_z) is filled with the k-space lines whose NAV position is within the i^th bin. This procedure will result in N randomly undersampled k-space matrices (39).

A 3D translation parameter ${\mathit{t}}_{\mathit{i}}=[t_x^i,t_y^i,t_z^i]$ is then assigned to the i^th bin to correct the k-space lines acquired at that bin:

$${\widehat{k}}_i(k_x,k_y,k_z,{\mathit{t}}_{\mathit{i}})=k_i(k_x,k_y,k_z).\exp (\frac{2\pi k_x}{{\mathit{FoV}}_x}{t}_x^i+\frac{2\pi k_y}{{\mathit{FoV}}_y}{t}_y^i+\frac{2\pi k_z}{{\mathit{FoV}}_z}{t}_z^i),$$

where k̂_i(k_x, k_y, k_z) is the motion-corrected k-space and FoV_x, FoV_y, and FoV_z are the field-of-views along the readout, phase, and slice encode directions, respectively. The 3D translation parameters t = [t₁, …, t_N] are estimated iteratively by maximizing the sharpness of the image reconstructed from the corrected k-space matrices:

$$\underset{t}{\mathrm{arg\; max}}[\mathit{sharpness}(\mathit{fft}(\sum _{i=1}^N{\widehat{k}}_i(k_x,k_y,k_z,{\mathit{t}}_{\mathit{i}})))].$$ [1]

To measure the sharpness of an image, the Tenengrad function (40) is used as follows. First, the gradient of the image is computed using a Sobel operator (41). The variance of the gradient image consisting of high frequency information is then defined as a measure of sharpness. Since the field-of-view (FoV) of whole-heart coronary MR acquisitions also includes static structures, such as the chest wall and spine, the proposed algorithm cannot optimally estimate the respiratory motion of the heart by maximizing the sharpness of the whole volume. Therefore, in the proposed technique only the sharpness of the moving object (i.e. heart) is optimized.

Finally, a fixed step signed gradient descent algorithm (42) is used to estimate the translation parameters such that the sharpness of the image reconstructed from all k-space lines is maximized. However to minimize the complexity of the cost function [1], rather than estimating all the translation parameters (t) at the same time, the translation parameter of each bin, t_i, is sequentially estimated in the optimization algorithm as follows (Figure 2):

1. Initialize the translation parameters t with zero.

2. Choose the i^th bin (start with i =1).

3. Select the k-space lines acquired at the i^th bin.

4. Correct the k-space lines from the i^th bin using t_i.

5. Reconstruct the image using the corrected k-space lines from all bins.

6. Cropped the image to only include the region of interest, i.e., heart.

7. Measure the sharpness of the cropped image.

8. If the sharpness of the cropped image is improved then update t_i and go to Step 4; otherwise go to Step 9.

9. Increment i and go to Step 2 until all the bins are processed. If all the bins are processed go to Step 10.

10. If the translation parameters are converged to a solution (i.e. the variation of the calculated translation parameter is less than a threshold α<0.1) or a maximum number of iteration is achieved, then exit the procedure; otherwise use the estimated translation parameters as initialization and go to Step 2.

Figure 2.

Different steps of the proposed motion correction algorithm for the calculation of the translational parameter for each bin. The 3D translation parameter assigned to each bin is updated by an iterative optimization algorithm until the sharpness of the image reconstructed from the motion-corrected k-space lines is maximized. This procedure is stopped when the maximum number of iteration is achieved or the variation of the calculated translation parameters is less than a threshold.

MATERIALS and METHODS

All images were acquired using a 1.5T scanner (Achieva, Philips Healthcare, Best, the Netherlands). Written informed consent was obtained from all the participants and the imaging protocol was approved by our Institutional Review Board. All reconstruction was performed off-line in Matlab (The MathWorks, Natick, MA).

Rigid Phantom Study

To investigate the feasibility of the proposed technique, we first performed a phantom study. A static phantom was imaged using a body-coil and an ECG-triggered 3D axial balanced-SSFP sequence with the following parameters: TR/TE = 4.0/2.0ms; field-of-view (FoV) = 280×280×140 mm³; spatial resolution 1.5×1.5×1.5 mm³; flip angle = 90°; bandwidth = 1.06 kHz. A NAV with a 100 mm gating window was placed at the edge of the phantom to measure the amount of displacement along the SI direction. When fifty percent of k-space was acquired, the scan was paused and the phantom was moved along the SI direction. The rest of scan was completed with the new phantom position. The NAV signal and raw k-space data were exported for off-line motion correction and image reconstruction using the proposed algorithm.

Similar to the previous experiment, another scan was performed by moving the phantom in the SI, AP, and RL directions. In this experiment, three NAVs were used to measure the amount of motion along each direction. As before, half of the k-space was acquired without any motion and the other half was acquired after the three-directional motion. The proposed algorithm was then employed to correct for the motion and to generate the motion-corrected image.

The phantom was also imaged without any motion with the same sequence parameters as a reference.

Non-rigid Phantom Study

The performance of the proposed technique was also examined on our MR-compatible pneumatic non-rigid heart phantom with respiratory and cardiac motion (43). A simulated respiratory motion pattern was used to control the respiratory motion of the phantom. The phantom was imaged with a body-coil and an ECG-triggered, 3D axial, balanced-SSFP sequence with the following parameters: TR/TE = 5.0/2.0ms; FoV = 280×150×150 mm³; spatial resolution of 2×2×2 mm³; flip angle = 70°; bandwidth = 1.32 kHz; and 32 k-space lines per segment. A NAV with a maximum gating window size of 15 mm was placed at the edge of the plate moving the heart to measure the respiratory displacement of the heart along the SI direction without respiratory gating. The proposed technique was then used to correct for the respiratory motion of the phantom. For comparison, the same sequence parameters were used to acquire another set of images (reference) using a NAV with a 5 mm gating window.

In vivo study

Eleven healthy adult subjects (7 females, mean age 25±9 years) without any contraindications to MRI underwent free-breathing coronary MRI using the proposed technique with a RHD gating window of 15 mm. In each scan session, scout images were acquired to localize the volunteer’s anatomy using a balanced-SSFP sequence with 3.1×3.1 mm² in-plane resolution and 10 mm slice thickness. On the scout images, a diaphragmatic NAV was placed at the dome of the RHD. The scan was followed by an axial breath-hold cine SSFP sequence with 1.2×1.2 mm² in-plane resolution and 48ms temporal resolution, to visually identify the delay from the R-wave and the duration of the mid-diastolic rest period of the right coronary artery (RCA). The coronary MRI sequence (44) was then used to acquire free-breathing 3D ECG-gated axial images with a 5-channel phased array coil and the following parameters: 320×280×(60-112) mm³, FoV; 1.3×1.3×1.3 mm³ spatial resolution reconstructed to 0.65×0.65×0.65 mm³; TE/TR = 4.2/2.1ms; flip angle 90°; bandwidth = 790 Hz; ~19 k-space lines per cardiac cycle; partial Fourier with a factor of 0.6-1; and a diaphragmatic NAV with a 15 mm gating window resulting in a scan time of 5 minutes and 33 seconds assuming the heart rate of 75 beats/minute and 100% gating efficiency. Slice tracking was not used in the acquisition. For comparison another coronary MRI dataset (reference) was acquired with the same imaging parameters using a RHD NAV with a 5 mm gating window without any slice tracking. Both the NAV signal and raw k-space data were recorded and transferred to a stand-alone workstation for motion correction and image reconstruction.

Image Analysis

We retrospectively corrected for respiratory motion using data acquired with the diaphragmatic NAV with 15 mm gating. We used 3, 5, and 15 bins in the proposed algorithm to correct for the respiratory motion of the heart. The motion-corrected images using different number of bins were then qualitatively and quantitatively compared with the reference images acquired with a diaphragmatic NAV with a 5 mm gating window. The normalized mean histogram of the breathing pattern of volunteers was computed using the RHD motion, measured by the NAV. The average correlation coefficient and the mean slope of regression line between the NAV and the shifts computed by the proposed technique were also calculated using the Pearson product-moment correlation function in Matlab (The MathWorks, Natick, MA).

Qualitative assessment of the images was performed by two experienced independent readers (both board certified cardiologists with level 3 training in cardiac MRI) using a four-point scale (45): 1, indicating poor or un-interpretable (coronary artery visible, with markedly blurred borders or edges); 2, fair (coronary artery visible, with moderately blurred borders or edges); 3, acceptable (coronary artery visible, with mildly blurred borders or edges); or 4, excellent (coronary artery visible, with sharply defined borders or edges). The readers were blinded to the imaging techniques. For each image, separate scores were given for the right coronary artery (RCA), left anterior descending (LAD), and left circumflex (LCX) coronary arteries. To quantitatively assess the images, Soapbubble software (46) (Philips Healthcare, Best, the Netherlands) was used to measure the vessel sharpness and length. Vessel sharpness was calculated for both sides of the vessel and final sharpness was defined as the average sharpness of the both sides. The calculated sharpness was then normalized to the lumen signal.

The visual scoring, vessel sharpness, and length are presented as mean ± one standard deviation. We used signed rank test, a conservative non parametric test, for all pair-wise measurements (SAS software, V9.3, SAS Institute Inc., Cary NC). A p-value of ≤ 0.05 was considered statistically significant.

RESULTS

Rigid Respiratory Phantom Study

Figure 3a depicts the pattern of motion corrupting the k-space lines measured by the NAV. As shown, half of the k-space lines were corrupted with a -5.2 mm displacement along the SI direction. Figure 3b shows the motion-corrupted image. The sharpness of image (Tenengrad function), which the proposed algorithm maximizes, is displayed in Figure 3c for different values of motion. The sharpness of image is maximized at -5.4 mm. The motion-corrected image using the proposed technique is shown in Figure 3d. Figure 3e demonstrates the motion-corrected image using the NAV information. The reference image is shown in Figure 3f.

Figure 3.

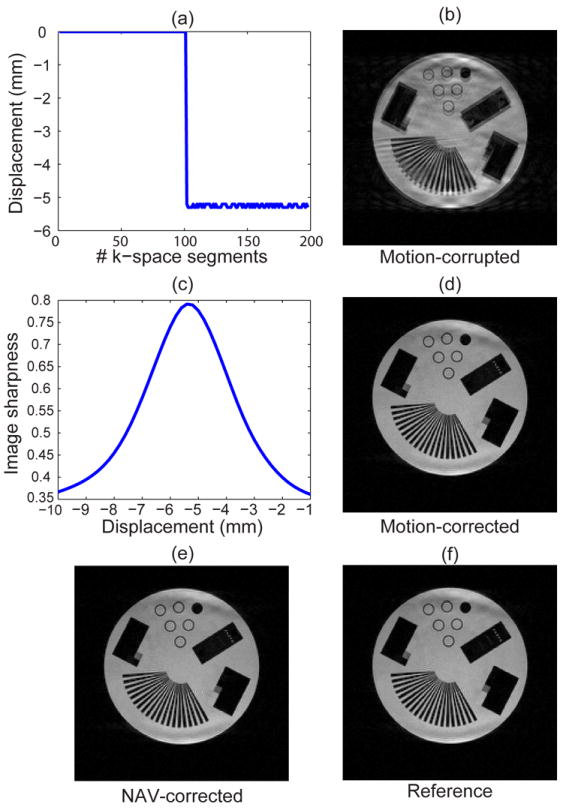
Performance of the proposed algorithm on the phantom undergoing a motion along the SI direction. The motion-corrupted image (b) is corrected using the proposed algorithm by maximizing the image sharpness cost function (c). The corrected image is shown in (d). The corrected image using the NAV information and the reference are shown in (e) and (f), respectively.

Figure 4a shows the amount of motion along the SI, AP, and RL directions measured by the three NAVs as -8.2, 27.2, and 2.5 mm. Figure 4b displays the generated motion-corrupted image. The NAV information along the SI direction is only used to detect the motion-corrupted k-space lines. Figures 4c-e depict the cost function that measures the sharpness of the image for different directions of SI, AP, and RL. As shown, the image sharpness has a global maximum at -8.0, 28.5, 2.5 mm along the SI, AP, and RL directions. These values were then used to correct the corrupted k-space lines and generate the motion-corrected image as shown in Figure 4f. Figure 4g displays the motion-corrected image using the NAV information. Figure 4h shows the reference image.

Figure 4.

Performance of the proposed algorithm on the phantom undergoing a motion along the SI, AP, and RL directions. The amount of motion along these directions is shown in (a). The motion-corrupted image is shown in (b). The sharpness cost function used to estimate the motion parameters and the motion-corrected image are shown in (c-f) and (f), respectively. The corrected image using NAV information and the reference are displayed in (g) and (h), respectively.

Non-rigid Respiratory Phantom Study

Figure 5a displays the image of the respiratory phantom acquired using the NAV with a 5mm gating window in ~6.4 minutes with 47% gating efficiency. The motion-corrupted image acquired using the NAV with a gating window of 15 mm is shown in Figure 5b. The scan time and gating efficiency for the acquisition of motion-corrupted images were ~3 minutes and 100%. Figure 5c displays the motion-corrected image using the proposed technique. The pattern of the respiratory motion and the histogram of the displacement of the phantom are shown in Figure 5d and e, respectively. The motion-corrected image of the moving heart phantom was comparable with the reference image while the scan time was reduced by a factor of 2 using a wider 15 mm gating window.

Figure 5.

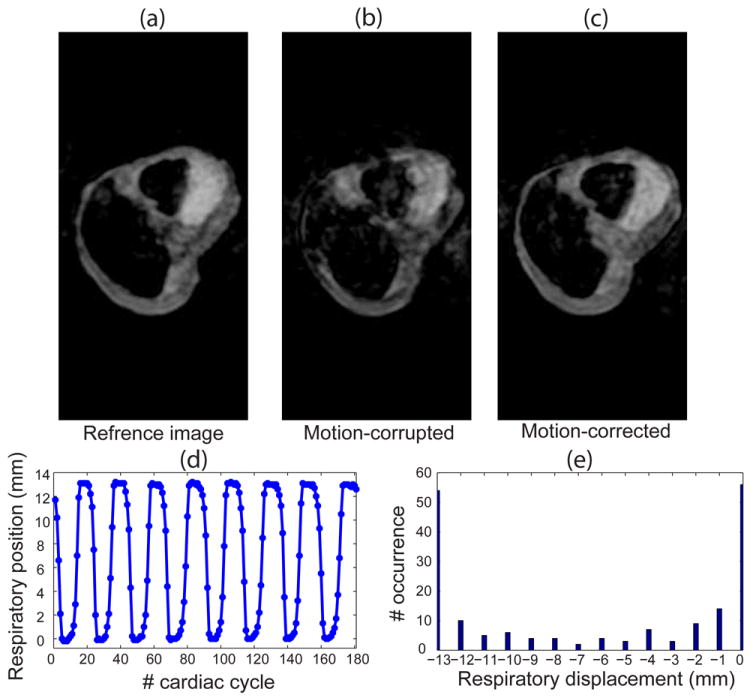
Performance of the proposed algorithm on a heart phantom with respiratory motion: (a) the reference image acquired using a diaphragmatic navigator (NAV) with 5 mm gating window; (b) the motion-corrupted image acquired without gating the respiratory motion of the heart phantom; (c) the motion-corrected image using the proposed algorithm; (d) the displacement of the heart phantom due to the respiratory motion through the scan acquisition time; and (e) the histogram of the position of the heart through the scan.

Coronary MRI

Figure 6 shows the axial and reformatted coronary MR images acquired from a 23-year-old male subject. The reference images were acquired using a diaphragmatic NAV with a 5 mm gating window in approximately 12 minutes with 56% gating efficiency. The motion-corrupted images were acquired using a diaphragmatic NAV with a 15 mm gating window in about 7 minutes with 84% gating efficiency. The motion-corrupted images were corrected using the proposed technique to generate the motion-corrected images. As shown, the motion-corrected image is very similar to the reference image, and scan time was reduced by 58%.

Figure 6.

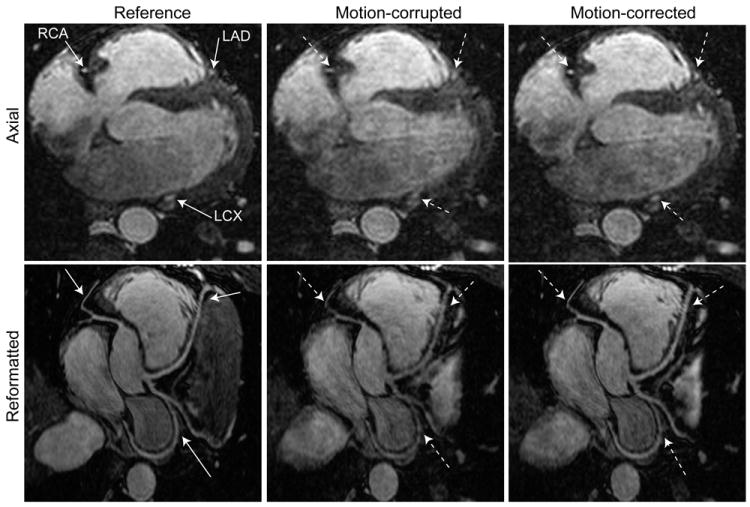
Axial and reformatted images of coronary MRI acquired from a male subject which shows the right coronary artery (RCA), left circumflex (LCX), and left anterior descending (LAD) arteries: the reference image is acquired using a diaphragmatic navigator (NAV) with a 5 mm gating window in ~12 minutes; the motion-corrupted image is acquired using a diaphragmatic NAV with a 15 mm gating window in ~7 minutes; the motion-corrected image is generated by retrospectively correcting the motion-corrupted image using the proposed algorithm.

Figure 7 displays another example of axial and reformatted whole-heart coronary images acquired from a 26-year-old female subject. The reference image shows the coronary images acquired using a diaphragmatic NAV with a 5 mm gating window in ~10 minutes with 44% gating efficiency. The motion-corrupted image displays images acquired with a 15 mm gating window in ~5 minutes with 97% gating efficiency. The proposed technique was used to correct the motion-corrupted image and generate the motion-corrected image. While the motion-corrected image is very similar to the reference image, the scan time was reduced by a factor of 2.

Figure 7.

Axial and reformatted images of coronary MRI showing the right coronary artery (RCA), left circumflex (LCX), and left anterior descending (LAD) systems that are acquired from a female subject: Reference shows the image acquired using a diaphragmatic navigator (NAV) with a 5 mm gating window in ~10 minutes; Motion-corrupted image is acquired using a diaphragmatic NAV with a 15 mm gating window in ~5 minutes. Motion-corrected image demonstrates the performance of the proposed algorithm in the correction of respiratory motion.

Figure 8 demonstrates the estimated translation parameters along the SI, AP, and RL directions with respect to the RHD motion. The slope of the linear regression line between the shift in the SI direction and the RHD motion is 0.51 ± 0.17. The average correlation coefficient between the shift in SI and the RHD motion is 0.90. The estimated translation parameters of the respiratory motion of the heart along the SI direction are strongly correlated with the RHD motion. The average slope of the regression lines between the RHD motion and the shift along SI direction is in agreement with previously reported values of 0.6 (6) and 0.45 (47). However, there is a negative, weak correlation between the estimated translation parameters along the AP and RL directions with the RHD motion. As expected, the amount of estimated motion along the SI direction shows high subject variability and is greater than the motion in the AP direction, and the motion in the AP direction is larger than the RL motion.

Figure 8.

Estimated three dimensional translation parameters with respect to the right hemi-diaphragm motion of eleven healthy subjects: (a-c) the estimated translation parameters along the superior-inferior (SI), anterior-posterior (AP), and right-left (RL) directions, respectively.

Figure 9 shows the occurrence of the NAV signal in each bin with the size of 1 mm (a) and 4 mm (b). Almost 50% of the RHD positions are within a 4 mm window around the respiratory end expiration.

Figure 9.

The mean and standard deviation of the number of occurrence of the NAV in each bin with the size of 1 mm (a) and 4 mm (b).

Table 1 displays the qualitative and quantitative comparison among three sets of images: (i) reference, (ii) motion-corrupted, and (iii) motion-corrected. The image quality score and vessel sharpness are similar between the motion-corrected and reference images (p>0.05), but both are significantly higher than the motion-corrupted images (p≤0.05). There is no statistically significant difference between the RCA, LAD, and LCX lengths in the reference and motion-corrected images (p>0.05). However, the lengths of RCA and LCX are significantly different between the motion-corrected and motion-corrupted images (p≤0.05).

Table 1.

Quantitative and qualitative measures for the images acquired using a diaphragmatic navigator with 5 mm gating window (Reference), 15 mm gating window without correction (Motion-corrupted), and with correction using the proposed algorithm (Motion-corrected).

Parameter (n=11)	Reference (Ref)	MC (15 bins)	Motion-corrupted	MC (15 bins) vs. Ref	Motion-corrupted vs. Ref	MC (15 bins) vs. Motion-corrupted
Imaging time (min)	12.0 ± 2.0	7.0 ± 1.0	7.0 ± 1.0	≤ 0.01*	≤ 0.01*	-
Scan efficiency	56 ± 9	92 ± 7	92 ± 7	≤ 0.01*	≤ 0.01*	-
RCA length (cm)	4.16 ± 1.67	3.87 ± 1.66	3.55 ± 1.53	0.46	0.10	≤ 0.03*
RCA sharpness (1/mm)	0.55 ± 0.08	0.54 ± 0.10	0.50 ± 0.10	0.64	≤ 0.01*	≤ 0.04*
RCA visual score	3.4 ± 0.7	3.3 ± 0.6	2.3 ± 0.8	1.00	≤ 0.02*	≤ 0.01*
LAD length (cm)	5.29 ± 1.45	5.16 ± 1.42	5.07 ± 1.50	0.76	1.00	0.81
LAD sharpness (1/mm)	0.43 ± 0.09	0.41 ± 0.07	0.38 ± 0.07	0.32	≤ 0.03*	≤ 0.01*
LAD visual score	2.6 ± 1.3	3.1 ± 0.8	1.8 ± 0.9	1.00	≤ 0.01*	≤ 0.01*
LCX sharpness (1/mm)	0.49 ± 0.12	0.45 ± 0.08	0.40 ± 0.06	0.07	≤ 0.03*	≤ 0.01*
LCX length (cm)	3.64 ± 1.33	3.67 ± 1.28	2.59 ± 1.03	0.16	0.08	≤ 0.01*
LCX visual score	2.7 ± 1.3	3.0 ± 1.0	1.7 ± 0.9	1.00	≤ 0.03*	≤ 0.03*

Ref = Reference, MC = Motion-corrected, RCA = right coronary artery, LAD = left anterior descending, and LCX = left circumflex. All values are reported as mean ± one standard deviation. Statistically significant p-values reported in the last three columns, are in bold.

Table 2 demonstrates the impact of using different number of bins (3, 5, and 15) in the proposed algorithm on the image quality. There is a strong agreement between the mean visual scores and the number of bins employed in the proposed algorithm. The mean visual scores of all vessels improved by increasing the number of bins from 3 to 5, and 15. However, there is no statistically significant difference between the scores of RCA, LAD, and LCX using 3, 5, and 15 bins; but the images corrected using 15 bins received the highest score and are the most similar to the reference images (p=1). Although, we did not observe statistically significant improvement using 5 and 15 bins, presumably due to small sample size, there is a trend toward better score using higher number of bins.

Table 2.

Qualitative measures for the images acquired using a diaphragmatic navigator with 5 mm gating window (Reference), 15 mm gating window with correction using the proposed motion compensation algorithm using 3, 5, and 15 bins, respectively.

Parameter (n=11)	Reference (Ref)	MC (3 bins)	MC (5 bins)	MC (15 bins)	MC (3 bins) vs. Ref	MC (5 bins) vs. Ref	MC (15 bins) vs. (3 bins)	MC (15 bins) vs. (5 bins)
RCA visual score	3.4 ± 0.7	3.0±0.9	3.2±0.9	3.3 ± 0.6	0.12	0.5	0.37	1.00
LAD visual score	2.6 ± 1.3	2.6±0.8	2.9±1.3	3.1 ± 0.8	1.00	0.53	0.06	1.00
LCX visual score	2.7 ± 1.3	2.5±0.9	2.8±1.3	3.0 ± 1.0	0.68	1.00	0.06	0.62

Ref = Reference, MC = Motion-corrected, RCA = right coronary artery, LAD = left anterior descending, and LCX = left circumflex. All values are reported as mean ± one standard deviation. Statistically significant p-values reported in the last three columns, are in bold.

DISCUSSION

In this study, a new respiratory motion compensation algorithm was presented for coronary MRI that shortens the scan time, without compromising image quality. The proposed technique maximizes the sharpness of an image by only changing the phase of the motion-corrupted k-space data. Therefore, the magnitude of the k-space data is not affected, and noise is not magnified. The phantom and in-vivo experiments demonstrated that the proposed technique is able to minimize respiratory motion of the heart and reduce the scan time with several advantages including: (i) it does not require any extra pre-pulse to acquire low resolution images to correct for the motion-corrupted k-space lines as previously shown in (38); (ii) it is compatible with any k-space sampling and profile ordering and imaging in any orientation, and (iii) it shortens the scan time by increasing navigator efficiency.

In our phantom experiment, there was a ~1 mm discrepancy between the estimated motion along the AP direction using the proposed algorithm and the NAV. This difference could be due to the circular shape and the displacement of the phantom along three directions. This displacement could cause the NAV to measure the motion of a different location.

In our in-vivo study, we used 15 bins in the proposed algorithm to achieve the highest image quality. This number of bins increases the processing time of the proposed algorithm up to 8 to 10 hours. However, the computation time can be minimized by reducing the number of the bins to 5 without significantly compromise image quality. We did not systematically study the optimal number of bins and further investigations are needed to determine the optimal bin size for better performance of the proposed motion correction algorithm considering the penalty of the reconstruction time. Furthermore, we used a suboptimal iterative optimization algorithm to estimate the translation parameters of each bin, one at a time. The ideal solution for computational time would be to simultaneously estimate all translation parameters from all bins.

In the current implementation, a 3D translation model is assigned to each bin since the translation of the heart has been shown to constitute the major components of the respiratory-induced heart motion (8,23,48). However, if a drift occurs or patients greatly change their breathing pattern, the scan still may not be completed. Increasing the gating window to its maximum size (i.e. 100 mm) and using an affine transformation (49) to more accurately model and correct for the respiratory motion of the heart in the proposed technique may potentially overcome this problem but was not studied.

In our study, the 3D k-space was fully sampled to allow simple 3D FFT reconstruction. However, the proposed algorithm has the potential to be combined with available accelerated imaging techniques such as parallel imaging (50,51) or compressed sensing (52,53) to further reduce the scan time, however combination of these two techniques requires further investigation and was not studied.

In the current implementation, a pencil-beam NAV (54) was used to divide the acquired k-space lines into multiple bins representing different locations of the RHD. Since there is a temporal delay between the acquisition of the pencil-beam NAV and data (55), it is quite possible that there is an error in the binning procedure (21). Using self-gating NAVs (20-23,27,56) or information acquired from multiple coils (57,58) may eliminate this temporal delay compared to the pencil beam NAV, and therefore, improve the image quality.

Our study has limitations. Our images were acquired using only respiratory gating without any slice tracking, which has lower scan efficiency compared to gate and track acquisition. The proposed algorithm has a very high computational complexity and with current implementation it takes approximately 8-10 hours for motion correction for a 3D whole heart imaging dataset. Although, the proposed algorithm will reduce the scan time, it is not known if it can improve diagnostic accuracy of a coronary MRI in patients.

CONCLUSIONS

The proposed retrospective algorithm iteratively corrects the respiratory-induced heart motion by maximizing the sharpness of image, and allows increasing the NAV window size to shorten the scan time without compromising image quality.