Improved in vivo diffusion tensor imaging of human cervical spinal cord

Abstract

We describe a cardiac gated high in-plane resolution axial human cervical spinal cord diffusion tensor imaging (DTI) protocol. Multiple steps were taken to optimize both image acquisition and image processing. The former includes slice-by-slice cardiac triggering and individually tiltable slices. The latter includes (i) iterative 2D retrospective motion correction, (ii) image intensity outlier detection to minimize the influence of physiological noise, (iii) a non-linear DTI estimation procedure incorporating non-negative eigenvalue priors, and (iv) tract-specific region-of-interest (ROI) identification based on an objective geometry reference. Using these strategies in combination, radial diffusivity (λ_⊥) was reproducibly measured in white matter (WM) tracts (adjusted mean [95% confidence interval]=0.25 [0.22, 0.29]µm²/ms), lower than previously reported λ_⊥ values in the in vivo human spinal cord DTI literature. Radial diffusivity and fractional anisotropy (FA) measured in WM varied from rostral to caudal as did mean translational motion, likely reflecting respiratory motion effect. Given the considerable sensitivity of DTI measurements to motion artifact, we believe outlier detection is indispensable in spinal cord diffusion imaging. We also recommend using a mixed-effects model to account for systematic measurement bias depending on cord segment.

Introduction

Spinal cord damage is a major cause of clinical disability in multiple sclerosis (MS), neuromyelitis optica (NMO), amyotrophic lateral sclerosis (ALS) and trauma. The spinal cord contains white matter (WM) tracts that carry information to and from the brain. The lateral corticospinal tracts (CST), located in the lateral portion of the cord, convey motor commands from the brain to all spinal segments; the posterior columns (PC), located in the dorsal portion of the cord, relay sensory impulses upwards to nuclei in the brainstem. The ability to evaluate tissue integrity within these specific WM tracts would have immediate clinical impact.

Conventional spinal cord magnetic resonance imaging (MRI), using T2-weighted (T2W), T1-weighted (T1W), and short-TI inversion recovery (STIR) sequences, can reveal the location of lesions that are either hyper- or hypo-intense. However, such qualitative assessments are not specific with respect to the underlying disease process leading to white matter pathology. Diffusion tensor imaging (DTI, Basser and Pierpaoli, 1996) improves pathologic specificity through the quantitative directional diffusivities, which measure water diffusion parallel (i.e., axial or longitudinal diffusivity equals λ₁ or λ_‖) and perpendicular (i.e., radial or perpendicular diffusivity equals λ_⊥ = λ₂ + λ₃/2) to the WM tracts (Song et al., 2002, 2003). These parameters have been shown to reflect axon and myelin damage in mouse models of spinal cord injury and disease (Budde et al., 2009; Kim et al., 2006).

However, quantitative in vivo DTI of the human spinal cord (Clark and Werring, 2002; Ellingson et al., 2008; Maier, 2007; Maier and Mamata, 2005) is challenging for several reasons (Barker, 2001): (i) The cord has a small cross-sectional area; (ii) magnetic field inhomogeneities from nearby vertebrae cause image distortions; and (iii) cerebrospinal fluid (CSF) pulsations, cardiac pulsation in surrounding vessels, and respiratory motion generate significant motion artifacts in the anterior-posterior and rostro-caudal directions. Thus, limited signal-to-noise ratio (SNR) resulting from physiological artifacts as well as thermal noise is a major concern in high in-plane resolution axial spinal cord DTI acquisition.

Reduced field-of-view (rFOV) sequences (Dowell et al., 2009; Finsterbusch, 2009; Jeong et al., 2005, 2006; Kim et al., 2010; Saritas et al., 2008; Wheeler-Kingshott et al., 2002a; Wilm et al., 2007, 2009; Xu et al., 2010) have shown promise in producing high quality, in vivo human spinal cord DTI. However, despite improvements in image quality and spatial resolution, tract-specific diffusion quantification within the individual spinal cord WM tracts has not been entirely satisfactory. Few studies have employed cardiac gating (Cohen-Adad et al., 2011a; Kharbanda et al., 2006; Summers et al., 2006; Wheeler-Kingshott et al., 2002a) to minimize the effect of CSF pulsations or have implemented outlier detection routines (Freund et al., 2010) as quality control measures. Consequently, overestimation of water diffusivities is likely prevalent in the human spinal cord DTI literature. In addition, motion correction, which depends on image registration, is challenging in rFOV spinal cord DTI because of limited tissue contrast and the small FOV.

Here we propose a slice-by-slice cardiac gated, rFOV cervical spinal cord DTI protocol. Features of this protocol include (i) iterative (Shimony et al., 2006) 2D image registration (Smith et al., 2010) optimized for rFOV spinal cord diffusion weighted (DW) images; (ii) outlier detection (Chang et al., 2005) to minimize the influence of physiological noise; (iii) a diffusion tensor estimation procedure incorporating positive eigenvalue priors, similar to (Cohen-Adad et al., 2008; Ducreux et al., 2007; Onu et al., 2010); and (iv) tract-specific region of interest (ROI) demarcation based on known anatomy (Klawiter et al., 2012; Xu et al., 2010). We offer this protocol as a comprehensive solution to the aforementioned challenges of tract-specific quantitative DTI of in vivo human spinal cord.

Methods

Subjects

Eighteen neurologically normal volunteers (median age 34±13 years, range 19–70 years; 8 females and 10 males) participated in this study. Each participant provided a written informed consent. All aspects of the study were approved by the Washington University Human Research Protection Office. Eight of the volunteers (1 subject, 4 times; 1 subject, 3 times, and 6 subjects, 2 times) were re-scanned over a 2-year period. Subjects were instructed to breathe and swallow normally during the entire data acquisition period.

Image acquisition

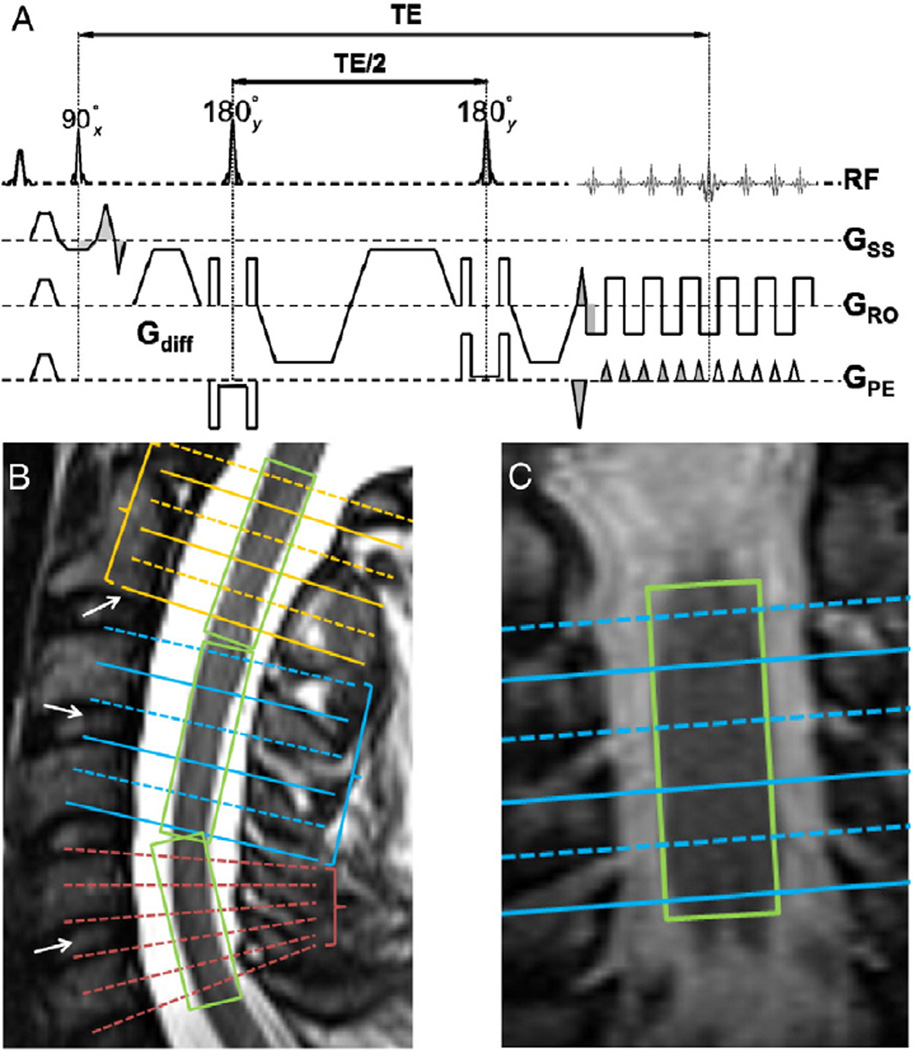
Magnetic resonance images were acquired on a 3 T scanner (Trio, Siemens, Erlangen, Germany) using either a 4-element (custom-fabricated) or a 2-element (neck posterior, vendor supplied) phased array receiver coil; coil choice depended on the subject's neck morphology with the objective of maximizing receive field penetration and SNR. A previously described rFOV single-shot SE-EPI sequence (Xu et al., 2008) was modified to improve gradient moment nulling (1st order in addition to the usual 0th order) in the slice-selective direction to reduce CSF flow artifacts. Reduced FOV was achieved by inner-volume imaging (i.e., orthogonal excitation and refocusing) using the driven equilibrium technique for efficient interleaved multi-slice acquisition (Jeong et al., 2005). Slice-selective gradients for the excitation pulse were velocity compensated and the spoiler gradients straddling the two refocusing pulses were removed in the slice-selective direction (Xu et al., 2010). Transaxial images were acquired with the following parameters: FOV 72×28.8 mm, matrix 80×32, resolution 0.9×0.9 mm, slice thickness 5 mm without gap, interleaved slice acquisition, bandwidth 1008 Hz/Pixel, echo spacing 1.04 ms, TE 99 ms, TR (6 cardiac cycles) ~5–6 s, no phase encoding partial Fourier or undersampling by parallel imaging. Three separate slice groups each spanning two vertebral segments (C1–2, C3–4, and C5–6), i.e., 6 slices each group (Fig. 1), were independently acquired over ~8–10 min per group. Each slice within a group was excited ~250–300 ms (Summers et al., 2006) after the rise of the sphygmic wave measured with a peripheral pulse oximeter. In the event of cardiac arrhythmia, acquisition was resumed at the next detected sphygmic wave (vendor supplied detection algorithm) without re-establishing steady state. Landmarks in slice positioning are crucial in our study because of the thick slices and lack of anatomical markers in rFOV images. The center of the last slice of C2 was aligned with the end of the 2nd vertebra, while the centers of the 2nd and 3rd slice groups were aligned with the intervertebral discs between the adjacent vertebrae (Fig. 1B, white arrows). Individual slices were tiltable (i.e., multi-slice-multi-angle, MSMA) in both the sagittal and coronal planes to follow the local curvature of the spinal cord. Shimming volume (Fig. 1B, green boxes) was restricted to the spinal cord in both sagittal and coronal views. After automatic field-map based shimming, the line width was further optimized (FWHM<45 Hz) by interactive adjustment. Diffusion encoding was achieved with twice-refocused spin echo diffusion preparation (Reese et al., 2003) to reduce eddy currents. Fat saturation was achieved by using both a conventional frequency selective fat saturation pulse with gradient spoiling and gradient reversal between the two refocusing/inversion pulses. Four balanced (i.e., reversed gradient polarity) averages of 25 diffusion encodings (a scaled version of the last 25 non-collinear vectors in Table 1 from Kroenke et al., 2006) with b values between 416 and 800 (b_mean ~600) s/mm² and two b₀ images were acquired (108 total image frames per acquisition). The b₀ image acquisitions were inserted into the diffusion encoding table, resulting in groups of 12 or 13 DW images after each b₀ image. Total acquisition time for the entire imaging session was about 45 min.

Fig. 1.

Reduced FOV diffusion sequence scheme (A) with gradient moment nulling (both 0th and 1st orders) in the slice-selective direction. Grey areas indicate matched gradient moments. Fat suppression was achieved with a frequency selective fat saturation module before the excitation pulse and gradient reversal between the two refocusing/inversion pulses. (B) Slice position with separate slice groups and tilted slices within the group. White arrows are landmarks for slice positioning. Green boxes (i.e., shimming volume) restrict the spatial region of B₀ homogeneity optimization to a relatively homogeneous tissue (i.e., spinal cord). (C) Slice position and shimming volume in the coronal view. This arrangement accommodated the natural curvature of the human spine and enabled compensating for positioning differences in the same subject on different visits. Furthermore, slices were individually tilted within the slice group to be parallel to the cross-section of the cord. Figure adapted from (Klawiter et al., 2012; Xu et al., 2010) with modification.

Table 1.

Results of statistical significances (p-values) comparing DTI parameters from WM tracts and GM between left (L) and right (R) hemicord, as well as between lateral CST and PC. There were no left and right differences in any of the WM or GM region (top three rows). A p-value of less than 0.0125 (with correction for multiple comparisons) was considered significant. Linear mixed-effects modeling was used to control for between-subject and nested slice level random effects, nSNR, translational motion, age and gender. Slightly larger diffusivity indices in PC than in lateral CST (supplementary data, Fig. 1) only manifest when controlling for slice level variance (last row).

	FA	MD	λ‖	λ⊥
GM (L vs. R)	p = 0.80	p = 0.78	p = 0.83	p = 0.44
CST (L vs. R)	p = 0.97	p = 0.18	p = 0.05	p = 0.47
PC (L vs. R)	p = 0.86	p = 0.10	p = 0.13	p = 0.66
CST vs. PC	p<0.01	p<0.001	p<0.001	p<0.001

Image registration

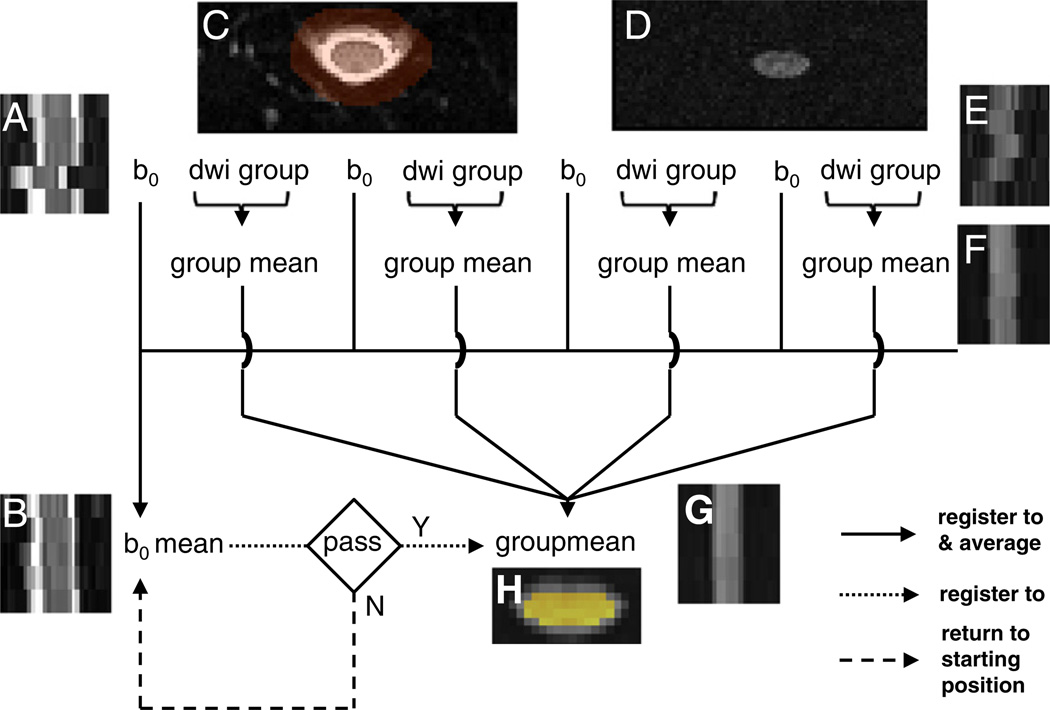
An iterative 2D rigid-body registration (FSL FLIRT, Jenkinson et al., 2002) restricted to translation (degree of freedom, DOF=2) was used for motion correction. The basic scheme is similar to that first described by Shimony et al. (2006) and was implemented in a bash shell script (http://sourceforge.net/p/spinedti). Thus, DW images representing encodings acquired in close temporal sequence were assigned to several realignment groups. The b₀ images constituted a separate alignment group. DW images were coregistered within group and between groups; the final DW group mean image then was registered with the b₀ group mean image. Each registration step was iterated three times. Transformation matrices were composed (i.e., T (individual DW image→final position)=T (individual DW image→intermediate DW group mean) × T (intermediate DW group mean→final DW group mean) and T (individual b₀ image→final position) =T (individual b₀ image→b₀ group mean) × T (b₀ group mean→final DW group mean), where T stands for affine transformation matrix). The voxel similarity measure (cost function=correlation ratio) was evaluated within a mask (i.e., used as both –inweight and – refweight by FLIRT) semi-automatically defined, encompassing the outer contour of the CSF in the b₀ images (Fig. 2C, transparent red-orange mask). Occasionally, mis-registration occurred because the outer CSF contour was aligned to cord contour; in such cases, the failed last registration step result was discarded and the average positions of the b₀ group and DW group images were taken as the final registration position (Fig. 2). The translations were composed and the registered images were resampled using a single sinc interpolation. The four balanced averages were concatenated as input to the next outlier rejection step.

Fig. 2.

Iterative registration scheme tailored for rFOV spinal cord diffusion imaging. DW images were mutually coregistered within alignment groups. (A) Sagittal b₀ image at original position. (B) Registered and averaged sagittal b₀ image. (C) Axial b₀ image (shown in entire in-plane FOV) at original position, overlaid with the registration mask (transparent red-orange). (D) Axial DW image (shown in entire in-plane FOV) at original position. (E) Sagittal DW image at original position. (F) Intermediate group registered and averaged sagittal DW image. (G) Final group registered and averaged sagittal DW image. (H) Final group registered and averaged axial DW image (cropped), overlaid with the outlier rejection mask (yellow). See Methods for details. The example shows one extreme case of severe motion disrupting the slice contiguity.

Based on the final transformation matrix, average translational motion during the acquisition for each slice was calculated as the mean across all b₀ and DW images (excluding outliers, see below) of the in-plane Euclidean distance from the original position to the final registered position.

DTI fitting with outlier rejection

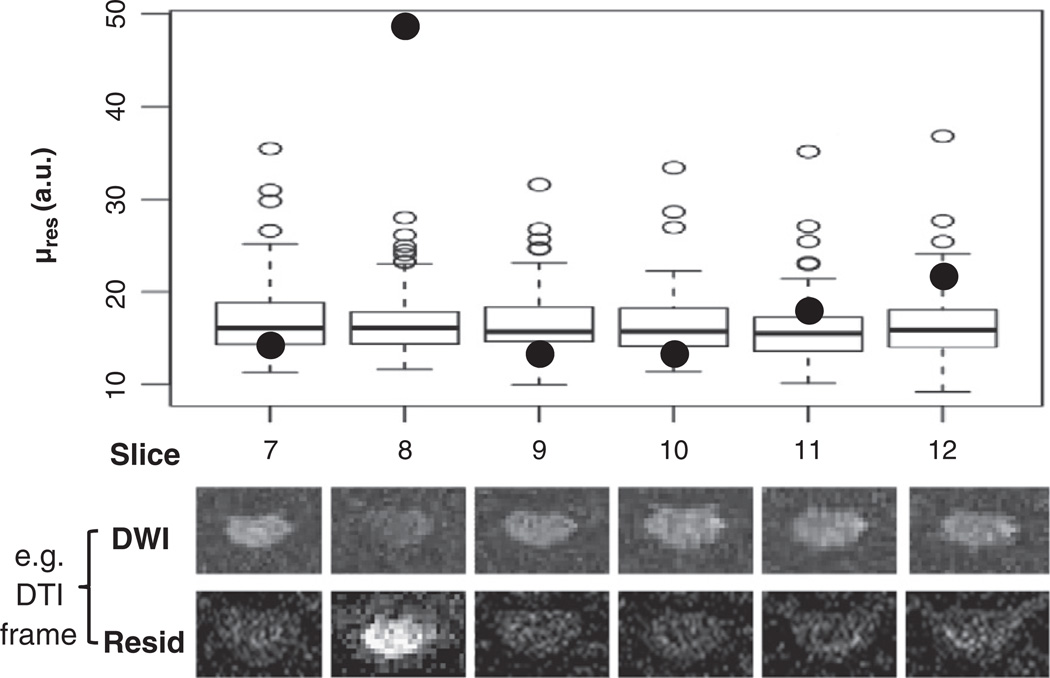
The first step in the outlier detection procedure was to remove images with excessive translation (i.e., failed registration) due to low SNR from the initial DTI fitting. A threshold for displacement >5 mm (~6 voxels) between the original and final position was empirically defined as excessive. After the initial DTI fitting, squared residual maps for each fitted image were produced. A mean cord residual score (µ_res) was generated for each acquired image by averaging the squared residuals from all voxels inside a cord mask, computed by intensity thresholding of the averaged DW images (Fig. 2, yellow mask, edge voxel removed). In our data, µ_res distributions were not normal. For each slice, a µ_res value of 3rd quartile + 1.5×inter-quartile range (approximately equivalent to mean + 2.7×standard deviation for a normal distribution) was used as an empirical lower threshold for potential outliers. The potential outlier image corresponding to the largest µ_res for each slice was removed and the reduced DTI data set was refit iteratively until all outliers were removed. Borderline cases were assessed by visual inspection of the potential outlier images. Box-plots were used to visualize the distribution of µ_res during the outlier identification process (Fig. 3). During each iteration, the diffusion tensor model (Basser and Pierpaoli, 1996) was fitted by a non-linear Levenberg–Marquardt (NLLM) algorithm with a non-negative eigenvalue Bayesian prior (Appendix I). For comparison, the same input datawere also fitted usingNLLMwithout the iterative outlier rejection scheme. The final output was resampled to 0.45 × 0.45 × 5 mm voxels.

Fig. 3.

Example of outlier rejection procedure for robust DTI fitting. See Methods section for details about the µ_res plotted here and the outlier rejection routine. Box-plots were used to visualize the distribution of µ_res. Solid points represent data for one diffusion encoding direction in six different slices. Only one of these (slice 8, solid point) was considered to be an outlier and removed from DTI fitting. The corresponding DW image and squared residual maps are shown for each slice below the Box-plots. Signal drop-out and, consequently, high residuals are evident for the outlier. The procedure was repeated until all outliers were removed. During each iteration, no more than one outlier (with the largest µ_res) was identified for each slice; which encoding was removed was not necessarily the same across slices.

The DTI fitting was implemented in C language (diff_4dfp). Visualization of µ_res distribution and outlier identification was implemented in an R language script. The entire pipeline was implemented with bash shell scripts (http://sourceforge.net/p/spinedti), using both FSL (fmrib.ox.ac.uk) and 4dfp tools (ftp://imaging.wustl.edu/pub/raichlab/4dfp_tools).

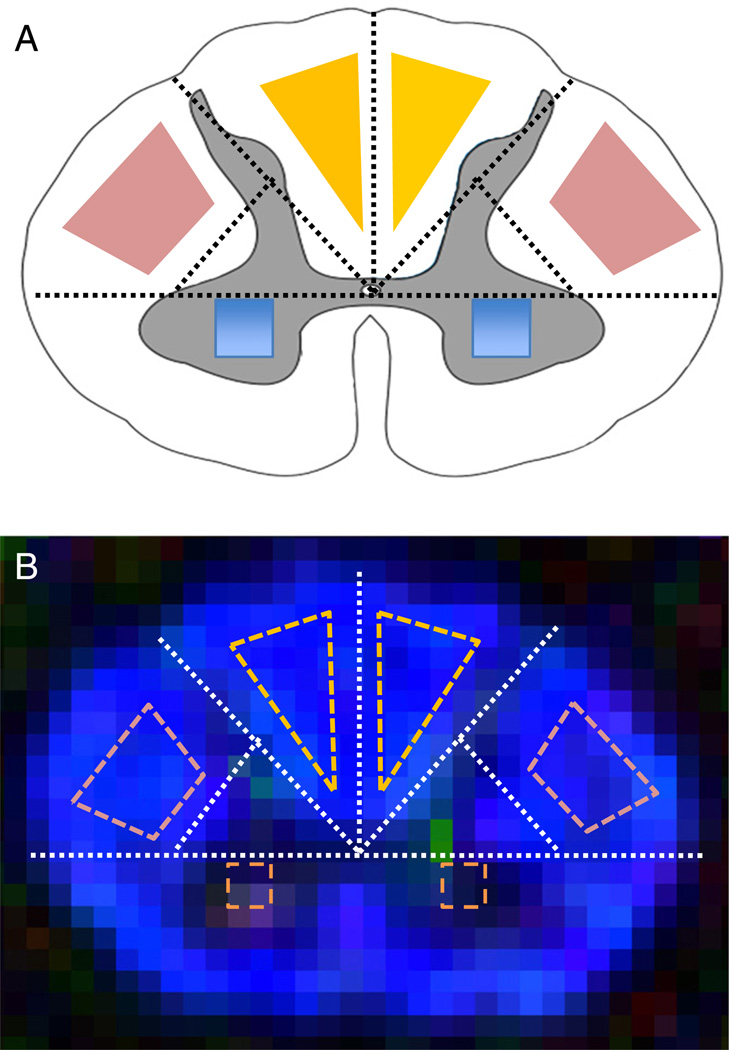
Region of interest demarcation

Regions-of-interest (ROI) for the lateral CST and PC WM tracts and gray matter (GM) were determined based on the geometry of the cord on the fractional anisotropy (FA) color map (Fig. 4B) and b₀ image (Klawiter et al., 2012; Xu et al., 2010). In addition, whole slice ROIs (denoted as “Whole” in tables and figures) were defined by the cord mask used in the outlier rejection section. A nominal SNR (nSNR, Appendix II) measure, accounting for the total number of artifact-free b₀ and DW images, was calculated for each ROI. No ROIs were defined in the ventral cord region, as the minimal layer of voxels and residual image distortion made such ROIs unreliable. The first slice from the C1–C2 acquisition was removed from further analysis to avoid the decussation of the lateral CST at the medullary– cervical cord junction.

Fig. 4.

Anatomical reference geometry (A) based ROI definition on a FA color maps of a representative slice from C4 (B), for lateral CST (A, pink), PC (A, yellow), and GM (C, blue). The same method was used for generating the ROIs at all cervical spinal cord levels in this study. Figure adapted from (Klawiter et al., 2012; Xu et al., 2010) with modification.

Simulation

Bloch equation simulation was performed to examine the perturbing effects of physiological cardiac rate variation on longitudinal magnetization (M_z), normalized to the non-cardiac triggered non-inner-volume acquisition. The numerical simulation followed Eq. (1) in Jeong et al. (2005) (Note typographic error: the second “+” sign should be a “–” sign). The R–R interval in healthy young adults typically is 0.8–1.0 s with a variability of about 5–10% (Akselrod et al., 1981; Dagli et al., 1999; Shmueli et al., 2007). We simulated baseline R–R intervals of 0.7 s (shorter than typical, hence more prone to propagated M_z fluctuations) and 0.9 s (typical). For each R–R interval, we simulated two variability levels (±10% and 20%)modeled as uniform distributions. The 20% figure doubles the typical range of cardiac rate variation to err on the side of caution. Simulated propagated variation in M_z was compiled into histograms (bin size=100) which were compared to the steady-state M_z value (i.e., fixed TR, as in non-cardiac triggered inner-volume acquisition). Parameters used in the Bloch equation simulations were specific to this study: spinal cord white matter T1 = 850 ms (Smith et al., 2008), T1 relaxation time between the two refocusing/inversion pulses=TE/2=54.5 ms, T1 relaxation time between the excitation and the first refocusing/inversion=16.5 ms, and number of slices=6.

Statistics

After proper transformation of DTI indices, linear mixed-effects modeling (Bates et al., 2011) was used to test for differences between ROIs in the left and right hemicord, as well as differences between lateral CST and PC ROIs. A p-value of less than 0.0125 (with correction for multiple comparisons) was considered significant. P-valuewas calculated with likelihood ratio test (R Development Core Team, 2011). Linear mixed-effects modeling allowed controlling for between-subject and nested slice level random effects, nSNR, translational motion, age and gender. Adjusted means for all types of ROIs, as a summary parameter including both population and slice level variances, were calculated from the linear mixed-effects model with 95% confidence intervals (CI) derived from Markov chain Monte Carlo resampling of the posterior probability distribution.

When population mean values were examined separately across cord segments, Pearson correlation coefficients (r) were used to assess the correlation between the mean translational motion (estimated from registration) and the DTI parameters across cord segments, as well as the influence of λ_⊥ and λ_‖ on the two summary parameters, mean diffusivity (MD) and FA.

To understand variance contribution and assess the reproducibility of the measurements, both intra-class correlation coefficient (ICC) and coefficient of variation (COV) were used. After linear mixed-effects modeling of the variances (Bates et al., 2011) for between-subject, within-subject (i.e., test-retest), and nested slice level, the ICC was calculated as the between-subject variance divided by the sum of between- and within-subject variance; COV was calculated as the square root of the within-subject variance (i.e., standard deviation) divided by the adjusted mean.

Results

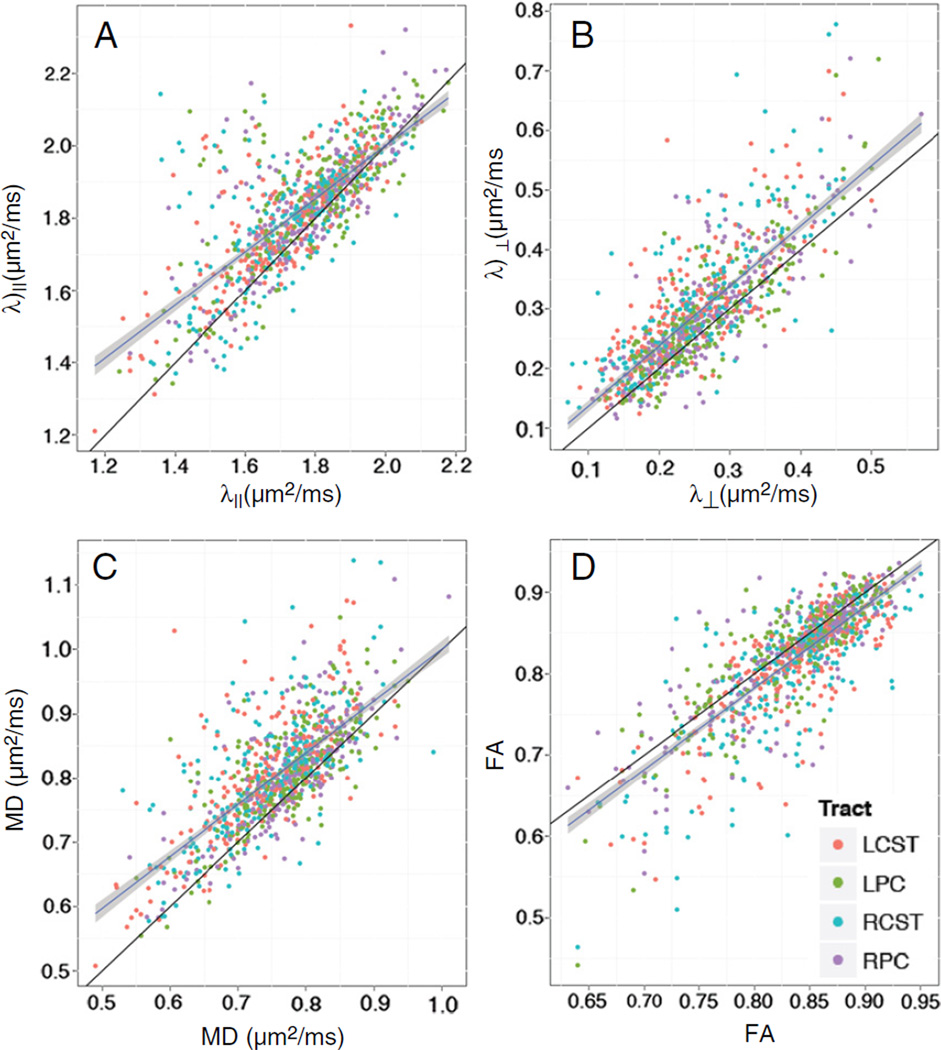
The average number of outlier images per slice was 6±5% (mean±sd). The number of outlier images varied substantially between slices and subjects with a trend of more outlier images towards the caudal slices. The outliers identified as excessive translation (i.e., failed registration) before the initial DTI fitting accounted for less than 1% of the total number of outlier images. In DTI data processed without outlier rejection there were appreciable overestimations of λ_⊥ (Fig. 5A), λ_‖ (Fig. 5B), MD (Fig. 5C), and underestimations of FA (Fig. 5D).

Fig. 5.

Self-correlation plots of λ_‖ (A), λ_⊥ (B), MD (C), and FA (D) with (x-axis) and without (y-axis) outlier rejection show significant overestimations of diffusivity measurements and underestimations of FA when outlier rejection was not applied. The black lines indicate line-of-identity. Ordinary linear regression lines were plotted in blue with 95% confidence intervals (shaded). Color represents left or right PC (LPC or RPC), and left or right lateral CST (LCST or RCST). The outlier rejection procedure did not bias any particular WM ROI. If the outlier rejection had not had any effect on the results, points would have been randomly distributed around the line-of-identity, due to the non-deterministic nature of diffusion tensor estimation with the non-negative eigenvalue Bayesian prior (Appendix I).

Representative DTI maps for each cord segment are shown in Fig. 6. There were no significant differences in any DTI measure between the left and right WM tracts or between left and right GM ROIs (Table 1). Slightly higher diffusivities were observed in PC compared to CST (Supplementary data, Fig. 1). However, in the adjusted mean for the entire cord (Table 2), these small differences were masked by variance across cord segments.

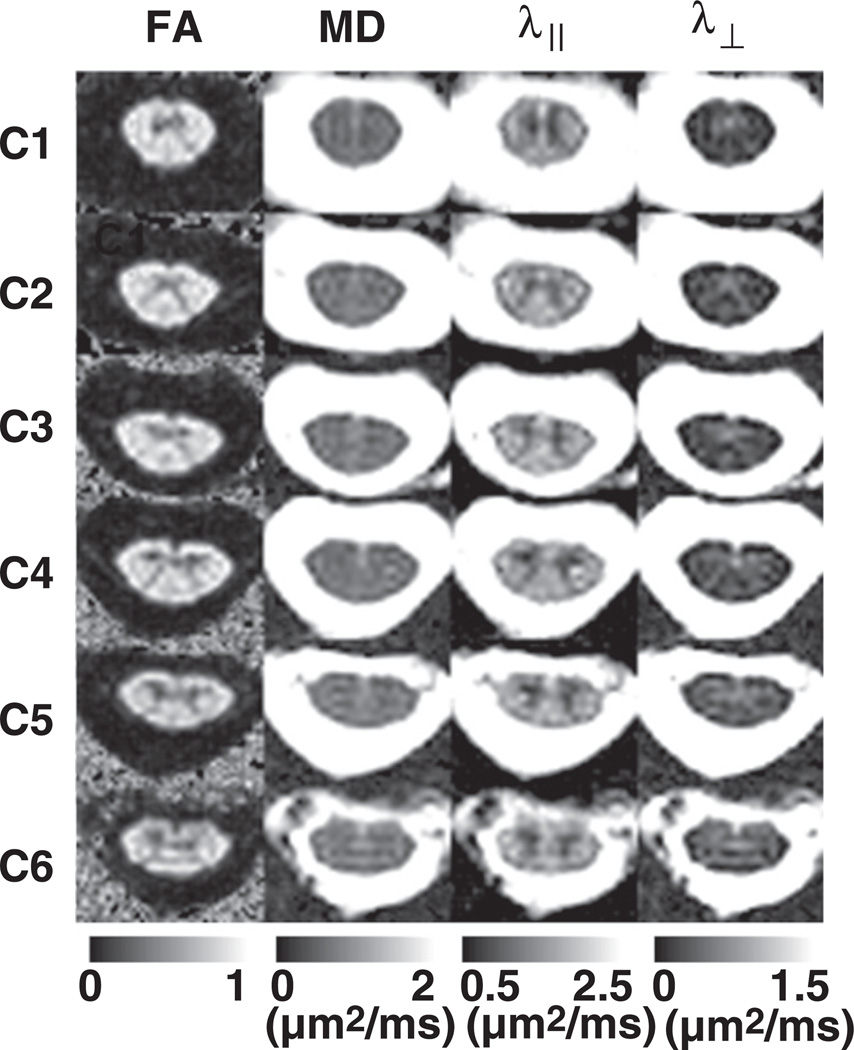
Fig. 6.

Representative DTI maps from the center slice in each cord segment (C1–C6) from a normal subject. The distinctive “butterfly” differentiation of GM and WM can be appreciated from FA, λ_‖, and λ_⊥ maps.

Table 2.

Adjusted means [95% confidence interval] of cervical spinal cord DTI parameters in WM (lateral CST and PC), GM and whole slice ROIs from 18 healthy subjects. The confidence intervals were calculated based on linear mixed-effects modeling of population, nested slice level, and left-right hemicord variances.

	FA	MD (µm2/ms)	λ‖ (µm2/ms)	λ⊥ (µm2/ms)
CST	0.84 [0.82,0.85]	0.74 [0.72,0.76]	1.71 [1.66,1.75]	0.24 [0.22,0.26]
PC	0.83 [0.81,0.85]	0.77 [0.74,0.80]	1.77 [1.71,1.83]	0.26 [0.23,0.29]
Whole	0.71 [0.70,0.72]	0.76 [0.74,0.77]	1.52 [1.48,1.56]	0.37 [0.35,0.38]
GM	0.42 [0.40,0.45]	0.74 [0.72,0.77]	1.11 [1.08,1.14]	0.55 [0.53,058]

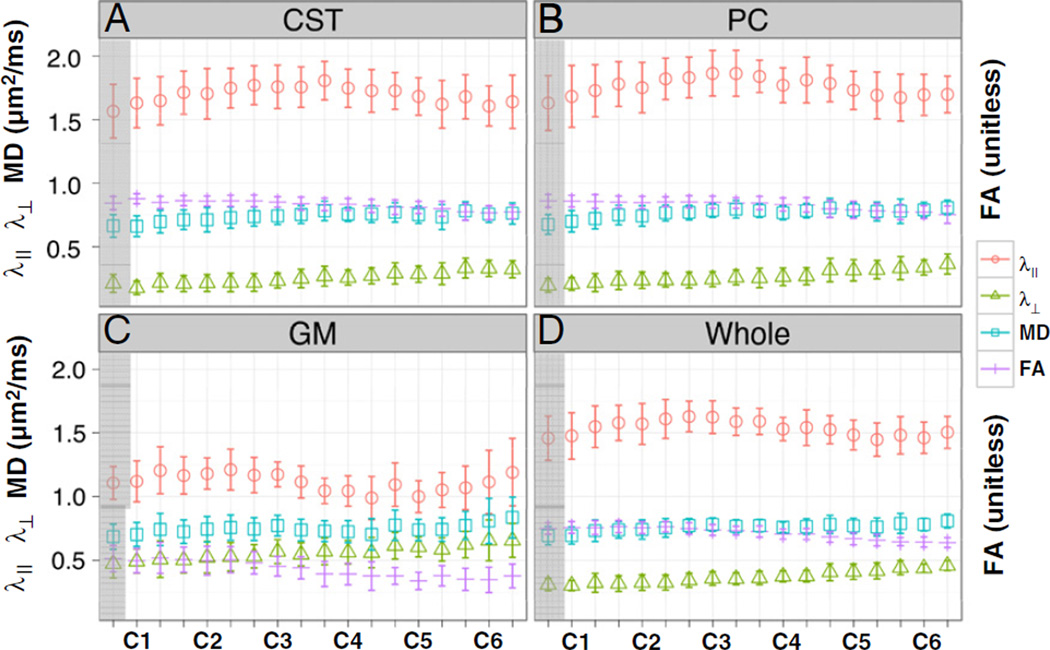
DTI parameters in lateral CST and PC were each left-right averaged and examined as a function of segment. Moving rostral to caudal, there was a steady increase in λ_⊥ (Fig. 7A and B, green) and a steady decrease in FA (Fig. 7A and B, purple). This systematic effect correlated with the increased mean translational motion from C1 to C6 (Supplementary data, Fig. 2, bottom trace). Quantitatively, mean translational motion was correlated with λ_⊥ (r = 0.70, p = 0.0059) and FA (r=−0.76, p = 0.0013), but not with λ_‖ (r = −0.42, p = 0.21) or MD (r = 0.31, p = 0.48). Rostro-caudal changes in the two summary indices, MD and FA, were dominated by λ_⊥ (r = 0.77, p<0.001 and r = −0.97, p<0.001, respectively) rather than λ_‖ (r = 0.56, p = 0.023 and r = 0.35, p = 0.28, respectively). Whole slice measurements (Fig. 7D), incorporating both WM and GM, yielded similar general trends for all DTI indices, as in WM. There was measureable fractional anisotropy (0.42 with 95% CI [0.40, 0.45]) in GM (Table 2, last row). Similar to WM and whole slice, there was a consistent trend of increase in λ_⊥ (Fig. 7C, green) and decrease in FA (Fig. 7C, purple), as well for GM from C1 to C6.

Fig. 7.

Distributions of DTI parameters in left-right averaged lateral corticospinal tracts (CST, A), left-right averaged posterior columns (PC, B), left-right averaged graymatter (GM, C), and whole slice ROI (Whole, D) through cord segments (C1–C6) for normal subjects (n = 18). Each tick mark on x-axis represents one slice. Error bars represent standard deviation among the population. The first slice in C1 (shadowed) was removed from other analyses to avoid the decussation of the lateral CST at the medullary–cervical cord junction.

After factoring out the nested slice-level variance, within-subject variances were about equal or smaller than between-subject variances (Table 3, ICC, upper panel), indicating reasonably low variance contribution from our measurement protocol. The relative magnitude of repeated measurement variability was less than 10% for all DTI parameters except for λ_⊥ in GM (Table 3, COV, lower panel), indicating overall good reproducibility. Specifically, FA values in WM and whole slice ROIs were consistently the most reproducible (ICC ≥ 0.70, COV ≤ 5%), while MD values in all ROIs were consistently less reproducible (ICC ~0.50, COV = 5–8%) than FA values. The reproducibility of λ_⊥ was high in WM (ICC = 0.82, COV = 8.8%) and whole slice (ICC = 0.72, COV = 5.9%) measures but not in GM (ICC = 0.52, COV = 10.6%). Conversely, high reproducibility in GM (ICC = 0.79, COV = 4.6%) and moderate reproducibility in WM (ICC< = 0.60, COV = 7–9%) was observed for λ_‖.

Table 3.

Test-retest intra-class correlation coefficients (ICC) and coefficients of variation (COV) for DTI parameters in the cervical spinal cord. Slice level variance was factored out in both ICC and COV calculations. Larger ICC value represents small within-subject test-retest variance as compared to between-subject variance, hence higher reproducibility. Smaller COV values represent small within-subject test-retest standard deviation (i.e., square root of variance) as compared to the adjusted mean (Table 2), hence higher reproducibility. Note, ICC did not always correlate with COV; hence these measures provide complementary information about reproducibility. DTI measures with relatively low within-subject variance contribution (ICC≥0.7) or low test-retest variability (COV≤5%) are shown in bold.

	FA	MD	λ‖	λ⊥
ICC	WM	0.70	0.50	0.47	0.82
	Whole	0.80	0.52	0.60	0.72
	GM	0.74	0.52	0.79	0.52
COV (%)	WM	3.6	5.9	8.4	8.8
	Whole	2.8	6.8	7.5	5.9
	GM	6.6	7.5	4.6	10.6

Simulated propagated fluctuation of longitudinal magnetization (M_z) due to physiological cardiac rate variation was observed to be minimal (Supplementary data, Fig. 3). Deviation from steady-state M_z increased with shorter baseline R–R intervals and greater cardiac rate variation, as expected. Nevertheless, the propagated error in M_z was small (<5%) even in the worse case of R–R interval = 0.7 s±20% (Supplementary data, Fig. 3D). Hyperintensity occurred more frequently than hypointensity in all simulated cases.

Discussion

Starting with the improved image quality and spatial resolution offered by rFOV diffusion imaging (Dowell et al., 2009; Finsterbusch, 2009; Jeong et al., 2005, 2006; Kim et al., 2010; Saritas et al., 2008; Wheeler-Kingshott et al., 2002a;Wilmet al., 2007, 2009),we employed slice-by-slice cardiac triggering and individually tiltable slices in spinal cord DTI acquisition (Klawiter et al., 2012; Xu et al., 2010). We further implemented several post-processing steps to achieve high quality DTI maps (Fig. 6) and tract-specific quantification (Table 2). We discuss these technical improvements and our DTI results in the following sub-sections.

Data acquisition

Reduced FOV was achieved with orthogonal excitation and refocusing (Jeong et al., 2005; Xu et al., 2008, 2010). Despite the double-inversion or driven equilibrium approach employed to minimize SNR loss due to longitudinal relaxation, adequate delay time within each TR was needed for optimal SNR. This constraint limited the number of slices acquired in each cardiac cycle, which reduced acquisition efficiency. We used a slice-by-slice cardiac triggering scheme to acquire each slice consistently at the most quiescent period in the diastole (Summers et al., 2006). Alternatively, with an oblique inner-volume arrangement (Wheeler-Kingshott et al., 2002a; Wilm et al., 2009), two or three slices may be acquired in one cardiac cycle without significant T1 saturation.

Achievable SNR in the spinal cord constrains the slice thickness in axial DTI protocols with high in-plane resolution. Although the cervical spinal cord is relatively straight, natural curvature exists and could be substantial in some subjects. To mitigate partial volume effects due to spinal cord curvature, the coverage from C1 to C6 was separated into three axial acquisitions. Furthermore, the diffusion sequence allowed each slice to be individually tilted (i.e., multi-slice-multi-angle, MSMA) in both the phase encoding (anterior-posterior) and readout (left-right) directions. In most cases, only modest tilt angles (<15°) are needed to follow the curvature of the cord. It should be noted that this imaging strategy leads to overlapping edges of neighboring slices. Also, tractography would not work correctly if the tracking algorithm did not take into account these slice tilts. Admittedly, slice tilting does not address local curvature within the 5 mm thick slice. However, fiber bundle bending within the long tracts of the cord is minimal (typically <3° over 5 mm). Nevertheless, this bending would lead to an underestimation of λ_‖ and overestimation of λ_⊥, even without partial volume effects.

We used gradient reversal (Gomori et al., 1988; Volk et al., 1987) between the two refocusing/inversion pulses (Xu et al., 2008), in addition to conventional frequency selective fat saturation to achieve fat suppression. Because of the wide slab, hence weak selective gradient in the phase encoding direction in the inner-volume sequence, the fat frequency shift at 3 T is large compared to the relatively low bandwidth refocusing/inversion pulses. This yields effective fat saturation even in the presence of field inhomogeneity. Gradient reversal in the slice direction with low bandwidth excitation and refocusing pulses have also been used in addition to spectral inversion recovery (SPIR), to achieve fat suppression (Wilm et al., 2007). Other fat suppression techniques, such as spectral–spatial excitation pulse (Dowell et al., 2009; Wheeler-Kingshott et al., 2002b) or judicially controlling fat and water excitation profiles (i.e., adjusting relative spatial shift) in 2D excitation pulse, have also been demonstrated.

The b values in our study were not optimized for imaging a particular pathology or for tractography (e.g., Lee et al., 2006), but for reliable diffusivity quantification in clinical applications. The upper limit (800 s/mm²) and mean b value (~600 s/mm²) were chosen to maximize the likelihood of satisfactory SNR (nominal SNR≥20, Klawiter et al., 2012) in DW images in a variety of situations (e.g., obese patients, poor shimming, fast heart rate, etc.). The lower limit (~400 s/mm²)was chosen to reliably suppress CSF signal around the cord in DW images, which otherwise could interfere with image registration. In addition, we used flow compensated slice-selective gradients for excitation and removed spoiler gradients in the slice direction to minimize sensitivity to CSF flow, which further reduced CSF artifacts in b₀ images and DW images without diffusion sensitization in the slice direction. A similar velocity compensation strategy has been used to facilitate z-shimming in T2* spinal cord imaging (Finsterbusch et al., 2012).

Image preprocessing (registration)

The customized rFOV diffusion sequence minimized susceptibility related image distortion in EPI. The twice-refocused diffusion preparation also substantially reduced eddy current effects (Reese et al., 2003). Nevertheless, residual geometric distortion in the phase encoding direction was still present. Generally available image registration based distortion correction (e.g., FSL eddy_correct) performed poorly during our initial testing with the reduced FOV cervical spine images, which has been reported by others as well (Cohen-Adad et al., 2009). Stretching or compression in the phase encoding direction significantly increased sensitivity to noise, and hence, was not enabled during our image registration. Other techniques such as reversed phase-encoding blips (Voss et al., 2006) or point spread function correction can potentially further reduce residual geometric distortion (Lundell et al., 2012). In our study, residual distortion was most pronounced in the ventral aspect of the spinal cord, which limited consistent and reliable ROI placement in that region. Moreover, given the limited layer of voxels (usually 1–2 voxels at 0.9 mm in-plane resolution) representing WM tracts in the ventral region, DTI measurement in that region is inevitably biased by partial volume effects from the nearby CSF and GM.

The choice of a 2D registration algorithm was dictated by the slice-by-slice cardiac triggered acquisition. In extreme cases, absolute frame-to-frame in-plane image shift before image registration (Fig. 2), even after cardiac gating, could be quite substantial (up to 4–6 mm, ~50% of the typical cervical spinal cord width in the phase encoding direction). Such disrupted contiguity of the anatomical structure was likely the result of B₀ variation due to respiration, exaggerated by the relatively long intervals between each slice excitation and the interleaved slice order. Although 2D registration precluded compensation for through-slice motion, spinal cord anatomy changes only very slowly from segment to segment. Although through slice motion was not corrected in our post-processing, the reduction in CSF pulsation artifacts obtained by cardiac triggering outweighed the inability to perform 3D registration. Image acquisition during the quiescent window of the cardiac cycle substantially reduced CSF pulsation related signal drop-out and ghosting (Kharbanda et al., 2006; Summers et al., 2006).

Due to the lack of anatomical contrast within the reduced FOV, we found correction for in-plane image rotation to be unreliable. Rotational freedom therefore was disabled (Smith et al., 2010). Presumably, the cervical cord shares the same amount of rotational motion as the brain (~0–1° on average in a typical scan session) (Power et al., 2012). CSF pulsation does not induce rotation of the spinal cord (Alperin et al., 1996; Hofmann et al., 2000; Mikulis et al., 1994; Summers et al., 2006). Hence, voxel mis-registration introduced by rotation even at the edge of the spinal cord was small compared to the voxel size, given the small in-plane radius (typically 5–8 mm) of the spinal cord.

Failure of the last registration step (i.e., registering the b₀ group mean image with the final DW group mean image) occurred in less than 2% of the total number of slices. All of the failures occurred in the upper cord segments (i.e., C1–C2) with clear cord – CSF contrast and not necessarily in low SNR cases. We have tried different cost functions (e.g., mutual information) or reversing the contrast of the b₀ group mean image, without consistent improvement. We conclude that contrast ambiguity between the outer CSF contour in the b₀ group mean image and the cord contour in the final DW group mean image led to false registration. However, the effect of discarding the final registration step on the overall registration accuracy was small, as long as the b₀ images were acquired without temporal bias. In our study, the average position of the eight b₀ images (interspersed within the diffusion encoding table) corresponded well to the position of the final group mean DW image. The last registration step typically moved the b₀ group mean image by less than half a voxel.

High SNR facilitates accurate registration of DW images. Accordingly, the least variation in translational motion was observed in C3 and C4, which had the highest mean SNR (Supplementary data, Fig. 2, upper trace). These results are not surprising, given that C3 and C4 are typically positioned, by default in most scanners, at the middle of the neck coil arrays. In addition, C3 and C4 are intrinsically less prone to respiratory motion as compared to the lower cord segments. Despite the absence of direct evidence, we attributed the increased rostral to caudal motion (i.e., from C1 to C6) to increased sensitivity to respiration. The observed trends from C1 to C6 of λ_⊥, FA, and MD in WM and whole slice ROIs were consistent with the literature (Smith et al., 2010; Van Hecke et al., 2009; Wheeler-Kingshott et al., 2002a), suggesting that unrecognized bias induced by respiratory motion could be a common problem. However we cannot rule out true biological causes of the rostro-caudal trend of the DTI parameters in WM, such as the collateral fibers running perpendicular to the primary longitudinal fiber orientation (Cohen-Adad et al., 2008; Lundell et al., 2011; Mamata et al., 2006) and/or the number and density of axons (DeLuca et al., 2004) in these WM tracts.

We have noticed motion artifacts attributable to swallowing. The extent and the severity of swallowing-induced artifacts need further investigation. If swallowing is indeed a common and severe problem, it is theoretically possible to introduce swallow-holding (i.e., swallowing suppression) during image acquisition, similar to breath-holding in abdominal imaging. The DTI acquisition protocol would need to be altered accordingly, perhaps divided into segments of duration on the order of a minute, depending on the subject's ability to suppress swallowing.

DTI model fitting

A sufficient number of artifact-free DW images are needed to robustly distinguish corrupted outlier images (Chang et al., 2012), since our outlier rejection procedure was model-based, as in the robust estimation of tensors by outlier rejection (RESTORE) (Chang et al., 2005). This can be achieved with a large number of unique diffusion vectors, many repetitions of a small set of diffusion vectors, or a combination of both. We chose four balanced (i.e., reversed diffusion gradient polarity) averages, to minimize residual b value cross-terms (Neeman et al., 1991), with 25 unique (in both direction and b value) diffusion vectors in this study. Each unique diffusion vector had a unique b value between ~400 and 800 s/mm² with an overall b_mean of ~600 s/mm². If SNR is adequate in each DW image, a single diffusion tensor estimated from such a multi-b-value scheme would differ little from a single shell scheme. However, when SNR is not adequate or borderline (norminal SNR<20), especially for diffusion encoding along the longitudinal direction, systematic bias could be introduced (Klawiter et al., 2012). The multi-b-value DTI scheme was chosen empirically to maximize the number of acquired DW images with sufficient SNR in clinical imaging. The multi-b-value scheme in this study provided not only enough redundancy for outlier rejection, but also greater searching space for the NLLM algorithm to avoid convergence to negative eigenvalues.

Occasional negative eigenvalues in brain imagingmay not appear as a serious artifact because DTI parameters typically are averaged over many voxels. However, this is not the case in spinal cord diffusion imaging, where only a limited number of voxels (for WM ROIs, typically ~4–6 voxels in native space, even fewer in atrophic cord) are available within individual tract-specific ROI. Hence, it is critical to constrain the diffusion tensor eigenvalues to positive values, for example, using MedINRIA (med.inria.fr) software (Cohen-Adad et al., 2008; Ducreux et al., 2007; Onu et al., 2010). Here, we used a positive prior based on Bayesian theory (Andersson, 2008) to address this problem (Appendix I). The implementation is simple, robust and computationally efficient. Alternative techniques for enforcing the same constraint have been described (Arsigny et al., 2006; Koay et al., 2006). All such methods share in common the same least squares objective function and theoretically converge to the same answer given the same input.

The lack of T1 or T2 contrast (Smith et al., 2008) between spinal cord GM and WM makes tract identification difficult. Tract specific ROI definition based on tractography (Ciccarelli et al., 2007; Smith et al., 2010; Van Hecke et al., 2008) or fuzzy-logic classification (Ellingson et al., 2007a, 2007b) is inherently biased by the diffusion measure. The geometry based ROI introduced by us (Xu et al., 2010) provides an objective basis for unbiased quantification with limited number of voxels. We used the FA color map to help locate the central canal as the center landmark in our ROI strategy and to conservatively define the CSF–WM boundary, which could be unreliable if based on the b₀ image alone. However, separation of the posterior portion of the cord into four quadrants does not strictly depend on the FA image, which makes the ROI strategy potentially applicable to lesioned cords with altered FA contrast. This ROI strategy was used in our study of MS and NMO patients (Klawiter et al., 2012) and adopted by another study of spinal cord injury (SCI) patients (Cohen-Adad et al., 2011a).

Outlier rejection

To our knowledge, outlier image rejection during post-processing of spinal cord DTI has been reported only once (Freund et al., 2010). The outlier identification routine used here was similar to the RESTORE (Chang et al., 2005) technique by comparing the fitted and the measured DWI signal. Instead of being voxel-based, we took the mean squared residuals (µ_res) inside the spinal cord mask, which forms a natural cluster of voxels. This spatially averaged µ_res criterion for outliers is much more conservative and appropriate in low SNR data. Theoretically, the WM of the spinal cord could be segmented first to forma WM mask for outlier rejection. However, practical resolution limits preclude such an approach. In addition to identifying outliers among DWI frames for each slice, µ_res can also be compared across slices to enhance the reliability of the outlier rejection procedure, a method that is unique to transverse spinal cord acquisition. This strategy assumes tissue structural consistency across slices, which only applies to healthy spinal cord without lesion or injury. Although this additional between-slice constraint was not used in the current study, outliers frequently clustered through slices and followed the slice interleave pattern (e.g., slices 2, 4, and 6 as a small cluster of outliers), indicating a contiguous period of intense motion.

Most of the outlier images were related to signal dropout with very few of them being hyperintense (Chang et al., 2012). The origin of outliers may have been either from physiological sources (signal dropout due to CSF pulsation, swallowing, or respiration), physical sources (table-vibration, scanner spike noise, or stimulated echo artifacts), or post processing (image mis-registration). The minimum time interval between acquired slices (i.e., TR/n) was equal to the cardiac cycle (typically ~800–1200 ms). Without cardiac triggering, steady state longitudinal magnetization had been reached (Dowell et al., 2009; Jeong et al., 2005). In case of cardiac arrhythmia, the inversion of magnetization outside of excited slices in the cardiac triggered inner-volume diffusion sequence (Jeong et al., 2005) makes the acquired signal more sensitive to disrupted steady state than in a cardiac triggered conventional, non-inner-volume diffusion sequence. This increased non-steady state sensitivity could lead to either hypointense or hyperintense outlier images. Ideally, the pulse sequence should re-establish steady state after each detected cardiac arrhythmia event before resuming DTI acquisition, which was not implemented in this study due to implementation complexity. Nevertheless, non-steady state outlier images only accounted for a minority (<15%) of all the outliers. The majority of the outliers were images with signal dropout artifacts.

Bloch equation simulation showed low sensitivity to normal cardiac rate variation (Supplementary data, Fig. 3). Even in the worst case (R–R interval=0.7 s±20%), variation of M_z was less than 5%. We conclude that non-steady-state outlier images were mostly attributable to cardiac arrhythmias instead of physiologic cardiac rate variation. The simulations also showed that hyperintensity was more likely than hypointensity, which suggests that the observed hyperintense outliers were non-steady-state artifact. Faster heart rates and therefore insufficient T1 relaxation to equilibrium could lead to a non-steady-state regime during cardiac gated inner-volume acquisition. Therefore, when the average R–R interval is less than 0.7 s, we suggest gating on every other pulse. In addition, we recommend acquiring enough slices (average gating interval × number of slices ≥ ~5 times tissue T1) to allow sufficient T1 relaxation.

While the percentage of outliers for any slice from this healthy cohort was low (typically <10%), noticeable overestimation of diffusivities could be appreciated (Fig. 5), similar to results from brain DTI studies (Walker et al., 2011). For healthy spinal cord WM, reduced variability of DTI parameters (most obvious for λ_⊥, Fig. 5B) suggests that the outlier rejection improved diffusion quantification. However, for injured WM or GM, assessing the value of outlier rejection would be challenging, because a single tensor may not well characterize the complicated tissue microstructure (Cohen and Assaf, 2002; Wang et al., 2011; Wedeen et al., 2005). Hence, auxiliary quality assurance parameters, such as SNR, percentage of outliers, or average motion, would be needed to ensure sufficient data quality.

In separate studies of multiple sclerosis patients (especially patients with acute lesions who were in pain or discomfort), we have observed significantly more outlier images (up to 25%, Xu et al., 2010) than in normal volunteers as in this study. This raises the important question when comparing patients vs. healthy controls of whether the measured DTI metrics reflect only the intrinsic tissue integrity, or also subject motion, which is more prevalent in patients. This issue has recently been highlighted in the context of resting state fMRI (Power et al., 2012). Even in longitudinal studies of the same patient population, there may be times when patients are more able to hold still, such as in the disease remission versus relapse, hence posing the same question as in cross-sectional studies. Thus, the outlier rejection routine, and the estimated nSNR (Appendix II, which takes the percentage of outlier images into account) and mean translational motion parameters are critical quality assurance tools and metrics to address this question for clinical spinal cord diffusion studies.

DTI quantification

There is both agreement and disagreement between our DTI results and those in the existing literature. The lack of left and right differences between WM tracts and GM ROI agrees with previous reports (Rossi et al., 2008; Smith et al., 2010), but differs from the observations by Lindberg et al. (2010). Studies in animals (Gullapalli et al., 2006; Schwartz et al., 2005a, 2005b) and in humans (Assaf et al., 2008; Onu et al., 2010; Rossi et al., 2008) have suggested that diffusion imaging can detect differences between spinal cord fasciculi. We observed slightly higher diffusivities in PC compared to lateral CST, but we cannot rule out measurement or post-processing bias as the origin, and the differences were relatively small compared to the variability across cord segments.

The λ_⊥ results in this study are consistent with in vivo animal DTI experiments (Budde et al., 2007; Kimet al., 2009) and ex vivo human spinal cord (Klawiter et al., 2011) findings. We found λ_⊥ to be smaller than most recent reports (Dowell et al., 2009; Freund et al., 2010; Onu et al., 2010; Qian et al., 2011; Smith et al., 2010), perhaps reflecting the optimizations implemented in our acquisition and post-processing. Recently, Ellingson et al. (2008) provided a meta-analysis of λ_⊥ and λ_‖ values from different spinal cord regions in both human and small animal. Specifically, the λ_⊥ in the cited in vivo small animal studies, consistent with current λ_⊥ results, was substantially lower than those inmost of the cited in vivo human literature. It is noteworthy that ageing effect on the white matter diffusivities and anisotropy (Agosta et al., 2007; Maier and Mamata, 2005; Van Hecke et al., 2008) was not accounted for in this study due to the small study size.

The whole slice DTI measures provided here as reference are similar to those from studies of axial acquisition with limited in-plane resolution (Van Hecke et al., 2009; Wheeler-Kingshott et al., 2002a) and are analogous to those from studies of sagittal acquisitions (Jeong et al., 2005, 2006; Kim et al., 2010; Ries et al., 2000), which amounts to volume weighted averages of GM and WM values. As expected, such measures show evident differences (Table 2), yet consistent offsets (Fig. 7D vs. Fig. 7A or B), from a tract-specific approach through all slice levels.

Diffusion anisotropy in GMhas been previously reported in both animals (Madi et al., 2005; Schwartz et al., 2005c) and humans (Mamata et al., 2006; Rossi et al., 2008). Complicated intravoxel fiber heterogeneity in GM, including commissural fibers, connections between the dorsal and ventral horns, as well as long tracts, has been observed with Q-ball or high angular resolution diffusion imaging (HARDI) techniques (Cohen-Adad et al., 2008; Lundell et al., 2011). Because conventional DTI cannot resolve such multiple fiber pathways, it underestimates the intrinsic anisotropy of individual fiber pathways. Given the complicated tissue structure in GM and inevitable partial volume effect from surrounding WM, due to either practical resolution limit or point spread function in the phase encoding dimension (Ries et al., 2000), we have refrained from over interpreting our GM λ_⊥ and λ_‖ results (Wheeler-Kingshott and Cercignani, 2009).

Reproducibility

The ICC calculated here was the ratio of between-subject variance to the total between and within-subject variance, while controlling for the nested-slice level variance. Thus, large ICC values indicate small within-subject variance as compared to between-subject variance, hence high within-subject reproducibility. This ICC definition is conceptually different from COV or the normalized Bland-Altman difference, D_BA (Bland and Altman, 1999; Smith et al., 2010), in which variations in repeated measurements are normalized to the mean, which averages away the between-subject variance. In our data, ICC did not always correlate with COV, hence provided complementary information about measurement reproducibility.

It is widely understood that image SNR can bias diffusion quantification (Jones and Basser, 2004) and influence the reproducibility in DTI indices (Farrell et al., 2007). Specifically, the low within-subject variance and high reproducibility of λ_⊥ in WM of our study likely reflected the high DW image SNR when diffusion encodings were applied relatively perpendicular to the tracts, and vice versa for λ_‖ in WM (i.e., low DW image SNR when diffusion encodings were applied relatively parallel to the tracts). The effect on λ_⊥ and λ_‖ propagated to the observed relatively high and moderate reproducibility of FA and MD in WM, respectively. Given the complicated tissue microstructure in GM, DTI provides a poor model for GM, hence the reproducibility of λ_⊥ and λ_‖ measures in GM should not be over-interpreted.

Slice level variance was partitioned out before calculating the reported ICC and COV values. Such reproducibility calculation is more appropriate for slice position dependent analyses (e.g., upstream or downstream of lesion, Klawiter et al., 2012),while the slice averaged reproducibility measure (e.g., the D^BA in Smith et al., 2010) is more appropriate if slice averaged measures are the object of study.

There was no evidence indicating that ROI placement introduced disproportional variability in our study as long as voxels with partial volume effects (CSF–WM and GM–WM) were avoided.

Cardiac pulsation has long been recognized as introducing artifacts in DW images in the lower part of the brain and even more so in the spinal cord. Outlier removal techniques (Chang et al., 2005, 2012) have been developed for DTI and implemented in software such as tortoise (http://www.tortoisedti.org) and dtistudio (http://www.dtistudio.org). However, to the best of our knowledge, neither cardiac gating nor outlier removal has been routinely used in spinal cord DTI. Constraining diffusion tensors to non-negative eigenvalues has also been studied before (Arsigny et al., 2006; Koay et al., 2006). Motion correction through registration is a common technique that has been used in almost all spinal cord DTI studies. Restriction of motion correction to in-plane translation is unique to our protocol and probably not suitable for non-reduced FOV or sagittal acquisitions. The multi-slice-multi-angle technique is common in anatomical imaging but almost all DTI acquisitions use parallel slices in interleaved multi-slice mode. Use of individually tiltable slices is novel in axial spinal cord DTI. In summary, none of the technique employed in this study is individually original. However, the combination of these techniques significantly improved the image quality and the reliability of diffusion quantification in specific spinal cord white matter tracts.

Conclusions

We report several improvements in cervical spinal cord DTI. However, challenges remain. Respiratory motion probably dominates the variance in the lower part of the cervical spinal cord and introduces bias in spinal cord diffusion quantification. At the high spatial resolution used in this study, SNR bias on measurement reproducibility may still be present. Given the non-uniform variances and bias sources revealed in this study, we offer the following recommendations for spinal cord DTI: (1) Locate the slice position, either through registration or reproducible slice prescription; (2) Estimate SNR and motion for each acquired slice level to control for potential biases; (3) Use mixed-effects models to account for systematic bias across cord segments. The effect of respiration and swallowing and the corresponding mitigation strategies need further investigation in future studies.

Advancements in phased-array coil technology (Cohen-Adad et al., 2011b; Kimet al., 2010; Kraff et al., 2009) and accelerated motion insensitive image acquisition may partially alleviate the current challenges faced by spinal cord diffusion quantification. However, standardization of sequence and protocol deployment, as well as centralized data analysis, should be considered prerequisites in multi-center spinal cord diffusion studies.

Appendix I

Positive priors for non-linear diffusion tensor (DT) calculation

The calculation of the DT elements is typically done after linearization of the DWI signal intensity attenuation equations via a logarithm operation. This has the advantage of simplicity and speed; however this method will occasionally produce non-physical, negative eigenvalues, especially in situations of low SNR and/or high anisotropy, such as in the in vivo human spinal cord diffusion imaging.

Non-linear methods, such as the Levenberg–Marquardt (LM) method (Press et al., 1992) are computationally slower, but have the advantages of not distorting the noise characteristics of the signal, and of having the flexibility of solving more complicated DT models (Kroenke et al., 2006) that cannot be easily linearized by the application of a logarithm. We demonstrate a method to add positive priors to the standard LM method that force the estimated diffusion eigenvalues to be positive, as required by the laws of physics, and hence to avoid the negative eigenvalue bias.

The incorporation of priors into the calculation requires the application of Bayes’ theorem to the calculation of the model parameters (abbreviated as λ_i in voxel i), which include a non-diffusion weighted signal amplitude (S₀), 3 eigenvalues (λ₁, λ₂, and λ₃), and 3 angles. Bayes’ theorem states that the posterior probability of the model parameters (Ω_i) given data, D_i, and relevant background information, I, can be expressed as (Jaynes and Bretthorst, 2003):

$$P({\Omega }_i|D_i,I)\propto P(D_i|{\Omega }_i,I)P({\Omega }_i|I),$$ (1)

for which P(D_i|Ω _i,I) is the likelihood of the data given the model parameters, and P(Ω_i|I) is the prior probability for the model parameters. The prior probability is factored into independent prior probabilities for each parameter, but only applied to the eigenvalues, that are constrained to remain positive:

$$P({\Omega }_i|I)\propto P({\lambda }_1|I)P({\lambda }_2|I)P({\lambda }_3|I).$$ (2)

Prior probabilities for these parameters were assigned the following function:

$$P({\lambda }_1|I)=\frac{{\lambda }_j}{{\lambda }_j^2+{\lambda }_{j0}^2},$$ (3)

with λ_j representing any of the eigenvalues, and λ_j0 representing a typical average value of λ_j in the problem. The search is done on the logarithm of the posterior probability, consequently the logarithm of this prior goes to negative infinity as the parameter approaches zero, effectively preventing the searching algorithm form making these parameters less than zero. The likelihood for the data from a voxel, given the model parameters, P(D_i|Ω_i,I), is expressible as a marginal probability when the standard deviation, σ_i, is removed using the sum and product rules:

$$P(D_i|{\Omega }_i,I)\propto \int P({\sigma }_i,D_i|{\Omega }_i,I)d{\sigma }_i\propto P(D_i|{\sigma }_i,{\Omega }_i,I)d{\sigma }_i.$$ (4)

Assigning Jeffreys’ prior probability to P(σ_i|I) and assigning the Gaussian distribution to P(D_i|σ _i,Ω_i,I), the marginal probability for the data may be written as the Student's t-distribution:

$$P(D_i|{\Omega }_i,I)\propto \frac{1}{2}\Gamma {\left(\frac{M}{2}\right(\frac{Q_i}{2}\left)\right)}^{-M/2}.$$ (5)

M is the number of data samples (diffusion measurements) per voxel. Q_i is the total squared residual:

$$Q_i=\sum _{k=1}^M{(E_{ik}-S_{ik})}^2,$$ (6)

with E_ik being the measured signal and S_ik being the model-estimated signal. The logarithm of the joint posterior probability is maximized using the LM method, and is of the form:

$$\text{log}P({\Omega }_i|D_i,I)\propto (-\frac{M}{2}\left)\text{log}\right(\frac{Q_i}{2})+\sum _{j=1}^3\text{log}(\frac{{\lambda }_j}{{\lambda }_j^2+{\lambda }_{j0}^2}),$$ (7)

which is formed by the commonly used first term, the likelihood, which is the logarithm of Eq. (5), added with the summation over j of the priors, which are the logarithm of Eq. (3) for all the eigenvalues. The addition of the prior terms necessitates modifications to the commonly used expression for the gradient (β) and Hessian or curvature matrix ([α]) (using the notation of Press et al., 1992). We accordingly add the first derivate of the log of the priors to β and the second derivative of the same to [α] when calculating these values for the positive model parameters. The remainder of the calculation proceeds using the standard LM method.

Appendix II

Nominal signal-to-noise ratio (nSNR)

The nominal SNR (nSNR) was defined for each ROI as:

$$n\mathrm{S}\mathrm{N}\mathrm{R}=0.665\frac{S_{b0}}{{\sigma }_{\text{noise}}}\sqrt{\frac{N_{\mathrm{D}\mathrm{W}\mathrm{I}}}{6},}$$ (8)

where S_b0 is the mean signal intensity of the ROI in the b₀ image; σ_noise is the standard deviation of signal intensity of an artifact-free noise region manually defined on the same slice as the ROI in the DW (b = 800 s/mm²) image before any image interpolation; and N_DWI is the number of acquired DW and b₀ images (excluding outliers). As the bias in the calculated DTI parameters are related to not only the SNR of the b₀ image, but also the number of acquired DW and b₀ images, N_DWI was normalized to the minimal six DT encoding directions to facilitate comparison across different protocols in literature. The 0.665 scaling factor takes account of the fact that magnitude images were used for the measurement of signal intensities in the presence of noise (Henkelman, 1985).

Appendix III

Supplementary data

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2012.11.014.