Comparison of Three Chain-of-States Methods: Nudged Elastic Band and Replica Path with Restraints or Constraints

Abstract

Chain-of-state methods are becoming important tools in studying the chemical reaction mechanisms, especially for biomacromolecules. In this article, three chain-of-state methods, nudged elastic band (NEB) method and the replica path method with restraints or constraints, were tested and compared using three model systems with various sizes and at different levels of theory: alanine dipeptide isomerization, β-alanine intramolecular condensation, and the matrix metalloproteinase 2 inhibition mechanism. The levels of theory used to describe the three model systems include molecular mechanics (MM), quantum mechanics (QM), and combined quantum mechanics and molecular mechanics (QM/MM). All three methods could correctly determine a reaction path with reasonable estimation of reaction barriers in most cases. The RMSD measurement with additional weighting schemes provides practically infinite choices of reaction coordinates to describe the reaction progress. These findings demonstrate that the chain-of-state methods are powerful tools when being used carefully to generate a plausible reaction mechanism with full pathway for complex systems at an affordable computational cost.

1. Introduction

Reaction mechanisms are important concepts in the understanding of the transition from reactants to products in chemistry.^1–4 In computational chemistry, the reaction mechanism can be represented as a reaction pathway on the potential energy surface (PES) of the system of interest through construction of a potential energy function of the nuclear coordinates.^5–9 A reaction pathway can be identified as the minimum energy path (MEP) connecting two local minima through one or more first-order saddle points that correspond to transition states (TS) on the PES. The MEP can be calculated in various methods. Walking on the PES either downhill from TS through the steepest descent pathway toward energy minima,^10–16 or uphill from energy minimum toward TS,^17–19 can produce the MEP. However, the need of TS a priori or posteriori makes the construction of MEP a difficult task for many systems.

To bypass the calculation of TS before the construction of MEP, there has been rapid development of so-called chain-of-states methods, in which a number of images (i.e., states) of a system are used to connect two end points, and are subject to minimization simultaneously. Restraints or constraints between images are added to maintain the distance between adjacent images to ensure the even distribution of the target reaction path. Some chain-of-state methods include the following: conjugate peak refinement,²⁰ nudged elastic band (NEB), ^21–28 replica path (RPATH),^29–32 line-integral, ^33–37 combined reaction path and stationary structures optimization,³⁸ zero temperature string (ZTS) methods,^39–42 finite temperature string (FTS) methods,⁴³, quadratic string method,⁴⁴ and growing string methods.^45–50

In the NEB method,²¹ the images are held together by harmonic spring forces. The orthogonal forces are projected out and do not affect the minimization of each image. Therefore, the NEB calculations can principally produce the MEP when fully converged. Chu et al. ⁵¹ developed the first superlinear minimizer for the NEB method. Their development was based on expanding the adopted basis Newton-Raphson (ABNR) method⁵² and is available in the CHARMM program suite.⁵³

Restraints have been implemented within the replica path (RPATH) method in CHARMM.³¹ Spring forces are introduced to harmonically restrain distances between adjacent images along the reaction pathway. Additional forces can also be added to maintain path smoothness. The study of the chorismate mutase mechanism using this approach demonstrated that this method can be effectively applied on macromolecules.³¹ Holonomic constraints have also been implemented within the replica path facility in CHARMM.³² The distances between adjacent images are maintained equal to each other up to convergence for each round of optimization. This can provide an even distribution of images to better represent the reaction process in the TS region.

It should be noted that the MEP is not sufficient to determine a mechanism in that entropic effects are ignored. Free energy of barrier crossing can be calculated or estimated by a variety of techniques starting from an MEP. The focus of this paper is the determination of MEP or approximate MEPs that are suitable for further investigation using free energy simulation techniques or entropy estimation such as those involving harmonic analysis approaches. ⁵⁴

Unlike single geometry optimization strategies, the chain-of-states methods have not been widely applied, especially in QM/MM enzymatic mechanism studies. A benchmark study with multiple test cases other than the original development work is necessary to demonstrate both the strengths and weaknesses of available methods and to promote their application and development. In this study, three chain-based optimization methods from CHARMM—NEB, RPATH with restraint and constraint—are tested using three reactions as test cases: alanine dipeptide isomerization, β-alanine (3-aminopropanoic acid) intramolecular condensation, and the matrix metalloproteinase 2 (MMP2) inhibition mechanism. The alanine dipeptide isomerization is a typical test case in computational methodology developments.^55–60 The β-lactam, the intramolecular condensation product of β-alanine, is part of the basic structure of widely used β-lactam antibiotics.^61,62 The MMP2 is a proteolytic enzyme that digests type IV collagens.⁶³ The structure and the catalytic mechanisms of MMP2 were under comprehensive studies.^64–69 All three systems together provide adequate assessment and discrimination of the efficiency of the methods under this study.

It has been shown that the reweighting of the atoms involved in the reaction path was crucial to obtain a reaction path in NEB calculations. ²⁷ In addition to mass-weighting scheme, user defined weighting schemes are also applied in some of the path calculations in this study for better results.

2. Method and Materials

2.1 NEB Method

The superlinear NEB minimizer⁵¹ is implemented on the basis of ABNR method⁵² in CHARMM.⁵³ The forces on each replica in NEB framework are projected using a tangent vector (τ_i) along the path

$$\begin{array}{l}{\mathbf{F}}_i={\mathbf{F}}_i^{\perp }+{\mathbf{F}}_i^{\left|\right|},\\ {\mathbf{F}}_i^{\perp }=-\nabla V({\mathbf{r}}_i)·(1-{\tau }_i{\tau }_i),\\ {\mathbf{F}}_i^{\left|\right|}=-{\nabla }_i\left(\frac{1}{2}k\sum _{j=1}^N{(\mathrm{\Delta }{l}^j-\overline{\mathrm{\Delta }l})}^2\right)·({\tau }_i{\tau }_i).\end{array}$$ (1)

where ${\mathbf{F}}_i^{\perp }$ and ${\mathbf{F}}_i^{\left|\right|}$ are force components perpendicular (off-path direction) and parallel (elastic band with force k) to the tangent vector of replica i (τ_i), respectively. V is the potential energy function, Δl is the distance between adjacent replicas. To improve the computational efficiency, both steepest-descent (SD) and Newton–Raphson (NR) in ABNR are extended to the NEB framework.

Various choices of tangent vector have been proposed and could lead to a different behavior of NEB calculations in terms of computational efficiency and smoothness of calculated reaction path.^22,25,26,28 The tangent vector used in the NEB method implemented in CHARMM is defined as

$${\tau }_i=\text{NORM}\left[\mathbf{w}·\left({\mathbf{r}}_{i+1,j}^{\text{RMS}\to i}-{\mathbf{r}}_{i-1,j}^{\text{RMS}\to i}\right)\right],$$ (2)

where NORM is the normalization operator, w is the weighting vector, and RMS → i superscript indicates that the neighboring replica is best fitted to replica i. ⁵¹

2.2 RPATH with Restraints

To optimize the reaction path represented by a series of replicas and their environment, penalty functions are needed to maintain the distance between adjacent replicas. In a restraint framework,³¹ each replica is restrained using best-fit root-mean-square distances (RMSD) to the adjacent replicas. The RMS restraint forces are defined by the following equation

$$E_{\mathit{rms}}=\sum _{i=1}^N\frac{1}{2}{k}_{\mathit{rms}}{\omega }_i{(r_i-\overline{r})}^2,$$ (3)

where N is the number of replicas, k_rms is the force constant used to restrain distances between adjacent replicas along the reaction pathway, r_i is the best-fit RMSD between replica i and i+1, and r̄ is the average distance between adjacent replicas. An atomic weight factor ω_i is used to select atoms and to determine their strength in the fitting procedure.

An additional force can be added to restrain the angle between replicas along the pathway through an angle energetic penalty term

$$\begin{array}{l}{E}_{\mathit{angle}}=\sum _{i=1}^N\frac{1}{2}{k}_{\mathit{ang}}{(\mathit{COSMAX}-cos{(\theta )}_i)}^2,if\mathit{COSMAX}>cos{(\theta )}_i,\\ E_{\mathit{angle}}=0,if\mathit{COSMAX}\le cos{(\theta )}_i.\end{array}$$ (4)

The angle θ, illustrated in Fig. 1, defines the deviation of the pathway from linearity. The force constant k_ang controls the rigidity of the pathway. The constant, COSMAX, determines the value of cos(θ) subject to the angle forces. Angle term forces are converted to best-fit RMSD radial forces using the definition of cosines. Best-fit RMSD forces are computed analytically. ⁵¹

Fig. 1.

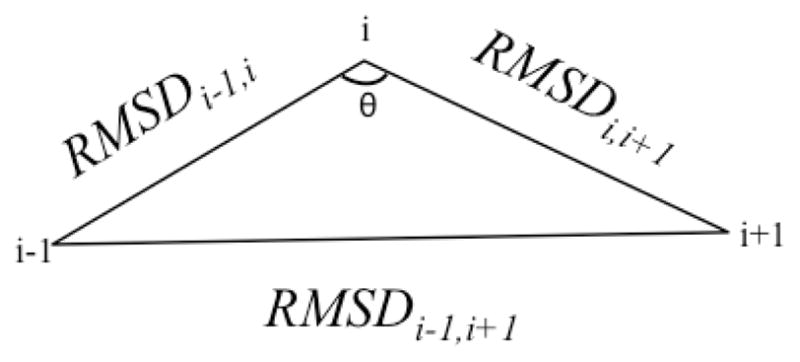
Illustration of angle θ for replica i in RPATH calculation. RMSD_i−1,i is the distance between replica i−1 and i. It is similar to RMSD_i,i+1 and RMSD_i−1,i+1.

2.3 RPATH with Constraint

Recently, the equal distance holonomic constraint³² method has been implemented in the RPATH framework in CHARMM. Given two states of a molecular system with N atoms, r⁰ and r^k, a chain of K+1 replicas can be constructed to connect these two states. The distance between each pair of adjacent replicas is set to be equal to each other

$$\mathrm{\Delta }{l}^0=•••=\mathrm{\Delta }{l}^i=•••=\mathrm{\Delta }{l}^{K-1}=\overline{\mathrm{\Delta }l}.$$ (5)

Here, Δlⁱ is the distance between replica i and i+1, and can be in any form, including best-fit RMS distance. $\overline{\mathrm{\Delta }l}$ is the average distance between adjacent replicas. The following scheme is used to propagate the reaction path, which satisfies eq. (5).

1. Set up and calculate initial average distance, $\overline{\mathrm{\Delta }l}$, for replicas r⁰⁽⁰⁾ through r^k(0). The superscript “(0)” indicates the optimization iteration step.

2. To maintain the equal distance, a set of K coefficients, (λⁱ)⁽ⁿ⁾(i=0,K−1), are used to update the coordinates of each replica i:

   $${\left({\mathbf{r}}^i\right)}^{(n+1)}={\left({\mathbf{r}}^i\right)}^{(n)}+{\left({\lambda }^{i-1}\right)}^{(n)}{\left(\frac{\partial \mathrm{\Delta }{l}^{i-1}}{\partial {\mathbf{r}}^i}\right)}^{(n)}+{\left({\lambda }^i\right)}^{(n)}{\left(\frac{\partial \mathrm{\Delta }{l}^i}{\partial {\mathbf{r}}^i}\right)}^{(n)}.$$ (6)
3. Solve (λⁱ)⁽ⁿ⁾ by setting the first-order Taylor expansion of each of $({({\lambda }^i)}^{(n)}-\overline{\mathrm{\Delta }l})(i=0,K-1)$ with respect to (λ^j)⁽ⁿ⁾ to zero:

   $$-\left({\left(\mathrm{\Delta }{l}^i\right)}^{(n)}-\overline{\mathrm{\Delta }l}\right)=\sum _{j=i-1}^{i+1}{\left(\frac{\partial \mathrm{\Delta }{l}^i}{\partial {\lambda }^j}\right)}_{{\lambda }^j}^{(n)}{\left({\lambda }^j\right)}^{(n)}.$$ (7)

4. If any of the values of $\mid {(\mathrm{\Delta }{l}^i)}^{(\text{n}+1)}-\overline{\mathrm{\Delta }l}\mid (i=0,K-1)$ is greater than a selected tolerance, then repeat steps (ii) and (iii).

5. After convergence, the RPATH calculation leads to a reaction path composed by K+1 equal distance replicas connecting states r⁰ and r^k.

When using constraints with RPATH, a kinetic energy potential can be added to the potential energy making the overall objective function to be minimized, a Hamiltonian.³² Therefore the optimized path is a so-called minimum Hamiltonian path (MHP) instead of an MEP. The kinetic energy component in the potential helps to prevent kinks and therefore helps to maintain the smoothness of the path. However, this smoothness comes at the cost of deviation from the MEP, resulting in higher reaction barriers.

2.4 Replication Schemes

Two replication schemes are available in CHARMM for chain-of-states calculations. In one scheme, all the replicas are contained in a single CHARMM protein structure file (PSF). Either the full system or specific “important” parts (e.g., active site of a catalytic enzyme) can be chosen and replicated. In the other scheme, the parallel distributed replicas (REPD) framework, a series of replicas with independent setup, are generated and run on different processors. Each replica has its own setup including PSF file, which contains the complete system information. With REPD, users have more flexibility to treat each replica differently with separate PSFs without affecting other replicas.

3. Results

3.1 Isomerization of Alanine Dipeptide

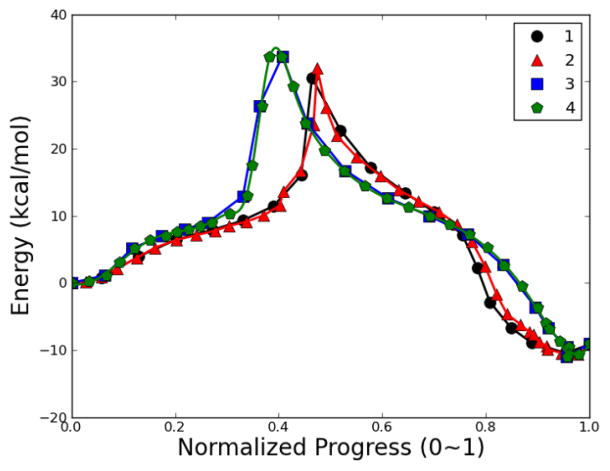
The first test case is the isomerization of the alanine dipeptide (N-acetylalanyl-N-methyl-amide). Two backbone dihedral angles (φ and ψ) are used to describe the isomerization process of this molecule (Fig. 2). The reaction path in the current study connects two conformers C_7eq and C_ax corresponding to two minima on the PES (Fig. 3). The CHARMM 22 force field⁷⁰ with CMAP backbone dihedral angle corrections⁷¹ was used for the calculation. No solvent molecules were present in the model system. All the RPATH calculations are carried out using 25 replicas. The initial guess of reaction path for optimization was constructed through linear interpolation (see Fig. S1 in Supporting Information). The TS structure of isomerization was optimized in CHARMM with the barrier as 8.74 kcal/mol with reference to conformer C_ax.

Fig. 2.

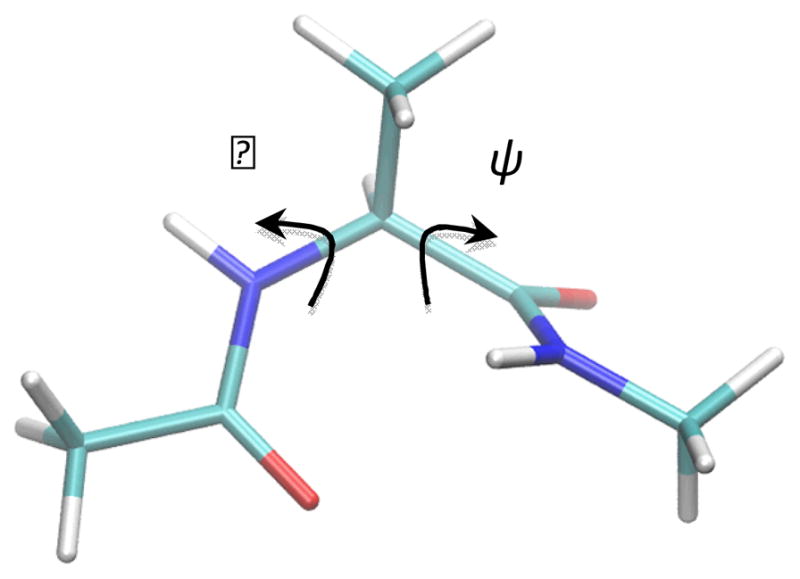
Structure of alanine dipeptide and two dihedral angles as reaction coordinate of isomerization. H, C, N, and O shown in white, cyan, blue, and red, respectively.

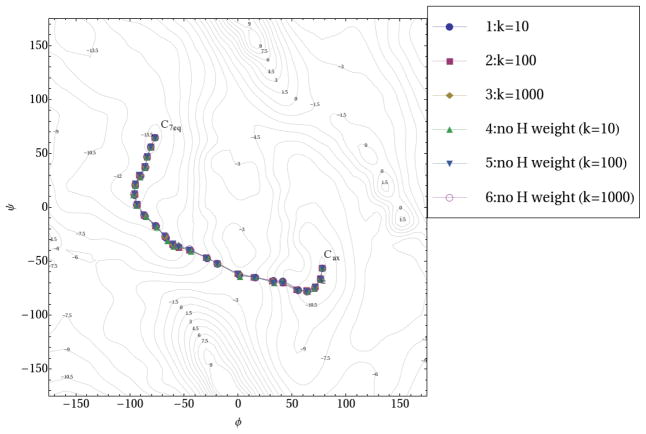
Fig. 3.

Reaction pathways of alanine dipeptide isomerization using NEB method. In pathways 1~3, the elastic force constant k is 10, 100 and 1000 kcal•mol⁻¹• Å⁻², respectively. The mass-weighted RMSD of all the atoms is used to measure the distance between replicas. The pathways 4~6 repeat the calculations of 1~3 with hydrogens excluded from mass-weighted RMSD calculation.

3.1.1 NEB Results

Six NEB calculations of alanine dipeptide were carried out as follows: In calculations 1~3, all atoms are used to calculate the mass-weighted RMSD between each adjacent replicas with a spring constant as 10, 100 and 1000 kcal•mol⁻¹• Å⁻², respectively. Calculations 4~6 repeat calculations 1~3, but have hydrogen atoms excluded from mass-weighted RMSD calculation. All six calculations lead to almost identical reaction pathways, which are presented on a contour plot using φ and ψ as reaction coordinates (Fig. 3). This observation demonstrates that the MEP obtained from NEB does not depend on the value of the spring constant k. The reaction barriers for isomerization with reference to C_7eq conformer obtained from these six calculations are within a very narrow range, which is between 8.74 and 8.81 kcal/mol (Table 1). For all six calculations, the ninth replica starting from the C_ax conformer represents an approximate transition state (TS) of the isomerization. From this point forward, the C_ax conformer always serves as the first replica for the replica numbering.

Table 1.

Calculations for alanine dipeptide isomerization

methods	parametersa		barrier (kcal/mol)	replica ID of approximate TS
NEB	1 k=10		8.78	9
	2 k=102		8.81	9
	3 k=103		8.81	9
	4 k=10, no H weight		8.74	9
	5 k=102, no H weight		8.81	9
	6 k=103, no H weight		8.78	9
restraint	kang=102, COSMAX=0.95	1 krms=103	8.52	8
		2 krms=104	8.64	8
		3 krms=105	8.63	7
		4 krms=103, no H weight	8.54	8
		5 krms=104, no H weight	8.77	8
		6 krms=105, no H weight	8.76	8
	krms=105, no H weight COSMAX=1.00	1 kang=102	8.64	8
		2 kang=103	8.78	9
		3 kang=104	8.87	10
		4 kang=2×104	10.37	10
constraint	1 kpki= 0, all atom mass-weighted		8.52	8
	2 kpki= 0, no hydrogen weight		8.73	9
	3 kpki=100, no hydrogen weight		9.63	15
	4 kpki=10, no hydrogen weight		9.59	11
	5 kpki=1, no hydrogen weight		8.78	9

^aUnit for force constant is kcal •mol⁻¹ •Å⁻².

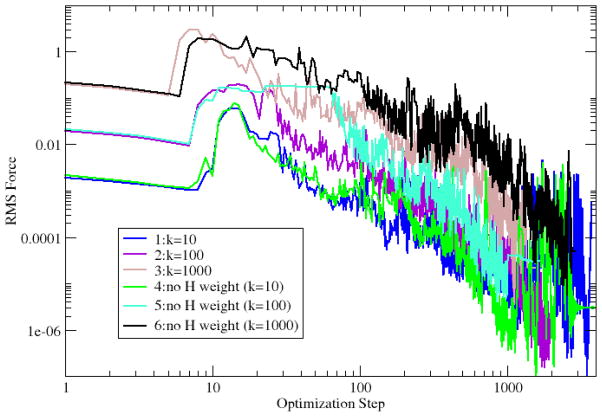
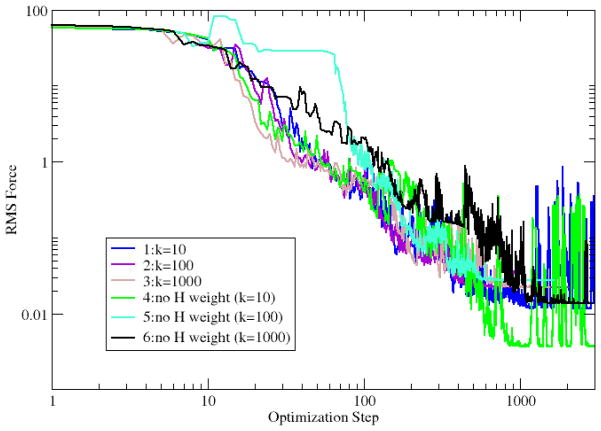
Both RMS forces perpendicular (off-path) and parallel to the tangent vector of the reaction pathway are plotted for calculations 1~6 (Fig. 4 and 5). The RMS forces fluctuate during optimization due to the fact that the tangent vector at each replica used for force projection is defined by a discrete reaction path and changes from one optimization step to the next. The plots of tangent forces in Fig. 4 start at different levels for the calculations with different spring force constants but converge toward zero, showing that a MEP can be obtained independently from spring constants (Fig. 4). The off-path RMS forces are independent from added spring forces, resulting from all six plots starting at the same level (Fig. 5). The RMS forces decrease smoothly but slowly for about ten steps initially before decreasing more rapidly. This is due to the ABNR optimizer implemented in CHARMM being combination of SD and NR methods with SD dominating the initial steps of the optimization. The convergence rates are not significantly different in these NEB calculations, except for calculation 5 with the force constant set to 100 kcal•mol⁻¹• Å⁻² and hydrogens excluded from the RMSD measurement.

Fig. 4.

The tangent RMS force (kcal•mol⁻¹•Å⁻¹) in NEB optimization of alanine dipeptide isomerization.

Fig. 5.

The off-path RMS force (kcal•mol⁻¹•Å⁻¹) in NEB optimization of alanine dipeptide isomerization.

3.1.2 RPATH/Restraint Results

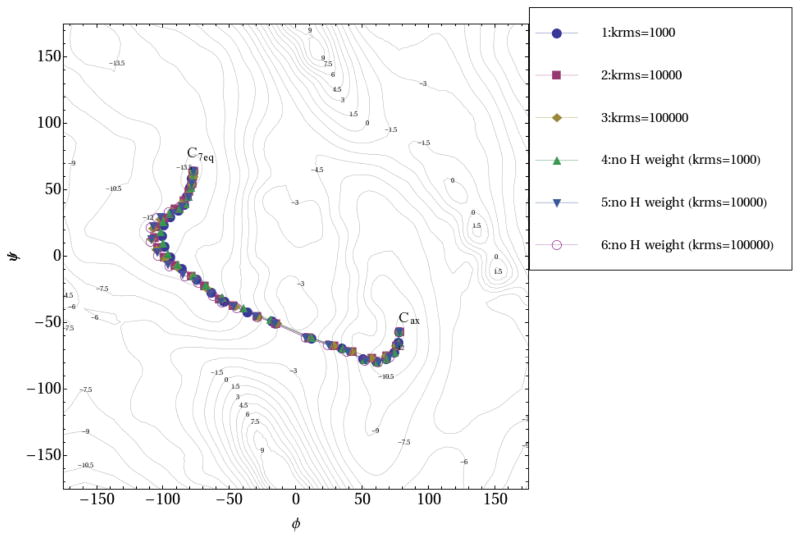
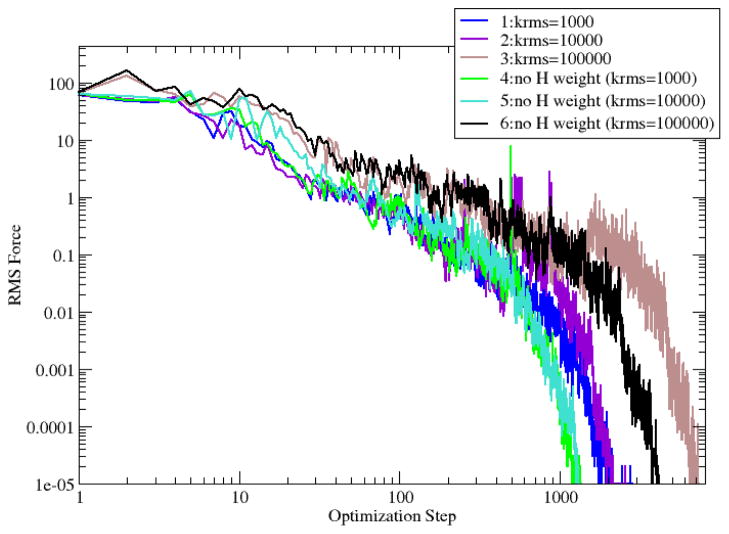
Six RPATH/restraint calculations of alanine dipeptide were carried out as the following. In calculations 1~3, all atoms are used to calculate the mass-weighted RMSD between each adjacent replica with a spring constant as 1000, 10000 and 100000 kcal•mol⁻¹• Å⁻², respectively. Calculations 4~6 repeat calculations 1~3, but have hydrogens excluded from the mass-weighted RMSD calculation. Larger spring constants are used in this setup, because smaller forces are not sufficient to maintain the close distance between adjacent replicas around a TS region (see Fig. S2 in Supporting Information). All six calculations have k_ang as 100 kcal•mol⁻¹• Å⁻², and COSMAX=0.95. The deviation among six pathways is noticeable around the region connecting C_7eq and the TS (Fig. 6). The barriers with reference to the C_7eq conformer range narrowly from 8.52 to 8.77 kcal/mol for all six pathways (Table 1), with barrier from pathway 6 (8.76 kcal/mol) as the closest to the one from the TS calculation in CHARMM (8.74 kcal/mol). Because no force projection is involved in RPATH with restraint calculations, the RMS forces actually converge toward zero for all six calculations (Fig. 7). Calculations 4 and 5 have the similar and the fastest convergence rates, while calculations 3 and 6 with largest k_rms display the slower convergence rates than other calculations.

Fig. 6.

Reaction pathways of alanine dipeptide isomerization using RPATH/restraint method. In pathways 1~3, the elastic force constant k is 1000, 10000 and 100000 kcal•mol⁻¹•Å⁻², respectively. The mass-weighted RMSD of all the atoms is used to measure the distance between replicas. The pathways 4~6 repeat the calculations of 1~3 with hydrogens excluded from the mass-weighted RMSD calculation.

Fig. 7.

The RMS force (kcal•mol⁻¹•Å⁻¹) in RPATH/restraint optimization of alanine dipeptide isomerization.

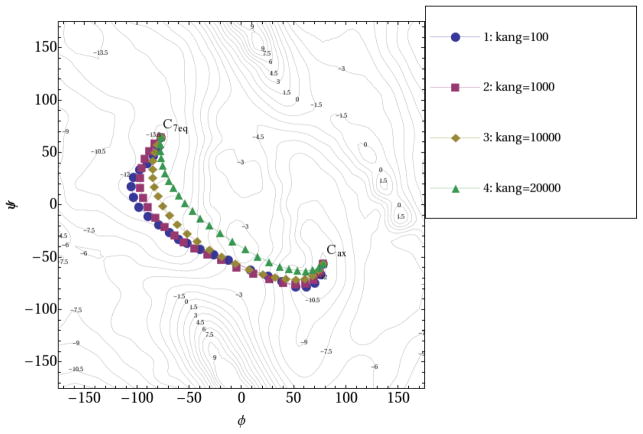
Different k_ang values were applied with k_rms = 100000 kcal•mol⁻¹• Å⁻² with hydrogen atoms excluding from mass-weighted RMSD measurement (Fig. 8). The COSMAX value was set to 1.00 for these calculations to increase the smoothness of the pathways further. With larger k_ang values, the pathways become more rigid and smoother and deviate significantly from the MEP. Interestingly, pathways 2 and 3 in Fig. 8 with k_ang as 1000 and 10000 kcal•mol⁻¹• Å⁻², respectively, still go through the TS region with barriers rather close to the one from TS calculation.

Fig. 8.

Reaction pathways of alanine dipeptide isomerization using RPATH/restraint method. The k_ang for the pathway curvature controlling is 100, 1000, 10000 and 20000, for pathways 1~4, respectively. For all the calculations, k_rms is 100000, and hydrogens are excluded from mass-weighted RMSD measurement. (force constant unit: kcal•mol⁻¹• Å⁻²)

Using k_ang values less than 10 kcal•mol⁻¹• Å⁻² leads to unusable pathways that tend to “hover” in a minimal basin (see Fig. S3 in Supporting Information). In this example, there is a two order-of-magnitude range of values for k_ang that provides a pathway that is very similar to the MEP. The optimal value will vary from system to system and also will depend on the number of replicas. Thus some care and preliminary investigation is required to use this method well.

3.1.3 RPATH/Constraint Results

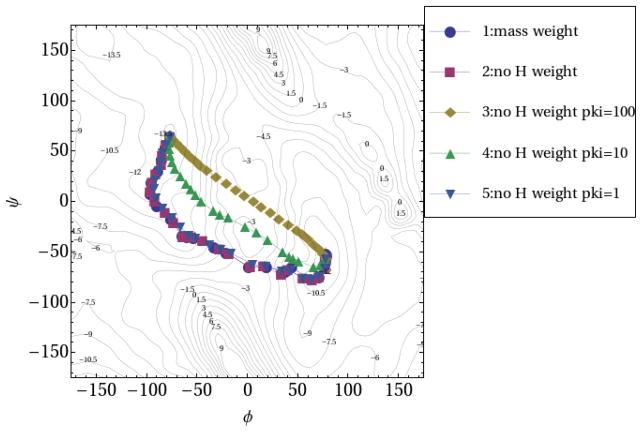
Five RPATH/constraint calculations of alanine dipeptide were carried out and plotted in Fig. 9. The reaction barrier obtained from calculation 1, with hydrogen included in the mass-weighted RMSD measurement, is 8.52 kcal/mol for replica 8. In calculation 2, with hydrogen excluded from RMSD measurement, replica 9 has a reaction barrier of 8.73 kcal/mol. The force constants of the kinetic energy potential (k_pki) as 100, 10 and 1 kcal•mol⁻¹• Å⁻² were applied in another three calculations, respectively. For calculation 3 with largest k_pki, the MHP as the reaction pathway resembles the straight-line interpolation between two end points. When reducing the kinetic energy force constant by an order of magnitude, the corresponding MHP is roughly in the middle between the MEP and the straight line connecting the two end points. The corresponding MHP for the smallest k_pki closely resembles the MEP with correct reaction barrier (8.78 kcal/mol) given by replica 9.

Fig. 9.

Reaction pathways of alanine dipeptide isomerization using RPATH/constraint method. The hydrogen is included for mass-weighted RMSD for pathway 1, but excluded in all other pathways. The kinetic energy potential is included in pathway 3~5 with force constant as 100, 10 and 1kcal•mol⁻¹• Å⁻², respectively.

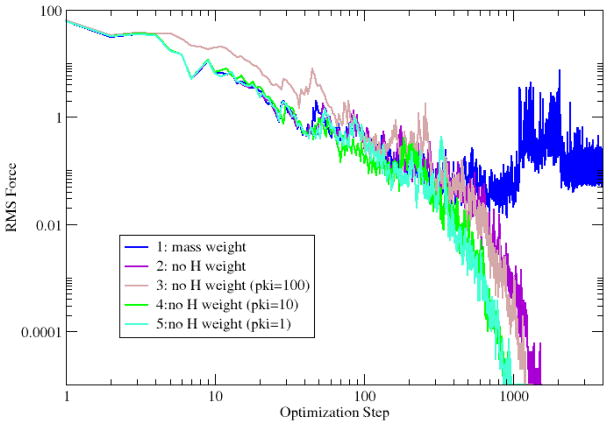
The RMS forces along the pathways during the path optimization are plotted in Fig. 10. Calculation 1 has difficulty to converge (1 in Fig. 10). This is due to the sensitivity of holonomic constraint iterations to the rotation of methyl groups. After excluding hydrogen from the RMSD measurement, the RPATH calculation converges rapidly (2 in Fig. 10). When including kinetic energy components, the convergence rate accelerates further.

Fig. 10.

The RMS force (kcal•mol⁻¹• Å⁻¹) in RPATH/constraint optimization of alanine dipeptide isomerization.

3.2 β-Alanine Intramolecular Condensation

The intramolecular condensation of β-alanine is a one-step reaction (Fig. 11) with a barrier of 56.79 kcal/mol at the B3PW91/6–31g(d,p) level of theory^72–74 calculated in Q-Chem.⁷⁵ It should be noted that this barrier is based on the internal energy from the QM calculations that do not include the zero point vibrational energy. Both the reaction barrier and TS structure from these QM calculations serve as benchmarks for the RPATH calculations. Due to the computational cost of the RPATH QM calculations, they were considered converged when the RMS force of the path is below 0.1 kcal•mol⁻¹• Å⁻¹ and the change of the total reaction path energy was less than 0.01 kcal•mol⁻¹ for the last optimization step of RPATH calculations.

Fig. 11.

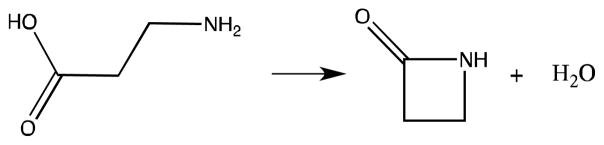
Intramolecular condensation of β-alanine.

3.2.1 NEB Results

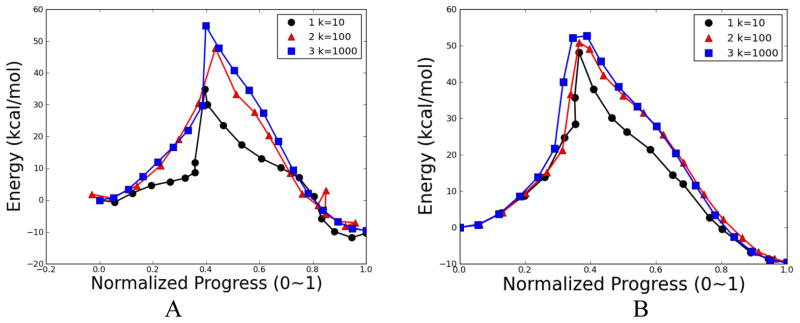
Four NEB calculations were carried out and plotted in Fig. 12. In calculations 1 and 2, all atoms are used to calculate the mass-weighted RMSD between adjacent replicas with a spring constant as 10 and 100 kcal•mol⁻¹• Å⁻², respectively. Calculations 3 and 4 repeat the first two calculations but with an additional weighting factor of 16 on the migrating hydrogen added to the mass-weighting scheme. For each NEB calculation, the structure with the highest energy is referred as the approximate TS structure. The approximate TS structures from these pathways are superimposed with the QM TS in Fig. 13.

Fig. 12.

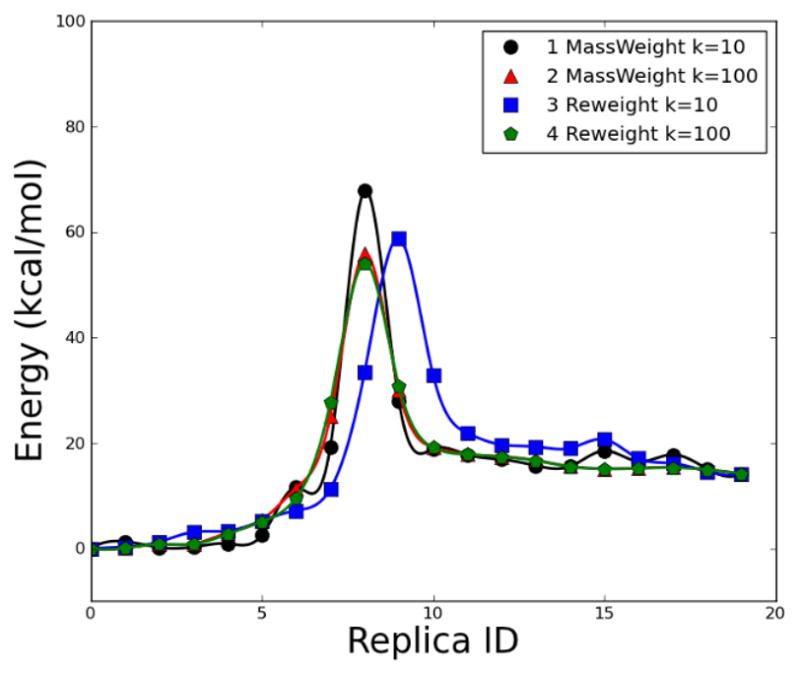
Energetic profile of β-alanine intramolecular condensation reaction using NEB method with 20 replicas. Four calculations with different force constant k (kcal•mol⁻¹• Å⁻²) and weighting schemes: 1, k=10, mass-weight; 2, k=100, mass-weight; 3, k=10, additional weight on migration hydrogen; 4, k=100, additional weight on migration hydrogen. All the calculations were carried out at B3PW91/6–31g(d,p) level of theory, which was applied for all other β-alanine calculations.

Fig. 13.

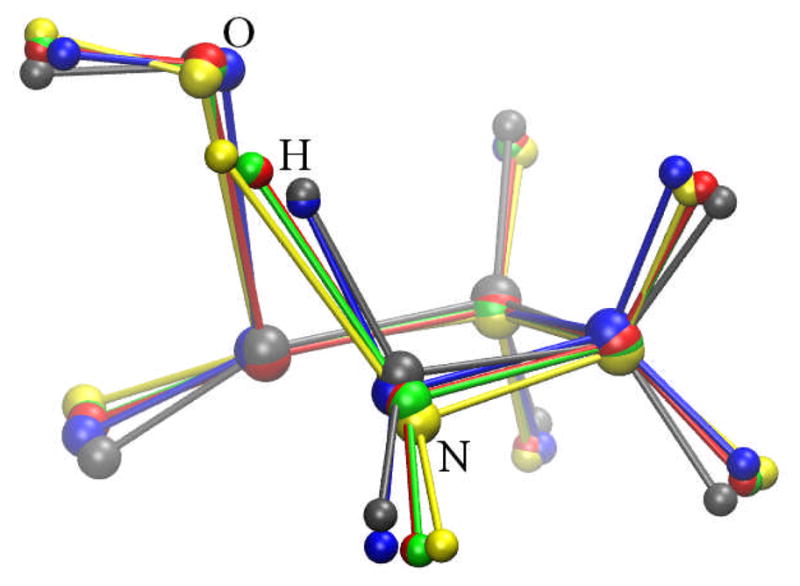
β-alanine intramolecular condensation reaction approximate transition states from NEB calculations using 20 replicas. Four calculations with different force constant k (kcal•mol⁻¹• Å⁻²): yellow, pathway 1, k=10, mass-weight; green, pathway 2, k=100, mass-weight; blue, pathway 3, k=10, additional weight on migration hydrogen; red, pathway 4, k=100, additional weight on migration hydrogen; gray: the TS obtained from QM calculation.

The barrier of pathway 1 is 67.83 kcal/mol, which is about 10 kcal/mol higher than the QM barrier. The barriers of pathways 2, 3, and 4 (55.83, 58.83, and 54.10 kcal/mol, respectively) are rather close to the QM barrier. The approximate TS structures from pathways 1, 2, and 4 (yellow, green, and red, respectively) in Fig. 13 show that the positions of migration hydrogen are significantly different from that in the QM TS structure. The position of migration hydrogen in the approximate TS structure from the pathway 3 (blue in Fig. 13) closely resembles the QM TS structure, but the overall structural difference between the approximate TS from pathway 3 and the QM TS is rather significant.

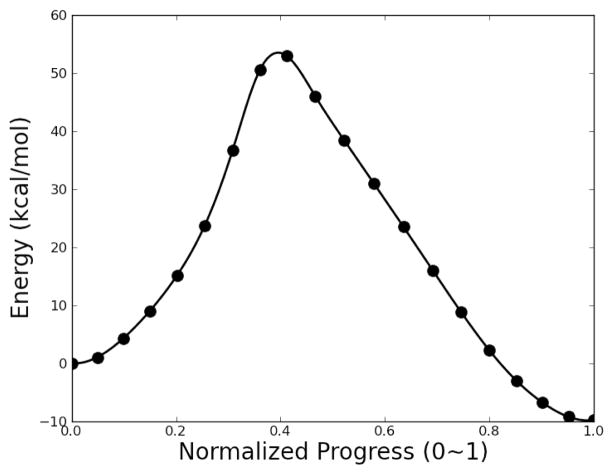
3.2.2 RPATH/Restraint Results

Four RPATH/restraint calculations are presented in Fig. 14. The mass-weighted RMSD was used as a measurement of the distance between replicas. The approximate TS structures from these pathways are superimposed with the QM TS in Fig. 15. The barriers of pathways 1 and 2 are around 40 kcal/mol, which is about 16 kcal/mol lower than the QM barrier. The approximate TS structures from pathways 1 and 2 (yellow and green, respectively) in Fig. 15 show that the positions of migration hydrogen are significantly different from that in the QM TS structure. Both energy and structure differences indicate that pathways 1 and 2 do not capture the TS accurately. Both calculations have large force constants for RMSD distance (k=10000 and 100000 kcal•mol⁻¹• Å⁻² for 1 and 2, respectively) and relatively small force constants for the angle term (k_ang=100 kcal•mol⁻¹• Å⁻²). Pathways 3 and 4 repeat the calculations of pathway 1 and with larger k_ang as 1000 and 10000 kcal • mol⁻¹ • Å⁻², respectively. The barriers of pathway 3 and 4 are 54.32 and 63.78 kcal/mol, respectively, and are closer to the barrier from the QM calculation than pathways 1 and 2. Both approximate TSs from pathway 3 and 4 (blue and red) have the same nonmass-weighted RMSD distance (0.10 Å) to the QM TS (gray), while the approximate TSs from pathways 1 and 2 also have the same value (0.18 Å) for such distance to the QM TS.

Fig. 14.

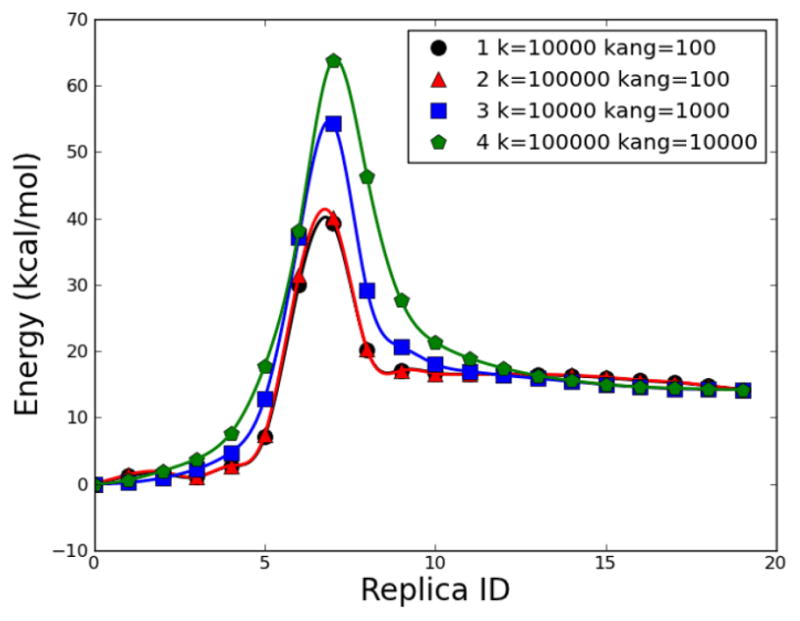
Energetic profile of β-alanine intramolecular condensation reaction using RPATH/restraint method with 20 replicas. Four calculations with different force constant k and angle force k_ang in kcal•mol⁻¹• Å⁻².

Fig. 15.

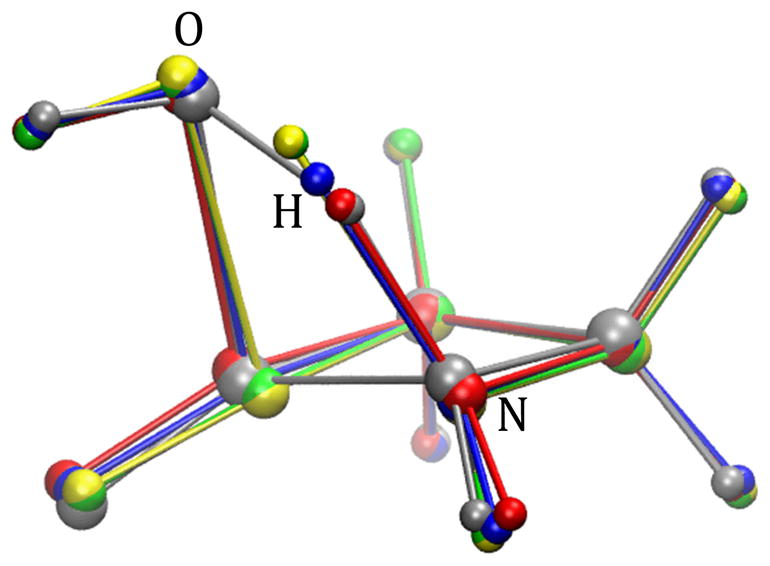
β-alanine intramolecular condensation reaction approximate transition states from RPATH/restraint calculations using 20 replicas. Four calculations with different force constant k and angle force k_ang in kcal•mol⁻¹• Å⁻²: yellow, pathway 1, k=10000, k_ang=100; green, pathway 2, k =100000, k_ang=100; blue, pathway 3, k =10000, k_ang=1000; red, pathway 4, k =100000, k_ang=10000; gray: the TS obtained from QM calculation.

These four RPATH/restraint calculations were repeated with an additional weighting factor of 16 on the migrating hydrogen added to the mass-weighting scheme. However, the added weighting factor on the migrating hydrogen did not improve the pathways in terms of smoothness and estimated reaction barriers (see Fig. S4 in Supporting Information).

3.2.3 RPATH/Constraint Results

Two sets of RPATH/constraint calculations are presented: one with mass-weighted RMSD (set A), and the other with an additional weighting factor of 16 on the migrating hydrogen added to the mass-weighting scheme (set B). For set A, pathways 1, 2 and 3 with k_pki as 100, 10 and 1 kcal•mol⁻¹• Å⁻², respectively, are plotted in Fig. 16A. Pathway 3 has the smallest k_pki and yields barrier that is the closest to the QM calculation, differing by only 3 kcal/mol. All three approximate TS structures from pathways 1, 2, and 3 are superimposed with the QM TS in Fig. 17A. The migrating hydrogen in all three approximate TSs shows a significant difference from QM TS. The RMSD of these approximate TSs in reference to the QM TS ranges from 0.13 to 0.45 Å, with the approximate TS of pathway 1 displaying the largest value.

Fig. 16.

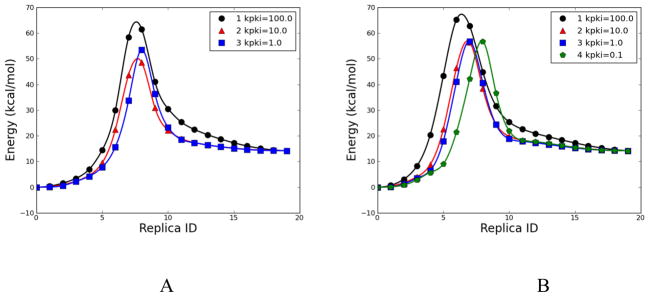
Energetic profile of β-alanine intramolecular condensation reaction using RPATH/constraint method with 20 replicas. A. Three calculations using mass-weighted RMSD with different k_pki (kcal•mol⁻¹• Å⁻²) values. B. Four calculations using mass-weighted RMSD and additional weighting factor on migration hydrogen with different k_pki values.

Fig. 17.

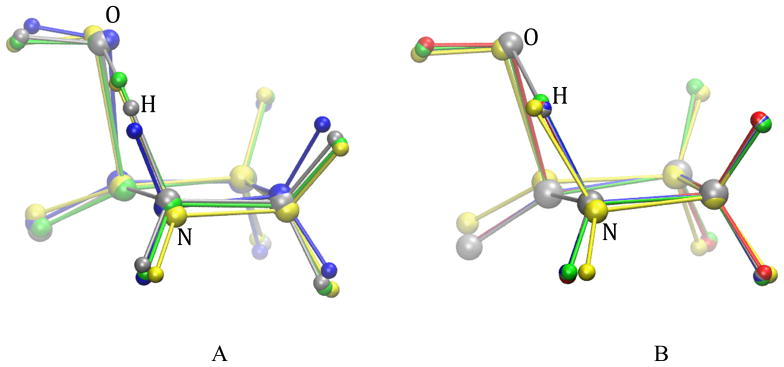
β-alanine intramolecular condensation reaction approximate transition states from RPATH/constraint calculations with 20 replicas. A. Three calculations using mass-weighted RMSD with different kinetic k_pki (kcal•mol⁻¹• Å⁻²) values: yellow, k_pki =100.0; green, k_pki =10.0; blue, k_pki =1.0; gray: the TS obtained from QM calculation. B. Four calculations using mass-weighted RMSD and additional weighting factor on migration hydrogen with different kinetic k_pki values: yellow, k_pki =100.0; green, k_pki =10.0; blue, k_pki =1.0; red, k_pki =0.1; gray: the TS obtained from QM calculation.

In set B, pathways 1, 2, 3 and 4 with k_pki as 100, 10, 1 and 0.1 kcal•mol⁻¹•Å⁻², respectively, are plotted in Fig. 16B. Pathway 1 has an overestimated barrier, 65.22 kcal/mol (Table 2). Pathways 2, 3, and 4 have reaction barriers very close to the QM barrier with less than 0.5 kcal/mol difference. The superimposed approximate TS structures in Fig. 17B show the extreme similarities between the approximate TSs from pathways 2, 3, and 4 (green, blue, and red, respectively) and the QM TS (gray), especially the position of the migrating hydrogen. All three approximate TSs have very small RMSDs, which are equal to or are less than 0.03 Å with reference to the QM TS (Table 2). By emphasizing the movement of the migrating hydrogen with a large weighting factor, set B showed significant improvement compared with set A.

Table 2.

Calculations for β-alanine intramolecular condensation reaction^a

methods	parametersb		barrier (kcal/mol)	RMSD with QM TS (Å)	replica ID of approximate TS
NEB	mass-weight	1 k=10	67.83	0.28	9
		2 k=102	55.88	0.19	9
	mass-weight with additional weight on migrating hydrogen	1 k=10	58.83	0.18	10
		2 k=102	54.10	0.18	8
restraint	1 krms=104, kang=102		39.19	0.18	8
	2 krms=105, kang=102		40.16	0.18	8
	3 krms=104, kang=103		54.32	0.10	8
	4 krms=105, kang=104		63.78	0.10	8
constraint	mass-weight	1 kpki= 102	61.52	0.45	9
		2 kpki= 10	48.52	0.13	9
		3 kpki=1	53.45	0.18	9
	mass-weight with additional weight on migrating hydrogen	1 kpki= 102	65.22	0.18	7
		2 kpki= 10	56.43	0.03	8
		3 kpki 1	56.79	0.01	8
		4 kpki=0.1	56.78	0.02	9

^aAll calculations were carried with whole system described in QM at B3PW91/6–31g(d,p) level of theory.

^bUnit for force constant is kcal•mol⁻¹•Å⁻².

3.3 Inhibition Mechanism of MMP2

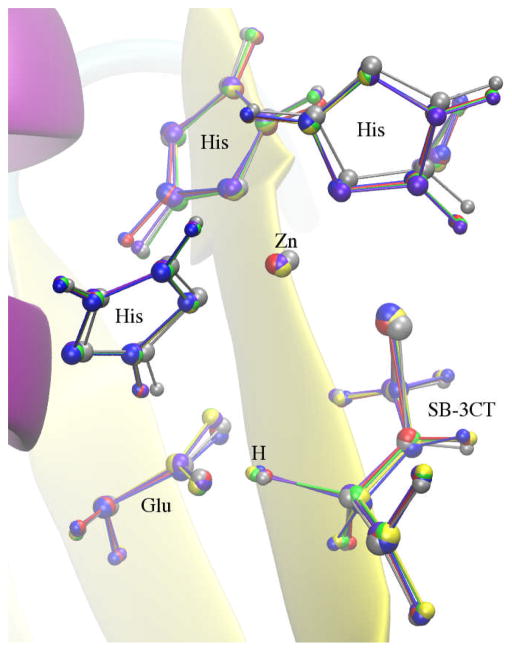
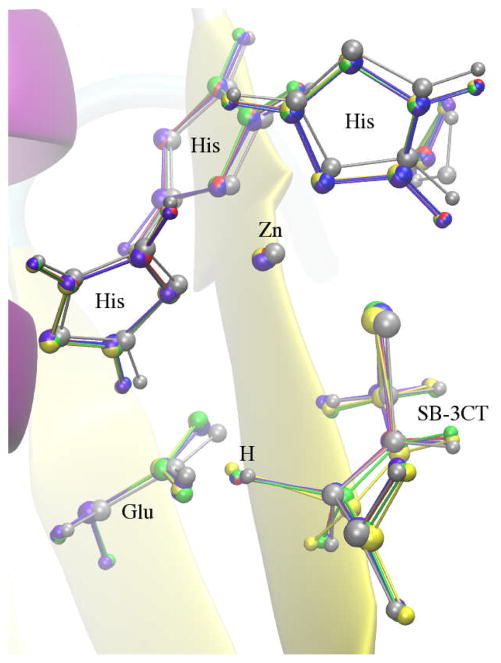
The inhibition mechanism of MMP2 by its potent inhibitor SB-3CT is a coupled deprotonation of the methylene group juxtaposed between the sulfone and the thiirane that opens the thiirane ring (Fig. 18). This reaction creates a thiolate anion that strongly coordinates with a zinc atom in the active site. This reaction has been previously studied by Tao et al using the ONIOM method, which is a QM/MM method.^76–78 In the present work, this reaction mechanism was employed as a test case for NEB and RPATH methods in CHARMM. The calculations were carried out using QM/MM methods through an interface of Q-Chem and CHARMM developed in our lab.⁷⁹ The CHARMM 22 force field⁷⁰ with CMAP backbone dihedral angle corrections⁷¹ is used for protein and the CHARMM general force field (CGenFF) for the inhibitor.⁸⁰ The B3LYP/6–31G(d) level of theory^73,74,81,82 was employed for all QM calculations. It should be noted that the QM/MM implementation for RPATH calculations through the CHARMM/Q-Chem interface⁷⁹ is an additive scheme using the electrostatic embedding method.⁸³ Unlike the ONIOM method,⁸⁴ the QM/MM geometry optimization of individual replica in this study is not an iterative procedure, i.e. no microiteration optimization was carried out for the QM subsystem.

Fig. 18.

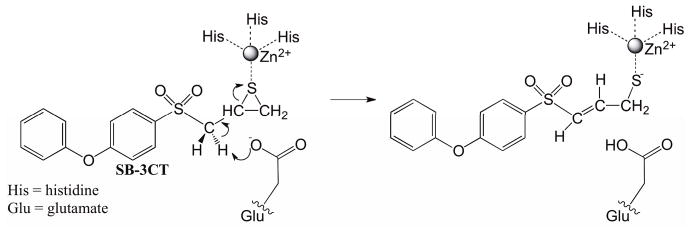
Inhibition mechanism of MMP2 by its inhibitor SB-3CT is coupled deprotonation of the methylene group juxtaposed between the sulfone and the thiirane and the opening of the thiirane ring.

Due to the high QM/MM computational cost, the RPATH calculations are considered as converged when the RMS force is less than 0.1 kcal•mol⁻¹• Å⁻² and the total energy change is less than 0.01 kcal/mol. A total of 20 replicas are employed in the RPATH optimization calculation for MMP2. For some of the calculations, additional replicas were inserted between each adjacent replica pair after optimization. The generated reaction path with 39 replicas in total was also subject to RPATH optimization to confirm the reaction barriers obtained in the calculations with 20 replicas. For the reaction pathways obtained from RPATH calculations, the approximate TS refer to the replica with the highest energy along the path.

An estimated TS of this reaction was obtained from restrained scan as benchmark. The restrained scan with 21 steps was performed between the two adjacent replicas for the replica with the highest energy from pathway 4 using RPATH/constraint. The breaking C–H and C–S bonds and forming O–H bond were restrained simultaneously while all other degrees of freedom are fully optimized for each calculation. This restrained scan generated a quadratic energetic profile (see Fig. S5 in the Supporting Information) with the highest energy structure as estimated TS, which leads to a barrier as 33.85 kcal/mol. In a previous study of this enzyme,⁷⁶ the reaction barrier of this inhibiting mechanism by SB-3CT was estimated as 19.9 kcal/mol using a subtractive QM/MM method, ONIOM.⁸⁴ The difference between the reaction barriers estimated in this and previous studies may originate from the fact that the initial MMP2 inhibitor complex structure used in this study with the CHARMM force field ^70,71 was directly taken from the previous study, in which the AMBER force field⁸⁵ was used in both molecular dynamics and QM/MM calculations. The ONIOM reactant and TS from the previous study were also subjected to a single point QM/MM calculation using the CHARMM/Q-Chem interface at the same level of theory in this study. However, due to the difference between the force fields applied in this and previous studies, the reaction barrier calculated in this way is too high to be meaningful (data not shown).

3.3.1 NEB Results

In NEB calculations, two sets of weighting schemes were applied for RMSD distance measurements between adjacent replicas. In scheme A, mass-weighted RMSD is calculated using only QM atoms including hydrogen. In an attempt to better describe the reaction progress, additional arbitrary weighting factors were added in addition to an atomic mass-weighting scheme emphasizing different atoms of the QM region. In scheme B, additional weighting factors were added to give a different emphasis on different parts of the QM region. A factor of 50.0 is given to the migrating hydrogen, a factor of 3.0 is given to the carboxylate group of Glu289, sulfone, thiirane ring, and the methylene group (excluding the migrating hydrogen) from SB-3CT, and a factor of 1.0 for all other QM atoms. Three harmonic spring constants, 10, 10² and 10³ kcal•mol⁻¹•Å⁻², were applied using weighting schemes A and B, and are plotted in Fig. 19A and B, respectively. The reaction pathway energetics are plotted against the progression parameter d, which is illustrated in Fig. 20.

Fig. 19.

Energetic profiles of MMP2 inhibition mechanism by SB-3CT using NEB method with 20 replicas and different force constant k in kcal•mol⁻¹• Å⁻². A. Three calculations using mass-weighted RMSD. B. Three calculations using combination of mass and additional weighting factor(See text for details).

Fig. 20.

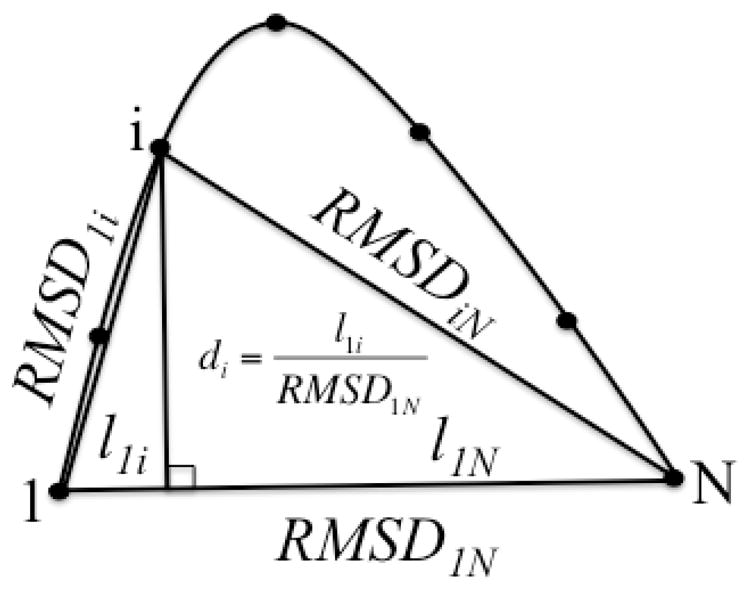
Illustration of progression parameter d_i for replica i.

For pathways using weighting scheme A, a single reaction barrier is present in all three calculations as 34.90, 47.76, and 54.80 kcal/mol, respectively, with the barrier from pathway 1 closest to the benchmark 33.85 kcal/mol. It is noticeable that the parameter d does not progress smoothly in pathways 1 or 2 (Fig. 19A). In comparison, the pathways using weighting scheme B display smoother progressing of parameter d (Fig. 19B). However, all the barriers of pathways using weighting scheme B (48.08, 50.86, and 52.66 kcal/mol) are much higher than the benchmark value. The approximate TS structures of all pathways using weighting schemes A and B are illustrated in Fig. 21 with the estimated TS and TS obtained from previous QM/MM study.⁷⁶ Pathway 1 with the weighting scheme A is more consistent with the estimated TS than the other five pathways in terms of reaction barrier and the nonmass-weighted RMSD of the atoms in QM region with reference to the estimated TS (Table 3). The position of migrating hydrogen in the estimated TS structures from the five pathways (Fig. 21A and B) except for pathway 1 with the weighting scheme A is significantly different from those in the benchmark TS structures.

Fig. 21.

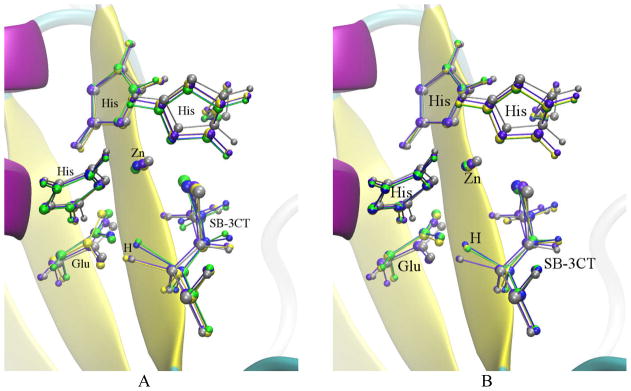
SB-3CT ring opening approximate transition states from NEB calculationsand different force constant k in kcal•mol⁻¹• Å⁻². A. Three calculations using mass-weighted RMSD. B. Three calculations using combination of mass and additional weighting factor (See text for details). In both figures: yellow: k=10; green: k=100; blue: k=1000; violet: the estimated TS; gray: the TS obtained from ONIOM calculation in the previous study.⁷⁶

Table 3.

Calculations for matrix metalloproteinase 2 (MMP2) inhibition mechanism^a

methods	parametersb (weighting scheme)	total replicas	barrier (kcal/mol)	RMSD with QM/MM TS (Å)	replica ID of approximate TS
NEB	1: k=10, (A)c	20	34.90	0.63	9
	2: k=100, (A)	20	47.76	0.75	8
	3: k=1000, (A)	20	54.80	0.74	9
	4: k=10, (B)d	20	48.08	0.72	9
	5: k=100, (B)	20	50.86	0.73	8
	6: k=1000, (B)	20	52.66	0.74	9
restraint	1: k=1000, (A)	20	35.88	0.73	10
	2: k=1000, (A)	39	40.31	0.71	17
	3: k=1000, (C)e	20	43.33	0.71	9
	4: k=1000, (C)	39	47.47	0.71	16
constraint	1: (A)	20	34.46	0.64	9
	2: (A)	39	34.73	0.64	17
	3: (B)	20	33.20	0.64	10
	4: (B)	39	34.74	0.63	18
	5: kpki=1, (A)	20	52.90	0.74	9
constraint/REPD	1: (A)	20	30.57	0.64	9
	2: (A)	39	32.00	0.63	17
	3: (D)f	20	33.76	0.62	9
	4: (D)	39	33.77	0.62	17

^aThe RPATH calculations were carried with whole system described in QM/MM at CHARMM22:B3LYP/6–31g(d) level of theory.

^bUnit for force constant is kcal•mol⁻¹• Å⁻².

^cWeighting scheme A: mass weighted RMSD is calculated using only QM atoms including hydrogen.

^dWeighting scheme B: In combination with weighting scheme A, a factor of 50.0 is given to the migrating hydrogen, a factor of 3.0 is given to the carboxylate group of Glu289, sulphone, thiirane ring, and the methylene group (excluding the migrating hydrogen) from SB-3CT, and a factor of 1.0 for all other QM atoms.

^eWeighting scheme C: In combination with weighting scheme A, a factor of 36 is given for the migrating hydrogen, a factor of 3 is given for the carboxylate group of Glu289, sulphone, thiirane ring, and the methylene group (excluding the migrating hydrogen) from SB-3CT, and a factor of 0.5 for all other QM atoms.

^fWeighting scheme D: In combination with weighting scheme A, a factor of 50.0 is given for the migrating hydrogen, a factor of 3.0 is given for the carboxylate group of Glu289, sulphone, thiirane ring, and the methylene group (excluding the migrating hydrogen) from SB-3CT, and a factor of 0.5 for all other QM atoms.

3.3.2 RPATH/Restraint Results

Force constants k_rms=1000 kcal•mol⁻¹• Å⁻², k_ang=100 kcal•mol⁻¹• Å⁻², COSMAX=0.95 were applied for RPATH/restraint calculations for the MMP2/SB-3CT system. First, the weighting scheme A was used as distance measurements between adjacent replicas. The single-point QM/MM energy of each replica is plotted as pathway 1 in Fig. 22 against the normalized reaction progress parameter. A single reaction barrier 35.88 kcal/mol is obtained from this pathway (Table 3). To obtain a better estimation of the reaction barrier, and confirm that no other reaction barrier along the obtained reaction pathway exists, an additional replica was inserted between each adjacent replica pair using linear interpolation. The new reaction pathway with 39 replicas was optimized (pathway 2 in Fig. 22), and shows an increased reaction barrier of 40.31 kcal/mol (Table 3), which is much higher than 33.85 kcal/mol, the estimated barrier.

Fig. 22.

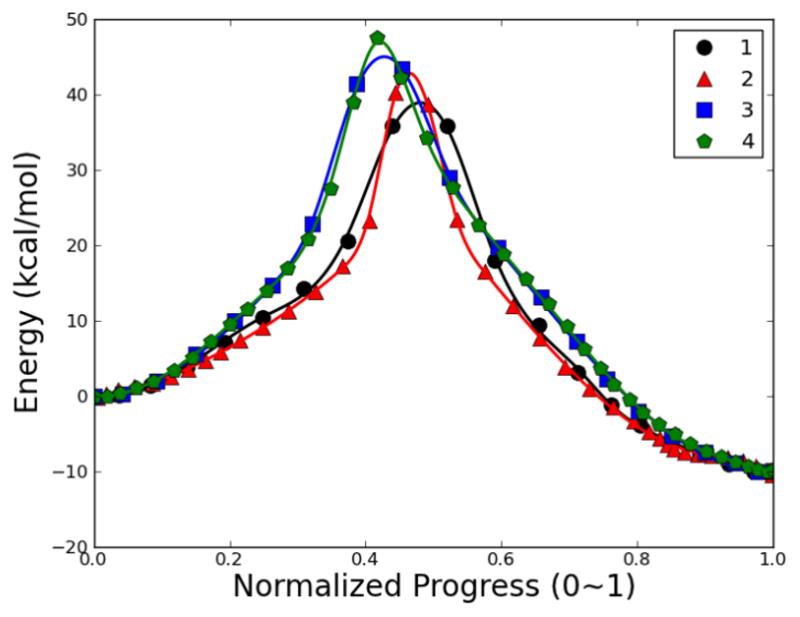
Energetic profile of MMP2 inhibition mechanism by SB-3CT using RPATH/restraint. 1: mass-weighted RMSD with 20 replicas; 2: mass-weight with 39 replicas; 3: combination of mass and additional weighting factors RMSD and with 20 replicas; 4: combination of mass and additional weighting factors RMSD and with 39 replicas.

In an attempt to better describe the reaction progress using RPATH/restraint, a weighting scheme C was added in addition to atomic mass-weighting scheme A. In this case, a factor of 36 is given for the migrating hydrogen, a factor of 3 is given for the carboxylate group of Glu289, sulfone, thiirane ring, and the methylene group (excluding the migrating hydrogen) from SB-3CT, and a factor of 0.5 for all other QM atoms. The reaction pathway shows a single barrier as 43.33 kcal/mol. Further optimization with an additional 19 replicas increases the barrier to 47.47 kcal/mol. Both barriers are much higher than 33.85 kcal/mol, the estimated barrier.

These plots demonstrate that the reaction proceeds from reactant to product smoothly. The inter-replica distance is larger in the vicinity around the TS region compared to the end point regions. When applying additional weighting factors, the distribution of replicas along reaction pathway is somewhat more even than just merely mass-weighting. All four pathways clearly show a single barrier in agreement with a concerted reaction mechanism for proton migration and thiirane ring-opening.⁷⁶

The approximate TS structures of all four pathways are illustrated in Fig. 23 with the estimated TS and the TS obtained from the previous QM/MM study.⁷⁶ All four structures have nonmass-weighted RMSD of the QM region close to 0.3 Å with reference to the estimated TS (Table 3).

Fig. 23.

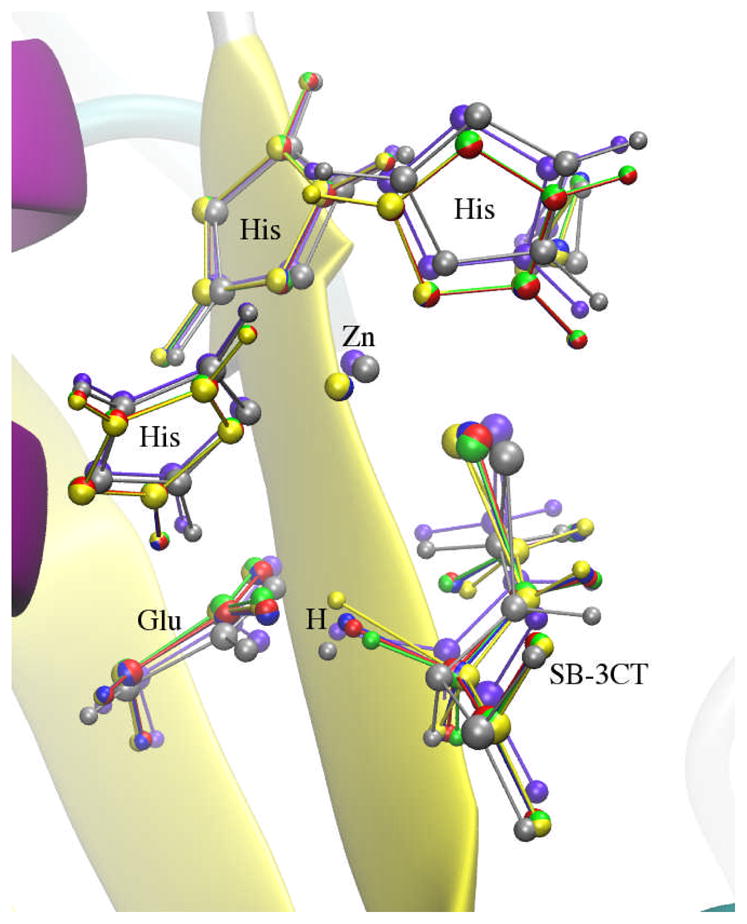
SB-3CT ring opening approximate transition states from RPATH/restraint calculations: yellow: calculation with 20 replicas using mass-weighted RMSD, green: calculation with 39 replicas using mass-weighted RMSD, blue: calculation with 20 replicas using mass-weighted RMSD with additional weighting factors, red: calculation with 39 replicas using mass-weighted RMSD with additional weighting factors, gray: the TS obtained from ONIOM calculation in the previous study. ⁷⁶

3.3.3 RPATH/Constraint Results

The RPATH calculation with 20 replicas using a constraint on the weighting scheme Ashows a single barrier of 34.46 kcal/mol (pathway 1 in Fig. 24). After inserting additional replicas between adjacent replicas, the new reaction pathway with 39 total replicas was optimized showing a single reaction barrier of 34.73 kcal/mol (pathway 2 in Fig. 24). The energetic profiles of these two pathways are consistent with each other and with differences less than 1 kcal/mol to the estimated barrier, 33.85 kcal/mol. The two approximate TSs have almost identical progression parameters.

Fig. 24.

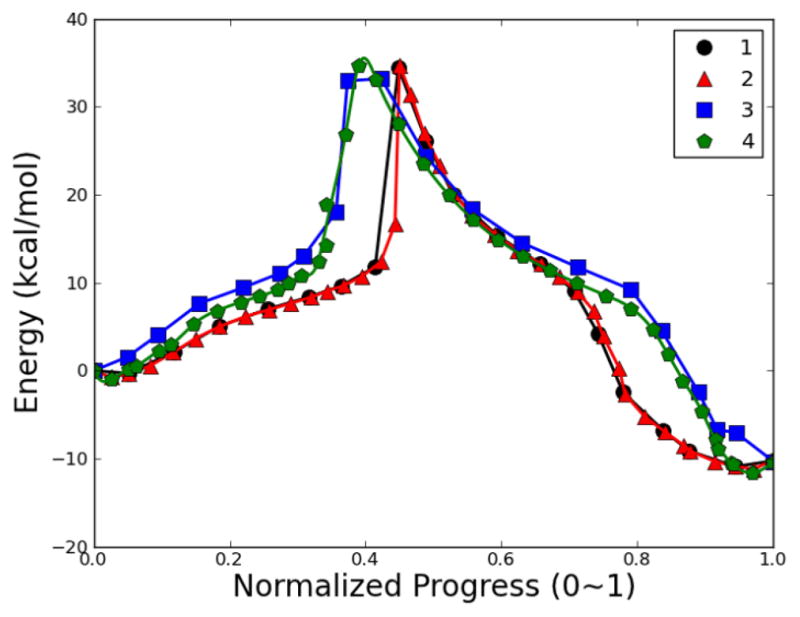
Energetic profiles of MMP2 inhibition mechanism by SB-3CT using RPATH/constraint. 1: mass-weighted RMSD with 20 replicas; 2: mass-weight with 39 replicas; 3: combination of mass and additional weighting factor RMSD and with 20 replicas; 4: combination of mass and additional weighting factor RMSD and with 39 replicas.

The weighting scheme B used in section 3.3.1 was used in addition to atomic mass-weighting scheme A. The reaction pathway has a single barrier of 33.20 kcal/mol (pathway 3 in Fig. 24). A further optimized pathway with 19 additional replicas (pathway 4 in Fig. 24) has two replicas close in energy around the TS region with a barrier of 34.74 kcal/mol. Both barriers have differences less than 1 kcal/mol to the estimated barrier, 33.85 kcal/mol. A kinetic energy force constant of 1 kcal•mol⁻¹•Å⁻² was applied to obtain a MHP of this reaction. The reaction pathway is rather smooth and evenly distributed (Fig. 26). However, the reaction barrier of this pathway is 52.90 kcal/mol and is much higher than the estimated barrier.

Fig. 26.

Energetic profile of MMP2 inhibition mechanism by SB-3CT using RPATH/constraint method with more weight on migration hydrogen and k_pki =1 kcal•mol⁻¹• Å⁻².

The approximate TS structures of all four pathways from Fig. 24 are illustrated in Fig. 25 with the estimated TS and the TS obtained from the previous QM/MM study.⁷⁶ All four approximate TSs obtained from RPATH calculations resemble with each other closely as well as with the two reference TSs. The migrating hydrogens in the approximate TSs from four pathways are almost on top of each other as well as the two reference TSs. The geometries of the thiirane ring-opening in all six approximate TSs are also very close. This observation shows that the RPATH/constraint is a very useful tool to produce the reaction pathway with accurate TS information.

Fig. 25.

SB-3CT ring opening approximate transition states from RPATH/constraint calculations: yellow: calculation with 20 replicas using mass-weighted RMSD, green: calculation with 39 replicas using mass-weighted RMSD, blue: calculation with 20 replicas using mass-weighted RMSD with additional weighting factors, red: calculation with 39 replicas using mass-weighted RMSD with additional weighting factors, gray: the TS obtained from ONIOM calculation inthe previous study. ⁷⁶

3.3.4 RPATH/Constraint with REPD Framework Results

The reaction path calculated using RPATH with constraints and the REPD framework computes a reaction barrier of 30.57 kcal/mol (pathway 1 in Fig. 27). After inserting additional replica between adjacent replicas, the new reaction pathway with 39 replicas was optimized and showed a single reaction barrier as 32.00 kcal/mol (pathway 2 in Fig. 27). Both barriers are lower than the estimated barrier, 33.85 kcal/mol. The two pathways are very consistent with each other.

Fig. 27.

Energetic profiles of MMP2 inhibition mechanism by SB-3CT using RPATH/constraint method in distributed replica (REPD) framework. 1: mass-weighted RMSD with 20 replicas; 2: mass-weighted RMSD with 39 replicas; 3: combination of mass and additional weighting factor RMSD and with 20 replicas; 4: combination of mass and additional weighting factor RMSD and with 39 replicas.

A weighting scheme D was added in addition to atomic mass-weighting scheme A. In this case, a factor of 50.0 is given for the migrating hydrogen, a factor of 3.0 is given for the carboxylate group of Glu289, sulfone, thiirane ring, and the methylene group (excluding the migrating hydrogen) from SB-3CT, and a factor of 0.5 for all other QM atoms. The pathways with 20 replicas (3 in Fig. 27) and 39 replicas (4 in Fig. 27) have barriers as 33.76 and 33.77 kcal/mol (4 in Fig. 27), respectively, very close to the estimated barrier, 33.85 kcal/mol.

The approximate TS structures of these four pathways are illustrated in Fig. 28 and are compared with the estimated TS and the TS from the previous QM/MM study.⁷⁶ Similar to the RPATH/constraint calculations, all four approximate TSs obtained from RPATH/constraint with the REPD framework are very close to the reference TSs, especially the position of the migrating hydrogen and geometry of the opening thiirane ring.

Fig. 28.

SB-3CT ring opening approximate transition states from RPATH/constraint calculations in REPD framework: yellow: calculation with 20 replicas using mass-weighted RMSD, green: calculation with 39 replicas using mass-weighted RMSD, blue: calculation with 20 replicas using mass-weighted RMSD with additional weighting factors, red: calculation with 39 replicas using mass-weighted RMSD with additional weighting factors, gray: the TS obtained from ONIOM calculation inthe previous study. ⁷⁶

4. Discussion

In the present study, we applied three chain-based methods implemented in CHARMM on three test cases: alanine dipeptide isomerization, β-alanine intermolecular condensation, and the inhibition mechanism of MMP2 by SB-3CT. The levels of theory applied for these three systems are MM, QM, and QM/MM, respectively.

4.1 Isomerization of Alanine Dipeptide

The NEB method works very well for alanine dipeptide isomerization. For all three spring constants applied in the calculations, the obtained reaction pathways are almost identical. Theoretically, the path optimization using the NEB method should provide a MEP of the target reaction. This is apparently the case for the alanine dipeptide isomerization. For mass-weighted RMSD either with or without hydrogen atoms, the same reaction pathways were obtained for six NEB calculations using spring constants that differ by 3 orders of magnitude. Because of the force projection applied in NEB calculation, the RMS fluctuates during the optimization. This fluctuation does not diminish when close to convergence. This is one undesired feature and leads to slow convergence for more complicated systems when applying the NEB method.

The force constants applied in the RPATH/restraint calculations are much stronger than those applied in the NEB calculations. When applying the same force constants as in NEB, the replicas in the TS region suffer significant sliding down, i.e. the distances between adjacent replicas around the TS are much larger than those close to the end points. For force constants, k_rms, larger than 1000 kcal•mol⁻¹• Å⁻², the RPATH/restraint method calculations gave reaction pathways close to the MEP. The angle force constant, k_ang, is a very useful tool to control the smoothness of the pathway. By increasing k_ang, the optimized pathway can vary between the MEP and a straight-line interpolation between the two end points. This feature can be important when studying a reaction with a rough PES to prevent kinks along the optimized pathway. Smooth pathways can also serve as the reference for off-path dynamic simulation to obtain the free energy of the reaction.

The RPATH/constraint calculations also give an MEP. The fast convergence of the RMS force shows that this method is promising for reaction path optimizations. However, the convergence failure when including hydrogen in the RMSD measurement reminds the user to be careful when choosing a reaction coordinate. It is noticeable that the replicas on the φ and ψ contour plot for calculations 1 and 2 in Fig. 9 are not evenly distributed as those obtained in NEB calculations. Including a kinetic potential energy in the objective function is an effective way to increase the smoothness of the reaction pathway but with the price of deviating from the MEP. By adjusting the kinetic energy force constant, one could obtain multiple reaction pathways that vary between the MEP and the straight line connecting the two end points (see calculations 3–5 in Fig. 9). Similar to the k_ang for the restraint method, this could be a convenient tool when studying pathways on rough PESs or generating references for an off-path simulation.

4.2 β-alanine Intermolecular Condensation

The NEB method provides rather smooth energetic profiles in all four calculations. The estimated reaction barriers using NEB from three pathways are also close to the barrier obtained from benchmark calculation. However, the estimated TS structures show significant deviation from the QM TS structure, even with an additional weighting factor on the migrating hydrogen. This observation suggests that caution needs to be used when applying the NEB method on more complex systems.

In calculations using the RPATH/restraint method, the force to control the smoothness of the path (k_ang) played an important role in the minimization. Only with a large k_ang, the RPATH calculations give a barrier and approximate TS that are close to the results from QM calculations. This is also likely due to the flatness of the PES around the product with two separate molecules.

The RPATH/constraint calculations with mass-weighted RMSD measurements do not show significant improvement compared with the restraint results. However, with an additional weighting factor on the migrating hydrogen, the constraint calculations reproduce the reaction barrier and the approximate TS structures of this reaction very accurately. It should be pointed out that the kinetic energy potential (with nonzero k_pki) is necessary in constraint calculations for convergence.

As a summary, special caution needs to be taken when applying the RPATH method on small organic systems using the QM methods, especially when separate molecules are present in either reactant or product or both. In such cases, additional forces or terms to maintain the pathway smoothness and rigidity are needed to ensure the convergence of the calculations and the accuracy of the reaction barrier and the approximate TS structure.

4.3 Inhibition Mechanism of MMP2

The barriers of two NEB calculations with larger force constants are higher than those with a force constant of 10 kcal•mol⁻¹•Å⁻². This suggests that further relaxation of the reaction path is needed for the NEB calculations with large force constants. The progression of the reaction pathways with two smaller force constants is not smooth. The pathway with the largest force constant has a smoother progression but with higher reaction barrier than the estimated value. The calculation with additional weighting factors led to smoother energetic profiles, but higher reaction barrier, especially with large force constants. When using the NEB method to study large systems at high level of theory, one needs to be very careful to choose the appropriate force constants to balance between the smoothness of pathway and the converging rate of the calculation.

The RPATH/restraint generated rather smooth pathways. The consistency of the four pathways shows the reliability of the RPATH/restraint method to capture the reaction mechanism. All the reaction barriers obtained from these calculations but one are much higher than the estimated barrier. The only one that is close to the estimated barrier, however, has the approximate TS structure with the largest RMSD from the estimated TS. The significant variation of the approximate TS structures and high reaction barriers indicates the difficulty of consistently converging to MEP for large systems when using various setups in the RPATH/restraint calculations. This inconsistency of RPATH/restraint calculations is also shown from β-alanine results.

The four RPATH/constraint calculations generate very consistent barrier heights, all between 33.20 and 34.74 kcal/mol, very close to the estimated barrier. The replicas are evenly distributed along the pathway, providing good coverage of the TS regions (Fig. 24). All four approximate TS structures obtained from the RPATH/constraint calculations are very similar to the reference TS (Fig. 25). The RPATH/constraint method seems to be a robust tool to study the reaction mechanisms of protein reactions. By including a kinetic energy potential, the RPATH/constraint calculation could produce a very smooth pathway, but the calculated reaction barrier may be significantly higher than the real barrier.

It should be pointed out that the different reaction progression parameters of approximate TSs shown in the energetic plots do not indicate significant difference among the approximate TS structures of the reaction, because this parameter depends on the definition of the RMSD and any additional weighting factors applied in the distance measurement. It is obvious that the approximate TS structures obtained from different RPATH calculations are very similar to each other as well as to the reference TSs. It should be emphasized that no universal setup of the RMSD distance will work well for all the RPATH calculations, especially for complicated protein systems. The users are suggested to try different RMSD schemes initially to find the best way for certain RPATH methods.

5. Concluding Remarks

In conclusion, replica path (RPATH) methods implemented in CHARMM are powerful tools to elucidate the reaction mechanism of systems with various sizes and complexity. Starting from reactant and product, a RPATH calculation could generate a reaction pathway represented by multiple replicas providing reaction barriers that can be used in comparisons with experimental results. There is no single option that will prevail in every case. Each method has its own strengths and weaknesses. The best choice for reaction pathway calculation clearly depends on the nature of the system of interest itself. In general, the NEB method works well on the system at low level of theory and low computational cost, i.e. molecular mechanics. After convergence, the NEB method could generate rather accurate MEP. The RPATH with restraints or constraints works well with large systems at higher levels of theory due to their computational efficiency and fast convergence rates.

For small organic reactions, most with separate reactants or products, special caution needs to be taken when applying RPATH methods to study reaction mechanisms. The separation of the molecules could bring difficulty to the optimization convergence. Options are available to control the rigidity of the pathway and therefore accelerate the convergence of the optimization. For small systems, it is always recommended to carry out a standalone TS search from the approximate TS structure obtained from the RPATH calculations. For many large systems, the choice of reaction coordinates may not be obvious. The RMSD measurement with additional weighting schemes provides practically infinite choices to describe the reaction progress. Our test calculations of the MMP2 system demonstrated that the choice of RMSD distance does not lead to different reaction mechanisms and has limited effects on the reaction barrier and approximate TS structures, especially with constraint methods.

The key point of this study is that the RPATH methods are powerful and useful tools to study the reaction mechanisms of macromolecular systems, such as enzymes. With these tools, plausible reaction mechanisms as a full pathway could be generated without TS information a priori. Currently, the RPATH minimization only provides MEPs and estimations of the reaction barrier without free energy information. In our future studies, the reaction paths will be subject to dynamics simulation to estimate the reaction free energy profile, which is directly connected to experimental observation.