There Is a World Outside of Experimental Designs: Using Twins to Investigate Causation

Abstract

This study introduces a co-twin control method commonly used in the medical literature but not often within educational research. This method allows for a comparison of twins discordant for an “exposure,” approximating alternative outcomes in the counterfactual model. Example analyses use data drawn from the Florida Twin Project on Reading to determine whether exposure to “teacher quality,” measured by growth in oral reading fluency (ORF) scores of classmates, causally affects ORF performance of twins in the subsequent years. The analysis highlights PROC MIXED in SAS, including a novel expansion to allow for the nested data. Results from 2,788 twins suggested that being in classrooms with lower teacher quality in first grade leads to lower ORF scores in second and third grade with little indication of possible genetic or environmental confounding.

Understanding causal mechanisms is a central aim of educational researchers. Without this causal understanding, educational interventions could not be developed or tested for effectiveness, the role of specific cognitive skills in educational outcomes could not be known, and policy issues and challenges could not be addressed. Experimental designs that use random assignment deserve the high status they are ascribed, given the causal inferences that are afforded by such methods (Shavelson & Towne, 2002). As such, randomized controlled trial (RCT) experiments are typically considered the gold standard in educational research (Shadish, Cook, & Campbell, 2002). However, in situations where random assignment to groups is not possible due to ethical or feasibility constraints, quasi-experimental designs can be used for causal inferencing but with more methodological difficulty (Rutter, 2007; Shadish et al., 2002). Designs with the greatest chance of yielding causal information are those that have strong counterfactual conditions (National Early Literacy Panel, 2008; Shadish et al., 2002).

However, it can be difficult for many educational researchers to achieve the standards necessary for causal inference making. Issues such as low fidelity, teacher and child attrition, and inability to randomly assign schools to conditions are just some of the possible barriers to achieving a more rigorous experimental design. Even with random assignment, there may be potential problems introduced if the schools or classrooms who volunteer to be in educational experiments are different from those who decline (Levitt & List, 2007; McGue, Osler, & Christensen, 2010). Given the possible limitations of using an experimental design in educational research, it is important to discuss different quasi-experimental designs available to the educational researcher. The primary goal of this article is to show how a twin sample can provide instances of natural experiments with the important possibility of ruling out genetic and environmental effects as potential confounders of the effect of an exposure in educational research. Specifically, this article will describe the logic of the co-twin control design, a type of quasi-experimental design that allows for a very strong matching of individuals on genetic and shared environmental background. Although this co-twin control design cannot typically rule out all possible alternatives to conclude a strong causal relationship, it can allow for an investigator to rule out many of the more important possible confounders in the relationship between exposure and outcome. This can provide an educational investigator a better understanding of where potential causal relationships may actually exist, which would suggest areas of further exploration. To fully explore the method, a practical example of the co-twin control method will be highlighted, namely, the role of “teacher quality” in Grade 1 on subsequent student reading performance in state testing in Grades 2 and 3.

Counterfactual Model of Causation

The counterfactual model is a framework for understanding casual implications in outcomes that have many causal sources, evaluating alternative approaches for the estimation of causal effects (Morgan & Winship, 2007). A true counterfactual comparison would require observing the same units during exposure to a treatment and nonexposure to a treatment simultaneously—a situation that is obviously impossible. The closest we can get to a true counterfactual comparison is by creating hypothetical counterfactuals that are as close as possible to the true counterfactual condition. Using the counterfactual model, researchers can then estimate what would have happened to a hypothetically similar group of people if they had not received treatment (Shadish et al., 2002). RCTs provide a strong methodology for using the counterfactual model of causation, as by randomly assigning individuals to conditions of exposure versus nonexposure, the control group can serve as the counterfactual to the treatment group. In other words, RCTs are able to rule out all other causes or nonmanipulated effects (known and unknown) by randomly distributing these causes across treatment and control groups. This creates a hypothetical counterfactual (i.e., control group) that is equated on expectation to the treatment group. Although the true counterfactual condition cannot be observed or measured, statistical comparisons of the two groups after exposure can then be made to determine whether the exposure caused a change in the treatment group only. Because quasi-experimental groups are formed via nonrandom assignment, there is no expectation that the treatment and control groups will be equated. As a minimal bar, the groups should at least show evidence of equality at pretest on measured variables.

Co-Twin Control Design: An Example of a Quasi-Experimental Design Using Discordant Twin Methodology

Behavioral genetics has long been known for twin designs, with the most well-known design used to estimate heritability (i.e., genetic influences) by comparing the similarity of monozygotic (MZ) twins (who share 100% of their genes) on an outcome to the similarity of dizygotic (DZ) twins (who share approximately 50% of their segregating genes) on the same outcome (Plomin, DeFries, McClearn, & McGuffin, 2008). When the similarity between MZ twins is greater than DZ twins, genetic influences are inferred. The extent to which the similarity between MZ twins is close in magnitude to the similarity between DZ twins, environmental influences are assumed. This methodology has been successfully used to determine the heritability of many educational outcomes, particularly in reading (for review, see Plomin & Kovas, 2005).

Key to this discussion, twin designs can also be used to determine the effect of an environmental influence on a given outcome, particularly when only one member of a twin pair is exposed to a proposed environmental exposure, resulting in discordant twin pairs. This exposure can be purposeful, such as only one member of a twin pair receives a vocabulary intervention and the other does not (e.g., Strayer, 1930). However, given the ethical dilemmas with such a design, the “exposure” can also be due to preexisting differences between the twins (Plomin & Haworth, 2010). For example, a recent report from the gerontology literature used the “co-twin control design” to explore whether there was a causal link between drinking and increased cognitive performance in old age (McGue et al., 2010). As assigning one member of the twin pair to a drinking treatment is not possible, the authors instead utilized a twin data set that had twin pairs discordant for drinking status. They were able to determine that there was genetic confounding between drinking and cognitive outcomes, suggesting that drinking was not necessarily causally associated with higher cognitive outcome.

The logic of the co-twin control design rests in the counterfactual model, similar to more commonly used educational quasi-experimental methods such as propensity scores and the regression discontinuity design (Rutter, 2007; Shadish et al., 2002). Different quasi-experimental designs make assumptions to draw casual inferences. Propensity scores assume that by modeling the selection process that created the groups being compared, and then controlling for those variables identified as important predictors in that process (either through matching or by covariance analysis), the control group, conditioned on the propensity score, will serve as a better counterfactual. The regression discontinuity design also uses elements of the counterfactual model to make causal inferences. In an RCT, a random variable is used to assign people to condition, as is the case in simple random assignment, or to people within a block, which is known as block or stratified random assignment. However, in a regression discontinuity design, it is a known variable, such as a pretest score. In both cases, the selection process that creates the groups is known and can be modeled. In a regression discontinuity design, a regression equation that estimates the relationship between the assignment variable and the outcome variable fits the treatment group and the control group, and the difference between the intercepts of the two models is used to estimate the effects of treatment. In essence, the control group regression line serves as the counterfactual for the treatment group regression line, much like the mean of the control group at the posttest serves as the counterfactual for the treatment mean at the end of the study. For the co-twin control design, the nonexposed member of the twin pair serves as the counterfactual to the exposed member, allowing for an estimation of what the exposed twin would have looked like if they had also been not exposed. Given that twins share all, or some, segregating genetic alleles and a common childhood environment, the nonexposed member of the pair can serve as a close match to the exposed member. Using the quantitative genetic design, individual differences on an outcome can be attributable to additive genetic influences (i.e., genes that are directly inherited from one’s parents; A), which are shared 100% by MZ twins and approximately 50% in DZ twins; shared environmental influences (i.e., those environmental influences that serve to make siblings more similar; C), which are shared completely by both twin types; and nonshared environmental influences (i.e., those environmental influences that serve to make siblings unique; E), which are not shared by any twin type.

Outside of the experimental design and in nontwin populations, any association of exposure to outcome has the possibility of being confounded due to genetic influences, shared environmental influences, and nonshared environmental influences. For example, more frequent instances of book reading in the home could be considered an “exposure” that is commonly associated with better reading outcomes in school (e.g., Scarborough, Dobrich, & Hager, 1991). This relationship could be due to causal influences of literacy experiences at home on reading outcomes in school. Alternatively, the association could be explained by a common genetic cause, such as attention-deficit/hyperactivity disorder, which could underlie children’s decisions to not read a book at home and perform poorly in the classroom (Willcutt et al., 2010). In the same vein, the association could be explained by a common environmental cause, such as low socioeconomic status (SES; Chall, Jacobs, & Baldwin, 1990). The power of the co-twin control design is the ability to reject these possibilities outside of an experimental design.

The co-twin control design assumes that any potential causal relationship will be seen as an association between exposure and outcome at the individual level (i.e., indicating an association at all), as well as within MZ and DZ discordant twins. This is because by examining the magnitude of the effect of exposure on outcome within MZ twins discordant for exposure, possible A and C confounding effects can be controlled for. If there is any exposure effect that remains after controlling for genetic and shared environmental influences (i.e., MZ twins have these in common), then a stronger claim toward causality can be made, if no other plausible untested alternative explanation exists. By also comparing same-sex DZ twins discordant for exposure, partial A and all of C confounding effects are controlled for (i.e., DZ twins shared 50% of their genes on average and all their shared environment), with added power given to the analyses due to the inclusion of more twins (Plomin & Haworth, 2010). Given E specifically measures environmental influences not shared within a twin pair, neither MZ nor DZ twin pairs can control for this possible confound.

The logic of the co-twin control method is shown in Figure 1 by hypothetical examples of the exposure effect, or the difference in outcome score between discordant individuals (Bergen, Gardner, Aggen, & Kendler, 2008; Burt et al., 2010; McGue et al., 2010; Rutter, 2007). Scenario A shows an effect of exposure on outcome between discordant pairs of unrelated individuals in the population, discordant pairs of DZ twins, and discordant pairs of MZ twins, suggesting a possible causal effect. In other words, the magnitude of the exposure effect between discordant individuals is the same even after controlling for genetic and shared environmental influences (i.e., within twin pair), suggesting that they had no effect on the association. It should be noted that this relationship may also indicate confounding due to nonshared environmental influences, as these serve to only make siblings different and, therefore, cannot contribute to any association between twin pairs. Scenario B represents a noncausal situation where genetic confounding is occurring. In this scenario, discordant unrelated individuals show the greatest exposure effect, discordant DZ twins show a smaller exposure effect than the unrelated individuals, and MZ twins suggest no exposure effect. In other words, discordant MZ twins on exposure look the same on the outcome. As the only other known linking factor between exposure and outcome in discordant MZ twins is that the twins share the same genotype, genetic influences underlying the association are indicated. Scenario C represents a noncausal situation where shared environmental confounding is occurring. For this, both discordant twin types are similar to each other in the extent of the exposure effect, and this effect is smaller than the unrelated discordant individuals who do not share a family environment. Finally, Scenario D shows a noncausal case of genetic and shared environmental confounding. In this situation, discordant unrelated individuals show an exposure effect on outcome, but neither twin type does.

Figure 1. Hypothetical scenarios representing potential results from the co-twin control design.

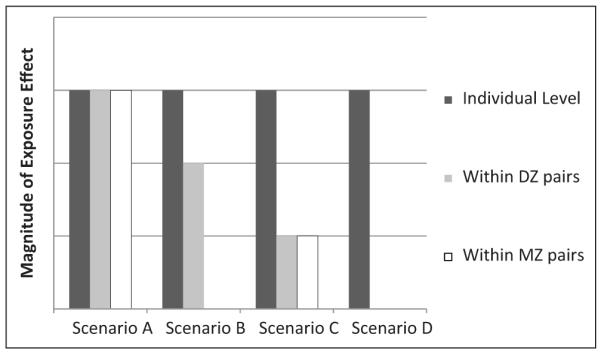
Note. DZ = dizygotic; MZ = monozygotic. Scenario A represents a similar effect of exposure no what matter the relatedness of the individuals, suggesting a possible causal effect. The remaining scenarios represent noncausal situations. Scenario B represents genetic confounding, whereas Scenario C represents shared environmental confounding. Scenario D represents genetic and shared environmental confounding.

Given the potential difficulty of conducting experimental methods in educational designs, the use of a co-twin control design is an exciting possibility. There are many ways an educational researcher interested in causal implications can use available twin data sets to test for these relationships. The most direct way an educational researcher can truly test for causal factors of interest is to recruit a twin sample and, if possible, experimentally manipulate the exposure factor or measure exposure differences that already exist in the sample. Although this may seem like a large undertaking, traditional experiments in education using RCT methods require approximately five times as many participants as a co-twin control design, suggesting that in fact less effort in comparison is needed (Carr, Martin, & Whitfield, 1981; Plomin & Haworth, 2010). This is because the comparisons made in the co-twin control design are within pair, which will have much less unexplained variance than the unexplained between groups variability seen in RCT designs (see Plomin & Haworth, 2010). Outside of primary data collection, the large and growing number of extant twin data sets with educationally relevant variables makes collaborations a real possibility for many educational researchers (see Plomin & Kovas, 2005, for a review of recent twin studies with reading performance outcomes). Finally, there are many publicly available data sets that have twinning information, such as the National Longitudinal Survey of Youth (Rodgers, Johnson, & Bard, 2005) and the Early Childhood Longitudinal Program Birth Cohort (Najarian, Snow, Lennon, & Kinsey, 2010). These large data sets have a wealth of educationally relevant data as well as many potential exposure variables that can be explored. Therefore, depending on the level of resources and research questions, most educational researchers will find that twin data are available to conduct these analyses.

The Co-Twin Control Design in Action

In an era of school and teacher accountability, it becomes even more important to understand the role of schools and teachers in the learning process. Reading is a highly genetically influenced process in early childhood, which suggests that only small portions of variance can be accounted for by the shared environment, which includes classroom influences and nested within that, teacher influences (e.g., Byrne et al., 2009; Petrill et al., 2010). Indeed, there are conflicting reports as to the extent to which individual teachers influence reading outcomes. Some work suggests that teachers have a significant, and possibly moderate, role in student’s reading performance (Connor, Morrison, Fishman, Schatschneider, & Underwood, 2007; Greenwald, Hedges, & Laine, 1996). However, much of this work has potential confounds due to nonrandom placement of children into classrooms based on achievement or behavior (Nye, Konstantopoulos, & Hedges, 2004). Attempts to control these possible biases have suggested that teacher influences, or more broadly classroom influences, show only small influences on student reading outcomes. Convincing work using randomized exposure to teacher suggested that teacher influences account for approximately 7% of the total variance in reading outcomes in the early school years (Nye et al., 2004). Byrne et al. (2010), using a version of a discordant twin analysis, found that approximately 8% of the difference in reading achievement scores for twins in different classrooms was attributable to classroom influences. More fine-tuned quantitative genetics work has suggested that Gene × Environment interactions may be at work when considering teacher quality, a term assigned to a measure of overall twin classmate growth on reading outcomes (Taylor, Roehrig, Soden-Hensler, Connor, & Schatschneider, 2010). When teacher quality, or classmate growth, is high, variability in reading outcomes is mostly due to genetic influences. However, when teacher quality, or classmate growth, is low, variance in reading performance is mostly attributable to the shared environment, including the teacher influence. This suggests that poorer classroom environments, and any potential teacher influence in that, have a larger impact on students than better classroom environments, including teachers, do (an effect also noted by Nye et al., 2004).

This work would suggest that the overall influence of any given teacher on student outcomes is small to moderate at best, but an interactive effect indicates that poorer teachers have a greater potential of influence than better teachers (Nye et al., 2004; Taylor et al., 2010). Despite this, genetic and other environmental sources of variance, such as school SES (e.g., Connor, Son, Hindman, & Morrison, 2005), affect reading outcomes to a much greater extent than teacher influences have been suggested to do. Moreover, most of the research on classroom or teacher effects has been correlational in nature. Thus, teacher effects associated with reading outcomes may be small to moderate, and the relationship may only be important in poor teachers, but it is unknown whether this association is causal beyond the initial evidence provided by Nye et al. (2004). Given the extent to which genetic and school SES effects influence reading outcomes (Byrne et al., 2009; McLoyd, 1998), it may be the case that there is an underlying genetic and/or environmental confounder in the relationship between teachers and reading performance.

The purpose of this study is not only to provide an illustration of the co-twin control design but also to explore the relationship of an individual teacher’s classroom environment and reading outcomes in future grades. As few reports could be found in the literature using this design to explore educationally relevant outcomes (Byrne et al., 2010 use a version of a discordant twin analysis in their work, but not the same co-twin control method as here), we will not only introduce the design but also offer a novel expansion to allow for the commonly found nested structure of educational data. Importantly, Byrne et al. (2010) made a strong argument that between-classroom variance, typically ascribed as “teacher influences” or “teacher quality” in the literature, should more generally be considered “classroom influences” with teacher influences as an unknown component of that variance. The present study does not intend to speak on potential difference between “classroom” versus “teacher” influences. We will use the term teacher quality as a label for a construct, which may likely include unknown classroom variance not attributable to the teacher, such as peer effects. We do so to maintain consistency with previous work from this project, which has used the same label (Taylor et al., 2010), and we caution the reader that these methods cannot speak to any individual teacher.

Therefore, we will explore the influence of “teacher quality” in Grade 1, measured via growth of oral reading performance by classmates of twins who are part of a large representative twin sample in Florida on reading outcomes (Taylor et al., 2010; Taylor & Schatschneider, 2010). Specifically, the reading outcome of interest is oral reading fluency (ORF) scores at the end of Grades 1 and 2. ORF, or rapid and accurate reading of connected text, has been highlighted as an efficient and reliable measure of reading skill in the primary grades (Roehrig, Petscher, Nettles, Hudson, & Torgesen, 2008), which is highly associated with reading comprehension (e.g., Roberts, Good, & Corcoran, 2005). In addition, ORF is an important measure of children’s progress through the education system (Fuchs, Fuchs, Hosp, & Jenkins, 2001). Given the previous work by Taylor et al. (2010), we will specifically examine the extent to which being exposed to poor teacher quality is related to subsequent reading performance as measured by ORF while controlling for genetic and shared environmental confounders.

Method

Participants

Data came from the Florida Twin Project on Reading, a cross-sequential project of reading development (Taylor & Schatschneider, 2010). Reading monitoring and achievement data were ascertained by school staff and maintained in the Florida Progress Monitoring and Reporting Network (PMRN), a statewide educational database. For the current report, reading data were collected over the 2003–2004 through 2008–2009 school years from 2,788 MZ (N = 1,382) and same-sex DZ (N = 1,406) twins. According to parent report, 20% of the twins were African American, 27% were Hispanic, 45% were White, and the remainder were mixed or other race/ethnicity.

Due to the cross-sequential nature of the study and data collection procedures, data were not available for all twins at all time points. However, all available data for each grade were analyzed, and the number of twins available for each grade level is presented in Table 1. Twins were approximately 7 years old at the beginning of Grade 1 (M = 6.76, SD = 0.49), 8 years old at the end of Grade 2 (M = 8.27, SD = 0.51), and 9 years old at the end of Grade 3 (M = 9.25, SD = 0.54).

Table 1.

Descriptive Statistics for All Environmental Exposure and Outcome Variables

Variable	M	SD	Minimum	Maximum	n
Overall class ORF gain Grade 1	59.58	10.52	6.14	102.39	1430
<50 percentile class ORF gain Grade 1	51.53	6.92	6.14	59.62	713
>50 percentile class ORF gain Grade 1	67.58	6.68	59.63	102.39	717
Twins’ spring ORF Grade 2	103.04	37.45	5.00	214.00	1,284
Twins’ spring ORF Grade 3	115.08	34.96	6.00	236.00	7,97

Note. ORF = oral reading fluency.

Procedure and Measures

School staff administered progress monitoring and achievement measures as part of normal school attendance, and all scores were entered into the PMRN web-based data collection system. Scheduled administration of measures was determined by the Florida Department of Education and local school districts. In the present analyses, data from the fall and spring administration for each grade were used, with each typically occurring within a 45-day time window.

Outcome

Dynamic Indicators of Basic Early Literacy Skills (DIBELS; Kaminski & Good, 2003) ORF scores from spring of Grades 2 and 3 were used to measure accurate and fluent reading of connected text. Students read grade-level calibrated passages aloud for 1 min. Fluency rate is assessed as the number of words read correctly in 1 min. Reported parallel forms reliability (.94) and predictive criterion-related validity (.78; October–May) with the Woodcock–Johnson Basic Reading Skills Cluster score demonstrate the technical adequacy of the measure (Speece & Case, 2001).

Environmental exposure

Following the methods used in Taylor et al. (2010), data from the twins’ classmates in Grade 1 were used to create an index of class ORF gain, or “teacher quality,” representing the environmental exposure of interest. This index of teacher quality was calculated as a residualized gain score of ORF for all nontwins in each twin’s classroom. Higher scores indicate greater gains in ORF than expected on average. To operationalize exposure to teacher quality, a mean split of class ORF gain was used with twins below the cut point labeled as having been exposed to lower teacher quality and therefore a potentially poorer environment, and twins above the cut point labeled as having been exposed to a higher teacher quality.

Statistical Analyses

The co-twin discordant design is based on a multilevel regression framework comparing an individual-level regression to within-pair and between-pair associations of exposure to outcome (see McGue et al., 2010). In this model, twins are considered as nested within twin pair, and the variances of twin pairs are fixed. The model is typically represented by the following two equations. Therefore, let y_ij be the observed outcome for the ith twin (i = 1, 2) in the jth twin pair (j = 1, 2, … N) and let x_ij be the exposure for the individual. The individual-level regression equation would be represented by

$$y_{\mathit{ij}}={\beta }_0+{\beta }_1{x}_{\mathit{ij}}+e_{\mathit{ij}},$$ (1)

where β₁ is the effect of exposure of teacher quality on ORF in Grades 2 and 3 for each individual, β₀ is the intercept, and e_ij is the residual correlated within a twin pair. Typically, this model is then further extended to account for twin pairings by including a within-pair (β_w) and between-pair (β_b) regression effect using the following regression model:

$$y_{\mathit{ij}}={\beta }_0+{\beta }_w(x_{\mathit{ij}}-{\overline{x}}_j)+{\beta }_B{\overline{x}}_j+e_{\mathit{ij}},$$ (2)

where ${\stackrel{‒}{x}}_j$ is the mean exposure for the jth twin pair, β_w is the direct estimate of the effect of teacher quality on ORF in Grades 2 and 3 within discordant twin pairs, and e_ij is the residual correlated within a twin pair.

The co-twin discordant design has typically been used in the medical epidemiological literature, and no reports could be found where it has been applied to educational data. As is typical in education research, the present data are not only nested at the twin pair level but also the twins are nested within schools, thus adding a third level to the nested structure of the data that needs to be considered. Therefore, we propose to extend the typical co-twin discordant model, as shown in Equations 1 and 2, to account for this nested structure. Let y_ijk be the observed outcome for the ith twin (i = 1, 2) in the jth twin pair (j = 1, 2, … N) in the kth school (k = 1, 2, … N), and let x_ijk be the exposure for the individual:

$$y_{\mathit{ijk}}={\beta }_0+{\beta }_w(x_{\mathit{ijk}}-{\overline{x}}_K)+{\beta }_B{\overline{x}}_j+{\beta }_S{\overline{x}}_k+r_k+r_{\mathit{jk}}+e_{\mathit{ijk}},$$ (3)

where ${\stackrel{‒}{x}}_j$ is still the mean exposure for the jth twin pair, β_S is the school effect, and β_w is still the direct estimate of the effect of teacher quality in Grade 1 on ORF in Grades 2 and 3 within discordant twin pairs, taking into account the twins share the same school. In addition, r_k is the random term for the school effect, r_ik is the random term for the twin pair effect, and e_ij is the residual correlated within a school. The model in Equation 3 was fit using SAS PROC MIXED (Singer, 1998) using all available raw data.

Results

At the beginning of Grade 1, 79% of the twin pairs were in different homeroom classrooms. Of these twin pairs in different classrooms, there were 353 pairs of MZ twins, 113 of them were concordant for exposure to better quality teachers, 138 were concordant for exposure to lower quality teachers, and 102 were discordant. Furthermore, there were 358 pairs of DZ twins, 120 were concordant for better quality teachers, 115 were concordant for lower quality teachers, and 123 were discordant. The rate of exposure to a lower quality teacher did not differ significantly between MZ (51.9%) and DZ (47.7%) twins. Tetrachoric correlations suggested that MZ twins were only slightly more similar to each other (r_t = .42) on exposure to teacher quality than DZ twins (r_t = .31), suggesting that in general, the twins were separated into different classrooms regardless of their zygosity.

Descriptive statistics for the exposure and outcome variables of interest are displayed in Table 1. It was determined that lower teacher quality in Grade 1 was significantly associated with lower performance in spring of Grade 2, t(643) = 3.40, p < .001, d = .27, and Grade 3, t(404) = 1.95, p < .05, d = .19.

Major results from the hierarchical linear modeling are displayed in Table 2 and Figure 2. Although all model information is presented in Table 2 from the unconditional and conditional models, the results of interest for the co-twin control design are the estimates of the difference estimates from the conditional model (see Figure 2). For Grades 2 and 3 spring ORF scores, the individual-level analysis suggested that there is a significant difference between individuals who were exposed to poorer teacher quality than those who were not. In general, children who experienced a lower quality teacher scored about 5 points lower in Grade 2, representing reading five less words in a minute, than children who experienced higher quality teachers (d = .13). The same was shown in Grade 3, with students of lower quality teacher in Grade 1 scoring approximately 6 points lower (d = .17). This effect was also significant within MZ and DZ discordant twin pairings. Within the 102 pairs of discordant MZ pairs, children who were exposed to the poorer teacher quality performed approximately 8 points (i.e., words) lower on ORF outcomes than their twins in Grade 2 (d = .23), and almost 10 points lower in Grade 3 (d = .26). Within the 123 discordant DZ twin pairs, children who experienced the poorer teacher quality exposure performed approximately 2 points lower on the Grade 2 spring ORF (d = .04) and 3 points lower on the Grade 3 spring ORF (d = .08).

Table 2.

HLM Results of the Co-Twin Control Analyses Exploring the Effect of Teacher Quality on Oral Reading Fluency Performance, Including the Magnitude of Difference in Words per Minute in Grades 2 and 3 (With SEs)

	Unconditional Model		Conditional Model		Unconditional Model		Conditional Model
	Grade 2		Grade 2		Grade 3		Grade 3
	Estimate	SE	Estimate	SE	Estimate	SE	Estimate	SE
Fixed effects
Intercept	102.29	1.43	103.98*	2.66	114.77	1.55	115.71*	2.99
Zygosity			−8.15*	3.33			−8.53*	3.77
Teacher quality			1.57	3.03			2.77	3.57
Zygosity × teacher quality			6.63*	3.82			6.90	4.56
Random effects
School level	171.12*	71.67	165.04*	72.15	9.97	83.23	.02	82.08
Family level	778.47*	84.57	755.42*	84.14	742.37	108.00	746.27*	110.21
Individual level	463.38*	27.62	465.28*	27.95	473.53	35.94	454.14*	34.80
Deviance	12,205.50		12,192.20		7,323.90		7,573.6
Difference estimates
Individual level			4.88*	2.10			6.21*	2.30
Within DZ pairs			1.56	3.03			2.77	3.57
Within MZ pairs			8.19*	2.62			9.66*	2.88

Note. HLM = hierarchical linear modeling; DZ = dizygotic; MZ = monozygotic.

^*p < .05.

Figure 2. Results from the co-twin control analyses exploring the effect of teacher quality on reading performance.

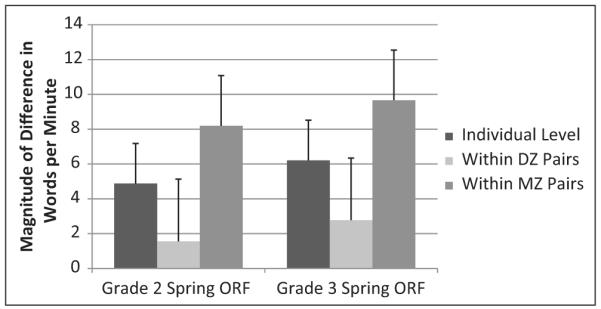
Note. DZ = dizygotic; MZ = monozygotic; ORF = oral reading fluency.

As suggested by the hypothetical examples in Figure 1, the pattern of results in Figure 2 is consistent (within error bars) with Scenario A, indicating that there are no genetic and shared environmental confounders, suggesting that there may be causal link between teacher quality in Grade 1 and subsequent scores on ORF testing for the following two school years. This is because the magnitude of the difference in ORF scores between discordant individuals is the same (within standard error bars) as the difference between MZ and DZ twins. If there was confounding due to genetic or environmental influences, the difference within the twin pairings would be smaller than that of unrelated individuals. This result is further supported by the low effect size of the difference in ORF scores between discordant individuals (see Table 2). In general, although there was a significant difference in number of words read in discordant twin pairs, this was small for all, indicating that the overall effect was equally small across the groups. This supports the idea that there were no differences between the groups and that the overall effect of teacher quality on student reading outcomes is small.

Discussion

The primary goal of this study was to introduce educational researchers to the co-twin control design as an alternative method for strengthening causal inferences outside of an experimental design (Rutter, 2007). We argue that maintaining stringent experimental designs can be difficult in educational research, for ethical and practical considerations. Aspects such as schools declining to participate, drop out of classrooms, children relocating during the intervention, and other potential biases to the counterfactual model are common threats in educational research. However, by comparing the mean difference on an outcome between discordant twins based on an exposure, it is possible to determine whether there may be a possible causal influence of exposure on outcome or whether there are instead genetic and/or environmental confounders in the relationship. It is important to note that the co-twin control design is tempered in the actual causal conclusions that can be made if there are other alternative explanations, or other confounding variables, that can be recognized as potentially occurring. This design is able to control for genetic and shared environmental confounders, but it does not directly test the causal relationship. Therefore, causal inferences can only be strengthened or reduced using this approach.

A practical example of the co-twin control design explored the extent to which teacher quality influenced reading performance outcomes in subsequent years. Previous work has suggested that the overall influence of teacher effects, nested within classroom influences, on children’s reading outcomes is low to moderate, with genetic influences and other environmental effects such as school SES playing a much larger role in student performance (e.g., Byrne et al., 2010). Given the work by Taylor et al. (2010), who found that poor teaching has a larger potential influence on student reading performance than good teaching, we specifically examined the possible causal role of exposure to poor teacher quality on reading outcomes. It should be emphasized that although the present work uses the same “teacher quality” variable as Taylor et al. (2010), this work cannot identify the genetic and environmental etiology of reading performance at any level of teacher quality but instead only attempts to control for the effects, no matter what their magnitude. The results suggested that the magnitude of the exposure effect was the same, even when controlling for genetic and environmental confounders by analyzing twin pairs, indicating a potential causal role of poorer teacher quality on reading outcomes in subsequent school years.

We temper our main conclusions for three reasons. First, the practical difference between children from discordant classrooms is not high, with an overall difference of five words in Grade 2 and six words in Grade 3, representing approximately 5% of the mean ORF score in those grades. Therefore, although there is a significant difference between the groups, it is a small one practically. Second, we note that by using a mean split of teacher quality (necessary to provide adequate power), a fake dichotomy was created where actual differences are most likely much smaller, similar to the previous work of Byrne et al. (2010) and Nye et al. (2004). We underscore that these results are not presented as a comprehensive exploration of the effect of teacher quality on ORF outcomes but instead as an example of a novel method in educational sciences. Finally, ORF passages, including those used in the present sample, have suggested form effects, in that difficulty is not uniform across all form administrations (Francis et al., 2008; Petscher & Kim, 2011). The present results may be an artifact of individuals getting test passages of different difficulty, which, if not random in this sample, may undermine the casual implications.

For this particular example of the role of teacher quality on reading outcomes, there was a potential for environmental confounders only, and not genetic. This is due to teacher quality being measured by class ORF gain, a truly environmental variable that does not include the twins’ data or twin or parent report, all of which could have introduced genetic sources of variability (Taylor et al., 2010). Indeed, potential confounders of note that were ruled out by this study were environmental aspects shared between the twins, most likely school-level influences such as school SES. However, many potential causal relationships in which educational researchers may be interested include the possibility of genetic confounders as well as environmental ones. For instance, if teacher quality had been measured by actual classroom observation of the twins’ teachers, genetic confounders are possible due to gene–environment correlations (e.g., DeThorne & Hart, 2009). More specifically, teachers may interact with children in their class differentially based on each child’s genetic predispositions, resulting in teacher quality changing depending on the students themselves. For example, preschool teachers can be affected by language abilities of the students in their classroom, changing their teacher style for lower or higher class ability. As language is a highly genetically influenced trait in early childhood, teacher quality would be associated with genetic variance (DeThorne et al., 2008).

As with any method, there are some limitations to the co-twin control design, which may be relevant to educational researchers. First, the co-twin control design cannot rule out reverse causation unless longitudinal designs are used. The present example, as with many other education research questions, is longitudinal, and researchers are best served to explore longitudinal hypotheses using this model. Second, this design cannot explore the impact of an exposure that is shared between MZ twins, as it relies on a natural experimental paradigm where the twins have to be discordant. Family SES or home language environment cannot differentiate twins living together and therefore cannot be explored with this design. Finally and most importantly, as mentioned in the introduction, it is not possible to control for nonshared environmental confounders using the design. This is important to note because this results in MZ twins not being the perfect counterfactual of each other, even though it does match them by genotype and shared environment in childhood. Therefore, the results of this study and others that use this design may indeed suggest causality or may reflect nonshared environmental alternative explanations, which cannot be controlled for. In the present example, tracking may have occurred, resulting in a selection bias toward which twin pairs were separated and into which classrooms they were assigned. Tracking is the phenomenon where a school puts students of similar ability levels into the same classroom, resulting in differences between classrooms in a given grade based on ability. It represents a possible nonshared environment confounder because tracking serves to make siblings less similar by placing them in different classrooms. The twins in this sample may have been grouped based on preexisting performance factors, and therefore, we are not able to rule out selection as a possible bias against causal conclusions.

Implications for Practitioners

Although there is no direct impact of the introduction of this novel method to educational scientists on practitioners, there are still implications. Researchers inform educational practice as well as policy decisions, which directly affect practitioners. Understanding causal relationships is an important part of understanding the mechanisms in education, particularly in curriculum setup. Although not a thorough analysis of teacher effects on reading outcomes, the present example of the co-twin control method explores just one out of the ways that this design, available to many educational researchers, could have implications for practitioners.

Although experimental designs are the gold standard in educational research for determining causal relationships, they are not the only options for researchers. Threats to the experimental design, such as nonrepresentativeness of participating schools and/or students, as well as dropout and other nonrandom influences, are a valid concern in the educational literature. Moreover, not all research questions in education are feasible using an experimental design. We suggest that quasi-experimental designs, such as observational approaches like the co-twin control design, provide an alternative method for an educational researcher (Rutter, 2007). Although MZ twins (and for power, DZ twins) do not provide the perfect counterfactual situation, they do allow for possible causal relationships to be explored with some limitations. If an exposure has a potential causal effect on an outcome, then the exposed member of a discordant twin pair will show higher rates of the outcome than the nonexposed member. If this is not the case, then there will be differential relationships of exposure to outcome based on the zygosity of the twin pair. This design requires smaller sample sizes than the experimental method and utilizes a natural experiment, which can be capitalized on by many educational researchers, including those with limited resources, making it an alternative to the gold standard.