High-Field ¹³C DNP with a Radical Mixture

Abstract

We report direct ¹³C dynamic nuclear polarization at 5 T under magic angle spinning (MAS) at 82 K using a mixture of monoradicals with narrow EPR linewidths. We show the importance of optimizing both EPR linewidth and electron relaxation times by studying direct DNP of ¹³C using SA-BDPA and trityl radical, and achieve ¹³C enhancements above 600. This new approach may be better suited for dissolution DNP and for studies of ¹H depleted biological and other non-protonated solids.

Over the past few decades, many techniques have been developed for studying chemical structure. NMR spectroscopy in particular has achieved widespread use due to its ability to characterize biological molecules ranging from chemical structure, dynamics, and medium-range (4–6 Å) intra- and intermolecular structure. Solid-state NMR in particular has been especially important in structurally characterizing disordered biological solids, which are inaccessible to traditional diffraction based methods. However, the success of these experiments is limited due to the low Boltzmann polarization of nuclear spins, leading to long acquisition times. To address this issue, solution NMR and magnetic resonance imaging focuses primarily on high-γ, abundant nuclei such as ¹H, ¹⁹F and ³¹P, while solid-state NMR methods utilizes magic angle spinning (MAS), cross-polarization (CP) and high magnetic fields to obtain modest gains in sensitivity and resolution.

More recently high-field dynamic nuclear polarization (DNP) has been a valuable approach for studying structure, function, and reaction pathways because it allows significant reduction in acquisition times. In a DNP experiment, the large thermal electron spin polarization of a paramagnetic compound is transferred to surrounding nuclei, a process that is driven by irradiating the sample with microwaves.^1,2 Immense gains in sensitivity have been reported for various low- nuclei (e.g., ¹³C, ¹⁵N, ¹⁷O, ²⁷Al and ²⁹Si) using indirect DNP polarization.^3–6 Typically, a nitroxide-based biradical (e.g., TOTAPOL) is used as the electron polarization source and polarizes ¹H (theoretically reaching (γ_e/γ_H) ε≈ 660).^7,8 This polarization is then transferred to lower-γ nuclei by a CP step, reaching enhancement factors (ε) as high as 248.⁹ This approach has been used successfully for structural biology and more recently surface science studies.^4,10–18

Indirect polarization is extremely attractive as many systems contain ¹H’s that are easily polarized. Strong ¹H–¹H and e′–¹H couplings allow for efficient DNP and dispersion of polarization via spin-diffusion. Additionally, the wide availability of nitroxide-based biradicals, with broad EPR lines, allows high-γ nuclei such as ¹H to be efficiently polarized by the cross-effect (CE). Unfortunately, many chemical systems do not fall into this category, because they are severely lacking ¹H’s which limits the ability to efficiently cross-polarize. An attractive approach in these circumstances is to perform direct polarization of low-γ nuclei such as ¹³C without the CP step from ¹H.

In this paper, we utilize a mixture of two narrow-linewidth radicals that have EPR resonance frequencies that are approximately separated by the ¹³C nuclear Larmor frequency as the polarizing agent. Concurrently, since that exhibit different relaxation rates, we can optimizing both the CE matching condition and the DNP kinetics. With this mixture, we obtain record ¹³C DNP enhancements > 600 (nearly 25 % of the theoretical enhancement (γ_e/γ_C) ε≈ 2620).

The development of high-field DNP has focused on the CE mechanism, since typical solid effect (SE) enhancements had been considerably lower than those for CE.¹⁹ However, recent results have shown that SE may be useful for polarization using transition-metal based polarizing agents²⁰ and can also give enhancements ~100;^21,22 with sufficient microwave field strength, sensitivity gains may match those of CE.²³ The dominant polarization transfer process depends on the nucleus being polarized and the EPR characteristics of the polarizing agent. In particular, the relative magnitudes of the electron homogeneous (δ) and inhomogeneous (Δ) linewidths, and the nuclear Larmor frequency (ω_0I) determine the dominant polarization mechanism.

The SE mechanism is a two-spin process which is dominant when ω_0I > δ, Δ and microwave irradiation is applied at the electron-nuclear zero- or double-quantum frequency.^24–26 This matching condition is given by

$${\omega }_{\text{mw}}={\omega }_{0S}\pm {\omega }_{0I}$$ (1)

where ω_0S is the electron Larmor frequency and ω_mw is the micro- wave frequency.

The CE mechanism may be described as a three-spin flipflop-flip process between two electrons and a nucleus, which is dominant when Δ> ω_0I > δ. In order to achieve maximum efficiency the difference between the two electron Larmor frequencies must be near the nuclear Larmor frequency.^27–31

$${\omega }_{0I}={\omega }_{0S_2}-{\omega }_{0S_1}$$ (2)

Optimizing the polarizing agents used for SE and CE is a non-trivial task, as discussed recently by Hu.³² Both the EPR line-shape and the electron spin-lattice relaxation time (T_1S) must be considered. For SE, one applies microwave irradiation at the matching condition given in (eq, 1); ideally, one uses a polarizing agent with a narrow EPR spectrum, thus allowing the matching condition to be met for the majority of unpaired electrons in the system. Also, a short electron T_1S allows quick ‘recycling’ of SE, since the electron must quickly recover its polarization in order to polarize many nuclei. However, there is an optimum T_1S since a short T_1S leads to paramagnetic relaxation of nearby nuclei, thus destroying the polarization already transferred to nuclei.

For CE, one destroys the thermal polarization of one electron with microwave irradiation. This electron then recovers its polarization via a flip-flop-flip process with a second electron and a nucleus. This process is efficient when eq. 2 is satisfied. Therefore, the ideal polarizing agent includes two different radicals, each with narrow EPR resonances, which are separated by the nuclear Larmor frequency. Note that the recovery of polarization of the first electron occurs via two competing processes. The first process is the CE mechanism as just described. However, the second process is the usual electron T_1S relaxation. Therefore, if the T_1S of the first electron is long, the CE mechanism dominates and polarization transfer is more efficient, as recently demonstrated by Zagdoun et al.⁸ This is not a complete picture, however. The second electron must provide polarization, as does the electron in SE. Therefore, quick ‘recycling’ of the CE mechanism relies on a sufficiently short T_1S of the second electron. If the two electrons have the same T_1S, as is the case for most nitroxide biradicals, then one must compromise on the T_1S. However, if two different radicals are used, then one can select polarizing agents such that the first electron has a long T_1S and the second electron has a shorter T_1S.

By using a mixture of SA-BDPA and trityl, we demonstrate efficient cross effect using two radicals with relatively narrow EPR linewidths, being 28 and 50 MHz, respectively. The centers of the EPR spectra are separated by roughly the ¹³C Larmor frequency (34 MHz separation vs. 53 MHz Larmor frequency at 5 T; trityl is broad enough to make up the difference). Additionally, SA-BDPA has a long T_1S, whereas the T_1S of trityl is shorter³³, giving improved CE performance when irradiating near the SA-BDPA resonance.

¹³C direct polarization magic-angle spinning NMR experiments were performed using two organic water-soluble polarizing agents, SA-BDPA³³ and trityl OX063,³⁴ which are depicted in Figure 1. Both SE and CE must be considered in this study. To evaluate the dominating DNP mechanism, the ¹³C DNP enhancement field-profiles were measured via direct detection, where the magnetic field was adjusted between 4977 and 4990 mT (Figure 2) and 8 W of microwave output power was chosen for long term stability (>6 hours).

Figure 1.

Narrowline monoradical chemical structures of SA-BDPA and trityl (OX063).

Figure 2.

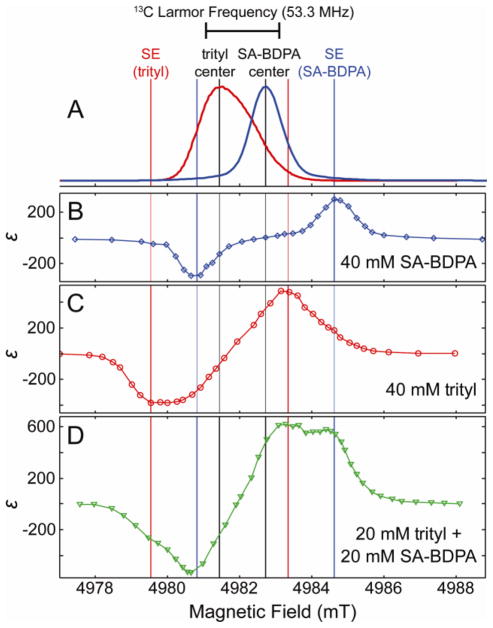
Field-dependent ¹³C DNP enhancement profiles of SA-BDPA (B), trityl (C), and a mixture (D), with EPR spectra of SA-BDPA and trityl (A). Field profiles were recorded at 82 K with a microwave frequency of 139.66 GHz, 8 W of microwave power and a MAS frequency of 4.8 kHz.

In Figure 2A, we show the EPR spectra of SA-BDPA and trityl, acquired at 140 GHz (the field axis is adjusted to align with the DNP experiments at 139.66 GHz). We also mark the center of each spectrum in black, and mark the field positions that are predicted to be optimal for SE DNP for both SA-BDPA (blue) and trityl (red). In Figure 2B–D, ¹³C-DNP field profiles are shown for SA-BDPA, trityl, and a 1:1 mixture, each with a total radical concentration of 40 mM.

Figure 2B shows the field profile using only SA-BDPA. From the EPR spectrum, we see that the line of SA-BDPA is narrower than the ¹³C Larmor frequency. Therefore, we expect that SE is strongly dominating the DNP transfer. This is confirmed by the fact that there is a plateau in the enhancement at the center of the DNP field profile, which is characteristic of a well-resolved SE. Also the position of maximum enhancement is in good agreement with the position predicted for SE.

The trityl EPR spectrum is considerably broader than that of SA-BDPA, and with a linewidth of 50 MHz it is possible for both SE and CE to contribute to the DNP enhancements. The trityl DNP profile is given in Figure 2C. The asymmetry of enhancements (−380 vs. 480), and the lack of a plateau in the center of the field profile suggest that CE is making some contribution to the DNP enhancement. However, the extrema of the DNP profile are in good agreement with those predicted for SE DNP, and so one sees that SE also likely is making a major contribution.

In Figure 2D, the ¹³C DNP field profile is shown for a mixture of SA-BDPA and trityl. In this case, there are many contributing DNP processes: SE resulting from SA-BDPA, SE and CE resulting from trityl, and finally CE resulting from the interaction between SA-BDPA and trityl. Careful examination reveals that the major features seen in the field profile are at nearly the same positions as seen in the pure SA-BPDA and trityl profiles. We first examine the features seen at 4980.7 and 4984.4 mT, which correspond to SE from SA-BDPA. The intensity of these features is remarkable, giving enhancements at these positions of ±535 and 575, respectively. Although other processes contribute to these large enhancements, it appears that SE from SA-BDPA is at least as effective in this sample as it was in the pure SA-BDPA sample, despite the total concentration of SA-BDPA of the mixed sample being half of that in the pure sample. This is further confirmed in Figure 3, where the SA-BDPA DNP field profile is subtracted from the mixture field profile, using a coefficient of 1.1. This coefficient was chosen in order to fully remove the features resulting from SE using SA-BDPA, without introducing other features. This implies that SE resulting from SA-BDPA is somehow more effective in this sample than it is in the pure sample. In fact, this is a result of a reduced electron T_1S for SA-BDPA in the mixed sample. Paramagnetic relaxation from trityl actually shortens the SA-BDPA T_1S, allowing SA-BDPA to become more efficient at polarizing the ¹³C nuclei. This is seen in Table 1, where T_1S of SA-BDPA changes from 28.9 ms in the pure SA-BDPA sample to 3.6 ms in the mixture. We also note that any change in the trityl T_1S is negligible.

Figure 3.

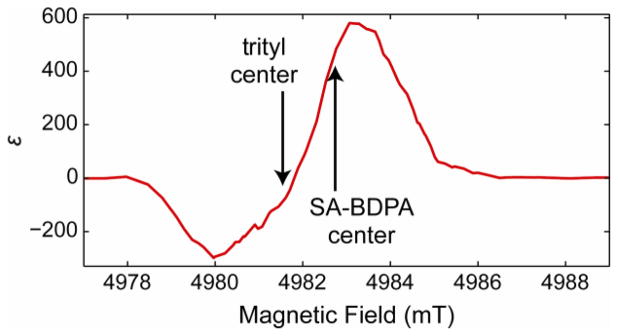
Subtracted DNP field profile, obtained by subtracting the SA-BDPA DNP field profile (Figure 2B) multiplied by 1.1 from the SA-BDPA and trityl mixture DNP field profile.

Table 1.

¹³C direct detection enhancement ε, electron spin relaxation time T_1S and DNP build-up time T_B.

Radical	ε	T1S (ms)	TB (s)
SA-BDPA (40 mM)	300	28.9	287 (16)
trityl (40 mM)	480	1.4	167 (7)
Mixture (20 mM of each)	620	3.6 (SA-BPDA) 1.4 (trityl)	216 (3)

Once the contribution of SE from SA-BDPA is removed, as is shown in Figure 3, we see a highly asymmetric DNP field profile remaining. This profile contains contributions from pure trityl SE and CE, but also CE resulting from SA-BDPA and trityl. We already know that the pure trityl field profile is not nearly as asymmetric as this profile, as seen in Figure 2C, and so this asymmetry is likely a result of CE from SA-BDPA and trityl. In fact, this is exactly what we expect. If we irradiate near to the center of the SA-BDPA spectrum, the SA-BDPA radical saturates easily, since it has a longer T_1S. Therefore, the polarization recovery of the SA-BDPA electron occurs primarily via the CE mechanism. Furthermore, the fast T_1S of trityl allows for quick recycling of the CE mechanism, giving an overall more efficient CE mechanism. However, when irradiating closer to the center of the trityl spectrum, saturation is more difficult because the T_1S of trityl is shorter, and the source of polarization, SA-BDPA, recovers more slowly. This leads to an overall less efficient CE mechanism. We note that the peaks do not lie exactly on the SA-BDPA or trityl centers. This is both because SA-BDPA and trityl do not have exactly the correct separation for the ¹³C cross effect matching, and also because contributions to the DNP enhancement remain from the pure trityl. One should note that previous experiments by Hu et al. showed that mixtures of TEMPO and trityl were efficient in polarizing ¹H.¹⁹ In particular, DNP was efficient when irradiating the narrow, trityl radical. However, it was not clear whether improvements were primarily due to a longer electron T₁ for trityl, or due to the considerably narrower lineshape of trityl compared to TEMPO.

Both nuclear spin-lattice relaxation (T_1I) and polarization build-up (T_B) times for ¹³C were measured at 82 K. Both T_B and T_1I values were within error of one another for each radical composition, and so only T_B is listed in Table 1. The polarization build-up times varied between the radicals, however, with trityl being the shortest and SA-BDPA being the longest. Radical concentrations and sample conditions were identical, enabling direct comparison between the effect of the nuclear and electron relaxation characteristics. The observed reduction in polarization times for each must be attributed to the inherent electron T_1S of the radical, and the type of DNP mechanisms that are active.

Direct ¹³C polarization enhancements were measured at the maximum positive field positions using optimized recycle delays (1.26 × T_B) for each radical composition. Off-signals (0 W micro-wave power) were acquired under identical conditions as the on-signals (10 W microwave power) for SA-BDPA (4984.5 mT), trityl (4983.2 mT), and mixture (4983.1 mT), respectively. SA-BDPA and trityl provided enhancements of 300 and 480, respectively, at 82 K. SA-BDPA is comparable to previous studies on ¹³C detection using TOTAPOL obtaining enhancements of 305 under similar sample conditions.³⁵ Trityl proves slightly more efficient in polarizing as the breadth better satisfies the cross-effect mechanism, and provides ~60% larger enhancement. The mixed radical sample satisfies the CE matching condition most efficiently, and the beneficial differences in electron relaxation times (T_1S) lead to a very effective cross-effect enhancement of 620. The mixture outperforms trityl (> 130 %) and SA-BDPA (> 200 %), and also outperforms previous experiments which utilize TOTAPOL for ¹³C DNP (> 200 %). ³⁵

These narrow line radicals may be ideally suited for directly polarizing low-γ nuclei that are either poorly cross-polarized by high-γ nuclei (e.g., ¹H or ¹⁹F) or are found within environments in which high-γ nuclei are absent. Introducing a mixture approach whereby better satisfying the CE matching condition and having different T_1S relaxation times could have drastic implications providing a more efficient CE mechanism and may help compensate the decrease in enhancements as DNP experiments move to higher magnetic fields. These findings may be beneficial for dissolution DNP methods that commonly use trityl radical, since one may combine SA-BDPA and trityl. Then, polarizing at liquid He temperatures could lead to significant polarization gains on labeled dissolution experiments without modification of any hardware. Finally, if trityl and SA-BDPA can be tethered together to create a biradical, it should be possible to reduce radical concentrations, increase the contribution of CE to the DNP enhancements, and potentially increase DNP gains in the future.

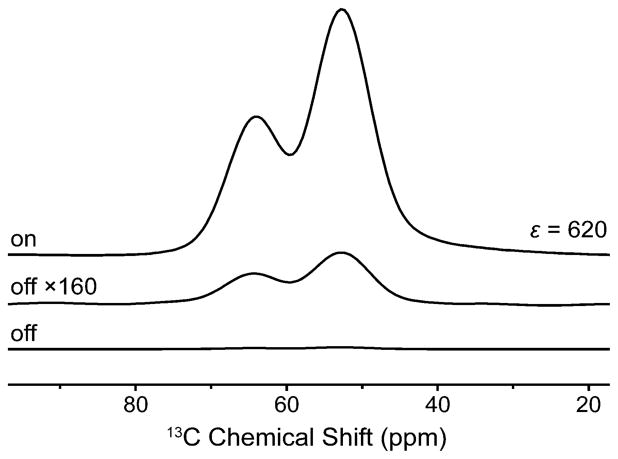
Figure 4.

¹³C direct polarization using the mixed radical SA-BDPA (20 mM) and trityl (20 mM) on U-¹³C-glycerol-d8 (60%) in D₂O (30%) and H₂O (10%) at 82 K and 10 W (B_o = 4983.1 mT).