A Bias Corrected Net Reclassification Improvement for Clinical Subgroups

Abstract

Background

Comparing prediction models using reclassification within subgroups at intermediate risk is often of clinical interest.

Objective

To demonstrate a method for obtaining an unbiased estimate for the Net Reclassification Improvement (NRI) evaluated only on a subset, or the clinical NRI. Study Design and Setting: We derived the expected value of the clinical NRI under the null hypothesis using the same principles as the overall NRI. We then conducted a simulation study based on a logistic model with a known predictor and a potential predictor, varying the effects of the known and potential predictors to test the performance of our bias-corrected clinical NRI measure. Finally, data from the Women’s Health Study, a prospective cohort of 24,171 female health professionals, were used as an example of the proposed method.

Results

Our bias-corrected estimate is shown to have a mean of zero in the null case under a range of simulated parameters and, unlike the naïve estimate, to be unbiased. We also provide two methods for obtaining a variance estimate, both with reasonable type 1 errors.

Conclusion

Our proposed method is an improvement over currently used methods of calculating the clinical NRI and is recommended to reduce overly optimistic results.

Introduction

In the analysis of a new predictive model, often an extension of the current model to include a new biomarker or other information, there is interest in assessing improvement in the ability to predict outcomes. The ability of a model to classify people into appropriate clinically relevant categories of risk has increasingly been used in addition to the traditional measures of discrimination and calibration (1) and has been included in guidelines for the evaluation of new markers and models.(2) The Net Reclassification Improvement (NRI) suggested by Pencina and colleagues (3) provides a statistic for comparing the overall reclassification of a new model compared to a reference model given a set of clinical cut-points.

To avoid unnecessary testing and restrict the comparison to the area of uncertainly in clinical decision making, there is often additional interest in the reclassification of only a subset of the population, defined by the reference model. In the case of the cut-points for cardiovascular disease risk, for example, the treatment implications are the clearest for the highest and lowest risk categories, while for those at intermediate risk, the risk to benefit tradeoffs are more ambiguous.(4) Consequently, it is often of interest to examine reclassification by the new model only in those people whom the reference model categorized as intermediate risk.(5) Such sequential testing can be more cost-effective and clinically useful.(6) The methodology for this process, however, is less developed. An extension of the NRI for the intermediate risk group, defined by the categories of the reference model, has been proposed, called the clinical NRI or cNRI, and has been used in multiple clinical and statistical publications to date.(7–12) This measure has been found to be biased, however, and a bias-correction for the cNRI has been proposed.(13) We explain and expand on this correction below.

Methods

Estimation

When the reference model and the new model are compared, predicted risks for each are generated and study subjects are sorted into risk categories according to the pre-specified clinical cut-points. From this, a reclassification table can be constructed as shown in Table 1 with the rows representing risk categories from the reference model and columns representing risk categories from the new model. Those falling in cells on the diagonal are placed in the same category by both models, those above the diagonal are classified as higher risk by the new model, and those below the diagonal are classified as higher risk by the reference model.

Table 1.

Reclassification Table for the Null Case^*

a) Observed Reclassification (cases / non-cases)
Reference Model	Low	New Model		High	Totals
		Intermediate Low	Intermediate High
Low	40 / 1708	0 / 19	0 / 0	0 / 0	40 / 1727
Intermediate Low	1 / 18	120 / 1304	2 / 11	0 / 0	123 / 1333
Intermediate High	0 / 0	0 / 13	173 / 958	3 / 10	176 / 981
High	0 / 0	0 / 0	0 / 6	173 / 441	173 / 447
Totals	41 / 1726	120 / 1336	175 / 975	176 / 451	512 / 4488

b) Expected Reclassification (cases / non-cases)
Reference Model	Low	New Model		High	Totals
		Intermediate Low	Intermediate High
Low	40 / 1708	0.5 / 18.5	0 / 0	0 / 0	40.5 / 1726.5
Intermediate Low	0.5 / 18.5	120 / 1304	1 / 12	0 / 0	121.5 / 1334.5
Intermediate High	0 / 0	1 / 12	173 / 958	1.5 / 8	175.5 / 978
High	0 / 0	0 / 0	1.5 / 8	173 / 441	174.5 / 449
Totals	40.5 / 1726.5	121.5 / 1334.5	175.5 / 978	174.5 / 449	512 / 4488

^*Cells include cases/non-cases

Reclassification from a simulation comparing a reference model based on X (true OR of 8) and a new model based on X and Y (true OR of 1) with a base event probability of 10% and reclassification cut points at 5%, 10% and 20%.

Using the reclassification table, the overall NRI is calculated as follows:

$$\mathit{NRI}=\frac{\#\mathit{cases}\_\mathit{moving}\_up-\#\mathit{cases}\_\mathit{moving}\_\mathit{down}}{\#\mathit{cases}}+\frac{\#\mathit{noncases}\_\mathit{moving}\_\mathit{down}-\#\mathit{noncases}\_\mathit{moving}\_up}{\#\mathit{noncases}}$$

The NRI follows McNemar’s (14) logic, wherein under the null hypothesis reclassification is symmetric and the expected NRI is 0. Consequently, a Z statistic can be calculated as

$$Z_{\mathit{NRI}}=\frac{\mathit{NRI}-0}{\sqrt{\frac{\#\mathit{cases}\_\mathit{moving}}{\#{\mathit{cases}}^2}+\frac{\#\mathit{noncases}\_\mathit{moving}}{\#{\mathit{noncases}}^2}}}$$

The data shown in Table 1a are from an example of the null hypothesis, in which there is no improvement using the new model. In this case, we would expect to see most of the subjects assigned to the same category by both models in the reclassification table, with any reclassification in the form of random and thus symmetric movement around the diagonal, e.g. equal movement into higher and lower categories for both cases and non-cases. As expected, there is little movement off the diagonal in Table 1a, and the movement that is observed is fairly symmetric, leading to an NRI of 0.7%, with a corresponding p-value of 0.17.

The naïve cNRI, calculated in this case by applying the NRI formula only to those cases and non-cases classified as Intermediate Low or Intermediate High by the reference model, is 1.8%. The same Z-statistic formula above has been applied to generate p-values and confidence intervals, in this case generating a p value of 0.04 (with estimated 95% CI 0.03 to 3.5), suggesting an improvement even in the null case where none exists. However, unlike the NRI, the expected value of the cNRI under the null is not 0. Following the same logic from McNemar as in the original NRI derivation (14) and in Bowker’s test of difference in matched pairs (15), the expected distribution of matched pairs of categorical predictions is symmetric around the diagonal of agreement, which allows the focus to be on the differences in direction of the responses. By extension, the expected CNRI can be estimated through application of the symmetric nature of this null hypothesis.(13)

Specifically, under the null we would expect the off-diagonals to be symmetric for both cases and non-cases. The expected number of cases and controls in each cell can be obtained by taking the average of the symmetric cells. For example, the expected number of cases in row r, column c would be the average of the cases in row r, column c and the cases in row c, column r. Using Table 1a as an example, there are no cases in the first row, second column (Low by the Reference Model and Intermediate Low by the New Model) and one case in the second row, first column (Intermediate Low by the reference model and Low by the New Model). As shown in Table 1b, the expected number of cases in both cells is the average of 0.5 cases. Once the expected table (shown in Table 1b) is constructed, an unbiased estimate of the cNRI can be obtained as follows:

$$\text{cNRI}=\text{na}\ddot{\text{1}}\text{ve}\text{cNRI}-\text{expected}\text{cNRI}.$$

Using Table 1b, the expected cNRI is obtained is 0.8%, and the bias-corrected cNRI is 1.0%.

Deriving a variance estimate for this test statistic is not straightforward. A simple variance estimate can be obtained, using the same formulation as the NRI as follows:

$${\mathit{Var}}_{\mathit{cNRI}}=\frac{\#\mathit{subset}\_\mathit{cases}\_\mathit{moving}}{\#\mathit{subset}\_{\mathit{cases}}^2}+\frac{\#\mathit{subset}\_\mathit{noncases}\_\mathit{moving}}{\#\mathit{subset}\_{\mathit{noncases}}^2}$$

A Z statistic can then be calculated, using the bias-corrected cNRI as follows:

$$Z_{\mathit{cNRI}}=\frac{\mathit{cNRI}-0}{\sqrt{\frac{\#\mathit{subset}\_\mathit{cases}\_\mathit{moving}}{\#\mathit{subset}\_{\mathit{cases}}^2}+\frac{\#\mathit{subset}\_\mathit{noncases}\_\mathit{moving}}{\#\mathit{subset}\_{\mathit{noncases}}^2}}}$$

However, we found this variance estimate to be slightly conservative in our simulations, as shown below.

Role of the funding sources

The funding sources had no role in this study.

Results

Simulations

To assess the performance of the proposed measure, including the standard error estimation, we conducted a simulation study based on a logistic model with two explanatory variables, X and Y, where X represented a known predictor (or combination) and Y represented a potential new predictor. Both X and Y were normally distributed with a mean of 0 and a standard deviation of 0.5. We used an overall probability of an event of 10% and varied the odds ratios (OR) associated with X (from 4 to 16) and Y (from 0 to 3), using 500 simulations of 5000 observations for each combination and refitting the models to the simulated data. The odds ratios were chosen to illustrate a scenario in which the known predictor (X) is a summary of all known predictors or an established score. For instance, the Framingham Risk Score has an OR of approximately 16 for a 2 SD increase. Similarly, an OR of 3 for the new predictor (Y) is used for illustration of a relatively large effect. Reclassification tables were constructed using 4 categories with cut points at half the overall event probability, the overall event probability, and twice the overall event probability, with the middle two categories considered intermediate risk. We also considered the situation of 3 risk categories by combining the two intermediate risk groups. The R program (version 2.13.0) was used for this and all other analysis in this paper.

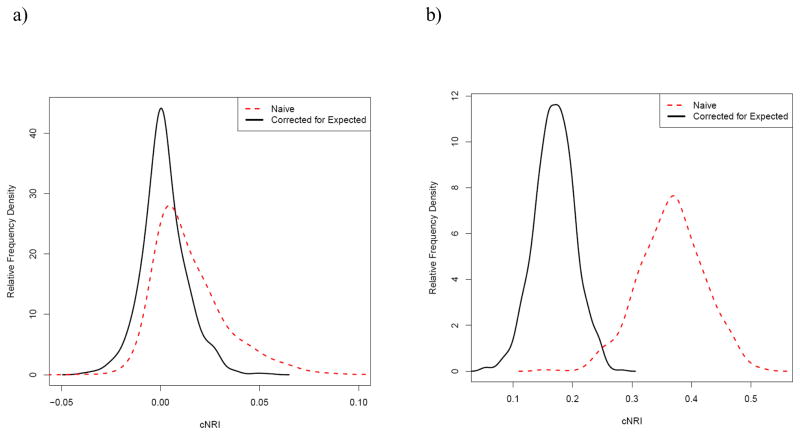
Figure 1 shows the distribution of the cNRI for the null case, using a combination of OR X of 8 and OR Y of 1. Using the reclassification cut point algorithm described above gave cutpoints of 5%, 10% and 20% in this combination. As shown, the distribution of the cNRI is only symmetric and centered around 0 after correction for the estimated value, while the naïve cNRI is shifted largely above zero with a non-symmetric positive tail. Figure 1b shows the distribution for similar parameters (OR X of 8, overall probability of 10%, sample size of 5000) using identical cut points as Figure 1a, but with a non-null OR for Y of 3. As shown, the correction shifts the distribution of the cNRI towards the null and the variability is decreased.

Figure 1.

Distribution of the cNRI with the proposed correction for the expected distribution and the naïve cNRI for simulations comparing reclassification for a model based on both X (true OR of 8) and Y (true OR of 1 for (a) and 3 for (b)) to a model based only on X. The sample size for each simulation was 5000, with a base event probability of 10% and reclassification cut points at 5%, 10% and 20%.

Table 2 shows the mean and median cNRI and the percent of p-values less than 0.05 for both the bias-corrected and the naïve cNRI for a variety of parameter combinations in the null situation with an OR Y of 1. As shown, the naïve cNRI is clearly biased with 20–39% of p-values less than 0.05. The cNRI corrected for the expected value behaves as expected in the null case (OR of Y = 1) with a mean of approximately zero. While the exact value for the cNRI varied slightly depending on the parameters, the effect of correction was similar across all parameter combinations. Using 3 risk categories by leaving out the middle cut-point at the overall probability led to similar results (Table 3).

Table 2.

Results of 500 Simulations for Each Parameter Combination for the Null Case with OR Y = 1

OR X	Naïve cNRI (%)			Bias-corrected cNRI (%)
	Mean	Median	p < 0.05 Simple Variance	Mean	Median	Simple Variance	p < 0.05
							Bootstrap
							Variance	95% CI
4 Categories
4	1.11	0.84	20.1%	0.21	0.12	3.0%	4.8%	7.0%
8	1.47	1.01	21.5%	0.19	0.08	3.2%	4.8%	6.6%
16	1.72	1.23	21.2%	0.21	0.10	3.6%	5.8%	8.4%
3 Categories
4	1.04	0.74	39.2%	0.13	0.08	3.1%	5.4%	8.6%
8	1.36	0.98	35.5%	0.07	0.03	5.9%	4.4%	6.8%
16	1.65	1.30	34.4%	0.14	0.04	4.3%	5.9%	9.0%

Table 3.

Reclassification Table When New Model Adds Predictive Information

a) Observed Reclassification (cases / non-cases)
Reference Model	Low	New Model		High	Totals
		Intermediate Low	Intermediate High
Low	39 / 1651*	9 / 193	3 / 14	0 / 0	51 / 1858
Intermediate Low	21 / 428	26 / 531	47 / 241	5 / 19	99 / 1219
Intermediate High	1 / 75	28 / 271	72 / 481	51 / 158	152 / 985
High	0 / 2	1 / 29	16 / 134	175 / 279	192 / 444
Totals	61 / 2156	64 / 1024	138 / 870	231 / 456	494 / 4506

b) Expected Reclassification (cases / non-cases)
Reference Model	Low	New Model		High	Totals
		Intermediate Low	Intermediate High
Low	39 / 1651*	15 / 310.5	2 / 44.5	0 / 1	56 / 2007
Intermediate Low	15 / 310.5	26 / 531	37.5 / 256	3 / 24	81.5 / 1121.5
Intermediate High	2 / 44.5	37.5 / 256	72 / 481	33.5 / 146	145 / 927.5
High	0 / 1	3 / 24	33.5 / 146	175 / 279	211.5 / 450
Totals	56 / 2007	81.5 / 1121.5	145 / 927.5	211.5 / 450	494 / 4506

^*Cells include cases/non-cases

Reclassification from a simulation comparing a reference model based on X (true OR of 8) and a new model based on X and Y (true OR of 3) with a base event probability of 10% and reclassification cut points at 5%, 10% and 20%.

While the formula based p-value calculation performs reasonably well in our simulations, bootstrap techniques have also been suggested for prediction metrics.(16) We explored 3 bootstrap approaches. The first approach used the X and Y variables from the bootstrap sample and refit both models, all predictions, and all statistics. The second approach stratified the bootstrap sampling by the risk categories of the Reference Model and did not refit the models. The naïve and expected cNRI were then recalculated for the sample. The third approach limited the resampling to the intermediate risk category of the Reference Model (e.g. the middle row of Table 1a in the example), did not refit the models, and retained the expected cNRI from the original model. The naïve cNRI was then recalculated for the sample Each approach used 1000 bootstrap samples to calculate the variance of the bias-corrected cNRI and a 95% confidence interval estimate using the 97.5 and 2.5 percentiles of the bias-corrected cNRI distribution.

The first bootstrap approach resulted in p-values which were highly conservative for both a substitution of the bootstrap estimate of variance into the Z-test formula and for a count of how often the 95% confidence interval includes 0. The type 1 error for an alpha of 0.05 was approximately zero, with no instances of a p<0.05 or 95% confidence intervals which did not include 0. The type 1 error rates resulting from the second bootstrap approach are shown in Table 2, along with the p-values obtained using the formula for the Z-test given above. The simple variance error rates are slightly conservative (most ranging from 3.0% to 4.3%, with one at 5.9%) while the bootstrap variance error rates are closer to the expected 5% (ranging from 4.4% to 5.8%). The error rates from the 95% confidence intervals were slightly optimistic, ranging from 6.6 to 8.4%. We suggest that the formula based method is reasonable for use and report the results from that approach in the rest of the paper, but note that it may be slightly conservative. Interestingly, the variance obtained with the third bootstrap approach corresponded nearly exactly with the simple variance. This suggests that the simple variance accounts for the variation in the naïve cNRI but not for the variance in the expected cNRI under the null.

In the example in Table 1, after subtracting the expected cNRI from the naïve cNRI of 1.8%, the bias-corrected cNRI is 0.9%, with a corresponding simple variance p-value 0.26 and 95% CI of −0.7 to 2.7. Table 3 shows the observed and expected reclassification tables for an example with a significant NRI. In this example, the new model improves prediction, with an NRI of 16.7% (95% CI = 11.0 to 22.4, p < 0.001). The naïve cNRI is 37.3% (95% CI = 27.0 to 47.5, p < 0.001), while the bias-corrected cNRI is still significant but much smaller at 19.6% (95% CI = 9.4 to 29.9, p < 0.001).

The bias corrected cNRI is also much closer to the overall NRI, with observed differences centered approximately at 0 and ranging from −2% to 3% for the null case with an OR X of 8 for 4 categories (for 3 categories the range was −0.2% to 0.3%). Under the same parameters, the difference between the NRI and naïve cNRI was centered at 1% and ranged from −2% to 9% (for 3 categories the range was −1% to 8%). In the non-null case where OR Y = 3 using 4 categories, the difference between the bias-corrected cNRI and the NRI was centered at 0.8% with a range from −4% to 7%, while the difference between the naïve cNRI and the NRI was centered at 20% with a range from 8% to 31%.

Example from the Women’s Health Study

The Women’s Health Study is a longitudinal cohort of initially health women, age 45 and older at entry, followed for incident cardiovascular disease (CVD). The data collection methods and study design have been described in detail elsewhere.(17, 18) CVD risk factors shown to be predictive in this population included age, blood pressure, total and high density lipoprotein (HDL) cholesterol, hemoglobin A1c if diabetic at baseline, smoking, and C-reactive protein in addition to family history of premature myocardial infarction (MI).(19) We used the 24,171 women with complete risk factor data and known CVD status at 8 years for this analysis to compare a model with all of the risk factors except HDL cholesterol to a complete model with HDL cholesterol. An additional analysis compared models with and without systolic blood pressure for illustration.

Cox-proportional hazards models were used to generate predicted probabilities of a CVD event at 8 years. The reclassification used the 8-year equivalents of the traditional 10-year categories (<5%, 5 to <10%, 10 to <20%, 20+%), which correspond to <4%, 4 to <8%, 8 to <16%, 16+%, respectively. As with the simulations, intermediate risk was considered to be the middle two categories.

The results of the comparison of models with and without HDL cholesterol are shown in Table 4, with the observed distribution of cases and non-cases (part a) followed by the expected distribution under the null (part b). The overall NRI was 4.0% (95% CI = 0.6 to 7.5%) with a p-value of 0.021. The naïve cNRI was 17.0% (95% CI = 10.4 to 23.7) and the p-value calculated without adjusting for the expected value was less than 0.001. However, the bias-corrected cNRI was 4.0%, with a p-value of 0.24 (95% CI = −2.7 to 10.7).

Table 4.

Reclassification of 8-year Predicted Risk of CVD Event Using Models With and Without HDL Cholesterol in the Women’s Health Study

a. Observed (cases / non-cases)
Model without HDL	Predicted 8-year Risk of CVD from Model with HDL				Total
	<4%	4 to <8%	8 to <16%	16+%
<4%	228 / 20093	23 / 493	0 / 0	0 / 0	251 / 20586
4 to <8%	12 / 431	105 / 1477	20 / 203	0 / 0	137 / 2111
8 to <16%	0 / 2	13 / 152	76 / 507	17 / 42	106 / 703
16+ %	0 / 0	0 / 1	10 / 48	56 / 162	66 / 211
Total	240 / 20526	141 / 2123	106 / 758	73 / 204	560 / 23611

b. Expected (cases / non-cases)
Model without HDL	Predicted 8-year Risk of CVD from Model with HDL				Total
	<4%	4 to <8%	8 to <16%	16+%
<4%	228 / 20093	17.5 / 462	0 / 1	0 / 0	245.5 / 20556
4 to <8%	17.5 / 462	105 / 1477	16.5 / 177.5	0 / 0.5	139 / 2117
8 to <16%	0 / 1	16.5 / 177.5	76 / 507	13.5 / 45	106 / 730.5
16+ %	0 / 0	0 / 0.5	13.5 / 45	56 / 162	69.5 / 207.5
Total	245.5 / 20556	139 / 2117	106 / 730.5	69.5 / 207.5	560 / 23611

Table 5 shows the results of comparing a model without systolic blood pressure to the full risk factor model. In this case, the overall NRI was 9.8% (95% CI = 5.6 to 14.0%) with a p-value of less than 0.001. In this case, the naïve cNRI was 29.1% (95% CI = 21.2 to 37.0), with a p-value < 0.001. The bias-corrected cNRI was 13.8%, with a simple variance p-value of 0.001 (95% CI = 5.9 to 21.7).

Table 5.

Reclassification of 8-year Predicted Risk of CVD Event Using Models With and Without Systolic Blood Pressure in the Women’s Health Study

a. Observed (cases / non-cases)
Model without Systolic BP	Predicted 8-year Risk of CVD from Model with Systolic BP				Total
	<4%	4 to <8%	8 to <16%	16+%
<4%	218 / 19933	38 / 642	0 / 23	0 / 0	256 / 20598
4 to <8%	22 / 589	96 /1291	36 / 263	1 / 6	155 / 2149
8 to <16%	0 / 4	7 / 188	59 / 434	24 / 58	90 / 684
16+ %	0 / 0	0 / 2	11 / 38	48 / 140	59 / 180
Total	240 / 20526	141 / 2123	106 / 758	73 / 204	560 / 23611

b. Expected (cases / non-cases)
Model without Systolic BP	Predicted 8-year Risk of CVD from Model with Systolic BP				Total
	<4%	4 to <8%	8 to <16%	16+%
<4%	218 / 19933	30 / 615.5	0 / 13.5	0 / 0	248 / 20562
4 to <8%	30 / 615.5	96 /1291	21.5 / 225.5	0.5 / 4	148 / 2136
8 to <16%	0 / 13.5	21.5 / 225.5	59 / 434	17.5 / 48	98 / 721
16+ %	0 / 0	0.5 / 4	17.5 / 48	48 / 140	66 / 192
Total	248 / 20562	148 / 2136	98 / 721	66 / 192	560 / 23611

DISCUSSION

As shown, extending the concept of reclassification and the NRI in particular to a subset is possible using a cNRI, but the naïve estimate is shown to be biased. Our proposed correction adjusts for the expected value under the null, reducing the bias of the naïve cNRI, and can easily be incorporated into analysis by drawing upon the information contained in the entire reclassification table.

Pauker and Kassirer, in an overview of medical decision making,(20) describe the scenario in which there is a low risk threshold below which no one is treated, and a high risk threshold, above which everyone in treated. In between the two threshold is the intermediate risk category, in which further testing is necessary to make a treatment decision; the cNRI addresses this scenario. Like the NRI, it depends on clinically relevant cut-points, with the additional requirement of a subset of the risk categories in which treatment decisions are unclear. This is the case in cardiovascular risk prediction, where the Adult Treatment Panel III guidelines suggest high and low risk cut-points.(4) Of note, the proposed test does not address movement from the original high and low groups into the intermediate group, but rather examines a sequential setting where only those classified as intermediate by the reference test are assessed for improvement using the new test. This same procedure could be used for other categories defined by the reference model.

While the bootstrap has been recommended for confidence intervals and the associated p-values for the NRI,(16) we found bootstrap approaches offered little type 1 error improvement over the formula based approach. As has been observed in other prediction applications,(21) we found the full bootstrap to be overly conservative. We also note that our proposed correction is not a correction for optimism as suggested by Harrell,(22) in the sense that it does not correct for the bias introduced through generating and testing a model on the same data. Instead, our correction returns the expected value under the null to 0. This reduces confusion in interpretation of the statistic, since the current (naïve) estimate does not have an expected value of 0 under the null. Correction for optimism would still be necessary to estimate performance in other data.

The power for the cNRI depends on the categories selected, the numbers crossing those boundaries, and the number classified as intermediate risk by the reference model. While the null hypothesis is similar to the test of association derived from the beta coefficient, both the NRI and cNRI have less power, as previously demonstrated.(13) The trade-off for the reduction in power is the ability to test a specific clinical question, as noted above. Consequently, we believe that the proposed effect estimate has clinical value and thus is worth evaluating.

As with the NRI, upward and downward movement of cases and controls are given equal weight in the calculation of the cNRI, though different weighting schemes could be accommodated by including weights as shown in the equation below.(16)

$$\mathit{weightedNRI}=W_1(\%\mathit{cases}\_\mathit{moving}\_up-\%\mathit{cases}\_\mathit{moving}\_\mathit{down})+W_2(\%\mathit{noncases}\_\mathit{moving}\_\mathit{down}-\%\mathit{noncases}\_\mathit{moving}\_up)$$

The cNRI would use the same equation, applied to those classified as intermediate risk and to the symmetric null case.

Clinical papers which have used the naive cNRI have been primarily in the cardiovascular literature. Recent examples have all examined improvement in either cardiovascular or coronary heart disease risk prediction, evaluating the addition of novel markers to established prediction models. Melander and colleagues examined the addition of multiple novel markers to traditional cardiovascular risk factors.(11) While their overall NRI was 0.0%, they found a significant cNRI of 7.3%. Using the tables provided in the manuscript, we computed a bias-corrected cNRI of 2.0% with a simple variance p-value of 0.56. Similarly, Ripatti and collagues, in assessing the addition of a genetic risk score to coronary heart disease risk prediction, found a non significant NRI of 2.2% and a highly significant cNRI of 9.7%.(12) Using the tables provided in the manuscript, we calculated a bias-corrected cNRI of 2.3% with a simple variance p-value of 0.38. Other recent examples have included the addition of genetic variation at chromosome 9p21(7) and subclinical measures to coronary heart disease risk prediction(9), but did not include sufficient information to calculate a bias-corrected cNRI.

Several statistical papers have also mentioned the cNRI. A recent paper by Chambless and colleagues extending the overall NRI to the survival setting also provided a formula for calculating the NRI for a subgroup which was similar to the calculation for the naive cNRI presented above.(8) However, the authors did not take into account the observed cNRI under the null and the performance of their measure under the null was not discussed. In addition, Whittemore provided a formula for a row specific NRI, but did not provide an estimate for the variance of the row NRI, nor take into account the expected value under the null.(23)

Lack of calibration can also affect the utility of reclassification measures. Assessment of calibration within the reclassification table offers a complementary reclassification measure to both the cNRI and the NRI.(13) This measure allows for the assessment of the match between observed and predicted values across the entire reclassification table, including the intermediate risk categories, and is a critical component of a clinically-based evaluation of reclassification.

Our proposed cNRI statistic addresses the clinical interest in intermediate risk reclassification, performed well under simulation, and was clearly interpretable in a relevant clinical example. We have provided a slightly conservative simple calculation for the p value and presented results for bootstrap methods for p-value calculations. R and SAS functions for the calculation of the cNRI with bootstrap confidence intervals are available from the authors upon request. The proposed cNRI, in replacing a naïve formulation, will correct an important source of bias in the medical literature and aid in appropriately answering an important clinical question of impact on intermediate risk patients.