Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Apr 5.
Published in final edited form as: J Biomech. 2013 Jan 30;46(6):1176–1183. doi: 10.1016/j.jbiomech.2013.01.001

Sensitivity of joint moments to changes in walking speed and body-weight-support are interdependent and vary across joints

Saryn R Goldberg 1, Steven J Stanhope 2,3,4,5
PMCID: PMC3605195  NIHMSID: NIHMS434523  PMID: 23374276

Abstract

We investigated the effect of simultaneous changes in body-weight-support level and walking speed on mean peak internal joint moments at the ankle, knee and hip. We hypothesized that observed changes in these joint moments would be approximately linear with both body-weight-support and walking speed and would be similar across joints. Kinematic and kinetic data were collected from 8 unimpaired adult subjects walking on an instrumented treadmill while wearing a dynamically controlled overhead support harness. Subjects walked with four levels of body-weight-support (0%, 20%, 40%, and 60% of bodyweight) at three walking speeds (0.4, 0.6, and 0.8 statures/s, ranging on average from 0.7 to 1.4 m/s). Data were used to calculate mean peak joint moments across subjects for each condition. In general, subjects’ mean peak joint moments decreased linearly with decreasing walking speed and with increasing body-weight-support, except the knee extension moment, which showed a quadratic relationship with walking speed and no significant change with body-weight-support. All joint moments, with the exception of knee extension, showed a significant interaction effect between walking speed and body-weight-support, indicating that the sensitivity of these joint moments to changes in these variables was interdependent. In most cases, the ankle and hip extension moments showed the largest sensitivity to walking speed. The ankle moment was observed to have the greatest sensitivity to body-weight-support. This finding, that altering walking speed and body-weight-support level results in non-uniform changes in peak moments across joints, suggests that further research is warranted to establish the set of combined speed and support conditions that produce motor patterns supportive of normal gait retraining.

Keywords: walking, gait, speed, body-weight-support, joint moments, treadmill

Introduction

The biomechanical demands of a walking task can be controlled by modulating walking speed and support load during gait. Researchers have used this concept in studies aimed at identifying the contributions of individual muscles to the tasks of support and forward progression during walking (Liu et al. 2008, Neptune et al., 2008, McGowan et al., 2009). In addition, body-weight-supported treadmill training, in which a therapist controls the difficulty of the walking task by varying walking speed and providing weight support, has come to play an important role in gait rehabilitation, particularly for individuals who have suffered a stroke or spinal cord injury (Dietz, 2009). One underlying assumption behind this rehabilitation approach is that the range of speeds and support levels employed will still result in the normal sensorimotor input and elicit the proportionately scaled motor responses required for successful gait retraining (Dobkin, 2004; Dietz, 2009). Importance has been placed on determining how gait speed (Lamontagne at al., 2000) and support level (Harkema et al.,1997) should be prescribed for maximal efficacy of rehabilitation.

In these research and rehabilitation paradigms, body-weight-support is typically provided by means of an overhead harness. Support systems that are designed to provide a constant upward unloading force, even as the body center of mass follows a natural sinusoidal trajectory, can deliver a constant, proportional level of unloading and do not interfere with the dynamics of normal gait (Gazzani et al., 2000). To achieve this goal, researchers have implemented a range of body-weight-support approaches, including the use of very long steel springs (Donelan and Kram, 1997), pneumatic systems (Gazzani et al., 2000), and mechatronic systems (Frey et al., 2006).

Walking with increasing levels of body-weight-support has resulted in large proportional decreases in vertical ground contact forces (Harkema et al., 1997; Griffin et al., 1999) and mechanical work (Griffin et al., 1999) across support levels up to 75% bodyweight or more. Increased body-weight-support levels have resulted in much smaller (15% or less) observed changes in kinematic parameters, such as stride frequency and length, stance and swing duration, and vertical displacement of the center of mass (Donelan and Kram, 1997; Farley and MacMahon, 1992; Finch et al., 1991; Griffin et al., 1999) over a wide range of support levels. Similarly, changes in joint kinematics with increasing levels of body-weight-support are relatively small, with larger changes not observed until support levels reach 50% bodyweight or more (Threlkeld et al., 2003; Finch et al., 1991).

Increases in overground walking speed have been found to have variable effects on sagittal plane gait kinematics, with some studies showing little (Winter, 1983) to no (Lelas et al., 2003) effect due to gait speed, with others showing increases with speed or stride rate (Murray et al., 1984, Oberg et al., 1994, Kirtley et al., 1985, Umberger and Martin, 2007). Kinetic parameters show a stronger and more consistent correlation with increases in gait speed or stride rate (Winter, 1983; Kirtley et al., 1985, Lelas et al., 2003, Umberger and Martin, 2007, Farris and Sawicki, 2012), with most sagittal plane peak moments and powers showing either linear or quadratic increases with increasing speed (Lelas et al., 2003).

Several researchers have performed comprehensive studies of subjects walking at a range of combinations of walking speeds and body-weight-support levels, reporting data on lower limb kinematics, timing of gait events, muscle EMG, and insole pressures (Ivanenko et al., 2002; venHedel et al., 2006; Klarner et al., 2010). The relatively small changes in lower extremity kinematics across a complete range of body-weight-support levels (0-100%) and walking speeds (0.2 – 1.4 m/s) observed by Ivenenko et al. (2002) is suggestive of a proportional motor response. However, the drastic changes in insole pressure forces and EMG patterns over the same range of support levels and speeds suggests that a more complex motor response likely exists. Reports of kinetic data while walking with body-weight-support across walking speeds are limited. Lewek et al. (2010) characterized how kinematics and joint moments at the ankle respond proportionately to a range of walking speeds and body-weight-support levels, but joint moment data have not been reported for the remaining joints of the lower limb.

The purpose of this study was to measure how the sensitivity of peak joint moments to changes in walking speed is affected by changes in body-weight-support level and conversely, how the sensitivity of peak joint moments to changes in body-weight-support level is affected by changes in walking speed. In this context, the term sensitivity refers to the linear change in a joint moment with changes in either walking speed or body-weight-support level. Specifically, we aimed to test the following three hypotheses:

  1. Joint moments will change linearly with a) changes in body-weight-support level across walking speeds, and with b) changes in walking speed across body-weight-support levels.

  2. For each joint, sensitivity of peak joint moments to walking speed will be the same across body-weight-support levels and sensitivity of peak joint moments to body-weight-support will be the same across walking speeds.

  3. Sensitivities of peak joint moments to walking speed and sensitivities of peak joint moments to body-weight-support will be the same across joints.

Methods

Motion capture and force platform data were collected from 8 unimpaired adult subjects (average ± sd height 177 ± 7.5 cm, average ± sd weight 74 ± 13.1 kg) as they walked at a prescribed range of combinations of walking speeds and body-weight-support (BWS) levels. Motion capture data were collected using a six-camera system (Vicon, Los Angeles, CA) and a marker configuration similar to that described by Holden et al. (1997). Modifications to the marker configuration included using an array of four-targets on the pelvis and trunk segments. Informed consent was obtained for this IRB-approved study.

Walking speed was controlled and force platform data were collected by having subjects walk on an instrumented, split-belt treadmill (Model TM-06-B, Bertec Corp., Columbus, OH) (Figure 1a). The treadmill was geared to maintain the set speed constant and was calibrated using the techniques described by Goldberg et al. (2009), resulting in a center of pressure measurement error of less than 3 mm when the treadmill was moving at slow speeds.

Figure 1.

Figure 1

Open in a new tab

a) Walking speed was controlled and force platform data were collected by having subjects walk on an instrumented, split-belt treadmill (Model TM-06-B, Bertec Corp., Columbus, OH). Custom-made handrails were positioned in front of the subject to minimize interference with motion capture data collection. Subjects were not permitted to hold the handrail during testing. b) BWS levels were controlled by having subjects walk while wearing a pelvic harness connected to a custom-designed, overhead BWS system (Intelligent Automation, Inc., Rockville, MD). The harness was suspended from as high a point as possible to minimize contributions of the BWS to horizontal forces on the subject.

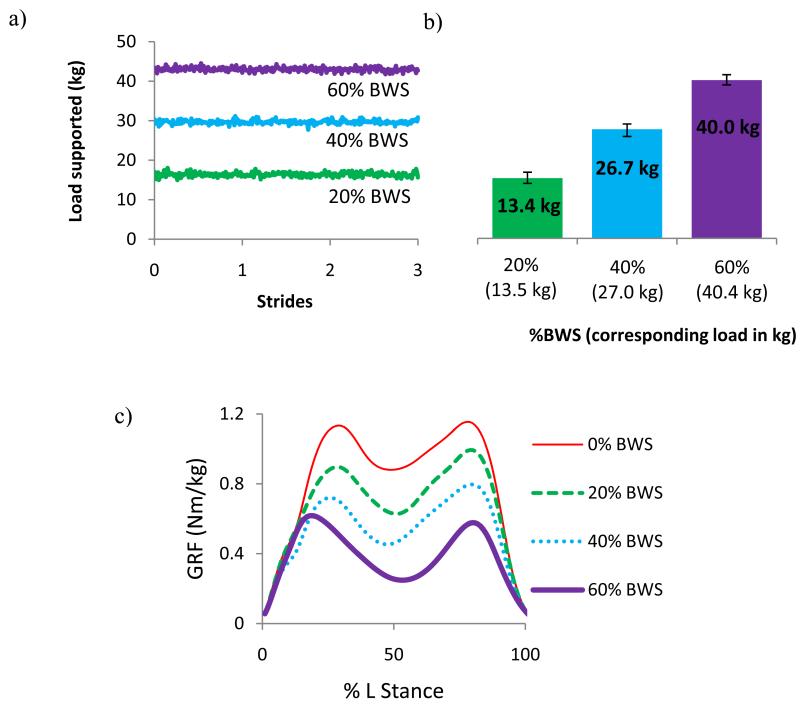
BWS levels were controlled by having subjects walk while wearing a pelvic harness connected to a custom-designed, overhead BWS system (Intelligent Automation, Inc., Rockville, MD) (Figure 1b). The BWS system used a dynamically controlled motor and two in-series load cells to actively supply a constant cable force independent of the height of the center of mass as it changed during the gait cycle. Specifically, the system was able to maintain an applied load within ± 2% bodyweight of the specified load across all walking speeds and support levels (Figure 2). The BWS system was suspended from a height of 4.5 m to minimize any horizontal contribution to the support load as the subject drifted fore or aft on the treadmill.

Figure 2.

Figure 2

Open in a new tab

a) Load supported by the active BWS system during 3 strides for a 67 kg individual walking at 0.6 statures/s. b) Average load supported by the active BWS system over the same time period. The set load support in BWS and kg is indicated underneath each bar. The error bars indicate the maximum and minimum loads that were applied by the system during the trial. c) Average vertical ground reaction force (GRF) normalized by subject bodyweight measured under the left foot with no BWS, 20%, 40%, and 60% BWS.

Subjects walked with four different levels of BWS (0%, 20%, 40%, and 60% of bodyweight) at each of three walking speeds (0.4, 0.6, and 0.8 statures/s, ranging on average from 0.7 to 1.4 m/s). Conditions were presented to subjects in a randomized order. Subjects were given 1.5 – 2 minutes to acclimate to each condition before data were collected for at least one minute. This acclimation time exceeds what Donelan and Kram (1997) concluded was sufficient for subjects to accommodate to walking on a treadmill with different levels of simulated reduced gravity. The majority of subjects readily adapted to each test condition. However, one subject was not able to adapt to the 60% BWS level at any speed, and their data at this support level were not collected. Two additional subjects adopted atypical ground reaction force patterns for the 60% BWS condition at 0.8 statures/s and their data at this condition were excluded. For all remaining trials, motion capture and force plate data were sampled at 120 and 1040 Hz, respectively, and low-pass filtered at 6 and 10 Hz, respectively.

Data were used to calculate hip, knee, and ankle net internal muscular moments during stance using Visual3D software (C-Motion, Inc. Germantown, MD) for the left leg for all clean treadmill strides (i.e. neither foot fell on the opposite belt as determined from force data and the subject did not drift too far fore or aft, such that the horizontal force component remained less than approximately 5% of the applied support load). Stance phase was defined as the interval when the vertical ground reaction force was greater than or equal to 20 N. Moment data were scaled by body weight and values for peak ankle plantarflexion moments and for peak flexion and extension moments at the knee and hip were averaged across trials within each condition for each subject. For each subject at each condition, data from a minimum of five strides were available for inclusion, with most subjects and conditions having more than 10 strides. Peak moment values were averaged across subjects for each condition.

The absolute value of the average peak moment data were analyzed using hierarchical linear regression. Each joint moment was modeled as a function of walking speed, BWS, and the interaction of walking speed and BWS. Second order terms for walking speed and BWS were included in the regression models to assess non-linearity. If these non-linear terms were statistically significant, they were employed in the model. The regressions were then used to predict the slope of joint moment vs. walking speed (i.e. the joint moment sensitivity to walking speed) at each BWS level for each joint and to predict the slope of joint moment vs. BWS level (i.e. the moment sensitivity to BWS) at each walking speed for each joint. Hierarchical regression was used to compare these slopes across joints. For the primary regression, p < 0.05 was taken to indicate statistical significance. For comparisons across joints, p < 0.01 was taken to indicate statistical significance to adjust for multiple comparisons.

Results

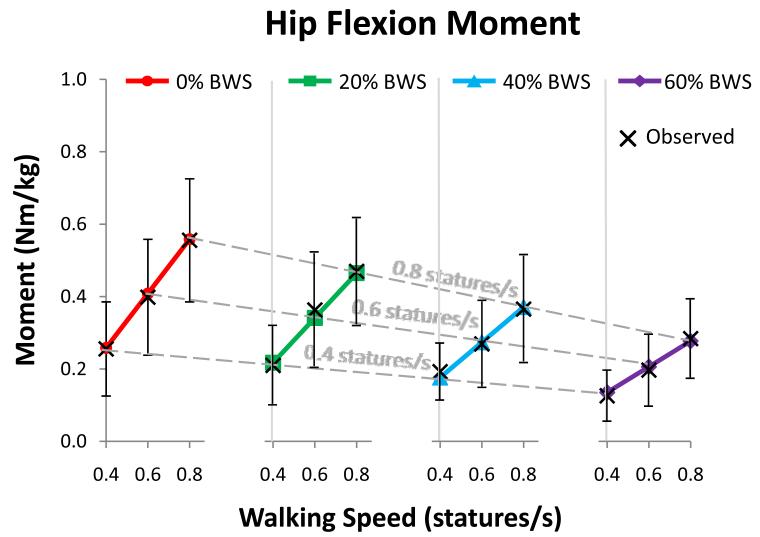
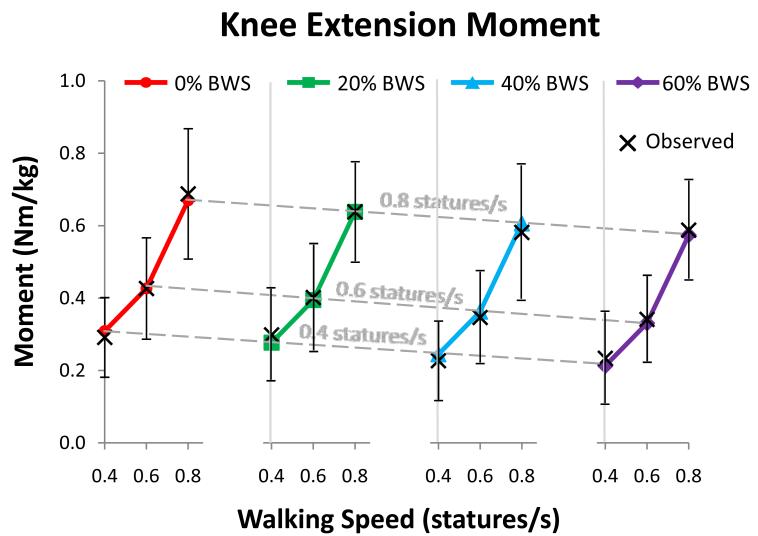
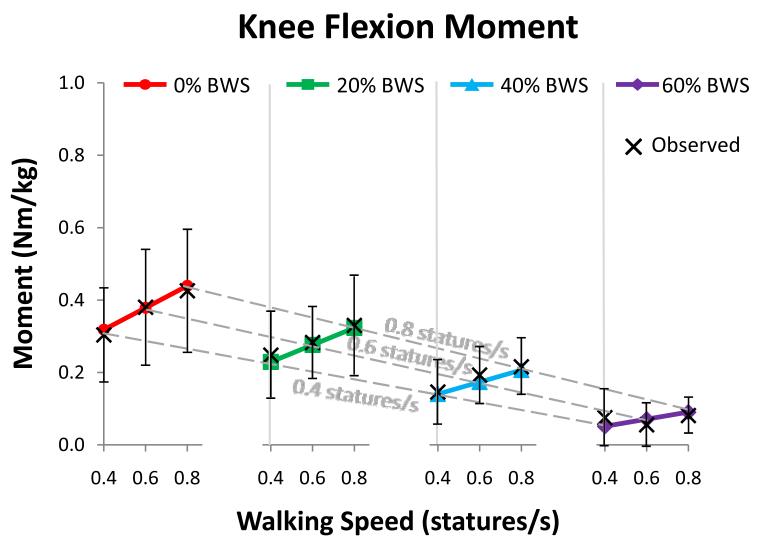
Changes in joint moment trajectories across subjects and conditions were confirmed to be well-represented by changes in peak moment values (see supplemental data, Figures S1 and S2). In general, subjects’ average peak joint moments increased in a linear manner with increasing walking speed and decreased in a linear manner with increasing BWS (as indicated by Figures 3-7). The exception to this finding was the knee extension moment, which showed a non-linear (quadratic) increase with walking speed and no statistically significant change with BWS level (Table 1 and Figure 4). There was a statistically significant interaction of walking speed and BWS for ankle (p = 0.001), knee flexion (p = < 0.001), hip extension (p = 0.003), and hip flexion moments (p = 0.002) (Table 1). These statistically significant interactions indicate that there was a statistically significant interdependence of these two variables. More specifically, they indicate that the moment sensitivities to BWS changed with walking speed (i.e. in Figures 3 and 5-7, the slopes of the solid lines within each plot were statistically significantly different from one another) and the moment sensitivities to walking speed changed with BWS (i.e. in Figures 3 and 5-7, the slopes of the dotted lines within each plot were statistically significantly different from one another). The interaction effect for knee extension was not statistically significant (p = 0.585) (Table 1).

Figure 3.

Figure 3

Open in a new tab

Predicted and observed average peak ankle plantarflexion moment as it changes with walking speed (varied from 0.4 to 0.8 statures/s) and BWS level (varied from 0% to 60% bodyweight). The values predicted by the linear regression models (Table 1) are shown by the filled shapes and the observed values are shown by “X”s, with error bars on the observed values indicating ± 1 standard deviation. Walking speed sensitivity at each BWS level was calculated as the slope of each solid line. BWS sensitivity at each walking speed was calculated as the slope of each dashed line (due to the even spacing between the four BWS plots). There was a significant interaction effect between walking speed and BWS level, so the slopes of the solid and dotted lines change with these variables. Note that the moment range on this plot differs from that of Figures 4-7.

Figure 7.

Figure 7

Open in a new tab

Predicted and observed average peak hip flexion moment as it changes with walking speed (varied from 0.4 to 0.8 statures/s) and BWS level (varied from 0% to 60% bodyweight). The values predicted by the linear regression models (Table 1) are shown by the filled shapes and the observed values are shown by “X”s, with error bars on the observed values indicating ± 1 standard deviation. Walking speed sensitivity at each BWS level was calculated as the slope of each solid line. BWS sensitivity at each walking speed was calculated as the slope of each dashed line (due to the even spacing between the four BWS plots). There was a significant interaction effect between walking speed and BWS level, so the slopes of the solid and dotted lines change with these variables.

Table 1.

Results for regression analysis of individual joint moments. All joints except for knee extension showed a linear relationship between both joint moment and walking speed and joint moment and BWS level (as evidenced by the insignificant p-values for the second order regression coefficients). The knee extension moment showed a non-linear relationship with walking speed and no significant relationship with BWS. All joints except for knee extension also showed a significant interaction between walking speed and BWS level. The bolded coefficients are those that were used in the regression model for each joint.

R-squared
Value		 Variable Regression
coefficient		 Standard
Error		 p value
Ankle
plantarflexion		 0.663 Speed 1.218 0.096 < 0.001
BWS −0.464 0.134 0.01
Speed × BWS −1.31 0.22 0.001
Speed2 −0.9897 0.4592 0.068
BWS2 −0.4862 0.2268 0.069
Knee extension 0.538 Speed −0.995 0.39 0.038
BWS −0.159 0.088 0.112
Speed × BWS −0.1548 0.2706 0.585
Speed2 1.5847 0.2748 0.001
BWS2 0.1531 0.3255 0.652
Knee flexion 0.516 Speed 0.305 0.037 < 0.001
BWS −0.244 0.094 0.035
Speed × BWS −0.425 0.06 < 0.001
Speed2 −0.0128 0.1418 0.931
BWS2 −0.2058 0.2110 0.362
Hip
extension		 0.699 Speed 1.053 0.083 < 0.001
BWS −0.126 0.068 0.105
Speed × BWS −0.498 0.115 0.003
Speed2 0.3777 0.2171 0.125
BWS2 −0.2891 0.1685 0.130
Hip
flexion		 0.457 Speed 0.75 0.076 < 0.001
BWS 0.058 0.099 0.577
Speed × BWS −0.658 0.139 0.002
Speed2 −0.0084 0.2777 0.977
BWS2 −0.1178 0.1755 0.524
Open in a new tab

Figure 4.

Figure 4

Open in a new tab

Predicted and observed average peak knee extension moment as it changes with walking speed (varied from 0.4 to 0.8 statures/s) and BWS level (varied from 0% to 60% bodyweight). The values predicted by the regression models (Table 1) are shown by the filled shapes and the observed values are shown by “X”s, with error bars on the observed values indicating ± 1 standard deviation. In general, mean peak knee extension moments increased in a non-linear manner with increasing walking speed (quadratic relationship), as the slope between 0.4 and 0.6 statures/s was less than the slope between 0.6 and 0.8 statures/s. Walking speed sensitivity was not calculated due to the non-linearity of the predicted values. There was no significant change in knee extension moment with BWS level. BWS sensitivity at each walking speed was calculated as the slope of each dashed line (due to the even spacing between the four BWS plots). There was no significant interaction effect between walking speed and BWS.

Figure 5.

Figure 5

Open in a new tab

Predicted and observed average peak knee flexion moment as it changes with walking speed (varied from 0.4 to 0.8 statures/s) and BWS level (varied from 0% to 60% bodyweight). The values predicted by the linear regression models (Table 1) are shown by the filled shapes and the observed values are shown by “X”s, with error bars on the observed values indicating ± 1 standard deviation. Walking speed sensitivity at each BWS level was calculated as the slope of each solid line. BWS sensitivity at each walking speed was calculated as the slope of each dashed line (due to the even spacing between the four BWS plots). There was a significant interaction effect between walking speed and BWS level, so the slopes of the solid and dotted lines change with these variables.

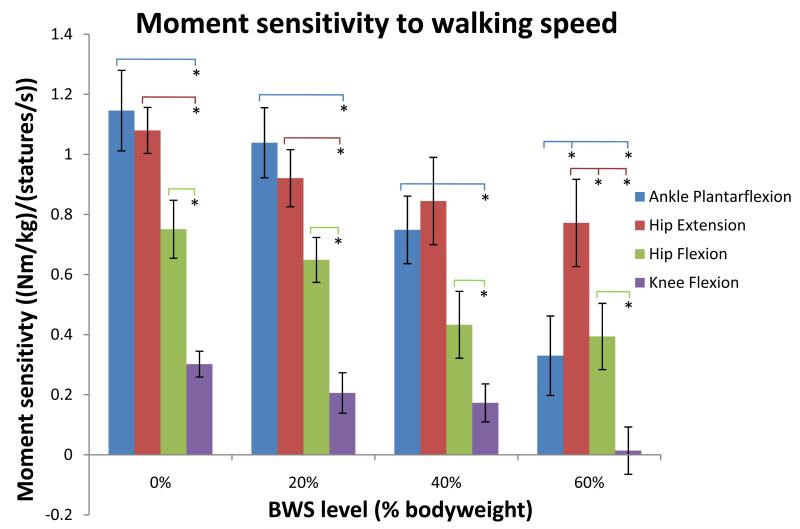
In most cases, the ankle and hip extension moments showed the largest sensitivity to walking speed across all BWS levels (Figure 8). The hip flexion moment and knee flexion moment in general had a lower sensitivity to walking speed across joint levels, with the knee flexion moment being statistically significantly smaller in almost all cases (Figure 8). The knee extension moment was not included in these comparisons due to the non-linearity of change in this moment across walking speeds.

Figure 8.

Figure 8

Open in a new tab

Comparison of moment sensitivity to walking speed across joints and BWS levels. An asterix indicates a statistically significant difference between comparisons. Error bars indicate ± 1 standard error. Knee extension is not included because of the non-linearity of change in moment across walking speeds.

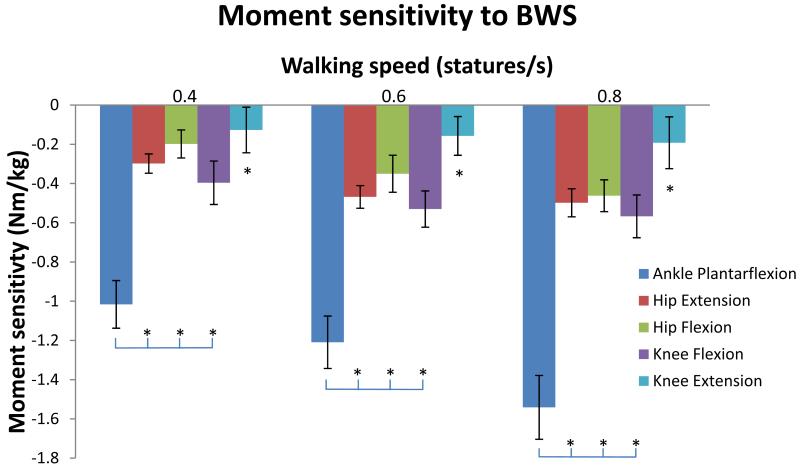
The ankle moment was observed to have a statistically significantly larger sensitivity to BWS (more than two times larger) than that of any other joint at each walking speed (Figure 9). The knee extension moment was observed to have a sensitivity to BWS that is statistically indistinguishable from zero at each walking speed, as the 95% confidence interval for this sensitivity (calculated as ± 2 times the standard error) encompassed zero. This sensitivity was statistically significantly smaller than that of every other joint at each walking speed.

Figure 9.

Figure 9

Open in a new tab

Comparison of moment sensitivity to BWS across joints and walking speeds. An asterix indicates a statistically significant difference between comparisons. The asterix above the knee extension sensitivity indicates that it was statistically significantly different from all other joints. Note that the knee extension moment sensitivity to BWS was not statistically distinguishable from zero, as the 95% confidence interval (± 2 times the standard error) encompasses zero. Error bars indicate ± 1 standard error.

Discussion

In this study walking speed and BWS level were modulated to determine the effects of these changes on mean peak sagittal plane joint moments. It was expected that joint moments would change linearly with changes in both variables. Mean peak joint moments were found to increase with increasing walking speed, as has been observed across joints by many other researchers (Winter, 1984; Kirtley et al., 1985, Holden et al., 1997; Lelas et al., 2003; Lewek et al., 2011). These increases were linear, supporting the first part of our first hypothesis, with the exception of the knee extension moment, which showed a non-linear (quadratic) increase. However, it is possible that our ability to distinguish between a linear or quadratic model being a best fit could have been enhanced by having data for more than three speeds.

Our hypothesis that joint moments would decrease linearly with BWS was also supported for all joints except for the knee extension moment, which did not show a statistically significant dependence on BWS level. While we are unaware of other published data showing knee joint moments as a function of BWS, reports of knee extensor muscle excitation data from subjects walking with various levels of BWS are consistent with this finding, indicating that EMG levels for the rectus femoris (Dietz et al., 1997; Ivanenko et al., 2002; Gravano et al., 2011) and vastus medialis and/or lateralis (van Hedel et al., 2006; Ivanenko et al., 2002; Gravano et al., 2011) change little with changes in BWS levels less than 60%. In contrast, there is some evidence that application of 40% BWS does significantly decrease quadriceps activity relative to fully loaded walking (Colby et al, 1999).

While the group mean knee extension moment data showed little change with BWS, individual subject average peak knee extension moment data were variable, with some subject moments increasing, some decreasing, and some showing little change with increasing levels of BWS. Despite this variability, all subjects walked with observed normal walking kinematics. This suggests that when considering peak knee extension moments, a range of strategies were available to subjects that enabled successful execution of a walking task. It is unclear whether an extended period for accommodating to a test condition would result in subjects choosing more consistent knee extensor moment strategies.

All joint moments, except for the knee extension moment, showed a significant interaction between walking speed and BWS, refuting our second hypothesis. This finding at the ankle is supported by the work of Lewek et al. (2011), who also reported a significant interaction effect between gait speed and BWS over a wider range of walking speeds and a narrower range of BWS levels than those tested here. Similar data for other joints is not available for comparison. However, dynamic simulation studies that examined how individual joint moments (Kepple et al., 1997) and individual muscles (Neptune et al. 2001; Anderson and Pandy 2003; Liu et al., 2006; McGowan et al. 2009) contribute to the tasks of support and forward progression indicate that most joints and muscles contribute to both functional tasks to some extent. It follows that changing the demands of one of these functional roles (by changing walking speed or providing BWS) would affect how much the joint or muscle contributes to the other functional role.

A possible explanation for the observation that the sensitivity of joint moments to changes in these variables was different across joints (refuting our third hypothesis) may stem from differences in how joints contribute to the combined tasks of support and forward progression. Induced acceleration results from Kepple et al. (1997) indicate that individual joint moments contribute to these two tasks in different ways. While induced acceleration analyses are known to be sensitive to the specifics of the musculoskeletal and ground contact models used in the analysis (Chen, 2006), results from Kepple et al. (1997) show that at the point in the gait cycle when the ankle plantarflexion moment is at its peak, the ankle moment is the largest contributor to vertical acceleration (i.e. support) and forward acceleration (i.e. forward progression) of the center of mass. In contrast, at the time of peak knee extension moment, the knee moment is a large contributor to both vertical and backward acceleration of the center of mass. These observations provide a possible functional explanation for why the peak knee extension moment is not significantly affected by changes in BWS level, and suggests that the knee extension moment’s functional role of slowing the body’s forward progression may be dominant in the face of perturbations to its functional role of providing support.

Results from the work of Liu et al. (2008), who used perturbation analysis of a dynamic simulation to determine how the peak contributions of individual muscles to support and forward progression are affected by changes in walking speed, are consistent with our finding that the ankle extensors and hip extensors had the highest sensitivity to walking speed when compared to other joints. Specifically, they found that the way in which walking speed altered muscular contributions to support and progression varied across muscles, and that the contributions of soleus and gluteus maximus were most strongly affected by walking speed. Further, their results appear to show that the contributions of the knee extensors (vasti) at slow speeds were significantly different than their contributions at higher speeds, which is consistent with our finding that the knee extension moments changed non-linearly with walking speed. Other researchers have reported how individual muscle function changed with walking speed (Neptune et al., 2008) or in response to altered demand for both support and forward progression during walking (McGowan et al., 2009), but their results are integrated across the entire gait cycle, which makes them difficult to compare to our results, which were evaluated at a single time point.

While changes in moment trajectories across subjects and conditions were observed to be well-represented by changes in peak flexion and extension moment values, there are some limitations to using the peak negative and positive joint moments to characterize muscular effort associated with a movement strategy. An increase or decrease in a peak moment is not necessarily representative of a similar change in the moments required throughout a movement, but instead represents a change in the peak net moment-production capacity required to execute the observed movement strategy. Changes in peak moments cannot characterize changes in the rate of force production required to execute a given movement strategy. Further, as is true for any moment-based analysis, the metric cannot discern when observed peaks were the result of co-contraction of antagonistic muscle groups and thus representative of higher levels of individual muscular effort.

One must use caution when applying the results from this study to clinical practice, as our unimpaired subject cohort does not reflect the abilities of an impaired patient group, and clinical body-weight-support systems, such as lift-style systems (Barbeau et al. 1987, Visintin et al. 1998, Field-Fote et al. 2011), are not typically designed to supply a constant unloading force throughout the gait cycle, as ours was. However, in cases when support is provided in a manner similar to that implemented here, the findings from this study may have implications for therapeutic gait retraining. If all joint moments scale in a uniform way with changes in speed and support, one would expect that the motor response to therapeutic combinations of BWS and walking speed would directly transfer to the retraining of normal over-ground gait. However, in light of the results presented in this study, that joint moments respond non-uniformly to changes with these variables, it is unclear if the kinetic adaptations reinforced while walking with BWS at faster speeds readily transfer to the slower, unsupported conditions experienced during activities of daily living. Therefore, our results support the potential benefit of clinical protocols that wean patients off BWS while targeting anticipated over-ground walking velocities. In addition, we observed an apparent upper threshold to combinations of significant unloading (60% BWS) and faster walking speeds that resulted in some subjects adopting a gait pattern that could no longer be characterized as walking. This suggests that therapeutic conditions that combine even higher levels of support with slower walking speeds (Beer et al. 2008, Pilutti et al. 2011) may exceed the threshold conditions that produce a walking response. While our study demonstrates the non-uniform adaptations of peak joint moments to combinations of walking speed and body-weight-support, further research is warranted to establish the set of combined speed and support conditions that produce motor patterns supportive of normal gait retraining and to understand the adaptations of individuals with impaired gait.

Supplementary Material

01

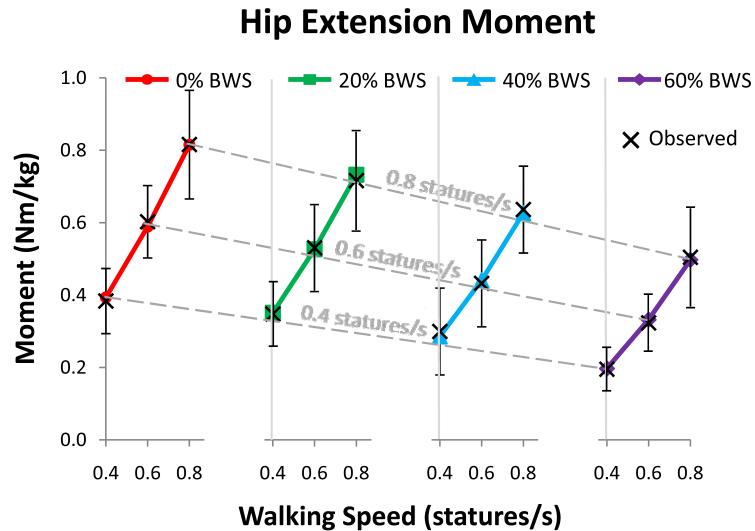
Figure 6.

Figure 6

Open in a new tab

Predicted and observed average peak hip extension moment as it changes with walking speed (varied from 0.4 to 0.8 statures/s) and BWS level (varied from 0% to 60% bodyweight). The values predicted by the linear regression models (Table 1) are shown by the filled shapes and the observed values are shown by “X”s, with error bars on the observed values indicating ± 1 standard deviation. Walking speed sensitivity at each BWS level was calculated as the slope of each solid line. BWS sensitivity at each walking speed was calculated as the slope of each dashed line (due to the even spacing between the four BWS plots). There was a significant interaction effect between walking speed and BWS level, so the slopes of the solid and dotted lines change with these variables.

Acknowledgements

This research was supported by an Intramural Research Program of the National Institute of Child Health and Human Development and the Clinical Center of the National Institutes of Health. The authors would like to thank Karen Lohmann Siegel and Alexander Razzook for assistance with data collection. The authors would also like to thank Dr. Paul Kolm of the Christiana Care Center for Outcomes Research for conducting the statistical analyses.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

Conflict of interest statement

Neither Dr. Goldberg nor Dr. Stanhope have financial or personal relationships with individuals or organizations that inappropriately influenced this work.

References

  1. Alexander RM. Optimization of gaits in the locomotion of vertebrates. Physiological Reviews. 1989;69(4):1199–1227. doi: 10.1152/physrev.1989.69.4.1199. [DOI] [PubMed] [Google Scholar]
  2. Anderson FC, Pandy MG. Individual muscle contributions to support in normal walking. Gait & Posture. 2003;17:159–169. doi: 10.1016/s0966-6362(02)00073-5. [DOI] [PubMed] [Google Scholar]
  3. Barbeau H, Wainberg M, Finch L. Description and application of a system for locomotor rehabilitation. Medical Biology and Computing. 1987;25:341–344. doi: 10.1007/BF02447435. [DOI] [PubMed] [Google Scholar]
  4. Beer S, Aschbacher B, Managlou D, Gamper E, Kool J, Kesserlring J. Robot-assisted gait training in multiple sclerosis: a pilot randomized trial. Multiple Sclerosis. 2008;14:231–236. doi: 10.1177/1352458507082358. [DOI] [PubMed] [Google Scholar]
  5. Chen G. Induced acceleration contributions to locomotion dynamics are not physically well defined. Gait and Posture. 23:37–44. doi: 10.1016/j.gaitpost.2004.11.016. [DOI] [PubMed] [Google Scholar]
  6. Colby SM, Kirendall DT, Bruzga RF. Electromyographic analysis and energy expenditure of harness supported treadmill walking: implications for knee rehabilitation. Gait & Posture. 1999;10:200–205. doi: 10.1016/s0966-6362(99)00035-1. [DOI] [PubMed] [Google Scholar]
  7. Dietz V, Leenders KL, Colombo G. Leg muscle activation during gait in Parkinson’s disease: influence of body unloading. Electroencephalography and Clinical Neurophysiology. 1997;105:400–405. doi: 10.1016/s0924-980x(97)00042-8. [DOI] [PubMed] [Google Scholar]
  8. Dietz V. Body weight supported gait training: from laboratory to clinical setting. Brain Research Bulletin. 2009;78:I–VI. doi: 10.1016/S0361-9230(08)00410-3. [DOI] [PubMed] [Google Scholar]
  9. Dobkin BH. Strategies for stroke rehabilitation. The Lancet Neurology. 2004;3:528–536. doi: 10.1016/S1474-4422(04)00851-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Donelan JM, Kram R. The effect of reduced gravity on the kinematics of human walking: a test of the dynamic similarity hypothesis for locomotion. Journal of Experimental Biology. 1997;200:3193–3201. doi: 10.1242/jeb.200.24.3193. [DOI] [PubMed] [Google Scholar]
  11. Farley CT, McMahon TA. Energetics of walking and running: insights from simulated reduced-gravity experiments. Journal of Applied Physiology. 1992;73:2709–2712. doi: 10.1152/jappl.1992.73.6.2709. [DOI] [PubMed] [Google Scholar]
  12. Farris DJ, Sawicki GS. The mechanics and energetics of human walking and running: a joint level perspective. Journal of The Royal Society Interface. 2012;9:110–118. doi: 10.1098/rsif.2011.0182. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Field-Fote EC, Roach KE. Influence of a locomotor training approach on walking speed and distance in people with chronic spinal cord injury: a randomized clinical trial. Physical Therapy. 2011;91:48–60. doi: 10.2522/ptj.20090359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Finch L, Barbeau H, Arsenault B. Influence of body weight support on normal human gait: development of a gait retraining strategy. Physical Therapy. 1991;71:842–855. doi: 10.1093/ptj/71.11.842. [DOI] [PubMed] [Google Scholar]
  15. Frey M, Colombo G, Vaglio M, Buvher R, Jorg M, Riener R. A novel mechatronic body weight support system. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2006;14:311–321. doi: 10.1109/TNSRE.2006.881556. [DOI] [PubMed] [Google Scholar]
  16. Gazzani F, Fadda A, Torre M, Macellari V. WARD: a pneumatic system for body weight relief in gait rehabilitation. IEEE Transactions on Rehabilitation Engineering. 2000;8:506–513. doi: 10.1109/86.895954. [DOI] [PubMed] [Google Scholar]
  17. Goldberg SR, Kepple TM, Stanhope SJ. In situ calibration and motion capture transformation optimization improve instrumented treadmill measurements. Journal of Applied Biomechanics. 2009;25:401–406. doi: 10.1123/jab.25.4.401. [DOI] [PubMed] [Google Scholar]
  18. Gravano S, Ivanenko YP, Maccioni G, Poppele RE, Lacquaniti F. A novel approach to mechanical foot stimulation during human locomotion under body weight support. Human Movement Science. 2011;30:352–367. doi: 10.1016/j.humov.2010.01.002. [DOI] [PubMed] [Google Scholar]
  19. Griffin TM, Tolani NA, Kram R. Walking in simulated reduced gravity: mechanical energy fluctuations and exchange. Journal of Applied Physiology. 1999;86:383–390. doi: 10.1152/jappl.1999.86.1.383. [DOI] [PubMed] [Google Scholar]
  20. Harkema SJ, Hurley SL, Patel UK, Requejo PS, Dobkin BH, Edgerton VR. Human lumbosacral spinal cord interprets loading during stepping. Journal of Neurophysiology. 1997;77:797–811. doi: 10.1152/jn.1997.77.2.797. [DOI] [PubMed] [Google Scholar]
  21. Holden J, Chou G, Stanhope S. Changes in knee joint function over a wide range of walking speeds. Clinical Biomechanics. 1997;12:375–382. doi: 10.1016/s0268-0033(97)00020-x. [DOI] [PubMed] [Google Scholar]
  22. Ivanenko YP, Grasso R, Macellari V, Lacquaniti F. Control of foot trajectory in human locomotion: role of ground contact forces in simulated reduced gravity. Journal of Neurophysiology. 2002;87:3070–3089. doi: 10.1152/jn.2002.87.6.3070. [DOI] [PubMed] [Google Scholar]
  23. Ivanenko YP, Labini FS, Cappellini G, Macellari V, McIntyre J, Lacquaniti F. Gait transitions in simulated reduced gravity. Journal of Applied Physiology. 2011;110:781–788. doi: 10.1152/japplphysiol.00799.2010. [DOI] [PubMed] [Google Scholar]
  24. Kepple TM, Siegel KL, Stanhope SJ. Relative contributions of the lower extremity joint moments to forward progression and support during gait. Gait & Posture. 1997;6:1–8. [Google Scholar]
  25. Kirtley C, Whittle MW, Jefferson RJ. Influence of walking speed on gait parameters. Journal of Biomedical Engineering. 1985;7:282–288. doi: 10.1016/0141-5425(85)90055-x. [DOI] [PubMed] [Google Scholar]
  26. Klarner T, Chan HK, Wakeling JM, Lam T. Patterns of muscle coordination vary with stride frequency during weight assisted treadmill walking. Gait & Posture. 2010;31:360–365. doi: 10.1016/j.gaitpost.2010.01.001. [DOI] [PubMed] [Google Scholar]
  27. Kram R, Domingo A, Ferris DP. Effect of reduced gravity on the preferred walk-run transition speed. The Journal of Experimental Biology. 1997;200:821–826. doi: 10.1242/jeb.200.4.821. [DOI] [PubMed] [Google Scholar]
  28. Lamontagne A, Fung J. Faster is better: implications for speed-intensive gait training after stroke. Stroke. 2004;35:2543–2548. doi: 10.1161/01.STR.0000144685.88760.d7. [DOI] [PubMed] [Google Scholar]
  29. Lelas JL, Merriman GJ, Riley PO, Kerrigan DC. Predicting peak kinematic and kinetic parameters from gait speed. Gait and Posture. 2003;17:106–112. doi: 10.1016/s0966-6362(02)00060-7. [DOI] [PubMed] [Google Scholar]
  30. Lewek MD. The influence of body weight support on ankle mechanics during treadmill walking. Journal of Biomechanics. 2011;44:128–133. doi: 10.1016/j.jbiomech.2010.08.037. [DOI] [PubMed] [Google Scholar]
  31. Liu MQ, Anderson FC, Pandy MG, Delp SL. Muscles that support the body also modulate forward progression during walking. Journal of Biomechanics. 2006;39:2623–2630. doi: 10.1016/j.jbiomech.2005.08.017. [DOI] [PubMed] [Google Scholar]
  32. Liu MQ, Anderson FC, Schwartz MH, Delp SL. Muscle contributions to support and progression over a range of walking speeds. Journal of Biomechanics. 2008;41:3243–3252. doi: 10.1016/j.jbiomech.2008.07.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. McGowan CP, Kram R, Neptune RR. Modulation of leg muscle function in response to altered demand for body support and forward propulsion during walking. Journal of Biomechanics. 2009;42:850–856. doi: 10.1016/j.jbiomech.2009.01.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Murray MP, Mollinger LA, Gardner GM, Sepic SB. Kinematic and EMG patterns during slow, free, and fast walking. Journal of Orthopaedic Research. 1984;2:272–280. doi: 10.1002/jor.1100020309. [DOI] [PubMed] [Google Scholar]
  35. Neptune RR, Kautz SA, Zajac FE. Contributions of the individual plantar flexors to support, forward progression and swing initiation during walking. Journal of Biomechanics. 2001;34:1387–1398. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
  36. Neptune RR, Kotaro S, Kautz SA. The effect of walking speed on muscle function and mechanical energetics. Gait & Posture. 2008;28:135–143. doi: 10.1016/j.gaitpost.2007.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Oberg T, Karszina A, Oberg K. Joint angle parameters in gait: references data for normal subjects, 10-79 years of age. Journal of Rehabilitation Research and Development. 1994;31:199–213. [PubMed] [Google Scholar]
  38. Pilutti LA, Lelli DA, Paulseth JE, Crome M, Jiang S, Rathbone MP, Hicks AL. Effects of 12 weeks of supported treadmill training on functional ability and quality of life in progressive multiple sclerosis: a pilot study. Archives of Physical Medicine and Rehabilitation. 2011;92:31–36. doi: 10.1016/j.apmr.2010.08.027. [DOI] [PubMed] [Google Scholar]
  39. Umberger BR, Martin PE. Mechanical power and efficiency of level walking with different stride rates. Journal of Experimental Biology. 2007;210:3255–3265. doi: 10.1242/jeb.000950. [DOI] [PubMed] [Google Scholar]
  40. van Hedel HJA, Tomatis L, Muller R. Modulation of leg muscle activity and gait kinematics by walking speed and bodyweight unloading. Gait & Posture. 2006;24:35–45. doi: 10.1016/j.gaitpost.2005.06.015. [DOI] [PubMed] [Google Scholar]
  41. Visintin M, Barbeau H, Korner-Bitensky N, Mayo NE. A new approach to retrain gain in stroke patients through body weight support and treadmill stimulation. Stroke. 1998;29:1122–1128. doi: 10.1161/01.str.29.6.1122. [DOI] [PubMed] [Google Scholar]
  42. Winter DA. Kinematic and kinetic patterns in human gait: variability and compensating effects. Human Movement Science. 1984;3:51–76. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

01
NIHMS434523-supplement-01.pdf (219.3KB, pdf)

RESOURCES