Abstract
Purpose
This study aimed to quantitatively investigate two main magnetization transfer (MT) effects at low B1: the nuclear Overhauser enhancement (NOE) and amide proton transfer (APT) in the human brain at 7 Tesla.
Methods
The MT effects in the human brain were characterized using a four-pool proton model, which consisted of bulk water, macromolecules, an amide group of mobile proteins and peptides, and NOE-related protons resonating upfield. The pool sizes, exchange rates, and relaxation times of these proton pools were investigated quantitatively by fitting, and the net signals of APT and NOE were simulated based on the fitted parameters.
Results
The results showed that the four-pool model fitted the experimental data quite well, and the NOE effects in human brain at 7 T had a broad spectrum distribution. The NOE effects peaked at a B1 of ~ 1 - 1.4 μT and were significantly stronger in the white matter than in the gray matter, corresponding to a pool-size ratio of approximately 2:1. Since the APT effect was relatively small compared to the NOE effects, MT asymmetry analysis yielded an NOE-dominated contrast in the healthy human brain in this range of B1.
Conclusion
These findings are important to identify the source of NOE effects and to quantify APT effects in human brain at 7 T.
Keywords: magnetization transfer, nuclear Overhauser enhancement, amide proton transfer, ultra high field, chemical exchange saturation transfer
INTRODUCTION
Magnetization transfer (MT) imaging is a well-known MRI technique that can indirectly detect macromolecules and other solutes in the tissue through the water signal (1). In the conventional MT imaging technique, macromolecular protons are selectively saturated, and the saturation is subsequently transferred to bulk water protons, generally through two mechanisms: 1) chemical exchange mediated by water-exchangeable protons of various macromolecules, such as -NH2, -NH and -OH; and 2) nuclear Overhauser enhancement (NOE) mediated by the aliphatic protons of lipids, proteins, and various metabolites due to dipole-dipole interactions (2).
Over the past decade, a new class of MRI contrasts, termed chemical exchange saturation transfer (CEST) (3), has been developed. Initially developed as an exogenous MRI contrast, CEST has also been utilized as an endogenous and an exogenous contrast to investigate a variety of macromolecules and metabolites (4-9). Several emerging endogenous CEST contrast types include APT (amide proton transfer) at +3.5ppm downfield from the water resonance (10), glycoCEST at +0.5 to +1.5ppm (-OH in glycogen) (11), gagCEST at +0.9 to +1.9ppm (-OH in glycosaminoglycan) (12), and GluCEST at ~3ppm (amino protons in glutamate) (13). Preliminary studies in animal models and clinical populations have demonstrated the feasibility and potential clinical value of these techniques for detecting mobile proteins, metabolites, and the pH level (14-20). However, the drawbacks of endogenous CEST include spillover of water saturation, asymmetric MT effects, and the potential cross-talk or overlap of various metabolite peaks due to their relatively broad spectra. Various strategies have been proposed to overcome these shortcomings (21-24). Ultrahigh magnetic fields (e.g., 7 T human MRI scanners), in particular are appealing for CEST imaging due to the wider spectrum separation between water and exchangeable protons as well as the improved signal-to-noise ratio (SNR) (19,25-27).
The NOE is a very common effect in NMR spectroscopy and is highly useful for characterizing chemical structures (28). While the NOE may be mixed with macromolecular pools and may not be visible in early studies at lower magnetic fields, it has been observed upfield in several recent CEST studies at ultrahigh magnetic fields (12,29). The NOE is important both as a potentially new MR contrast, and as a confounding factor for the quantification of APT and other CEST effects. Recently, this effect has been carefully investigated in phantoms and animal models by Jin et al. (30). These studies demonstrated a low optimal B1, higher distribution in white matter (WM) than in gray matter (GM), and insensitivity to pH. To date, however, this upfield effect has not been thoroughly studied, based on the literature, in the human brain.
The general MT process can be characterized by a number of proton pools that exchange magnetization, and thus, by corresponding Bloch equations with exchange terms. Such an MT model was first developed with 2 pools (31) and later extended to three or four pools (32). In CEST imaging, similar quantification methods were also developed (33,34). In the present study, we aimed to systematically investigate NOE and APT effects in the human brain by fitting the experimental data to a four-pool model containing bulk water, macromolecules, mobile amide protons, and NOE-related protons. The fitting procedures directly solve Bloch equations with exchange terms (35,36). The advantage of this method is that it makes few assumptions (e.g., no assumptions of a steady state). After the parameters are fitted, any process of interest (e.g., NOE and APT effects) can be simulated. Our primary purpose was to quantitatively investigate pool sizes, exchange rates, and relaxation times, as well as the B1 dependence and WM-GM contrast of the NOE and APT effects at 7T, which may contribute to identifying the source of, and subsequently quantifying, these NOE and APT effects.
MATERIALS AND METHODS
Theory
In our study, four proton pools were considered: free water protons; solid-like macromolecular protons; amide protons of mobile proteins and peptides; and the upfield NOE-related protons. We used a four-pool model as in the study by Woessner et al. (35) to describe the evolution of magnetizations, in which it was assumed that the magnetization exchanges between any two of the solid-like macromolecular proton pool, amide proton pool, or the upfield NOE-related proton pool were negligible. We assumed the solid-like pool to be resonating at the same frequency center as water, which yielded a Lorentzian line-shape. Generally, the solid-like macromolecular pool is believed to be more complicated than a single pool resonating at a single frequency, but with the absorption of a super-Lorentzian line-shape (37,38). However, in a small spectral range, the line-shape of the macromolecular pool can be approximated as a Lorentzian shape, with T2 adjusted (36,39). MT generally relies on CEST or NOE. Although the mechanisms are different, CEST and NOE have quite similar effects on MRI procedure, except that the exchange rate is higher for CEST than NOE (40).
Assuming the saturation field is in the x-direction in the rotation frame, the Bloch equations with exchange terms can be written as:
| [1] |
| [2] |
| [3] |
| [4] |
| [5] |
| [6] |
| [7] |
| [8] |
| [9] |
| [10] |
| [11] |
| [12] |
where a, b, c, and d represent pools of bulk water protons, macromolecular protons, amide protons, and NOE related protons, respectively; T1i and T2i are the longitudinal and transverse relaxation times of pool i, respectively; Cij is the transition rate of protons from pool i to pool j; Ca = Cab + Cac + Cad; ω is the frequency of the saturation pulse; ωi is the Larmor frequency of pool i; ω1 is the saturation power; Mixyz is the x-, y-, and z- magnetizations of pool i; and Mi0 is the initial magnetization of pool i. Under the mass balance, we have:
| [13] |
The coupled differential equations [1]-[12] are linear and can be rewritten in a matrix form as:
| [14] |
which can be solved analytically and the parameter fitting can be performed using the minimum norm estimate (35). By assuming the exchange rate(s) of a particular pool or two particular pools to be zero, the four-pool model can be reduced to a two-pool or a three-pool model. By subtracting experimental data or simulated four-pool data from simulated two-pool or three-pool data, one can obtain the MT signals related to the particular pool of interest, such as the NOE- or APT-related pool.
Pulse Sequence
Ideal MT pulses should contain long, continuous RF waveforms for the system to reach a steady state. However, due to scanner hardware limitations, we employed an RF pulse train consisting of forty rectangular pulses, with a duration of 98.4 ms for each pulse and a gap of 1.6 ms between RF pulses. The total length of the pulse train was 4 sec. Such a long pulse ensured that the system could reach a steady state even with a very low B1 (which was proven in our pilot study). A centric order turbo-FLASH (TFL) readout was used for image acquisition with TR/TE=7.5/2.86 ms. The TR between MT pulse trains was 10 sec. For each B1 level, a total of 36 images were acquired at different offset frequencies, including 34 frequencies between −6 and 6ppm (±0, ±0.25, ±0.5, ±0.75, ±1, ±1.25, ±1.5, ±1.75, ±2, ±2.5, ±3, ±3.5, ±4, ±4.5, ±5, ±5.5, ±6ppm), and also at ±150ppm as reference images. More images around the water resonance (with a step of 0.25ppm between ±2ppm) were sampled for B0 inhomogeneity corrections.
MR Scanning
This study was performed on a Siemens MAGNETOM 7.0 Tesla whole-body human Scanner (Erlangen, Germany) with a custom-made eight-channel elliptical, octagonal Tx/Rx head coil (41). The coil has a horizontal inner diameter of 23 cm, a vertical inner diameter of 25 cm, and a mechanical length of 28 cm (length of the driven elements: 20 cm). It was made of eight rectangular phased-array loops with inter-loop capacitors for mutual inductance decoupling. The eight coil elements could be excited simultaneously with shifted phases, achieving a relatively homogenous RF or B1 field at high field (a variation of about 16% in the slice of human brain covering the region of interest in this study). The saturation as described by the saturation factor (33) is not sensitive to the variation of B1. Indeed, the effect of B1 inhomogeneity on the CEST signal seems small, according to Fig. 2.
Fig. 2.
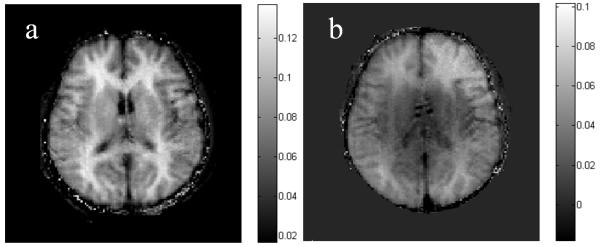
MT asymmetry maps calculated by subtracting the MT images of 3.5 ppm from –3.5 ppm. a: At B1 = 0.9 μT. The WM is brighter than the GM. b: At B1 = 2.3 μT. The WM-GM contrast is weaker.
Seven healthy volunteers (four males, three females, 21 - 26) were studied, after they provided written, informed consent according to a human MRI protocol approved by the Institutional Review Board. Two experiments were performed. In Experiment 1, six different B1 levels were tested (0.2, 0.5, 0.9, 1.4, 1.9, 2.3 μT) in five volunteers using the pulse sequence described. Because in this B1 range, the pools of free water protons, solid-like macromolecular protons, APT related protons, and NOE-related protons consist of the main components of MT effects in human brain as in our data (see Results). Therefore, the four-pool model should be appropriate for characterizing the major line-shape of the MT spectrum. For comparison, we also performed a second experiment, in which seven B1 levels (0.2, 0.5, 0.9, 1.9, 2.8, 3.8, 4.7 μT) were tested in the remaining two volunteers to demonstrate the MT effect with higher levels of saturation power. With B1 higher than 3 μT, several proton pools (e.g., amino protons and protein side chains) other than the four pools described above may become apparent, which may violate the four-pool model. Thus, in the second experiment, we attempted to investigate the asymmetry of MT as a function of B1, and we believe that two volunteers would be enough to demonstrate the effect. Due to SAR limitations, the duration of saturation pulses was shortened from 4 s to 0.8 s, at which point, the system may not reach a steady state. The imaging parameters common to Exps. 1 and 2 were: a single slice of 8 mm through the motor cortex; FA = 14 degrees; TR (between MT pulses) = 10s; and a BW of 130 Hz for a resolution of 1.7 × 1.7 × 8 mm3. TR was set to 10 s so that the longitudinal magnetization would be fully recovered, and each scan at a particular B1 level with 36 frequency offsets took eight min.
Data Analysis
All data analyses, fitting, and statistical analysis were performed in Matlab 6.5 (Mathworks, Natick, MA). In order to correct for B0 field inhomogeneity effects, the z-spectrum collected with 0.2 μT was fitted using a 12th-order polynomial function and interpolated using an offset resolution of 0.01ppm (42). The water resonance was assumed to be at the frequency of the lowest signal intensity, and the B0 inhomogeneity map was obtained. Then, all measured MT curves were also interpolated to 0.01ppm and shifted accordingly, based on the fitted B0 inhomogeneity map. Finally, the corrected z-spectra were interpolated back to the 35 sampling points. All of the analyses were performed on a pixel-by-pixel basis. Regions of interest (ROIs) in the gray matter (GM) and the white matter (WM) were carefully chosen manually in each individual volunteer. The size of each ROI was 0.23 mL.
The starting parameters for T1, T2, exchange rate, and chemical shift values of free water, macromolecular, and amide proton pools used values published in the literature (25,27,33,38). Since no previous study included fitting of the upfield NOE pool, we set the starting values for T1 and exchange rate to be the same as those of the APT pool. The starting NOE-related T2 value was set to 0.3 ms. The NOE-related chemical shift value was set to –3.5ppm since the peak appeared at this frequency in our data. The fitting algorithm that we used was the trust-region-reflective, so the results depend on initial guesses. However, we tried many different initial guesses in a reasonable range. The results were relatively stable for these initial guesses. After the NOE and APT signals were simulated, a paired t-test was performed to compare the NOE and APT signals of the WM and the GM.
RESULTS
Experiment 1
Z-spectra and Asymmetry Plots
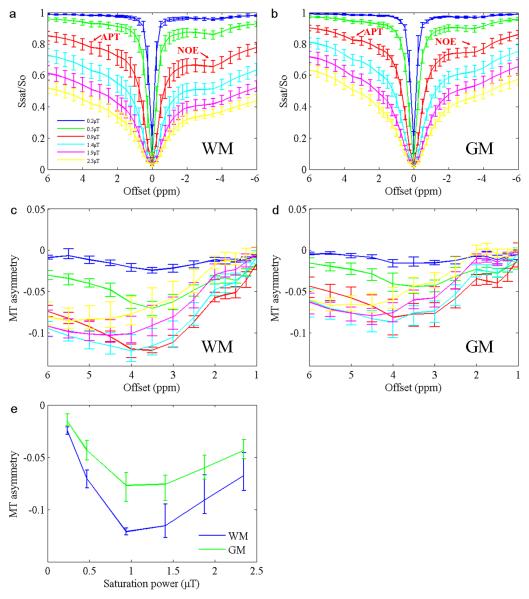
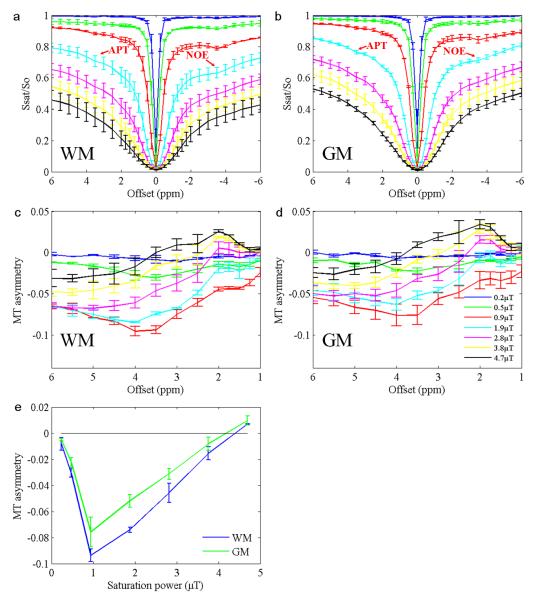
Figure 1 shows the average curves (n = 5) of the z-spectra in GM (Fig. 1a) and WM (Fig. 1b), as well as the associated MT asymmetry plots (Fig. 1c and d; defined as upfield signals minus downfield signals) acquired in Experiment 1. MT asymmetry signals calculated at 3.5ppm from the water resonance as a function of saturation power are also shown in Fig. 1e. The results clearly show the presence of the NOE signals at approximately –3.5ppm. APT signals at 3.5ppm are also visible. MT asymmetry plots in the WM are generally lower than those in the GM, indicating that the NOE-related proton pool is more abundant in the WM. The lowest asymmetry signal occurred at the B1 of 0.9 μT, suggesting that the NOE may be best saturated around this saturation power. However, quantification of the net signal is required to confirm these observations. Although the figures shown here are the average results of five volunteers, all reported trends were similar and robust for each individual volunteer.
Fig. 1.
a: Average z-spectra (n = 5) of the WM. b: Average z-spectra of the GM. c: Average MT asymmetry plots of the WM. d: Average MT asymmetry plots of the GM. e: Average MT asymmetry signals at 3.5ppm as a function of saturation power. Error bars indicate SD.
Figure 2 shows an example of MT asymmetry maps at two different B1 levels calculated by subtracting the images of –3.5ppm from those of +3.5ppm. The contrast between WM and GM is obvious in the asymmetry map at the B1 of 0.9 μT (Fig. 2a), which is consistent with Fig. 1e and close to the optimal B1 for NOE (see below). The map at B1 = 2.3 μT (Fig. 2b) has a reduced contrast.
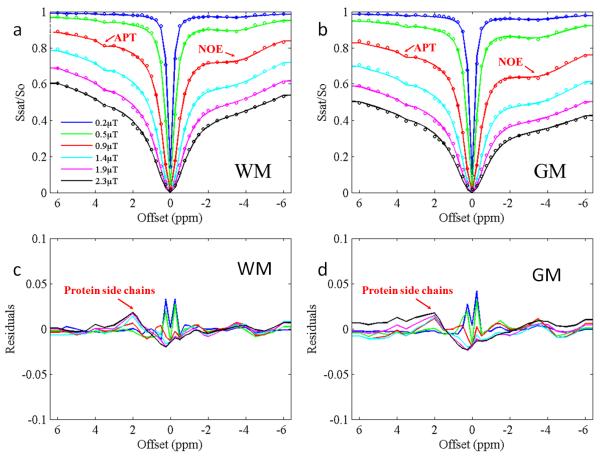
Figure 3 shows four-pool fitting results in the WM (Fig. 3a) and the GM (Fig. 3b) and corresponding residuals (Fig. 3c and Fig. 3d) from a representative volunteer. The four-pool model provided an excellent explanation of experimental data, with an R-square of 0.9893 - 0.9990 between the fitted and measured z-spectra curves. Table 1a and b summarize all fitted parameters and the corresponding 95% confidence interval of APT and NOE effects in the WM and the GM of all volunteers. The pool size was defined as the relative spin quantities assuming that of bulk water to be one. The magnetization exchange rates of three solute proton pools with the bulk water pool (Cba, Cca and Cda) are also shown. Fitting errors, defined as the mean residual deviation per point, were 0.14%-1.14%. These results confirm that NOE is larger in the WM than in the GM (p < 0.0001). The fitted magnitudes of NOE and APT effects showed variability across volunteers. However, the ratio of the NOE effects between the GM and the WM was relatively stable, at approximately 2:1. The APT pool size was small compared with that of NOE, and was larger in the GM than in the WM (p < 0.0001). The fitted APT exchange rate was relatively large (~280 Hz) compared to a previous study at 4.7 T (~28 Hz) (43), suggesting that a greater amount of faster exchanging amide protons might have contributed to the effect at 7T, as expected. The fitted macromolecular proton T2 was longer than reported values in the literature, which was to be expected given the Lorentzian approximation of the macromolecular line-shape (39). The macromolecular proton pool size and APT T2 matched well with literature values (33,44).
Fig. 3.
Fitted results of a typical volunteer using a four-pool model. a: Fitted results of the WM. b: Fitted results of the GM. c: Fitted residuals of the WM. d: Fitted residuals of the GM. Experimental data are shown as dots and fitted plots are shown as lines. R-square is in a range of 0.9893 - 0.9990.
Separation of APT and NOE Signals
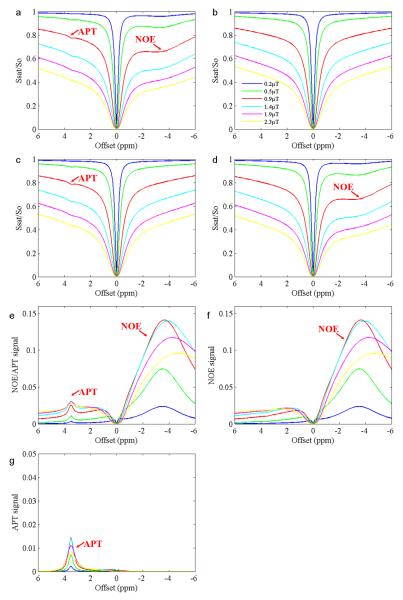
In order to obtain the net signals of APT and NOE, the two-pool and three-pool simulations were carried out and compared with the four-pool model simulation. The results using the WM parameters are shown in Fig. 4. When the four-pool model (bulk water protons, solid-like macromolecular protons, APT-related amide protons, and NOE-related protons) was used, both NOE and APT effects could be seen in the simulated z-spectra (Fig. 4a), as observed experimentally (Figs. 1a and 2a). However, when the two-pool model (bulk water protons and solid-like macromolecular protons) was used, neither NOE nor APT existed in the simulated z-spectra (Fig. 4b). We further performed two three-pool simulated results. In the first three-pool model (without the NOE-related proton pool), no NOE effects could be seen (Fig. 4c). Similarly, in the second three-pool model (without APT-related proton model), no APT effects could be seen (Fig. 4d). Based on these simulated z-spectra results, the combined signals of APT and NOE signals (Fig. 4e) could be obtained by subtracting the four-pool (Fig. 4a) from the two-pool (Fig. 4b) simulated data; the net NOE signals (Fig. 4f) could be obtained by subtracting the four-pool (Fig. 4a) from the first three-pool (Fig. 4c) simulated data; and the net APT signals (Fig. 4g) could be obtained by subtracting the four-pool (Fig. 4a) from the second three-pool (Fig. 4d) simulated data. Based on Fig. 4f, it is important to note that the NOE effects showed a broad-spectrum distribution and had a strong effect on the APT signals downfield of the water resonance.
Fig. 4.
Simulated z-spectra, NOE signals, and APT signals of the WM at several power levels. All these simulations were done using the mean fitted parameters of the WM for all five volunteers. a: Z-spectra from the four-pool model (bulk water protons, solid-like macromolecular protons, APT-related amide protons, and NOE-related protons). b: Z-spectra from the two-pool model (bulk water protons and solid-like macromolecular protons). c: Z-spectra from the first three-pool model (bulk water protons, solid-like macromolecular protons, and APT-related amide protons). No NOE effects can be seen. d: Z-spectra from the second three-pool model (bulk water protons, solid-like macromolecular protons, and NOE-related protons). No APT effects can be seen. e: (b) - (a). Both NOE and APT signals are observed. f: (c) - (a). Only NOE signals are observed. g: (d) - (a). Only APT signals are observed.
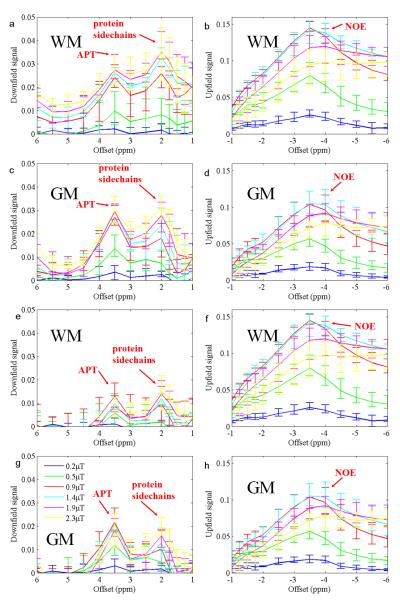
Figure 5 shows the experimental results of the net APT and NOE signals obtained from five subjects, in which the experimental data were subtracted from simulated z-spectrum curves using two-pool (Fig. 5a-d) and three-pool (Fig. 5e-h) models. These downfield and upfield signals were quite similar to the APT and NOE signals shown in Fig. 4e-f, except that experimental data were used rather than the simulated four-pool data, and the two-pool and three-pool simulations here were based on the fitted parameters of each single volunteer rather than the average of all. Note that the experimental data contained additional proton pools (e.g., protein side chains). Indeed, the signal of protein side chains appeared at 2ppm. Notably, both APT and protein side chain CEST signals were higher when subtracting the experimental data from the two-pool simulation than from the three-pool simulation due to the influence of the NOE signals on the downfield range, as demonstrated in Fig. 4. The NOE signal was very similar for both two-pool and three-pool simulations, which further confirmed that APT had little distribution upfield.
Fig. 5.
Experimental upfield and downfield signals in the GM and the WM, calculated by subtracting experimental data (n = 5) from simulated data. a - d: Simulated two-pool data minus experimental data. e - h: Simulated three-pool data minus experimental data. Protein side chain signals at 2ppm downfield also appear. Error bars indicate SD.
Figure 6 shows the plots of the net signals of APT and NOE as a function of the saturation power by subtracting the simulated four-pool data (Fig. 6a) or experimental data (n = 5) (Fig. 6b) from the three-pool simulation data at 3.5ppm. Both results were very similar. It is clear that both APT and NOE signals peak around 1~1.4 μT. The APT signal was an order of magnitude smaller compared to that of the NOE signal. Thus, the asymmetry analysis at the optimal B1 for NOE yielded an NOE-dominated contrast map, as shown in Fig. 2a. The NOE signals were stronger in the WM than in the GM, while the APT signals were higher in the GM than in the WM in each volunteer (p < 0.0001). These results are consistent with previous preclinical studies in rats by Jin et al. (30).
Fig. 6.
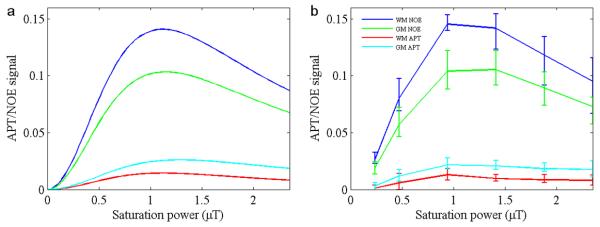
Simulated (a) and experimental (b) signals from NOE and APT, as a function of B1 for Experiment 1. Simulated results (a) were obtained based on the subtraction of the four-pool model from the three-pool simulation. Experimental results (b) were obtained based on the subtraction of experimental data (n=5) from the three-pool simulation. Error bars indicate SD. Both APT and NOE signals peak around 1 - 1.4 μT.
Experiment 2
Figure 7 shows the results of the second experiment (n = 2), in which shorter but higher B1 saturation pulses were employed. Plots of the lower B1 in the second experiment were similar to those of Exp 1. With higher B1, the downfield signals began to dominate and the asymmetry of the z-spectra was reversed. However, with B1 higher than 3 μT, the downfield signals at 3.5ppm could not be solely attributed to APT, because amino protons and protein side chains may contribute (2). Therefore, a four-pool model may be insufficient to accurately model the data at B1 values greater than 3 uT. In the asymmetry plots, proton side chain signals appeared to be very strong at high saturation power levels. Fig. 7e shows the asymmetry signal obtained by subtracting the 3.5ppm signal from the –3.5ppm signal as a function of saturation power. The asymmetry of MT effects was smallest at 0.9 μT, and kept increasing with greater B1, and finally reversed at 4~5 μT, which is higher than the values in a previous study at 3T (2 μT) (17).
Fig. 7.
Experimental data (n = 2) from Experiment 2. a: Average z-spectra of the WM. b: Average z-spectra of the GM. c: Asymmetry plots of the WM. d: Asymmetry plots of the GM. e: MT asymmetry signal as a function of saturation power. Error bars indicate SD. The asymmetry is reversed at B1 > 4.5 μT.
DISCUSSION
In this work, we systematically investigated the B1 dependence of the two main components of MT signals in the human brain at 7 T, including downfield APT and upfield NOE effects. The upfield signals centered around –3.5ppm, with an optimal RF power of approximately 1 μT. At this B1, the MT asymmetry effect was strongest and the APT effect was relatively small; thus, the asymmetry analysis at this saturation power may yield an NOE-dominated contrast.
A four-pool fitting model was performed to quantitatively characterize the z-spectra in the healthy human brain. To the best of our knowledge, this is the first study employing a four-pool model to quantify the endogenous MT effects in the human brain. Certainly, there are other proton pools in the human brain z-spectra, such as protein side chains and amino protons. We did not include these in our model because their influences on the z-spectra seemed to be negligible in our results when B1 was lower than 3 μT. However, conventional MT and NOE have to be included, since they influence the major portion of the z-spectra from –6ppm to 6ppm, as in our study. We also calculated the net signals of APT and NOE by subtracting four-pool simulation data and experimental data from two-pool or three-pool simulations. The results showed that NOE has a broad peak and even extends downfield of the water resonance. This suggests that it is necessary to consider NOE signals when analyzing downfield APT in the human brain. Further, when comparing Fig. 4f with Fig. 5f, the line-shape of simulated NOE signals (Fig. 4) was very similar to the upfield signals shown in Fig. 5, suggesting that our model is valid for describing the upfield MT effect in the human brain. The amplitude and width of the simulated APT peak in Fig. 4 were also similar to the 3.5ppm peak of Fig. 5, suggesting that although the APT peak was relatively small, it could still be well-fitted.
Using the optimal B1 that we observed, we investigated the spatial distribution of the upfield NOE effect in the human brain, and found that the effect was much more abundant in the WM than in the GM. The pool-size ratio was approximately 2:1. There are potentially many possible sources for this NOE signal, including lipids, mobile proteins, or various metabolites (e.g., lactate). Because the signals were larger in the WM than in the GM, lipids might have been a very likely source. However, we should keep in mind that lipids in myelin are commonly believed to be in solid phase and have a very short T2, so that the peak is unlikely to be visible. Therefore, only relatively mobile lipids with a longer T2 may contribute to the observed NOE signals. Further, this NOE signal may originate from the aliphatic protons of mobile proteins. Consequently, it is very possible that the NOE signal may not arise from a single proton pool, but rather, a mixture of various proton pools resonating at close frequencies. Further detailed study is needed to investigate the source of this signal.
In our model, the solid-like macromolecular pool was approximated as a Lorentzian line-shape (39), rather than the more accurate super-Lorentzian line-shape used in MT studies (36). This simplification is acceptable in CEST studies in a small frequency range. Because the T2 of solid-like macromolecules is very short and the NMR signal should thus be very wide, the difference between Lorentzian and super-Lorentzian line-shapes is negligible in a small frequency range. This approximation may cause uncertainty in quantification of solid-like macromolecule (e.g., an increase in T2) because the super-Lorentzian line-shape is wider than the Lorentzian line-shape. However, this should not affect the quantification of APT and NOE because they will be distinguished from solid-lineshape by asymmetry analysis.
The present findings have several implications in MT studies at 7 T. Currently, the APT signal is the primary endogenous CEST contrast for exploiting mobile proteins and pH levels in tissue. However, it has been shown recently that amino protons in glutamate (~3ppm) and protein side chains (~2ppm) may contribute to downfield CEST signals (13,42). It remains challenging to separate the contributions of APT, amino protons, and protein side chains in CEST experiments, although manipulating the duration and magnitude of B1 helps. Our results show that the NOE signals should be considered in future CEST experiments for accurate quantification. Indeed, accurate quantification can be achieved by the use of three- or four-pool model fitting, as shown in the present study. Our results are helpful for investigating the sources of the NOE signal. The sources of NOE may contain a mixture of proton pools, and its upfield location and B1 dependence (which peaked at low B1) are unique from those of the downfield CEST effects. Currently, it is still unclear whether the NOE signal could be developed into a useful MRI contrast for mapping lipids, protein, or other metabolites.
In conclusion, we quantitatively investigated MT signals in the human brain at 7 T. The upfield NOE signal (-3.5ppm) was found to peak around the B1 of 1 μT, with an amplitude greater than that of downfield CEST signals, and was more abundant in the WM than in the GM. These findings may have implications for future CEST studies in the human brain at 7 T.
Table 1a.
Fitted parameters for WM for all volunteers (n = 5) for experiment 1.
| No. | APT pool size (‰) |
APT pool T2 (ms) |
APT pool exchange rate (Hz) |
NOE pool size (%) |
NOE pool T2 (μs) |
NOE pool exchange rate (Hz) |
MT pool size (%) |
MT pool T2 (μs) |
MT pool exchange rate (Hz) |
R-squ are |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.34 | 15.0 | 281.34 | 2.98 | 334.5 | 20.01 | 7.38 | 86.9 | 50.0 | 0.9945 |
| 95% CI | 0.24 - 0.43 |
12.0 - 30.0 |
229.3 - 314.5 |
2.41 - 3.09 |
324.8 - 341.8- |
16.24 – 21.78 |
4.94 – 8.13 |
81.4 – 94.5 |
42.8 – 58.8 | — |
| 2 | 0.24 | 23.6 | 280.42 | 2.72 | 311.1 | 27.33 | 6.69 | 85.8 | 63.3 | 0.9987 |
| 95% CI | 0.12-0.2 8 |
15.0 – 47.5 |
191.1 – 347.0 |
1.72 - 2.73 |
282.8 – 322.2 |
17.2 – 28.3 | 4.14 – 6.80 |
80.8 – 87.8 |
42.0 – 63.6 | — |
| 3 | 0. 20 | 16.5 | 281.80 | 2.01 | 330.2 | 30.85 | 5.74 | 80.1 | 71.2 | 0.9910 |
| 95% CI | 0.15-0.2 7 |
14.5 – 32.5 |
244.20 – 289.44 |
1.63 - 2.20 |
290.2 – 342.4 |
27.76 – 33.25 |
4.78 – 5.75 |
77.6 – 86.0 |
67.5 – 74.9 | — |
| 4 | 0.15 | 42.3 | 281.42 | 2.29 | 298.6 | 29.28 | 5.90 | 81.4 | 88.3 | 0.9957 |
| 95% CI | 0.10 – 0.21 |
0.17 – 43.7 |
247.42 – 311.00 |
1.72 - 23.2 |
276.3 – 326.6 |
27.99 – 44.25 |
4.65 – 6.69 |
75.1 – 83.6 |
76.5 – 91.0 | — |
| 5 | 0.16 | 16.1 | 281.06 | 1.97 | 315.4 | 29.76 | 5.19 | 84.6 | 64.6 | 0.9986 |
| 95% CI | 0.16 – 0.21 |
15.4 – 28.2 |
255.82 – 349.99 |
1.83 – 2.04 |
295.2 – 320.2 |
22.26 – 31.19 |
4.80 – 5.29 |
74.6 – 90.4 |
42.0 - 68.0 | — |
| Mean | 0.22 | 22.7 | 281.21 | 2.39 | 318.0 | 27.45 | 6.18 | 83.8 | 67.5 | 0.9957 |
| Standard error |
0.04 | 5.8 | 0.6 | 0.22 | 7.3 | 2.18 | 0.43 | 1.5 | 6.98 | — |
Table 1b.
Fitted parameters for GM for all volunteers (n = 5) for experiment 1.
| No. | APT pool size (‰) |
APT pool T2 (ms) |
APT pool exchange rate (Hz) |
NOE pool size (%) |
NOE pool T2 (μs) |
NOE pool exchange rate (Hz) |
MT pool size (%) |
MT pool T2 (μs) |
MT pool exchange rate (Hz) |
R-squ are |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.41 | 15.2 | 283.94 | 1.51 | 443.4 | 20.14 | 4.53 | 103.7 | 50.0 | 0.9946 |
| 95% CI | 0.25-0.4 3 |
13.0 – 42.5 |
250.04 – 320.26 |
0.75 – 15.5 |
333.7 – 452.4 |
20.00 – 22.51 |
3.44 – 5.31 |
98.0 – 115.3 |
45.0 – 52.7 | — |
| 2 | 0.33 | 25.7 | 283.21 | 1.21 | 497.2 | 24.92 | 3.56 | 96.4 | 59.5 | 0.9952 |
| 95% CI | 0.17 - 0.35 |
15.4 – 37.2 |
280.7 - 305.0 |
0.70 – 1.26 |
377.3 – 501.3 |
23.47 – 30.81 |
2.06 – 3.89 |
93.1 – 106.9 |
34.2 – 60.8 | — |
| 3 | 0.21 | 16.0 | 282.09 | 1.01 | 465.5 | 23.86 | 3.17 | 113.2 | 65.7 | 0.9893 |
| 95% CI | 0.14 - 0.28 |
14.2 – 33.7 |
274.27 – 322.76 |
0.72 – 1.19 |
406.1 – 512.3 |
22.67 – 31.54 |
2.97 – 3.28 |
109.6 – 118.0 |
52.1 – 86.4 | — |
| 4 | 0.21 | 37.5 | 279.81 | 1.42 | 359.9 | 24.24 | 3.62 | 97.4 | 71.3 | 0.9981 |
| 95% CI | 0.15 - 0.25 |
16.7 – 49.7 |
196.39 – 318.16 |
1.20 – 1.63 |
348.0 – 394.5 |
21.59 – 25.80 |
2.78 – 3.65 |
87.6 – 106.9 |
57.6 – 76.9 | — |
| 5 | 0.27 | 48.3 | 280.60 | 0.75 | 433.8 | 29.36 | 2.25 | 110.7 | 70.9 | 0.9990 |
| 95% CI | 0.18 – 0.29 |
17.5 – 48.6 |
178.37 – 345.00 |
0.64 – 0.98 |
378.0 – 434.5 |
27.42 – 32.91 |
2.20 – 2.75 |
106.7 – 111.6 |
69.2 – 88.2 | — |
| Mean | 0.25 | 28.54 | 281.93 | 1.18 | 402.7 | 24.50 | 3.426 | 104.28 | 63.48 | 0.9952 |
| Standard error |
0.05 | 7.14 | 0.87 | 0.16 | 25.48 | 1.65 | 0.42 | 3.80 | 4.5 | — |
Acknowledgements
We thank Dr. A. Dean Sherry (University of Texas at Dallas) for providing the simulation codes that we modified for use in this study. We also thank Dr. Bida Zhang for his advice about modifying the pulse sequence we used in this study. This work was supported by the Ministry of Science and Technology of China (grant numbers: 2012CB825500 and 2009IM030900), the Knowledge Innovation Project (grant number: KSCX2-YW-R-259), the Major Scientific & Research Equipment and Instrument Developing Project (grant number: ZDYZ2010-2) of the Chinese Academy of Science, the National Natural Science Foundation of China (NSFC, grant numbers: 91132302, 90820307, and 81128006), and the National Institutes of Health (grant number: R01EB009731 and R01MH080892-04S1).
REFERENCES
- 1.Wolff SD, Balaban RS. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn Reson Med. 1989;10:135–144. doi: 10.1002/mrm.1910100113. [DOI] [PubMed] [Google Scholar]
- 2.Liepinsh E, Otting G. Proton exchange rates from amino acid side chains-implication for image contrast. Magn Reson Med. 1996;35:30–42. doi: 10.1002/mrm.1910350106. [DOI] [PubMed] [Google Scholar]
- 3.Ward KM, Aletras AH, Balaban RS. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST) J Magn Reson. 2000;143(1):79–87. doi: 10.1006/jmre.1999.1956. [DOI] [PubMed] [Google Scholar]
- 4.Zhou J, van Zijl PC. Chemical exchange saturation transfer imaging and spectroscopy. Progr NMR Spectr. 2006;48:109–136. [Google Scholar]
- 5.Sherry AD, Woods M. Chemical exchange saturation transfer contrast agents for magnetic resonance imaging. Annu Rev Biomed Eng. 2008;10:391–411. doi: 10.1146/annurev.bioeng.9.060906.151929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hancu I, Dixon WT, Woods M, Vinogradov E, Sherry AD, Lenkinski RE. CEST and PARACEST MR contrast agents. Acta Radiol. 2010;51(8):910–923. doi: 10.3109/02841851.2010.502126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Terreno E, Castelli DD, Aime S. Encoding the frequency dependence in MRI contrast media: the emerging class of CEST agents. Contrast Media Mol Imaging. 2010;5(2):78–98. doi: 10.1002/cmmi.369. [DOI] [PubMed] [Google Scholar]
- 8.van Zijl PC, Yadav NN. Chemical exchange saturation transfer (CEST): what is in a name and what isn’t? Magn Reson Med. 2011;65(4):927–948. doi: 10.1002/mrm.22761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pacheco-Torres J, Calle D, Lizarbe B, Negri V, Ubide C, Fayos R, Larrubia PL, Ballesteros P, Cerdan S. Environmentally sensitive paramagnetic and diamagnetic contrast agents for nuclear magnetic resonance imaging and spectroscopy. Curr Top Med Chem. 2011;11(1):115–130. doi: 10.2174/156802611793611904. [DOI] [PubMed] [Google Scholar]
- 10.Zhou J, Payen JF, Wilson DA, Traystman RJ, van Zijl PC. Using the amide proton signals of intracellular proteins and peptides to detect pH effects in MRI. Nat Med. 2003;9(8):1085–1090. doi: 10.1038/nm907. [DOI] [PubMed] [Google Scholar]
- 11.van Zijl PC, Jones CK, Ren J, Malloy CR, Sherry AD. MRI detection of glycogen in vivo by using chemical exchange saturation transfer imaging (glycoCEST) Proc Natl Acad Sci U S A. 2007;104(11):4359–4364. doi: 10.1073/pnas.0700281104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ling W, Regatte RR, Navon G, Jerschow A. Assessment of glycosaminoglycan concentration in vivo by chemical exchange-dependent saturation transfer (gagCEST) Proc Natl Acad Sci U S A. 2008;105(7):2266–2270. doi: 10.1073/pnas.0707666105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cai KJ, Haris M, Singh A, Kogan F, Greenberg JH, Hariharan H, Detre JA, Reddy R. Magnetic resonance imaging of glutamate. Nat Med. 2012;18(2):302–306. doi: 10.1038/nm.2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Sun PZ, Zhou J, Sun W, Huang J, van Zijl PC. Detection of the ischemic penumbra using pH-weighted MRI. J Cereb Blood Flow Metab. 2007;27(6):1129–1136. doi: 10.1038/sj.jcbfm.9600424. [DOI] [PubMed] [Google Scholar]
- 15.Wen Z, Hu S, Huang F, Wang X, Guo L, Quan X, Wang S, Zhou J. MR imaging of high-grade brain tumors using endogenous protein and peptide-based contrast. NeuroImage. 2010;51:616–622. doi: 10.1016/j.neuroimage.2010.02.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhou J, Tryggestad E, Wen Z, Lal B, Zhou T, Grossman R, Wang S, Yan K, Fu DX, Ford E, Tyler B, Blakeley J, Laterra J, van Zijl PC. Differentiation between glioma and radiation necrosis using molecular magnetic resonance imaging of endogenous proteins and peptides. Nat Med. 2011;17:130–134. doi: 10.1038/nm.2268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhao X, Wen Z, Huang F, Lu S, Wang X, Hu S, Zu D, Zhou J. Saturation power dependence of amide proton transfer image contrasts in human brain tumors and strokes at 3 T. Magn Reson Med. 2011;66:1033–1041. doi: 10.1002/mrm.22891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jia G, Abaza R, Williams JD, Zynger DL, Zhou J, Shah ZK, Patel M, Sammet S, Wei L, Bahnson RR, Knopp MV. Amide proton transfer MR imaging of prostate cancer: A preliminary study. J Magn Reson Imaging. 2011;33(3):647–654. doi: 10.1002/jmri.22480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schmitt B, Zbyn S, Stelzeneder D, Jellus V, Paul D, Lauer L, Bachert P, Trattnig S. Cartilage quality assessment by using glycosaminoglycan chemical exchange saturation transfer and Na-23 MR imaging at 7T. Radiology. 2011;260(1):257–264. doi: 10.1148/radiol.11101841. [DOI] [PubMed] [Google Scholar]
- 20.Jia G, Takayama Y, Flanigan DC, Kaeding CC, Zhou J, Chaudhari A, Clark D, Sammet S, Liang J, Choi S, Knopp MV. Quantitative assessment of mobile protein levels in human knee synovial fluid: feasibility of chemical exchange saturation transfer (proteinCEST) MRI of osteoarthritis. Magn Reson Imaging. 2011;29:335–341. doi: 10.1016/j.mri.2010.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J Magn Reson. 2011;211(2):149–155. doi: 10.1016/j.jmr.2011.05.001. [DOI] [PubMed] [Google Scholar]
- 22.Scheidegger R, Vinogradov E, Alsop DC. Amide proton transfer imaging with improved robustness to magnetic field inhomogeneity and magnetization transfer asymmetry using saturation with frequency alternating RF irradiation. Magn Reson Med. 2011;66(5):1275–1285. doi: 10.1002/mrm.22912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lee JS, Regatte RR, Jerschow A. Isolating chemical exchange saturation transfer contrast from magnetization transfer asymmetry under two-frequency rf irradiation. J Magn Reson. 2012;215:56–63. doi: 10.1016/j.jmr.2011.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zu Z, Janve VA, Li K, Does MD, Gore JC, Gochberg DF. Multi-angle ratiometric approach to measure chemical exchange in amide proton transfer imaging. Magn Reson Med. 2011 doi: 10.1002/mrm.23276. DOI 10.1002/mrm.23276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Mougin OE, Coxon RC, Pitiot A, Gowland PA. Magnetization transfer phenomenon in the human brain at 7 T. NeuroImage. 2010;49(1):272–281. doi: 10.1016/j.neuroimage.2009.08.022. [DOI] [PubMed] [Google Scholar]
- 26.Dula AN, Asche EM, Landman BA, Welch EB, Pawate S, Sriram S, Gore JC, Smith SA. Development of chemical exchange saturation transfer at 7T. Magn Reson Med. 2011;66(3):831–838. doi: 10.1002/mrm.22862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jones CK, Polders D, Hua J, Zhe H, Hoogduin HJ, Zhou J, Luijten P, van Zijl PC. In vivo 3D whole-brain pulsed steady state chemical exchange saturation transfer at 7T. Magn Reson Med. 2012;67:1579–1589. doi: 10.1002/mrm.23141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kumar A, Ernst RR, Wuthrich K. A two-dimensional nuclear Overhauser enhancement (2D NOE) experiment for the elucidation of complete proton-proton cross-relaxation networks in biological macromolecules. Biochem Biophys Res Commun. 1980;95(1):1–6. doi: 10.1016/0006-291x(80)90695-6. [DOI] [PubMed] [Google Scholar]
- 29.Jones CK, Huang AJ, van Zijl PC. Exchange-relayed nuclear Overhauser effect MRI; Proceedings of 19th Annual Meeting ISMRM; Montreal, Canada. 2011.p. 2735. [Google Scholar]
- 30.Jin T, Wang P, Zong X, Kim SG. MR imaging of the amide-proton transfer effect and the pH-insensitive nuclear overhauser effect at 9.4 T. Magn Reson Med. 2012 doi: 10.1002/mrm.24315. DOI 10.1002/mrm.24315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magn Reson Med. 1993;29(6):759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- 32.Tessier JJ, Dillon N, Carpenter TA, Hall LD. Interpretation of magnetization transfer and proton cross-relaxation spectra of biological tissues. J Magn Reson B. 1995;107(2):138–144. doi: 10.1006/jmrb.1995.1069. [DOI] [PubMed] [Google Scholar]
- 33.Zhou J, Wilson DA, Sun PZ, Klaus JA, van Zijl PC. Quantitative description of proton exchange processes between water and endogenous and exogenous agents for WEX, CEST, and APT experiments. Magn Reson Med. 2004;51(5):945–952. doi: 10.1002/mrm.20048. [DOI] [PubMed] [Google Scholar]
- 34.Sun PZ. Simplified and scalable numerical solution for describing multi-pool chemical exchange saturation transfer (CEST) MRI contrast. J Magn Reson. 2010;205(2):235–241. doi: 10.1016/j.jmr.2010.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Woessner DE, Zhang S, Merritt ME, Sherry AD. Numerical solution of the Bloch equations provides insights into the optimum design of PARACEST agents for MRI. Magn Reson Med. 2005;53(4):790–799. doi: 10.1002/mrm.20408. [DOI] [PubMed] [Google Scholar]
- 36.Li AX, Hudson RHE, Barrett JW, Jones CK, Pasternak SH, Bartha R. Four-pool modeling of proton exchange processes in biological systems in the presence of MRI-paramagnetic chemical exchange saturation transfer (PARACEST) agents. Magn Reson Med. 2008;60(5):1197–1206. doi: 10.1002/mrm.21752. [DOI] [PubMed] [Google Scholar]
- 37.Morrison C, Henkelman RM. A model for magnetization transfer in tissues. Magn Reson Med. 1995;33(4):475–482. doi: 10.1002/mrm.1910330404. [DOI] [PubMed] [Google Scholar]
- 38.Sled JG, Pike GB. Quantitative imaging of magnetization transfer exchange and relaxation properties in vivo using MRI. Magn Reson Med. 2001;46(5):923–931. doi: 10.1002/mrm.1278. [DOI] [PubMed] [Google Scholar]
- 39.Zaiss M, Schmitt B, Bachert P. Quantitative separation of CEST effect from magnetization transfer and spillover effects by Lorentzian-line-fit analysis of z-spectra. J Magn Reson. 2011;211(2):149–155. doi: 10.1016/j.jmr.2011.05.001. [DOI] [PubMed] [Google Scholar]
- 40.Mori S, Eleff SM, Pilatus U, Mori N, van Zijl PC. Proton NMR spectroscopy of solvent-saturable resonances: a new approach to study pH effects in situ. Magn Reson Med. 1998;40(1):36–42. doi: 10.1002/mrm.1910400105. [DOI] [PubMed] [Google Scholar]
- 41.Zuo Z, Park J, Li Y, Li Z, Yan X, Zhang Z, Zhuo Y, Cho ZH, Zhou XJ, Xue R. An Elliptical Octagonal Phased-Array Head Coil for Multi-Channel Transmission and Reception at 7T; Proceedings of the 20th Annual Meeting of ISMRM; Melbourne, Australia. 2012.p. 2804. [Google Scholar]
- 42.Zhou J, Lal B, Wilson DA, Laterra J, van Zijl PC. Amide proton transfer (APT) contrast for imaging of brain tumors. Magn Reson Med. 2003;50:1120–1126. doi: 10.1002/mrm.10651. [DOI] [PubMed] [Google Scholar]
- 43.van Zijl PC, Zhou J, Mori N, Payen JF, Wilson D, Mori S. Mechanism of magnetization transfer during on-resonance water saturation. A new approach to detect mobile proteins, peptides, and lipids. Magn Reson Med. 2003;49(3):440–449. doi: 10.1002/mrm.10398. [DOI] [PubMed] [Google Scholar]
- 44.Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T-1, T-2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med. 2005;54(3):507–512. doi: 10.1002/mrm.20605. [DOI] [PubMed] [Google Scholar]