Abstract
Understanding radiation responses of Fe-based metals is essential to develop radiation tolerant steels for longer and safer life cycles in harsh reactor environments. Nanograined metals have been explored as self-healing materials due to point-defect recombination at grain boundaries. The fundamental defect-boundary interactions, however, are not yet well understood. We discover that the interactions are always mediated by formation and annealing of chain-like defects, which consist of alternately positioned interstitials and vacancies. These chain-like defects are closely correlated to the patterns of defect formation energy minima on the grain boundary, which depend on specific boundary configurations. Through chain-like defects, a point defect effectively translates large distances, to annihilate with its opposite, thus grain boundaries act as highly efficient defect sinks that cannot saturate under extreme radiation conditions.
In fission reactors where stainless steels are widely used as in-core structural components, materials are exposed to high fluence neutrons with accumulated radiation damage up to a few hundred displacements per atom (dpa)1,2. High energy fission product particles resulting from neutron-solid interactions create collision cascades. Majority of interstitials and vacancies in the cascades can quickly recombine within a fraction of one picosecond, but those point defects escaping the dynamic annealing process develop into extended defects such as dislocations, stacking fault tetrahedra and voids3,4,5,6,7. The radiation-induced microstructure and microchemistry changes eventually lead to various structural failures including swelling, hardening, embrittlement, stress corrosion cracking, and creep2,8,9. Towards development of radiation tolerant materials with self-repairing capabilities, previous studies have shown that free surfaces, grain boundaries, and precipitate-matrix interfaces can act as defect sinks to trap and recombine defects10,11,12. Among various structure-engineered materials, nanograined or nanolayered metals have been a subject of great interest13,14,15,16. Although thermal stability of nanograins, i.e. grain coarsening upon annealing, presents a challenge for practical usage, grain stabilizations have been achieved through introducing additives or by fine tuning of plastic deformation conditions17,18. Most recently, nanocrystalline metals having exceptional thermal stability have been reported with the design guided by a new thermodynamic model19. These findings show great promises for applications of grained-engineered metals in reactors. Further materials developments require atomic scale details, often beyond direct experimental observations. One complexity of the boundary effect is found in recent modeling studies, which show that boundaries act as not only interstitial sinks but also interstitial sources if the vacancies become supersaturated within the bulk12. However, many fundamental mechanisms, i.e. atomic scale details of defect annihilation on grain boundaries, remain unknown.
Using single-phase bcc Fe as the model material, we shed light onto atomic scale details of boundary defect sink and annihilation through molecular dynamics (MD) simulations. One key finding is that boundary-defect interactions are not realized by movements of individual defects which keep their identities through the whole processes. Instead, a chain-like group defect is always involved. The study identified two kinds of chain defects, both consisting of alternately positioned interstitials and vacancies. One is denoted as “bulk chain-like” (BC) defect, and the other is denoted as “grain boundary chain-like” (GBC) defect. A point defect can induce BC or GBC defects and, through localized recombination of neighboring interstitial-vacancy pairs along the chain, realizes an equivalent transport from one end of the chain to the other end. BC or GBC defects can also be induced between a well-separated interstitial-vacancy pair to realize defect annihilation. The present study identifies three defect removal processes and for all of them, BC and GBC defects are both relevant to the patterns of the defect formation energy minima on the boundary.
Results
The MD simulations started with a Fe unit cell containing a (013)[100]Σ = 5 symmetric-tilt grain boundary created with a tilt angle of 36.8°. In the beginning the modeling intentionally introduced one vacancy on one side of the grain boundary and one interstitial on the other side. The interstitial quickly changes into a dumbbell defect (a stable small defect complex having one vacancy sitting between interstitials). Fig. 1 shows three modeling identified defect annihilation processes. In case #1 denoted as “BC model” in the figure (Fig. 1a–g, also Supplementary movie S1), a dumbbell defect in the bulk rotates (Fig. 1b) and induces a BC defect (Fig. 1c). Through subsequent defect annihilation between neighboring interstitials and vacancies on the chain, the inducing defect disappears and leaves one interstitial on the boundary (Fig. 1d), which is equivalent to transporting the bulk interstitial to the boundary. Next, with presence of an isolated vacancy in the bulk, the interstitial loaded on the boundary induces another BC defect between the two defects (Fig. 1e), which eventually leads to complete defect annihilation. One BC defect can be treated as a chain of linked interstitial-vacancy pairs. Different from previously reported crowdion defect, which is a chain of displaced atoms aligned along one crystal axis direction and is often observed around a damage cascade when the inducing defect has sufficiently high kinetic energy20,21, a BC defect is induced by atoms at thermal vibration energies and is not formed by kinetically displacing the neighboring lattice atoms one after the other in a subsequent manner. Instead, the interstitial-vacancy pairs on the BC defect appear without time orders. Some BC fragments are found to form first at a distance away from the inducing defect, then these fragments connect and complete the chain formation. This means that a BC defect is induced by the stress fields between two ending locations. Our modeling shows that the landing of the BC defect on the boundary always correspond to the sites having the lowest defect formation energies, which appear as periodical patterns on the boundary with the site density determined by the boundary configuration (to be discussed in the present study). This finding reveals the governing factor to determine the capability to transport a defect to the boundary.
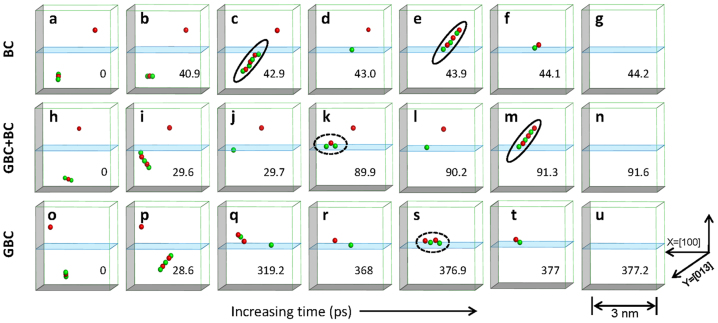
Figure 1. Representative snapshots of a MD simulation of three different defect annihilation processes for (013)[100]Σ = 5 symmetric title grain boundary.
All simulations start with one bulk vacancy and one bulk dumbbell defect close to a grain boundary. (a–g) The process involving BC defect for annihilation: A BC defect is created at time t = 42.9 ps to transport an interstitial to the boundary and then another BC defect is created t = 43.9 ps to annihilate a bulk vacancy. (h–n) The process involving GBC defect for boundary migration and BC defect for annihilation: A GBC defect is created at t = 89.9 ps to move a boundary trapped interstitial, and then a BC defect is created at t = 91.3 ps to annihilate a bulk vacancy. (o–u) The process involving GBC defect for annihilation on the boundary: A GBC defect is created at t = 376.9 ps to annihilate a defect pair separated and trapped on the boundary. The boundary is represented with a blue shadowed plane. The green balls refer to interstitial and red balls refer to vacancy. The solid circles refer to BC defects and dash circles refer to GC defects.
Since a BC defect is induced by stress fields between chain's starting and ending sites, defect removal through BC model may not occur if two ends are separated too far away. In a more general situation, described as case #2 and denoted as “GBC + BC model” in Fig. 1, h to n and also shown in Supplementary movie S2, a boundary-loaded interstitial migrates first on the boundary (Fig. 1k), then induce a BC defect (Fig. 1m) to recombine with a bulk vacancy. The case #3, denoted as “GBC model” in Fig. 1, o to h, and also shown in Supplementary movie S3, is a defect annihilation mechanism involving the step of trapping one interstitial and one vacancy on the boundary but the defect pair is separated over a distance more than one lattice spacing (Fig. 1, o to r). Although vacancy is less mobile, it still can “transport” to the boundary through BC defect formation (Fig. 1q). Induced by stress fields between the defect pair, each defect migrates on the boundary through GBC defect formations. Eventually, one GBC defect links the two defects and realizes defect removal (Fig. 1s).
A GBC defect has specific configurations: its interstitial corresponds to the boundary site of the lowest interstitial formation energy 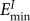 and its vacancy corresponds to that of lowest vacancy formation energy
and its vacancy corresponds to that of lowest vacancy formation energy 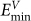 . MD simulation shows that a GBC defect is formed by displacing a lattice atom from
. MD simulation shows that a GBC defect is formed by displacing a lattice atom from 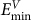 site to the immediate neighboring
site to the immediate neighboring 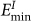 site. Figure 2 shows the correspondence between a GBC defect and defect formation energy on the boundary. The GBC defect shown in Fig. 2a was obtained from modeling (Fig. 1s). When bonding two bcc crystals to form a symmetric grain boundary, joining regions of the 1st planes and the 2nd planes have different atomic interactions, where the 1st plane refer to the top surface plane of a bcc unit cell, and the 2nd plane refers to the middle plane, consisting of the center atoms of the unit cell. Interstitials and vacancies in the GBC defect are alternately positioned and each defect takes only one site on each plane (Fig. 2b). The white arrows in Fig. 2c point to sites occupied by the defects, over two dimensional mapping of vacancy formation energy (
site. Figure 2 shows the correspondence between a GBC defect and defect formation energy on the boundary. The GBC defect shown in Fig. 2a was obtained from modeling (Fig. 1s). When bonding two bcc crystals to form a symmetric grain boundary, joining regions of the 1st planes and the 2nd planes have different atomic interactions, where the 1st plane refer to the top surface plane of a bcc unit cell, and the 2nd plane refers to the middle plane, consisting of the center atoms of the unit cell. Interstitials and vacancies in the GBC defect are alternately positioned and each defect takes only one site on each plane (Fig. 2b). The white arrows in Fig. 2c point to sites occupied by the defects, over two dimensional mapping of vacancy formation energy (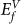 ) and interstitial formation energy (
) and interstitial formation energy (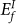 ). Obviously, the defect location correspond to
). Obviously, the defect location correspond to 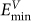 and
and 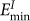 , i.e. the vacancy in a GBC defect takes one
, i.e. the vacancy in a GBC defect takes one 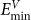 site and the interstitial takes one neighboring
site and the interstitial takes one neighboring 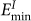 on the next plane. The
on the next plane. The 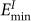 site corresponds to boundary open volume, where the surrounding atoms have inward relaxation and the region is energetically favorable to insert an interstitial type defect. The
site corresponds to boundary open volume, where the surrounding atoms have inward relaxation and the region is energetically favorable to insert an interstitial type defect. The 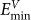 region are caused by close vicinity of two meeting atoms and their repulsive interactions lead to outward relaxation of surrounding atoms which favors vacancy formation.
region are caused by close vicinity of two meeting atoms and their repulsive interactions lead to outward relaxation of surrounding atoms which favors vacancy formation.
Figure 2. Comparisons of (a) MD simulation observed GBC defect and (b) schematics of lattice locations of defects in the GBC defect and (c) corresponding 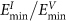 sites for (013)[100]Σ = 5 symmetric tilt grain boundary.
sites for (013)[100]Σ = 5 symmetric tilt grain boundary.
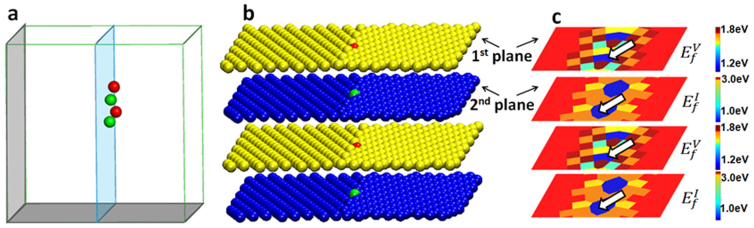
The arrows mark the allowable sites for interstitial and vacancy formation as predicted by formation energy minima, which agree with GBC defect configurations. The GBC defect forms on the boundary plane represented by the blue shaded area. The MD simulation corresponds to Fig. 1s.
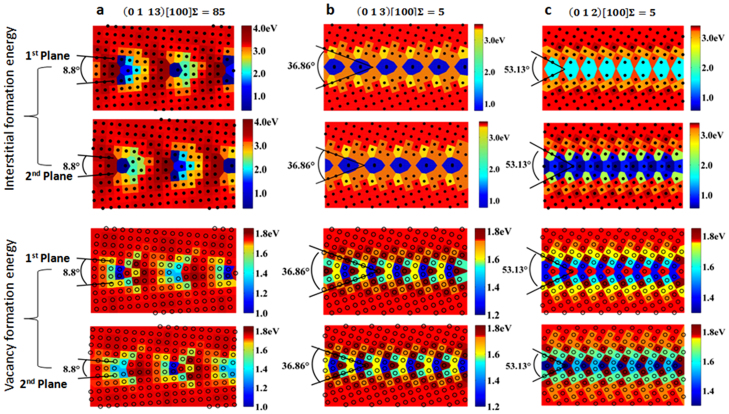
To show the dependence of 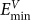 and
and 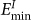 patterns on boundary configurations, Figure 3 plots the energy mapping of
patterns on boundary configurations, Figure 3 plots the energy mapping of 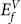 and
and 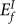 over symmetric tilt grain boundaries of three different angles, with θ = 8.8° for (0113)[100]Σ = 85 (Fig. 3a), θ = 36.86° for (013)[100]Σ = 5 (Fig. 3b), and θ = 53.13° for (012)[100]Σ = 5 (Fig. 3c). Viewed along the rotation axis forming symmetric boundary, i.e. the direction perpendicular to planes shown in Fig. 2b,
over symmetric tilt grain boundaries of three different angles, with θ = 8.8° for (0113)[100]Σ = 85 (Fig. 3a), θ = 36.86° for (013)[100]Σ = 5 (Fig. 3b), and θ = 53.13° for (012)[100]Σ = 5 (Fig. 3c). Viewed along the rotation axis forming symmetric boundary, i.e. the direction perpendicular to planes shown in Fig. 2b, 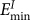 regions are periodically spaced with separation distances decreasing with increasing boundary angles, the same as
regions are periodically spaced with separation distances decreasing with increasing boundary angles, the same as 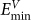 regions. The neighboring interstitial-vacancy pairs on the GBC defect cannot be separated more than, roughly, one lattice spacing distance, which means for small angle boundary (θ = 8.8°, Fig. 3a), the separation distance between neighboring
regions. The neighboring interstitial-vacancy pairs on the GBC defect cannot be separated more than, roughly, one lattice spacing distance, which means for small angle boundary (θ = 8.8°, Fig. 3a), the separation distance between neighboring 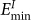 (or
(or 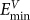 ) sites is too large, and the GBC defect can only form along the rotation axis, since this direction guarantees one
) sites is too large, and the GBC defect can only form along the rotation axis, since this direction guarantees one 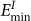 or one
or one 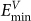 sites over every plane distance. Each
sites over every plane distance. Each 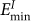 and
and 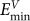 region contains, usually, multiple sites for interstitials or vacancies to occupy, which leads to zigzag like configurations of GBC defect. A GBC defect can form on the same plane (The 1st or 2nd planes denoted in Fig. 2b) if neighboring
region contains, usually, multiple sites for interstitials or vacancies to occupy, which leads to zigzag like configurations of GBC defect. A GBC defect can form on the same plane (The 1st or 2nd planes denoted in Fig. 2b) if neighboring 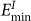 −
− 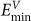 pairs on the plane has a separation distance comparable to one lattice spacing, which occurs only for large angle boundary, θ = 53.13° (Fig. 3c). In comparison with small angle boundaries, very large angle boundary leads to higher
pairs on the plane has a separation distance comparable to one lattice spacing, which occurs only for large angle boundary, θ = 53.13° (Fig. 3c). In comparison with small angle boundaries, very large angle boundary leads to higher 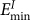 (or
(or 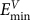 ) densities and provides more GBC defect formation directions.
) densities and provides more GBC defect formation directions.
Figure 3. Formation energy of interstitials and vacancies in the bulk and at the boundaries, created with tilt angles of (a) 8.8°, (b) 36.8°, and (c) 53.13°, respectively.
The energy scale bar is provided. The hollow circles refer to vacancies and the solid circles to interstitials. These interstitials sites are not octahedral and tetrahedral interstitials since both are not energetically favorable. For interstitials in the bulk, energy minimization favors dumbbell defect formation around one lattice location. Close to the boundary, isolated interstitials become energetically favorable to form and corresponding stable locations are identified by allowing structural relaxations in simulations.
Discussion
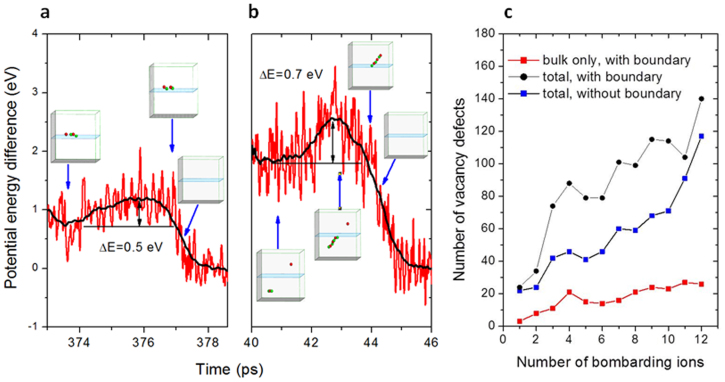
The BC and GBC mediated defect removal processes have relatively small energy barrier, which can be analyzed from time changes of total potential energy of the selected volume containing reacting defects. Figure 4 plots the potential change covering the steps of formation and annihilation of a GBC defect (Fig. 4a) and of a BC defect (Fig. 4b). The potential energy changes have fluctuations resulting from thermal vibrations and also attempted interstitial-vacancy pair formation/rotation. The energy difference judged by the averaged values between starting step and the energy maximum suggest energy barriers of ~0.5 eV for GBC defect and ~0.7 eV for BC defect. For GBC mediated defect removal, several successive steps, i.e. forming the first BC and then the second BC, occur vary fast and individual energy barrier for each step cannot be differentiated. Overall, the energy barriers are much less in comparison with the energy required to form a crowdion defect, which requires a minimum energy of 6.3 eV, even for the most favorable direction of [111], according to our MD simulations.
Figure 4.
(a) Time dependent potential changes of a localized volume involving the step of forming a GBC defect between a boundary-trapped, well-separated interstitial-vacancy pair and the step of its annihilation, and (b) the potential changes of the volume involving the successive steps of forming a BC defect to transport an interstitial to the boundary and subsequent forming another BC defect to annihilate a bulk vacancy, and (c) numbers of vacancy defects left after repeated ion bombardments with or without a grain boundary presented.
Our study further suggests that similar GBC defect formation and annihilation mechanisms would apply to dislocations. For an isolated interstitial dislocation in bulk, the edge of the inserted atomic plane expects to have similar atomic scale zigzag roughness. For a given atom on the edge, paired compressive and tensile strain regions are created on each side of the atom. These paired stress fields are zigzag like along the dislocation line. Consequently, GBC like defect chains are allowed to create along the dislocation lines, to assist defect migration and recombination. In fact, for boundaries of ultra small angle misalignment, they essentially relax into periodically separated dislocations.
Considering ultra high dpa encountered by reactor structural components, the stability of boundaries and preservability of boundary effects under extreme radiation conditions need to be evaluated. Fig. 4c compares the number of residual defects left in the system by repeating ion bombardments of 3 keV in the bulk, with or without the presence of a boundary in close vicinity. Between two successive ion bombardments, structural relaxation is allowed to model interactions among the newly introduced defects and defects left in the previous damage cascades. The damage-overlapping region promotes the formation of large defects due to intense defect interactions. The immobile defect clusters reduce the overall defect mobilities, thus reducing dynamic interstitial-vacancy recombination, and nonlinear damage buildups are expected. For the bulk containing a grain boundary, the boundary effect can be saturated or disappear at high damage levels, if one of the following occurs (1) the boundary defect sink properties favor one particular type of defect (interstitial vs. vacancy) and creates large defect imbalance on the boundary which makes defect recombination difficult; (2) boundary loses its sink properties due to mixing; (3) boundary loses its annihilation property beyond certain limits. Our simulations show that the boundary still has high efficiency in defect removal under repeated ion bombardments. As shown in Fig. 4c, for a cell containing a grain boundary, the numbers of residual defects (red) in bulk are systematically lower than that without a boundary (blue). However, if not excluding boundary defects, the numbers of total defects (black) are higher than that without a boundary. This can be explained by observation that a boundary vacancy, in addition to forming chain-like defect, can induce displacing of one nearest lattice atom and forms a small vacancy-interstitial-vacancy complex, which increases the vacancy numbers. At longer times, majority of these boundary defects will be removed through defect annihilation.
Methods
The MD simulations were performed by using LAMMPS (Large-scale Atomic Molecular Massively Parallel Simulator)22. In order to accurately describe Fe-Fe interactions at equilibrium separation distances and much closer distance when repulsive nucleon-nucleon interaction is significant, embedded-atom method (EAM) potential (Ref. 23) was smoothly connected to Ziegler-Biersack-Litmark (ZBL) potentials24. The Fe unit cell contains about 70000 atoms, and periodical boundary conditions are applied for cell surfaces. The atomic coordinates for the symmetric tilt grain boundary structures were generated using GB studio25.
To calculate the defect formation energies, the created cell was structurally relaxed through energy minimization. Then an interstitial or a vacancy was introduced in the region of interest and the second energy minimization was performed, to allow the point defect find its stable location. The formation energies of point defects are calculated by
and
where E1 is potential energy for the whole system, E2 is potential energy of system with one vacancy or one interstitial, and N is the total atom number in the system.
To model dynamic defect-boundary interactions, one interstitial and one vacancy were positioned at each side of boundary to avoid their annihilation. The defect-loaded cell was then relaxed through energy minimization. As a consequence of the energy minimization, introduced interstitial forms a dumbbell defect by displacing one lattice atom and forming an interstitial-vacancy-interstitial defect complex. At 450 K, simulations started under canonical (NVT) ensemble with moles (N), volume (V) and temperature (T) conserved. The selection of 450 K is able to obtain sufficient defect mobility. The starting of the step performing NVT corresponds to time t = 0 ps in Fig. 1. To avoid interference with thermal vibration, a vacancy is defined to exist when an empty lattice site has no atoms found in the radius of one third of lattice parameter (0.287 nm). The same radius is used to define interstitials if their displacements from the nearest lattice sites are larger than this value. The criterion is sensitive enough since the modeling can identify a dumbbell configuration. On the other hand, the radius is larger enough to avoid overestimation of defect numbers under thermal vibration. Further reducing the radius will increase statistic fluctuations of defect numbers but will not change the conclusion on chain like defect formation and its transport mechanism.
In MD simulations of repeating ion bombardments, a 3 keV Fe ion continuously hits the cell at an incident angle of 9° to avoid channeling ion irradiation. The damage cascade is roughly 0.5 nm away from the grain boundary. The time period between two successive ion bombardments is 100 ps. For irradiation in bulk Fe without grain boundary, this time period is much longer than the time required, typically a few picoseconds, to finish energy/heat dissipation and to form saturated defect population with stable defect clusters formed. For each ion bombardment, microcanonical ensemble (NVE, with the system isolated without heat exchange) was applied for the first 45 ps, followed by NVT for the rest of 55 ps, prior to introducing the next bombarding ion. This is necessary to avoid beam heating from energy contributed by the bombarding ions.
Author Contributions
D.C. performed the simulations of defect trapping and annihilation. J.W. performed the simulations on defect formation energies. T.C. performed the simulations of repeated ion bombardments. L.S. designed and guided the overall modeling activities, provided knowledge on data interpretation and drafted the manuscript. All authors discussed the results and commented on the manuscript.
Supplementary Material
Movie 1
Acknowledgments
This work was supported by National Science Foundation (US) under grant no. CMMI-0846835. We acknowledge the Texas A&M Supercomputing Facility (http://sc.tamu.edu/) for providing computing resources useful in conducting the research reported in this paper.
References
- Charit I. & Murty K. L. Structural materials issues for the next generation fission reactor. JOM 62, 67–74 (2010). [Google Scholar]
- Yvon P. & Carré F. Structural materials challenges for advanced reactor systems. J. Nucl. Mat. 385, 217–222 (2009). [Google Scholar]
- Rose M., Balogh A. G. & Hahn H. Instability of irradiation induced defects in nanostructured materials. Nucl. Instrum. Methods Phys. Res. B 127–128, 119–122 (1997). [Google Scholar]
- Chimi Y. Accumulation and recovery of defects in ion-irradiated nanocrystalline gold. J. Nucl. Mater. 297, 355–357 (2001). [Google Scholar]
- Nita N., Schaeublin R. & Victoria M. Impact of irradiation on the microstructure of nanocrystalline materials. J. Nucl. Mater. 329–333, 953–957 (2004). [Google Scholar]
- Wirth B. D., Bulatov V. & Diaz de la Rubia T. Atomistic simulation of stacking fault tetrahedral formation in Cu. J. Nucl. Mat. 283–287, 773–777 (2000). [Google Scholar]
- Arakawa K. et al. Observation of the One-Dimensional Diffusion of Nanometer-Sized Dislocation Loops. Science 318, 956–959 (2007). [DOI] [PubMed] [Google Scholar]
- Wirth B. D. How does radiation damage materials? Science 318, 923–924 (2007). [DOI] [PubMed] [Google Scholar]
- Soneda N. & Diaz de la Rubia T. Defect production, annealing kinetics and damage evolution in alpha-Fe: an atomic-scale computer simulation. Phil. Mag. A 78, 995–1019 (1998). [Google Scholar]
- Cawthorne C. & Fulton E. J. Voids in irradiated stainless steel. Nature 216, 575–576 (1967). [Google Scholar]
- Diaz de la Rubia T. et al. Multiscale modelling of plastic flow localization in irradiated materials. Nature 406, 871–874 (2000). [DOI] [PubMed] [Google Scholar]
- Singh B. N., Foreman A. J. E. & Trinkaus H. Radiation hardening revisited: role of intracascade clustering. J. Nucl. Mater. 249, 103–115 (1997). [Google Scholar]
- Demkowicz M. J., Hoagland R. G. & Hirth J. P. Interface structure and radiation damage resistance in Cu-Nb multilayer nanocomposites. Phys. Rev. Lett. 100, 136102 (2008). [DOI] [PubMed] [Google Scholar]
- Fu E. G., Misra A., Wang H., Shao L. & Zhang X. Interface enabled defects reduction in helium ion irradiated Cu/V nanolayers. J. Nucl. Mater. 407, 178–188 (2010). [Google Scholar]
- Bai X-M. et al. Efficient annealing of radiation damage near grain boundaries via interstitial emission. Science 327, 1631–1634 (2010). [DOI] [PubMed] [Google Scholar]
- Samaras M., Derlet P. M., Swygenhoven H. V. & Victoria M. Computer simulation of displacement cascade in nanocrystalline Ni. Phys. Rev. Lett 88, 125505 (2002). [DOI] [PubMed] [Google Scholar]
- McClintock D. A., Sokolov M. A., Hoelzer D. T. & Nanstad R. K. Mechanical properties of irradiated ODS-EUROFER and nanocluster strengthened 14YWT. J. Nucl. Mater. 392, 353–359 (2009). [Google Scholar]
- Saldana C., Murthy T. G., Shankar M. R., Stach E. A. & Chandrasekar S. Stabilizing nanostructured materials by coherent nanotwins and their grain boundary triple junction drag. Appl. Phys. Lett. 94, 021910 (2009). [Google Scholar]
- Chookajorn T., Murdoch H. A. & Schuh C. A. Design of stable nanocrystalline alloys. Science 337, 951–954 (2012). [DOI] [PubMed] [Google Scholar]
- Paneth H. R. The mechanism of self-diffusion in alkali metals. Phys. Rev. 80, 708–711 (1950). [Google Scholar]
- Chen D. & Shao L. Molecular dynamics simulation of ion focusing and crowdion formation in self-ion-irradiated Fe. Nucl. Instrum. Methods Phys. Res. B 272, 33–36 (2012). [Google Scholar]
- Plimpton S. J. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 117, 1–19 (1995). [Google Scholar]
- Mendelev M. I. et al. Development of new interatomic potentials appropriate for crystalline and liquid iron. Phil. Mag. 83, 3977–3994 (2003). [Google Scholar]
- Ziegler J. F. & Biersack J. P. The stopping and range of ions in solids. Springer Series in Electronics 10, 122–156 (1982). [Google Scholar]
- Ogawa H. GBstudio: a builder software on periodic models of CSL boundaries for molecular simulation. Materials Transactions 47, 2706–2710 (2006). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Movie 1