Detection of Acoustic Temporal Fine Structure by Cochlear Implant Listeners: Behavioral Results and Computational Modeling

Abstract

A test of within-channel detection of acoustic temporal fine structure (aTFS) cues is presented. Eight cochlear implant listeners (CI) were asked to discriminate between two Schroeder-phase (SP) complexes using a two-alternative, forced-choice task. Because differences between the acoustic stimuli are primarily constrained to their aTFS, successful discrimination reflects a combination of the subjects’ perception of and the strategy’s ability to deliver aTFS cues.

Subjects were mapped with single-channel Continuous Interleaved Sampling (CIS) and Simultaneous Analog Stimulation (SAS) strategies. To compare within- and across- channel delivery of aTFS cues, a 16-channel clinical HiRes strategy was also fitted. Throughout testing, SAS consistently outperformed the CIS strategy (p ≤ 0.002). For SP stimuli with F₀ =50 Hz, the highest discrimination scores were achieved with the HiRes encoding, followed by scores with the SAS and the CIS strategies, respectively. At 200 Hz, single-channel SAS performed better than HiRes (p = 0.022), demonstrating that under a more challenging testing condition, discrimination performance with a single-channel analog encoding can exceed that of a 16-channel pulsatile strategy.

To better understand the intermediate steps of discrimination, a biophysical model was used to examine the neural discharges evoked by the SP stimuli. Discrimination estimates calculated from simulated neural responses successfully tracked the behavioral performance trends of single-channel CI listeners.

1. Introduction

Despite good speech perception in quiet, cochlear implant (CI) users have great difficulty perceiving speech in the presence of fluctuating background noise (Kang et al., 2009; Lorenzi et al., 2006; Nelson et al., 2003; Qin and Oxenham, 2003; Zeng et al., 2005). Furthermore, CI listeners perform worse than normal-hearing listeners on tests of binaural sound localization, pitch perception, and melody recognition (Gfeller et al., 2002; Jung et al., 2010; Kong et al., 2004; Smith et al., 2002; Spahr and Dorman, 2004; Drennan et al., 2008; Zeng et al., 2004). A number of studies suggest that acoustic temporal fine structure (aTFS; rapid variations in the acoustic pressure) is an important cue necessary for good performance on the above tasks (Hopkins et al., 2008; Moore, 2008; Smith et al., 2002; Xu and Pfingst, 2003; Sheft et al., 2008).

Poor perception of aTFS by CI users is in part due to the pulsatile strategies currently used in the clinical setting: these strategies do not explicitly encode temporal fine structure of the ambient sounds. Instead, they divide the incoming audio signal into several channels (frequency bands), discard the TFS, and encode only the slowly-varying amplitude – the temporal envelope – of each channel. A certain amount of fine structure may be still be conveyed to the CI users, however, as a byproduct of signal processing. This can occur in two ways: either within-channel, as a discharge pattern within auditory nerve fibers; or across-channel, by varying the location of neural discharges along the length of the cochlea (Drennan et al., 2008; Wilson and Dorman, 2008). If a broadband, flat-envelope stimulus is supplied as an input to the CI processor, some aTFS may be perceived by the listener as a within-channel pitch cue because of processor–created changes in the narrow-band envelope of the electric waveform (Ghitza, 2001; Gilbert and Lorenzi, 2006; Zeng et al., 2004). Yet, only low-frequency TFS cues may be delivered in such a way — the CI users are often unable to follow temporal envelope modulations above 300 Hz (Shannon, 1992; Townshend et al., 1987; Zeng, 2002). Alternatively, fine structure information may be represented as an across-channel, “channel balance”, cue that arises when closely-spaced electrodes are stimulated in a rapid sequence (e.g., Fig. 9; (Dorman et al., 1996; Kwon and van den Honert, 2006; McDermott and McKay, 1994; Nobbe et al., 2007)). While it is unclear how much of the acoustic fine structure information is conveyed by each of the mechanisms (Wilson and Dorman, 2008), the aggregate amount is considerably less than what is available to normal-hearing (NH) listeners.

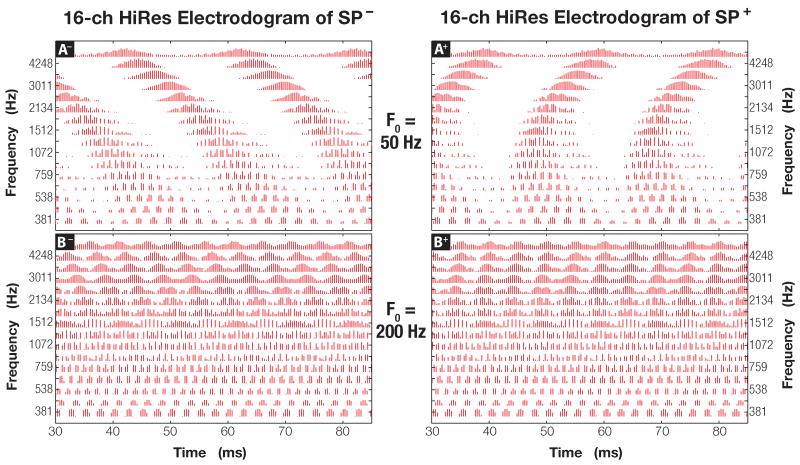
Figure 9.

An electrodogram showing multi-channel HiRes encoding of a negative (left column) and a positive (right column) Schroeder-phase signal with F₀ = 50 and 200 Hz (top and bottom, respectively). Biphasic pulses are plotted as vertical lines in the graph. The y-axis shows center frequencies of each of the 16 electrodes (e.g., 381 Hz corresponds to the apical-most electrode #1).

To improve the design of new sound-encoding strategies, a quantitative test measuring how well aTFS cues are delivered to CI users is needed. In 2008, Drennan et al. developed a two-alternative, forced-choice (2AFC) task that measures CI listeners’ ability to discriminate across-channel changes in acoustic temporal fine structure of Schroeder-phase stimuli. The test is straightforward and can efficiently evaluate multi-channel CI sound-encoding strategies (Drennan et al., 2010): it is nonlinguistic, is relatively brief (~ 20 minutes per administration), has a good test-retest reliability, and is moderately correlated with speech perception in CI users (Drennan et al., 2008). Most importantly, however, is that the differences between positive and negative Schroeder-phase stimuli are primarily constrained to the signals’ aTFS; opposite-phase signals have perceptually-indistinguishable envelopes (Lauer et al., 2009) and identical long-term spectra. Consequently, discrimination performance measured with acoustic Schroeder-phase stimuli reflects the ability of the encoding strategy to convey aTFS differences to the CI listeners as well as the listeners’ ability to detect the strategy’s cues.

In the following, we describe an analogous test to measure sensitivity of cochlear implant listeners to changes in acoustic TFS. However, instead of measuring temporal cues across multiple channels, as is done by Drennan et al. (2008), we propose to measure how well acoustic temporal fine structure is delivered within a single channel. This modification allows us to compare how well aTFS cues are delivered within-channel, rather than across-channel. We hypothesize that if a signal-processing strategy improves within-channel encoding of aTFS, then this improvement would be reflected by the test results.

To evaluate this hypothesis, two complementary approaches were pursued. First, we measured the discrimination performance of the cochlear implant subjects using two single-channel sound encoding strategies. Second, we simulated responses of the auditory nerve (AN) fibers to the encoded stimuli using a computational model. Whereas the first approach reflects how well the aTFS cues are ultimately perceived by the cochlear implant listeners, modeling provides an insight on how these cues are represented during the intermediate steps of perception, on the level of neural impulses along the AN fibers (e.g., Heinz et al., 2001; Heinz and Swaminathan, 2009). By evaluating the discrimination task with this two-pronged approach, we become better-informed about where and how the majority of the fine structure cues are lost — whether they are discarded during sound encoding, during the conversion of electrical stimuli into neural responses, or whether aTFS cues are lost during the downstream processing stages of the auditory pathway.

In addition to measuring Schroeder-phase discrimination with single-channel strategies, we also measured listeners’ performance with 16-channel HiResolution–P or –S clinical strategies (–paired or –sequential, respectively; Advanced Bionics Corp., Valencia, CA). These additional data allow us to evaluate how listeners’ scores change if the aTFS cues are delivered via both across- and within- channel mechanisms.

2. Methods

2.1. Behavioral

2.1.1. Listeners

Eight postlingually-deafened adult cochlear implant users participated in this study. Listeners’ age ranged from 32 to 77 years of age, with a mean age of 58 years. On average, the subjects had 5.2 years of hearing loss and 4.5 years of experience with their implants. The etiology of the subjects’ hearing loss varied, with the most frequent cause cited as “unknown”. A summary of the participants’ information is provided in Table 1. Clinically, all subjects used either the Advanced Bionics CII Bionic Ear® or the HiRes 90K® device. This study was approved by the University of Washington Institutional Review Board.

Table 1.

Demographic data of participating CI listeners. Multi-channel strategy to measure across-channel delivery of TFS was set closest to the subject’s clinical strategy (see “Methods” for details). Subject S52 did not test with multi-channel strategy.

Subject	Gender	Age	Years of Hearing Loss	Years with Implant	Etiology	Multi-channel Strategy Used
S34	M	55	5	3	Noise exposure	HiRes-S
S48	F	67	10	1.5	Familial	HiRes-P
S52	M	77	0.1	1	Noise exposure	HiRes-S
S58	M	64	7	7	Noise exposure, antibiotics	HiRes-P
S59	M	47	12	2.5	Unknown	HiRes-S
S62	F	32	3	1	Unknown	HiRes-S
S65	F	56	2	7	Unknown	HiRes-S
S66	F	66	2.5	13	Unknown	HiRes-S
S71	F	72	16	3	Autoimmune	HiRes-S
S80	M	60	2	2	Otosclerosis	N/A
S84	M	48	0	1.5	Familial	N/A
Average:	M: 6, F: 5	58.5	5.4	3.9

2.1.2. Fitting Procedure & Encoding Parameters

Prior to administering the test, an experienced implant audiologist created single-channel maps on a Platinum Series™ Sound Processor (PSP; Advanced Bionics Corp., Sylmar, CA) using a clinical processor interface and the SClin 2000™ Software Suite v1.08.

Two single-channel encoding strategies were mapped for each of the subjects: 1) Continuous Interleaved Sampling (CIS; Wilson et al., 1991), and 2) Simultaneous Analog Stimulation (SAS; e.g., Nie et al., 2008b). For each strategy, all channels on the sound processor were turned off, except for the one to be tested. Either the apical-most, 1^st channel, chosen because TFS is naturally perceived in the lower-frequency region of the cochlea, or the middle channel (4^th, chosen to measure discrimination in a different location of the cochlea) was used for fitting and stimulation. Thus, during the testing, stimuli for each listener were presented under the following conditions, in random order: CIS encoding strategy active on either the 1^st or the 4^th channel of the implant electrode; or the SAS strategy active on either of the same channels. Results for multi-channel testing with the HiResolution strategy (HiRes; e.g., Firszt, 2003; Koch et al., 2004) were collected during a separate session, after a brief fitting procedure described below.

2.1.3. Single-channel CIS Settings

Although all of the listeners had a 16–electrode implant device (either Advanced Bionics CII or 90K), the SClin fitting software could only generate programs with a maximum of eight channels. Therefore, when monopolar mode with odd coupling was used with the CIS encoding, channel 4 activated electrode 7, approximately mid-way on the electrode array, and channel 1 stimulated the apical-most electrode 1.

Behavioral threshold (T) and maximum comfortable loudness (M) levels were measured on each channel using default timing durations for pulsatile, monopolar measurements (M-level: 50 μs, T-level: 200 μs, inter-stimulus time: 1000 μs). Threshold level was determined by adaptively tracking a 50% detection rate, as indicated by the listener’s feedback. Comfort levels were established by asking each study participant to track loudness until they judged the stimulation to be “loud, but comfortable”. One independent CIS program was generated for each test electrode and then uploaded to the PSP.

On either channel, a 350 to 5500 Hz bandpass filter with a center frequency of 1652 Hz (SClin’s default for one-channel maps) was used to preprocess the incoming audio. A half-wave, instead of a full-wave rectifier was used to avoid frequency-doubling effects during the envelope extraction. To represent rapid variations in the envelope with minimal distortions, the pulse rate of the stimuli was set to 3250 Hz (cathodic phase first). The duration of each pulse was 75 μs, and no gap was present between cathodic and anodic pulses. Prior to testing, volume and sensitivity knobs on the processor were set to the 12 o’clock orientation, approximately mid-way of their range.

2.1.4. Single-channel SAS Settings

Programs for SAS were created analogously. However, instead of monopolar stimulation, in the analog programs, we used the BP+0 bipolar stimulation mode. This was necessary because the excitation threshold for monopolar analog stimulation is below the stimulus resolution of the Advanced Bionics current sources, and thus, the SClin 2000™ software allows only bipolar stimulation to be used with the SAS strategy. Consequently, the middle channel used electrode 8 as ground and stimulated on electrode 7, while the apical-most channel 1 activated electrodes 1 (output) and 2 (ground). Timing parameters for fitting SAS were set as follows: 1000- μs duration for M- and T-levels, and 200- μs inter-stimulus time.

Encoding parameters for SAS were chosen to correspond as closely as possible to those used for CIS. Bandpass filter on the active channel spanned 250 to 5500 Hz, with the center frequency of 1652 Hz. The stimulation rate was set to 11,375 Hz, which corresponds to an 87.912 μs–wide “sample-and-hold” digitisation of the input sound.

2.1.5. Multi-channel HiRes Settings

If the listener was clinically using HiRes-S or HiRes-P, no fitting of the multi-channel strategy was performed prior to test administration. However, if either Fidelity120-S or Fidelity120-P was used, the subject’s speech processor was connected to the SoundWave™ program (v1.1.38, by Advanced Bionics Corp.) and the clinical map residing on the processor was downloaded. The Fidelity120 feature (Litvak et al., 2003; Trautwein, 2006) was disabled to create either a HiRes-S or a HiRes-P map, the program was turned on “live”, and global changes were made to the M-levels until the patient judged the loudness of the program to be “loud, but comfortable”. The multi-channel programs were subsequently saved and uploaded to the PSP. Assignments of paired or sequential HiRes strategies used for multi-channel testing are listed in Table 1.

2.1.6. Test Stimuli

Schroeder-phase (SP) harmonic stimuli were chosen to test subjects’ detection of acoustic temporal fine structure because the positive– and the negative– phase complexes differ in their TFS, with both signals exhibiting identical spectral content and minimal envelope differences (Schroeder, 1970). Test stimuli used in this study were generated in a manner identical to that described by Drennan et al. (2008). Specifically, each SP frequency sweep was generated by summing N equal-amplitude cosine harmonics from the fundamental frequency (F₀) to 5 kHz. The phase q_n of each n^th harmonic was set as follows:

$$q_n=\pm p\cdot n(n+1)∕N,$$

where either a plus or a minus was used to construct a positive or a negative Schroeder-phase signal, respectively. Because the period of each SP frequency sweep is either 20 or 5 ms in duration (for F₀ = 50 Hz and 200 Hz signals, respectively), the sweeps were replicated and concatenated until a 500 ms test stimulus was created. To minimize onset and offset cues of the test stimuli, the starting point of the generated stimulus was randomly shifted and multiplied by a 500 ms constant-amplitude window with a 10 ms linear onset and offset.

Increasing the fundamental frequency of the generated stimuli while keeping the signal’s frequency sweep range fixed decreases the differences between positive and negative Schroeder complexes (Dooling et al., 2002). To assess a wide range of CI listeners’ performance during the discrimination test, we elected to generate stimuli with fundamental frequencies of 50 and 200 Hz. Performance scores at these frequencies have been shown to predict a variety of clinical outcome measures and to reflect the changes in the sound processors (Drennan et al., 2010). Additionally, using these two fundamental frequencies makes it possible to compare single-channel results gathered in this study to those published earlier (e.g., Dooling et al., 2002; Drennan et al., 2008).

2.1.7. Test Administration

The test was administered in a sound-attenuating IAC booth. A program written in MATLAB (MathWorks Inc., Natick, MA) played sound stimuli to the cochlear implant user and recorded the listener’s selection via a graphical user interface. Sounds were played through an Apple PowerMacG5 sound card connected to a Crown D45 amplifier (Crown Int’l; Elkhart, IN) and a free-standing studio monitor (B&W DM303 speaker from Bowers & Wilkins, North Reading, MA) placed at head level, 1 m in front of the listener (0° azimuth).

Each trial consisted of four 500-ms test stimuli interleaved with 100 ms of silence, with three of the four stimuli presenting a negative Schroeder-phase and the remaining stimulus presenting a positive phase. At the onset of this four-interval, 2AFC test the listeners were instructed to discriminate Schroeder-phase complex pairs by identifying which of the two intervals – the second or the third one – corresponded to a sound different from the other three intervals. After each decision, visual feedback of the correct answer was provided to the listener. For each of the five processor maps (i.e., CIS1, CIS4, SAS1, SAS4, and the multi-channel HiRes), and every fundamental frequency (50 Hz or 200 Hz), a single administration of the test consisted of one short training block followed by a total of 144 discrimination tasks, grouped into six test blocks of 24 trials. The dependent variable measured was percent of correct identifications of the positive-phase stimuli.

2.1.8. Measuring Effects of Level Roving

To examine the effects of loudness on single–channel Schroeder phase discrimination, four subjects (S48, S71, S80, and S84) participated in tests where the presentation level of the stimuli was roved either 0 or 6 dB (i.e., the intensity of the stimulus varied either 0 dB or ±3 dB). The roving test was administered for SAS and CIS strategies at F₀ =50 Hz and F₀ =200 Hz. Because tests with level roving were conducted after non–roved data was already collected and effect of the stimulating electrode was determined not to be significant, all of the roving stimuli were supplied on the 4th electrode. This caveat aside, the roving test was conducted in the same manner as its non–roving counterpart, described above.

2.1.9. Analysis of Results

Percent correct was calculated from the mean score of six test blocks for each fundamental frequency/testing condition pair (e.g., CIS1 @ F₀ =50 Hz, CIS4 @ 50 Hz, SAS1 @ 50 Hz, SAS4 @ 50 Hz, CIS1 @ 200 Hz, …, SAS4 @ 200 Hz) and for each subject. Block scores were calculated by averaging the discrimination scores of 24 stimulus presentations that comprised each individual test block. To examine the effect of within- and across- channel delivery of aTFS cues, paired t-tests between CIS, SAS, and HiRes scores at 50 and 200 Hz were performed. The effect of the stimulation channel, the fundamental frequency, and single-channel sound-encoding strategy was evaluated with a 2×2×2 repeated-measures ANOVA.

2.2. Computational Modeling

To estimate the amount of acoustic temporal fine structure conveyed to the auditory nerve, the electrical output of the sound processor in response to the audio stimuli was recorded and membrane potentials along the auditory nerve fibers were simulated. Our aim was to learn whether neural responses evoked by processor-encoded SP complexes presented a bottleneck in subjects’ discrimination of the opposite-phase stimuli and whether discrimination estimates based on the simulated spiketrains could follow listeners’ performance.

2.2.1. Rationale for Modeling Spiral Ganglion Cells

There are several reasons why auditory nerve fibers were chosen for modeling. Firstly, the anatomic properties and electrophysiological response of spiral ganglion cells (SGCs) have been studied in detail (e.g., Arnesen and Osen, 1978; Hu et al., 2010; Liberman and Oliver, 1984; Matsuoka, 2000; Miller et al., 2001; Runge-Samuelson et al., 2004). Secondly, Type I SGCs present the locus where electrical stimuli from the CI processor are first converted into neural potentials; spiral ganglion cells are the sole source of audio information to the brain. From the principles of information theory, no additional information about the stimuli can be created de novo through subsequent processing: the nervous system can transform the sensory information it receives from SGCs, perform computations on it, or manipulate it in other ways, but no new information can be created as a result (Cover and Thomas, 1991, ; pg. 576). Neural responses of the spiral ganglion cells constrain the amount of auditory information that is available to the brain and thus provide an upper bound on potential discrimination performance of CI listeners. Thus, the similarity of spike trains evoked by the test stimuli could be used to estimate discrimination performance of an ideal observer (e.g., Wohlgemuth and Ronacher, 2007). Furthermore, we hypothesized that neural responses from a population of peripheral auditory fibers capture the majority of the informational content used by the CI listeners to discriminate processor-encoded Schroeder-phase stimuli.

2.2.2. Description of the Model

Each neural fiber is modeled by a passive resistor-capacitor network at the myelinated internodes, and the nodes of Ranvier are represented by stochastic, voltage-dependent channels (Na, K_fast, and K_slow), a leakage current, and membrane capacitance. Morphology of the model is spatially-distributed and is based on a typical Felis catus Type I spiral ganglion cell. The model replicates a number of physiological properties of a single fiber – relative spread, spike latency and jitter, chronaxie, relative refractory period, and conduction velocity – within 10% of that measured in vivo (cf. Imennov and Rubinstein, 2009). Furthermore, a population of diameter-distributed model fibers successfully matches response characteristics of the same number of in vivo fibers. Due to the computational cost of modeling neural responses to behavioral stimuli, we used 25 diameter-distributed fibers during our simulations. As in prior studies, the diameters of the fibers were sampled from a Gaussian distribution with the mean of 2.0 μm and 0.5 μm standard deviation. Details on implementation of the model are presented by Mino et al. (2004), while an in-depth description of the model’s parameters and its physiological response properties is provided by Imennov and Rubinstein (2009).

2.2.3. Stimuli Acquisition

Current discharge waveforms supplied as an input to the model were acquired from the CI processor used in the behavioral part of the study. Because the model provides an upper bound on listeners’ performance, we wanted to minimize the limitations imposed by a particularly poorly-performing user and thus programmed the CI processor with the map of our best-performing user, S65. To measure voltage with maximum precision, the manual volume control on the processor was set to the maximum (3 o’clock). This increased the current output of the electrode without altering the automatic gain control (AGC) settings of the device. After digitization, the increased amplitude of the acquired signal was compensated for by lowering the current density of the model electrode until about half of the model fibers responded to the supplied CIS and SAS stimuli. The manual sensitivity control knob on the body-worn processor was set to the same position as in behavioral testing, at 12 o’clock.

For acquisition, the CI processor was placed inside the sound booth, in approximately the same location as the subject’s head. All of the acquisition equipment, except for the Implant-In-a-Box connected to the head coil on the PSP, was placed outside of the booth. Voltage output of the active channel was sampled at 2.5 MHz using the Tektronix MSO4000 oscilloscope (Tektronix Corp., Richardson, TX). The acquired waveform was then used to drive the current output of a spherical, monopolar electrode in the computational model. Because the model does not simulate electrical field interactions from multiple electrodes, no modeling of the multi-channel strategy was conducted in this study.

2.2.4. Estimating Discriminability of Neural Responses

Unlike the task of calculating informational capacity of an engineered system (Shannon and Weaver, 1949), quantifying discrimination performance of a biological system is more appropriately handled by a metric-driven signal detection procedure (Grewe et al., 2007; Thomson and Kristan, 2005). To estimate the discriminability of processor-encoded stimuli from the neural responses, we followed an approach similar to the one utilized by de Ruyter Van Steveninck and Bialek (1995). Although there are a number of distance metrics which can be used to quantitatively measure the similarities of spike trains (cf. Houghton and Sen, 2008; van Rossum, 2001; Victor, 2005), we opted to use a “direct” method (de Ruyter Van Steveninck and Bialek, 1995), closest to the Hamming distance (Hamming, 1950). It makes the least number of assumptions about the underlying neural code (Rieke et al., 1997), needs only a single parameter, bin width, and is the simplest applicable approach (spike count, which is simpler, is unsuitable for time-sensitive stimuli (Joris and Yin, 1992; Machens et al., 2001)).

The discriminability of neural responses was estimated as follows. First, spike times of each fiber were discretised with bin width Δτ, such that if any spikes occurred in the i^th time interval [i*Δτ, i*Δτ+Δτ], the i^th bin in the discretised spike train would be assigned a “1”. Conversely, if no spikes were recorded during a time interval, the corresponding bin would be set to “0”.

Given a particular discretised spike train, the estimation procedure must decide which stimulus — the positive– or the negative– phase Schroeder signal — evoked the observed response. Because presentation of either of the stimuli is equally likely, the estimation method that will give the maximum fraction of correct decisions is maximum likelihood (Green and Swets, 1966; Rieke et al., 1997; Dayan and Abbott, 2001). Having observed a particular spike train Q, we can calculate the probability of correctly identifying positive Schroeder-phase stimulus, P_c(SP⁺), as the source of the spike train by summing over the set of all possible firing patterns {Q}:

$${\mathrm{P}}_{\mathrm{c}}\left({\mathrm{SP}}^{+}\right)=\sum _{\left\{Q\right\}}\mathrm{P}(Q\mid {\mathrm{SP}}^{+})\cdot \mathrm{H}\left[\mathrm{P}\right(Q\mid {\mathrm{SP}}^{+})-\mathrm{P}(Q\mid {\mathrm{SP}}^{-}\left)\right],$$

where H[−] is the Heaviside step function (NIST, 2010). Swapping SP⁻ for SP⁺ yields the percentage of correct negative-phase identifications. The fraction of correct judgments for the discrimination task is then P_c(SP⁺, SP⁻) = [P_c(SP⁺) + P_c(SP⁻)]/2 (Rieke et al., 1997). This fraction was calculated for each modeled fiber, and fibers’ aggregate mean was subsequently compared to the “percent correct” score obtained during behavioral testing.

To maintain parity with behavioral testing, discrimination estimates were computed from neural output evoked by 500-ms –long test stimuli. Temporal patterns in response to individual SP sweeps (20 ms in duration for F₀ =50 Hz and 5 ms for 200 Hz) within each 500-ms test stimulus were ergodic^*, which allowed us to build an ensemble of neural responses {Q} from a single test stimulus. Correspondingly, depending on the fundamental frequency, either 25 (= 500 ms/20 ms) or 100 (= 500 ms/5 ms) –element ensemble was produced during each model run. To generate several P_c(SP⁺, SP⁻) estimates, 21 model (i.e., Monte Carlo) runs were executed. Despite a considerable number of trials conducted in this computational study (525 = 25 · 21 and 2100 = 100 · 21, depending on F₀), we did not sample the entire set of the possible response patterns. However, our experimentation has shown that adding more trials to the discrimination procedure did not have a marked effect on the performance estimates.

All experimental conditions used in single-channel behavioral tasks (CIS or SAS encoding of SP^+/− at 50 and 200 Hz) were modeled and then supplied to the estimation routines.

3. Results

3.1. Behavioral Tasks

All subjects but one completed the full battery of non-roving, single-channel tests. Subject S52 did not like the sound of SAS and thus did not use the analog strategy. Four subjects, S48, S71, S80, and S84, also participated in tests where the level of the single-channel stimuli was roved. Of these four subjects, S71, S80, and S84 did not complete multi-channel HiRes testing due to time constraints.

3.1.1. Stimuli Without Level Roving

Subjects’ discrimination performance with single-channel strategies and non-roving stimuli is shown in Figs. 1 and 2 (fundamental frequencies of 50 and 200 Hz, respectively). Because the stimulation channel did not produce any effect on the listeners’ scores (p = 0.9993), results for the two channels were pooled together. Note how behavioral results compare to chance performance (50% on a 2AFC task) and the 95% confidence interval expected of 144 (=6 blocks * 24 trials) binomially-distributed stimulus presentations, indicated by the shaded region surrounding the 50% line in the figures. Both figures exhibit a common trend: subjects’ Schroeder-phase discrimination scores with the SAS strategy are consistently better than with the CIS strategy.

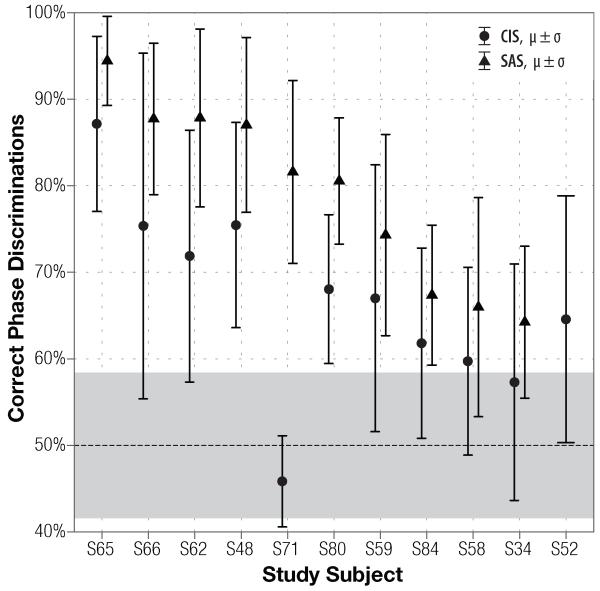
Figure 1.

Subjects’ discrimination of non-roving 50 Hz Schroeder-phase stimuli using single-channel CIS (filled circles) and SAS (triangles) encoding strategies. Average score and standard deviation are plotted for each subject. At-chance performance is 50%, grey shading around it indicates 95% confidence interval expected on 144 binomially–distributed trials. Subject S52 did not test with the SAS strategy.

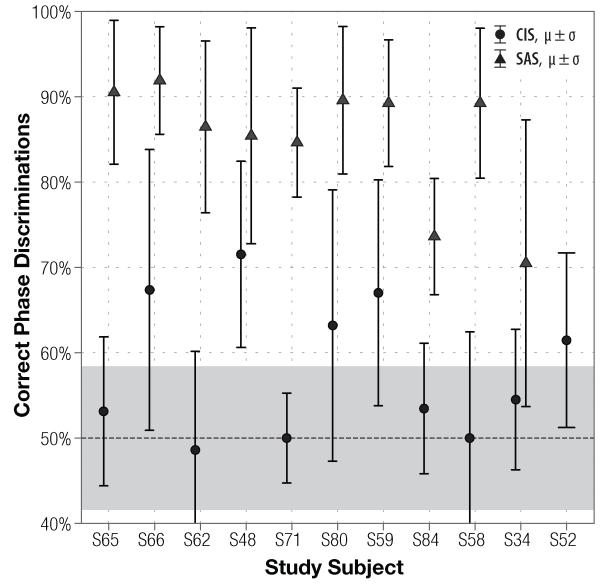
Figure 2.

Subjects’ discrimination of non-roving 200 Hz Schroeder-phase stimuli using single-channel CIS (filled circles) and SAS (triangles) encoding strategies. Plot layout and legend is identical to those in Fig. 1. Subject S52 did not test with the SAS strategy.

Broad distribution of the results demonstrates that the task is well-suited to measuring a range of discrimination abilities: at the fundamental frequency of 50 Hz, scores with CIS and SAS strategies span from 46% to 87% and from 64% to 94% percent correct, respectively. Comparatively, scores at 200 Hz (Fig. 2) span a narrower range: with CIS, subjects scored as low as 48% and as high as 72%, and with SAS, scores varied from 70% to 92%. Although SAS scores appear to be higher at 200 Hz than at 50 Hz, the difference is not statistically significant (p = 0.128).

A 2×2×2 repeated-measures ANOVA was performed to measure associations among single-channel strategies (CIS or SAS), stimulation channels (1 or 4), and the fundamental frequencies (50 or 200 Hz). Encoding strategy and F₀ were found to be statistically-significantly associated with discrimination performance (p = 0.004 and p = 0.024, respectively). Additionally, we detected an interaction between encoding strategy and fundamental frequency (p = 0.033; Table 2); therefore, our summary of the strategies’ performance in Table 3 is separated by fundamental frequency.

Table 2.

Repeated measures ANOVA results for non-roving stimululus presentations.

Factor	p-value
channel	0.9999
strategy	0.0043 **
F0	0.0244 *
channel : strategy	0.5091
channel : F0	0.4631
strategy : F0	0.0331 *
channel : strategy * F0	0.7936

Significance codes are:

^*for p ≤ 0.05,

^**for p ≤ 0 01.

Table 3.

Comparison of multi-channel HiRes performance to single-channel results under the no-rove condition. For each fundamental frequency, first row lists percent of correct discriminations with a given strategy, second row shows t-test scores of neighboring strategies, and third row lists t-test scores of the CIS/SAS strategies. Significant differences with p-values < 0.05 are listed in bold.

	CIS	HiRes	SAS
	68.4%	86.0%	81.1%
F0 = 50 Hz	p = 0.013		p= 0.428
	p = 0.002
	59.3%	68.0%	86.1%
F0 = 200 Hz	p = 0.212		p= 0.022
	p = 0.001

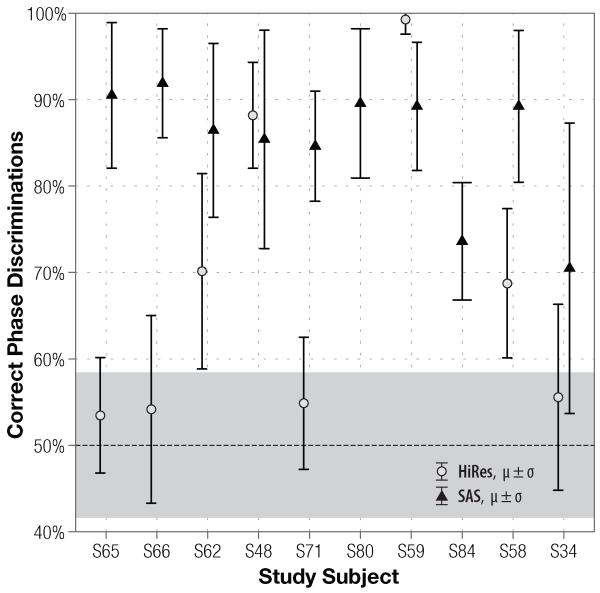
Discrimination of Schroeder-phase with a 16-channel HiRes map is compared to the subjects’ results with a single-channel SAS map in Fig. 3 (F₀ =50 Hz) and Fig. 4 (F₀ =200 Hz). Because CIS performance was consistently worse than that of SAS, and these results were already presented in prior figures, CIS scores were omitted from Figs. 3 and 4 for clarity. To determine if the differences between the stimulation strategies are significant, we analyzed the population data with a paired t-test, as shown in Table 3.

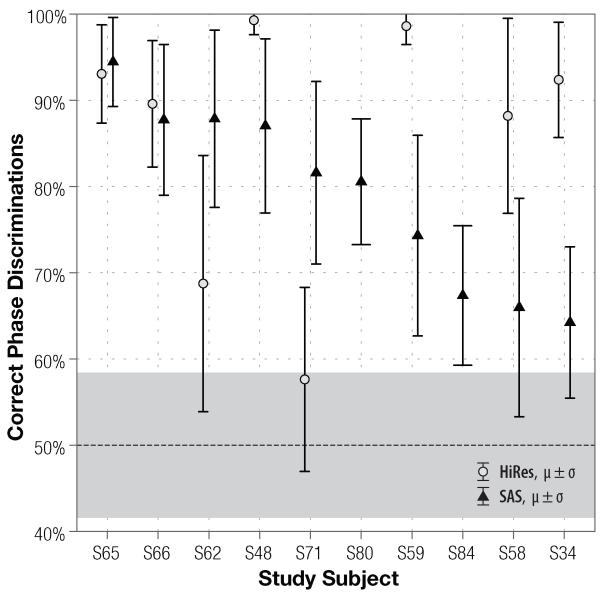
Figure 3.

Comparison of subjects’ discrimination performance of 50-Hz stimuli using single–channel SAS (triangles) and multi–channel HiRes (light circles) strategies. Average score and standard deviation are plotted for each subject. At-chance performance is 50%, grey shading around it indicates 95% confidence interval expected on 144 binomially–distributed trials.

Figure 4.

Comparison of subjects’ discrimination performance of 200-Hz stimuli using single-channel SAS (triangles) and multi-channel HiRes (light circles) strategies. Legend and layout are identical to the ones used in the previous figure.

On average, at F₀ =50 Hz, 16-channel HiRes yielded significantly (p = 0.013) better performance than the single-channel CIS, but not the SAS strategy (p = 0.428). Once the fundamental frequency was raised to 200 Hz, performance ranking changed: HiRes performed just was well as CIS (p = 0.212), but subjects using single-channel SAS scored higher than with the 16-channel HiRes strategy (86.1% vs. 68.0%). Statistically, the SAS improvement over HiRes is significant at the 0.05 level (p = 0.022). Moreover, the significance between the different scores persists even once the α level is adjusted for multiple comparisons.

Paired t-tests did not show any statistically-significant differences between subjects’ performance on the first and the last test blocks for any of the strategies (CIS, SAS, or the HiRes). This leads us to conclude that, similar to the multi-channel version of the test (Drennan et al., 2008), there are no significant training effects on the within-channel SP discrimination task.

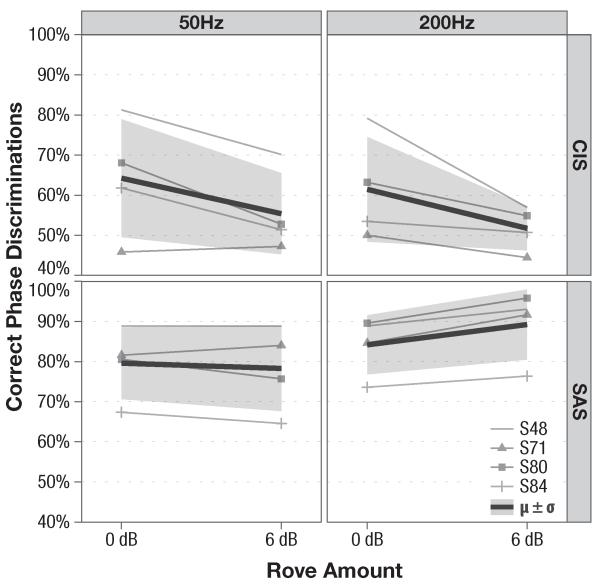
3.1.2. Effects of Level Roving

Effects of roving are shown in Fig. 5. Mean intra-subject performance is graphed as individual lines (see legend, inset in lower right corner of the figure). The thick black line plots the aggregate, inter-subject performance on the test, while the shading surrounding the black line corresponds to one standard deviation of the aggregate data. Overall, roving the level did not have a statistically–significant effect on subjects’ performance, suggesting that the level cues were not used to discriminate the test stimuli. Although roving the level of the CIS stimuli appears to decrease subjects’ discrimination scores (64.2% and 61.5% vs. 55.4% and 51.7% at 50 and 200 Hz, respectively), this decrease is not statistically-significant (p = 0.364 and p = 0.241 at F₀ =50 and 200 Hz). Analogously, SAS remained unaffected by the 6 dB rove at 50 Hz and at 200 Hz (p = 0.858 and p = 0.411, respectively).

Figure 5.

Effects of level roving on subjects’ discrimination performance using single-channel SAS and CIS strategies. Mean intra–subject scores are marked with thin lines and shapes displayed in the inset legend (lower right), while the overall, inter–subject performance is plotted as a thick black line, surrounded by a shaded region, whose height corresponds to ± standard deviation.

3.2. Modeling

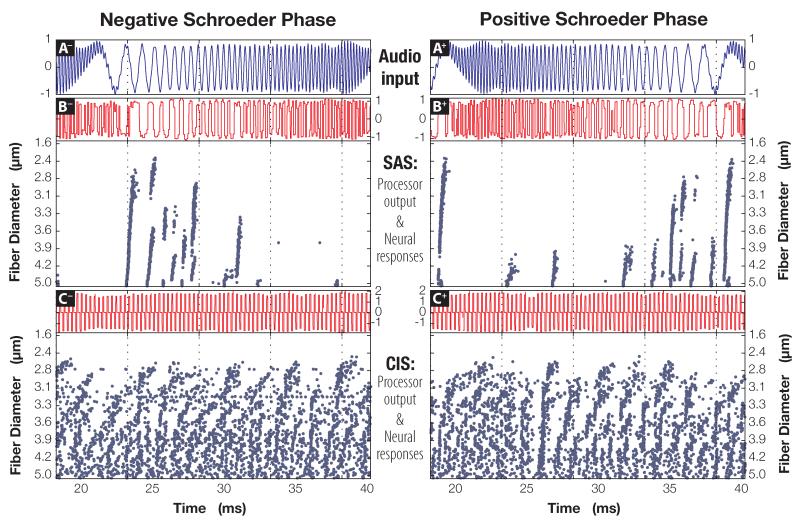
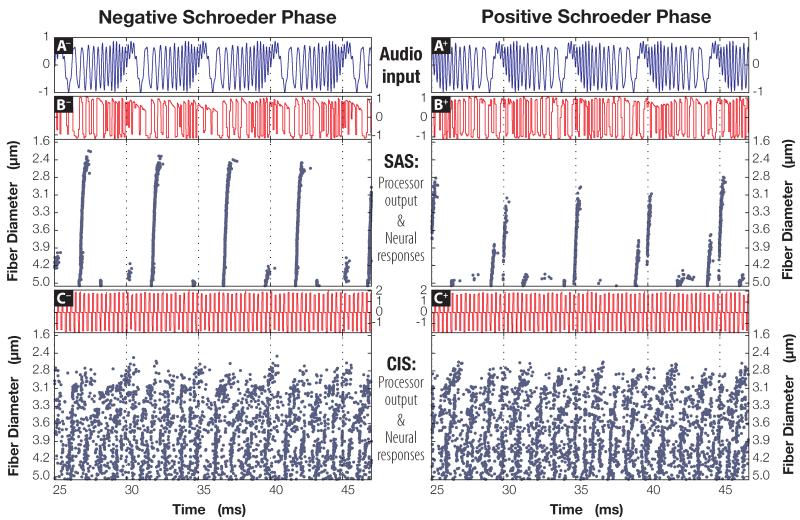
The cochlear implant output from four sound stimuli (F₀ =50 or 200 Hz; negative or positive Schroeder phase) encoded with either the CIS or the SAS strategy were used as an input to the neural model (cf. “Methods” section). Acoustic signals with the fundamental frequencies of 50 Hz and 200 Hz, the processor output, and the corresponding neural responses are shown in Figs. 6 and 7, respectively. To display the stimuli and the neural responses in sufficient detail, only part of the simulation output is shown. In both figures, subpanels on the left side of the figures correspond to the negative SP stimuli, while subpanels on the right are associated with positive-phase stimuli; this relationship is also indicated by the suffxes in the panel names. Panels A⁻ and A⁺, topmost in both figures, plot Schroeder-phase signals that were played through the speaker, while voltage traces acquired from the processor (subpanels B and C) show the SAS- and CIS- encodings of the acoustic signal, respectively. Raster plots at the bottom of subpanels B and C show times at which 25 differently-sized fibers exhibited a spike in the trans-membrane voltage potential.

Figure 6.

Responses of a neural population model to 50 Hz positive and negative Schroeder-phase input signals (+ and −, respectively; for clarity, only part of the simulated response shown). A) Waveforms of audio signals; B) Top panel: Input sound encoded with SAS encoding strategy; bottom panel: spike output of a neural population model in response to input sound encoded with SAS. C) Same as “B”, only coding was performed with CIS strategy.

Figure 7.

Responses of a neural population model to 200 Hz positive and negative Schroeder-phase input signals (+ and −, respectively; for clarity, only part of the simulated response shown). Layout is identical to that used in Fig. 6.

By design, the envelopes of the SP signals are nearly identical, with the primary difference between the two complexes contained in the temporal fine structure of the sounds (Schroeder, 1970). Consequently, once Schroeder-phase signals are encoded with the CIS strategy, the resultant waveform primarily captures the envelope of the signal. Comparatively, SAS encoding preserves aTFS better than CIS, which is reflected both in the encoded waveforms (compare signal traces in subpanels B and C), as well as in the corresponding neural responses (compare raster plots in B to spike patterns in C).

Drennan et al. (2008) showed that discriminating positive and negative Schroeder-phase complexes becomes progressively harder for the CI listeners as the fundamental frequency of the test stimuli is increased. This relationship is also supported by Figs. 6 and 7. Even a cursory examination of the SAS raster plots in Fig. 6 (F₀ =50 Hz; subpanels B⁻ and B⁺) reveals larger and more conspicuous differences between the neural responses to opposite-phase stimuli, compared to those in Fig. 7 (F₀ =200 Hz). As the fundamental frequency increases further, the neural responses to opposite phases of Schroeder complexes become more alike, eventually producing an identical, albeit time-shifted, response in auditory nerve fibers (data not shown). To a smaller degree, similar behavior can be observed in the neural responses to CIS-encoded Schroeder-phase signals. Note how the spiking behavior in C⁺ differs from that in C⁻ at 50 Hz (Fig. 6), especially in 3.5- μm and 3.9- μm fibers. Such differences are not preserved once the fundamental frequency is increased to 200 Hz in Fig. 7; by then, responses become desynchronized and very much alike, regardless of the stimulus phase supplied to the model.

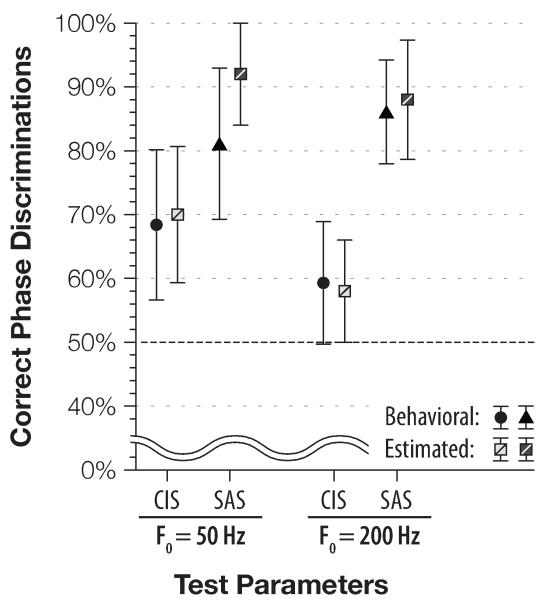
To quantitatively compare modeling results to those obtained in behavioral testing, we estimated the likelihood that an ideal observer (viz., the maximum likelihood classifier) would perceive the simulated spike trains as coming from distinct stimuli (see Estimating Discriminability of Neural Responses above). The estimates, obtained with a discretisation bin width of 1.6667 ms, are shown in Fig. 8 (the rationale for picking this bin width is explained in the “Quantitative Estimates of Discriminability” subsection of Discussion). Under all testing conditions, the ideal observer performs better than the study subjects, which is in line with our expectation that the optimal decisions of a maximum likelihood classifier provide an upper bound on the behavioral performance. Moreover, the modeled discrimination performance follows the general trends observed in the single-channel behavioral data: overall, performance decreases at higher fundamental frequency, and SAS consistently outperforms CIS-encoded stimuli.

Figure 8.

Comparison of single–channel behavioral results (average and standard deviation) from Figs. 1 and 2 with discrimination estimates based on the simulated responses. Chance performance (dashed line) is correct discrimination of phase on 50% of trials.

4. Discussion

First, the caveats. Discrimination results presented in this paper may not describe how well aTFS differences in non-SP stimuli will be perceived by a CI listener because other auditory stimuli may exhibit acoustic fine structure and neural response patterns distinct from those evoked by Schroeder phase complexes. Schroeder phase stimuli, however, serve as a good starting point — they provide a compact measure of how well acoustic TFS, absent of any confounding differences in the envelope or the spectrum, is conveyed by a particular sound-encoding strategy. Additionally, although our test demonstrates that acoustic TFS is perceived by the listeners, it does not measure the efficacy of this delivery. It is possible that aTFS cues could potentially be transmitted in a manner detrimental to speech perception. However, while delivery of acoustic TFS cues may be necessary but not sufficient for an improved speech performance, listeners’ discrimination of Schroeder-phase stimuli has been shown to correlate with clinical outcomes^†.

4.1. Behavioral Task

This paper described a behavioral task that measures within-channel detection of acoustic temporal fine structure cues delivered by the cochlear implant processor. Because the audio stimuli are supplied through the processor, the discrimination performance measured reflects the strategy’s encoding of aTFS cues as well as listeners’ ability to perceive these cues during the test.

When comparing behavioral results of a single-channel CIS program to that of a single-channel SAS, one has to remember that these encoding strategies employed different modes of stimulation: the CIS map used monopolar stimulation, while SAS relied on bipolar excitation (see SAS Settings in Methods). It is possible, but unlikely, that the difference in the stimulation modes had a significant effect on the reported single-channel results. Because CIS and SAS strategies in our experiments are supplied within a single channel, differences in the current spread between mono– and bi– polar stimulation modes are unlikely to influence subjects’ performance, especially given that the loudness of each strategy was custom-fitted for every listener participating in the test. For these reasons, we expect that the greatest influence on Schroeder-phase discrimination stems from the disparate CI strategies rather than from the modes of stimulation. Along the same line of reasoning, we do not expect significant differences to arise due to monopolar, rather than bipolar, SAS stimulation employed in our computational model.

As expected a priori, single-channel scores demonstrate a clear advantage of the analog strategy over the pulsatile encoding in conveying SP aTFS: throughout the study, SAS consistently yielded better performance than CIS. At the low fundamental frequency of the test stimuli, when phase discrimination is easy, SAS provided a 13% improvement over CIS results (81% vs. 68%, respectively). Once the difficulty of the task was increased, the differences between SAS and CIS scores became even more pronounced: at 200 Hz, SAS outperformed CIS by 27% (86% vs. 59%). Because the 95% confidence interval for at-chance performance on 144 trials ranges from 42 to 58 percent, we can conclude that single-channel CIS listeners’ ability to discriminate aTFS changes at 200 Hz is practically nonexistent.

As suggested by Table 2, changing F₀ from 50 to 200 Hz affected single-channel CIS and SAS strategies in different ways. While the increased fundamental frequency significantly depressed CIS scores, no comparable decrease in subjects’ SAS performance was observed. Although the behavioral SAS scores at 200 Hz appear to be higher than those at 50 Hz, this increase is not statistically-significant (p = 0.128). Similarly, while the estimates from our model do follow the expected trend and project a decrease in subjects’ SAS performance at 200 Hz, this decrease is statistically-insignificant (p = 0.75), bringing it in-line with our behavioral results. It is likely that the divergent effects of the fundamental frequency on CIS and SAS results are driven by how well aTFS is encoded by their respective strategies. Ultimately, CIS can encode aTFS information only in the amplitude of its pulses, where it also represents the envelope of its acoustic input. Comparatively, SAS encoding is less constrained, and is thus, more robust — aTFS cues are presented apart from other acoustic information, as electrical TFS (eTFS) in the current-discharge waveform, at the stimulating electrode (see SAS signal in Fig. 7B^−/+).

4.1.1. Discrimination Cues

Because we did not rove the level at which the audio was presented, one might argue that level differences between opposite-phase audio waveforms were the source of listeners’ discrimination performance. According to the data, roving the level did not significantly affect subjects’ performance. As can be observed in the top two panels of Fig. 5, roving presentation level of the CIS stimuli decreased subjects’ performance by ~ 4%, but this decrease was not statistically–significant (p = 0.364 and p = 0.241 at 50 & 200 Hz). Comparatively, effects of roving the SAS stimuli are even smaller — at 50 Hz, 6 dB rove resulted in performance difference of 1.3%, corresponding to p = 0.858, and at 200 Hz, the effect of roving differences resulted in p = 0.411. Taken together, these results indicate that listeners of neither the CIS-encoded stimuli nor the SAS-encoded stimuli relied on loudness cues to perform the discrimination task described in this paper. We allow the speculation that a larger study may have the power to discern a small, yet statistically-significant difference between the roved/non-roved CIS discrimination. However, the consistency of the SAS listeners’ performance suggests that the conclusions based on the SAS data are applicable to a larger pool of cochlear implant listeners, underscoring that the discrimination of the SAS-encoded Schroeder-phase stimuli is performed based on the aTFS differences.

Given the identical spectra and perceptibly identical envelopes of the audio SP stimuli, the discrimination cues used by our test subjects arose as a result of aTFS. The question then arises: how did the CIS users achieve a discrimination performance well above chance (Fig. 1) when the CIS strategy explicitly discards acoustic temporal fine structure? In contrast to the idealized diagram illustrating the CIS strategy (Wilson et al., 1991), the CIS encoding does not strictly reproduce the envelope of its audio input. So long as incoherent demodulation (e.g.,, half-wave rectification followed by lowpass filtering) is used to separate envelope and TFS information from the input signal, some of the aTFS information will invariably “leak” into the extracted envelope (Clark and Atlas, 2009). Thus, all of the CI encoding strategies that rely on incoherent demodulation (e.g.,, Hilbert transformation, half– or full– wave rectification followed by lowpass filtering) are inadvertently encoding at least some aspect of the acoustic TFS in the extracted envelope. Given that the original, audio stimuli supplied to the CI listeners are perceptually indistinguishable aside for the content of their aTFS, it stands to reason that the modulation cues that aided CIS listeners’ discrimination arose as a result of aTFS leakage into the encoded waveform’s envelope.

4.1.2. Within– vs. Across– Channel TFS Delivery

At the fundamental frequency of 50 Hz, the best discrimination of acoustic temporal fine structure was achieved with the multi-channel HiRes encoding, followed by performance scores obtained with the single-channel SAS and CIS strategies. Individual CI listeners in our study achieved performance levels comparable to those observed in normal-hearing subjects: on average, NH listeners correctly discriminated 50 Hz Schroeder phases 97% of the time (Drennan et al., 2008). Using a 16-channel HiRes strategy, our listeners S48 and S59 achieved 99%–correct discrimination. These, and previously-published results (Drennan et al., 2008) demonstrate that at low fundamental frequencies of the stimuli, a multi-channel strategy is fully capable of detecting changes in acoustic temporal fine structure of Schroeder-phase signals through the FM-to-AM conversion process. When a broadband frequency modulated (FM) signal is passed through narrow-band bandpass filters, the frequency excursions of FM are converted into the amplitude modulation (AM) of the output levels (e.g., Moore and Sek, 1996; Saberi and Hafter, 1995; Heinz and Swaminathan, 2009). Previous studies demonstrated that listeners with normal-hearing (Gilbert and Lorenzi, 2006) and CIs (Won et al., 2012) can understand speech using AM cues recovered from FM. The present study demonstrated that, a multi-channel CI processor generates AM cues recovered from broadband FM components of Schroeder-phase stimuli as a result of the audio-filtering process and CI users were able to use these recovered AM cues for robust Schroeder-phase discrimination at 50 Hz.

Once the difficulty of the task was increased, single-channel SAS outperformed multi-channel HiRes: 86% correct vs. 68%, p = 0.022; Fig. 4. Two of our best performers, S66 and S59 (using SAS and HiRes, respectively) scored very close to the SP discrimination observed in a NH population (92 and 99% vs. 96%; (Drennan et al., 2008). Furthermore, our inter-subject average of 68% –correct discrimination with the HiRes strategy is consistent with the 67% –correct rate obtained in a different cohort of multi-channel listeners^‡ (Drennan et al., 2008).

Although the SAS strategy is now rarely used for multi-channel CI stimulation, it does demonstrate the capacity of analog strategies to deliver aTFS cues. In fact, considering that single-channel SAS enabled its users to achieve a better level of performance than with the HiRes strategy using all of its 16 channels (see Fig. 9), one can speculate that on a per-channel basis, within-channel delivery of aTFS is more advantageous compared to across-channel cue delivery. Given the significant role that temporal fine structure plays in perception of tonal languages, speech in noise, and in enjoyment of music, it is not surprising that a number of groups are attempting to overcome the shortcomings of conventional strategies by utilizing within-channel encoding of temporal cues, either through novel analog (Sit et al., 2007; Sit and Sarpeshkar, 2008) or pulsatile encoding strategies (Li et al., 2010; Nie et al., 2005, 2008a; Wilson et al., 2005; Zeng et al., 2005). Currently, however, none of these strategies has yet been realized commercially, and it still remains to be seen whether implant listeners will be able to take advantage of the additional aTFS information in the real-world setting (cf. Kovačić and Balaban, 2009).

4.2. Modeling Results

Figs. 6 and 7 demonstrate how the representation of the audio Schroeder phase signals change as they are processed by the encoding strategies and output as spikes along the auditory nerve fibers. The audio stimuli that were played through the free-field speaker inside the soundbooth are shown in subpanels A⁺ and A⁻ of the figures. Waveforms at the top of subpanels B and C plot the current that was output on the only electrode active in the S65-fitted CI processor. Compare the shape and fluctuation of these electric waveforms to their acoustic source and note that the differences between CIS– and SAS– encoded waveforms (top of subpanels B and C, respectively) are plain even after a cursory examination: SAS preserves the overall appearance of the audio input, while the CIS encoding tracks only the fluctuations of the sound’s envelope and does not explicitly encode the acoustic temporal fine structure. Increasing the fundamental frequency of the SP stimuli from 50 to 200 Hz decreases the period of the individual frequency sweeps from 20 to 5 ms, which causes a marked decrease in the fidelity of both SAS and CIS encodings, as can be seen by comparing Fig. 7 to Fig. 6.

During the discrimination task, the listener was asked to identify which stimulus sounded unlike the other three. To relate Figs. 6 and 7 to the performance observed on the behavioral task, one has to judge the similarity (i.e., the discriminability) of neural responses elicited by positive and negative sound-encoded stimuli. In visually examining the provided figures, note the difference between the orderly periodicity of current waveforms and the neural responses they elicit. From one period to the next, the spiking patterns are more variable, a byproduct of stochastic response properties such as relative spread, latency, and jitter, which constrains how well the encoded waveforms alone can predict the behavioral results (cf. Huettel and Collins, 2004).

4.2.1. Neural Responses to SAS-encoded Stimuli

Designating negative-phase responses (subpanel B⁻ in either of the figures) as a point of reference allows one to evaluate how well the phase differences will be perceived by SAS-mapped listeners. For example, at 50 Hz, the negative-Schroeder waveform initially elicits response from both large- and small-diameter fibers alike (Fig. 6B⁻, at t = 23 ms). As time continues, the spiking fibers form a “decreasing triangle” pattern, where large-diameter fibers continue to fire and smaller-diameter fibers become progressively quiescent (ibid., t = 25 to 30 ms). Responses to the positive-phase SAS waveform, on the other hand, exhibit an opposite trend: first, rapid oscillations of the current cause only the largest of the fibers to reach action potential (Fig. 6B⁺, at t = 24 ms), but as the period of the amplitude oscillations increases, progressively smaller fibers respond, forming an “increasing triangle” spike pattern (cf. Paintal, 1966).

Likewise, opposite-phase SAS stimuli with the fundamental frequency of 200 Hz produce distinct neural responses. The spiking pattern produced by the 200-Hz stimuli, however, is different from the one produced by 50-Hz Schroeder-phase complexes. Because the period of each frequency sweep decreases from 20 ms to 5 ms, both absolute and relative refractory periods begin to constrain nerve fibers’ response rates^§. As a result, the spike count in response to 200-Hz stimuli is significantly smaller than in response to 50-Hz stimuli. Still, the positive and the negative neural responses at 200 Hz can be visually discriminated from each other. Note how action potentials elicited by the negative-phase SAS stimulus occur contemporaneously along all of the responding fibers (Fig. 7B⁻; at t = 27, 32, …, 47 ms). Fibers stimulated with positive Schroeder-phase stimulus respond differently: the fibers’ spikes are often staggered and diameter-dependent (B⁺; t = 30, 40, 45 ms). It is likely that these differences in neural response pattern are primarily driven by the time-reversed nature of the SAS stimulus waveforms, specifically, the order in which rapid and slow oscillations occur (Brittan-Powell et al., 2005).

4.2.2. Neural Responses to CIS-encoded Stimuli

Both positive and negative phases of CIS-encoded 50-Hz SP stimulus produced seemingly identical responses of equal magnitude. However, a closer examination of subpanels C⁻ and C⁺ in Fig. 6 reveals that there are consistent differences in response timings. Overall, subpanel C⁺ exhibits a more synchronized response pattern across differently-sized fibers. For example, compare spike timing of 3.3 – 4.1 μm diameter fibers across both panels. Responses evoked by the negative-phase stimulus exhibit a stochastic firing pattern, while same-sized fibers in subpanel C⁺ respond in lockstep, at approximately the same time (Fig. 6C⁺; fibers ~3.3 μm and 3.9 μm at t = 27, 28, 29, 31, 32, 33, 34, 35 ms).

Regularly observed differences in response timing between the two response sets disappear once the fundamental frequency of the CIS-encoded stimuli is increased from 50 to 200 Hz. In Fig. 7, both of the subpanels C⁻ and C⁺ exhibit an identical pattern: smaller-diameter fibers respond rarely, and with little periodicity, while larger-diameter fiber populations (~3.8 μm) exhibit highly regular responses.

4.2.3. Quantitative Estimates of Discriminability

Although gross differences between neural responses evoked by opposite-phase stimuli can be assessed visually, such comparison is subjective and imprecise: the stochastic nature of neural responses introduces variability in spike times (e.g., due to jitter, latency, and relative spread (White et al., 2000)) that can potentially manifest itself as “false” differences to the observer. To overcome this challenge, the similarity of neural responses was measured quantitatively, using a method that intrinsically accounts for the stochasticity of spike times.

Discriminability calculated from the modeled output is compared to within-channel behavioral data in Fig. 8. The estimated results track two main trends observed during psychophysical testing: 1) SP discrimination tends to be harder at higher fundamental frequencies (observed in our CIS tasks, as well as in previous studies: (Dooling et al., 2001; Drennan et al., 2008), and 2) SAS listeners tend to outperform subjects using the CIS encoding strategy.

Because duration of discretisation bins controls the sensitivity of the estimation method, the calculated percent correct scores are directly affected by the precision with which the neural data is discretised. To establish a range of plausible bin widths with which to perform our analysis, we reasoned that the precision (∞ 1/binWidth) of the peripheral auditory system lies somewhere between the jitter of its fibers and the duration of the stimulus. Bins whose duration is less than the fiber’s jitter would erroneously discretise responses from identical stimuli into different bit patterns, and bins as long as the stimulus itself can only detect the stimulus’ presence or absence, but not its temporal structure.

The bin width used to generate Fig. 8 is 1.6667 ms; we have found it to be a plausible duration that demonstrates the trends and provides an upper limit on behavioral results. As we varied the bin width between the two extremes (jitter and duration of the frequency sweep), the observed trends are preserved, so long as the estimated percent correct scores are unencumbered by the ceiling and floor effects (i.e., are above at-chance performance and below the saturation values). Furthermore, we confirmed that the estimates are insensitive to changes in the starting phase of the neural responses: we repeated the estimation procedure and delayed one, or both, of the neural responses by d ∈ {0.00, 0.25, 0.50, …, 20} ms. While holding the bin width fixed at 1.6667 ms, the variable-phase score estimates diverged no more than 1% from the non-shifted estimates. Relative to the magnitude of the estimates’ standard errors shown in Fig. 8, these differences in score values were deemed insignificant.

5. Conclusion

The present study has demonstrated that although both single- and multi- channel strategies are capable of delivering temporal cues to the listeners, under challenging discrimination conditions, a single-channel analog signal is capable of encoding aTFS changes better than a 16-channel pulsatile strategy. Moreover, the authors described a novel test that measures within-channel perception of acoustic temporal fine structure cues and demonstrated that a stochastic biophysical model of auditory nerve fibers exhibits some of the same major trends as those observed in single-channel behavioral experiments. These results suggest the potential utility of computational models in predicting broad outcomes in behavioral studies of cochlear implant listeners.

Highlights.

• We tested detection of acoustic temporal fine structure in cochlear implant listeners

• Subjects using 1-channel SAS strategy consistently outperformed those using CIS

• At F0=200 Hz, 1-channel SAS listeners outperformed those using 16-channel HiRes

• We modeled neural spikes evoked by Schroeder-phase stimuli using a biophysical model

• Discrimination estimated based on the model tracked behavioral performance