Central Synapses Release a Resource-Efficient Amount of Glutamate

Abstract

Why synapses release a certain amount of neurotransmitter is poorly understood. Here we combine patch-clamp electrophysiology with computer simulations to estimate how much glutamate is discharged at two distinct central synapses of the rat. We find that, regardless of some uncertainty over synaptic microenvironment, synapses generate the maximal current per released glutamate molecule while maximizing signal information content. Our result suggests that synapses operate on a principle of resource optimization.

Information processing in the brain involves excitatory events generated by release of glutamate from a synaptic vesicle into the synaptic cleft. The vesicle content of glutamate depends on the vesicle volume and activity of vesicular transporters. Small central synapses tend to release glutamate in single-vesicle mode, without saturating postsynaptic receptors ^{1, 2}. This adds to the variability of transmitted signals, arguably reducing the computational certainty of brain circuits. The adaptive significance of having this mode of operation is not known.

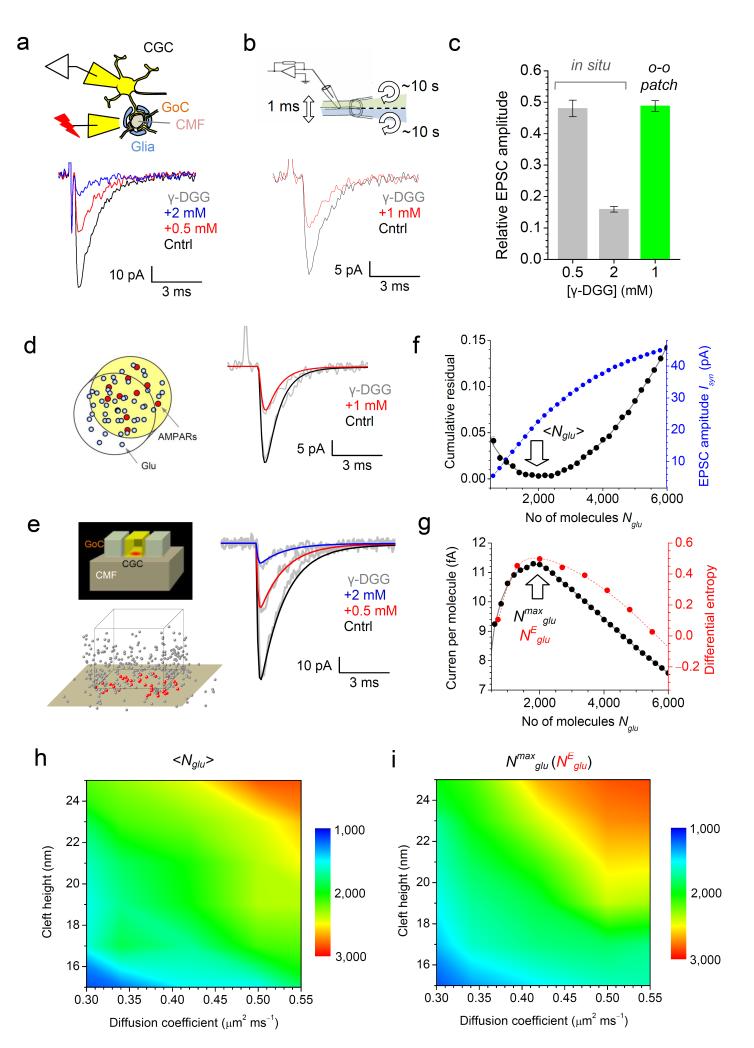
We first sought to estimate the amount of released glutamate at synapses between cerebellar mossy fibers (CMFs) and granule cells (CGCs): CGCs are among the most electrically compact neurons in the brain, with negligible voltage-clamp errors in somatic recordings. Furthermore, functional features and the environment of CMF-CGC synapses have been explored in exhaustive detail ^{3, 4}. To gauge how much glutamate is released there we examined activation of synaptic α-amino-3-hydroxy-5-methylisoxazole-4- propionic acid receptors (AMPARs) using the fast-dissociating antagonist γ-D-glutamylglycine (γ-DGG): its inhibitory action is inversely related to the intra-cleft glutamate concentration ^{2, 5}. γ-DGG at 0.5 mM and 2 mM produced stable reductions of AMPAR EPSCs, by 52 ± 3% and 84 ± 1%, respectively (Fig. 1a,c). This reduction reflects the AMPAR kinetics plus the effects pertinent to diffusion and escape of glutamate. To isolate geometry and diffusion, we monitored AMPAR kinetics in outside-out patches of CGCs using 1 ms pulses of glutamate ⁶, with and without γ-DGG. Because AMPARs in CGCs in situ are almost exclusively intra-synaptic, we used cultured CGCs in which AMPARs migrate to the soma ^{4, 7}. 1 mM γ-DGG reduced AMPAR responses recorded in the same patch (Methods) by 48 ± 3 % (n = 6, Fig. 1b,c). These data incorporated into the Monte Carlo model of AMPAR activation by glutamate ^{8, 9} (Fig. 1d) gave us finely-tuned kinetic constants for AMPAR interaction with γ-DGG (Methods), in accordance with ⁵ (Supplementary Fig. 1).

Figure 1.

The amount of glutamate released at CMF-CGC synapses corresponds to the maximal current per released molecule.

(a) Diagram: in-situ configuration (GoC, Golgi cell axons). Traces, one-cell example EPSCs, as indicated. (b) Diagram: fast ligand-application system (~0.2 ms constant, ~10 s full exchange ⁶) for patch probing. Traces: one-patch AMPAR responses (cultured CGC excision) to 1 ms pulses of 1 mM glutamate, as indicated. (c) Summary of experiments depicted in (a-b). (d) Diagram: Monte Carlo model of AMPAR activation in patches⁹. Traces: model outcome (color-coded) matches experimental traces (grey, as in b). (e) Top: CMF-CGC synapse model geometry (adapted from ³); bottom: a model snapshot of diffusing glutamate molecules 2 ms post-release (for clarity, every other molecule is depicted; red and gray, inside and outside the cleft, respectively). Traces: simulated (color-coded) and experimental EPSCs (grey, as in a). (f) In black: matching simulated and experimental data through mean-square minimization (residuals combined for three conditions) predicts <N_glu> = 2001 ± 86 (mean ± 95% confidence, here and elsewhere; arrow). In blue: simulated dependence between I_syn and N_glu. (g) The maximum current-per-molecule ratio corresponds to N^max_glu = 1970 ± 55 molecules (black) which coincides with N^E_glu value for the maximal differential entropy H (red). (h) Parametric map for <N_glu> (color coded) over a physiological range of the (unknown) intra-cleft glutamate diffusion coefficients and cleft heights. (i) Parametric map for N^max_glu (notations as in h) which is virtually indistinguishable from that of N^E_glu (Supplementary Fig. 2c).

Equipped with the receptor kinetics, we simulated AMPAR activation in the known average microenvironment of CMF-CGC synapses, which has been adapted for modeling ^{3, 4} (Fig. 1e diagrams). We used the previously validated Monte Carlo approach ^{6, 8, 9} in which molecules are tracked every 0.1 μs (Methods). Varying the number of released molecules N_glu led to an excellent fit between simulated and recorded EPSCs (Fig. 1e traces). This optimization procedure was robust (clear single minimum for residuals, Fig. 1f, black) giving ‹N_glu› = 2001 ± 86 (mean ± 95% confidence limits; arrow in Fig. 1f). ‹N_glu› was broadly within the limits of previous estimates ¹⁰, but what could be its adaptive meaning? Our simulations indicated that although the EPSC amplitude I_syn depended on N_glu monotonically, the relationship was not linear (Fig. 1f, blue). This non-linearity robustly predicted that the value N^max_glu = 1970 ± 55 corresponded to the maximal AMPAR current per molecule (Fig. 1g, black; arrow, N^max_glu). Notably, this value was indistinguishable from ‹N_glu› (Fig. 1f, black). We also asked how the information content of the EPSC signal changes with N_glu: in Shannon theory, information content gauges the amount of uncertainty in the signal, which could be important for efficient neural code transfer ^{11, 12}. We therefore calculated the differential entropy ¹³ H of I_syn (Methods) for all simulated N_glu values and found that, again, H peaked at the N^E_glu value indistinguishable from either ‹N_glu› or N^max_glu (Fig. 1g, red). To understand whether this was simply a fortuitous coincidence for one particular set of (average) synaptic parameters, we examined the relationship between ‹N_glu›, N^max_glu and N^E_glu further.

First, we calculated ‹N_glu› using the same γ-DGG experiments (Fig. 1a) while varying two poorly accessible features of the synaptic environment, the synaptic cleft height and the intra-cleft glutamate diffusion coefficient. This produced the parametric map for ‹N_glu› (Fig. 1h). Second, we carried out a similar exploration for N^max_glu and found that the parametric map for N^max_glu was virtually undistinguishable from that of ‹N_glu› (Fig. 1i). We carried out further map comparisons exploring the size of the postsynaptic density (PSD, populated with AMPARs) and the membrane apposition area; again, a correspondence between parametric maps for N^max_glu and ‹N_glu› was evident (Supplementary Fig. 2a). We repeated the parameter exploration for N^E_glu values and, reassuringly, found little discrepancy (less than 50-80 glutamate molecules, or 3-4%) between N^max_glu and N^E_glu across the tested range (Supplementary Fig. 2b-c). Taken together, these results indicated that ‹N_glu› was close to both N^max_glu and N^E_glu, regardless of the uncertainty about the exact architecture of CMF-CGC synapses.

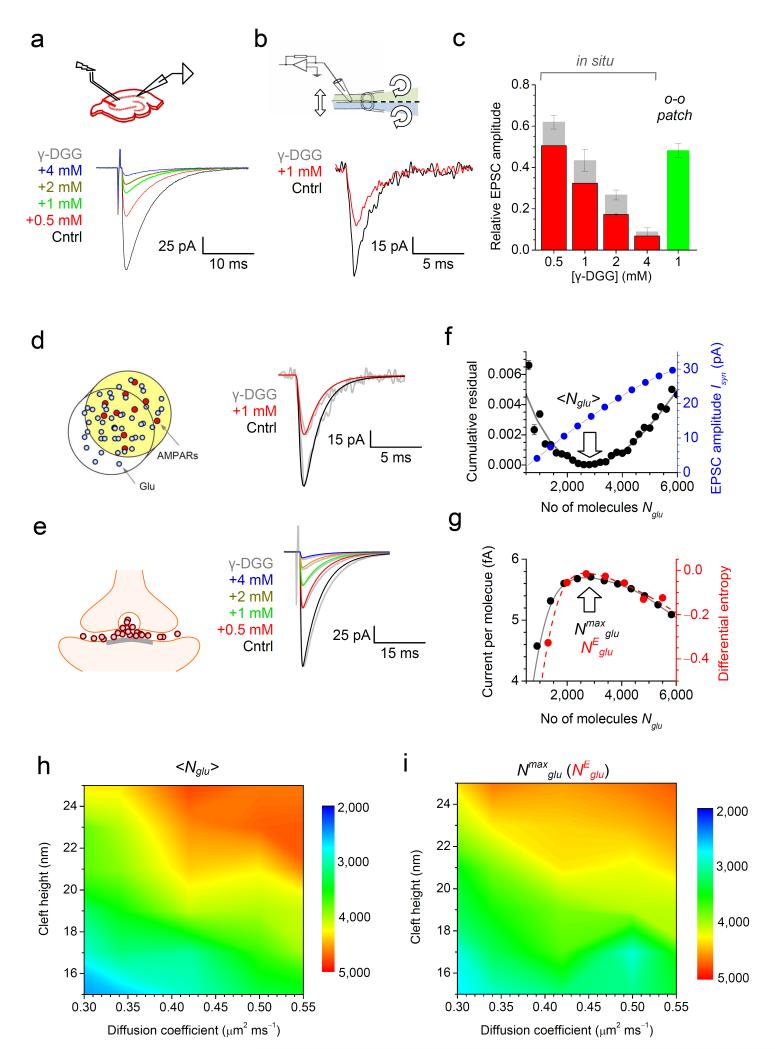
To test if the close association between ‹N_glu› and N^max_glu was a unique feature of these synapses we also investigated hippocampal CA3-CA1 connections. Here, we examined the reduction of AMPAR EPSC by four concentrations of γ-DGG (Fig. 2a) and tested AMPAR kinetics in outside-out patches from CA1 pyramidal cells with and without 1 mM γ-DGG (reduction to 48 ± 3% of control; n = 6; Fig. 2b). To account for voltage- and space-clamp errors in large CA1 pyramids ¹⁴, we conducted a separate investigation. Briefly, we documented the relationship between the EPSC amplitude and the effect of one γ-DGG concentration (0.5 mM) for n = 109 cells and then used a NEURON-built CA1 pyramid model to obtain corrections for the other three γ-DGG concentrations (Methods, Supplementary Fig. 3). The resulting data (Fig. 2c; grey and red columns) provided several constraints to analyze γ-DGG effects in the synaptic cleft gauging them against the effect of 1 mM γ-DGG in membrane patches (reduction to 48 ± 3% of baseline; n = 6; Fig. 2c, green). Reassuringly, the best-fit kinetic constants finely tuned to the CA1 pyramid patch recordings (Fig. 2d, traces) were undistinguishable from those for CGC AMPARs (Methods). Based on these data, a detailed Monte Carlo model of the CA3-CA1 synapse, which has been extensively tested ^{6, 9}, gave ‹N_glu› = 2780 ± 20 molecules, with the excellent experiment-theory match (Fig. 2e, traces) obtained with robust optimization (Fig. 2f, black). Again, the value of ‹N_glu› for these synapses coincided with N^max_glu (2690 ± 95 molecules; Fig. 2g) and followed both N^max_glu and N^E_glu values over a wide range of synaptic cleft heights, glutamate diffusion coefficients (Fig. 2h-i), the postsynaptic density size or the membrane appositions areas (Supplementary Fig. 4).

Figure 2.

The amount of glutamate released at CA3-CA1 synapses corresponds to the maximal postsynaptic current per released molecule.

(a) Top: experimental diagram. Traces: one-cell example EPSCs recorded in a CA1 pyramidal cell, as indicated (color-coded). (b) Traces: example AMPAR responses recorded in one outside-out patch from a CA1 pyramid (1 ms pulses of 1 mM glutamate), as indicated. (c) Summary of experiments depicted in (a-b); grey and red columns, raw data and the data corrected for voltage-clamp errors (Supplementary Fig. 3), respectively. (d) Traces: modeled patch responses (color-coded) match recorded traces (grey, as in b). (e) Diagram: a CA3-CA1 synapse model ^{6, 9}; traces: simulated (color-coded) and recorded (grey, as in a) EPSCs; small decay-time mismatch reflects the fact that real voltage-clamp is not instantaneous. (f) In black: the matching of simulated and experimental data through minimization of the mean-square residual (combined for five conditions) predicts <N_glu> = 2780 ±120 (arrow). In blue: simulated dependence between I_syn and N_glu. (g) The maximum current-per-molecule ratio corresponds to N^max_glu = 2690 ± 95 molecules (black, arrow) which virtually coincides with N^E_glu value corresponding to the maximal differential entropy H (red). (h) Parametric map for <N_glu> (color coded) over a range of the intra-cleft glutamate diffusion coefficients and cleft heights. (i) Parametric map for N^max_glu (notations as in h) which is virtually indistinguishable from that of N^E_glu (Supplementary Fig. 4c).

Our results thus suggest that glutamate discharges at small excitatory synapses tend to provide both the highest “signal-to-molecule” ratio and the highest information content of synaptic signals. Indeed, vesicle-stored glutamate is a precious resource: metabolic recycling and transporting glutamate into the vesicle lumen is a highly energy-consuming process. Providing the strongest synaptic signal per released molecule thus suggests the principle of energy resource optimization. Similarly, preserving as much information as possible during signal processing in the brain has been an important notion of theoretical studies into the machinery of neural coding ^{11, 12}. How could such optimization impact on synaptic structure and function? One possibility is that formation of synaptic connections may involve structural adaptations leading to the optimal configuration. To test the plausibility of this scenario, we asked whether immature cerebellar CMF-CGC synapses are “sub-optimal”. We therefore repeated our tests in CMF-CGC synapses (as Fig. 1) using P6 preparations: at this early age synaptic architecture is distinctly different from that of mature CMF-CGC connections ⁴ (Methods; Supplementary Fig. 5a-b). We found that ‹N_glu› and N^max_glu diverged significantly at P6 (Supplementary Fig. 5c) thus lending support to the hypothesis that resource optimization may result from developmental adaptation of synaptic configuration. Notably, CMF-CGC synapses showed substantially larger values of the maximal current per molecule and information entropy compared with CA3-CA1 synapses (Figs. 1g and 2g). Whether this can be attributed to the fact that CGCs receive only four CMF inputs, compared to thousands of CA3-CA1 connections per cell, remains to be ascertained.

Will resource optimization hold during use-dependent plasticity? First, our samples are likely to contain synapses expressing various degrees of potentiation/depression. Second, we have observed the same principle at two different synapses, with distinct architectures and numbers of released molecules. Finally, it appears that varying major features of the synaptic environment does not impinge on the correspondence between ‹N_glu›, N^max_glu, and N^E_glu. It is therefore reasonable to hypothesize that during homeostatic or use-dependent plasticity the amount of released glutamate, or synaptic architecture, or both, could be adjusted in accord with the minimum resource / maximum information transfer requirement. Intriguingly, the synaptic cleft height also appears optimized for boosting the synaptic current ⁸ while energy resource optimization has been suggested to underlie spike generation in central neurons ¹⁵, failures of presynaptic release ¹⁶, and dendritic integration of synaptic inputs ¹⁷. It remains an open question whether such observations represent elements of a free energy minimization regime which has recently been proposed to govern the brain machinery of perception and learning ¹⁸.

METHODS (on-line)

Electrophysiology in situ: acute slices from cerebellum and hippocampus

Animal experimentation met all relevant national and EU regulations. 250 μm parasagittal slices from the cerebellar vermis, or transverse 300 μm hippocampal slices, were cut from 3-4-week old male Sprague-Dawley or Wistar rats (or P6 pups where specified) and incubated for one hour in a solution containing (in mM): 124 NaCl, 3 KCl, 1 CaCl₂, 3 MCGCl₂, 26 NaHCO₃, 1.25 NaH₂PO₄, 10 D-glucose, and bubbled with 95:5 O₂/CO₂, pH 7.4. Slices were next transferred to a recording chamber superfused with an external solution which was similar to the incubation solution plus 2 mM CaCl₂ and 2 mM MCGCl₂. AMPAR EPSCs were isolated by adding 1 μM CGP55845, 100 μM D-APV, 250 μM S-MCPG, 1 μM strychnine and 100 μM picrotoxin. The intracellular solution for voltage-clamp recordings contained (mM): 117.5 Cs-gluconate, 17.5 CsCl, 10 KOH-HEPES, 10 BAPTA, 8 NaCl, 5 QX-314, 2 Mg-ATP, 0.3 GTP (pH 7.2, 295 mOsm). Patch-clamp recordings were performed at 33-35°C using Multiclamp-700B amplifier; signals were digitized at 10 kHz. The pipette resistance was 7-9 MOhm for CGCs and 3-6 MΩ for CA1 pyramids.

To stimulate the bulk of Schaffer collaterals in hippocampal slices, a bipolar stimulating electrode was placed in stratum radiatum approximately 200 μm from stratum pyramidale. In cerebellar slices, mossy fiber axons were stimulated with a bipolar tungsten electrode placed in the cerebellar white matter near the gyrus crest to stimulate fibers entering the granule cells layer. 100 μs electrical stimuli were applied to afferent fibers evoke EPSCs. Individual recording sweeps were collected at 15 s intervals. Other receptor and transporter blockers were added as indicated. All animal handling procedures followed current UK regulations. Data were routinely represented as mean ± SEM; Student’s unpaired or paired t-test (or non-parametric Wilcoxon paired tests when distribution was non-Gaussian) was used for statistical hypothesis testing.

Electrophysiology: fast glutamate application in outside-out patches

Patches were excised from cerebellar granule cells or CA1 pyramidal cells held in whole-cell mode in the respective acute slices. The fast ligand application method was adapted from ¹⁹. We used a θ -glass application pipette pulled out to a ~200 μm tip diameter. The pipette was fixed in a micro-clamp, which was glued directly on a piezo bending actuator mounted on an electrode holder. Pipette channels were filled with the bath solution or bath solution containing different pharmacological agents (Fig. 1b). Three separate micro-capillaries inserted into each of two channels provided application solution supply; solutions in each channel could be replaced within ~10 s by toggling the pressure pump circuit between the supplying micro-capillaries. Pressure in the application pipette channels was adjusted using the two-channel PDES-02DX pneumatic micro ejector (npi electronic GmbH) using compressed nitrogen. The ~1 ms electric pulses were applied via a constant voltage stimulus isolator; stimulus duration and amplitude were adjusted using a control test in which one pipette channel was filled with distilled water and the current was recorded by an open patch pipette. The characteristic time constant of the rapid switch response in these control experiments was 150-250 μs, as documented earlier ⁶.

Kinetic model: AMPA receptors

We used the kinetic scheme published earlier ⁵ which included state transitions dealing with effective concentrations of local glutamate and γ-DGG (Supplementary Fig. 1). To accurately reproduce the kinetics of native AMPARs in our experiments, we adjusted some of the above kinetic constants to match the experimental AMPAR kinetics in well-controlled conditions of ligand application (1 ms pulse of 1 mM glutamate, with and without 1 mM γ-DGG) to outside-out patches. For fine-tuning purposes, we introduced proportionality factors P_glu and P_DGG to scale the constants dealing with receptor interaction with glutamate and γ-DGG, respectively, as indicated above. The values of P_glu = 0.851 ± 0.012 for CA1-CA3 synapses and P_glu = 0.898 ± 0.078 for CMF-CGC synapses were obtained through accurate fitting of outside-out AMPAR responses (n = 5); with these values and best-fit P_DGG = 0.98 ± 0.02 (n = 5) the kinetic scheme provided an excellent match with the AMPAR activation time course in patches including the 48% amplitude reduction by 2 mM γ-DGG (Figs. 1d, 2d).

Monte-Carlo model: main notations and symbols

R – radius of the synaptic apposition zone; δ – synaptic cleft height; Q – the number of released neurotransmitter molecules; D – effective diffusion coefficient of glutamate in the cleft; t – time variable; r – radial distance from the cleft centre; N – total number of receptors (AMPA) within the active zone; r_PSD – radius of the postsynaptic density; P(r) – fraction of open receptors; I_syn – total peak synaptic current through open receptors; γ – conductivity of a single receptor-channel; V_o – the postsynaptic resting membrane potential outside the cleft; V_c = 0 – the receptor reversal potential of AMPAR; C(r,t) – local glutamate concentration.

Monte-Carlo model: receptor activation

The model duty cycle following glutamate release event was as follows. At each time step (dt = 0.1 μs), the model first updated the co-ordinates of all individual glutamate molecules that follow Brownian movement. Next, it calculated the concentration profile of glutamate C(r,t) in the cleft based on all molecular positions. In conditions of approximate rotational symmetry (again, rectangular shapes of synaptic elements at 250-300 nm from the center had a negligible effect on these calculations), this corresponded to C(r,t) = Q(2πrδΔr)⁻¹, where Q stands for the number of glutamate molecules occurring at time point t inside the flat cylindrical ring of height δ, width Δr and radius r. The average occurrence (concentration) of open receptors [O](r) within the PSD was then calculated at the same time point from the multi-stage AMPAR kinetic scheme, in accordance with the local glutamate concentration C(r,t) . When the fast-dissociating antagonist γ-DGG was present in the extracellular medium, the AMPA receptor activation kinetics were computed accordingly. These calculations gave the total synaptic current in the analytical and discrete forms, respectively, as

$$I_{\mathit{syn}}=2\pi {\Sigma }_{i=1}^{r_{\mathit{PSD}}I\Delta r}{\mathit{iV}}_0{\gamma }^2\left(\Delta r\right)\left[O\right]\left(r\right)$$

where r_PSD / Δr was rounded to the nearest integer. We routinely verified that reducing the time step did not change the outcome of simulations.

Monte Carlo model: synaptic environment

Computations were carried using an ad hoc built in-house 64-node PC cluster optimized for parallel computing ⁹. The modeling methodology and computational Monte Carlo algorithms adapted our approach which was outlined in detail previously ^{6, 9}. Geometric features of mossy fiber (CMF) -cerebellar granule cell (CGC) synapses were approximated by the pre- and postsynaptic rectangular elements representing the structure of cerebella glomeruli, as described in a previously published model ³. 200 to 6000 glutamate molecules (N_glu) were released in the center of the 600 nm wide apposition area separated by a 50 nm space from neighboring structures (Fig. 1e); the average synaptic cleft height was 16 nm (varied between 15-25 nm), and the postsynaptic density (PSD) width was 160 nm (varied between 140-300 nm). 50-300 AMPARs were scattered inside the postsynaptic density, with the channel conductance of 10 pS, respectively. In the trials focusing on immature P6 synapses, synaptic geometry was amended, in accordance with 3D microscopy data documented for P8 animals (Supplementary Fig. 5b) ⁴: notably, the PSD was expanded to 400 nm with the synaptic cleft having a simple 2D geometry (as opposed to the 3D structure depicted in Fig. 1e) characteristic of immature CMF-CG connections ⁴. The default glutamate diffusion coefficient was 0.3 μm²/ms, as estimated earlier ³, and varied between 0.2-0.6 μm²/ms in parameter exploration tests.

CA3-CA1 synapses were modeled by two cylindrical elements (diameter 150-600 nm, PSD diameter 120-360 nm) separated by the apposition cleft (varied between 15-25 nm), as detailed earlier ^{6, 8}. Movements of individual glutamate and γ-DGG molecules, their binding to individual receptor molecules, and receptor state transitions were computed with a time step of 0.1 μs (further reduction of the time step by an order of magnitude improved computation accuracy by only <1%). Because electrodiffusion phenomena in the cleft could only manifest themselves as a 15-20% deceleration of the EPSC decay upon reversal of the synaptic current, with no effect on the EPSC amplitude ⁶, they were not considered in the present model.

NEURON model

To correct for space-clamp errors, a NEURON ²⁰ library model of a CA1 pyramidal cell was used incorporating distributed membrane ion channel kinetics known to date ^{21, 22} (accession 2796 and 7509; Supplementary Fig. 3).

Information content: Differential entropy

To gauge the information content of the EPSC amplitude I_syn(N_glu) at each vesicular content N_glu, we used differential entropy, a version of Shannon entropy extended for continuous distributions ¹³:

$$H\left(x\right)=-\underset{-\infty }{\overset{+\infty }{\int }}f\left(x\right){\log }_{2}f\left(x\right)\mathit{dx}$$

where f(x) stands for the probability density function of stochastically generated I_syn(N_glu) at each value of N_glu. In evaluating H(x) we noticed that, across the explored range of synaptic parameters, stochastic fluctuation of I_syn(N_glu) was indistinguishable from the Gaussian distribution. Therefore, we could calculate H(I_syn) as $H\left(I_{\mathit{syn}}\right)={\log }_2\left(\sigma \sqrt{2e\pi }\right)$ where σ stands for the standard deviation of I_syn(N_glu) values.