The zipper groups of the amyloid state of proteins

A formal derivation is provided of the 15 symmetry groups (zipper groups) available to the amyloid homosteric zipper.

Abstract

Fibrous proteins in the amyloid state are found both associated with numerous diseases and in the normal functions of cells. Amyloid fibers contain a repetitive spine, commonly built from a pair of β-sheets whose β-strands run perpendicular to the fiber direction and whose side chains interdigitate, much like the teeth of a zipper. In fiber spines known as homosteric zippers, identical protein segments sharing identical packing environments make the two β-sheets. In previous work based on atomic resolution crystal structures of homosteric zippers derived from a dozen proteins, the symmetries of homosteric zippers were categorized into eight classes. Here, it is shown through a formal derivation that each homosteric zipper class corresponds to a unique set of symmetry groups termed ‘zipper groups’. Furthermore, the eight previously identified classes do not account for all of the 15 possible zipper groups, which may be categorized into the complete set of ten classes. Because of their foundations in group theory, the 15 zipper groups provide a mathematically rigorous classification for homosteric zippers.

1. Introduction  

Amyloid fibers were first found associated with denatured proteins and diseases (Eisenberg & Jucker, 2012 ▶), but have more recently been discovered in a variety of normal cellular processes (Chapman et al., 2002 ▶; Si et al., 2003 ▶; Fowler et al., 2006 ▶; Maji et al., 2009 ▶; Kato et al., 2012 ▶). Apparently, evolution has harnessed this tight but reversible mode of protein association for numerous biological functions.

Although models of amyloid fibers are varied (Nelson & Eisenberg, 2006 ▶), several models contain a structural feature known as the amyloid spine (Fig. 1 ▶ a). The spine consists of a pair of β-sheets that run the length of the fiber (Nelson et al., 2005 ▶). The β-strands of the two spinal β-sheets are small adhesive segments of potentially larger polypeptide chains that constitute the fiber (Sambashivan et al., 2005 ▶). β-­Hydrogen bonding within the spinal β-sheets mediates β-­strand adhesion along the spine axis and provides cooperative forces that bestow fibers with high thermodynamic stability (Nelson et al., 2005 ▶; Tsemekhman et al., 2007 ▶). Tightly interdigitated side chains of the β-strands (Fig. 1 ▶ b) bind the two β-sheets together in a spine geometry termed a ‘steric zipper’ (Nelson et al., 2005 ▶; Sawaya et al., 2007 ▶). Along with numerous examples from single-crystal diffraction (Eisenberg & Jucker, 2012 ▶), the steric zipper model is consistent with models derived from other types of data. For instance, a fiber-diffraction model of polyglutamine satisfies the requirements for a steric zipper (Sikorski & Atkins, 2005 ▶), as do models of amyloid-β fibrillar oligomers derived from powder diffraction (Stroud et al., 2012 ▶).

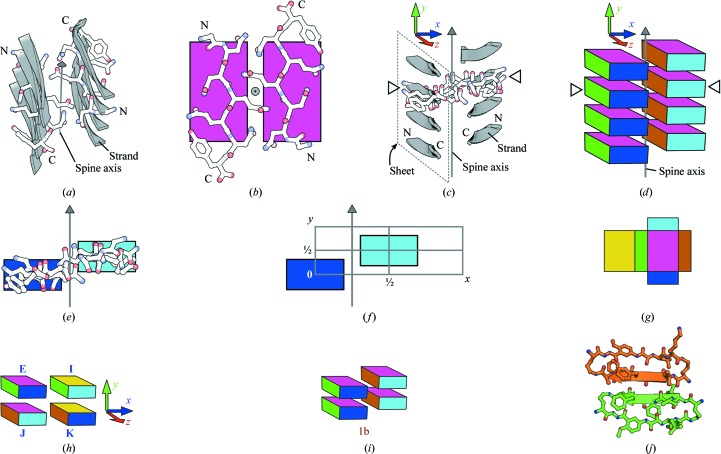
Figure 1.

(a) Overview of a GNNQQNY amyloid spine (PDB entry 1yjp; Nelson et al., 2005 ▶). Four β-strands from each of the two spinal β-sheets are shown. β-­Strands are depicted in gray as cartoons. One β-strand from each β-sheet is also shown as sticks with N- and C-termini labeled. All strands of a given sheet in this spine run in the same direction from the N-terminus to the C-terminus. The spine axis is shown as a gray arrow running through the center of the spine. Here, the spine axis is oblique to the viewer. (b) View down the GNNQQNY spine axis showing one pair of β-strands, each from a different β-­sheet. The arrow representing the spine axis in (a) points towards the viewer here (gray circle with dot). The N- and C- termini of the two β-strands are labeled. The magenta laminae are faces of boxes that represent the two β-strands and indicate the orientation of the β-strands, as described for (d). Here, the magenta faces are orthogonal to the spine axis. (c) A view of the GNNQQNY spine looking perpendicular to the spine axis. This vantage point is similar to that in (e), but slightly rotated around the spine axis. The x, y and z axes of the coordinate system for this GNNQQNY spine are shown in blue, green and red, respectively. The y axis is parallel to the spine axis. One β-sheet of the spine is outlined by a dashed parallelogram. One β-strand from each β-sheet is labeled at the N- and C-termini. Open triangles indicate two β-strands that are also indicated in (d). (d) The GNNQQNY spine is represented as stacks of boxes with colored faces, seen from the same vantage point as in (c). Each box represents a different β-strand. Colors indicate orientation such that various landmarks of the β-strands point towards the different colored faces of a representative box. For this GNNQQNY example, landmark features and the faces to which they point are as follows: N-terminus of each β-strand, cyan face; C-terminus, blue face; side chain of the first Q, amber face; backbone carbonyl of the first Q, magenta face; side chain of the second Q, green face; backbone carbonyl of the second Q, yellow face. (e) A view down the z axis of the GNNQQNY spine, showing only two β-strands, one from each sheet. The two β-strands are depicted as both sticks and colored boxes. Here, the blue and cyan faces of the boxes are in the xy plane, which is also the plane of the figure, so the other faces of the boxes are not visible. The spine axis is shown as a gray arrow. This vantage point, similar to those in (c) and (d), is created from the vantage point of (b) by a 90° rotation around the x axis, where the now hidden magenta faces point towards the top of the figure. (f) The homosteric zipper lattice (gray grid) is made from half-unit translations along the x and y axes at z = 0. The grey arrow represents the spine axis, which is defined to be at x = ¼ and z = 0. (g, h, i) The rotations E ₃ (identity), I ₃ (180° rotation around x), J ₃ (180° around y) and K ₃ (180° around z) on a single β-strand are illustrated using the colored box. This box is set into the zipper lattice to schematize homosteric zippers, as in (d) and (i) and in Fig. 2 ▶. β-Strands run from the N-terminus to the C-terminus parallel to the z axis (from the cyan side of the box to the blue side). The y axis is perpendicular to the magenta and yellow sides. The x axis, which is perpendicular to the green and amber sides, runs through the interface of the two spinal β-sheets. (g) The exterior surface of the box is shown as if the box were unfolded. (h) The box is shown in four orientations representing the four rotations on the reference (labeled with the identity operation, E). The subscripts have been dropped from the rotation labels E, I, J and K. (i) The GNNQQNY homosteric zipper (zipper group 1b) is depicted as two stacks of colored boxes. Two repeats (unit cells) are shown. The two β-sheets are staggered along the y axis as dictated by the zipper group 1b generators (E and Jxy), producing 2₁ symmetry along the spine axis. (j) The atomic resolution crystal structure of mcLVFFA (Liu et al., 2011 ▶) contains a parallel, face=back β-sheet. The structure of one dimer of a macrocycle tetramer is shown as a ball-and-stick model with the β-strands (LVFFA) represented as cartoons. In the top macrocycle (amber), the residues Leu1, Phe3 and Ala5 project toward the viewer, given the numbering 1–5. In the bottom macrocycle (green), the residues Val2 and Phe4 project toward the viewer.

A variety of steric zipper symmetries have emerged from X-­ray crystallographic studies of the adhesive segments of amyloid fibers (Nelson et al., 2005 ▶; Sawaya et al., 2007 ▶; Wiltzius et al., 2009 ▶; Colletier et al., 2011 ▶). In these studies the spinal β-­sheets have identical β-strands running nearly perpen­dicular to the spine axis (Fig. 1 ▶ c). Additionally, all of the β-­strands in a given spine have identical packing environments. Given the growing catalog of amyloid interactions, it is useful to enumerate the symmetries of these interactions, just as it was useful to enumerate the space groups: all possible ways to pack identical objects. Here, I derive and illustrate all possible steric zipper interactions between identical protein segments wherein all segments share identical packing environ­ments: the so-called homosteric zippers.

In all steric zipper X-ray structures determined to date, two β-sheets form the spine (Sawaya et al., 2007 ▶). The spinal β-­sheets of a zipper are identical in that (i) both β-sheets are parallel (i.e. all β-strands run in the same direction) or antiparallel (alternate β-strands run in opposite directions) and (ii) both β-sheets have the same β-hydrogen-bonding pattern such that identical residues make the same β-hydrogen-bonding contacts in both β-sheets. Additionally, these atomic resolution structures reveal steric zippers that consist exclusively of β-strands of a single sequence, called ‘homosteric zippers’ (Eisenberg & Jucker, 2012 ▶). Homosteric zippers differ from ‘heterosteric zippers’, in which the β-strands of the spine have more than one sequence.

Sawaya and coworkers classified the known homosteric zipper structures using three class constraints to specify zipper features: (i) how each β-strand interacts with its nearest-neighboring β-strands in the same β-sheet (‘parallel’ or ‘antiparallel’), (ii) whether the same sides of both β-sheets are up (‘up–up’) or whether one is up and other is down (‘up–down’) or whether both can be rotated by 180° around an axis perpendicular to the β-sheets to yield identical β-sheets (‘up=down’) and (iii) whether identical (‘face-to-face’) or opposite (‘face-to-back’) faces of the β-­sheets create the zipper interface or whether the β-sheets can both be flipped around an axis parallel to the spine axis to yield the same β-­sheets (‘face=back’). Eight classes of homo­steric zippers arise from the possible combinations of these class constraints (Sawaya et al., 2007 ▶).

The group-theoretic treatment herein establishes a mathematically rigorous classification of 15 zipper groups and shows that the full set of homosteric zipper classes should expand to ten. To enumerate all homosteric zipper classes, I describe their symmetries in terms of a coordinate system in which the homosteric zipper spine is oriented with its β-­hydrogen bonds (backbone C=O and N—H groups) running nearly parallel to the y axis and with its β-­strands running nearly parallel to the z axis (Fig. 1 ▶ c). The spine axis is parallel to the y axis, lying in the interface between the β-sheets at a defined location in the coordinate system (Fig. 1 ▶ f).

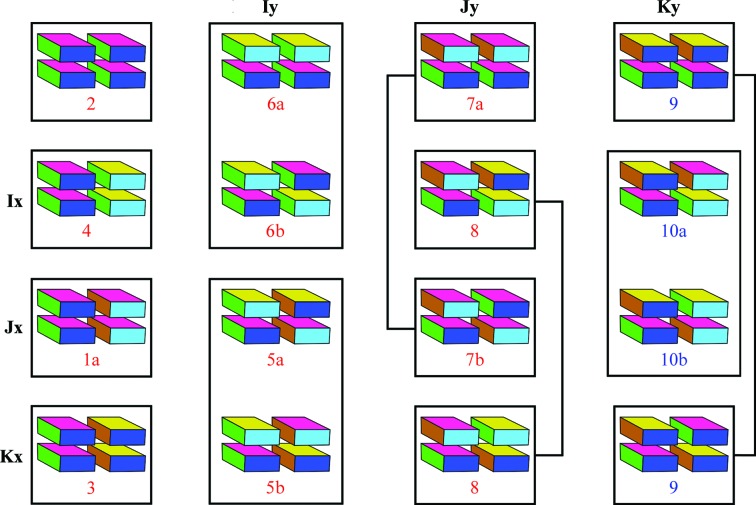
By enumerating all possible combinations of symmetry operations (Table 1 ▶), I demonstrate the existence of 15 distinct symmetry groups, termed ‘zipper groups’ (Table 2 ▶). Each of the eight homosteric zipper classes identified by Sawaya and coworkers corresponds to a subset of the zipper groups, accounting for 12 of the 15 zipper groups. Two novel classes of homosteric zippers correspond to the three remaining zipper groups (Fig. 2 ▶), extending the number of homosteric zipper classes to ten.

Table 1. Representations of the zipper-group generators.

Indices listed in the first column specify elements that differ from the 1 ₄ identity projective transformation matrix.

Element	E	Ix	Jx	Kx	Iy	Jy	Ky	Ixy	Jxy	Kxy
1 1	1	1	1	1	1	1	1	1	1	1
2 2	1	1	1	1	1	1	1	1	1	1
3 3	1	1	1	1	1	1	1	1	1	1
1 4	0				0	0	0
2 4	0	0	0	0

Table 2. The 19 possible combinations of generators produce 15 distinct zipper groups.

Zipper-group names are based on the homosteric zipper classes described previously (Sawaya et al., 2007 ▶). Underlined positions are group generators. Each homosteric zipper class corresponds to two distinct zipper groups except for homosteric zipper classes 2, 3, 4, 8 and 9. The penultimate column indicates alternate symmetry that arises from the shift of one -sheet relative to the other along the z axis (described in the text). The last column indicates whether the symmetry of the zipper group requires the -sheets to be eclipsed, where neighboring -strands in the two -sheets are in the same plane.

Zipper group	Positions	Layer group	Principal axis	Alternate symmetry	Eclipsed
2	E	1 (p111)			N
4	E, Ix	9 (p2111)	x (21)		N
6a	E, Iy	8 (p211)	x (twofold)	p2111	Y
4	E, Ixy	9 (p2111)	x (21)		N
1a	E, Jx	8 (p121)	y (twofold)		Y
7a	E, Jy	9 (p1211)	y (21)		N
1b	E, Jxy	9 (p1211)	y (21)		N
3	E, Kx	3 (p112)	z (twofold)	p1121	N
9	E, Ky	3 (p112)	z (twofold)	c112	N
3	E, Kxy	3 (p112)	z (twofold)	p1121	N
6b	E, Ix, Iy, xy	10 (c211)	x (21 and twofold)	p2111	Y
8	E, Ix, Jy, Kxy	21 (p21212)		p212121	N
10a	E, Ix, Ky, Jxy	21 (p21212)			N
5a	E, Jx, Iy, Kxy	19 (p222)		p121	Y
7b	E, Jx, Jy, xy	10 (c121)	y (21 and twofold)		Y
10b	E, Jx, Ky, Ixy	20 (p2122)			Y
5b	E, Kx, Iy, Jxy	20 (p2212)		p1211	Y
8	E, Kx, Jy, Ixy	21 (p21212)		p212121	N
9	E, Kx, Ky, xy	3 (b112)	z (twofold)	i112	N

Figure 2.

Relationship of zipper groups to the ten homosteric zipper classes, eight of which have previously been described (Sawaya et al., 2007 ▶). Zipper groups are organized by the rotation and translation components of the generators. Zipper groups that satisfy previously identified homosteric zipper classes are labeled in red. Zipper groups that do not satisfy any of the previously identified classes are labeled in blue. E (identity) and the generators in the row and column headings produce the zipper groups listed in each cell of the chart (see also Table 2 ▶). Not shown here is zipper group 1b (shown in Fig. 1 ▶ i), which is generated by E and Jxy. Zipper groups that satisfy the same homosteric zipper classes are shown connected by a line or boxed together.

2. Methods: derivation of the 15 homosteric zipper groups  

2.1. The zipper-group positions  

I represent the homosteric zipper lattice by a set of translations, {e ₃, x ₃, y ₃, xy ₃} (1), such that one β-sheet is centered on e ₃ and another on x ₃, with the spine axis halfway between e ₃ and x ₃ and running parallel to the y axis (Fig. 1 ▶ f),

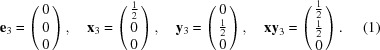β-Strands that occupy a zipper lattice can be in one of four orientations (2) that correspond to a reference (E ₃) or π rotations (I ₃, J ₃ and K ₃) around each of the three principal axes (x, y and z, respectively),

A multicolored box (shown as if unfolded in Fig. 1 ▶ g) illustrates these orientations. Different sides of the box are visible depending on the orientation (Fig. 1 ▶ h).

Combining the translations {e ₃, x ₃, y ₃, xy ₃} with rotations {E ₃, I ₃, J ₃ and K ₃} produces positions. For example, J ₃ and x ₃ combine to produce the position Jx. Positions are represented as 4 × 4 projective transformation matrices. An example is shown in (3):

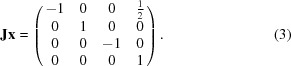The resulting positions (E, I, J, K, x, Ix, Jx, …, Kxy) form a finite group under matrix multiplication wherein the translation component (elements [1 4], [2 4] and [3 4]) of the product matrix is under modulo 1. This modulo operation simply implies that a translation as large or larger than a unit cell moves to a position in a different unit cell.

2.2. Ten generators produce the 15 zipper groups  

Every symmetry group available to zipper lattices may be produced from ten generators (Table 1 ▶) combined such that no more than one generator with a given translation (e ₃, x ₃, y ₃ or xy ₃) is used in each combination. This requirement simply implies that no two segments may occupy the same lattice position. The resulting 15 distinct zipper groups are layer groups of non-enantiomorphic objects expanded to include multiple settings for several of the layer groups (Table 2 ▶).

To illustrate a zipper group, I place multicolored boxes that represent specific orientations (Fig. 1 ▶ h) into a lattice. An example is Fig. 1 ▶(i), which illustrates two repeats of a GNNQQNY homosteric zipper (PDB entry 1yjp; Nelson et al., 2005 ▶) which belongs to zipper group 1b. Fig. 1(f) depicts one unit cell of the zipper group 1b lattice.

2.3. Zipper groups have layer-group symmetry  

Although the zipper-group settings are different from the standard layer-group settings, the zipper groups have layer-group symmetry. For example, the generators for zipper group 1b (E and Jx) combine to generate layer group 8 with C ₂ ^y point symmetry. This symmetry is demonstrated by changing the basis such that the translation components of the two positions shift by (−¼ 0 0)^T (4),

Different zipper groups may have the same layer-group symmetry (Table 2 ▶). For example, zipper groups 1b and 7a both have layer group 9 symmetry. These two groups are distinguished by their settings, which places symmetry axes at different locations in the two zipper groups. Zipper group 1b has 2₁ symmetry along the spine axis at x = ¼. In contrast, zipper group 7a has 2₁ symmetries coincident with the centers of the β-sheets at x = 0 and x = ½. Because of the stereochemistry of β-hydrogen bonding, some symmetries along the z axis in zipper groups 9, 10a and 10b are imperfect.

3. Discussion  

3.1. Nomenclature of the zipper groups reflects their relation to the homosteric zipper classes  

Because zipper-group symmetries satisfy homosteric zipper classes, the names of the zipper groups have been assigned to reflect the names of homosteric zipper classes (Table 2 ▶). For example, zipper groups 1a and 1b satisfy the homosteric zipper class 1 constraints (parallel, up–up, face=back). Fig. 2 ▶ illustrates the relationships between zipper groups, their generators and the homosteric zipper classes.

3.2. Zipper groups predict novel homosteric zipper symmetries  

A complete enumeration of zipper groups (Table 2 ▶) reveals that three zipper groups (9, 10a and 10b) remain after accounting for all eight previously identified homosteric zipper classes (Sawaya et al., 2007 ▶). Zipper groups 9, 10a and 10b satisfy the novel combination of parallel, face=back. Zipper group 9 differs from 10a and 10b in that both β-sheets of zipper group 9 run in the same direction along z (a class constraint termed ‘head-to-head’; Fig. 2 ▶). Zipper groups 10a and 10b have β-sheets that run in opposite directions along z (‘head-to-tail’). Although not yet observed in atomic structures of homosteric zippers, a parallel, face=back β-sheet has been observed in the atomic resolution crystal structure of the mcLVFFA macrocyclic β-sheet mimic (Liu et al., 2011 ▶). In this structure (Fig. 1 ▶ j), the sequence LVFFA makes a parallel, face=back β-sheet, suggesting that LVFFA has the potential to form zipper group 9, 10a or 10b.

3.3. Rationale for the preponderance of certain zipper groups  

Some zipper groups are observed in crystal structures more frequently than expected, perhaps because symmetry influences the stability of the amyloid spine. For example, the symmetries of several zipper groups require that interacting β-­strands from different β-sheets be in the same plane, where the plane is perpendicular to the spine axis. Such zipper groups are described as ‘eclipsed’ (Table 2 ▶). Of the 15 zipper groups, seven are eclipsed. Yet among all 44 published crystallo­graphic homosteric zippers (Table 3 ▶), eclipsed zipper groups are rare, comprising only seven of the 44 zippers. This bias towards ‘staggered’ zipper groups (groups that are not eclipsed) may arise from the profile method used to identify amyloidogenic segments, which employs the zipper group 1b NNQQNY zipper as a template (Nelson et al., 2005 ▶; Thompson et al., 2006 ▶). However, a strong bias towards staggered zippers exists even when group 1b zippers are excluded, with only seven of the 24 remaining zippers being eclipsed. The bias towards staggered zippers may reflect the fact that staggered zippers more readily interdigitate than eclipsed zippers, increasing the surface complementarity and hence the energetic favorability of sheet adhesion.

Table 3. The zipper groups of 44 published homosteric zipper crystal structures.

Zipper-group symmetries are related to crystallographic symmetry. The layer-group symmetries of the zippers are shown in the column ‘Layer symmetry’. The ‘Cryst’ column shows the crystallographic symmetry of the structure. The following annotations are used. , : for a structure, the crystallographic symmetry bearing the given annotation produces the zipper symmetry bearing the same annotation. : noncrystallographic symmetry or pseudosymmetry. a: the twofold component of the C2 crystallographic symmetry creates the twofold component of the C2 zipper symmetry. b: the 2₁ crystallographic symmetry creates the 2₁ component of the C2 zipper symmetry, c: the same crystal structure has two different zipper interfaces. Parentheses: the strict layer-group symmetry indicated is broken by a z-shift.

	Sequence	PDB code	Layer symmetry	Layer group	Zipper group	Cryst
1	GDVIEV	3sgs	p 2111	9	4	P1211
2	AIIGLM	2y3j	p111	1	2	P111
3	MVGGVVIA	2y3k	p111	1	2	P111
4	MVGGVVIA	2y3l	p1211	9	7a	P1211
5	KLVFFA	2y29	p1211	9	7a	P21 2121
6	KLVFFA	2y2a	p1211	9	7a	P 212121
7	GAIIGL	3pzz	p 211	10	6b	P111
8	NKGAII	3q2x	p1211	9	1b	P1211
9	KLVFFA	3ow9	c1a21	10	7b	C1a21
10	VQIVYK	3ovl	p1211	9	1b	C121
11	GGVLVN	3ppd	p1211	9	1b	P2121 21
12	MMHFGN	3nve	p 211	8	6a	P1211
13	IIHFGS	3nvf	p121	8	1a	P2121 2
14	MIHFGN	3nvg	p1211	9	1b	P21 2121
15	MIHFGND	3nvh	p1211	9	1b	P21 2121
16	LSFSKD	3loz	p1211	(20)	5b	P1211
17	GYMLGS	3nhc	p 21 21 21	(21)	8	P 21 2121
18	GYVLGS	3nhd	p 21 21 21	(21)	8	P 21 212
19	LVEALYL	3hyd	p1211	9	1b	C121
20	HSSNNF	3fpo	p 2111	9	4	P1211
21	VQIVYK	3fpq	p1211	9	1b	C121
22	NFLVHS	3fr1	p1211	9	7a	P21 2121
23	NFLVHSS	3fth	c b211	10	6b	P1b211
24	NVGSNTY	3ftk	p1211	9	1b	P1211
25	NVGSNTY	3ftl	p1211	9	1b	P1211
26	SSTNVG	3ftr	p1211	9	1b	P21 2121
27	NNQNTF	c 3vfa	p1211	9	1b	P1211
28	NNQNTF	c 3vfa	p1211	9	1b	P1211
29	AILSST	3fod	p 21 21 2	21	8	P1211
30	SSTNVG	3dg1	p1211	9	1b	C121
31	NNFGAIL	3dgj	p1211	9	1b	P21 2121
32	GGVVIA	2onv	p 2111	9	4	P 21212
33	SSTSSA	2onw	p1211	9	1b	P21 2121
34	NNQQ	2onx	p 2111	9	4	P1211
35	MVGGVV	2okz	p 21 21 21	(21)	8	P1211
36	SNQNNF	2ol9	p111	1	2	P111
37	NNQQ	2olx	p1211	9	1b	P21 2121
38	GNNQQNY	2omm	p1211	9	1b	P21 2121
39	LYQLEN	2omp	p1211	9	7a	P1211
40	VEALYL	2omq	p1211	9	7a	P111
41	VQIVYK	2on9	p1211	9	1b	P1211
42	MVGGVV	2ona	p 21 21 21	(21)	8	P111
43	NNQQNY	1yjo	p1211	9	1b	P1211
44	GNNQQNY	1yjp	p1211	9	1b	P1211

3.4. Zipper-group pseudo-symmetry is observed in some crystal structures  

In experimental structures, the strict layer-group symmetries of several zipper groups are broken by a shift along the z axis (termed ‘z-shift’) of one β-sheet relative to the other (Table 2 ▶, ‘Alternate Symmetry’). This z-shift produces a 2₁ screw from C ₂ ^z point symmetry of zipper groups 3, 8 and 9. Similarly, the z-shift creates 2₁ symmetry from C ₂ ^x point symmetry of zipper groups 6a and 6b. The potential for some of these 2₁ screw axes in x and z has been recognized previously (Sawaya et al., 2007 ▶). In zipper groups 5a and 5b, the z-shift completely removes any symmetries in x and z. Because zipper groups are defined by generators with only x and y translations, the z-shift does not influence the ability of the affected zipper groups to satisfy homosteric zipper classes.

4. Conclusion  

Here, I develop a mathematically rigorous classification of homosteric zippers using group theory to derive the 15 zipper groups that specify all possible symmetries available to homosteric zippers. Zipper groups extend previous work in which eight symmetry classes of homosteric zipper spines were identified from crystal structures and from an intuitive analysis of the ways that pairs of β-sheets can interact (Sawaya et al., 2007 ▶). Zipper groups may be categorized such that the complete homosteric zipper classification developed by Sawaya and coworkers expands to ten classes. Subsequent to the work of Sawaya and coworkers, a sheet satisfying this expanded set of symmetries was observed in a crystal structure (Liu et al., 2011 ▶). I anticipate that structures of amyloid spines belonging to the new homosteric zipper symmetries will be discovered in the future.