Basic Concepts in Population Modeling, Simulation, and Model-Based Drug Development

Abstract

Modeling is an important tool in drug development; population modeling is a complex process requiring robust underlying procedures for ensuring clean data, appropriate computing platforms, adequate resources, and effective communication. Although requiring an investment in resources, it can save time and money by providing a platform for integrating all information gathered on new therapeutic agents. This article provides a brief overview of aspects of modeling and simulation as applied to many areas in drug development.

Modeling as a Tool in Drug Development

Overview

This tutorial serves as an introduction to model (and simulation)-based approaches for drug development for novice modelers and for those who, while not being modelers themselves, nevertheless use the approach and want to increase their understanding of the process. The tutorial provides some history, describes modeling and simulation (e.g., pharmacometrics) with emphasis on population modeling and simulation, and discusses some regulatory, project management, and information technology issues. This is the first in a series of articles aimed at providing basic information on pharmacometrics.

Brief history

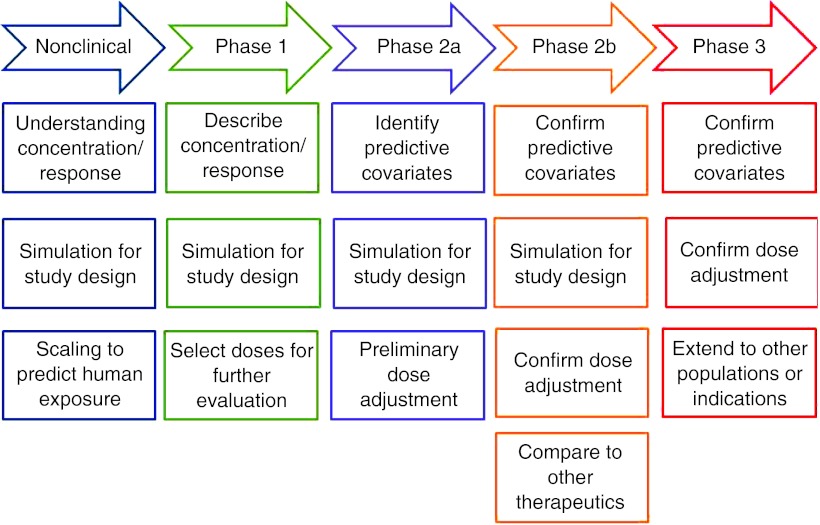
Atkinson and Lalonde¹ stated that “dose selection and dose regimen design are essential for converting drugs from poisons to therapeutically useful agents.” Modeling and simulation have emerged as important tools for integrating data, knowledge, and mechanisms to aid in arriving at rational decisions regarding drug use and development. Figure 1 presents a brief outline of some areas in which modeling and simulation are commonly employed during drug development. Appropriate models can provide a framework for predicting the time course of exposure and response for different dose regimens. Central to this evolution has been the widespread adoption of population modeling methods that provide a framework for quantitating and explaining variability in drug exposure and response.

Figure 1.

Modeling and simulation during drug development.

All drugs exhibit between-subject variability (BSV) in exposure and response, and many studies performed during drug development are aimed at identifying and quantifying this variability. A sound understanding of the influence of factors such as body weight, age, genotype, renal/hepatic function, and concomitant medications on drug exposure and response is important for refining dosage recommendations, thereby improving the safety and efficacy of a drug agent by appropriately controlling variability in drug exposure.

Population modeling is a tool to identify and describe relationships between a subject's physiologic characteristics and observed drug exposure or response. Population pharmacokinetics (PK) modeling is not a new concept; it was first introduced in 1972 by Sheiner et al.² Although this approach was initially developed to deal with sparse PK data collected during therapeutic drug monitoring,³ it was soon expanded to include models linking drug concentration to response (e.g., pharmacodynamics (PD)).⁴ Thereafter, modeling has grown to become an important tool in drug development.

Population parameters were originally estimated either by fitting the combined data from all the individuals, ignoring individual differences (the “naive pooled approach”), or by fitting each individual's data separately and combining individual parameter estimates to generate mean (population) parameters (the “two-stage approach”). Both methods have inherent problems, which become worse when deficiencies such as dosing compliance, missing samples, and other data errors are present,⁵ resulting in biased parameter estimates. The approach developed by Sheiner et al. addressed the problems associated with both the earlier methods and allowed pooling of sparse data from many subjects to estimate population mean parameters, BSV, and the covariate effects that quantitate and explain variability in drug exposure. This approach also allowed a measure of parameter precision by generation of SE.

At first glance, the term “population PK” suggests that the individual patient is ignored; however, the importance of the individual in population models is highlighted by the description of variability, with data from each individual contributing to the identification of trends such as changes in drug exposure with changing age or weight, and the subsequent estimation of the population characteristics. Pharmacometrics can be used to improve our understanding of mechanisms (e.g., linear or saturable metabolism), inform the initial selection of doses to test, modify or personalize dosage for subpopulations of patients, and evaluate the the appropriateness of study designs.⁶

What are Models?

In the broadest sense, models are representations of a “system” designed to provide knowledge or understanding of the system. Models are usually simplified representations of systems, and it is the simplification that can make them useful. The nature of the simplification is related to the intended use of the model. Models are therefore better judged by their “fitness for purpose” rather than for being “right” or “true.” For example, one scale model of an airplane may be made for testing its aerodynamics in a wind tunnel, while another may be made for visualizing and choosing the exterior colors. Neither of the models is meant to do the job of the real airplane. Furthermore, neither is a “true” model, but each may be fit for its intended purpose. This idea was famously articulated by George Box who stated: “Essentially, all models are wrong, but some are useful.”⁷ Fitness for purpose implies “credibility” and “fidelity.” Credibility implies that the model conforms to accepted principles and mechanisms that can be justified and defended. Credible models are ones for which the assumptions made in the construction are understood and clearly stated. Fidelity is gauged by comparing the model to components of the system (reality) that are considered important (note that fidelity does not always imply credibility). Model development can therefore be envisaged as ranking credible models according to a range of metrics that distil their “fitness for purpose,” preferably including considerations of timeliness and economy.

Models can be physical objects as in the airplane example mentioned earlier, or abstract representations; this is also true of pharmacometrics models. It is possible to represent PK models as analog electric circuits or hydraulic systems.^8,9 However, in PK it is more convenient to consider conceptual models—models that define a collection of mathematical relationships. Like all mathematical concepts, these exist as ideas that can be represented in various terminologies and through different physical media (from a piece of paper, to a spreadsheet to programming language).

Models provide a basis for describing and understanding the time-course of drug exposure and response after the administration of different doses or formulations of a drug to individuals, and provide a means for estimating the associated parameters such as clearance and volume of distribution of a drug. Population models can be developed using relatively few observations from each subject, and the resulting parameter estimates can be compared to previous assessments to determine consistency between studies or patient populations. The data can also be compared with those relating to other drugs in the same therapeutic class, as a means of evaluating the development potential of a new therapeutic agent. Consequently, one of the primary objectives of any population modeling evaluation is to develop a mathematical function that can describe the pharmacologic time course of a drug over the range of doses evaluated in clinical trials.

Types of Models

PK models

PK models describe the relationship between drug concentration(s) and time. The building block of many PK models is a “compartment”—a region of the body in which the drug is well mixed and kinetically homogenous (and can therefore be described in terms of a single representative concentration at any time point¹⁰). Compartments have proven to be ubiquitous and fundamental building blocks of PK models, with differences between models often being defined by the way the compartments are connected. Mammillary models generally have a central compartment representing plasma with one or two peripheral compartments linked to the central compartment by rate constants (e.g., k₁₂ and k₂₁).¹¹ Compartments in mammillary models can sometimes be real physiologic spaces in the body (such as the blood or extravascular fluid), but are more typically abstract concepts that do not necessarily represent any particular region of the body.

In contrast, physiology-based PK models (PBPK) use one or more compartments to represent a defined organ of the body, with a number of such organ models connected by vascular transport (blood flow) as determined by anatomic considerations.¹² Mammillary PK models can generally be informed by blood or plasma concentrations alone whereas, with PBPK models, tissue and plasma concentrations are typically required, or parameters may have to be set according to values mentioned in the literature. This makes it complicated to apply PBPK models to clinical data; on the other hand, it provides a greater scope to understand the effect of physiologic perturbations and disease on drug disposition, and often improves the ability to translate findings from preclinical to clinical settings.

PKPD models

PK/PD (PKPD) models include a measure of drug effect (PD). They have been the focus of considerable attention because they are vital for linking PK information to measures of activity and clinical outcomes.¹³ Models describing continuous PD metrics often represent the concentration–effect relationship as a continuous function (e.g., linear, E_max, or sigmoid E_max). The concentration that “drives” the PD model can be either the “direct” central compartment (plasma) drug concentration, or an “indirect” effect wherein the PD response lags behind the plasma drug concentration. Models describing discrete PD effects (e.g., treatment failure/success, or the grade of an adverse event) often use logistic equations to convert the effect to a probability within a cohort of subjects. This probability can be related to a PK model. Exposure–response models are a class of PKPD models wherein the independent variable is not time, but rather, a metric describing drug exposure at steady-state (e.g., dose, area under the curve (AUC), or peak plasma concentration (C_max)).

Disease progression models

Disease progression models were first used in 1992 to describe the time course of a disease metric (e.g., ADASC in Alzheimer's disease¹⁴). Such models also capture the inter-subject variability in disease progression, and the manner in which the time course is influenced by covariates or by treatment.¹⁵ They can be linked to a concurrent PK model and used to determine whether a drug exhibits symptomatic activity or affects progression.¹⁶ Models of disease progress in placebo groups are crucial for understanding the time course of the disease in treated groups, as well as for predicting the likely response in a placebo group in a clinical trial.¹⁷

Meta-models and Bayesian averaging

Meta-analyses means “the analysis of analyses.”¹⁸ They are prospectively planned analyses of aggregate (e.g., mean) results from many individual studies to integrate findings and generate summary estimates. Meta-models are used to compare the efficacy or safety of new treatments with other treatments for which individual data are not available, such as comparisons with competitors' products. They can also be used to re-evaluate data in situations involving mixed results (e.g., some studies showed an effect and others did not).¹⁹ Meta-models can describe PD or disease progression,²⁰ and are now frequently used to underwrite go/no go decisions during drug development. There are several important factors to consider in relation to meta-analysis: (i) the objectives and goals should be clearly defined before initiating any work; (ii) the data incorporated in the analysis must be complete, compatible, and unbiased (e.g., not limiting data only to those from successful trials); (iii) between-study and between-treatment-arms variability should be accounted for; and (iv) combining individual data with aggregate data must be done carefully, the method of combination depending partly on the structure of the model.²¹

The practice of selecting one model from a series of proposed models and making inferences on the basis of the selected model ignores model uncertainty. This could impair predictive performance and overlook features that other models may have captured better. Bayesian model averaging combines models and accounts for model uncertainty.²² A typical application of this Bayesian approach is where several models for a drug exist in the literature and it is not clear which model should be used for simulating a new study. It is certainly possible to fit the predictions of the available models and develop a single model that incorporates the contributions of multiple models. However, the Bayesian method of model averaging allows all existing models to contribute to a simulation, with the input being weighted on the basis of prespecified criteria such as the quality of the data or the model, or other factors. This approach, therefore, incorporates the uncertainty inherent in each contributing model.

The Components of Population Models

Population modeling requires accurate information on dosing, measurements, and covariates. Population models are comprised of several components: structural models, stochastic models, and covariate models. Structural models are functions that describe the time course of a measured response, and can be represented as algebraic or differential equations. Stochastic models describe the variability or random effects in the observed data, and covariate models describe the influence of factors such as demographics or disease on the individual time course of the response. These components are described in detail later in this article.

Data and database preparation

It is axiomatic that models are only as good as the data they are based on. Databases used for modeling are frequently complex, requiring accurate information on timing, dates, and amounts of the drug administered, sample collection, and associated demographic and laboratory information. In addition, because data are collated in a unique fashion (so that patient factors are recorded together for each patient, rather than as separate listings which is the more traditional method of presenting demographic and laboratory data), errors can sometimes be found that would not ordinarily be noted. For example, an 80-year-old female subject weighing 40 kg, with an estimated creatinine clearance of 120 ml/min, would seem unlikely to be included in a model database; however, when considered individually, each of the records would not have been thought to be problematic during routine data checks. Units for all values must be consistent throughout the database, and this requirement can make it more difficult to pool data from several studies. Establishing quality assurance of both the merged database and the final results is more intensive, and generally requires special training.

Structural models as algebraic equations

The simplest representation of a PK model is an algebraic equation such as the one representing a one-compartment model, the drug being administered as a single intravenous bolus dose:

This model states the relationship between the independent variable, time (t), and the dependent variable, concentration (C). The notation C_(t) suggests that C depends on t. Dose, clearance (CL), and distribution volume (V) are parameters (constants); they do not change with different values of t. Note the differences in the uses of the terms “variable” and “parameter.” The dependent and independent variables are chosen merely to extract information from the equation. In PK, time is often the independent variable. However, Equation (1) could be rearranged such that CL is the independent variable and time is a constant (this may be done for sensitivity analysis for example).

Linearity and superposition

Equation (1) produces an exponential curve of concentration vs. time. Fitting Equation (1) to the data is therefore known as nonlinear regression. Unfortunately, the term “linearity” can be used to describe distinctly different properties of equations in pharmacometrics. Despite the nonlinear time course that it produces, Equation (1) is linear with respect to its parameters (i.e., a plot of C vs. CL or C vs. V produces a straight line), which has useful properties. The concentration–time curve for any one dose can be added to that for another dose, and the sum will produce a curve that is the same as that for the two doses given together. This principle of “superposition”²³ also applies if there are temporal differences in the timings of the doses, and can be exploited to model the outcome of complex dose regimens simply by summing the results for each of the single doses as defined by their corresponding algebraic equations.

Structural models as differential equations

Some complex pharmacometrics systems cannot be stated as algebraic equations. However, they can be stated as differential equations. Rewriting Equation (1) as a differential equation:

A differential equation describes the rate of change of a variable. In this example, dC/dt is the notation for the rate of change of concentration with respect to time (sometimes abbreviated as C′). Note that differential equations require specification of the initial value of the dependent variables. Here, the value of C at time zero (C₀) is Dose/V.

Numerical methods are needed to solve systems of differential equations. Euler's method is a simple example and can be easily coded. Numerically solving Equation (2) requires approximating the value of the variable (C₂) after an increment in time (t₂ – t₁) based on the previous value (C₁) and the implied rate of change (–CL/V*C₁):

An initial value is needed for this process (to give the first value for C₁, see Equation (2)). Computational errors are minimized by keeping the time increments very small. There has been extensive development of algorithms to solve differential equations numerically, and in most contexts the difference between an analytical solution and the approximate numerical solution is inconsequential. However, solving a system of equations is computationally intensive and, even with automated, rapid processors, there is a time penalty for using differential equations to describe a model. Generally, algebraic equations and superposition are exploited unless the model is complex or nonlinear with respect to its parameters (e.g., saturable metabolism), in which case differential equations are necessary.

Stochastic models for random effects

Population models provide a means of characterizing the extent of between-subject (e.g., the differences in exposure between one patient and another) and between-occasion variability (e.g., the differences in the same patient from one dose to the next) that a drug exhibits for a specific dose regimen in a particular patient population. Variability is an important concept in the development of safe and efficacious dosing; if a drug has a relatively narrow therapeutic window but extensive variability, then the probability of both subtherapeutic and/or toxic exposure may be higher,²⁴ making the quantitation of variability an important objective for population modeling.

In classical linear regression, there is only one level of unexplained variability, namely, the difference between a particular observation and the model-predicted value for that observation (residual unexplained variability (RUV)). In contrast, population models often partition unexplained variability into two or more levels (sometimes called hierarchies). Commonly, the first level is variability between parameter values for a particular subject and the population value of the parameters (random BSV). The second level is the unexplained residual variability (RUV), common to standard linear regression.

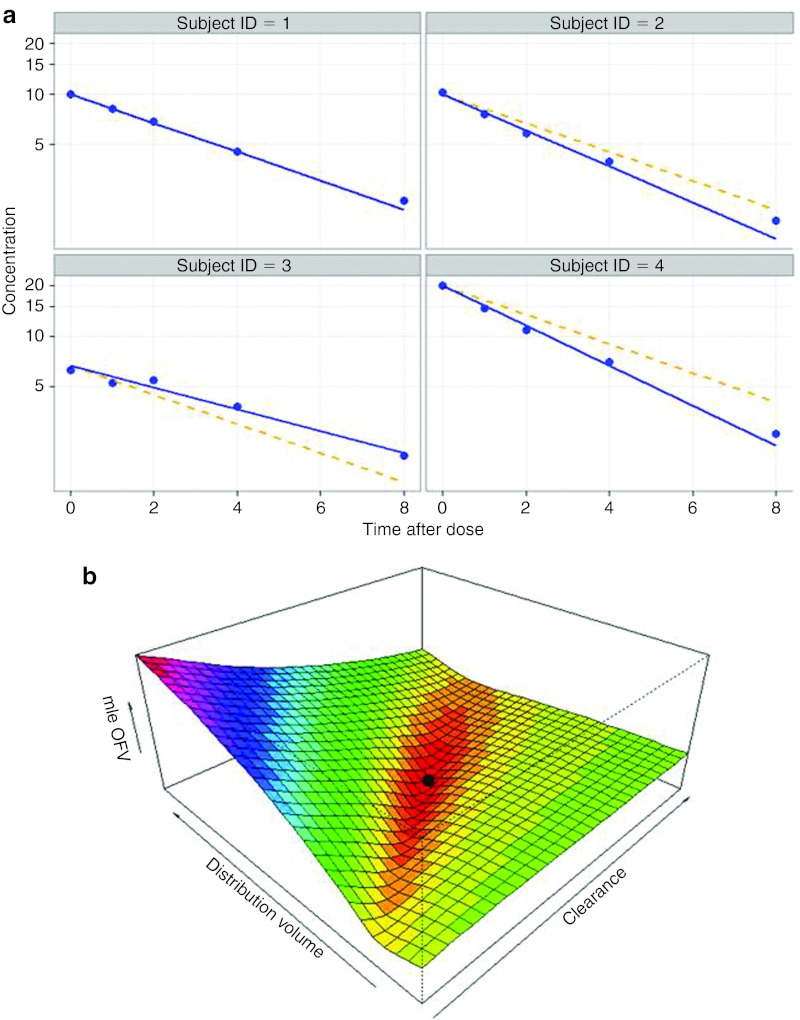
A proper understanding of population models requires an understanding of some of the key concepts and terminology relating to these different levels of variability. As an example, consider a PK study involving four subjects (Figure 2) to each of whom an intravenous bolus dose of a drug was given, with the kinetics of the drug being capable of being described in terms of a one-compartment model (Equation (1)). Each subject's data can be described by the same structural model described in Equation (1), but each subject is described by unique parameter values for CL and V (Table 1). The model may have either a “fixed” parameter (no BSV) or a “random-effect” parameter (including BSV). Confusingly, the term “fixed” is also used in modeling to indicate a parameter that is not estimated from the data; however, the different uses of the term “fixed” can usually be inferred from the context. In the example cited, CL is a random-effect parameter and V is a fixed-effect parameter. Fixed effects are represented by parameters (THETA) that have the same value for every subject. THETA is typically estimated from the data (e.g., “V was estimated to be 13.6 l in the population”). Random effects are represented as a quantity (ETA) reflecting the difference between an individual's parameter value and the population value. ETA is assumed to be normally or log-normally distributed across the population being evaluated, is centered around zero, and is summarized by its variance (or SD), often termed as OMEGA. OMEGA describes the distribution of BSV for the parameter across the population being studied (e.g., Figure 3c). Typically, both THETA and OMEGA are estimated from the data (e.g., “CL was estimated to be 2.1 l/min with a BSV of 28%”). Population models usually have fixed effect as well as random-effect parameters, and are therefore called “mixed-effect” models.

Figure 2.

Best fit for a simple population pharmacokinetics model. (a) Goodness-of-fit plots for the model shown in Table 1. Symbols represent the observed data. The solid blue line denotes individual predicted concentration (C_IPRED). The broken line denotes the population predicted concentration (C_PRED). C_PRED accounts for the explainable between-subject differences (e.g., dose and covariates). C_IPRED accounts for both explainable and unexplainable differences (e.g., BSV in CL) between subjects. (b) When only two parameters are fitted (CL_POP and V_POP in this case) the OFV is a three-dimensional surface. The best fit parameters are shown by the black symbol in the “trough” in the objective function value (OFV) surface.

Table 1. Equations for a simple population pharmacokinetic model.

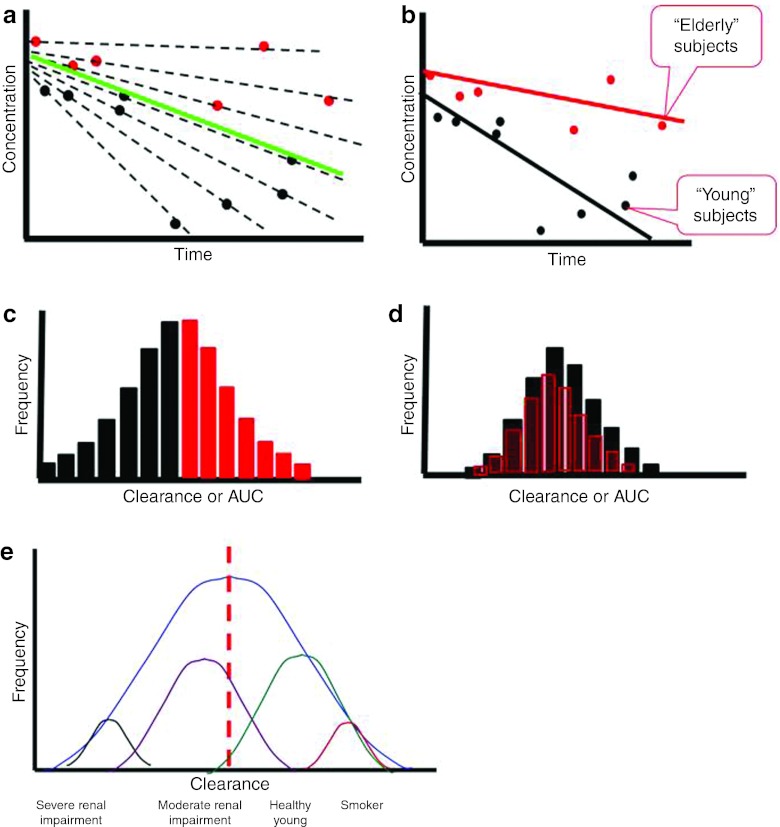
Figure 3.

Effect of covariates on variability. (a) Plot of concentrations vs. time. The solid green line denotes population average, the broken black lines denote individual averages, the red symbols represent concentration values in elderly subjects, and the black symbols represent concentration values in young subjects. (b) The solid red line denotes the population average for elderly subjects, and the solid black line represents the population average for young subjects. (c) Frequency histogram of exposures (area under the curve (AUC)) or clearances across the entire population. (d) Frequency histogram of exposures or clearances after adjusting for age. (e) A representative distribution of clearance values with underlying distributions being associated with patient factors and covariates.

Population models need to include a description of RUV. RUV is defined by a quantity (EPS) reflecting the difference between the observed data for an individual and the model's prediction (the residual). EPS is assumed to be normally distributed and centered around zero, and is summarized by its variance (or SD), often termed as SIGMA. SIGMA is estimated from the data (e.g., “RUV was estimated to be 18%”). There are four estimated parameters in the model that have been described as an example: THETA1, THETA2, OMEGA, and SIGMA. The relationships between parameter values and variables in the example model are summarized in Table 2.

Table 2. Parameter and variable values for a simple population model.

Covariate models for fixed effects

The identification of covariates that explain variability is an important objective of any population modeling evaluation. During drug development, questions such as “how much does drug exposure vary with age?” are often answered by the results of clinical trials in healthy young and elderly subjects. However, such information can also be garnered through population modeling. Population modeling develops quantitative relationships between covariates (such as age) and parameters, accounting for “explainable” BSV by incorporating the influence of covariates on THETA. Figure 3a shows a hypothetical range of concentration–time profiles arising from an intravenous bolus of identical doses of a test drug to elderly and young patients. Taken together, without introducing a covariate into the population model, the range of clearance (and therefore AUC) values is quite wide (Figure 3b). However, when a covariate effect (age) is introduced into the model, characterizing the difference in clearance between young and elderly subjects (Figure 3b), the overall BSV in the AUC is reduced (Figure 3d). In this example, if dosing were adjusted to allow different doses for young and elderly patients, the range of exposures that patients experience in a clinical trial or in clinical use would be more consistent. In the example shown in Table 1, both CL and V scale linearly with body weight (WT), reflecting the explainable variability in these parameters attributable to body size. WT is normalized to a value of 70 kg, so that subjects with a weight of 70 kg take the typical population value. Mandema et al.²⁵ describe several well recognized approaches that have been used to evaluate the effects of covariates on population models. In general, however, graphical evaluations of the data are usually the best place to start.

The variability often encountered in the metrics of exposure, such as in AUC or peak or trough concentrations, can be thought of as a continuous distribution of values that is comprised of subpopulations arising from different demographic, laboratory, and pathological factors, as shown in Figure 3e. Identification and quantification of these differences can support dose recommendations for special populations of patients; conversely, they can show that dose adjustments are not warranted. Such recommendations are often derived through the use of simulation.

Concepts of Estimation and Simulation

The processes of estimation of parameters for models from data, and simulation of new data from models are fundamental to pharmacometrics. These topics are discussed further in this paper.

Estimation methods

The concept of estimating the “best parameters” for a model is central to the modeling endeavor. There are clear analogies to linear regression, wherein the slope and intercept parameters of a line are estimated from the data. Linear regression is based on “least squares” minimization. The difference between each pair of observed (e.g., C_obs) and predicted (e.g., “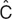”) values for the dependent variables is calculated, yielding the residual (C_obs – 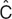). The best parameters achieve the lowest value of the sum of the squares of the residuals (which is used so that positive and negative residuals do not cancel each other out). The “sum of squares” term can be thought of as an “objective function.” It has a given value for each unique pair of slope and intercept parameters, and is lowest for the line of best fit.

Most pharmacometric models need some extensions to this least squares concept for estimating the parameters. The first extension is needed because the least squares objective function is dependent on the magnitude of the data (i.e., high data points can be given more “weight” than low data points) and, because there is often a subjective component to the choice of weights, it is best to avoid this situation. Maximum likelihood estimation is commonly used because it avoids the need for data weighting. For a given pair of observed and predicted data values, 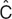is considered to have a possible range of values described by a normal distribution, with a mean of 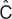and a SD given by the estimate of sigma (see Table 1). The likelihood of the observed data (closely associated with probability) is a metric summarizing the deviation of the observed data (C_obs) from the center of this distribution. For ease of computation, the maximum likelihood estimation objective function is usually expressed as the negative sum of the log of the likelihoods, yielding a single number—the maximum likelihood estimation objective function value (OFV). The minimum value of the OFV for a particular model and data set is associated with the “best fit” parameter values, but the absolute value of the OFV is not important. It is used within a model for comparing parameter values, and is compared between models for ranking them in order of goodness of fit for the same dataset. The OFV also offers some advantages. It allows simultaneous fitting of random effects and residual error (crucial to population models) and has a distribution (approximately χ²) that facilitates the use of statistical tests to make comparisons between models.

The second extension arises from the fact that, unlike linear models, most PK models are too complex to solve for the minimum value of the OFV by means of algebraic methods. Optimization approaches are used, involving searching for combinations of parameter values that produce the lowest value of the OFV. When two parameters are fitted, it is possible to show the OFV as a three-dimensional surface (Figure 2b). There are many optimization algorithms (“estimation methods”) for finding the minimum value of this OFV surface. The simplest of these is the “gradient method.” Starting at one point on the surface, the parameters are evaluated to determine the direction in which the OFV decreases the most. The next set of parameters is chosen to take a “step” in this direction, and the process is repeated until the minimum OFV is found. There are some key features of optimization processes, regardless of the actual algorithm used (the algorithm is usually chosen on the basis of accuracy, robustness, and speed). First is the need to specify initial parameter values (essentially telling the search algorithm where to start on the OFV surface). Second is the concept of local minima on the OFV surface. There is a risk that the search algorithm will find a local minimum rather than the lower global minimum. Local minima arise for some combinations of models and data when there are two sets of parameter values that, although different, provide similar fits to the data. Appropriate choice of initial values helps reduce the risk of finding a local minimum in estimation (for instance, by starting the search nearer the global minimum). Finally, as can be seen in Figure 2b, the minimum of the OFV sits in a “trough” on the OFV surface. The shape of this trough provides important information about the uncertainty in the parameter estimates. For a steep sided trough, there are a limited range of parameter values that can describe the data for this model. In contrast, a broad, shallow trough implies that a greater range of parameter values can describe the data for this model (i.e., uncertain/imprecise parameter estimates). This uncertainty in parameter estimates can be quantified from the shape of the “trough” on the OFV surface, and is usually reported either as SE of the parameter estimate or as confidence intervals for the parameter. For example, the statement “V was estimated to be 13.6 l with a SE of 11%” means that, given the model and data, there is a high certainty in the prediction of V. Precise parameter estimates are a desirable feature of a model, particularly when the parameter value is crucial in making inferences from the model. Over-parameterized models generally have one or more parameters with high imprecision (i.e., there is not enough information in the data to estimate the parameter) and may therefore benefit from simplification.

Simulation methods

Using models to simulate data is an important component of pharmacometric model evaluation and inference. For the purpose of evaluation, the model may be used to simulate data that are suitable for direct comparison with the index data. This can be done either by using a subset of the original database used in deriving the model (internal validation) or a new data set (external validation). For the purpose of inference, the model is generally used to simulate data other than observed data. Interpolation involves simulation of nonobserved data that lie within the bounds of the original data (e.g., simulating AUC for a 25 mg dose when the observed data used in building the model was for 20 and 30 mg doses). Extrapolation involves simulation of nonobserved data that lie outside the bounds of the original data (e.g., simulating AUC for a 100 mg dose when the observed data was for 20 and 30 mg doses). Extrapolation requires confidence in the assumptions of the underlying model. In this example, if the model has been designed with the assumption of dose linearity, and if the drug has saturable metabolism, the model predictions may be erroneous. Simulations should therefore be interpreted with a clear understanding of the limitations and assumptions inherent in the model. Nevertheless, using models to frame mechanisms and hypotheses, and for extrapolating and experimentally testing the model predictions, is part of the “Learn and Confirm” paradigm of model building.

Simulating from models with fixed-effect and random-effect parameters (i.e., stochastic simulation with population models) is more complex than non-stochastic simulation from simple fixed-effect models. Random-effect parameters account for unexplained variability in the data that must be recreated during simulation. This is done by using a random number generator to sample parameter values from a distribution, with the mean and SD of the distribution of random effects as found from the estimation process. Most modeling software has random number generators for a variety of distributions (e.g., uniform, normal, log-normal, binomial, etc.) as appropriate for a given model.

For stochastic simulations, the model needs to be simulated repeatedly so that the distribution of the simulated output can be summarized (e.g., mean values and SD). In theory, more simulation replicates are better, but the number that are actually performed is often limited by considerations of time and data size. A common “rule of thumb” is that at least 200 simulations are needed when summarizing simulated data as mean values, and at least 1,000 are needed when summarizing as confidence intervals. When simulating stochastic models with more than one random effect parameter, it is important to understand potential correlations among the parameters, and to account for this factor during simulation so as to avoid implausible combinations of parameters in individual subjects.

Clinical trial simulation is an important application of the simulation method. It is not a new method; it involves the application of old technologies to the problem of maximizing the information content obtained in earlier trials in order to ensure the greatest chance of conducting a new clinical trial with the desired outcome. Bonate²⁶ has reviewed applications for clinical trial simulation, and reported successful evaluations by several researchers. Simulation is a useful tool for determining key aspects of study design such as the appropriate doses for First-in-Humans trials, dose selection for proof-of-concept and pivotal studies, study design, subject numbers, sample numbers, timing, and other factors. When designing a clinical trial, it is important to ensure that sufficient information to estimate model parameters is collected, while also ensuring that the schedule is not onerous. Although it has been referenced in the Guidance to Industry,²⁷ the collection of a single trough value from each subject is insufficient to estimate parameters. A process referred to as “D-optimization” uses information from previous models to optimize the numbers and timing of samples collected from subjects.²⁸ Potential study designs can then be tested using simulations to ensure appropriateness of the design.

As described by Miller et al.,²⁹ clinical trial simulation is a part of the “Learn and Confirm” cycle of drug development. Information from previously conducted studies can be used to simulate expected ranges of responses for upcoming trials. Subsequently, information gathered in the new trial can be used to confirm the model and potentially augment information provided by the model. With each cycle, the robustness and suitability of the model becomes better established.

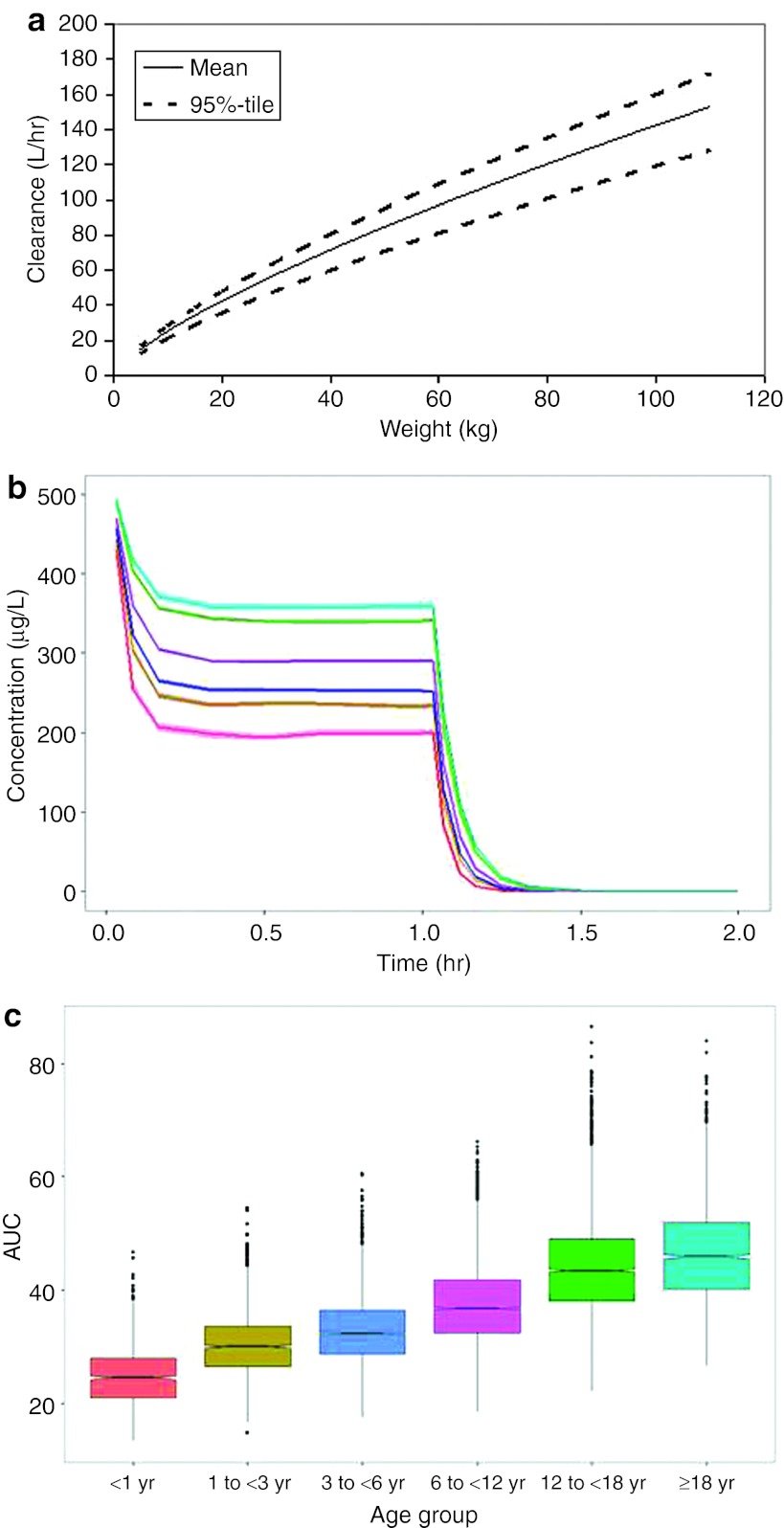
A hypothetical example of clinical trial simulation is provided in Figure 4. In panel a, the effect of weight on clearance of a drug is provided. Based on the narrow confidence intervals for this trend, the effect is well estimated and should be robust for simulation. A simulation of expected concentration–time profiles after a 1-h infusion of a 10 mg/kg dose to neonates, infants, young children, older children, adolescents, and adults is shown in Figure 4b. With this weight-based dose strategy, neonates and infants show a concentration–time profile that is substantially lower than expected as compared to adults. When the data are summarized into AUC values, it can be seen that the overall exposure levels in neonates, infants, and young children are markedly different from those in adults. In this example, higher doses are required in pediatric patients in order to obtain exposure levels comparable to those in adults. Therefore, a study that is designed such that all subjects receive the same weight-based (mg/kg) dose regardless of age would be unlikely to succeed in younger patients, for whom alternative dose recommendations would have to be considered. It is common to find that weight-based dosing is an inappropriate dose metric for use in children. This is because the relationship between weight and clearance is usually not linear, and weight-based dosing does not take into account the extent of maturation of organs.³⁰

Figure 4.

Simulated exposures for different age groups. (a) Relationship between clearance and weight. The solid line denotes the mean relationship, and the upper and lower broken lines denote the upper and lower 95% confidence intervals, respectively. (b) Simulation of mean concentration–time profiles after a 1-h infusion of a 10 mg/kg dose to neonates (pink line), infants (brown line), young children (blue line), older children (purple line), adolescents (green line), and adults (cyan line). (c) Box and whisker plots of simulated (area under the curve (AUC)) values for neonates (pink), infants (brown), young children (blue), older children (purple), adolescents (green), and adults (cyan) after the 10 mg/kg dose regimen.

Regulatory Aspects

The US Food and Drug Administration (FDA), through the FDA Modernization Act of 1997³¹ and the FDA “effectiveness” guidance of 1998³² allowed the use of exposure–response information in combination with a single pivotal clinical trial as sufficient evidence of effectiveness. Although the use of an exposure–response evaluation to replace a pivotal trial is not common, population PK modeling and exposure–response evaluations are frequently used to support registration decisions and labeling. This is because population PK modeling enables the identification of the sources of variability that ultimately have an impact on both safety and efficacy. In particular, the FDA has acknowledged the use of population modeling as being informative in extending information from adult indications to pediatric indications.³³ In a recent review of the impact of population modeling,³⁴ the authors evaluated 198 submissions from January 2000 through December 2008. The number of submissions wherein pharmacometrics analyses were included increased sixfold over 9 years (from 45 submissions during the 5 years from 2000 to 2004 to 87 submissions during the 2 years 2007–2008). The impact of these analyses on labeling decisions has also increased across all sections of the drug label. Among the 198 submissions surveyed, pharmacometrics analyses of 126 submissions (64%) contributed to drug approval decisions, while those of 133 submissions (67%) contributed to labeling decisions. Modeling and simulation also play a large role in personalized medicine.

Modeling and simulation also play a large role in personalized medicine. Personalized medicine aims to provide more accurate predictions of individual responses to therapy based on the characteristics of the individuals.³⁵ Pharmacogenetics tests allow clinicians to individualize treatment, potentially improving compliance because the medication and dosage are more likely to be safe and effective. The warfarin drug label changes made in 2007 and 2010 provide a good example. These changes were based, in part, on research conducted by the C-Path Institute and others.³⁶ Work by Hamberg et al.³⁷ on warfarin exposure and response identified the CYP2C9 genotype and age as being predictive of exposure, and the VKORC1 genotype as being predictive of response. The authors showed the importance of CYP2C9 and VKORC1 genotypes and the patient's age for arriving at strategies to improve the success of warfarin therapy.

In a recent commentary on the impact of population modeling on regulatory decision making, Manolis and Herold³⁸ described three broad classifications of model-based evaluations: (i) those that are generally well accepted, (ii) those that may be acceptable if justified, and (iii) those that are controversial.

Examples of the first category are:

• Hypothesis generation and learning throughout drug development.

• The use of modeling and simulation to optimize designs, select doses to be further tested in clinical trials, and develop minimal sampling schedules.

Examples of the second category are:

• The use of modeling and simulation for final recommendation of intermediate doses that were not specifically tested in phase II/III trials or to bridge efficacy data across indications.

• Modeling of phase II/III data to support regulatory claims (e.g., absence of suspected drug–drug interactions, effect of pharmacogenetics on exposure).

Examples of the third category are:

• Model-based inference as the “sole” evidence of efficacy/safety, or based on simulated data for efficacy and safety (notwithstanding exceptional scenarios).

Reporting requirements

In 1999, Sun et al. published a detailed description of the general expectations by regulators for submission of population modeling work.³⁹ In addition, there are guidance documents from FDA²⁷ and the Committee for Medicinal Products for Human Use (CHMP) of the European Medicines Agency (EMA)⁴⁰ which should always be considered when conducting population modeling evaluations. In general, a prespecified analysis plan is useful and should be included in the final report. Because of the importance of the quality of the data in determining the modeling results, it is essential to spend the necessary time to ensure that the data are of good quality, and to describe the methods used for data merging and evaluation. Both the analysis plan and the report should describe all data editing procedures that have been used to detect and correct errors, including the criteria used for declaring data unusable (e.g., missing information on dates or times of doses or measurements). The rationale for declaring a data point to be an outlier needs to be statistically convincing and should be specified in the analysis plan. The methods used for handling concentrations below quantitation limits and missing covariate data must also be specified.

A final report should be sufficiently descriptive so as to allow a reviewer to understand how the conclusions were reached. The objectives of the analyses, the hypotheses being investigated, and the assumptions imposed should be clearly stated, both in the analysis plan and in the report. The steps taken to develop the population model should be clearly described. This can be done through the use of flow charts or decision trees. The criteria and rationale for the model-building procedures adopted should be specified. Often, one or more tables showing the models tested and summaries of the results of each evaluation are also included to provide a clear description of the results and decision-making process.

The reliability and robustness of the results can be supported by generating standard diagnostic plots, key parameter estimates and associated SE, and other metrics. A model that is appropriate for a specific purpose (e.g., describing data) may or may not be appropriate for other purposes (such as simulation). The objective of model qualification is to examine whether the model is suitable for the proposed applications. For example, if the model is to be used for simulation and dosage recommendation, the predictive performance of the model should be tested.

Project Management Aspects

Reviews of filings in the United States and Europe made between 1991 and 2001 showed that the average success rate for all candidate drugs in all therapeutic areas was ~11%,⁴¹ and that the success rate was lower during preclinical development. With the cost of conducting clinical trials increasing with each stage in drug development, failure at late stages of development is problematic. The costs associated with drug development are staggeringly high. In 2010, the cost of developing a new drug was estimated to be ~$1.2 billion (costs vary depending on the therapeutic indication).⁴² Part of the problem is difficulty in making informed decisions at critical junctures during the drug development process.

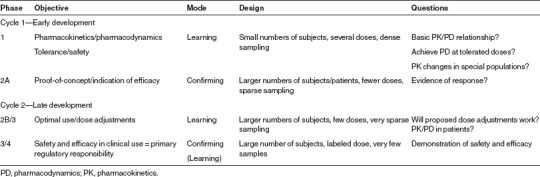
In 1997, Sheiner⁴³ introduced the concept of “Learn and Confirm” as a means to improve decision making by using information more effectively. Sheiner outlined a drug development process that involved two cycles of learning and confirming (Table 3). During the learning phases of each cycle, studies should be designed to answer broader questions, and require more elaborate evaluations to answer; in contrast, during the confirming phases, questions are typically of the “yes/no” variety and can be answered using traditional statistical approaches. Sheiner advocated the use of modeling as a means of addressing the learning questions and of improving the information from confirming questions by providing a basis for explaining the variations in the data and increasing the power to detect meaningful clinical results.⁴⁴

Table 3. Learning vs. confirming by development stage.

In a report in 2004, the FDA addressed the issue of decline in new drug submissions and escalating development costs.⁴⁵ The report indicated a need for applied scientific work to create new and better tools to evaluate the safety and effectiveness of new products, in shorter time frames, with more certainty, and at lower cost. The FDA has advocated model-based drug development as an approach to improving knowledge management and decision making relating to drug development (in line with the “Learn and Confirm” paradigm) and has taken an active role in encouraging model development for various therapeutic areas.⁴⁶ A recent review on model-based drug development by Lalonde et al.⁴⁷ suggested that prior information is often ignored when analyzing and interpreting results from the most recent clinical trial. However, modeling allows data from different studies to be combined in a logical manner, based on an understanding of the drug and the disease. The authors suggested that drug development can be viewed as a model-building exercise, during which knowledge about a new compound is continuously updated and used to inform decision making and optimize drug development strategy.

Resources

Modeling and simulation require investments in resources, because input is needed from several areas. Input from the clinical team is essential for the design of the protocol including implementation and monitoring, so as to ensure that the necessary data are collected. The creation of population modeling databases usually involves assistance from either database management staff or statistics staff. Database preparation calls for special attention because it is important to have the exact times and dates for all doses and measurements/observations. The results of the evaluation should be available sufficiently early so that the information can either be used in new clinical trials or included in the filing. It may be helpful to use preliminary data to meet important timelines, but the risks of using data that are not final should be weighed and considered.

The generating of a model usually requires the inputs of an analyst, and because the science changes continually, analysts should have their training updated regularly. Interpretation of the results may require input from clinical staff. The results of any modeling evaluations should also be discussed within the project team to ensure that the results are reasonable, understandable, and applicable to development decisions.

The report must also be checked for accuracy and completeness. Depending on the size of the database (the number of subjects and the number of observations per subject) and the complexity of the model, the process of development, qualification, and report generation for a model can take many weeks to complete.

Software and Modeling Environment

Most modeling programs can be run on any computer. However, models may take a long time to estimate parameters, thereby making it impractical to run models on a laptop computer. Given the large number of models that are usually tested during learning evaluations, and the occasionally protracted run times seen with complex models, investment in a dedicated computer system to house modeling software should be considered.

NONMEM was the first software available for population PK modeling, but subsequently other packages have been developed and are in use. After the first version of NONMEM was released, a wide range of applications was tested. Thereafter, improvements were implemented in the related statistical and estimation approaches to the methodology, in a series of upgrades. Alternatively, they were developed into other modeling platforms.⁴⁸ Table 4 shows timelines in respect of several key software packages used for population modeling. The selection of a software package for model-based evaluations depends on the experience of the modeling staff, and their training and education levels.

Table 4. Timeline for population modeling software development.

However, the selection and installation of the modeling software are not the only prerequisites for conducting population modeling. In many cases, a supporting programming language is necessary to run the modeling package (e.g., NONMEM requires Fortran). Because some modeling packages do not have user-friendly interfaces, “front-end” software may be needed (for example, there are several of these available for NONMEM, free of cost or for commercial licensing). Similarly, “back-end” packages for generating graphical outputs of modeling results, along with supporting languages, may also be necessary. It should also be noted that the analysts themselves should have appropriate experience, education and/or training. User-written model codes, subroutines, and scripts should also be provided for review as part of a regulatory submission.

Software validation vs. qualification

The FDA Guidance for Industry: Computerized Systems Used in Clinical Trials⁴⁹ defines “Software Validation” as the confirmation by examination and provision of objective evidence that software specifications conform to user needs and intended uses, and that the particular requirements implemented through the software can be consistently fulfilled. The document states that purchasers of off-the-shelf software should perform functional testing (e.g., with specified test data sets), adjust for the known limitations of the software, detect problems, and correct defects. Documentation should include software specifications, test plans, and test results for the hardware and software used for data management and modeling, and such documentation should be available for inspection. It is crucial that the software used for population analysis be adequately supported and maintained. Change control should be documented and revalidation should be performed as necessary. In the FDA guidance, 21 CFR Part 11⁵⁰ indicates that off-the-shelf software should be validated for its intended use. It should be noted that all software used in a regulated environment must conform to these standards.

While some modeling packages provide validation test kits, most do not. Running the same modeling problem in another package may or may not be possible, and manual calculation of the results to check for accuracy is not feasible for most population problems.

The definition of “software defect” is “a variance from a desired product attribute.” Two types of defects exist in software: variance from product specifications and variance from customer expectation (such as the wrong function being implemented). However, such defects have no impact unless they affect the user or the system, at which time they are classified as failures. Relationships between defects and failures are complex; some defects may not cause any failures, while others may cause critical failures. Critical failures involve one or more of the following: production of incorrect results; inability to reconstruct processing; inability of the processing to comply with policy or governmental regulation; unreliability of system results; nonportable systems; and unacceptable performance level. The testing of modeling software to identify defects, failures, and critical failures is difficult because of the complexity of the software itself. In addition, some modeling packages such as NONMEM can produce different results depending on the compiler (e.g., Fortran vendor or version) and compiler options used. Consequently, system qualification rather than the more comprehensive validation is generally performed for modeling software. Test kits provided by the vendor are run and compared with vendor-supplied results, and other test kits assessing patches and updates are also evaluated. Vendors should also provide a log of known problems and “work-around” strategies or changes that can be made to the software to address known problems.

User training

Modelers have a wide variety of backgrounds, including medicine, pharmacy, pharmacology, biophysics, engineering, and statistics. Given the complexity of population modeling approaches, user training is as important as ensuring software functionality. Unfortunately, the method of determining whether a user has sufficient education, training, and experience to conduct these assessments is not clearly defined. Many universities have training programs in population modeling, but the curriculum content and hands-on experience available to students vary substantially. Similarly, there are numerous postgraduate training courses, but these generally focus on introductory training, and users may require further training or mentoring before undertaking an analysis. Continuing education through courses, meetings, and other forums is important to ensure that analysts are familiar with new concepts and approaches.

Conclusions

There is no doubt that the use of model-based approaches for drug development and for maximizing the clinical potential of drugs is a complex and evolving field. The process of gaining knowledge in the area is continuous for all participants, regardless of their levels of expertise. The inclusion of population modeling in drug development requires allotment of adequate resources, sufficient training, and clear communication of expectations and results. For one who is approaching the field for the first time, it can be intimidating and confusing. A wise approach is to break the task into manageable pieces (“divide and conquer”). One should try to understand one topic or master one piece of software at a time, seek literature and training appropriate for one's level and needs and, most importantly seek the advice of mentors and develop sources for collaboration and support.

Conflict of Interest

The authors declared no conflict of interest.