Abstract
Single-nucleotide polymorphism (SNP) data are routinely obtained by sequencing a region of interest in a small panel, constructing a chip with probes specific to sites found to vary in the panel, and using the chip to assay subsequent samples. The size of the chip is often reduced by removing low-frequency alleles from the set of SNPs. Using coalescent estimation of the scaled population size parameter, Θ, as a test case, we demonstrate the loss of information inherent in this procedure and develop corrections for coalescent analysis of SNPs obtained via a panel. We show that more accurate Θ-estimates can be recovered if the panel size is known, but at considerable computational cost as the panel individuals must be explicitly modeled in the analysis. We extend this technique to apply to the case where rare alleles have been omitted from the SNP panel. We find that when appropriate corrections for panel ascertainment and rare-allele omission are used, the biases introduced by ascertainment are largely correctable, but recovered estimates are less accurate than would be obtained with fully sequenced data. This method is then applied to recombinant multiple population data to investigate the effects of recombination and migration on the estimate of Θ.
Keywords: panel single-nucleotide polymorphisms (SNPs), SNP chips, ascertainment, statistical correction, minor allele frequency
DATA for genetic studies are commonly obtained by typing only those single-nucleotide polymorphisms (SNPs) previously identified using a panel of fully sequenced individuals. Use of a panel to guide SNP genotyping clearly misses some variation in the samples, thus reducing the power of the resulting data. Lost variation is not randomly distributed: recent mutations, which are generally of low frequency, drop out at a higher rate than older mutations (Nielsen 2000), and this may bias analysis of the resulting data (Nielsen 2004). Previous articles (Kuhner et al. 2000; Nielsen et al. 2004) have addressed this potential bias and concluded that, if the composition of the panel is known, its effects can be accounted for. It may also be possible to reconstruct the relevant properties of the panel if one has access to SNP and sequence data from the same individuals (Albrechtsen et al. 2010).
SNP collections are then often stripped of rare alleles, using various allele-frequency cutoffs (International HapMap Consortium 2003) in an attempt to reduce the impact of sequencing error (which introduces spurious, low-frequency alleles) as well as to reduce the size, and therefore the cost, of the resulting SNP chip. This again biases the SNP collection toward higher-frequency alleles. Panel use and allele-frequency cutoffs both remove rare alleles, so the potential bias is substantial and can easily mask the signature of population growth (Coventry et al. 2010).
In this study, we demonstrate the bias produced by SNP panels and provide an appropriate correction. We consider the case in which the number of panel sequences is known but their genotypes are unknown, as well as exploring the consequences of missing or inaccurate information about panel size. We also consider the effects of sequencing error and of the deletion of rare alleles on inference from panel-based SNPs. Our correction is an implementation of the “reconstituted DNA” method (Kuhner et al. 2000), which requires knowing the count of invariant sites from the region of the genome from which SNPs were taken. To model recombination, the location of the SNPs is also required. SNP chips not providing this information cannot be used for recombinant coalescent analyses.
SNP data are used for diverse purposes including gene mapping, association studies, and inference of population parameters. As our test platform for the ability to correctly analyze panel-ascertained SNP data, we use inference of the scaled population size parameter , where is the effective population size and μ is the per-site mutation rate. Some of our experiments also infer recombination rate , where C is the recombination rate per interlink site per generation, and immigration rates , where m in the immigration rate per generation. To infer these parameters, we use the coalescent genealogy-sampler strategy in the LAMARC program (Kuhner 2006). Inference of Θ in coalescent genealogy samplers is based on the inferred distribution of branch lengths. It is therefore broadly sensitive to the distribution of mutations in the underlying sequences and reacts strongly to the systematic loss of rare alleles. Inability to accurately estimate Θ from panel-SNP data will skew the search of coalescent trees and therefore perturb recovery of other population parameters.
In this study we measure the biases of single-population SNP panels, both with and without the removal of rare SNPs, and develop methods for correcting for these, yielding less biased Θ-estimates within credibility intervals more often containing the truth. We also demonstrate that our method can be used in cases with population subdivision and recombination. Our corrections have been implemented in LAMARC but the principles involved are broadly applicable to coalescent analysis of SNP data gathered with a panel.
In this article we consider only the case in which panel members were surveyed from all populations in the analysis. We expect the bias inherent in use of a panel wholly drawn from a different population to be more severe, but we defer consideration to a future article.
Materials and Methods
We have added two new capabilities to LAMARC: panel corrections and error-aware likelihood analysis. This article focuses primarily on panel corrections, although the error correction method is also discussed.
Panel correction
Coalescent samplers make use of what has been called the “Felsenstein equation” (Felsenstein 1988):
| (1) |
The probability of the observed data D for a given value of Θ is here expressed as a sum, over all possible genealogies G, of the combined probability of the genealogy with regard to Θ and the data with regard to that genealogy. As the summation over genealogies is intractably large for realistic data sets, this equation is usually evaluated via Markov chain Monte Carlo methods (see Kuhner 2009 for a review).
For DNA data the term can be computed under a variety of mutational models (Felsenstein 2004). Use of fully ascertained SNP data requires modification of this term to include the probability of omitted invariant sites. Kuhner et al. (2000) give a correction for SNP data, termed the “reconstituted DNA” method. This correction assumes that the panel captures all variation in the sequences (as would happen if the samples themselves were used as the panel) and that the number of invariant sites is known, but their sequence is not. Using this correction, becomes as follows where s ranges over the SNP (variant) sites and u over the unobserved (invariant) sites:
| (2) |
For nonrecombinant genealogies, the rightmost product term in Equation 2 above simplifies as follows, where I represents invariant data at a single site and is the number of invariant sites. The equation for recombinant genealogies would be the product of several such right-side terms, one for each nonrecombinant marginal tree:
| (3) |
Summing over all possible values of (the refinement of I to a specific base, x), this becomes
| (4) |
This basic correction is not sufficient for panel-ascertained data, as it assumes that every unobserved site is known to be invariant. When data are ascertained based on a panel, some variable sites in the sample will be missed because they did not vary in the panel. Treating them as if they are invariant will bias estimates of Θ downward.
Kuhner et al. (2000) proposed, but did not implement, a correction for panel-based SNPs that relies on explicitly representing panel sequences as proxy samples in each sampled coalescent genealogy. Thus if 10 haplotype samples were collected using a SNP panel originally taken from 6 haplotypes, each genealogy would contain 16 haplotypes: 10 sample haplotypes and 6 panel-proxy haplotypes. We refer to all of these haplotypes as “tips” as they are at the tips, or leaves, of the genealogy.
Calculating the likelihood of the data on such an expanded genealogy is a little more complicated than the method given above as we now have four different classes of site data based on the division of sites into assayed and unassayed and of haplotypes into sample and panel. These four classes are as follows:
: Data samples at assayed sites. Variation here is fully captured.
Data samples at unassayed sites. Nothing is known about these sites’ data.
: Panel proxies at assayed sites. Bases are unspecified but known to vary within the set of proxies.
: Panel proxies at nonassayed sites. Bases are unspecified but known to be invariant across the set of proxies.
These data can be combined to calculate with the following decomposition:
| (5) |
Calculation of data likelihood for the assayed and unassayed sites is similar, with Figure 1 giving an overview of the procedure. For assayed sites, one first calculates with sample tips as measured and panel tips unknown and then subtracts each of four likelihoods with sample tips as measured and panel sites all invariant for one of the four possible bases. For unassayed sites the procedure is to sum each of four possible likelihoods in which the panel sites are invariant for a single base, while assuming all sample data are unknown. Likelihood calculation is done with the tree-peeling algorithm of Felsenstein (1981), as previously implemented in LAMARC. The calculation must be done five times for assayed sites and four times for unassayed sites.
Figure 1.
Pseudocode for calculating with panel correction. For simplicity’s sake, sequencing error is ignored here. Assayed and unassayed sites are calculated in separate steps, each simultaneously handling data samples and panel proxy members. Likelihood calculations are performed as in previous LAMARC versions.
The algorithm for searching among genealogies—the term in Equation 1—does not change to accommodate panels, other than inclusion of the panel tips. Instead, adding panel proxies to the genealogy allows us to approximately integrate over the unknown relationship between the panel sequences and the sample sequences. This in turn allows us to calculate the probability of the data given the genealogy while conditioning on panel ascertainment.
Error-aware likelihood analysis
Neither the sequencing of the original panel nor application of the resulting SNP chip to samples is an error-free process. Sequencing error typically manifests as observation of a novel allele in a single sample. Such errors can bias population parameter estimation (Clark and Whittam 1992; Johnson and Slatkin 2008). In this study we make use of a correction for sequencing error proposed by Felsenstein (2004) and briefly described below. This correction has been implemented and was released in LAMARC version 2.1.5.
In a naive (error-unaware) likelihood analysis, an observation of nucleotide c, for example, is represented at the tip with likelihood 1.0 under the hypothesis that the underlying nucleotide was indeed c and likelihood 0.0 under the hypotheses that it was any of . Under a uniform, randomly distributed sequencing error of rate ε, the likelihoods become for c and for each of . That is, when the true base is c, there is a probability that c will be observed and for each of as the true base there is a probability that c will be observed.
Our current implementation and experiments assume that error is randomly distributed and that sequencing error affects both the panel and the subsequent samples with the same error rate. The error rates of DNA sequencing and SNP detection will generally differ. Accommodating this would be a straightforward enhancement, as modeling error requires only one-time calculation of error-aware tip data likelihoods.
Throughout this article, whenever the data were simulated with sequencing error, errors were introduced at a rate of 0.001 per observed nucleotide and were random with respect to the base introduced. LAMARC’s error correction feature was used on all error-containing data, except in cases where minor allele-frequency cutoff (MAFC) (described below) was performed.
MAFC and effective panel size
It has been common practice when constructing a SNP chip to discard minor alleles observed in less than 1–3% of the panel sequences (International HapMap Consortium 2003). We know of no standard name for this practice. We call it the MAFC procedure. MAFC methods are used both to reduce the impact of sequencing error and to reduce the size, and thus the cost, of SNP chips. This approach necessarily discards some real information, particularly recent (and thus rare) mutations. Users expect that the chip’s power to detect variation will be only slightly reduced since the omitted SNPs are likely to be rare in the analyzed samples as well. We examine this assumption in Table 5 in Results.
Table 5. Performance comparison of different panel corrections.
| MAFC level | Panels declared | Panels correction used | Error correction used in LAMARC analysis | Average run time (sec) | Mean point estimate | Mean C.I. width | % rejection | Figure 5 letter |
|---|---|---|---|---|---|---|---|---|
| 12.5 | — | No | No | 864 | 0.000461 | 0.000955 | 49.0 | A |
| 6.2 | — | No | No | 1,038 | 0.000672 | 0.001377 | 24.0 | B |
| 3.1 | — | No | No | 1,174 | 0.000806 | 0.001637 | 11.0 | C |
| 1.6 | — | No | No | 1,349 | 0.000888 | 0.001798 | 8.0 | D |
| 12.5 | 4 | Yes | No | 12,591 | 0.000950 | 0.002040 | 20.0 | E |
| 6.2 | 9 | Yes | No | 25,391 | 0.000877 | 0.001258 | 11.0 | F |
| 3.1 | 16 | Yes | No | 45,552 | 0.001023 | 0.001158 | 10.0 | G |
| 1.6 | 29 | Yes | No | 91,148 | 0.001182 | 0.001108 | 11.0 | H |
| True Panels | ||||||||
| — | 4 | Yes | Yes | 33,373 | 0.001023 | 0.002541 | 8.0 | J |
| — | 8 | Yes | Yes | 82,430 | 0.001070 | 0.001882 | 8.0 | K |
| — | 16 | Yes | Yes | 244,245 | 0.001098 | 0.001550 | 8.0 | L |
| Complete SNP data | ||||||||
| — | — | No | Yes | 2,729 | 0.000962 | 0.002128 | 7.0 | M |
One hundred independent coalescent trees were generated, DNA data were simulated for each, and 0.1% sequencing error was applied. SNP data were then obtained using the panel sizes and MAFC procedures listed, with LAMARC runs completed using the corrections listed.
Removing rare alleles from a panel has an effect similar to using a smaller panel created earlier in the history of the population. A requirement that a site appears three times in the panel to be included in a SNP chip is similar to a requirement that a mutation happened long enough ago to appear in at least three contemporary panel members. Mutations arising recently are unlikely to have three descendants and are lost. Thus the MAFC procedure makes it difficult to resolve and evaluate the most tipward portions of the genealogies.
We have chosen to model this effect by determining an “effective panel size” for the MAFC procedure. Our technique is very simple: we estimate the size of a non-MAFC panel that would be expected to yield the same number of retained SNPs as our MAFC panel. Two potential alternatives we did not explore are determining an effective panel size to match SNP frequency spectrums, as has been done to correct summary statistics (Adams and Hudson 2004; Nielsen et al. 2004) and principal component analyses (Albrechtsen et al. 2010), and using a coalescent genealogy sampler that allows for multiple time points [such as the BEAST sampler (Drummond and Rambaut 2007)] to model the MAFC panel as a panel taken in the past.
To estimate the effective panel size, we convert Watterson’s estimator (Watterson 1975) from per-locus θ to per-site Θ and use it “backward” to estimate the count of segregating sites from Θ, sequence length, and panel size. We then similarly adapt Ewens’ formula (Ewens 1972; Ewens 2000, Equation 3.83, p. 114) for the distribution of n samples with a per-locus θ under the infinite-alleles model to the simpler case of biallelic loci and switching to per-site Θ. This provides the probability that a given site has j copies of the minor allele among m samples. Combining the two formulas, we produce the equation below. Determining a suitable effective panel size corresponds to finding a value, p, which minimizes the expression below, where m is the number of original MAFC panel members, and c is the highest minor allele size discarded by the MAFC correction. Small Θ-terms factor out and some of the summation terms cancel. The full derivation is given in Supporting Information, File S1:
| (6) |
Note that while Watterson’s estimate relies on the infinite-sites model and Ewens’ equation on the infinite-alleles model, the two should be reasonably comparable for low values of Θ. This is supported by the low counts of SNPs with three or more alleles found in our simulated data (see Table 1). Additional effort to model the process may be wasted as one is forced to choose an integer value for the effective panel size, p, the number of panel-proxy tips to include.
Table 1. Comparison of SNP counts in data sets.
| Θ | Length of DNA | Median no. SNPs in 100 generated trees | Mean no. SNPs in 100 generated trees | Mean % SNPs with more than two alleles |
|---|---|---|---|---|
| 0.1 | 500 | 215 | 212.8 | 12.34 |
| 0.01 | 5,000 | 260 | 268.6 | 1.21 |
| 0.001 | 50,000 | 268 | 290.1 | 0.13 |
For each Θ-value, 100 trees were generated, each with 148 tips. DNA was simulated for the sequence length given. Sequence lengths were chosen to recover a similar number of SNPs for each Θ-value. Watterson’s estimator predicts 278.6 SNPs for each of these data sets.
Panel correction adds tips to the genealogy corresponding to the panel sequences. When an effective panel size as given in Equation 6 is used, the tips added to the genealogy do not correspond to real sequences. Instead, Ewens’ formula and Watterson’s estimator combine to give an effective panel size that should discover a similar number of SNPs as the original panel size with a given MAFC. Since nothing is known about the panel sequences as individuals, there is little information lost by this approximation.
Calculating effective panel sizes for multiple population cases is more difficult as each panel proxy tip must be assigned to a specific population while MAFC considers minor allele count across all populations. For our two-population case, we calculated the effective panel size as if all SNPs surviving the MAFC cutoff did so by meeting the MAFC minimum within their subpopulation of origin. This will tend to result in too-large effective panel sizes, as SNPs occurring fewer times than the cutoff in a single population might still meet the cutoff when all populations are considered. A more accurate correction would require modeling the migration rates and we cannot rely on that if we are attempting to recover those rates.
As the formulas we used involve constant population sizes, neither the single-population nor the multipopulation MAFC corrections will be appropriate for data sets including growth, shrinkage, or population divergence.
An alternative to the effective panel size approach would be to compute the probability of the observed data conditional on a position being variable under MAFC, as is done in the basic SNP correction (Kuhner et al. 2000). This probability is quite expensive to compute as it involves a sum over all possible data configurations containing fewer than the required number of minor allele occurrences. While this computation can be simplified for reduced mutational models such as Jukes–Cantor, it suffers from combinatorial explosion for more realistic mutational models. We therefore use the effective panel size approach, which does not restrict our choice of mutational model.
Generation of simulated data
For each distinct set of population parameters under study, we began by simulating 100 random coalescent genealogies with enough tips to supply the maximum number of samples and panels examined across all studies on that parameter set. DNA sequences were simulated at the tips of each tree. This allowed us to compare the effect of different sequencing and panel schemes on the same “true” underlying data.
Genealogies were created using software based on Hudson’s simulator, ms (Hudson 1983, 2002). DNA sequences were simulated at the tips of each of the trees under the Kimura two-parameter mutational model (Kimura 1980) with a transition/transversion ratio of 2.0, using the program treedna.c (J. Felsenstein, unpublished data). We do not expect our results to be sensitive to the mutational model used.
In some cases we added 0.1% simulated sequencing error. This was done before the SNPs were identified, so it had the effect of increasing the number of SNPs. This error value is somewhat optimistic as the HapMap estimate is 0.5% (Akey et al. 2002), although high-quality sequencing can achieve lower error rates (Murray et al. 2004).
Panel and sample members were randomly chosen from the tips present in each tree. A random ordering was chosen for the panel members and used across all simulations generated for the given tree. Thus, all SNPs included in the panel of size 8 for a given set of conditions are also included in the panel of size 16 over the same conditions. The unused tips were eliminated before the analysis was done. The same choice of panel members was used for each pair of simulations that had the same conditions save for the application of sequencing error.
We identified a site as a SNP if it varied in the panel, or for analyses with the MAFC procedure, if its minor allele frequency in the panel was above the cutoff. Once a site was identified as a SNP in the panel, we assumed it to be fully typed in the sample. This procedure captures slightly more information than the industry standard. In practice, if at a particular site the panel individuals possessed only nucleotides A and C, the SNP chip would contain probes only for A and C, and a T nucleotide in a sampled individual analyzed with the chip would not be identified. For our smallest Θ-value (0.001), the difference between these approaches is small as sites with more than two nucleotides present are rare. For our highest Θ-value (0.1), however, our approach would result in correct detection of more variants than the standard SNP-chip approach.
LAMARC analysis conditions
For the simple, single-population experiments, we began with LAMARC (Kuhner 2006) version 2.1.5 and added the panel correction method. LAMARC 2.1.5 had a known bug (corrected in LAMARC 2.1.6) in analysis of recombination, but no recombination was present in these studies. The multipopulation experiments were performed with LAMARC 2.1.8, which contains the panel correction method. All analyses used a Bayesian approach with logarithmic priors. Specific prior details, start values, and parameter-sampling strategies are available in File S3 and File S4.
Single-population experiments
Our single-population experiments began by generating sets of 100 trees, each containing 148 tips, for each of three different Θ-values: 0.1 to simulate fast mutating populations such as viruses, 0.001 to approximate human mutation rates, and 0.01 to confirm that the trends seen at the extremes held at intermediate rates.
To keep information content similar across these, we chose sequence lengths expected to produce the same number of SNPs. Table 1 shows the median and mean SNP counts for these three values as well as the percentage of SNPs with more than two alleles. Straightforward modification of Watterson’s estimate to predict segregating sites from sequence length, sample count, and per-site Θ predicts 278.6 SNPs for each of these data. Our observed counts depart from this number. We used a finite-sites mutational model and at the higher values of Θ multiple mutations at the same site occur more often, bringing the mean SNP count lower. Mean SNP count for the smallest Θ value appears high, but is within 1.75 standard deviations of the expectation of the mean over 100 trials (Watterson 1975; Ewens 2000, p. 310).
Table 1 also shows that for , positions with more than two alleles were quite rare. This suggests that results for a conventional SNP chip capable of detecting only two alleles would be very similar to the results presented in this study.
All single-population experiments were performed on subsets or variants of these original 300 coalescent trees. The details of the naming of the subsequent data sets are found in File S2.
Panel correction and declaration of error:
This key experiment measured the effects of the number of panel members, use or nonuse of the panel correction, and sequencing error.
Sample size:
The effect of using larger samples was investigated by comparing cases with 8 and 20 samples.
Incorrect panel size declaration:
The effect of incorrectly declaring the panel size was studied by taking data sets generated with 8 panels and declaring them to have been created using 2, 4, 8, 12, or 16 panels.
MAFC and effective panel size correction:
From data sets created with a panel size of 128 we removed SNPS whose minor alleles appeared 2, 4, 8, and ≤16 times (frequencies 1.6%, 3.1%, 6.2%, or 12.5%). For triallelic (or more) sites, the cutoff was applied whenever the sum of all minor allele counts failed to clear the cutoff. Thus when a major allele appeared 98% of the time with two minor alleles each appearing 1% of the time, the site would be included with the 1.6% cutoff, but not for 3.1% or above. These data sets were analyzed with effective panel sizes derived from Equation 6: 29, 16, 8, and 4, respectively.
Multiple-population experiment
To explore the effect of panel and MAFC corrections on more sophisticated population models, we generated a single set of 100 independent genealogies with the following parameter values: Θ = 0.002 for population “North”, Θ = 0.003 for population “South”, no migration into population North from South, migration rate into population South from North, and recombination rate .
Where error was modeled the rate was 0.1%. Each population had 64 original panels and MAFC corrections with cutoffs 3, 7, and 15 were applied. SNP data were taken for eight samples in each population.
For these data we analyzed parameter recovery for the following conditions: fully sequenced data, with error, for analyses with and without error modeling; data as from a MAFC chip with cutoffs of 3, 7, and 15 (frequencies 2.3%, 5.5%, and 11.7%, respectively), analyzed without any correction for the MAFC procedure; and the same MAFC data, analyzed with an effective panel size correction (10, 5, and 2 proxy panels per population, respectively).
Results
Recovery rate of SNPs using panels
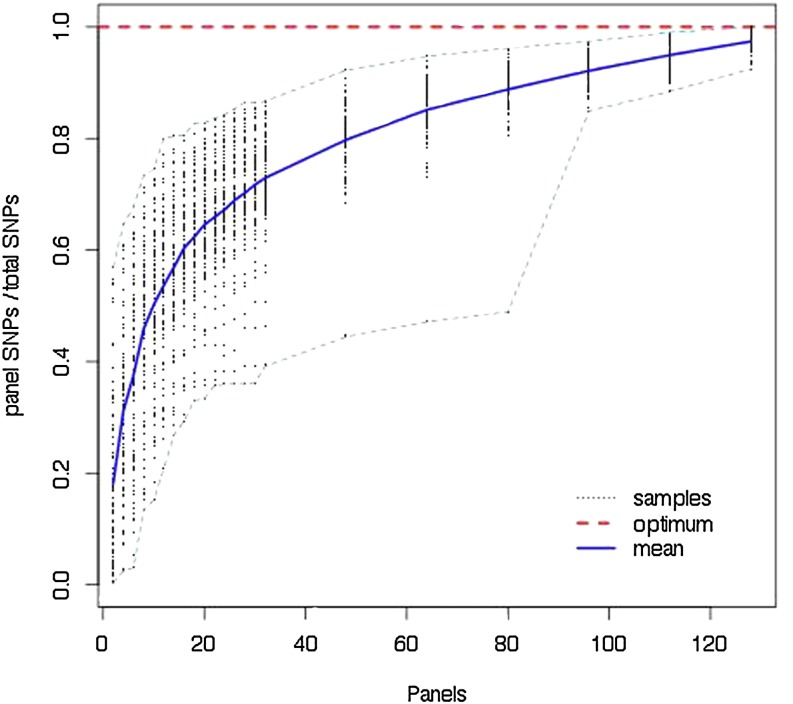
To explore the loss of SNPs due to the panel process, we compared the number of variable sites in our data sets with the number of SNPs detected using panels of various sizes. Figure 2 presents the results. Focusing on the mean, one is tempted to conclude that panels of size 8–10 recover 50% of all SNPs and panels of size 28–30 recover 75%. While on average this is true, some individual data sets show severe loss of SNPs due to statistical fluctuation. Note, for example, the case where 80 panel members recovered <50% of the SNPs. This occurs when, due to chance, the sample contains one or more divergent lineages not encountered by the panel. The plots of and and a plot comparing all three Θ-values are found in Figure S1, Figure S2, and Figure S3.
Figure 2.
Proportion of SNPs recovered with increasing panel size. One hundred trees with 148 tips and were generated and DNA was simulated for 50,000 bases. For each data set a random ordering of all tips was chosen and the proportion of the total SNPs found as the ordered panel members were added is plotted. Dashed lines show the edge of the results envelope and the solid line is the mean.
These sequences were simulated without recombination. Recombination would tend to move the number of SNPs detected toward the mean, because a lineage that was unusually divergent for one part of the sequence would not necessarily be divergent elsewhere.
Panel correction and declaration of error
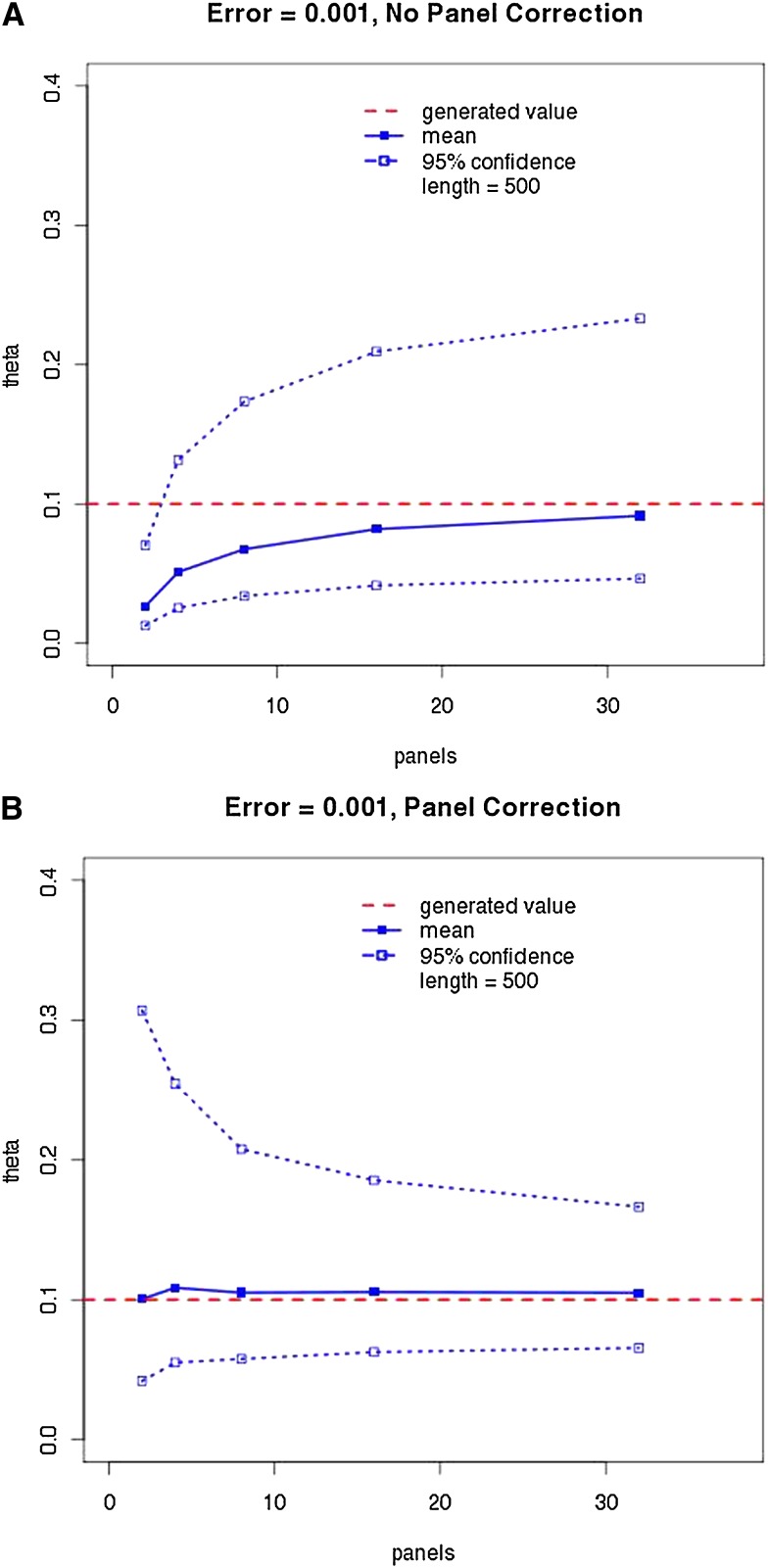
To gauge the effectiveness of panel correction, we performed LAMARC analyses on data sets produced with panels of various sizes, with and without simulated sequencing error. These results with sequencing error applied are summarized in Table 2 for all Θ-values and a graphical representation of the results for in the presence of sequencing error is given in Figure 3. (Figures and tables covering the case without sequencing error and the remaining Θ-values are given in Table S1 and Figure S4, Figure S5, Figure S6, Figure S7, Figure S8, and Figure S9 and include plots of most probable estimates for all cases.)
Table 2. Ability of LAMARC to recover θ-values from panel data with sequencing error.
| % LAMARC runs rejecting simulation Θ-value |
||||||
|---|---|---|---|---|---|---|
| Θ | Panel correction | 2 panels | 4 panels | 8 panels | 16 panels | 32 panels |
| 0.100 | No | 75.8 | 47.0 | 25.0 | 9.0 | 4.0 |
| Yes | 7.1 | 7.0 | 3.0 | 3.0 | 1.0 | |
| 0.010 | No | 74.0 | 53.0 | 35.0 | ||
| Yes | 8.0 | 11.0 | 7.0 | |||
| 0.001 | No | 79.0 | 64.0 | 50.0 | ||
| Yes | 8.0 | 8.0 | 8.0 | |||
Percentage of LAMARC runs rejecting their generating Θ-value, given 0.1% sequencing error and panel correction, is shown. All cases used the LAMARC error-aware correction. Except in the cases noted in the main text, each rejection rate was calculated from 100 LAMARC runs on data obtained from the same set of 100 independently generated trees. Successive panel sizes include the panel members of the smaller sizes.
Figure 3.
(A and B) Effect of panel correction on mean recovered most probable estimate (MPE) and credibility intervals. The solid line and points are the average MPE over 100 data sets and the average 95% credibility interval is enclosed by the dotted lines and outline points. The horizontal dashed line indicates the 0.1 Θ used in generating the data. Data were simulated with 0.1% sequencing error and the LAMARC correction was applied.
Throughout our experiments, we calculated that for an experiment size of 100 instances, rejecting the truth between 0 and 10 times was consistent with a nominal rejection rate of 5%. Therefore we consider experiments in which LAMARC excluded the simulation value from its 95% credibility interval ≤10 times to be successful.
In the two-panel data sets for the case, only 99 data sets were analyzed as in one case no SNPs were found in the panel. Results for this case are given as a percentage of the number of data sets actually run.
Panel and sample size
Felsenstein (2005) showed that a small number of samples are sufficient for accurate inference of Θ for a single isolated population of fixed size. Table 3 shows that this is also true for panel-ascertained SNPs. We measured improvement in LAMARC’s ability to recover Θ when switching from 8 to 20 samples for panels of various sizes. Both with and without the panel correction, larger panels captured the true value of Θ more often than smaller ones. Without the correction, however, the truth was rejected at a high rate, especially with larger sample sizes. Scatter plots of most probable estimates (MPEs) and credibility interval widths (Figure S10) show tighter credibility intervals with increasing sample size both with and without the panel correction. This is expected, as additional information should allow tighter bounds. In uncorrected cases, there is a strong downward bias in the MPE of Θ, leading to increased rejection of the truth as the credibility intervals tighten. While Table 3 suggests a trend toward increased rejection of the truth with sample size even in corrected cases, the corrected formula captured the truth an acceptable proportion of the time for all panel/sample combinations tested. Table S2 summarizes similar data without error.
Table 3. Ability of LAMARC to recover Θ with different panel and sample sizes.
| % LAMARC runs rejecting simulation Θ-value |
||||||
|---|---|---|---|---|---|---|
| Panel correction | 4 panels, 8 samples | 4 panels, 20 samples | 8 panels, 8 samples | 8 panels, 20 samples | 16 panels, 8 samples | 16 panels, 20 samples |
| No | 47.0 | 78.0 | 25.0 | 60.0 | 9.0 | 27.0 |
| Yes | 7.0 | 9.0 | 3.0 | 5.0 | 3.0 | 6.0 |
Percentage of LAMARC runs rejecting their generating Θ-value, given 0.1% sequencing error and panel correction, is shown. All cases used the LAMARC error-aware correction. Each rejection rate was calculated from runs on the same set of 100 independently generated trees. Successive panel sizes and sample sizes include the members of the smaller sizes. Plots of these data are found in Figure S11.
Incorrect panel size declaration
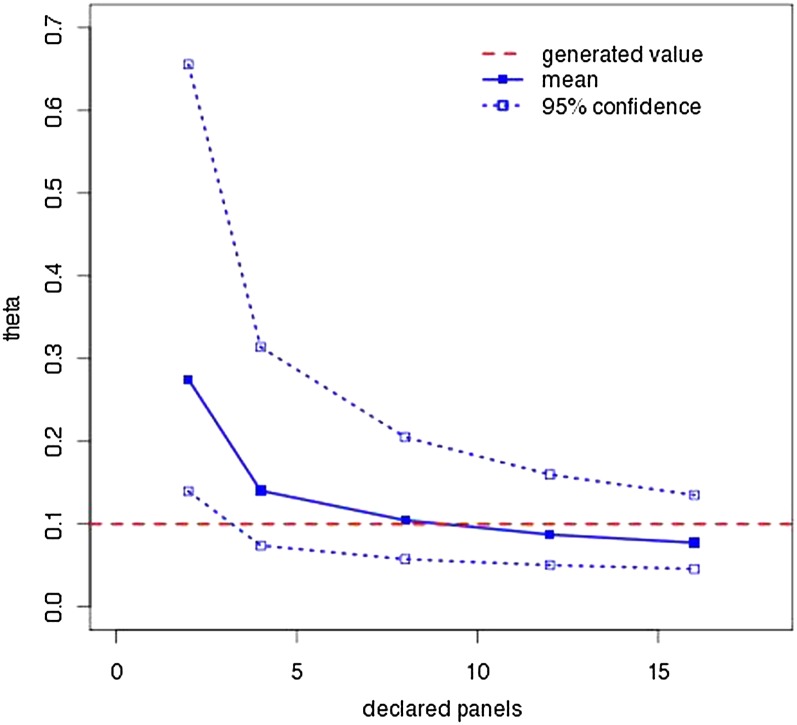
Given that panel correction greatly improves our ability to recover Θ, a natural question is whether one must know the panel size to achieve this improvement. Figure 4 confirms one must know the panel size by comparing the results of SNPs generated with a panel size of 8 and declared panel sizes of 2, 4, 8, 12, and 16 for correction. The values used for Figure 4 are found in Table S3.
Figure 4.
Effect of incorrect panel sizes on MPE and credibility intervals. One hundred data sets generated with and eight panels were analyzed using LAMARC with different declared panel sizes. The solid line and points are the average MPE; the dotted lines and outline points enclose the average 95% credibility interval. The horizontal dashed line indicates the 0.1 Θ used in generating the data.
MAFC procedure and effective panel size correction
We began our exploration of the MAFC data by examining the number of SNPs found with and without sequencing error for several minor allele-frequency cutoff levels applied to the 128-member panel. Table 4 shows the effective panel sizes calculated for each MAFC correction, along with the corresponding average SNP counts both with and without sequencing error. Note that at an error rate of 0.1%, the vast majority of SNPs occurring due to error were removed from the panel at the lowest MAFC level.
Table 4. MAFC effective panel sizes and number of variable sites for Θ = 0.001.
| MAFC % | Largest minor allele count removed by MAFC | Effective panel size | Expected SNP count, no sequencing error | Approximate expected SNP count, 0.1% sequencing error | Observed mean SNP count, no sequencing error | Observed mean SNP count, 0.1% sequencing error |
|---|---|---|---|---|---|---|
| 0 | 0 | 128 | 271.3 | 6248.8 | 283.02 | 6259.6 |
| 1.6 | 2/128 | 29 | 195.5 | 214.2 | 210.2 | 226.0 |
| 3.1 | 4/128 | 16 | 165.5 | 166.8 | 183.0 | 180.5 |
| 6.2 | 8/128 | 9 | 132.1 | 132.2 | 149.0 | 144.7 |
| 12.5 | 16/128 | 4 | 95.5 | 94.2 | 102.8 | 100.7 |
Shown are effective panel sizes, expected SNP counts without and with error, and mean observed SNP counts without and with error for 100 data sets with .
The trend of higher than expected observed mean SNP counts at each MAFC level was consistent with the higher than expected total SNP count seen in Table 1. The smaller observed SNP count for higher MAFC rejection levels on data with sequencing error was not intuitive. We therefore calculated an approximation to the expected distribution of observed minor allele counts under sequencing error. Drawing on earlier work modeling restriction site observations from underlying sequence data (Nei and Tajima 1985, Equation 4; Felsenstein 1992), we modeled the transformation from true, unobserved minor allele count to observed count with error. The observed decrease in MAFC SNP counts from error-free to error-containing data does not track exactly, but the same pattern is seen.
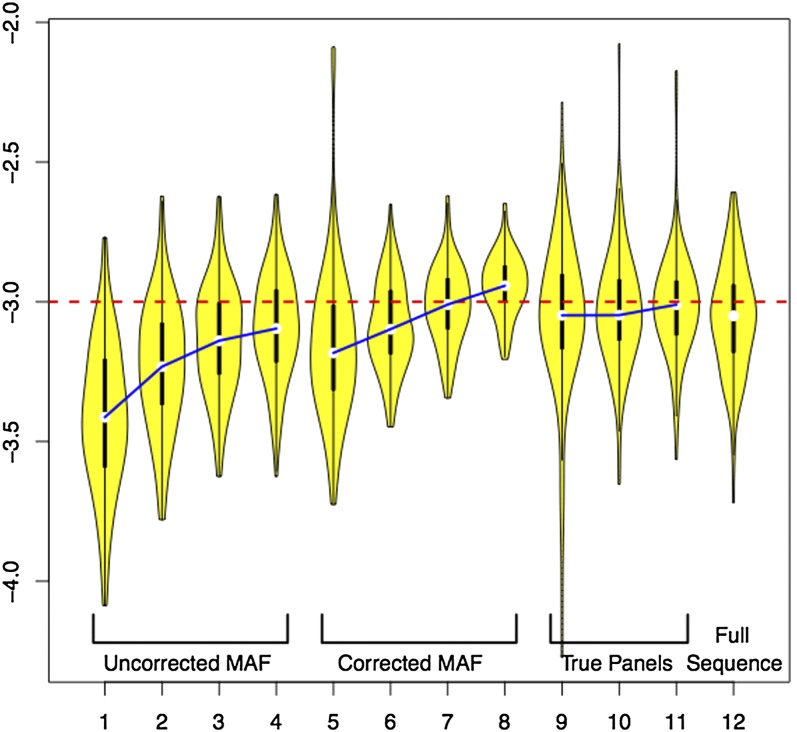
Table 5 summarizes LAMARC’s ability to recover Θ from MAFC data with and without the effective panel size correction. It also includes the results for smaller panel runs and fully sequenced data for the same eight samples. Figure 5 gives a visual representation of the distribution of recovered Θ-values for each of the 12 cases listed in Table 5. The average MPEs and high and low credibility interval bounds for the MAFC data are plotted in Figure S12.
Figure 5.
Distribution of MPE of Θ for different panel corrections. Violin plots show the log base 10 of the distribution of recovered Θ-estimates for the runs in Table 5. Medians of analyses using the same corrections and data ascertainment schemes are linked for clarity.
Effect of MAFC procedure and effective panel size correction on multipopulation data with recombination
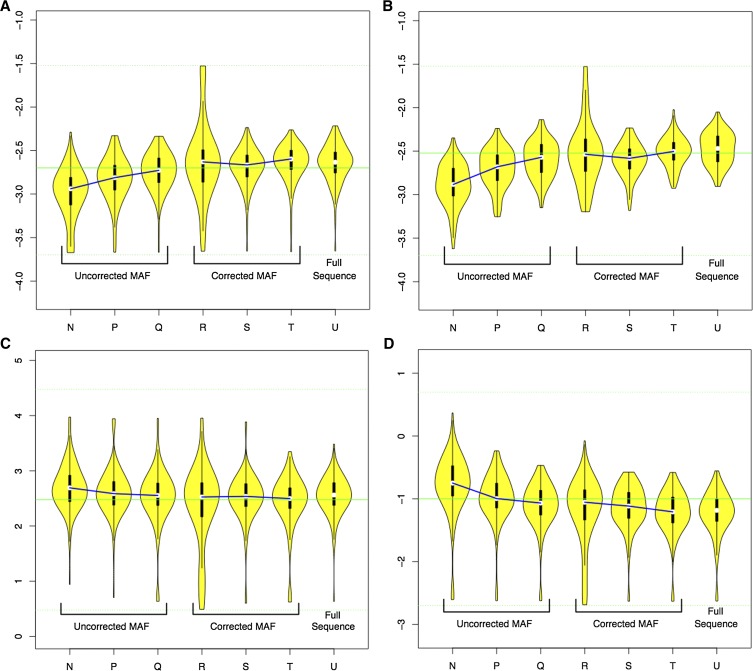
Tables 6 and 7 summarize LAMARC’s ability to recover population parameters from the two-population case for MAFC data without and with correction as well as fully sequenced data. Figure 6 gives a visual representation of recovered parameter values for each of the seven cases listed in Table 6. No data are reported for the migration rate into population North as the simulated value, zero, is not recoverable by LAMARC.
Table 6. Rejection rates for MAF panel corrections on multipopulation data.
| MAFC level | Panels declared | Panels correction used | Error correction used in LAMARC analysis | % rejection, Θ-North | % rejection, Θ-South | % rejection, mig rate into South | % rejection, rec rate | Figure 6 letter |
|---|---|---|---|---|---|---|---|---|
| 11.7 | — | No | No | 28 | 30 | 10 | 33 | N |
| 5.5 | — | No | No | 9 | 11 | 7 | 14 | P |
| 2.3 | — | No | No | 6 | 3 | 8 | 12 | Q |
| 11.7 | 2 | Yes | No | 22 | 20 | 18 | 23 | R |
| 5.5 | 5 | Yes | No | 7 | 7 | 9 | 14 | S |
| 2.3 | 10 | Yes | No | 8 | 6 | 8 | 14 | T |
| Complete SNP data | ||||||||
| — | — | No | Yes | 7 | 1 | 9 | 13 | U |
One hundred independent coalescent trees were generated, DNA data were simulated for each, and 0.1% sequencing error was applied. SNP data were then obtained using the panel sizes and MAFC corrections listed, with LAMARC runs completed using the corrections as listed. mig, migration; rec, recombination.
Table 7. Recovered MPEs for MAF panel corrections on multipopulation data.
| MAFC level | Panels declared | Panels correction used | Error correction used in LAMARC analysis | Mean recovered MPE Θ-North | Mean recovered MPE Θ-South | Mean recovered MPE mig rate into South | Mean recovered MPE rec rate | Figure 6 letter |
|---|---|---|---|---|---|---|---|---|
| 11.7 | — | No | No | 0.001243 | 0.001483 | 883.8 | 0.2563 | N |
| 5.5 | — | No | No | 0.001736 | 0.002227 | 763.4 | 0.1407 | P |
| 2.3 | — | No | No | 0.002049 | 0.002817 | 606.0 | 0.1018 | Q |
| 11.7 | 2 | Yes | No | 0.004600 | 0.004576 | 660.1 | 0.1034 | R |
| 5.5 | 5 | Yes | No | 0.002255 | 0.002717 | 542.6 | 0.0929 | S |
| 2.3 | 10 | Yes | No | 0.002487 | 0.003337 | 404.3 | 0.0768 | T |
| Complete SNP data | ||||||||
| — | — | No | Yes | 0.002517 | 0.0036601 | 466.0 | 0.0750 | U |
One hundred independent coalescent trees were generated, DNA data were simulated for each, and 0.1% sequencing error was applied. SNP data were then obtained using the panel sizes and MAFC corrections listed, with LAMARC runs completed using the corrections as listed.
Figure 6.
Distribution of MPE for two population parameter cases. (A) Recovered Θ-North values; (B) recovered Θ-South values; (C) recovered migration from North to South; (D) recovered recombination rates. Violin plots show the log base 10 of the distribution of recovered parameter estimates for the runs in Table 6. Medians of analyses using the same corrections and data ascertainment schemes are linked for clarity.
Discussion
Information is lost whenever a panel is used to guide SNP typing, and additional information is lost when a MAFC procedure is applied. Chip-based SNP typing is attractive because it is less expensive than full resequencing and provides the possibility of performing additional sequencing quickly. MAFC procedures appeal because a chip made with MAFC will see more variation per SNP included than one without and therefore appears more cost efficient. When these methods are used without correction, they bias coalescent analysis of the collected data to underestimate Θ. It is not possible to remove error without also removing low-frequency signal. Therefore, knowing which low-frequency data are missing is essential.
We have demonstrated that for coalescent-based inference of population parameters, data ascertained via a panel can be analyzed with reduced bias through use of the panel correction suggested in Kuhner et al. (2000). Information loss is severe with the smallest panel sizes, as seen in the widened credibility intervals for panel sizes 2 and 4 (Figure 3), whereas increasing from 16 panel members to 32 does not have much effect on the credibility intervals.
As previously shown by Felsenstein (2005), the sample size needed for accurate inference of Θ is quite small. This is confirmed in the presence of panel correction by our results showing only modest improvement in credibility interval tightness when going from 8 to 20 samples. Consequently, researchers undertaking coalescent analysis should consider full resequencing of a smaller number of individuals as an alternative to panel-based ascertainment of a larger number, especially in the case where the panel is to be created as part of the study. Panel-based ascertainment will sometimes lose unexpectedly large amounts of information. This is seen in Figure 2, in which a panel of size 80 missed over half the SNPs in a sample. Similar ill luck can befall the selection of samples for a resequencing study, but when it happens to a panel, all studies using that panel will be affected.
Use of MAFC is likely a false economy for coalescent analyses. Considerable work goes into sequencing of panel individuals to make the SNP chip and, as we have shown, even a modest MAFC procedure reduces the effective size of the panel drastically. An allele-frequency cutoff of 1.6% on a 128-member panel is comparable to a 29-member panel without MAFC. In data with 0.1% sequencing error and a human-like Θ, a 1.6% MAFC removes the vast majority of error SNPs. More aggressive MAFCs likely remove more signal than error. Appropriate statistical procedures can compensate for but not fully correct this loss of information.
Our two-population experiments suggest that Θ-population parameters are more susceptible to panel-introduced bias than other parameters. In our experiments, rejection of the simulated migration and recombination values was comparable among fully sequenced, corrected, and uncorrected MAFC data for all but the most aggressive (11.7%) MAFC procedures.
Population growth raises additional concerns for panel-based methods. In a growing population, branches of the coalescent tree at the tips are elongated compared to the more ancient branches. This increases the proportion of private polymorphisms in the data (Coventry et al. 2010) and it is exactly these polymorphisms that are lost through the use of panel and MAFC approaches. While the proxy-based true panel correction we present remains applicable in the presence of growth, we expect the loss of information and therefore corresponding loss of accuracy will be greater. Our effective panel size correction is not expected to apply in the presence of growth, as the formulas we used assumed a stable population.
We do not expect panel-ascertained and MAFC data to vanish in the near future. If data must be collected in this way, several steps can be taken to retain as much information as possible.
Panel size must be documented. We have shown that there is no conservative solution when panel size is not known: both guessing low and guessing high lead to bias (Figure 4). While Albrechtsen et al. (2010) suggest methods for inferring panel size, this does not justify omitting such information from the documentation of future SNP chips, as exact knowledge must be better than inference. Even if a SNP chip represents a heterogeneous collection of SNPs ascertained from different panel sizes, this information should be made available, as future analyses may be able to take it into account. Without panel size information the correction given here is impossible.
Information about any MAFC in effect is also essential, for similar reasons. We have shown that misstating panel size leads to bias. Although we did not measure this explicitly, misstating MAFC level is essentially the same as misstating panel size and should therefore also lead to bias.
Aggressive MAFC should be avoided. Sequencing error can be better handled by a statistical correction on the raw data. If MAFC must be used, the cutoff should be set as low as possible. While the “rare SNPs” are individually rare, they are collectively numerous and contain a substantial part of the information in a population survey. They should not be considered irrelevant or uninteresting. Table 5 shows that aggressive MAFC leads to very poor estimates even with correction.
Appropriate statistical corrections should be used for panel ascertainment, MAFC, and sequencing error. The panel corrections shown in this article will be released in LAMARC version 2.1.8 and can be implemented in other coalescent-based analytic tools. The sequencing error correction was introduced in LAMARC version 2.1.5 and can be used in any coalescent or phylogenetic analysis of DNA data, with or without reduction to SNPs, as long as the error rate is known.
Resequencing should be considered as an alternative to use of a SNP chip, particularly in cases with population growth or strong positive selection near the sampled genomic regions. We expect the loss of information to be more severe in such cases.
Avoiding error in one’s data sets is laudable, but insisting that all error be removed will lead to removing valuable information. When possible, error should be dealt with via statistical correction rather than mechanical removal. For coalescent analyses, this implies that collecting a small, high-quality set of data samples including both common and rare variants is superior to collecting a larger sample of common variants only.
Acknowledgments
The authors thank Joe Felsenstein, Josh Akey, and Bob Giansiracusa for their help. This work was supported by National Institutes of Health grant R01 HG004839 (to Mary Kuhner). Many of the two-population simulations were completed with support from an Amazon Web Services in Education Grants Award from Amazon.com.
Footnotes
Communicating editor: M. A. Beaumont
Literature Cited
- Adams A. M., Hudson R. R., 2004. Maximum-likelihood estimation of demographic parameters using the frequency spectrum of unlinked single-nucleotide polymorphism. Genetics 168: 1699–1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akey J. M., Zhang G., Zhang K., Jin L., Shriver M. D., 2002. Interrogating a high-density SNP map for signatures of natural selection. Genome Res. 12: 1805–1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Albrechtsen A., Nielsen F. C., Nielsen R., 2010. Ascertainment biases in SNP chips affect measures of population divergence. Mol. Biol. Evol. 27: 2534–2547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark A. G., Whittam T. S., 1992. Sequencing errors and molecular evolutionary analysis. Mol. Biol. Evol. 9: 744–752. [DOI] [PubMed] [Google Scholar]
- Coventry A., Bull-Otterson L. M., Liu X., Clark A. C., Maxwell T. J., et al. , 2010. Deep resequencing reveals excess rare recent variants consistent with explosive population growth. Nat. Commun. 1: 131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A. J., Rambaut A., 2007. BEAST: Bayesian evolutionary analysis by sampling trees. BMC Evol. Biol. 7: 214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewens W., 1972. The sampling theory of selectively neutral alleles. Theor. Popul. Biol. 3: 87–112. [DOI] [PubMed] [Google Scholar]
- Ewens W., 2000, Mathematical Population Genetics, 1. Theoretical Introduction, p. 114 Springer-Verlag, New York. [Google Scholar]
- Felsenstein J., 1981. Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 17(6): 368–376. [DOI] [PubMed] [Google Scholar]
- Felsenstein J., 1988. Phylogenies from molecular sequences: inference and reliability. Annu. Rev. Genet. 22: 521–525. [DOI] [PubMed] [Google Scholar]
- Felsenstein J., 1992. Phylogenies from restriction sites: a maximum-likelihood approach. Evolution 46: 159–173. [DOI] [PubMed] [Google Scholar]
- Felsenstein J., 2004. Inferring Phylogenies. Sinauer Associates, Sunderland, MA. [Google Scholar]
- Felsenstein J., 2005. Accuracy of coalescent likelihood estimates: Do we need more sites, more sequences, or more loci? Mol. Biol. Evol. 23: 691–700. [DOI] [PubMed] [Google Scholar]
- Hudson R. R., 1983. Properties of a neutral allele model with intragenic recombination. Theor. Popul. Biol. 23: 183–201. [DOI] [PubMed] [Google Scholar]
- Hudson R. R., 2002. Generating samples under a Wright-Fisher neutral model of genetic variation. Bioinformatics 18(2): 337–338. [DOI] [PubMed] [Google Scholar]
- International HapMap Consortium , 2003. The International HapMap Project. Nature 426: 789–796. [DOI] [PubMed] [Google Scholar]
- Johnson P. L. F., Slatkin M., 2008. Accounting for bias from sequencing error in population genetic estimates. Mol. Biol. Evol. 25: 199–206. [DOI] [PubMed] [Google Scholar]
- Kimura M., 1980. A simple model for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. J. Mol. Evol. 16: 111–120. [DOI] [PubMed] [Google Scholar]
- Kuhner M. K., 2006. LAMARC 2.0: maximum likelihood and Bayesian estimation of population parameters. Bioinformatics 22: 768–770. [DOI] [PubMed] [Google Scholar]
- Kuhner M. K., 2009. Coalescent genealogy samplers: windows into population history. Trends Ecol. Evol. 24: 86–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhner M. K., Beerli P., Yamato J., Felsenstein J., 2000. Usefulness of single nucleotide polymorphism data for estimating population parameters. Genetics 156: 439–447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray S. S., Oliphant A., Shen R., McBride C., Steeke R., et al. , 2004. A highly informative SNP linkage panel for human genetic studies. Nat. Methods 1: 113–117. [DOI] [PubMed] [Google Scholar]
- Nei M., Tajima F., 1985. Evolutionary change of restriction cleavage sites and phylogenetic inference for man and apes. Mol. Biol. Evol. 2: 189–205. [DOI] [PubMed] [Google Scholar]
- Nielsen R., 2000. Estimation of population parameters and recombination rates from single nucleotide polymorphisms. Genetics 154: 931–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., 2004. Population genetic analysis of ascertained SNP data. Hum. Genomics 1: 218–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen R., Hubisz M. J., Clark A. G., 2004. Reconstituting the frequency spectrum of ascertained single-nucleotide polymorphism data. Genetics 168: 2373–2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watterson G. A., 1975. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 7: 256–276. [DOI] [PubMed] [Google Scholar]