The anisotropic hyperelastic biomechanical response of the vocal ligament and implications for frequency regulation: A case study

Abstract

One of the primary mechanisms to vary one's vocal frequency is through vocal fold length changes. As stress and deformation are linked to each other, it is hypothesized that the anisotropy in the biomechanical properties of the vocal fold tissue would affect the phonation characteristics. A biomechanical model of vibrational frequency rise during vocal fold elongation is developed which combines an advanced biomechanical characterization protocol of the vocal fold tissue with continuum beam models. Biomechanical response of the tissue is related to a microstructurally informed, anisotropic, nonlinear hyperelastic constitutive model. A microstructural characteristic (the dispersion of collagen) was represented through a statistical orientation function acquired from a second harmonic generation image of the vocal ligament. Continuum models of vibration were constructed based upon Euler–Bernoulli and Timoshenko beam theories, and applied to the study of the vibration of a vocal ligament specimen. From the natural frequency predictions in dependence of elongation, two competing processes in frequency control emerged, i.e., the applied tension raises the frequency while simultaneously shear deformation lowers the frequency. Shear becomes much more substantial at higher modes of vibration and for highly anisotropic tissues. The analysis was developed as a case study based on a human vocal ligament specimen.

INTRODUCTION

The human voice has the capability to achieve a fundamental frequency F₀ range of five octaves.1 Many mechanisms contribute to sound production of the voice and F₀ control. Following the myoelastic-aerodynamic theory of phonation, these mechanisms are associated with the biomechanical properties of the vocal folds and the aerodynamic driving forces via the subglottal pressure.2 The biomechanical characteristics of the vocal folds can be categorized into passive (e.g., mass, length, elasticity) and active features (e.g., isotonic and isometric muscle contraction), which are inter-dependent, to regulate F₀.3 The vocal ligament (middle and deep layers of the lamina propria) is considered to be the primary load-bearing portion of the vocal fold, especially at high longitudinal stretches. It is part of the vocal fold structure that is the focus of the present study. Therefore, the vocal ligament has a critical functional role in phonation-enabling high vocal pitches by supporting large longitudinal stresses.

The string model of phonation is often used to model the change in F₀ due to variation of length and tension. Modeling experimental results of the vocal folds with the ideal string law dates back at least to the mid-20^th century.4 While the string model of phonation has widely been used to estimate the natural frequencies of phonation, such a model ignores the bending stiffness (flexural rigidity) of the vocal fold structure and thus underestimates frequencies.5 Beam models inherently account for bending stiffness allowing the prediction of a non-zero F₀ even in an unstretched state (with no applied tension), which is not possible in the string model.6, 7 The nonlinear biomechanical properties of the vocal folds have been integrated in F₀ predictions using string and classical (i.e., Euler–Bernoulli) beam models.5, 7, 8 The Euler–Bernoulli beam model is appropriate for structures with high length-to-thickness ratios (> 100) and for isotropic or nearly isotropic materials. Such conditions are typically not met in vocal folds.

Recent clinical studies have measured the vocal fold elongation using high-speed endoscopy and the acoustic signal (i.e., F₀) during a glissando in professional singers9, 10 and non-singers.11 Older techniques have used photography to inspect the vocal fold membranous length during an arpeggio.12, 13, 14 Still others have utilized radiographic methods such as traditional x-ray imaging15 or computed tomography.16 Finally, vocal fold elongation during frequency rise has been investigated in vitro with human larynges.4

The extracellular matrix of the vocal fold lamina propria is comprised of fibrous (e.g., collagen and elastin) and interstitial proteins (e.g., proteoglycans). These proteins are attributed to providing the elastic and viscous properties necessary to sustain the stresses and strains during phonation.17 A microstructural arrangement of elastin and collagen fibers aligned primarily in the anterior-posterior direction has been demonstrated in histological studies.18, 19, 20 The anisotropy of the vocal fold tissue was also confirmed in measurements of the biomechanical properties. A protocol was recently developed for the characterization of the tissue anisotropy in the small strain regime by combining longitudinal stretch experiments with transverse indentation experiments.21 The anisotropy, expressed as the ratio of the anterior-posterior elastic modulus and the longitudinal shear, was found to range typically from 15 to 40, while for an incompressible, isotropic tissue the ratio would equal three. As it was shown in Kelleher et al.,22, 23 the effect of shear deformation can be of substantial magnitude in the vibration of vocal fold tissue, and thus seems crucial for accurate predictions of the fundamental frequency. Furthermore, it is understood that during the stretching of a tissue (i.e., during posturing of the vocal folds) a re-orientation of the fibrous proteins can occur which will alter the effective anisotropy.

Based on these findings, it is argued here that vocal fold tissue should be described as a nonlinear and anisotropic solid. It is then hypothesized that shear deformation would play a significant role in vocal fold vibration. A structural model for vocal fold vibration accounting for longitudinal and shear stiffnesses is thus employed to provide relevant insight into vocal fold vibration during phonation.

In the present study, the vocal ligament is characterized by a microstructurally informed, anisotropic, nonlinear, hyperelastic constitutive model, specifically the Gasser–Ogden–Holzapfel (GOH) model.24 The GOH model is a histomechanical model with constitutive parameters obtained from the tissue's histology and from biomechanical experiments. For the present investigation, the microstructural data was obtained using multiphoton microscopy techniques, see Miri et al.25 for a recent application of this technique to vocal fold tissue. Multiphoton microscopy has emerged as a powerful tool for imaging a tissue's collagen fiber architecture without using exogenous stains.26 In order to accomplish this non-linear excitation, highly focused femtosecond pulsed lasers are typically used. Since the laser source is in the infrared range, the scattered light is minimized allowing for relatively deep imaging into the tissue (approximately 500 μm) while limiting the adverse effects of photobleaching.27 The biomechanical experiments commonly employed are uniaxial or biaxial stretch experiments. Then, the biomechanical parameters of the GOH model are inversely fitted to the experimental test data. This approach commonly causes uncertainty in the accuracy of the model predictions in the small strain regime. Here, this problem is overcome by supplementing the information from the stretch experiment in the longitudinal direction of the vocal folds with data from a transverse indentation experiment.21

The structural model of phonation considers the vocal ligament as a beam. The geometry of the vocal ligament may be approximated as a beam, though the beam representation may not be suitable for the vocal fold structure as a whole (cover, ligament, and muscle). For beams with small length-to-thickness ratios and/or relatively high levels of anisotropy (longitudinal elastic modulus to longitudinal shear modulus ratio > 10), the Timoshenko beam theory is appropriate.28 Timoshenko beam theory allows the beam's cross-section to rotate with respect to the neutral axis; hence, two additional effects are included: shear deformation and rotary inertia. Therefore, with longitudinal stretch during vocal fold posturing, the vibration characteristics will depend on the current longitudinal tangent stiffness and the longitudinal shear stiffness in the stretched state.

The purpose of this study was to develop a microstructural constitutive model of vocal ligament tissue deformation which is then linked to a beam model for computation of the modal frequencies. An experimental protocol for tissue testing and microscopy techniques is defined. To exemplify the proposed approach, the protocol is applied to an investigation of a vocal ligament specimen to obtain biomechanical and microstructural parameters. Bounds of the tissue constitutive model are evaluated and the vibration response of these limits is discussed. The present study is developed in the context of a case study. Thereby, one specific vocal ligament specimen excised from a human larynx is considered.

MATERIALS AND METHODS

Materials

The specimen under consideration was a vocal ligament carefully dissected from an excised 45 year-old Caucasian male larynx. The larynx was procured from the Willed Body Program of the University of Texas Southwestern Medical Center approximately 18 hours postmortem, and gross examination of the vocal folds revealed no abnormalities or pathologies. The sample preparation and testing protocols were approved by the Institutional Review Board of University of Texas Southwestern Medical Center. The ligament specimen was dissected with portions of the thyroid and arytenoid cartilages remaining to maintain the natural anterior and posterior attachments. The ligament specimen was separated from the underlying vocalis muscle and immediately placed in phosphate buffered saline (PBS).

Biomechanical testing

Upon dissection, biomechanical testing was conducted at the University of Texas South-western Medical Center. The vocal ligament specimen was subjected to longitudinal tension in the anterior-posterior direction following the approach described in detail in Kelleher et al.23 The displacements of two points on the specimen surface at the anterior commissure and vocal process were measured optically by use of a CCD camera system and an image analysis program. Therefore, the stretch λ of the ligament specimen due to elongation ΔL and with an initial length L₀, was calculated as λ = 1 + ΔL/L₀. Distance measurements were calibrated by taking an image of an object of known dimensions to establish a pixel-to-mm ratio. The specimen diameter of the entire tissue specimen was optically measured at thirteen equidistant locations, and the cross-sectional area was calculated assuming the tissue specimen to be of circular cross-section. A second CCD camera, orthogonal to the first, confirmed the circular cross-section to be a reasonable assumption (the diameter measurements from each camera were within 10% on average). Then the thirteen area measurements were averaged to estimate the initial cross-sectional area A₀. Finally, the nominal stress σ^N = P/A₀ was determined from the force output P and the specimen's cross-sectional area A₀ in the undeformed state. After the stretch experiments, the specimen was placed in PBS and allowed to rest for approximately 2 h.

Subsequently, a transverse (i.e., medial-lateral direction) indentation experiment was also performed on the vocal ligament specimen in a state where longitudinal stretch was absent.21 The compressive force-displacement response was evaluated using an anisotropic contact model.29 The force-displacement relation for an anisotropic half-space contacted by a rigid frictionless sphere, which leads to the same solution for two contacting cylinders with perpendicular axes, is

$$P^{\prime }=\frac{4M\sqrt{R}}{3}{\delta }^{3/2},$$ (1)

where $P^{\prime }$ is the indentation force, R is the radius of curvature, δ is the indentation depth, and M is the indentation modulus. The indentation modulus is an integral function of components of the elastic stiffness tensor, considering the ligament to be transversely isotropic (see Appendix A). For a known longitudinal elastic modulus (measured from the tensile test), the transverse elastic modulus and longitudinal shear modulus were obtained by inversely fitting Eq. 1 to the experimental P′-δ curve.21 An estimate of the “degree of anisotropy” in the unstretched state was defined as the ratio of the longitudinal elastic modulus to the longitudinal shear modulus. For purposes of estimating the anisotropy only, the longitudinal elastic modulus was computed by measuring the localized stretch of the mid-membranous region, which was where the indentation was performed. Since vocal fold tissue has been shown to be heterogeneous, it was important that the elastic properties be measured in the same region.22, 30 However, for the constitutive and vibration modeling the elastic properties of the overall tissue (i.e., from the anterior commissure to the vocal process) were used.

Microscopy and image processing

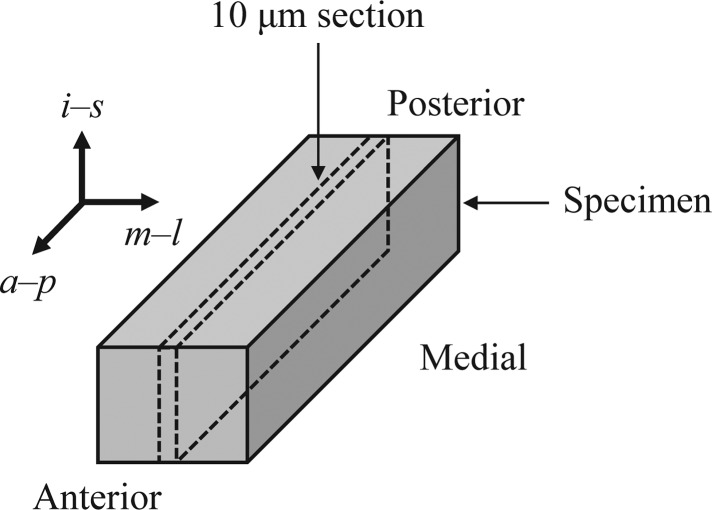
In order to utilize a microstructurally informed constitutive model, knowledge of the tissue's micro-architecture (specifically the directionality and dispersion of collagen fibers) is needed. Immediately following mechanical testing, the vocal ligament specimen was embedded in Optimal Cutting Temperature (Tissue-Tek^®, Sakura Finetek, Inc., Torrance, CA) compound, where the medial-lateral and anterior-posterior directions were labeled, and placed in a −20 °C freezer until sectioning. Once the specimen was frozen, it was transferred to a cryostat (i.e., a microtome in an enclosure maintained near −20 °C) and sectioned into 10 μm slices in the sagittal plane. The section taken from the mid-plane between the medial and lateral surfaces was placed onto a glass slide for viewing under a microscope. Figure 1 provides a depiction of the location and orientation of the section used for imaging.

Figure 1.

The location and orientation of the vocal ligament section used in the microscopy. a-p is the anterior-posterior, m-l is the medial-lateral, and i-s is the inferior-superior direction, respectively.

Microscopy was performed at the Live Cell Imaging Facility at University of Texas Southwestern Medical Center. Microstructural images of the vocal ligament specimen were acquired using a Zeiss laser scanning confocal microscope 510 META using an Achroplan water immersion objective with 40× magnification, 0.8 numerical aperture, and a working distance of 3.6 mm. Excitation was achieved using a tunable (705–980 nm) coherent Chameleon Ti:Sapphire pulsed near-infrared laser at an average power of 1.3 W. The excitation wavelength in this study was 900 nm. The resulting 512 × 512 pixel image had a field of view of 230 × 230 μm, which revealed the micro-architecture of the unstained samples. The backward (i.e., reflected light) and forward (i.e., transmitted light) second harmonic generation (SHG) signals of the microstructure of the vocal ligament specimen were simultaneously detected in two channels. The reflected image was not considered in this investigation because it produced a weaker signal than the transmitted image. Thus, only the transmitted image was analyzed for resolving the microstructural arrangement.

The raw SHG image from the mid-membranous location (mid-coronal plane) was loaded into matlab^® (The Mathworks, Natick, MA) and analyzed using an automated, custom-programed script to determine the distribution of fiber orientation. Initially, the image was contrast enhanced such that 1% of data was saturated at low and high intensities of the original image, and then padded with the mean gray scale value increasing the image size to 1024 × 1024 pixels. To reduce edge effects in the spectral analysis, a two-dimensional Hanning window was applied. The two-dimensional discrete Fourier transform was implemented and the power spectrum was displayed.31 The fiber alignment was calculated by analyzing the pixel intensity values of the power spectrum in polar coordinates, while omitting the pixels with a radial component less than 5 pixels to avoid erroneous low frequency effects. The relative intensity (RI) in angular increments of ±2° was

$$\text{RI}(\Theta )=\frac{\sum _{\theta \ge \Theta -2}^{\theta <\Theta +2}g(r,\theta )}{\sum _{\theta \ge 0°}^{\theta <180°}g(r,\theta )},$$ (2)

where g is the intensity value of the pixel with polar coordinates (r, θ) in the power spectrum.32 Two post-processing steps were performed on $\text{RI}(\Theta )$ before the preferred fiber orientation was determined. First, $\text{RI}(\Theta )$ was shifted such that the maximum value was now centered at $\Theta =0°$. This step was necessary in order to fit the data to a statistical (e.g., von Mises) distribution. Finally, the minimum value of the intensities was subtracted off of all $\text{RI}(\Theta )$ to remove the “dc” or baseline component of the grayscale intensities.

From the power spectrum, a parameter was extracted which characterized the microstructure. A single population of fibrous proteins is assumed, aligned in a transversely isotropic orientation while allowing for dispersion around the preferred/main axis of orientation. Following an approach suggested in Gasser et al.,24 the $\text{RI}(\Theta )$ from the SHG image was fitted to a von Mises distribution to find the density distribution function $\rho (\Theta )$:

$$\begin{array}{c}\rho (\Theta )=\frac{2\overline{\rho }(\Theta )}{{\int }_0^{\pi }\overline{\rho }(\Theta )\sin \Theta \hspace{0.17em}d\Theta },\\ \overline{\rho }(\Theta )=\frac{A\hspace{0.17em}\exp [b\hspace{0.17em}\cos \hspace{0.17em}(2\Theta )]}{2{\int }_0^{\pi }\exp \hspace{0.17em}[b\hspace{0.17em}\cos \hspace{0.17em}\Theta ]\hspace{0.17em}d\Theta },\end{array}$$ (3)

where A and b are fitted parameters of the von Mises distribution. The dispersion of the collagen fibers was subsequently quantified by using the parameter κ which represents the degree of fiber dispersion around the preferred anterior-posterior direction:

$$\kappa =\frac{1}{4}{\int }_0^{\pi }\rho (\Theta ){\sin }^3\Theta d\Theta .$$ (4)

The fiber dispersion coefficient ranges from κ = 0 for perfectly aligned fibers to κ = 1/3 for randomly distributed fibers (i.e., isotropic).

Microstructural constitutive model

The constitutive model employed for this investigation is the Gasser–Ogden–Holzapfel (GOH) model.24 The GOH model regards the tissue's mechanical response as a superposition of contributions from ground substances and from fibers. The interstitial proteins (“ground substances”) were modeled with an incompressible, isotropic, neo-Hookean model, and the fibrous proteins were modeled by an exponential, anisotropic, hyperelastic stress potential.

The GOH model was solved for the case of uniaxial tensile stretch λ along with longitudinal shear strain γ simultaneously. The longitudinal shear strain was included in the prescribed deformation so that an expression of the shear modulus as a function of λ may be obtained. The actual value of γ was set to zero so that no shear strain was present in the model, but derivatives with respect to γ are available. For tensile stretch λ applied in the longitudinal direction (treated as the x-axis or 11 subscript) and a longitudinal shear strain γ, the resulting Cauchy stress in the anterior-posterior direction σ₁₁ is

$$\begin{array}{c}{\sigma }_{11}=\frac{2}{3}({\tilde{\tau }}_{11}-{\tilde{\tau }}_{22}),\\ {\tilde{\tau }}_{11}=c({\lambda }^2+{\gamma }^2)+2{\psi }_f[{\lambda }^2(1-2\kappa )+\kappa {\gamma }^2],\\ {\tilde{\tau }}_{22}=(c+2\kappa {\psi }_f)/\lambda ,\\ {\psi }_f=k_1\overline{e}\exp (k_2{\overline{e}}^2),\\ \overline{e}={\lambda }^2(1-2\kappa )+\kappa {\gamma }^2-1+2\kappa /\lambda .\end{array}$$ (5)

The detailed algebraic and matrix manipulations leading to Eq. 5 are given in Appendix B. The mechanical response of Eq. 5 is described by four parameters: the isotropic neo-Hookean parameter c, a modulus-like parameter k₁, a dimensionless parameter indicative of the degree of nonlinearity k₂, and a microstructural parameter κ representing the collagen fiber dispersion. In order to compare to the experimental stress-stretch data, the nominal stress (which was equivalent to the first Piola–Kirchhoff stress in this case) is defined as

$${\sigma }_{11}^N=\frac{2}{3\lambda }({\tilde{\tau }}_{11}-{\tilde{\tau }}_{22}).$$ (6)

The tangent longitudinal elastic modulus (i.e., the instantaneous tensile stiffness at a given level of stretch) was obtained by partial differentiation of the Cauchy stress σ₁₁ with respect to λ. Partial differentiation was necessary because σ₁₁ was a function of two variables: λ and γ. The tangent elastic modulus E_t is

$$\begin{array}{c}{E}_t=\frac{\partial {\sigma }_{11}}{\partial \lambda }=\frac{2}{3}\left(\frac{\partial {\tilde{\tau }}_{11}}{\partial \lambda }-\frac{\partial {\tilde{\tau }}_{22}}{\partial \lambda }\right),\\ E_t=\frac{4}{3}\left[c\lambda +\frac{\partial {\psi }_f}{\partial \lambda }\left({\lambda }^2(1-2\kappa )-\frac{\kappa }{\lambda }+\kappa {\gamma }^2\right)+2{\psi }_f\lambda (1-2\kappa )+\frac{1}{2{\lambda }^2}(c+2{\psi }_f\kappa )\right],\\ \frac{\partial {\psi }_f}{\partial \lambda }=2k_1\left[\lambda (1-2\kappa )-\frac{\kappa }{{\lambda }^2}\right]\exp (k_2{\overline{e}}^2)+k_2{\psi }_f\frac{\partial ({\overline{e}}^2)}{\partial \lambda }.\end{array}$$ (7)

The tangent longitudinal shear modulus G_t as a function of λ is obtained by differentiating the longitudinal Cauchy shear stress σ₁₃ with respect to the shear strain as

$$\begin{array}{c}{G}_t=\frac{\partial {\sigma }_{13}}{\partial \gamma }=\frac{1}{\sqrt{\lambda }}\left(c+2\kappa \gamma \frac{\partial {\psi }_f}{\partial \gamma }+2\kappa {\psi }_f\right),\\ \frac{\partial {\psi }_f}{\partial \gamma }=2\kappa k_1\gamma \exp (k_2{\overline{e}}^2)+4\kappa k_2\gamma {\psi }_f\left[\kappa {\gamma }^2+{\lambda }^2(1-2\kappa )+\frac{2\kappa }{\lambda }-1\right].\end{array}$$ (8)

Considering the unstretched state (λ = 1, γ = 0) and known ratio E_t,0/G_t,0, the number of parameters for the GOH model reduce to two as the following expression emerges:

$$\frac{E_{t,0}}{G_{t,0}}(\lambda =1,\hspace{0.17em}\gamma =0)=2+\frac{8k_1}{3c}{(1-3\kappa )}^2.$$ (9)

The experimental stress-stretch response was fit to the expression of Eq. 6 using an optimization process executed with the Global Optimization Toolbox^™ of matlab^®. The algorithm solves the least-squares problem for multiple start points of k₁ and k₂ in an effort to find the global minimum rather than local minima. Constraints were imposed on the parametric search space so that the upper bounds of k₁ and k₂ were [1000 kPa, 1000], respectively, and the lower bounds were zero. 50 start points were randomly selected over the range of possible values in the optimization process. The set of k₁ and k₂ that was deemed the optimal solution was one that minimized the residual sum of squares (RSS). As a measure of the goodness-of-fit, the coefficient of determination R² = 1 − RSS/TSS, where TSS is the total sum of squares, was calculated.

For comparison and discussion purposes, two hypothetical constitutive characterization cases are considered: (1) a case assuming initial isotropic response and (2) a case assuming near-perfect microstructural alignment. For the ideal isotropic case (κ = 1/3), the measured anisotropy in the unstretched state E_t,0/G_t,0 cannot be imposed as a constraint, and therefore an approximate isotropic case is considered with κ = 0.3. For κ = 0 (perfectly aligned fibers), the equations significantly reduce in complexity. In particular, the tangent shear modulus becomes $G_t=c/\sqrt{\lambda }$ which indicates the absence of load transfer across the fibers in shear. A near-perfect microstructure alignment with κ = 0.01 will be used instead.

Vibration-dynamic beam models

The vocal ligament vibration characteristics were derived from the analysis by treating the ligament structure as a beam with circular cross-sections and an incompressible, anisotropic elastic solid. At each level of applied longitudinal stretch, the tangent stiffnesses E_t and G_t were computed and subsequently inserted into the beam model equations. The length, diameter, cross-sectional area, and second moment of inertia in the current/deformed configuration, $L=\lambda L_0,$$D=D_0/\sqrt{\lambda },$$A=A_0/\sqrt{\lambda },$ and $I=0.25\pi {\left(D/2\right)}^4$ (assuming incompressibility), respectively, were used rather than the quantities in the reference/undeformed configuration, as in Zhang et al.7

For an Euler–Bernoulli beam subjected to a longitudinal tensile load, the governing equation is

$$E_{t}I\frac{{\partial }^{4}w}{\partial x^4}-P\frac{{\partial }^{2}w}{\partial x^2}+{\rho }_{t}A\frac{{\partial }^{2}w}{\partial t^2}=0,$$ (10)

where w is the deflection of a beam segment located a distance x from the anterior end, t is time, P is the applied longitudinal tension which is P = σ₁₁ A, and ρ_t is the tissue density.33 The first term on the left hand side of Eq. 10 constitutes the bending resistance (flexural rigidity) of the beam, the second term accounts for the applied tension, and the last term is the inertial effects of the lateral (translational) displacement. The solution can be written as a linear superposition of four terms (sine, cosine, hyperbolic sine, and hyperbolic cosine) along with arbitrary constants to be determined by the boundary conditions. Therefore, the frequency of the nth mode for a pinned-pinned Euler–Bernoulli beam as a function of the longitudinal stretch is34

$$F_n^{EB}(\lambda )=\frac{{(n\pi )}^2}{L^2}\sqrt{\frac{E_{t}I}{{\rho }_{t}A}}{\left[1+\frac{P{L}^2}{{(n\pi )}^2{E}_{t}I}\right]}^{1/2}.$$ (11)

For a Timoshenko beam under a longitudinal tensile load, the two governing equations are35

$$\begin{array}{c}\left(1+\frac{P}{k_s{G}_{t}A}\right)\hspace{0.17em}{E}_{t}I\frac{{\partial }^{4}w}{\partial x^4}-P\frac{{\partial }^{2}w}{\partial x^2}+{\rho }_{t}A\frac{{\partial }^{2}w}{\partial t^2}-{\rho }_{t}I\left[1+\frac{P}{k_s{G}_{t}A}+\frac{E_t}{k_s{G}_t}\right]\frac{{\partial }^{4}w}{\partial x^2\partial t^2}=0,\\ \left(1+\frac{P}{k_s{G}_{t}A}\right)\hspace{0.17em}{E}_{t}I\frac{{\partial }^4\varphi }{\partial x^4}-P\frac{{\partial }^2\varphi }{\partial x^2}+{\rho }_{t}A\frac{{\partial }^2\varphi }{\partial t^2}-{\rho }_{t}I\left[1+\frac{P}{k_s{G}_{t}A}+\frac{E_t}{k_s{G}_t}\right]\frac{{\partial }^4\varphi }{\partial x^2\partial t^2}=0,\end{array}$$ (12)

where ϕ is the rotation of the beam's cross-section and k_s is Timoshenko's shear coefficient. In Eq. 12, shear deformation and rotary inertia are accounted for. The last term on the left hand side constitutes the joint action of shear deformation and rotary inertia but is of negligible proportions, according to Abramovich,35 so it is omitted in the solution process. After the separation of variables method and applying boundary conditions, the nth mode frequency variation with applied stretch of a pinned-pinned Timoshenko beam is

$$\begin{array}{c}\hfill F_n^T(\lambda )=\frac{{(n\pi )}^2}{L^2}\sqrt{\frac{E_{t}I}{{\rho }_{t}A}}{\left[\frac{1}{\beta }\left(1+\frac{P{L}^2}{{(n\pi )}^2{E}_{t}I}+\frac{P}{k_s{G}_{t}A}\right)\right]}^{1/2},\\ \hfill \beta =1+{(n\pi )}^2\left\{\frac{I}{A{L}^2}\left(1+\frac{P}{k_s{G}_{t}A}\right)+\frac{E_{t}I}{k_s{G}_{t}A{L}^2}\right\}.\end{array}$$ (13)

Timoshenko's shear (correction) coefficient k_s is a constant which depends upon the shape of the beam's cross-section.36 For a circular cross-section and incompressible tissue k_s = 0.964. It is important to note that the beam models developed here reveal the modal frequencies of the vocal ligament tissue and do not encompass flow-induced, self-sustained vibration.

RESULTS

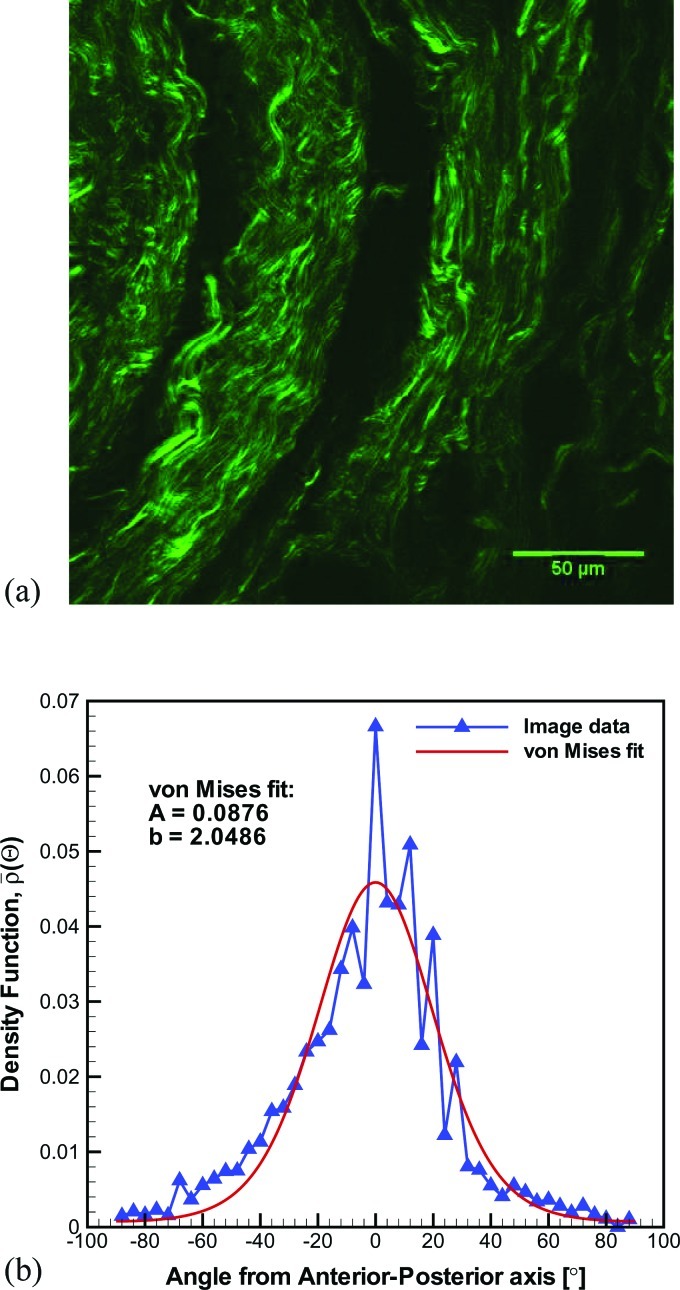
The SHG microstructural image and the results of subsequent image processing steps for the specimen of the present case study are displayed in Fig. 2. The image revealed the extracellular matrix fibrous proteins, Fig. 2a. A waviness or crimp typical of collagen fibers is evident. The main fiber direction, assumed to be associated with the anterior-posterior direction, was approximately 70° counter-clockwise from the SHG image's horizontal axis (i.e., abscissa). Figure 2b depicts the relative intensity distribution, shifted such that the maximum was centered at $\Theta =0°$ (i.e., the anterior-posterior axis). The von Mises density distribution fit, which has a goodness-of-fit R² = 0.88, is also shown. The value of the fiber dispersion coefficient computed from this particular ligament's microstructure was κ = 0.1444. Thus, the ligament specimen of the present case study displayed a microstructure that is strongly aligned but possesses significant dispersion. This level of dispersion was found to be representative for the mid-membranous region of the vocal ligament.37

Figure 2.

Microscopy and digital image processing.

The vocal ligament specimen exhibited a time dependent response with the stress at maximum load declining continuously with the number of load cycles in both the stretch and the indentation experiments. Even after 180 cycles, no steady state response was reached, consistent with other studies.23, 38 Thus, the analysis considers one representative cycle such that transient effects associated with cyclic loading were minimized. In particular, data is presented for the 55th loading cycle of the stretch and indentation tests. From cycles 1 to 180 in the stretch test, the peak force decayed by 33%. From cycles 1 to 60 in the indentation test, the peak force decayed by 25%. The detailed analysis of the ligament specimen was conducted for the 55th cycle where the peak force had experienced 76 and 99% of the total decay for the stretch and indentation tests, respectively.

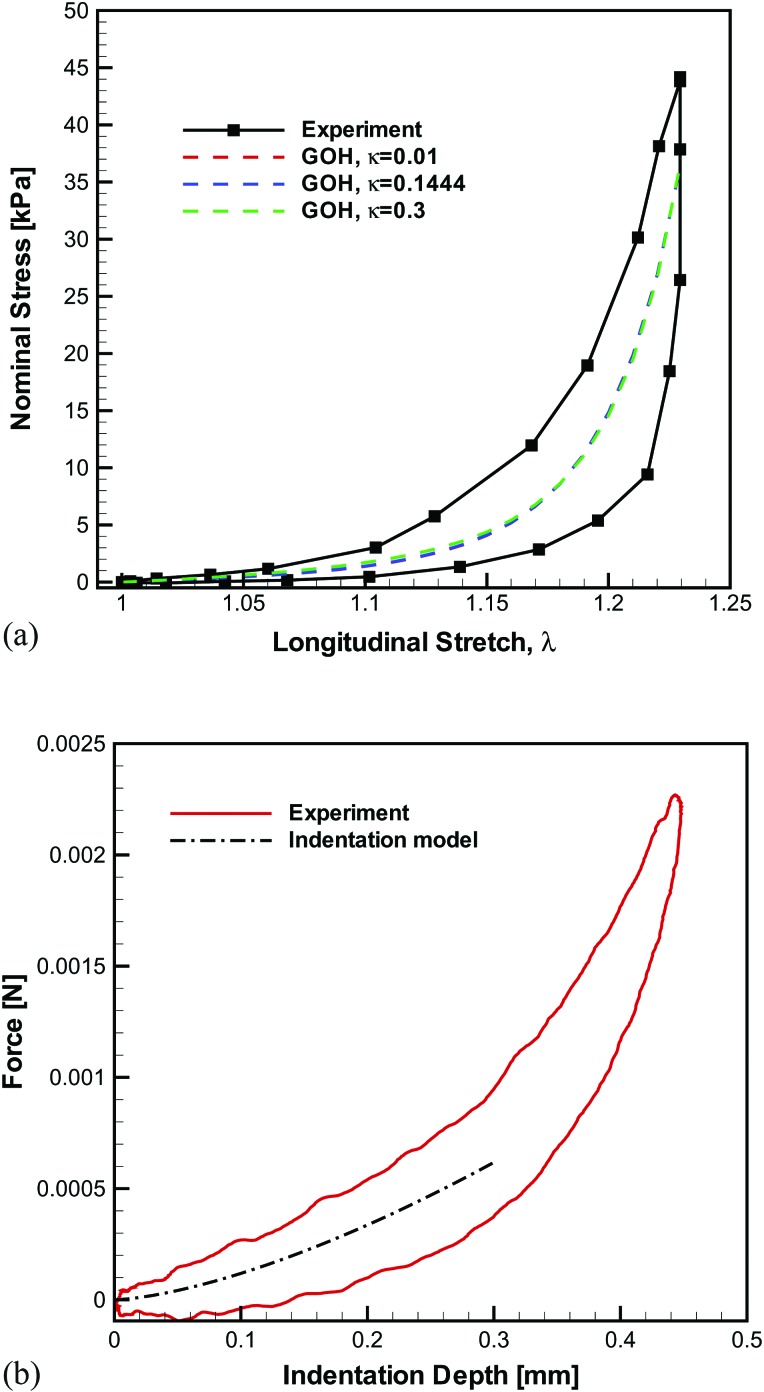
The tensile stress-stretch curve for the overall tissue (i.e., from anterior commissure to the vocal process) of the 55th cycle is depicted in Fig. 3a with the σ^N-λ response being highly nonlinear and hysteretic. The tensile response of the middle segment (i.e., mid-membranous region) exhibited an initial longitudinal elastic modulus of 28 kPa. Analysis of the transverse indentation experiment [see Fig. 3b] revealed that the transverse elastic modulus was 2.5 kPa and the longitudinal shear modulus was 0.9 kPa. Therefore, E_t,0/G_t,0 = 25 was used to approximate the degree of anisotropy in the unstretched state for this ligament specimen, which is a typical value for the vocal ligament.21 The modeled curve in Fig. 3b was fitted to only the initial 0.3 mm of the indentation depth due to the transverse indentation model's restriction to the small strain regime.21

Figure 3.

The biomechanical stretch and indentation experiments.

The GOH model with constitutive parameters k₁ = 8.14 kPa, k₂ = 27.32 for κ = 0.1444 and c = 0.30 kPa was found to approximate the experimental stress-stretch curve well (R² = 0.8360), Fig. 3a. It should be noted again that these parameters were determined under constraint of Eq. 9. Figure 3a depicts the outcome of the constitutive description by assuming a priori a near perfectly aligned microstructure (κ = 0.01) together with the measured anisotropy ratio. The constitutive parameters for this approximation were k₁ = 2.85 kPa, k₂ = 11.18, and c = 0.31 kPa. Again, a good description of the uniaxial stretch data was achieved, R² = 0.8359. Finally, assuming a nearly isotropic (κ = 0.3) tissue and E_t,0/G_t,0 = 3 representative of the isotropic response, the parameters were k₁ = 119.89 kPa, k₂ = 243.65, and c = 3.20 kPa (R² = 0.8362). It should be noted that the cases of κ = 0.01 and κ = 0.3 are introduced for comparison only and do not represent the actual tissue specimen in this case study.

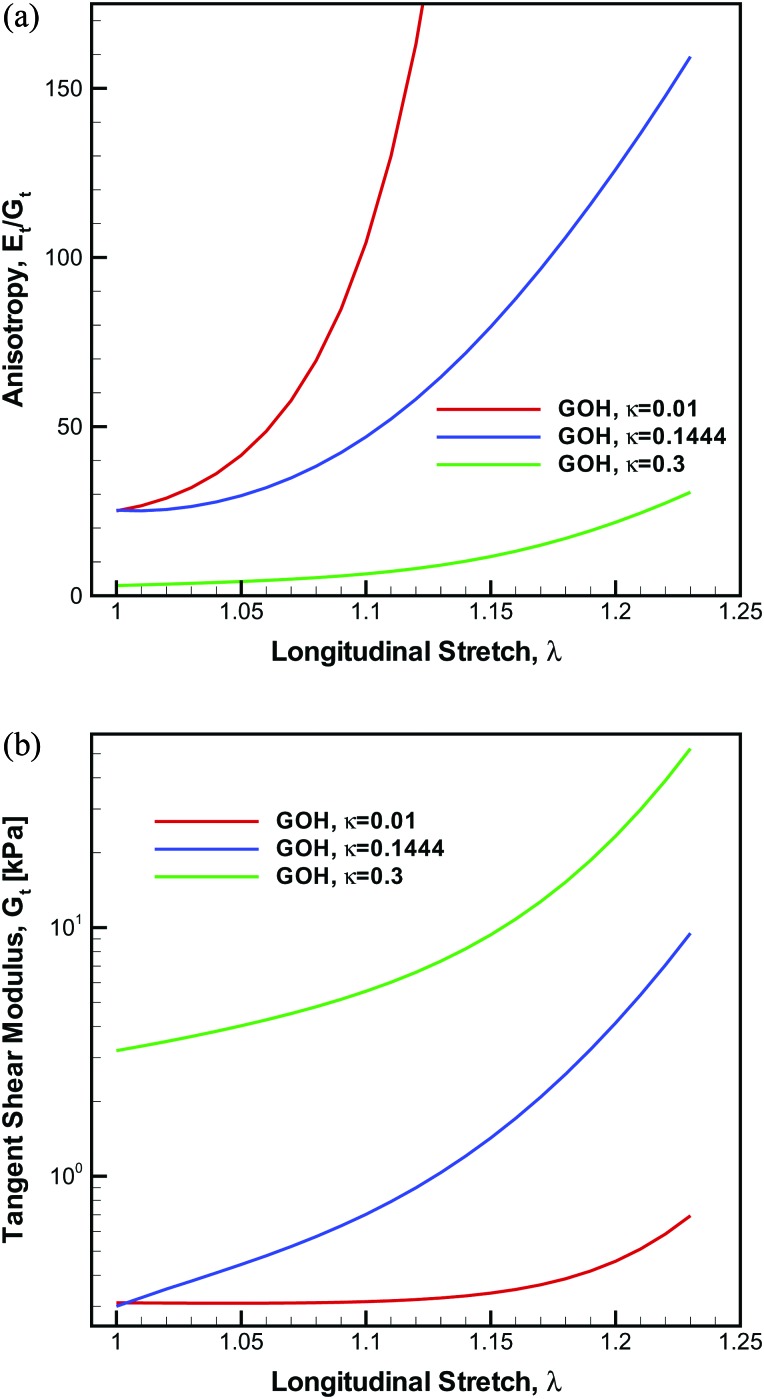
Figure 4a shows the evolution of the degree of anisotropy E_t/G_t with longitudinal stretch, as predicted by the GOH model for three values of fiber dispersion: κ = 0.1444 (the measured value of fiber dispersion), κ = 0.01 (virtually no fiber dispersion), and κ = 0.3 (nearly random dispersion). For κ = 0.1444 and the tissue specimen in this case study, the anisotropy is initially 25 and was predicted to increase nonlinearly with λ. At λ = 1.23 the ratio E_t/G_t reaches a value of 159. For the assumed value of κ = 0.01, the anisotropy was also set to 25 initially, but subsequently increased more substantially, reaching 2162 at λ = 1.23. For the nearly isotropic case κ = 0.3, the anisotropy was set to 3 in the unstretched state but increased to merely 31 at λ = 1.23. The stress-stretch curves and the longitudinal tangent stiffness values were nearly identical for all three cases. Therefore, the variations in the anisotropy between κ = 0.01, κ = 0.1444, and κ = 0.3 were due to drastically different responses in the tangent shear moduli, Fig. 4b. For κ = 0.01, G_t was essentially constant until λ = 1.15; yet when the fiber dispersion is accounted for G_t increases exponentially even from λ = 1.0. The impact this nonlinearity and evolution of the anisotropy with applied stretch has on the dynamic beam models is examined next.

Figure 4.

The anisotropy and tangent shear modulus predicted from the GOH model for three levels of fiber dispersion (κ = 0.01, κ = 0.1444, and κ = 0.3).

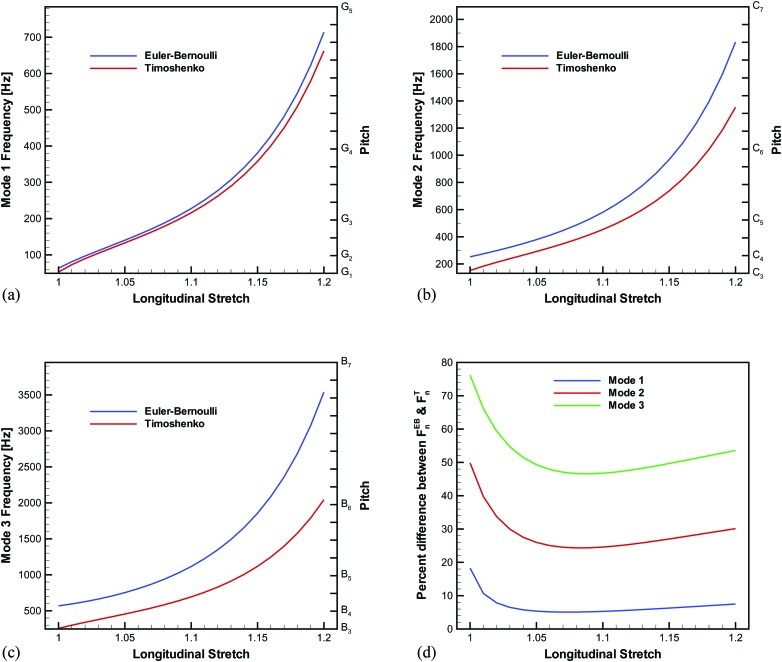
The first three natural frequencies of vibration in dependence of the longitudinal stretch for the vocal ligament specimen computed using the Euler–Bernoulli and the Timoshenko beam models [Eqs. 11, 13] are displayed in Fig. 5. The first three modes of vibration were studied because these have been projected to account for 99% of the energy at the onset of self-oscillation.39 The ligament specimen had an initial length and diameter of L₀ = 17.12 mm and D₀ = 2.78 mm, respectively, and was assumed to have a density of ρ_t = 1040 kg/m³. In the unstretched state, the fundamental frequency was 63 and 53 Hz for the Euler–Bernoulli and the Timoshenko models, respectively. Contrary to the beam models, the string model equation $(F_0=(1/2L)\sqrt{{\sigma }_{11}/{\rho }_t\hspace{0.17em}})$ would predict F₀ = 0 Hz in the unstretched state. The $F_n^T-\lambda$ curves were essentially linear in the small stretch region (λ < 1.10) but then increased strongly beyond λ = 1.15. This increase of the frequency for large stretch domain was due to exponential stiffening of the beam (i.e., ligament) as indicated in Fig. 3a. The percent difference between $F_n^{EB}$ and $F_n^T$ (for n = 1, 2, 3) as a function of the longitudinal stretch is given in Fig. 5d. For the first mode, the percent difference was initially 18% in the undeformed state. As longitudinal stretch was applied, the percent difference decreased until λ = 1.05, but then began increasing monotonically yet was still within 10% difference. Comparable trends were noted for modes two and three; however, the percent difference values were much larger. In the unstretched state of mode three, the Euler–Bernoulli model estimated a frequency more than double that of the Timoshenko model. Therefore, the effects of transverse shear deformation and rotary inertia had an even greater influence on the natural frequencies at higher modes, similar to other studies.40

Figure 5.

Euler–Bernoulli and Timoshenko beam model predictions of the natural frequencies for the GOH constitutive model and κ = 0.1444, with the pitch displayed on the secondary vertical axis.

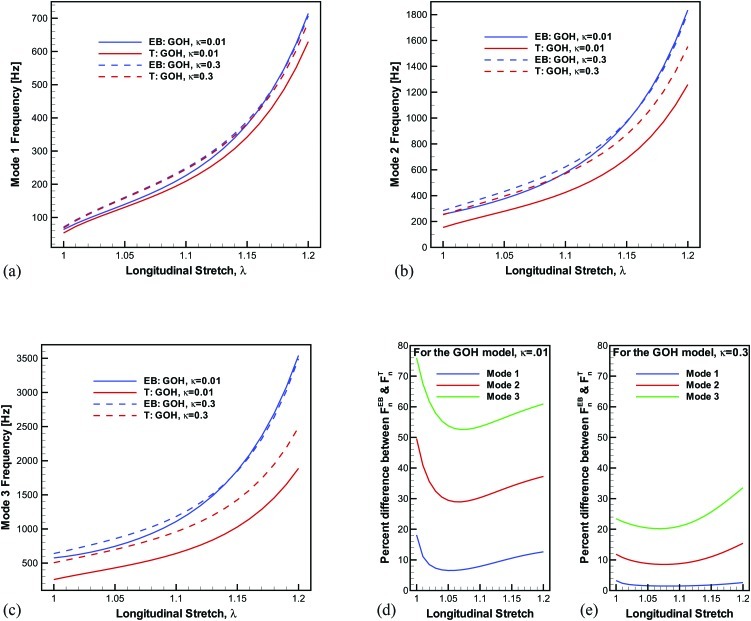
The natural frequency predictions are compared for the two extreme microstructural cases (κ = 0.01 and κ = 0.3) in Fig. 6. Since the case of κ = 0.3 has a low level of anisotropy, the shear effects are inhibited which causes the differences between Euler–Bernoulli and Timoshenko models to be minimal, particularly for the fundamental mode [Fig. 6e].

Figure 6.

Euler–Bernoulli and Timoshenko beam model predictions for the extreme cases of near perfectly aligned fibers (κ = 0.01) and near isotropy (κ = 0.3). (d) and (e) show the percent difference of the frequency predictions from the Euler–Bernoulli and Timoshenko beam models for κ = 0.01 and κ = 0.3, respectively.

DISCUSSION

This investigation presented an approach connecting the microstructure of the vocal ligament to its biomechanical characteristics and functional role during phonation. The microstructural arrangement of the extracellular matrix fibrous proteins, identified by the inherent crimp to be primarily collagen fibers, was quantified via a fiber dispersion coefficient. This particular microstructure was subsequently correlated to the macro-scale biomechanical response under uniaxial tension. Once the biomechanical properties were determined, dynamic beam models were developed to gain insights into phonation processes, in our case vocal fold posturing during a glissando. Consequently, a novel structure-property-function technique was illustrated for a vocal ligament specimen.

The biomechanical response was modeled by the nonlinear, anisotropic Gasser–Ogden–Holzapfel constitutive model. The nonlinearity of the stress-stretch curve at large deformations was predominantly due to increased contribution of the fibrous proteins. In the unstretched state, the fibers were dispersed about the anterior-posterior axis through the definition of the fiber dispersion coefficient κ which was measured from the SHG image. As the tensile stretch was applied, the fibers began to align further along the longitudinal axis which caused the exponential growth in the stress-stretch response and stiffness at large stretch levels. Furthermore, the evolution of the anisotropy as tension was applied was also a direct outcome of the GOH model. This result could not be replicated in phenomenological models that do not account for the changing microstructure.

There are distinct advantages of the microstructurally based constitutive model as opposed to a macro-scale anisotropic constitutive model (e.g., Fung-type hyperelastic model). First, a macro-scale model can be prone to mathematical deficiencies such as non-convexity when fitting parameters, where convexity implies that the stiffness tensor (i.e., second derivative of the strain-energy potential with respect to $\overline{e}$) is positive definite.41 Besides the mathematical advantages of material stability, a microstructural model is favorable regarding the biomechanics as well. A macro-scale anisotropic model can be approximated with the current model by setting κ = 0.01 (approximating perfectly aligned fibers). This would be the scenario if one was to use a typical transversely isotropic model of the vocal folds. While the longitudinal properties (i.e., tangent Young's modulus) from the tensile test could be properly modeled with a macro-scale anisotropic model, the macro-scale model is incapable of replicating other physical characteristics such as the evolution of the shear modulus [Fig. 4b]. A microstructural model accounting for the fiber dispersion is critical to accurately model the biomechanical properties in multiple directions. Complex loading configurations occur in vivo during phonation, where longitudinal tension is present with shear deformation. In other biological systems, such as arterial tissues of the cardiovascular system, multi-axial loading conditions are present. This study suggests that a macro-scale anisotropic constitutive model would be unable to accurately model the multi-axial behavior. Hence, a microstructural model accounting for fiber dispersion is obligatory for functional biomechanics. Furthermore, this emphasizes the need to experimentally measure the fiber dispersion and not simply fit the parameter. Considering κ = 0.01, κ = 0.1444, and κ = 0.3 in the analysis above, the curve fits to σ^N − λ yielded a nearly identical R² values, making it impossible to distinguish between κ values. Thus, knowledge of κ is essential to determine the evolution of the tissue anisotropy.

One limitation of the current approach was the assumption that the fiber dispersion κ computed from the SHG image at the mid-membranous (i.e., mid-coronal) location was uniform throughout the vocal ligament specimen. We speculate that the microstructural arrangement likely varies based upon the anterior-posterior location along the vocal ligament as indicated by the heterogeneous elastic response measured in previous studies.22, 30 A more complete analysis should include the fiber dispersion at several locations along the vocal ligament to account for the histological heterogeneity. A recent study has documented the dispersion and density of collagenous fibers of the vocal ligament with more samples and provided a statistical range.37 Another limitation was that only one specimen was analyzed since this was a case study. The anatomical and biomechanical variations in the vocal fold lamina propria will likely lead to a distinct vibrational frequency paradigm for each subject. Nevertheless, the specimen analyzed in the present case study represents a typical male vocal ligament in terms of geometry (e.g., length and thickness) and mechanical properties.

The continuum dynamic beam models of vocal ligament vibration described above are attractive due to their simplicity. The number of required parameters is small (8 for this investigation) compared to lumped mass models, which can involve many parameters (e.g., 28 parameters in Tokuda et al.42). Euler–Bernoulli (i.e., classical) beam theory is typically intended for long slender structures (length-to-thickness ratio > 100), and it assumes isotropy. The shear mode of deformation is known to be a primary factor contributing to the mucosal wave of vocal fold vibration.43 Yet this mode cannot be captured in an Euler–Bernoulli beam model (or a string model) of phonation. This can be remedied by employing Timoshenko beam theory. A Timoshenko beam accounts for shear deformation, which is especially important for highly anisotropic structures, and is applicable for thick beams, which seems to be relevant for the vocal ligament (length-to-thickness ratio ≈ 15). In the Timoshenko beam model of Eq. 13, the role of bending resistance and rotary inertia only (i.e., Rayleigh beam theory) can be elicited by letting G_t approach infinity, which suppresses shear deformation. The F₀-λ curve of this model is within 1% of the Euler–Bernoulli prediction. Conversely, the role of bending resistance and shear deformation only (i.e., Shear beam theory) can be seen by setting the first I/AL² term of β to zero, which suppresses rotary inertia. The F₀-λ curve of this model is virtually identical to the Timoshenko model in Fig. 5a, with the differences being less than 1.5%. Therefore, one can deduce that the major difference between the Euler–Bernoulli and Timoshenko beam models is the inclusion of shear deformation not rotary inertia.

In the unstretched state, which is more applicable to normal speaking conditions, the Euler–Bernoulli model predicted a fundamental frequency that was 20% greater than the Timoshenko model. However, this study suggests that there may not be a drastic difference between $F_0^{EB}$ and $F_0^T$ as the vocal ligament is elongated. The difference is much larger at higher modes of vibration. The importance of transverse shear deformation and rotary inertia are more pronounced on the second and third natural frequencies because the effective “beam” length is shortened in these higher mode shapes and shear deformation has more influence in shorter beams. During singing (e.g., a glissando), these higher modes may play an even larger role than in normal speaking conditions. Thus, Timoshenko beam theory should be used when studying vocal fold vibration, especially the higher modes of vibration.

There are several recommendations for future studies. First, frequency rise in this investigation was modeled only as vibration of the passive elastic properties of the vocal ligament. Biological tissues commonly exhibit a hysteretic response, and the vocal ligament of this case study does so too, as indicated in Fig. 3. The viscous tissue response underpinning the hysteresis is not accounted for presently and model predictions are based on the centerline of the hysteresis loop of the stress-stretch data. Tissue characterization and constitutive modeling accounting for the anisotropy in the viscous tissue response is currently ongoing work. Also, the active properties of the vocalis (thyroarytenoid) muscle should be incorporated along with the longitudinal tension since vocalis muscle contraction would stiffen the foundation of the vocal fold, which could be modeled with a Winkler foundation as developed in Nielsen.44 Lastly, the microscopy technique detailed in this investigation could be used to test the premise that the vocal ligament is transversely isotropic. Most models of the vocal fold lamina propria that account for tissue anisotropy, suppose the tissue to be transversely isotropic (e.g., Ref. 45). Acquiring three dimensional multiphoton images of the vocal fold microstructure, as in Miri et al.,25 could allow one to assess if the fibrous proteins do truly possess rotational symmetry about the anterior-posterior axis. If this rotational symmetry is absent then more advanced material models may be required.

CONCLUSION

The present work contributes two primary aspects to the understanding of phonation: (1) a microstructurally informed, nonlinear, anisotropic hyperelastic constitutive model was employed to characterize the biomechanics of vocal fold tissue, and (2) the effects of the anisotropy in mechanical properties on the natural frequency of vibration during vocal ligament elongation were evaluated. Therefore, a new understanding of the microstructure-property-function relationship emerged. The approach was illustrated as a case study for a vocal ligament specimen. The constitutive model integrated information about the ligament's micro-architecture, specifically the dispersion of collagen fibers. The GOH model allowed the uniaxial test data to be fit independent of the microstructure characteristics. However, the model became uniquely defined once data from the transverse indentation and the microstructure analysis was added. Only with such a complete set of information provided is it possible to appropriately describe the evolution of the vocal ligament anisotropy with posturing. Such knowledge is relevant in the context of frequency control. In order to investigate effects of shear deformation on phonation, the fundamental frequency predictions of an Euler–Bernoulli beam model and a Timoshenko beam model of vocal ligament vibration were compared. Not unexpectedly, the Timoshenko beam model predicted lower frequencies than the Euler–Bernoulli model. The magnitude of the influence of shear deformation on vocal ligament vibration increased with the mode number, and was found to be strongly dependent on the elongation as well as the microstructure as reflected in the anisotropy. Shear deformation on vocal ligament vibration was predicted to be most significant in the unstretched state, and subsequently decline since elongation increases the axial stress in the vocal ligament. A minimum of shear influence on vibration was found to occur at stretches 1.05 to 1.15 depending on the microstructure. At high stretches, shear again becomes important as the anisotropy of the tissue significantly increases.

APPENDIX A: INDENTATION MODEL

Details of the anisotropic contact model used to characterize the transverse indentation experiment are provided here. The indentation modulus M is

$$M=\frac{2\pi }{{\int }_0^{\pi }\frac{a_{3i}{B}_{\mathit{i}\mathit{j}}^{-1}(\gamma )a_{3j}}{{[(a_1/a_2){\cos }^2\gamma +(a_2/a_1){\sin }^2\gamma ]}^{1/2}}d\gamma },$$ (A1)

where a_3i are the direction cosines of the indentation load normal to the surface, B is a Barnett–Lothe tensor, a₁ and a₂ are the semiaxes of the contact ellipse, and γ is the angle between a vector t and a coordinate axis lying in the plane of the contact surface.29 The Barnett–Lothe tensor B is

$$\mathbf{B}(\mathbf{t})=\frac{-1}{\pi }{\int }_0^{\pi }\left[(\mathbf{mn})\hspace{0.17em}{(\mathbf{nn})}^{-1}(\mathbf{nm})-(\mathbf{mm})\right]d\phi ,$$ (A2)

with φ being the angle between a unit vector m and an arbitrary datum in the plane normal to t. The second-order tensors (ab) are defined as (ab)_jk = a_iC_ijklb_l, where C_ijkl is the elastic stiffness tensor. The unit vectors with respect to the (x, y, z) coordinate system are m = [−cosφ sinγ cosφ cosγ sinφ]^T and n = [sinφ sinγ − sinφ cosγ cosφ]^T, where T denotes the transpose. Therefore, fitting the indentation force-displacement response to Eq. 1 allows one to calculate M and to resolve the individual components of the elastic stiffness tensor C_ijkl.

APPENDIX B: GOH MODEL

The Gasser–Ogden–Holzapfel24 model is solved for the case of uniaxial tensile stretch λ and longitudinal shear strain γ. For stretch λ applied in the anterior-posterior direction (treated as the x-axis) the unimodular (distortional) portion of the deformation gradient, $\overline{\mathbf{F}}$ is

$$\overline{\mathbf{F}}\mathit{=}\left[\begin{array}{ccc}\lambda & 0& \gamma \\ 0& 1/\sqrt{\lambda }& 0\\ 0& 0& 1/\sqrt{\lambda }\end{array}\right]$$ (B1)

such that the material is incompressible [i.e., det($\overline{\mathbf{F}}$) = 1]. The longitudinal shear strain is included in $\overline{\mathbf{F}}$ so an analytical expression of the shear modulus as a function of λ may be obtained from the final solution. The actual value of γ will be set to zero so that no shear strain is present in the model. The left Cauchy–Green deformation tensor is

$$\overline{b}={\overline{\mathbf{F}\mathbf{F}}}^T=\left[\begin{array}{ccc}{\lambda }^2+{\gamma }^2& 0& \gamma /\sqrt{\lambda }\\ 0& 1/\lambda & 0\\ \gamma /\sqrt{\lambda }& 0& 1/\lambda \end{array}\right].$$ (B2)

The unit vector defining the preferred fiber orientation is a₀, which is assumed to be aligned along the x-axis. The current spatial fiber orientation is

$$\overline{\mathbf{a}}=\overline{\mathbf{F}}{\mathbf{a}}_0=\left\{\begin{array}{ccc}\lambda & 0& \gamma \\ 0& 1/\sqrt{\lambda }& 0\\ 0& 0& 1/\sqrt{\lambda }\end{array}\right\}\left\{\begin{array}{c}1\\ 0\\ 0\end{array}\right\}=\left\{\begin{array}{c}\lambda \\ 0\\ 0\end{array}\right\}.$$ (B3)

The unimodular (i.e., incompressible) structure tensor is

$$\begin{array}{c}\overline{\mathbf{h}}=\kappa \overline{\mathbf{b}}+(1-3\kappa )(\overline{\mathbf{a}}\otimes \overline{\mathbf{a}})\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\left[\begin{array}{ccc}{\lambda }^2(1-2\kappa )+\kappa {\gamma }^2& 0& \kappa \gamma /\sqrt{\lambda }\\ 0& \kappa /\lambda & 0\\ \kappa \gamma /\sqrt{\lambda }& 0& \kappa /\lambda \end{array}\right],\end{array}$$ (B4)

where ⊗ denotes the outer product or tensor product of two vectors. The Green–Lagrange strain-like quantity $\overline{e}$ is

$$\overline{e}=\text{tr}\hspace{0.17em}(\overline{\mathit{h}})-1={\lambda }^2(1-2\kappa )+\kappa {\gamma }^2+\frac{2\kappa }{\lambda }-1.$$ (B5)

The anisotropic hyperelastic potential of the vocal ligament is assumed to be composed of non-collagenous ground substances (matrix) and one family of collagen fibers. The matrix (denoted with subscript “g”) is represented with an isotropic neo-Hookean model, and the family of collagen fibers (denoted with subscript “f”) is defined with an exponential scalar stress function ${\psi }_f=k_1\overline{e}\exp (k_2{\overline{e}}^2)$. Thus, the isochoric Kirchhoff stress tensor $\overline{\mathit{\tau }}$ (which is equivalent to the Cauchy stress tensor σ for incompressible materials), is a superposition of the ground substance and fiber stresses. The fictitious Kirchhoff stress tensor $\tilde{\mathit{\tau }}$ is computed first and subsequently transformed into the true Kirchhoff stress tensor $\overline{\mathit{\tau }}$ (or σ) via the fourth-order projection tensor $\mathbb{P}=\mathbb{I}-(1/3)\mathit{I}\otimes \mathit{I}$ (or in indicial notation ${\mathbb{P}}_{\mathit{i}\mathit{j}\mathit{k}\mathit{l}}=(1/2)[{\delta }_{\mathit{i}\mathit{k}}{\delta }_{\mathit{j}\mathit{l}}+{\delta }_{\mathit{i}\mathit{l}}{\delta }_{\mathit{j}\mathit{k}}]-(1/3){\delta }_{\mathit{i}\mathit{j}}{\delta }_{\mathit{k}\mathit{l}}).$ The fictitious Kirchhoff stress tensor is

$$\begin{array}{c}\tilde{\mathit{\tau }}={\tilde{\mathit{\tau }}}_g+{\tilde{\mathit{\tau }}}_f=c\overline{\mathbf{b}}+2{\psi }_f\overline{\mathbf{h}}=\left[\begin{array}{ccc}c({\lambda }^2+{\gamma }^2)+2{\psi }_f[{\lambda }^2(1-2\kappa )+\kappa {\gamma }^2]& 0& (c+2{\psi }_f\kappa )\gamma /\sqrt{\lambda }\\ 0& (c+2{\psi }_f\kappa )/\lambda & 0\\ (c+2{\psi }_f\kappa )\hspace{0.17em}\gamma /\sqrt{\lambda }& 0& (c+2{\psi }_f\kappa )/\lambda \end{array}\right],\end{array}$$ (B6)

where c is the neo-Hookean parameter. The true Kirchhoff stress $\overline{\tau }=\mathbb{P}:\tilde{\tau }$ (with: being the double-dot product) is

$$\overline{\mathit{\tau }}=\sigma =\frac{1}{3}\left[\begin{array}{ccc}2{\tilde{\tau }}_{11}-2{\tilde{\tau }}_{22}& 0& 3{\tilde{\tau }}_{13}\\ 0& {\tilde{\tau }}_{22}-{\tilde{\tau }}_{11}& 0\\ 3{\tilde{\tau }}_{13}& 0& {\tilde{\tau }}_{22}-{\tilde{\tau }}_{11}\end{array}\right]$$ (B7)

and ${\tilde{\tau }}_{33}$ is eliminated from the result above because ${\tilde{\tau }}_{22}={\tilde{\tau }}_{33}$.