Short desynchronization episodes prevail in synchronous dynamics of human brain rhythms

Abstract

Neural synchronization is believed to be critical for many brain functions. It frequently exhibits temporal variability, but it is not known if this variability has a specific temporal patterning. This study explores these synchronization/desynchronization patterns. We employ recently developed techniques to analyze the fine temporal structure of phase-locking to study the temporal patterning of synchrony of the human brain rhythms. We study neural oscillations recorded by electroencephalograms in α and β frequency bands in healthy human subjects at rest and during the execution of a task. While the phase-locking strength depends on many factors, dynamics of synchrony has a very specific temporal pattern: synchronous states are interrupted by frequent, but short desynchronization episodes. The probability for a desynchronization episode to occur decreased with its duration. The transition matrix between synchronized and desynchronized states has eigenvalues close to 0 and 1 where eigenvalue 1 has multiplicity 1, and therefore if the stationary distribution between these states is perturbed, the system converges back to the stationary distribution very fast. The qualitative similarity of this patterning across different subjects, brain states and electrode locations suggests that this may be a general type of dynamics for the brain. Earlier studies indicate that not all oscillatory networks have this kind of patterning of synchronization/desynchronization dynamics. Thus, the observed prevalence of short (but potentially frequent) desynchronization events (length of one cycle of oscillations) may have important functional implications for the brain. Numerous short desynchronizations (as opposed to infrequent, but long desynchronizations) may allow for a quick and efficient formation and break-up of functionally significant neuronal assemblies.

Neural synchrony is hypothesized to be important for many physiological processes. Most of the time, this synchrony is not very strong, so that while neural signals may be synchronous on the average, they go in and out of phase. We found that neural synchronization in human brain follows very specific temporal pattern: synchronous states are interrupted by frequent, but short desynchronization episodes. In general, the same synchrony strength may result from many short desynchronization events or from few long desynchronization events (as well as from a wide spectrum of possibilities in between these extremes). However, in human brain rhythms, the probability for a desynchronization episode to occur decreased with its duration. In addition, the transition matrix between synchronized and desynchronized states has eigenvalues close to 0 and 1 (the latter has multiplicity 1) promoting a very quick convergence to a (presumably beneficial) stationary state after a perturbation. The qualitative similarity of the fine temporal structure of synchrony patterns across different subjects, brain states and parts of the brain suggests that this may be a general type of dynamics for the brain. Earlier studies indicate that not all oscillatory networks have this kind of patterning of synchronization/desynchronization dynamics. Thus, the observed prevalence of short (but potentially frequent) desynchronization events is likely to have important functional implications for the brain. From a cell assembly theory view point, the results may suggest that whenever a cell assembly must be formed to facilitate a particular function or task, short desynchronization dynamics may allow for a quick and efficient formation and break-up of such an assembly.

INTRODUCTION

Neural synchrony is believed to be an important mechanism underlying many phenomena in the human brain.^{1, 2, 3} It has been extensively studied using approaches and methods of physics and nonlinear dynamics (see Refs. ^{4, 5}). Neural synchrony strength is likely to be variable in time. The neural oscillations are known to exhibit intermittent synchronization in both healthy and diseased human and animal brain even at rest (see Refs. ^{6, 7, 8, 9, 10}). It was suggested that transient dynamics in the nervous system is generic.¹¹ Neural signals may go in and out of synchrony due to variety of factors and approaches to detect and quantify the presence of this variable and weak synchrony have been considered (see Refs. ^{12, 13}). However, the properties of how this synchrony is patterned in time have not being explored in normal human subjects.

Since this synchrony is not perfect, the same synchrony strength may be achieved with markedly different temporal patterns of activity (roughly speaking oscillations may go out of the phase-locked state for many short episodes or few long episodes). However, synchrony is a non-instantaneous phenomenon and from the data analysis perspective one considers synchrony in a statistical sense, observed over a sufficiently large number of cycles of oscillations.¹⁴ Yet if this synchrony is present on the average, one can look at each cycle of oscillations and see how far away it is from a synchronized state.¹⁵ This approach can describe the differences in the dynamics and temporal structure of synchronization/desynchronization events for the systems with similar overall level of phase locking or similar stability of synchronized state.¹⁵ This is especially important given that the neural synchrony in the current study, and a number of other neural systems, is not very strong. The underlying network of presumably weakly coupled oscillators spends a substantial fraction of time in the non-synchronous state. Thus the focus on desynchronization episodes is very reasonable.

This approach has been recently applied to study the temporal patterns of the pathological synchronization in subcortical brain areas in a group of patients with Parkinson's disease.^{10, 16} Locally measured synchronous (on the average) oscillatory activity was observed to follow a specific pattern: the synchronized state was interrupted by numerous but mostly short desynchronization states. However, it was not known if this was a signature of Parkinson's disease, a feature of the specific subcortical location, or a more general phenomenon. Here, we show that the latter is more likely to be the case. Since synchrony is important to facilitate interactions between neurons,^{1, 2, 3} the temporal patterning of this synchrony becomes a salient issue. We study synchronous patterns of neural activity in a large sample of healthy humans at rest and during an execution of a task. Similar temporal patterning of synchronous activity in large cortical areas in different states may suggest that (i) this type of patterning is a generic phenomenon in the brain, (ii) it may have some functional advantages for oscillating neural networks receiving, processing, and transmitting information, (iii) it may be grounded in some general properties of neuronal networks calling for the development of appropriate nonlinear dynamical theory.

EXPERIMENTAL DATA

We used 64-channel electroencephalograms (EEG) of the international 10-10 system at the sampling rate of 160 Hz recorded from 109 normal human subjects using the BCI2000 system^{17, 18} and available at PhysioNet.^{19, 20} To exclude very closely positioned electrodes we used the data from only 19 electrodes (corresponding to the international 10–20 system).

Each subject was recorded in two different experimental conditions: 1 min baseline recording (rest, eyes open) and total of 6 min of recordings of fist movement tasks. During the task period, each subject would perform a series of visually triggered 4 s long series of opening and closing fist movements (followed by 4 s rest intervals excluded from the analysis). In this study, we analyze three different groups of data: Baseline All, Task All, and Task C3-C4. Baseline All includes data from all 19 EEG electrodes during baseline recordings. Task All includes data from all 19 EEG electrodes during the task periods. Task C3-C4 includes only the data from C3 and C4 electrodes (which are close to the motor cortex) during the task periods.

ANALYSIS TECHNIQUES

Phase domain is an appropriate way to analyze weakly synchronized neural signals.^{12, 13, 21, 22} As the coupling strength increases from low to moderate values synchrony may be observed in the phase domain while the amplitudes of oscillations remain uncorrelated.¹⁴ Thus phase may provide a more sensitive and appropriate metric to explore the relatively moderately synchronized dynamics we study here.

All signals were referenced to the mean EEG of two ears. EEGs first filtered in $\alpha (8-13\text{Hz})$ and $\beta (13-30\text{Hz})$ frequency bands with Kaiser windowed digital FIR filter sampled at 160 Hz and zero-phase filtering was implemented to avoid phase distortions. Phase was then extracted via Hilbert transform resulting in the time-series of phases (see Refs. ^{12, 14}). For each pair of this time-series (measured at the same time) ${\varphi }_k(t)$ and ${\varphi }_l(t)$ we consider a standard index to characterize the strength of the phase locking between these two signals

$$\gamma =\left|\right|\frac{1}{N}{\displaystyle \sum _{j=1}^N{e}^{i\theta (t_j)}}|{|}^2,$$

where $\theta (t_j)={\varphi }_k(t_j)-{\varphi }_l(t_j)$ is the phase difference. This synchronization index varies from 0 (complete lack of phase locking) to 1 (perfect phase locking). However, this phase locking index is not designed to describe the fine temporal structure of the dynamics, rather it provides an overall index of phase synchrony.^{10, 15} Thus even if it is evaluated on the short time window, it should necessarily include sufficiently large number of oscillations and cannot be used to inspect whether the oscillations are at the preferred phase lag or not at each cycle.

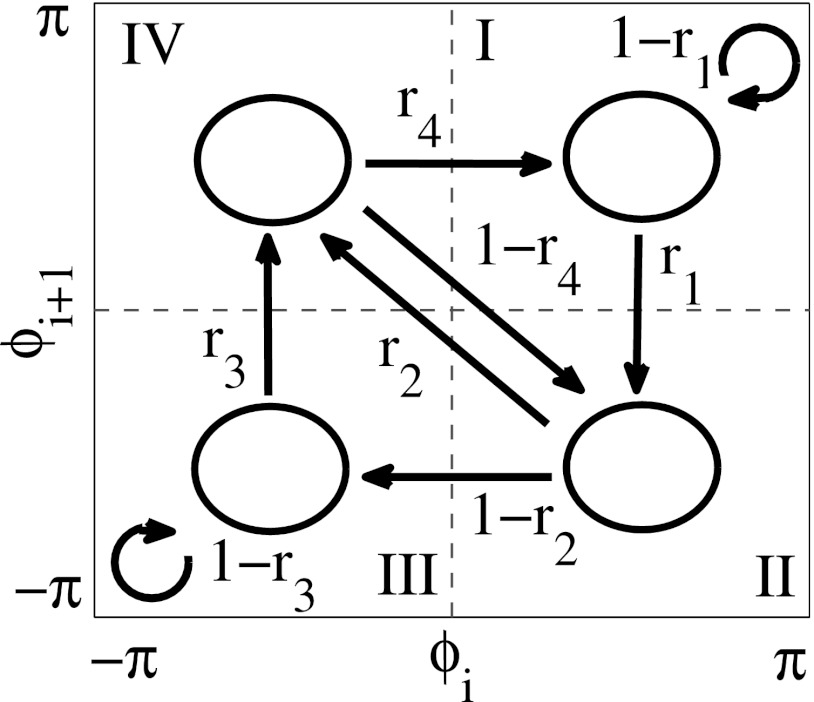
In order to assess the fine temporal structure of synchronous dynamics of the signal, we employed the analysis of phase synchronization on short time scales via first-return maps.¹⁵ This method allows for an analysis of the temporal development of phase difference if some level of synchrony (some preferred phase-locking angle) is present. Briefly, whenever the phase of the reference signal crossed from negative to positive values, we recorded the phase of the other signal, generating a set of consecutive phase values ${\left\{{\varphi }_i\right\}}_{i=1}^N,$ where N is the number of such crossings. Then ${({\varphi }_i,{\varphi }_{i+1})}_{i=1}^{N-1}$ was plotted. The predominantly synchronous dynamics appeared as a cluster of points, with the center at the diagonal ${\varphi }_{i+1}={\varphi }_i.$ We used the Kolmogorov-Smirnov test to detect non-uniform distribution of ${\left\{{\varphi }_i\right\}}_{i=1}^N$ with the significance level of 0.05 to include a recording in the further analysis (the results were not qualitatively affected by this level). After determining the center of the cluster for each pair of analyzed signals, all values of the phases were shifted by the same amount to position the center of the cluster at the center of the region I (see Fig. 1).

Figure 1.

Diagram of the $({\varphi }_i,{\varphi }_{i+1})$ map. The arrows indicate all possible transitions between regions and the expressions next to the arrows indicate the rates for these transitions.

This phase space was then partitioned into four regions numbered in a clockwise manner, since this is the primary direction of the dynamics. The region I is centered around the state with the most frequently observed (preferred) phase difference and is defined as a synchronized state. In this sense, other three regions are considered as desynchronized states. Note that the system can stay in the third region near diagonal for several iterations of the map (several cycles of oscillations). However, this happens relatively rarely. So region I is the region which corresponds to the most preferred time lag; it is a synchronized state in this essentially data-driven approach. Thus, the synchronized state here is the one where the deviation from the preferred phase angle is less than $\pi /2.$

Transition rates $r_{1,2,3,4}$ for the transitions between four regions of the map are defined as the number of points in a region, from which the trajectory leaves the region to another region, divided by the total number of points in the original region (see Fig. 1). For example, r₁ is the ratio of the number of trajectories escaping the region I for the region II to the number of all points in the region I. All rates vary between 0 and 1. The transition rates $r_{2,3,4}$ are related to the durations of desynchronizations and define them completely if transitions are independent. However, as we will show below, transitions were not fully independent in the data considered here. In addition to this four-state model, we will also consider a two-state model, where all three desynchronized states are lumped together into a single desynchronized state.

TRANSITIONS BETWEEN SYNCHRONIZED AND DESYNCHRONIZED STATES AND DURATIONS OF DESYNCHRONIZATION INTERVALS

Figs. 2a, 2b show examples of raw data and the corresponding filtered data for 3 s during task execution from C3 (panel A) and C4 (panel B) electrodes at the beta band. Fig. 2c shows that the preferred phase difference between two signals (presented here as ${\varphi }_i(t_j)$) is bounded (although within relatively large bounds fitting the discussion in Sec. 3) so that two phases are locked for a prolonged (with respect to the period of oscillations) intervals, interrupted by escapes to desynchronous states.

Figure 2.

An example of raw (light gray line) and filtered EEGs (solid line) for 3 s during task execution from C3 (panel a) and C4 (panel b) electrodes at the beta band. (c) The phase difference of the above signals plotted as ${\varphi }_i(t_j)$, where t_j is the time when the phase of C3 crosses from negative to positive values as described in the text.

An example of first-return map from the data is shown at Fig. 3. The transition rates $r_{1,2,3,4}$ correspond to panels (B), (D), (C), and (A), respectively. In one map iteration, most points in region I evolve into points within the region while relatively few points evolve to region II (Fig. 3b). So r₁ is relatively small. Other transition rates are computed similarly.

Figure 3.

An example of the first-return map for C3 and C4 EEGs for one subject during Baseline eyes open for the first 15 s. All four plots have the same data points (gray dots), but each subplot (a)-(d) presents the evolution of points from one region. If a point evolves from one region to another region, then we represent it as $°-\ast$. If a point evolves within the same region, then we represent it as $°-°$.

We also computed the relative frequencies (probabilities) of desynchronization events of different durations. In the considered first-return map approach, the duration of a desynchronization event is the number of steps that system spends away from region I minus one. This number of steps minus one is essentially a number of cycles of oscillations the signals are desynchronized. The shortest duration of a desynchronization event corresponds to the shortest path $\text{II}\to \text{IV}\to$ I. This corresponds to the desynchronization length of one cycle (in other words, in two steps the phases are back in a locked state).

Fig. 4 shows examples of desynchronization events of different durations. The number of origination points for the desynchronizations lasting for one cycle of oscillations (Fig. 4a) was much larger than that for other durations. This suggests that the probability of the desynchronization lasting for one cycle was high, while probabilities of longer durations were low. We now present the cumulative results for all 109 healthy human subjects for three different cases: Baseline All, Task All, and Task C3-C4.

Figure 4.

Examples of desynchronizations of different durations (same data as in Fig. 3 for 40 s). The gray line represents the trajectory during a desynchronization episode. For example, the trajectory for the shortest possible desynchronization (panel a) leaves region I, passes through regions II and IV, and returns to region I. Bold symbols in each panel represent the initial points for each desynchronization. (a)-(d) present all desynchronizations of duration of one to four cycles of oscillations, respectively.

At both α and β frequency bands, the means of overall synchrony index γ between any two EEGs were between 0.18 and 0.43 for all three different cases. That is, the overall levels of synchrony were moderate. The results for both frequency bands were largely similar to each other. Thus, we will present the illustrations only for β band.

The transition rates and distributions of durations of desynchronizations are presented in Fig. 5. The rate r₁ for all three cases (Baseline All, Task All, and Task C3-C4) was significantly lower than 0.3 while rates $r_{2,3,4}$ were significantly higher than 0.6 ($p<{10}^{-16}$, t-test was used here and below). These low r₁ and high $r_{2,3,4}$ values promote high probability of short desynchronization episodes. Note that in spite of their overall similarity, the transition rates $r_{1,2,3,4}$ vary across different conditions (baseline and task) and set of electrodes (all and C3-C4), as should be expected as EEGs in these cases should reflect different underlying neurophysiology.

Figure 5.

(a) Transition rates $r_{1,2,3,4}$, (b) distribution of desynchronization durations, (c) mean duration of desynchronizations at β-band. The last bin of the histogram (b), “$>8$”, is a sum of the relative frequencies of all desynchronizations longer than eight. Mean ± SD is presented in (a) and (b).

Fig. 5b shows that the probability to observe desynchronization lasting for one cycle of oscillations was significantly higher than 0.5, while the probabilities of longer desynchronizations were significantly lower than 0.2 $(p<{10}^{-16})$ for all three cases considered. The probabilities to observe the shortest desynchronization (length of one cycle of oscillations) for all three cases were at least 3 times higher than the probabilities of other lengths of desynchronizations (including those lasting for two or three cycles $(p<{10}^{-16})$). These high probabilities of the shortest desynchronization (length of one cycle of oscillations) imply the short mean desynchronization duration. The mean lengths of desynchronization episodes were between 1.9 and 2.7 (Fig. 5c). The modes and medians of distributions of desynchronization durations were always just one cycle of oscillations. For all pairs of signals analyzed, for Baseline All only in 0.06% of cases the desynchronization duration of one cycle was less frequent than the desynchronization duration of two or three cycles. For the Task All and Task C3-C4 this fraction was 4.9% and 3.4%.

The rates $r_{1,2,3,4}$, the averages and the distributions of durations of desynchronization events for Task All and Task C3-C4 were more or less similar to each other and more different from those distributions for Baseline All. This is not surprising because subjects performed a motor task in response to an external cue, which may involve a change in oscillatory activity in large cortical areas.

We now will consider how well the observed desynchronization intervals may be described in the framework of a Markov chain model: independent transitions between synchronized and desynchronized states. Fig. 6 shows the distribution of desynchronization durations in two-state model and four-state model. In the two-state model there are synchronized state (region I) and the desynchronized state (regions II, III, and IV). In this model, there are only two transition rates: ${\widehat{r}}_1$ (transition rate from the synchronized state to the desynchronized state) and r_R (return rate of resynchronization). The duration of desynchronization is the number of time-steps that system spends in the desynchronized state.

Figure 6.

Distribution of desynchronization durations from the data (white bars, the same as in Fig. 5), from the four-state model rates $r_{1,2,3,4}$(Fig. 1), and two-state model rates. (a) Baseline dynamics. (b) Dynamics during the task execution.

As can be seen at Fig. 6, the distributions of desynchronization durations generated by four-state model were almost (although not completely) identical to the distribution of durations obtained directly from the data. Although the distributions generated by the two-state model were visibly different from those from the data, the general pattern of the distributions was well captured by two-state model as well. That is, the probability of the shortest desynchronization (length of one cycle of oscillations) is much larger than probabilities for other desynchronizations.

An interesting observation is that although the rates $r_{1,2,3,4}$ depend on conditions (Baseline or Task) and set of electrodes, $r_1+r_{2,3,4}\approx 1$ (see Fig. 5a). This leads to the following ramification. The transition matrix of two-state model is

$$\left(\begin{array}{cc}1-{\widehat{r}}_1& {\widehat{r}}_1\\ r_R& 1-r_R\end{array}\right).$$

If ${\widehat{r}}_1+r_R=1$, then this system is in the detailed balance. Moreover, the eigenvalues of this matrix are 0 and 1. So that if the system is perturbed from a stationary distribution, it settles back to a stationary distribution after just one time-step (if there is small, but non-zero eigenvalue, the convergence is exponential, but very fast). Roughly speaking, ${\widehat{r}}_1\approx 1/4$ and $r_R\approx 3/4$ so that for synchronous on the average episodes we look at about a quarter of pairs of locations of the studied brain network are in non-synchronous state and about three quarters are in synchronous state. If this distribution is perturbed, the system gets back to the stationary state within just one cycle of oscillations given the observed transition rates.

Similar considerations are valid for the four-state model as well. The transition matrix of four-state model (see Fig. 1) is

$$\left(\begin{array}{cccc}1-r_1& r_1& 0& 0\\ 0& 0& 1-r_2& r_2\\ 0& 0& 1-r_3& r_3\\ r_4& 1-r_4& 0& 0\end{array}\right).$$

If $1-r_1=r_2=r_3=r_4$, then the eigenvalues of this matrix are 0 (multiplicity of 3) and 1. The square of this matrix projects any vector to the subspace corresponding to the eigenvalue 1. Thus again, if the stationary distribution is perturbed, the system will be back to the stationary distribution of synchronized and desynchronized states very quickly.

According to our measurements $r_1+r_{2,3,4}$ are close, but not identical to 1. This can be either due to the features of the time-series analysis or due to the nature of the observed system. However, even in the latter case, the considered brain networks will be in a state where the perturbed system rapidly converges to the stationary distribution.

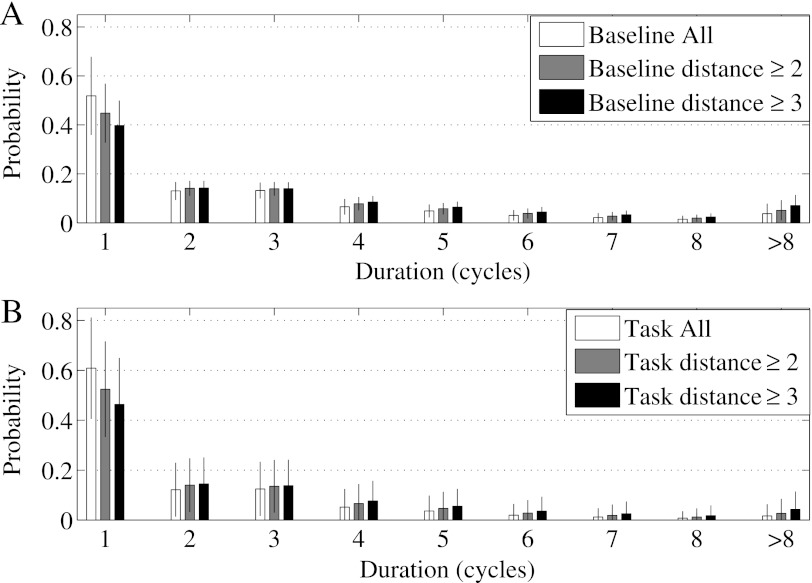
Finally, we analyzed the data from pairs of distant electrodes to eliminate volume conduction effects, which may potentially affect the analysis of the patterning of synchrony. We computed the durations of desynchronization events for pairs of electrodes separated by at least one and at least two other electrodes (Fig. 7). Strictly speaking, electrodes are not exactly equidistant, however, the distance between neighboring electrodes is not very much different and as we exclude immediate and next neighbor electrode pairs, we obtain results for substantially remote electrodes. While consideration of only remote pairs of electrodes affected the distribution of durations of desynchronization events, this effect was small for both baseline and task activity. In both considered cases, the probabilities to observe the shortest possible desynchronizations were at least two times higher than the probabilities of longer desynchronizations for both Baseline and Task cases $(p<{10}^{-16})$.

Figure 7.

Distribution of desynchronization durations for all electrode pairs (the same as in Fig. 5) in comparison with the distributions obtained from pairs of electrodes separated by at least one (distance $\ge 2$), and at least two (distance $\ge 3$) other electrodes. (a) Baseline dynamics. (b) Dynamics during the task execution.

DISCUSSION

The present study analyzed the fine temporal structure of neural synchrony in α and β frequency bands in healthy human EEG during resting state and a motor task. We found that in all considered cases oscillations go out of synchrony frequently, but primarily for only a small number of cycles of oscillations. The chances of longer desynchronization episodes decreased as the duration of the desynchronization episodes increases. Moreover, the studied system appears to be in a detailed balance between synchronized and desynchronized states within the framework of the two-state model.

Both the two-state model and four-state model can capture the temporal pattern of the short desynchronization events (length of one cycle of oscillations) in the considered study. However, the two-state model cannot distinguish the difference between two different systems with the same stability of the synchronized state or synchrony level and ${\widehat{r}}_1$, while the four-state model can effectively discriminate the difference.¹⁵ Moreover, from an experimental viewpoint, we do not know a priori whether the two-state model is sufficient to capture most of the important temporal dynamics of complex systems. We also would like to reiterate that both models are a way to describe synchronizations/desynchronizations in pairs of different brain areas as they develop in time rather than a detection of multiple patterns of synchronous and nonsynchronous pairs or clusters in spatially complex partially synchronized regime (like in Ref. 23).

Moderate coupling strength in a system of two coupled oscillators may induce the same strength of phase-locking, while the dynamics may be dominated by both long or short desynchronization episodes depending on the type of oscillators.¹⁵ Thus different desynchronization patterns provide different means to generate the same moderate synchrony levels. However, our analysis of EEG data indicates that the brain networks favor moderate synchrony with frequent short desynchronizations. While the particulars of the fine temporal structure in each frequency band are different, qualitatively our observations hold true both at rest and during task execution, for pair-wise synchrony across all brain areas as measured by EEG and for synchrony in the motor cortex. Note that the analysis of micro-electrode measured neural activity from subcortical areas of parkinsonian patients also showed the dominance of short desynchronization events.¹⁰ Thus, this dominance of short desynchronizations may be a generic feature of brain networks.

In line with this, it is interesting to note that dynamics of the phase synchronization of neuroimaging data from the human brain shows power law probability distribution, compatible with dynamical criticality, of both periods of phase-lock interval and rapid change of synchronization at broad frequency bands.²⁴ While that study was focused on a longer time scales (the analysis involved averaging, thus desynchronization was not followed from cycle to cycle of oscillations), those results suggest functional implications similar to ours. This criticality of the human brain may have capacity to change the configuration rapidly in response to external inputs more efficiently.²⁵

Even though the functional significance of the observed distribution of desynchronization events is yet unknown, we can speculate on potential functional implications. As noted in the beginning of this paper, neural synchrony has been conjectured to be important for several neural functions, including the formation of neuronal assemblies. Short desynchronizations may be more likely to facilitate the function of synchrony in the overall low-synchrony environment, because the synchronous state frequently gets a chance to reestablish itself (although for short time). Numerous short desynchronizations (as opposed to infrequent, but long desynchronizations) are likely to indicate that synchrony is both easy to form and easy to break. The probability of the shortest desynchronization (length of one cycle of oscillations) increases during a task, then it decreases to the baseline state during the resting state. This may suggests that whenever a cell assembly must be formed to facilitate a particular function or task, short desynchronization dynamics may allow for a quick and efficient formation and break-up of such an assembly. On the other hand, the ramifications of the transition matrices, whose eigenvalues are only 0 and 1 where eigenvalue 1 has multiplicity 1, which we discuss above, suggest that once the stationary distribution of synchronized and desynchronized states is perturbed, the system converges back to this stationary (and presumably beneficial) distribution very fast.

Finally, we need to note that our analysis does not explore the potential role of noise in our observations. Noise can have a substantial effect on intermittent phenomena, however, it is hard to manipulate in neurophysiological experiment. Nevertheless, time-series analysis used here does not make assumptions regarding the noisy component of the data. Moreover, modeling of neural-like (conductance-based) oscillators suggested that transition rates and the duration of desynchronization events are only weakly affected by noise of mild intensity.¹⁵

Our results call for a search for dynamical mechanisms responsible for the short desynchronizations.