Abstract
Because voice signals result from vocal fold vibration, perceptually meaningful vibratory measures should quantify those aspects of vibration that correspond to differences in voice quality. In this study, glottal area waveforms were extracted from high-speed videoendoscopy of the vocal folds. Principal component analysis was applied to these waveforms to investigate the factors that vary with voice quality. Results showed that the first principal component derived from tokens without glottal gaps was significantly (p < 0.01) associated with the open quotient (OQ). The alternating-current (AC) measure had a significant effect (p < 0.01) on the first principal component among tokens exhibiting glottal gaps. A measure AC/OQ, defined as the ratio of AC to OQ, was proposed to combine both amplitude and temporal characteristics of the glottal area waveform for both complete and incomplete glottal closures. Analyses of “glide” phonations in which quality varied continuously from breathy to pressed showed that the AC/OQ measure was able to characterize the corresponding continuum of glottal area waveform variation, regardless of the presence or absence of glottal gaps.
INTRODUCTION
The voice source represents the excitation signal to the vocal tract system (Fant, 1970), and carries information about voice quality, emotion, personal identity, and prosodic cues to sentence structure. Many measures have been used to parameterize the voice source and to study acoustic and perceptual consequences of changes in glottal pulse shapes, including open quotient (OQ, the relative duration of the open part of the glottal vibratory cycle), speed quotient (SQ; Timcke et al., 1958), closing quotient (ClQ), alternating-current to direct-current ratio (AC-DC ratio; Holmberg et al., 1988, 1989), and normalized amplitude quotient (Alku et al., 2002). The ability of conventional source measures (commonly used for glottal flow) to relate area waveform variations to spectral changes is limited by the difficulty of modeling both complete and incomplete glottal closure appropriately (Kreiman et al., 2012). In this study, we investigated the aspects of the glottal area pulse shape that vary with voice quality by using high-speed videoendoscopy of the vocal folds. We then propose and test a new measure of the glottal area to adequately capture variations in pulse shapes and relate them to corresponding acoustic changes, across glottal configurations both with and without complete closure of the cartilaginous and/or membranous glottis.
Measures of the voice source differ due to the different types of data and observations from which the measures are derived. One way of recovering the voice source signal from the acoustic sound pressure or oral airflow signal is via inverse filtering, which removes the vocal tract filtering effect. Inverse filtering is sensitive to recording conditions and experimental setup, and several methods have been proposed (e.g., Rothenberg, 1973; Javkin et al., 1987; Alku, 1992; Alku et al., 2006, 2009). A more direct way of observing vocal fold vibration is through high-speed video recording. The glottal area waveform can be extracted from high-speed images to represent the voice source signal. Because the production of glottal flow involves the interaction between lung pressure and the glottal area function (Fant, 1982) as well as the interaction between the glottal area and the vocal tract system (Titze and Story, 1997; Titze, 2008), the glottal area function is not identical to the glottal flow (e.g., glottal area pulses are known to be less rightward-skewed than the volume velocity pulses; Rothenberg, 1981; Stevens, 1998). When the vocal tract is inertive, this nonlinear source-filter interaction has the effect of increasing the maximum flow declination rate, peak glottal area, and peak glottal flow (Titze, 2004). The maximum flow declination rate is proportional to the maximum area declination rate, with an additional multiplication factor that depends on vocal tract inertance (Titze, 2006).
Once it is recovered, the voice source can be parameterized by fitting the source data with a pre-defined mathematical model subject to certain optimization criteria, so that the source can be represented by a set of model parameters. Models to describe flow functions include the Liljencrants-Fant (LF) model (Fant et al., 1985); the Fujisaki-Ljungqvist model (Fujisaki and Ljungqvist, 1986); and the Rosenberg model (Rosenberg, 1971). The LF model of the glottal flow derivative is the most commonly used of these, but analyses of singing (and other) voices showed that it provides a suboptimal fit to some source spectra, suggesting that it is not able to accommodate all observed variability in vocal production (Henrich et al., 2001). Similar results were reported by Shue et al. (2009), who estimated OQ using a codebook of the LF model from voices of four subjects. The estimated OQ and physiological measurements from the high-speed imaging data were well-correlated for only two of four speakers, suggesting again that the LF model may be suboptimal for representing some source signals.
Research efforts have also been devoted to studying the spectral and perceptual consequences of changes in source waveform shape, as represented by source model parameters. For example, Mehta et al. (2011) parameterized the glottal area waveform from high-speed videoendoscopy to obtain OQ, plateau quotient (PQ), SQ, and ClQ. PQ did not correlate significantly with any spectral tilt measures, while OQ and ClQ exhibited statistically significant but small correlations (|r| = 0.27 to |r| = 0.48) with spectral tilt measures. As the OQ increases, energy in the first source harmonic relative to the second (denoted as H1-H2) is assumed to increase, which presumably contributes to increased “breathiness” in perceived voice quality (e.g., Klatt and Klatt, 1990). However, a recent study based on high-speed imaging of the vocal folds during a “glide” phonation, where quality changed continuously from breathy to pressed, showed that two different relationships hold between H1-H2 and OQ, depending on whether glottal closure is complete or not (Kreiman et al., 2012). In the presence of a glottal gap, H1-H2 was best predicted by glottal pulse skewness (also called the asymmetry coefficient; Henrich et al., 2001),1 with no significant contribution of OQ; but in the absence of a posterior gap, H1-H2 was best predicted by OQ, with pulse skewness making no significant contribution to prediction. An additional study of the same data showed that the size of the glottal gap was strongly correlated with H1-H2 when glottal closure was incomplete (Chen et al., 2011). Thus, although quality changed continuously in this utterance, it appears that the relationship between glottal configuration and quality is discontinuous when described in terms of existing measures of the voice source like OQ, which do not reflect the presence or absence of a glottal gap. A measure that reflects both the timing of glottal opening and closing and the presence and size of a posterior glottal gap could overcome this difficulty, giving insight into the physical precursors of changes in perceived quality and providing a linkage between changes in glottal vibratory patterns and perceptual consequences. Such a measure is of particular importance because glottal gaps commonly occur during phonation in both normal and clinical subjects, especially in women (Koike and Hirano, 1973; Morrison et al., 1983; Södersten and Lindestad, 1990).
Current time-domain source models lack an effective way of modeling incomplete glottal closure, which has been shown to be an important physiological parameter in voice production (Cranen and Schroeter, 1995; Hanson and Chuang, 1999). Two approaches have been used to study the spectral and perceptual consequences of glottal gaps. In the first, spectral effects were compared for cases with and without glottal gaps, but glottal gap size was either not varied (Cranen and Schroeter, 1995) or not measured (Shue et al., 2010). Computer simulation compared gaps extending to the membranous glottis (“linked leaks,” corresponding to variations in AC flow) to gaps forming an orifice in the cartilaginous glottis separated from the vibrating part of the glottis (a DC component, or “parallel chink”; Cranen and Schroeter, 1995). Modeling results showed that gaps in the cartilaginous glottis and corresponding DC flow components had little or no effect on spectral slope relative to cases with no cartilaginous gap, while persistent gaps in the membranous glottis and corresponding AC modulations in flow resulted in increasingly steep spectral rolloffs. In the second approach, varying glottal gap size was quantified and related to spectral shape, but without comparison to no-gap cases (Omori et al., 1998; Chen et al., 2011). For example, Omori et al. (1998) measured glottal gap area at the most closed point of vibration from video-stroboscopic images of speakers with varying vocal pathologies. Glottal gap area affected pitch perturbation, the harmonics-to-noise ratio, high-frequency power ratio, mean flow rate, and maximum phonation time. Acoustic and aerodynamic measures were similar when glottal gap sizes (and presumably DC flow levels) were similar, regardless of the underlying vocal pathologies. In Chen et al. (2011), glottal gap size was shown to affect the cepstral peak prominence (CPP; Hillenbrand et al., 1994) and the harmonics-to-noise ratio (de Krom, 1993), indicating the presence of relatively more spectral noise with increasing glottal gap size. Simulation using a computational, kinematic model of the vocal folds showed that the acoustic measure CPP decreased with increased separation of the vocal processes, which was partially manifested as the size of the glottal gap during the maximum glottal closure (Samlan and Story, 2011).
Studies of the acoustic consequences of changing glottal configurations are limited by the lack of a measure of glottal configuration that varies continuously with quality, as described above. To the best of our knowledge, no measure has been proposed that reflects both overall pulse shape and the presence and size of a glottal gap. Studies of the perceptual consequences of changes in the voice source can also benefit from a source measure that adequately relates variations in glottal area waveforms to spectral variations, across a wide range of glottal configurations. For example, the analyses described above (Kreiman et al., 2012) did not reveal any abrupt quality change at the instant when the glottal gap disappeared. The continuous, smooth transition in voice quality suggests that a single physiologically based glottal measure might successfully map the continuum in waveform variation to corresponding changes in voice quality, particularly if that measure reflects the changing relationship between quality, OQ, and glottal gap described above. We describe such a measure, AC/OQ (the ratio of AC to OQ; see Sec. 2C. for the definition of AC), which was developed based on analyses of high-speed videoendoscopy of vocal fold vibrations during productions of steady-state vowels that varied statically in voice quality. We then test the ability of this measure to capture continuous variations in voice quality across a range of glottal configurations by analyzing additional high-speed videoendoscopy of phonation during which quality varied continuously along a continuum from breathy to pressed.
DATA AND METHODS
High-speed videoendoscopy data and audio recording
Two sets of synchronous audio recordings and high-speed videoendoscopic images of the vocal folds were collected. The first set included recordings from six phonetically knowledgable subjects, three females (denoted by F1–F3) and three males (denoted by M1–M3) (Kreiman et al., 2012). None of the subjects had a history of voice disorder. Speakers were asked to sustain the vowel /i/ for approximately 10 s while holding voice quality, fundamental frequency (F0), and loudness as steady as possible. Across tokens, speakers varied their F0 (low, normal, and high) and voice quality (pressed, normal, and breathy) quasi-orthogonally, resulting in nine steady-state recordings from each speaker. The vowel /i/ was selected to optimize the view of the vocal folds (Draper et al., 2007); across tokens vowel quality ranged from /I/ to approximately cardinal vowel /ε/. Voice quality was modeled by a phonetician prior to each recording. Because the purpose of the quality and pitch variations was simply to generate a variety of glottal configurations, no effort was made to ensure that voice quality types produced were comparable across speakers. For example, one person's modal phonation might have resembled another speaker's breathy or pressed.
Images were recorded at 3000 frames/s at a resolution of 512 × 512 pixels using a 70° rigid laryngoscope (KayPentax, Lincoln Park, New Jersey) with a 300 W Xenon light source (KayPentax, Lincoln Park, New Jersey) and a FASTCAM-ultima APX camera (Photron Ltd., San Diego, CA). Audio signals were synchronously recorded with a Brüel & Kjær microphone (1.27 cm diameter; type 4193 -L-004) and directly digitized at a sampling rate of 60 kHz, with a conditioning amplifier (NEXUS 2690, Brüel & Kjær, Denmark). Microphone signals were bandpass filtered between 20 Hz and 22.4 kHz. The A/D converter (PCI-DAS64/M1/16, Measurement Computing, Norton, MA) had a voltage resolution of 16 bits with input range +/−5 V. The audio recordings were later downsampled to 16 kHz for analysis.
The second set of recordings was gathered from four speakers, two of whom (speaker F1, M1) participated in the previous recording session, and two additional male speakers (no history of voice disorder, denoted as M4 and M5). These speakers gradually changed their phonations from breathy to pressed while holding F0 and vowel quality as constant as possible. High-speed images of the vocal folds were recorded using a Phantom V210 camera (Vision Research, Wayne, NJ) at a sampling rate of 10 000 frames/s, with a resolution of 208 × 352 pixels. The camera was mounted on a Glidecam Camcrane 200 (Glidecam Industries, Kingston, MA). The A/D converter (Module 9223, National Instruments, Austin, TX) had a voltage resolution of 16 bits with input range +/−10 V. Synchronized audio and high-speed images were recorded for 6 s. The other recording settings were identical to those described in the previous paragraph.
In both sets of recordings, most tokens provided satisfactory views of the posterior glottis, but additional tokens were recorded when necessary. The recording that provided the best view of the complete glottis (as judged by a speech-language pathologist) was selected for subsequent analysis.
Glottal area waveform extraction
For the first set of data, a 1-s sample of auditorily stable phonation was excerpted from each high-speed videoendoscopic recording. This sample excluded the beginning of the recording in order to avoid possible transient information from initiation of vibration. The glottal area waveform was calculated from the first 150 frames (50 ms) of each sample using a series of edge-detection and region-growing algorithms, described in detail in Shue (2010a). Factors such as shadows, random noises, over-exposures, and variations in contrast levels affected visualization of the glottis and the accuracy of glottal area extraction. Hence, we limited these analyses to 150 frames (50 ms) instead of the entire token (1 s) allowing visual examination on a frame-by-frame basis and manual adjustment if necessary for accuracy. For several tokens from speaker F1, glottal area waveforms were extracted for the entire 1 s (3000 frames) period and compared with data from the first 150 frames. Comparison showed that the glottal area waveform of the first 150 frames was representative of the entire token. The number of glottal cycles contributed by each speaker depended on the speaker's F0. A total of 442 glottal cycles were included for analysis, among which speakers F1, F2, F3, M1, M2, and M3 contributed 98, 89, 83, 47, 53, and 72 cycles, respectively. Subsequent analyses were also performed on the glottal waveforms from each speaker separately, which minimized the effect of different number of cycles contributed by different speakers.
For the second set of video recordings, glottal area waveforms of the complete utterances were extracted using “GlotAnTools,” a software toolkit that automatically segments the glottal area from high-speed images (supplied by the Department for Phoniatrics and Pedaudiology of the University Hospital, Erlangen, Germany). Note that in both sets of recordings, each glottal area cycle was kept rather than averaging across cycles within each recording.
Calculation of glottal measures
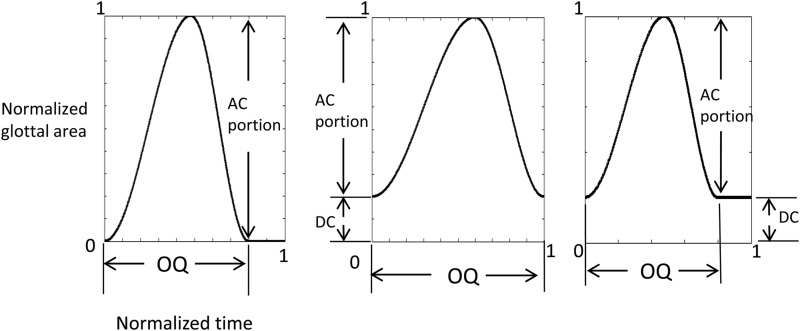
Based on analyses showing a trading relationship between changing OQ and glottal gap size as quality varied continuously (Kreiman et al., 2012), we hypothesized that a measure capturing these two aspects of vocal function would correspond reasonably well to changing quality in a larger set of voice samples. As part of the process of developing this measure, we calculated values of OQ, DC, and AC for each glottal cycle in the glottal area waveforms. Figure 1 shows how these measures were determined from sample waveforms. Each cycle of glottal vibration was tracked from the extracted glottal area waveforms by marking the first instants of glottal opening when glottal closure was complete. When no complete glottal closure occurred, the moments of minimal glottal area were tracked. DC offsets of the glottal area waveforms were maintained so that when closure was incomplete, the minimum glottal area was non-zero. The glottal area waveform amplitude was measured in numbers of pixels, and therefore did not represent the actual glottal area. Further, due to variable positioning of the laryngoscope relative to the vocal folds across recordings, glottal area waveform amplitudes were not directly comparable across recordings. Thus, for each glottal cycle, the waveform was normalized by the maximum glottal area within each cycle, so that the maximum amplitude was always 1. DC was defined as the minimum normalized glottal area in each glottal cycle. This process results in a smaller AC waveform when a DC component is present, relative to cases with full glottal closure (see Fig. 1 for an example). Because this normalization factors the DC component into the AC value, AC was then defined as the root-mean-square (rms) of the AC portion around its mean (Holmberg et al., 1988).2 Finally, following Kreiman et al. (2012), when the glottis did not close completely, the moment when glottal area began to increase and the onset of maximum closure was treated as opening and closing instants, respectively. For each individual cycle of phonation, OQ was calculated as the time from the first opening instant to the onset of maximum closure (or minimum area), divided by cycle duration (the time from the opening instant to the opening instant of the following cycle). Note that these measurements, although commonly used for glottal flow waveforms (e.g., Holmberg et al., 1988), were calculated from glottal area waveforms in this study.
Figure 1.
Examples showing how glottal measures (AC, DC, and OQ) were determined from glottal area waveforms. (a) Complete glottal closure. (b),(c) Incomplete glottal closures.
Acoustic measures
The CPP (Hillenbrand et al., 1994), which robustly measures the relative energy in the harmonic and inharmonic aspects of a voice signal, was measured pitch-synchronously from the audio signals with VoiceSauce software (Shue, 2010b) using an analysis window of four periods with a 1 ms shift. F0 values were obtained from the STRAIGHT algorithm (Kawahara et al., 1999) to determine the period of a glottal cycle. Values were aligned with glottal area waveforms extracted from the imaging signal for subsequent analysis.
Principal component analysis
On the first set of data, principal component analysis (PCA) was applied to investigate factors that describe variations in the glottal pulse shape. The first PCA was conducted using glottal waveforms from all speakers. Each cycle of each waveform from every speaker was resampled to 1000 points to normalize for differences in F0. Resampled waveforms were visually examined to ensure the pulse shapes of the original waveforms were preserved after the resampling procedure. The amplitude values for each glottal pulse at each sampling instant served as input to the PCA. A second PCA was performed on glottal area waveforms from tokens that exhibited glottal gaps, and a third was performed on glottal area waveforms from tokens where no glottal gap presented. An additional set of PCAs was performed on the glottal waveforms from each speaker separately. The waveforms with maximum and minimum projections on the first two principal components (PCs) were plotted to visualize the variation in waveforms for each speaker. Finally, we conducted regression analyses relating source measures to PCs.
ANALYSIS AND RESULTS
PCAs
Results of the PCAs and multiple regression analyses relating PCs to measures of pulse shape are shown in Table TABLE I.. In the first PCA (which included glottal area waveforms from all speakers), PC1 and PC2 accounted for 66.4% and 19.4% of the variance in pulse shapes, respectively. PC1 was most strongly related to OQ and PC2 was most strongly related to AC. The measures of AC and DC were highly correlated (r = −0.96, p < 0.001). As noted in Sec. 2C, the varying glottal gap size directly affects AC, which decreases with increasing glottal gap size, indicating more inharmonic noise relative to the harmonic energy. In this sense, the measure AC incorporates the glottal gap effect and provides a basis for capturing this aspect of glottal area waveform variation. In the second PCA (which included only tokens with glottal gaps), PC1 was best predicted by AC, with no significant contribution of OQ. In the third PCA where tokens without glottal gaps were included, PC1 was best predicted by OQ, with AC making no significant contribution to prediction.
TABLE I.
Standardized regression coefficients for multiple linear regression analyses relating source measures to the first two PCs. Percentage of variance accounted for by each PC is shown in parentheses. “All” denotes PCA using glottal area waveforms from all speakers. “Gap” denotes PCA using only tokens that exhibited glottal gaps. “No gap” denotes PCA using only tokens with no glottal gap. All values except those with an asterisk (*) are significant at p < 0.01.
| All | Gap | No gap | ||||
|---|---|---|---|---|---|---|
| PC1 (66.4%) | PC2 (19.4%) | PC1 (55.2%) | PC2 (29.8%) | PC1 (74.9%) | PC2 (10.7%) | |
| OQ | −0.88 | 0.51 | 0.07* | −0.41 | −0.87 | −0.24 |
| AC | 0.06* | 0.97 | 0.87 | 0.07* | 0.08* | 0.06* |
| R2 | 0.86 | 0.60 | 0.75 | 0.19 | 0.72 | 0.06 |
For the PCAs performed on the glottal waveforms from individual speakers, results of multiple regression analyses relating PCs to measures of pulse shape are shown in Table TABLE II.. The time-based measure OQ and the amplitude-based measure AC showed significant effects on PC1 and PC2 for all speakers except M3. For speaker M3, PC1 accounted for 82% of the variance and was best predicted by OQ only, with AC making no significant contribution to prediction.
TABLE II.
Standardized regression coefficients and R2 values for multiple linear regression analyses relating source measures to the first two PCs for each speaker. “—” denotes not significant. All other values are significant at p < 0.01. Percentage of variance accounted for by each PC is shown in parentheses.
| Speak | OQ | AC | R2 | |
|---|---|---|---|---|
| F1 | PC1 (80%) | −0.92 | 0.08 | 0.95 |
| PC2 (12%) | −0.77 | −1.17 | 0.82 | |
| F2 | PC1 (54%) | −0.29 | 0.66 | 0.75 |
| PC2 (23%) | −0.97 | −0.91 | 0.73 | |
| F3 | PC1 (74%) | −0.68 | 0.38 | 0.94 |
| PC2 (20%) | −0.93 | −1.14 | 0.78 | |
| M1 | PC1 (78%) | −0.57 | 0.42 | 0.93 |
| PC2 (16%) | −0.99 | −1.14 | 0.23 | |
| M2 | PC1 (76%) | −0.69 | −0.34 | 0.96 |
| PC2 (16%) | 1.13 | 1.25 | 0.58 | |
| M3 | PC1 (82%) | −0.92 | — | 0.86 |
| PC2 (8%) | — | — | 0.05 |
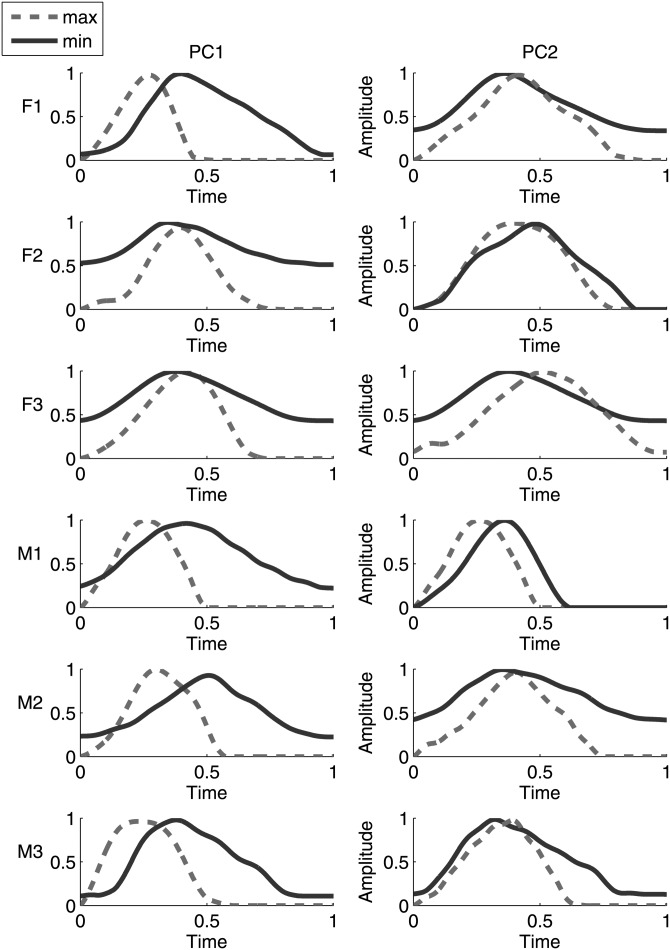
Figure 2 shows the waveforms representing extreme cases on the first two PCA factors, for each speaker. For PC1, the minimum and the maximum cases differ greatly in OQ for all speakers. Changes in AC (easiest to see in Fig. 2 as changes in DC offset) between the minimum and the maximum cases also exist for PC1 for speakers F2, F3, M1, and M2. For PC2, speakers F1 and M2 exhibit differences in OQ and AC; speakers F2 and M1 show differences mainly in OQ; speaker F3 exhibits differences in AC. These analyses show that, across speakers and voice qualities, variations in glottal area waveforms (including the effects of glottal gaps on normalized pulse amplitude) are well-summarized by the combination of AC and OQ.
Figure 2.
(Color online) Waveforms representing extreme cases on the first two PCA factors for each speaker (F1, F2, F3, M1, M2, and M3).
Data distribution in the PCA space
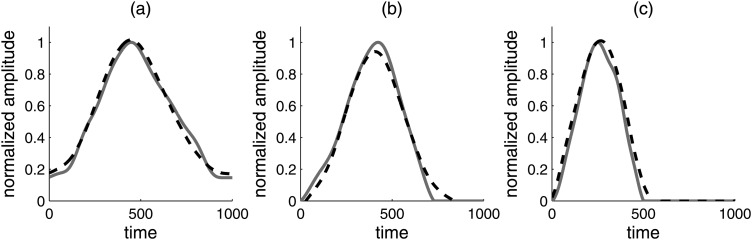
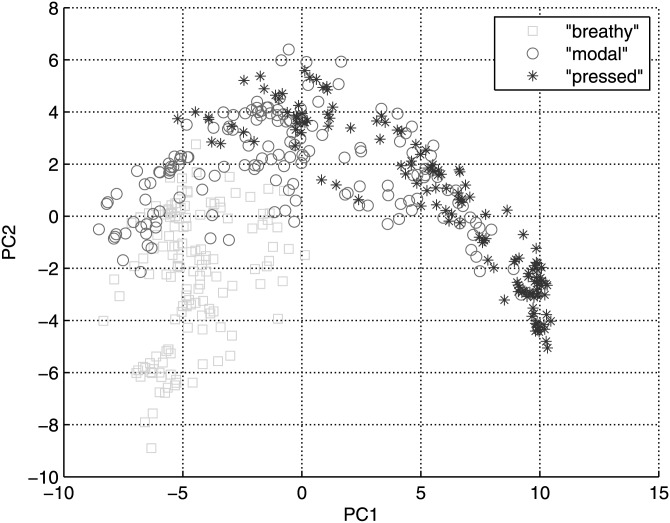
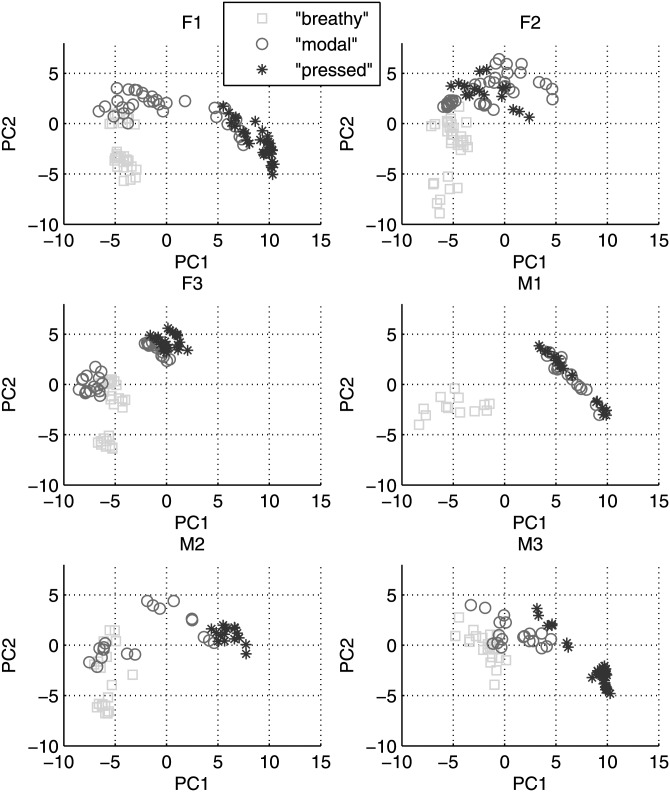
Projections (scores) on the first two PCs were calculated for each of the glottal area waveforms on the first set of data. Waveforms were reconstructed using the first two PC scores and visually examined to ensure that they captured the shape of the original waveforms. Figure 3 shows three examples (breathy, modal, and pressed) of reconstructed and original waveforms from speaker F1. Although detailed differences exist, the reconstructed waveform represents the gross shape of the original waveform because the first two PCs accounted for 85.8% of the variance. The distribution of nominally breathy, modal, and pressed cases across speakers is shown in Fig. 4, and the distribution of data in the PCA space for each individual speaker is shown in Fig. 5. Although the speakers were asked to produce sounds in three “categories” of voice qualities, the highly overlapped data distribution between categories indicates the existence of a continuous axis to which the voice source variation continuum can be mapped. This axis should approximately capture the glottal area pulse shape variation along a breathy-to-pressed dimension, from bottom left to bottom right clockwise as shown in Fig. 4. For speaker M1, the modal and pressed cases overlap substantially, while the breathy cases are well separated from the other two types. For the other speakers, modal cases overlap partially with breathy cases and partially with pressed cases. Neither PC1 nor PC2 alone quantified the three voice qualities sequentially, as expected given the large interspeaker differences in how the stimuli were produced.
Figure 3.
(Color online) Examples of reconstructed waveforms using the first two PC scores (dashed line) and original waveforms (solid line) from speaker F1. (a) Breathy, (b) modal, and (c) pressed.
Figure 4.
(Color online) Data distribution, for all speakers, in the PCA space labeled by nominal voice qualities.
Figure 5.
(Color online) Data distribution in the PCA space labeled by voice qualities for each speaker.
The proposed measure: AC/OQ
Measures of the physical voice source ideally should quantify the most prominent factors characterizing glottal pulse shapes, and should also reflect physical precursors of voice quality variation, including the overall glottal pulse shape variations and glottal gap configurations. PCA results showed that pulse shape variations can be efficiently characterized by the time-based measure OQ and the pulse-amplitude-based measure AC. Further, as noted above, the relationship between acoustic measures, quality, and OQ varies depending on the extent of glottal closure (Kreiman et al., 2012). A measure AC/OQ is proposed to combine both amplitude and temporal characteristics of the glottal area waveform in cases of both complete and incomplete glottal closures. In the numerator, the AC component (reflecting glottal gap presence and size) quantifies the oscillating energy elicited during the glottal open phase. In the denominator, OQ measures the relative duration of the open phase during a glottal period. In this sense, the AC/OQ measure quantifies the oscillating energy produced within a unit time slot. AC/OQ reaches its minimum value of 0 when the glottal area waveform is a constant (i.e., vocal folds are open and no sound is being produced). Theoretically, AC/OQ can reach infinity when the glottal pulse is an impulse (delta function), but this does not occur in human phonation (although following this logic values should be highest for vocal fry, in which the laryngeal excitations are a discrete train of pulses; e.g., Hollien et al., 1966).
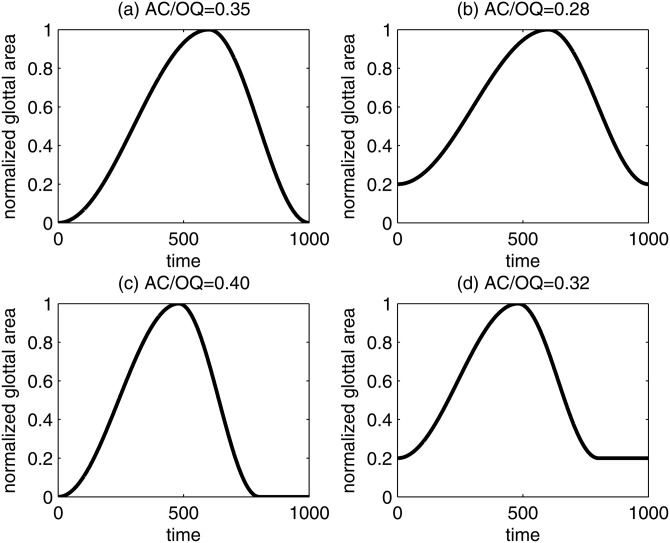
Figure 6 shows AC/OQ values for four examples of glottal area waveforms. Figure 6a shows an area waveform with no DC offset normalized to peak amplitude; Fig. 6b shows the same area waveform with the addition of a DC offset. The presence of a DC offset in Fig. 6b has the effect of “compressing” the area waveform as described in Sec. 2C, and hence, AC/OQ decreases. In Fig. 6c, OQ decreases from 1 to 0.8 for the waveform in Fig. 6a, and in Fig. 6d a DC offset is added to the waveform in Fig. 6c. As illustrated in this figure, the decrease in OQ results in an increase in AC/OQ [compare Fig. 6c to 6a]. Adding the DC offset reduces the AC/OQ value [compare Fig. 6b to 6a and Fig. 6d to 6c]. Similar to kurtosis in probability theory, AC/OQ measures the “peakedness” of the glottal area waveform. A higher AC/OQ value indicates a sharper peak in the glottal area pulse and stronger periodic oscillating energy in the spectral domain. On the other hand, a lower AC/OQ value corresponds to a flatter glottal pulse and weaker periodic oscillating energy. Values in Fig. 6 show how the AC/OQ measure captures the tradeoff evident in the glide phonation described in Sec. 3F between effects of changing OQ and changing DC levels on voice quality. As quality moved from breathy toward pressed, glottal configuration initially resembled Fig. 6b (with the lowest AC/OQ value), then Fig. 6a, with an intermediate value, and finally Fig. 6c, with the highest value. The prediction implied by the comparison between Figs. 6a, 6d is that voices with a smaller OQ plus a DC offset should fall perceptually in roughly the same range along a breathy-to-pressed continuum as those with a large OQ but no DC offset. This prediction remains to be tested. Such a comparison requires a comparatively large glottal gap only in the cartilaginous region that is separated from the vocal fold vibration (the membranous glottis vibrating with a relatively small OQ). This scenario was not available in the current data.
Figure 6.
Four synthetic glottal area waveforms showing how the changes in OQ and DC offset affect AC/OQ values. Note that OQ for (a) and (b) is equal to one.
Evaluating AC/OQ in parameterizing differences in glottal area waveforms across voice qualities
Assuming a quality continuum from breathy to pressed, Table TABLE III. shows regression analyses relating AC/OQ to the nominal voice quality continuum for each speaker, and Table TABLE IV. shows the means and standard deviation of AC/OQ for the three productive categories for the six speakers in the first set of data. AC/OQ was significantly correlated with the voice quality continuum for all 6 speakers (p < 0.001). Except for modal vs pressed for speaker M1, AC/OQ values also differed significantly between categories (p < 0.001) for each speaker. For speaker M1, whose modal phonation is quite pressed-sounding, neither OQ nor H1-H2 differed significantly between pressed and modal phonations (p > 0.05). Previous studies have argued that pressed phonation has lower OQ and H1-H2 values than modal phonation (Klatt and Klatt, 1990; Hanson, 1997), suggesting that speaker M1's productions of the designated voice qualities were inconsistent with the most usual understanding of quality labels. Despite these anomalies, the correlation between AC/OQ and the productive continuum was still significant for this speaker (r2 = 0.63).
TABLE III.
Regression coefficients and r2 values for linear regression analyses relating AC/OQ to the nominal voice quality continuum for each individual speaker. All values are significant at p < 0.001.
| Speaker | Regression coefficients | r2 |
|---|---|---|
| F1 | 0.25 | 0.85 |
| F2 | 0.27 | 0.80 |
| F3 | 0.30 | 0.76 |
| M1 | 0.25 | 0.63 |
| M2 | 0.23 | 0.71 |
| M3 | 0.37 | 0.80 |
TABLE IV.
Mean and standard deviation (in parentheses) of AC/OQ with changes in the target voice quality for the six individual speakers.
| Speaker | Breathy | Modal | Pressed |
|---|---|---|---|
| F1 | 0.25 (0.03) | 0.35 (0.03) | 0.46 (0.04) |
| F2 | 0.24 (0.04) | 0.36 (0.03) | 0.42 (0.02) |
| F3 | 0.25 (0.04) | 0.35 (0.04) | 0.41 (0.01) |
| M1 | 0.28 (0.02) | 0.46 (0.01) | 0.45 (0.02) |
| M2 | 0.24 (0.05) | 0.31 (0.06) | 0.44 (0.04) |
| M3 | 0.32 (0.02) | 0.36 (0.01) | 0.46 (0.03) |
Relating the physical measure AC/OQ to the acoustic measure CPP
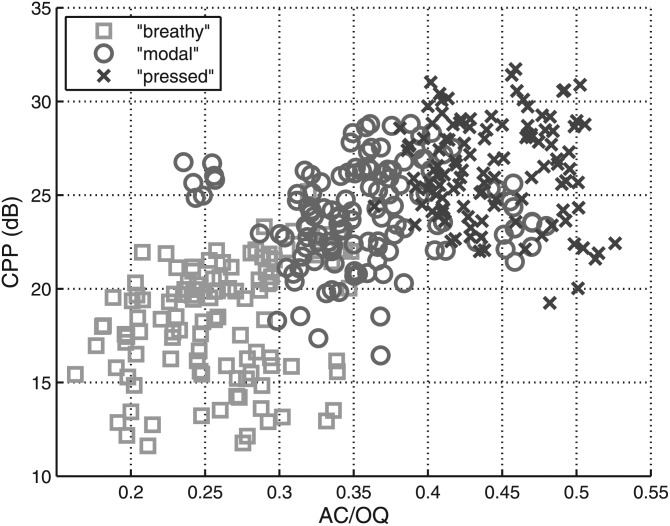
Previous studies (Fischer-Jorgensen, 1967; Klatt and Klatt, 1990; Södersten and Lindestad, 1990; Chen et al., 2011) showed that an increase in glottal gap size results in a higher spectral noise level; and changes in OQ are related to changes in the shape of the harmonic source spectral shape (e.g., Fant, 1995). Thus, the changes in glottal configuration measured by AC/OQ should be manifest in the cepstral domain as the prominence of the cepstral peak, which can be quantified by the acoustic measure CPP (Hillenbrand et al., 1994), reflecting the relative amounts of periodic and aperiodic energy in a voice signal. AC/OQ and CPP values for the six speakers on the first set of data are shown in Fig. 7 (r = 0.68, p < 0.001). Note that the function relating these measures flattens out for large values of AC/OQ, for which OQ is small and glottal gaps are small or absent. When these conditions pertain, noise levels are relatively constant across stimuli, reducing variability in the CPP and consequently reducing the overall correlation between these measures.
Figure 7.
(Color online) AC/OQ and CPP values with changes in the target voice quality (breathy, modal, and pressed) for the six speakers (F1, F2, F3, M1, M2, and M3).
Testing AC/OQ on glide phonations from breathy to pressed
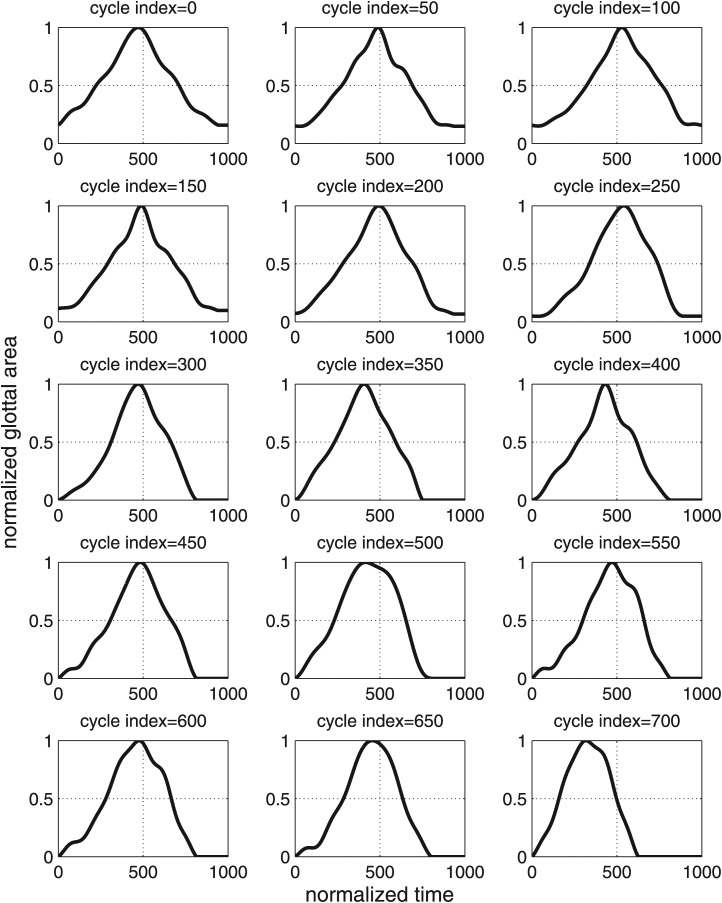
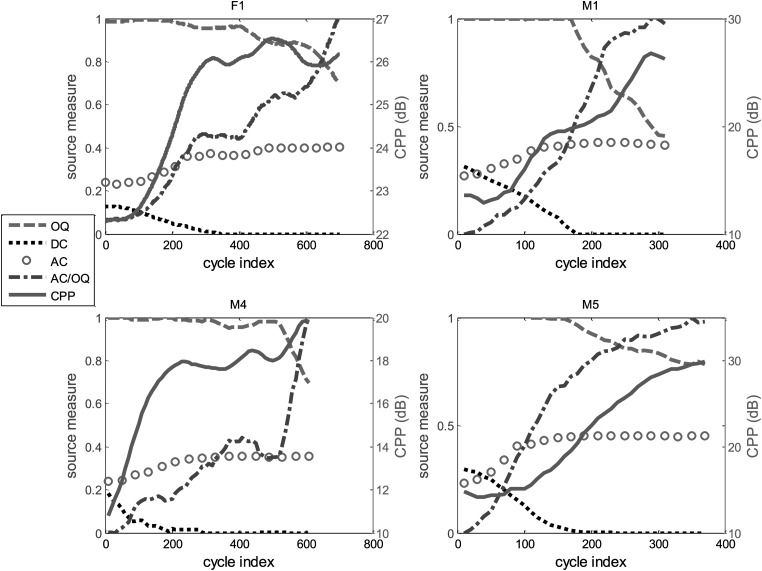
The large interspeaker variability in how stimuli in different voice quality “categories” were produced limited our ability to validate the relationship between AC/OQ and changes in voice quality. To address this limitation, we further measured AC/OQ for the second set of high-speed recordings, in which four speakers (F1, M1, M4, and M5) produced voice quality glide phonations during which voice quality changed continuously from breathy to pressed within a single utterance. The glottal area waveforms for a glide phonation from speaker F1 are shown in Fig. 8. As observed previously (Kreiman et al., 2012), the DC component (i.e., the glottal gap size) gradually decreases during the first half of the recording (from cycle index 0 to 300 with incomplete glottal closures). During the second half of the recording (from cycle index 300 to 700 when glottal closure is complete), the OQ continuously decreased as quality became increasingly pressed.
Figure 8.
The glottal area waveforms during a voice quality “glide” phonation (from breathy to pressed) from speaker F1. The plots are sequential from left to right and top to bottom, according to cycle index numbers.
The measures OQ, DC, AC, AC/OQ, and CPP during glide phonations from all four speakers are plotted in Fig. 9. The glottal configuration is mainly characterized by a decrease in DC over approximately the first half of the recording, and by decreasing OQ during the phonatory phase with complete glottal closure (approximately the second half of the recording). This two-part physical process is captured by AC/OQ as illustrated in Fig. 9. Recall that AC reflects the effect of DC in the presence of a glottal gap. Despite this effect of glottal gap, for all speakers, AC/OQ increased approximately steadily as quality changed from breathy to pressed, apparently capturing the waveform variation along the voice quality axis of breathy-to-pressed. Linear regression analyses modeling AC/OQ as a function of time show r2 = 0.96, 0.96, 0.80, and 0.89 for speakers F1, M1, M4, and M5, respectively. AC/OQ is also strongly correlated with the CPP for these four speakers (r = 0.86, 0.95, 0.77, and 0.92, p < 0.001, for speakers F1, M1, M4, and M5, respectively). In this sense, AC/OQ appears to map between glottal vibratory patterns, acoustic consequences, and quality.
Figure 9.
(Color online) The voice source measures (OQ, DC, AC, and AC/OQ) and the acoustic measure CPP for voice quality “glide” phonations from breathy to pressed for four speakers (F1, M1, M4, and M5). For clarity, AC/OQ has been normalized to a maximum value of 1 and a minimum value of 0.
DISCUSSION
PCA was applied to glottal area waveforms to investigate the factors that vary with voice quality, based on the assumption that perceptually meaningful vibratory measures should quantify those aspects of vibration that correspond to differences in voice quality. Because the PCAs on which this measure is based weigh each sample of the glottal pulse equally and capture the dimensions with the largest variation, AC/OQ (which is based primarily on the first two principal components) mostly reflects the gross shape of the glottal pulse, which corresponds largely to the low-frequency part of the source spectrum (Stevens, 1998). Listeners are highly sensitive to the relative amplitudes of the lower harmonics (Kreiman et al., 2010), which convey both paralinguistic information about a variety of personal and interpersonal attributes [see Kreiman and Sidtis (2011), for review] and linguistic information in languages like Gujarati (Fischer-Jorgensen, 1967) and White Hmong (Huffman, 1987). In this sense, AC/OQ potentially provides insight into how changes in glottal vibration patterns result in acoustic patterns that are perceptually salient.
The primary advantage of AC/OQ relative to existing source measures (and OQ in particular) is that it provides a unified framework for measuring the glottal area waveform along a voice quality axis of breathy-to-pressed, regardless of whether glottal closure is complete or not. Examination of changes in glottal area functions with changes in quality showed that the breathiest voice qualities were accompanied by glottal gaps which decreased in size with increasing pressedness. Only after the membranous glottal gap had completely disappeared did OQ begin to decrease with ongoing changes in voice quality. Despite this two-part physical process, AC/OQ is linearly related to continuous changes in quality and to the acoustic measure CPP, linking these three domains in a straightforward manner. These findings are consistent with results of Samlan and Story (2011), whose computer simulation showed that increasing the separation between the vocal processes at maximum closure (controlled by a vocal fold adduction parameter) generally led to decreased harmonic energy and increased random (noise) energy, which resulted in decreased CPP. The two-way physical process (captured by AC/OQ) and CPP values observed in this study lend experimental support to the simulated relationship between kinematic (anatomical) parameters and acoustics measures in Samlan and Story (2011).
Additionally, glottal measures derived from the glottal flow (or the flow derivative) usually involve measuring the characteristics of the glottal closing phase (e.g., the negative peak of the flow derivative) because of its association with the main acoustic excitation of the vocal tract (Fant, 1993). AC/OQ captures the gross shape of the glottal area pulse, and thus is able to quantify the variation in glottal area waveforms. Finally, the calculation of AC/OQ does not rely on the sample value of the waveform at a single time instant (i.e., the negative peak of the waveform derivative). Thus, distortion of glottal area functions due to recording conditions or the area calculation algorithm does not significantly affect the accuracy of AC/OQ.
Measures of the glottal area waveform pulse skewness (speed quotient/closing quotient/asymmetry coefficient) have been linked with acoustic measures. Previous studies on this topic commonly made measures on glottal flow signals (e.g., Henrich et al., 2001; Holmberg et al., 1988). However, recent studies using laryngeal high-speed videoendoscopy report varying levels of correlation between glottal area waveform skewness and acoustic measures. For example, Mehta et al. (2011) reported that the speed quotient of the glottal area function showed only weak correlation with spectral tilt measures. Kreiman et al. (2012) reported that the relationship between the glottal area pulse skewness and H1-H2 depended on whether a glottal gap existed (see Kreiman et al., 2012, Table TABLE IV.) and regression model parameters were also speaker dependent. Simulations using a computational model of the kinematics of vocal fold showed that speed quotient of the glottal area function was not a direct measure of the maximum area declination rate and had significant variability due to adduction, vertical difference, and glottal convergence (Titze, 2006). Measures of glottal area waveform skewness were initially tested in the current study but did not vary consistently with variations in voice quality and/or acoustic measures. Because the goal of this study was to investigate the aspects of the glottal area waveform that vary consistently with acoustic measures and voice qualities, the skewness measures were not included in the results.
CONCLUSION
In conclusion, this study investigated the aspects of the glottal area pulse shape that vary with voice quality, by using high-speed videoendoscopy of the vocal folds. A new measure, AC/OQ, was proposed to capture variations in glottal area pulse shapes in a manner that reflects both acoustic and perceptual consequences of those variations. This measure is defined as the AC component divided by OQ, so that an increase in glottal gap size (DC) or an increase in OQ results in lower AC/OQ values. Analyses of phonations differing both discretely and continuously in voice quality showed that across speakers AC/OQ values also increased monotonically along a breathy-to-pressed continuum. Thus, AC/OQ is capable of characterizing the continuum of glottal area waveform variation corresponding to a range of voice qualities, regardless of the existence or absence of glottal gaps.
Some limitations to this work should be noted. First, the audio and high-speed video recordings of the vocal folds were collected from speakers with normal voices. In producing breathy phonation, these speakers usually demonstrated a gap through the cartilaginous glottis, which may extend continuously through some or all of the membranous glottis (Holmberg et al., 1988; Södersten and Lindestad, 1990). However, speakers with voice disorders may have a gap that appears only in the membranous glottis, as occurs in presbylaryngis (the aged larynx) or in some patients with Parkinson disease who have breathy voices (Hanson et al., 1984). Because this glottal configuration was not included in our study, it is possible that AC/OQ may not measure these voices adequately. Second, this study examined only a single dimension of voice quality. The extent or manner in which AC/OQ may generalize to other voice qualities or glottal configurations remains for future research.
ACKNOWLEDGMENTS
This work was supported in part by NSF Grant No. IIS-1018863 and by NIH/NIDCD Grant Nos. DC01797 and DC011300. We thank Marc Garellek and Dinesh Chhetri for help recording high-speed images. We also thank Michael Döllinger for kindly providing GlotAnTools software for high-speed image segmentation.
Footnotes
Defined as to/(to + tc), where to is the duration of opening phase and tc is the duration of closing phase.
The actual measure used in Holmberg et al. (1988) was an AC-DC ratio, defined as the rms of the AC portion around its mean divided by the mean of the AC portion. In that study, glottal flow was calculated by inverse-filtering the oral flow measured using a flow mask, which quantified the absolute amount of glottal flow. The division by the mean of the AC portion compensated for the dynamic range of actual glottal flow. In studies using laryngeal high-speed videoendoscopy, the absolute glottal area is not available due to the varying distance between the laryngoscopy and the glottis across recordings. Therefore, in this study the extracted glottal area waveforms were normalized to have a maximum value of 1 (divided by the maximum glottal area in each glottal period) so that waveforms were comparable across recordings. This normalization process compensated for the dynamic range of the glottal area. Therefore, the AC component (calculated as rms of the AC portion) was directly used in the study without being divided by the mean of the AC component.
References
- Alku, P. (1992). “ Glottal wave analysis with pitch synchronous iterative adaptive inverse filtering,” Speech Commun. 11, 109–118. 10.1016/0167-6393(92)90005-R [DOI] [Google Scholar]
- Alku, P., Bäckström, T., and Vilkman, E. (2002). “ Normalized amplitude quotient for parameterization of the glottal flow,” J. Acoust. Soc. Am. 112, 701–710. 10.1121/1.1490365 [DOI] [PubMed] [Google Scholar]
- Alku, P., Magi, C., Yrttiaho, S., Bäckström, T., and Story, B. (2009). “ Closed phase covariance analysis based on constrained linear prediction for glottal inverse filtering,” J. Acoust. Soc. Am. 125, 3289–3305. 10.1121/1.3095801 [DOI] [PubMed] [Google Scholar]
- Alku, P., Story, B., and Airas, M. (2006). “ Estimation of the voice source from speech pressure signals: Evaluation of an inverse filtering technique using physical modeling of voice production,” Folia Phoniatr. Logop. 58, 102–113. 10.1159/000089611 [DOI] [PubMed] [Google Scholar]
- Chen, G., Kreiman, J., Shue, Y.-L., and Alwan, A. (2011). “ Acoustic correlates of glottal gaps,” in Interspeech, pp. 2673–2676.
- Cranen, B., and Schroeter, J. (1995). “ Modeling a leaky glottis,” J. Phonetics 23, 165–177. 10.1016/S0095-4470(95)80040-9 [DOI] [Google Scholar]
- de Krom, G. (1993). “ A cepstrum-based technique for determining a harmonics-to-noise ratio in speech signals,” J. Speech Hear. Res. 36, 254–266. [DOI] [PubMed] [Google Scholar]
- Draper, M. R., Blagnys, B., and Premachandra, D. J. (2007). “ To ‘EE’ or not to ‘EE’,” J. Otolaryngol. 36, 189–193. 10.2310/7070.2007.0019 [DOI] [PubMed] [Google Scholar]
- Fant, G. (1970). Acoustic Theory of Speech Production, 2nd ed. (Mouton, The Hague, Paris: ), pp. 15–20. [Google Scholar]
- Fant, G. (1982). “ Preliminaries to analysis of the human voice source,” Speech Transm. Lab. Q. Prog. Status Rep. 4, 1–27. [Google Scholar]
- Fant, G. (1993). “ Some problems in voice source analysis,” Speech Commun. 13, 7–22. 10.1016/0167-6393(93)90055-P [DOI] [Google Scholar]
- Fant, G. (1995). “ The LF-model revisited. Transformations and frequency domain analysis,” Speech Transm. Lab. Q. Prog. Status Rep. 36, 119–156. [Google Scholar]
- Fant, G., Liljencrants, J., and Lin, Q. (1985). “ A four-parameter model of glottal flow,” Speech Transm. Lab. Q. Prog. Status Rep. 4, 1–13. [Google Scholar]
- Fischer-Jorgensen, E. (1967). “ Phonetic analysis of breathy (murmured) vowels in Gujarati,” Indian Linguist. 28, 71–139. [Google Scholar]
- Fujisaki, H., and Ljungqvist, M. (1986). “ Proposal and evaluation of models for the glottal source waveform,” in ICASSP, pp. 1605–1608.
- Hanson, D. G., Gerratt, B. R., and Ward, P. H. (1984). “ Cinegraphic observations of laryngeal function in Parkinson's disease,” Laryngoscope 94, 348–353. 10.1288/00005537-198403000-00011 [DOI] [PubMed] [Google Scholar]
- Hanson, H. M. (1997). “ Glottal characteristics of female speakers: Acoustic correlates,” J. Acoust. Soc. Am. 101, 466–481. 10.1121/1.417991 [DOI] [PubMed] [Google Scholar]
- Hanson, H. M., and Chuang, E. S. (1999). “ Glottal characteristics of male speakers: Acoustic correlates and comparison with female data,” J. Acoust. Soc. Am. 106, 1064–1077. 10.1121/1.427116 [DOI] [PubMed] [Google Scholar]
- Henrich, N., d'Alessandro, C., and Doval, B. (2001). “ Spectral correlates of voice open quotient and glottal flow asymmetry: Theory, limits and experimental data,” in Eurospeech, pp. 47–50.
- Hillenbrand, J., Cleveland, R., and Erickson, R. (1994). “ Acoustic correlates of breathy vocal quality,” J. Speech Hear. Res. 37, 769–778. [DOI] [PubMed] [Google Scholar]
- Hollien, H., Moore, P., Wendahl, R. W., and Michel, J. (1966). “ On the nature of vocal fry,” J. Speech Hear. Res. 9, 245–247. [DOI] [PubMed] [Google Scholar]
- Holmberg, E. B., Hillman, R. E., and Perkell, J. S. (1988). “ Glottal airflow and transglottal air pressure measurements for male and female speakers in soft, normal, and loud voice,” J. Acoust. Soc. Am. 84, 511–529. 10.1121/1.396829 [DOI] [PubMed] [Google Scholar]
- Holmberg, E. B., Hillman, R. E., and Perkell, J. S. (1989). “ Glottal airflow and transglottal air pressure measurements for male and female speakers in low, normal, and high pitch,” J. Voice 3, 294–305. 10.1016/S0892-1997(89)80051-7 [DOI] [PubMed] [Google Scholar]
- Huffman, M. K. (1987). “ Measures of phonation type in Hmong,” J. Acoust. Soc. Am. 81, 495–504. 10.1121/1.394915 [DOI] [PubMed] [Google Scholar]
- Javkin, H., Antoñanzas-Barroso, N., and Maddieson, I. (1987). “ Digital inverse filtering for linguistic research,” J. Speech Hear. Res. 30, 122–129. [DOI] [PubMed] [Google Scholar]
- Kawahara, H., Masuda-Katsuse, I., and de Cheveigne, A. (1999). “ Restructuring speech representations using a pitch-adaptive time-frequency smoothing and an instantaneous-frequency-based F0 extraction: Possible role of a repetitive structure in sounds,” Speech Commun. 27, 187–207. 10.1016/S0167-6393(98)00085-5 [DOI] [Google Scholar]
- Klatt, D., and Klatt, L. (1990). “ Analysis, synthesis, and perception of voice quality variations among female and male talkers,” J. Acoust. Soc. Am. 87, 820–857. 10.1121/1.398894 [DOI] [PubMed] [Google Scholar]
- Koike, Y., and Hirano, M. (1973). “ Glottal-area time function and subglottal-pressure variation,” J. Acoust. Soc. Am. 54, 1618–1627. 10.1121/1.1914458 [DOI] [PubMed] [Google Scholar]
- Kreiman, J., Gerratt, B. R., and Khan, S. D. (2010). “ Effects of native language on perception of voice quality,” J. Phonetics 38, 588–593. 10.1016/j.wocn.2010.08.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreiman, J., Shue, Y. L., Chen, G., Iseli, M., Gerratt, B. R., Neubauer, J., and Alwan, A. (2012). “ Variability in the relationships among voice quality, harmonic amplitudes, open quotient, and glottal area waveform shape in sustained phonation,” J. Acoust. Soc. Am. 132, 2625–2632. 10.1121/1.4747007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreiman, J., and Sidtis, D. (2011). Foundations of Voice Studies: An Interdisciplinary Approach to Voice Production and Perception (Wiley-Blackwell, Malden, MA: ), pp. 1–504. [Google Scholar]
- Mehta, D. D., Zañartu, M., Quatieri, T. F., Deliyski, D. D., and Hillman, R. E. (2011). “ Investigating acoustic correlates of human vocal fold vibratory phase asymmetry through modeling and laryngeal high-speed videoendoscopy,” J. Acoust. Soc. Am. 130, 3999–4009. 10.1121/1.3658441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison, M., Rammage, L., Belisle, G., Pullan, B., and Nichol, H. (1983). “ Muscular tension dysphonia,” J. Otolaryngol. 12, 302–306. [PubMed] [Google Scholar]
- Omori, K., Slavit, D., Kacker, A., and Blaugrund, S. (1998). “ Influence of size and etiology of glottal gap in glottic incompetence dysphonia,” Laryngoscope 108, 514–518. 10.1097/00005537-199804000-00010 [DOI] [PubMed] [Google Scholar]
- Rosenberg, A. (1971). “ Effects of the glottal pulse shape on the quality of natural vowels,” J. Acoust. Soc. Am. 49, 583–590. 10.1121/1.1912389 [DOI] [PubMed] [Google Scholar]
- Rothenberg, M. (1973). “ A new inverse-filtering technique for deriving the glottal air flow waveform during voicing,” J. Acoust. Soc. Am. 53, 1632–1645. 10.1121/1.1913513 [DOI] [PubMed] [Google Scholar]
- Rothenberg, M. (1981). “ Acoustic interaction between the glottal source and the vocal tract,” in Vocal Fold Physiology, edited by Stevens K. N. and Hirano M. (University of Tokyo Press, Tokyo: ), pp. 305–323. [Google Scholar]
- Samlan, R. A., and Story, B. H. (2011). “ Relation of structural and vibratory kinematics of the vocal folds to two acoustic measures of breathy voice based on computational modeling,” J. Speech Lang. Hear. Res. 54, 1267–1283. 10.1044/1092-4388(2011/10-0195) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shue, Y.-L. (2010a). “ The voice source in speech production: Data, analysis and models,” Ph.D. thesis, University of California Los Angeles, http://www.ee.ucla.edu/~spapl/paper/shue_dissertation.pdf (Last viewed Nov. 30, 2012). [Google Scholar]
- Shue, Y.-L. (2010b). “ VoiceSauce: A program for voice analysis,” http://www.ee.ucla.edu/~spapl/voicesauce/ (Last viewed Apr. 30, 2012).
- Shue, Y.-L., Chen, G., and Alwan, A. (2010). “ On the interdependencies between voice quality, glottal gaps, and voice-source related acoustic measures,” in Interspeech, pp. 34–37.
- Shue, Y.-L., Kreiman, J., and Alwan, A. (2009). “ A novel codebook search technique for estimating the open quotient,” in Interspeech, pp. 2895–2898.
- Södersten, M., and Lindestad, P. -Å. (1990). “ Glottal closure and perceived breathiness during phonation in normally speaking subjects,” J. Speech Hear. Res. 33, 601–611. [DOI] [PubMed] [Google Scholar]
- Stevens, K. N. (1998). Acoustic Phonetics (The MIT Press, Cambridge, MA: ), pp. 55–126. [Google Scholar]
- Timcke, R., Von Leden, H., and Moore, P. (1958). “ Laryngeal vibrations: Measurements of the glottic wave. Part I. The normal vibratory cycle,” Arch. Otolaryngol. 68, 1–19. 10.1001/archotol.1958.00730020005001 [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (2004). “ A theoretical study of F0-F1 interaction with application to resonant speaking and singing voice,” J. Voice 18, 292–298. 10.1016/j.jvoice.2003.12.010 [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (2006). “ Theoretical analysis of maximum flow declination rate versus maximum area declination rate in phonation,” J. Speech Lang. Hear. Res. 49, 439–447. 10.1044/1092-4388(2006/034) [DOI] [PubMed] [Google Scholar]
- Titze, I. R. (2008). “ Nonlinear source-filter coupling in phonation: Theory,” J. Acoust. Soc. Am. 123, 2733–2749. 10.1121/1.2832337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titze, I., and Story, B. (1997). “ Acoustic interactions of the voice source with the lower vocal tract,” J. Acoust. Soc. Am. 101, 2234–2243. 10.1121/1.418246 [DOI] [PubMed] [Google Scholar]