Efficient and Robust Model-to-Image Alignment using 3D Scale-Invariant Features

Abstract

This paper presents feature-based alignment (FBA), a general method for efficient and robust model-to-image alignment. Volumetric images, e.g. CT scans of the human body, are modeled probabilistically as a collage of 3D scale-invariant image features within a normalized reference space. Features are incorporated as a latent random variable and marginalized out in computing a maximum a-posteriori alignment solution. The model is learned from features extracted in pre-aligned training images, then fit to features extracted from a new image to identify a globally optimal locally linear alignment solution. Novel techniques are presented for determining local feature orientation and efficiently encoding feature intensity in 3D. Experiments involving difficult magnetic resonance (MR) images of the human brain demonstrate FBA achieves alignment accuracy similar to widely-used registration methods, while requiring a fraction of the memory and computation resources and offering a more robust, globally optimal solution. Experiments on CT human body scans demonstrate FBA as an effective system for automatic human body alignment where other alignment methods break down.

1. Introduction

Many medical imaging applications involve aligning 3D volumetric images, e.g. CT volumes of the human body or MR images of the human brain, to a standard frame of reference or model. For example, comparative studies of biomedical image data often require aligning images of different subjects to a normative atlas (Li et al., 2003; Baiker et al., 2010), and model-to-image alignment can serve as the basis for volumetric object identification (Criminisi et al., 2009; Flitton et al., 2010) or computer-assisted diagnosis (Kloppel et al., 2008; Toews et al., 2010). Alignment is typically addressed via image registration or model fitting methods, where an optimal spatial transform is determined between an image and a template (Collins et al., 1994; Ourselin et al., 2001; Jenkinson and Smith, 2001; Avants et al., 2008; Klein et al., 2010) or model (Cootes et al., 2001; Criminisi et al., 2009; Tao et al., 2011), based on a combination of image similarity and geometrical constraints. Volumetric image alignment has been the focus of an important body of research for several decades, and a number of solutions now exist that are effective for analysis of well-curated data. For example, brain images of healthy subjects acquired in prospective studies can be aligned via diffeomorphic warps guaranteeing smooth, one-to-one correspondence between different subjects (Avants et al., 2008; Klein et al., 2009).

The limitations of existing approaches become apparent when considering applications that require robust, efficient alignment of difficult data. For example, increasing numbers of publicly available human body scans (Johnson et al., 2008; Cleary, 2010) may potentially lead to important developments in analyzing and classifying disease, possibly via large-scale data mining or content-based image retrieval methods (El-Naqa et al., 2004; Lehmanna et al., 2005; Akgul et al., 2011) similar to those that have emerged in the context of 2D image data (Nister, 2006; Tao et al., 2011). Volumetric alignment remains a primary bottleneck, however, for several reasons. The human body varies greatly, due to deformations such as scaling, articulation, breathing motion, etc., but also due to the fact that the same structure may not be identifiable or present in all images, e.g. in the cases of pathology, variable organ configurations, bowel contents, partially overlapping or truncated images, etc. Accurate alignment throughout the entire image is difficult to achieve in such cases, motivating the need for robust, meaningful alignment solutions despite a lack of one-to-one correspondence. Alignment routines typically operate on entire image volumes, requiring on the order of minutes to compute a single robust linear alignment solution on an average PC. Storing, transmitting and aligning large numbers of image volumes imposes a significant burden on memory, bandwidth and computational resources, motivating the need for improved efficiency. Algorithms often require initialization within a ’capture radius’ of the correct solution, where initialization is typically provided via external labels, e.g. the body part and patient orientation as encoded in the Digital Imaging and Communications in Medicine (DICOM) protocol. DICOM labeling error rates as high as 15% have been reported (Guld et al., 2002), however, motivating the need for globally optimal alignment of image content independent of external labels.

This paper proposes a method for efficient, robust volumetric model to- image alignment, entitled feature-based alignment (FBA). In FBA, all image data are represented as 3D scale-invariant features: distinctive, local image patterns characterized geometrically in terms of location, scale and orientation within the image, and equipped with an encoding of local image appearance. This representation is particularly useful for alignment, as features arising from the same anatomical tissues be automatically extracted and identified in different images despite global variations in image geometry and intensity, e.g. due to misalignment, sensor non-uniformity, etc. FBA models the posterior probability of a transform aligning an image to a standard reference frame or atlas, conditional on features extracted in the image. The model incorporates a latent variable enumerating a set of features characteristic of an imaging domain, e.g. features arising from ventricles or gyri in MR brain images. Model features are characterized by their occurrence probability and by conditional densities over feature appearance and geometry within atlas space, and are marginalized out in computing a maximum a-posteriori (MAP) alignment solutions. The model is trained from pre-aligned image data, automatically identifying a set of features most characteristic of anatomical structure present in training images. Efficient, globally optimal alignment is then achieved from a sparse set of highly probably feature correspondences between the model and a new image. Alignment is particularly robust to missing or unrelated image structure, and produces a set of model-to-image correspondences that can be used to initialize more detailed registration, segmentation or analysis procedures. FBA is generally applicable to a variety of imaging domains, and is efficient in both execution time and memory footprint.

The primary contribution of this article is a novel model for volumetric image alignment based on 3D scale-invariant image features. Scale-invariant features are widely used for robust, efficient matching (Lowe, 2004; Mikolajczyk and Schmid, 2004; Stewart et al., 2003; Yang et al., 2011) and appearance modeling (Fergus et al., 2006; Toews and Arbel, 2007, 2009) of 2D image data. 3D scale-invariant features extracted from volumetric data have been used for image matching (Allaire et al., 2008; Cheung and Hamarneh, 2009; Flitton et al., 2010) and classification (Toews et al., 2010), however leveraging 3D orientation information in determining feature geometry and efficiently encoding image intensity has proved challenging. We present novel techniques for assigning feature orientation and encoding intensity, both of which are necessary to achieve efficient, globally optimal alignment. Experiments investigate model-to-image alignment of MR brain images and CT images of the human body. In the case of brain images, FBA achieves alignment accuracy similar to established registration algorithms a fraction of the cost in terms of computation and memory, while offering a more robust, globally optimal solution. FBA is demonstrated for robust, global alignment of human body CT image volumes, in difficult scenarios including arbitrary image truncation and inter-subject variability where other alignment routines break down.

1.1. Prior Work

This article presents a general model for fast and robust volumetric image alignment, based on 3D scale-invariant image features. Here we review prior work on volumetric model-to-image alignment and the use of invariant image features.

1.1.1. Model-to-Image Alignment

Model-to-image alignment seeks identify a mapping between a model defined in particular imaging domain, e.g. brain scans, and a new image. Models used for alignment generally combine appearance and geometrical information within a standard geometrical frame of reference, e.g. the Talairach stereotaxic brain reference space (Talairach and Tournoux, 1988). Domain-specific image features and alignment strategies can be used, e.g. specialized detectors for specific structures such as the midsagittal plane of the brain (Brummer, 1991; Nowinski et al., 2006), bones (Baiker et al., 2010), branch points in lung airways (Li et al., 2003), retinal vasculature structures (Stewart et al., 2003), etc. Such strategies are difficult to generalize to new imaging domains, however, as optimal features for alignment may not be known a-priori and are prone to inter-rater variability. Furthermore, alignment tends to break down if structures of interest are not present in new images, e.g. due to image truncation.

Image registration can be used as a general alignment solution, where the model is represented as an average template (Collins et al., 1994; Avants et al., 2008) or template collection (Blezek and Miller, 2006). Registration is effective in aligning images related by a smooth, one-to-one mapping, e.g. inter-subject alignment of healthy brain images (Klein et al., 2009) or intrasubject lung image registration (Murphy et al., 2011). It is difficult to generalize registration to scenarios where a smooth one-to-one mapping may not apply, for example in the case of abnormality, outliers or missing data. Outlier modeling strategies have been proposed (Periaswamy and Farid, 2006), however coping with significant truncation or multiple modes of anatomical morphology remains challenging. Robust image-to-image matching techniques can be used to overcome sensitivity to outliers and missing data. The FLIRT (Functional Linear Image Registration Tool) algorithm (Jenkinson and Smith, 2001) involves a coarse-to-fine strategy using the robust mutual information similarity measure. Block matching methods (Ourselin et al., 2001; Clatz et al., 2005) achieve robust alignment by matching subsets of image data, e.g. the robust block matching (RBM) algorithm (Ourselin et al., 2001) computes alignment from a subset of blocks with a best image matching score, via a multi-resolution matching strategy with pre-defined block sizes and resolutions. Registration formulations focusing on distinctive local features (Amit and Kong, 1996; Yang et al., 2011) or emphasizing salient image regions (Ou et al., 2011) can improve robustness to outliers. A potential weakness of registration and matching techniques is that they do not explicitly learn and exploit domain-specific image structure, and thus may be prone to aligning unrelated image content.

Model-based alignment involves learning a domain-specific model from training examples that can then be reliably fit to new images. Global models of image appearance (Barber, 1976; Turk and Pentland, 1991) or combined appearance and geometry (Cootes et al., 2001) capture data variation efficiently using principal component analysis (PCA). As with image registration, robust modeling strategies have been proposed (Beichel et al., 2005), however outliers, localized variation or missing data remain challenging. Modeling the image as a collection of local parts or features provides a mechanism for coping with localized variations and occlusions. Parts-based models can be described in terms of the modeling of inter-feature geometrical relationships. Naive Bayes models consider features as conditionally independent given a single feature or reference frame (Wells III, 1997; Leibe et al., 2004; Toews and Arbel, 2007, 2009), and lead to efficient, occlusion-resistant algorithms for recovering low-parameter image deformations, e.g. linear transforms. Markov models impose constraints between neighboring features and can represent deformable or articulated transforms (Fischler and Elschlager, 1973; Felzenszwalb and Huttenlocher, 2005; Fergus et al., 2006; Potesil et al., 2010; Zhang and Cootes, 2012), however computational efficiency and occlusion resistance may be more difficult to achieve.

The Haar wavelet-based strategy popularized in the context of face detection (Viola and Jones, 2001) is an important local feature modeling technique. Relatively uninformative Haar wavelet features are computed efficiently via the integral image representation, and feature selection techniques such as AdaBoost (Freund and Schapire, 1997) are used to combine features into a strong classifier. These models are typically used to reproduce manually assigned labels or landmarks, e.g. fetal anatomical measurements in ultrasound images (Carneiro et al., 2008), brain structure segmentation (Wels et al., 2009) or annotations in radiographs (Tao et al., 2011). There two primary disadvantages of this approach. First, while translation and scaling can be recovered efficiently, recovering rotation requires an explicit search over orientation and increases the computational complexity and error rate of fitting. Effectively coping with a single orientation parameter is challenging in 2D image data (Carneiro et al., 2008; Tao et al., 2011), difficulties are more pronounced in higher dimensions (Criminisi et al., 2009). Secondly, model training requires a high degree of supervision, and anatomical landmarks or structures of interest need to be specified manually, however it may not necessarily be obvious which structures are most useful for alignment.

1.1.2. Modeling Local Invariant Features

Local image features offer a mechanism for representing image appearance in a manner robust to local variations, occlusions and missing structure, and are widely used in the computer vision (Grimson and Lozano-Perez, 1987; Wells III, 1997; Viola and Jones, 2001; Fergus et al., 2006; Toews and Arbel, 2009) and medical imaging communities (Amit and Kong, 1996; Rohr, 1997; Pennec et al., 2000; Stewart et al., 2003; Toews and Arbel, 2007; Toews et al., 2010; Yang et al., 2011). Early work proposed local interest operators for identifying salient points for image matching in the context of binocular stereo vision (Marr and Poggio, 1977) and robotic mapping (Moravec, 1979). Subsequent work proposed detectors for corners (Harris and Stephens, 1988) and landmarks (Amit and Kong, 1996; Rohr, 1997) based on spatial derivatives. Local feature geometry is useful in characterizing image patterns in a manner independent of image intensity, e.g. via landmarks (Pennec et al., 2000) or point sets (Jian and Vemuri, 2011). Image intensity information associated with features can be encoded for efficient image correspondence (Tomasi and Shi, 1994; Rohr et al., 2001; Urschler et al., 2006). Scale-space theory extends interest operators to consider the size or scale of image patterns in addition to location (Lindeberg, 1998; Romeny, 2003), as the notion of an image pattern is intimately linked to the scale at which it is observed. Local invariant image features have been widely adopted for image matching in the computer vision community (Lowe, 2004; Mikolajczyk and Schmid, 2004), e.g. the scale-invariant feature transform (SIFT) method (Lowe, 2004), and are an attractive basis for modeling. They can be repeatably extracted and used to compute correspondence in the presence of global geometrical similarity or affine deformations (Mikolajczyk et al., 2005) and intensity changes.

Scale-invariant feature extraction typically involves a search for image regions that maximize a criterion of saliency, for example the magnitude of Gaussian derivatives in scale (Lowe, 2004) and/or space (Mikolajczyk and Schmid, 2004), image phase (Carneiro and Jepson, 2003) or information-theoric measures such as entropy (Kadir and Brady, 2001) or mutual information (Toews and Wells III, 2010). Once regions have been identified, they can be assigned an orientation in order to achieve invariance to image rotation. In 2D images, this is typically done by identifying dominant gradient orientations within the image region. The method of Lowe involves generating a 1D histogram of image gradient orientations, smoothing the histogram to reduce noise and finally identifying histogram maxima (Lowe, 2004). With location, scale and orientation identified, features can be spatially normalized and encoded for efficient image-to-image matching. Due to normalization, matching can be accomplished without requiring an explicit search over geometrical transformations under which features are invariant. In conventional 2D images, the image gradient orientation histogram (GoH) representation, popularized by the SIFT descriptor (Lowe, 2004), has been shown to be among the most effective encoding strategies for image-to-image matching (Mikolajczyk and Schmid, 2004). Gradient orientation samples are set into coarse histogram bins over space and orientation, providing a representation that is informative regarding yet robust to geometrical image deformations. Rank-ordering of the GoH descriptor further improves the encoding performance, providing invariance to arbitrary monotonic deformations of image gradients (Toews and Wells III, 2009).

In the context of volumetric images, 3D scale-invariant feature methods have been used by several authors in the context of intra-subject image matching (Allaire et al., 2008; Ni et al., 2008; Niemeijer et al., 2009; Cheung and Hamarneh, 2009; Flitton et al., 2010). They have not been widely adopted in more difficult contexts, for example inter-subject or atlas-to-subject alignment, as popular 2D methods for orientation assignment and intensity encoding do not generalize trivially to 3D. The primary difficulty is that 3D orientation is characterized by 3 parameters, e.g. azimuth, elevation and tilt angles, instead of a single parameter. When images do not exhibit significant orientation changes, orientation assignment can be neglected (Toews et al., 2010; Laptev, 2005) or partially characterized (Ni et al., 2008; Niemeijer et al., 2009; Cheung and Hamarneh, 2009). Orientation assignment is required for efficient alignment in the presence of orientation changes, however. Most authors have followed the approach of (Scovanner et al., 2007; Allaire et al., 2008; Flitton et al., 2010), whereby maxima are first identified in a 2D histogram of local gradient orientations parameterized by azimuth and elevation angles, after which an orthogonal tilt angle is determined. The azimuth/elevation parameterization is subject to sampling bias, as bins are non-uniformly sized. This can be partially mitigated by normalizing histogram bins according to solid angle area (Scovanner et al., 2007), however bias remains a difficulty for histogram smoothing and interpolation operations. Furthermore, the popular GoH intensity encoding is difficult to generalize to 3D due to the curse of dimensionality. For example, the 2D SIFT descriptor (Lowe, 2004) accumulates gradient orientations over 4² spatial bins and 8 orientation bins, resulting in a 128-element vector. Approaches extending this quantization to 3D have resulted in large descriptors with 2000+ elements (Allaire et al., 2008; Niemeijer et al., 2009; Flitton et al., 2010), which introduce a significant burden in memory and computational resources.

2. Material and Methods

Feature-based alignment aims to identify a globally optimal spatial mapping between a volumetric image and an atlas or model, based on a sparse set of scale-invariant feature correspondences. This section describes FBA, including local invariant feature extraction, a probabilistic model that can be learned from training images, and a technique for robust model-to-image alignment.

2.1. Invariant Feature Extraction

The goal of invariant feature extraction is to identify and characterize informative image patterns in a manner independent of global variations in image geometry and appearance, e.g. due to misalignment or intensity changes. A scale-invariant feature in 3D is defined geometrically by a scaled local coordinate system S within image I. Let S = {X, σ,Θ}, where X = {x, y, z} is 3-parameter location specifying the origin, σ is a 1-parameter scale and Θ = {θ̂₁, θ̂₂, θ̂₃} is a set of three orthonormal unit vectors θ̂₁, θ̂₂, θ̂₃ specifying the orientations of the coordinate axes.

Invariant feature extraction begins by identifying a set of location/scale pairs {(X_i, σ_i)} in an image. This is done by detecting spherical image regions centered on location X_i with radius proportional to scale σ_i that locally maximize a function f(X, σ) of image saliency. For example, SIFT feature extraction detects local maxima of the difference-of-Gaussian (DoG) function (Lowe, 2004):

$$\{(X_i,{\sigma }_i)\}=\underset{X,\sigma }{\text{local}\text{argmax}}\mid f(X,\kappa \sigma )-f(X,\sigma )\mid ,$$ (1)

where f(X, σ) is the convolution of the image I with a Gaussian kernel of variance σ², κ is a multiplicative scale sampling rate, and the expression ‘ $\underset{X}{\text{loca}\text{argmax}}\{f(X)\}$’denotes a set of values of the argument X that locally maximize f(X). DoG region detection generalizes trivially from 2D to higher dimensions and can be efficiently implemented using Gaussian scale-space pyramids (Lowe, 2004). Following detection, each region is assigned an orientation Θ, after which image intensity is encoded. Orientation assignment and intensity encoding in 3D are non-trivial extensions of 2D techniques, the following sections describe the methods adopted here.

2.1.1. Orientation Assignment

Orientation assignment involves determining the local coordinate system axes Θ for each location/scale pair (X, σ) identified via feature detection. This can be done by maximizing histograms of image gradient orientation computed within the image region surrounding X. Histograms based on angular parameterizations such as azimuth/elevation (Scovanner et al., 2007) are affected by sampling bias due to non-uniform bin geometry. Bias is avoided by here by adopting a non-parametric 3D histogram of gradient orientation, as follows. For each pair (X, σ), a cubical image patch centered on X with side length proportional to σ is cropped and rescaled to a fixed size. Image gradient samples are then computed at each voxel within the inscribed sphere of the patch, and used to populate bins on the surface of a unit sphere in a 3D gradient orientation histogram. For each gradient sample ∇I, the histogram bin location is determined by a unit vector of gradient orientation $\widehat{\nabla }I=\frac{\nabla I}{\left|\right|\nabla I\left|\right|}$, and bins are incremented by the gradient magnitude ||∇I||. Note that the orientation histogram is sparsely populated, as only bins intersected by the unit sphere surface contain non-zero counts. Trilinear interpolation is used to spread increments over neighboring bins, and the histogram is smoothed via a standard 3D Gaussian kernel in order to reduce noise, approximating smoothing on a unit sphere (Chung, 2006). Note that while operations such as interpolation, incrementing and smoothing operations may be affected by minor discretization effects due to volumetric histogram binning, they are unaffected by angular parameterization bias.

A three-step orientation assignment procedure is used to identify Θ from 3D orientation histograms, as illustrated in Figure 1a). First, a primary orientation vector θ̂₁ is identified as the maximum of a 3D histogram H₁(θ̂) generated from gradient samples ∇I:

$${\widehat{\theta }}_1=\underset{\widehat{\theta }}{\text{argmax}}\left\{H_1(\widehat{\theta })\right\}.$$ (2)

Figure 1.

Diagram a) illustrates the bin structure of the 3D volumetric histogram during orientation assignment, shaded regions indicate non-zero histogram bins. From left to right, the primary orientation vector θ̂₁ is first determined, followed by a perpendicular secondary orientation θ̂₂ and finally θ̂₃. Diagram b) illustrates the GoH image intensity encoding in 3D that quantizes gradient samples uniformly in 8 spatial bins and 8 orientations bins.

Next, a secondary orientation vector θ̂₂ is determined in the great circle orthogonal to θ̂₁. This is done by maximizing a second histogram H₂(θ̂) generated from the components of gradient samples orthogonal to θ̂₁, i.e. defined by the operation θ̂₁ × (∇I × θ̂₁):

$${\widehat{\theta }}_2=\underset{\widehat{\theta }}{\text{argmax}}\left\{H_2(\widehat{\theta })\right\}.$$ (3)

Finally, the remaining orientation vector θ̂₃ is defined as the cross product θ̂₃ = θ̂₁ × θ̂₂. Note that quadratic interpolation is used to refine histogram maxima locations to sub-bin precision.

In general, orientation histograms for a single region (X, σ) may contain multiple informative maxima. Alternatively, orientation may be ambiguous for either θ̂₁ and/or θ̂₂, e.g. for spherical image patterns where unique orientations cannot be reliably assigned. As in 2D orientation assignment Lowe (2004), these cases are handled by generating multiple features for each region from multiple primary and secondary orientation maxima, while limiting the number of features due to ambiguous maxima. For each region, a new feature is generated for each primary histogram peak within 0.8× the maximum primary peak, and for each secondary peak with 0.8× the maximum secondary peak. This results in an average of approximately 3 features per region in MR and CT volumes used later in experiments, which allows the representation of multi-modal local orientation structure while limiting multiple peaks due to orientation ambiguity.

2.1.2. Image Intensity Encoding

Once feature geometry is determined, a volumetric image patch is cropped, rescaled and reoriented according to the local coordinate system defined by {X, σ,Θ}, after which intensities are encoded for subsequent matching. The goal of encoding is to convert volumetric intensity data into a small and distinctive representation for computing correspondence efficiently. We adopt a gradient orientation histogram (GoH) encoding that quantizes space and orientation uniformly into octants, resulting in a 64-bin histogram indexed by 2³ = 8 spatial bins and 2³ = 8 orientation bins, as illustrated in Figure 1b). Gradient samples computed within the image patch are used to populate the histogram bins. For each gradient sample, the spatial histogram bin coordinate is determined by the sample location, the orientation bin coordinate is determined by the gradient vector orientation, and the bin is incremented by the gradient magnitude. Finally, the histogram is normalized by rank-ordering (Toews and Wells III, 2009), resulting in a 64-element descriptor consisting of a permutation of the integers {1,…, 64}.

The encoding proposed here is attractive for several reasons. Spatial histogram weighting schemes used in 2D encoding are unnecessary (Lowe, 2004), as spatial bins are distributed symmetrically about the origin. The octant sampling scheme generalizes to arbitrary spatial dimensions by considering orthants, where vectors in N-dimensions are of length 2^N×2^N = 2^2N. Dissimilarity measures such as the L² distance can be used to compare rank-ordered vectors in a manner invariant to monotonic deformations in gradient magnitude (Toews and Wells III, 2009). Furthermore, rank-ordered vectors are small, requiring 48 bytes, and lead to efficient storage and matching.

2.2. Feature-based Model for Alignment

Let I_j represent the intensity encoding associated with feature geometry S_j, and let = {(I_j, S_j)} represent a set of feature appearance/geometry pairs extracted in a single image I. Furthermore, let T represent a global linear transform mapping image I to an atlas or standard reference space, about which non-linear deformations can be identified and quantified locally. FBA aims to estimate the maximum a-posteriori (MAP) transform T_MAP = argmax {p(T| )} maximizing the posterior probability of T conditional on . Assuming conditionally independent feature observations (I_j, S_j), Bayes rule results in:

$$p(T\mid \mathcal{I})=\frac{p(T){\prod }_{j}p(I_j,S_j\mid T)}{p(\mathcal{I})}.$$ (4)

In Equation (4), p( ) is constant as are fixed data during alignment and p(T) is a prior density over transform parameters. Factor p(I_j, S_j|T) is a density over the appearance and geometry of an observed feature conditional on T, and is constructed by marginalizing over feature data extracted from training images as follows. Images are naturally described in terms of distinctive local structure shared across similar images, for instance the human brain can be described by the corpus callosum, ventricles, etc. Distinctive structure is incorporated here by defining density p(I_j, S_j|T) via the marginalization of a latent discrete random variable f taking on values {f₀,…, f_N}:

$$p(I_j,S_j\mid T)=\sum _i^{N}p(I_j,S_j,f_i\mid T)=\sum _i^{N}p(I_j,S_j\mid f_i,T)p(f_i).$$ (5)

In Equation (5), f_i can be viewed as an indicator for a specific image pattern or model feature i that occurs with stable appearance and geometry across a population. p(f_i) quantifies the probability of observing model feature f_i; we assume statistical independence of f and T. p(I_j, S_j|f_i, T) is a joint density over observed feature data (I_j, S_j) conditional on model feature f_i and global transform T. This density can be thought of intuitively as quantifying the probability of feature (I_j, S_j) when brought into correspondence with f_i via transform T. For different distinctive model features, these densities are generally concentrated and non-overlapping, meaning that for a single fixed observed feature, p(I_j, S_j|f_i, T) ≈ 0 for all but at most one f_i. A special case is reserved for f₀, which represents a generic, spurious background feature. The density p(I_j, S_j|f₀, T) associated with f₀ by definition exhibits high variance in appearance and geometry, and is thus approximated as uniform or constant, i.e. p(I_j, S_j|f₀, T) ≈ α for some positive constant α. As a result, Equation (5) is locally approximated as:

$$p(I_j,S_j\mid T)\approx p(I_j,S_j\mid f_i,T)p(f_i)+\alpha p(f_0),$$ (6)

In Equation (6), the value of p(I_j, S_j|T) for a single fixed observed feature (I_j, S_j) is approximated by contributions from the background f₀ and at most one distinctive model feature f_i. The approximation in Equation (6) is key to model learning and alignment procedures described later. Model feature-conditional densities p(I_j, S_j|f_i, T) are defined as:

$$p(I_j,S_j\mid f_i,T)=p(I_j\mid S_j,f_i,T)p(S_j\mid f_i,T),$$ (7)

$$=p(I_j\mid f_i)p(S_j\mid f_i,T),$$ (8)

where Equation (7) follows from Bayes rule and Equation (8) from the assumption of conditional independence of I_j and (S_j, T) given f_i. p(I_j|f_i) is taken to be an isotropic Gaussian density over intensity descriptor elements. Density p(S_j|f_i, T) represents the local variation of feature geometrical variation associated with model feature f_i, given global transform T. This accounts for local deformations about T due to inter-subject variability, and is factored into conditional densities over feature location, scale and orientation:

$$p(S_j\mid f_i,T)=p(X_j\mid f_i,T)p({\sigma }_j\mid f_i,T)p({\mathrm{\Theta }}_j\mid f_i,T).$$ (9)

In Equation (9), factor p(X_j|f_i, T) is an isotropic Gaussian density over feature location conditioned on (σ_j, f_i, T). p(σ_j|f_i, T) is a Gaussian density over log feature scale ln σ_j conditioned on (f_i, T). p(Θ_j|f_i, T) is a von Mises density (Evans et al., 1993) over independent angular deviations of coordinate axes, here approximated as an isotropic Gaussian density over Θ for simplicity under a small angle assumption. Note that all densities used here take the computational form of the isotropic Gaussian density, which for an n-dimensional random vector Y is parameterized by an n-dimensional mean vector μ and a scalar variance λ:

$$Y~\mathcal{N}(\mu ,\lambda )=\frac{exp(-\frac{1}{2\lambda }{(Y-\mu )}^T(Y-\mu ))}{{(2\pi \lambda )}^{\frac{n}{2}}}.$$ (10)

Thus for densities over feature appearance and geometry in Equations (8) and (9), variables (Y, n) in Equation (10) take on the values of (Y = I_j, n = 64), (Y = X_j, n = 3), (Y = lnσ_j, n = 1) and (Y = Θ_j, n = 9).

2.2.1. Learning

Learning aims to identify a set of model features {f_i} and to estimate associated distribution parameters from training images. Training images are first pre-aligned into a standard reference space and features are extracted as in Section 2.1. Pre-alignment fixes T as a constant in Equation (4), allowing estimation of parameters for factors p(S_j, I_j|f_i, T) and p(f_i) in Equation (5) that takes the form of a Gaussian mixture model. Parameter estimation could potentially be achieved via clustering approaches such as expectation-maximization (Duda et al., 2001) or Dirichlet process modeling (Rasmussen, 2001). The number of model features N is generally large and unknown, however, making these approaches difficult to apply. A process similar to the mean-shift algorithm (Comaniciu and Meer, 2002) is thus adopted to identify concentrated clusters of features extracted across subjects that are similar both in geometry and appearance, where features in a cluster represent instances of the same underlying anatomical structure or model feature f_i.

First, for each extracted feature index i, set G_i of geometrically similar features is identified such that:

$$G_i=\left\{\begin{array}{r}\hfill j:\frac{\left|\right|X_i-X_j\left|\right|}{{\sigma }_i}\le {\epsilon }_x,\\ \hfill \left|ln\frac{{\sigma }_j}{{\sigma }_i}\right|\le {\epsilon }_{ln\sigma },\\ \hfill {\mathrm{\Theta }}_j·{\mathrm{\Theta }}_i\ge {\epsilon }_{cos\theta }\end{array}\right\}.$$ (11)

In Equation (11), ε_x and ε_lnσ are thresholds on the maximum acceptable difference in location and scale. ε_{cos θ} is a threshold on the minimum acceptable angular difference cosine, where Θ_j·Θ_i represents the maximum dot product between corresponding orientation unit vectors. These three thresholds define a binary measure of inter-feature geometrical similarity, and can be set to fixed values that generally apply to all features.

Next, a set A_i of features similar in appearance to i is identified such that the L² distance ||I_i − I_j|| is less than a threshold ε_Ii:

$$A_i({\epsilon }_{I_i})=\{j:||I_i-I_j||\le {\epsilon }_{I_i}\}.$$ (12)

Threshold ε_Ii is feature-specific, as the amount of appearance information varies from one feature to the next, and is maximized for each i as follows:

$${\epsilon }_{I_i}=sup\left\{{\epsilon }_I\in [0,\infty ):\gamma \le \frac{\mid G_i\cap A_i({\epsilon }_{I_i})\mid }{\mid \overline{G_i}\cap A_i({\epsilon }_{I_i})\mid }\right\}.$$ (13)

Features in intersection C_i = G_i ∩ A_i(ε_Ii) are considered to be samples of f_i for which p(I_j, S_j|f_i, T)p(f_i) ≫ 0 in Equation (6). In Equation (13), ε_Ii is thus maximized such that the relative probability of distinctive vs. background features $\frac{\mid G_i\cap A_i({\epsilon }_{I_i})\mid }{\mid \overline{G_i}\cap A_i({\epsilon }_{I_i})\mid }\approx \frac{p(f_i)}{p(f_0)}$ within A_i(ε_Ii) is greater than a positive constant γ. Here, γ = 1 is empirically used, reflecting equal probabilities of distinctive vs. background features. Much smaller γ result in large ε_Ii and inefficient alignment, much larger γ result in small ε_Ii and inaccurate estimation of p(I_j, S_j|f_i, T)p(f_i). Note the set in Equation (13) contains at least one element, i.e. feature i corresponding to ε_I = 0, and ε_Ii is thus always defined.

Note that learning produces many similar, redundant clusters, as each extracted image feature results in a cluster. Redundant clusters are discarded to obtain a reduced set of model features. Here, all clusters C_j associated with features j that are themselves elements of a larger cluster j ∈ C_i,|C_i| > |C_j| are discarded. Finally, parameters of distributions in Equation (8) are estimated from remaining clusters. For densities over appearance and geometry associated with cluster C_i, mean parameters are taken to be the values of I_i and S_i, respectively. Density means, variances and discrete distribution parameters for p(f) are estimated via maximum likelihood (ML).

2.2.2. Alignment

Alignment seeks to identify T_MAP maximizing p(T| ) given feature data extracted in a new image. A two-step algorithm similar to the Interpretation Tree approach (Grimson and Lozano-Perez, 1987) is adopted, where candidate image-model correspondences are first identified and used to generate transform candidates, after which candidate transforms are evaluated under p(T| ). Candidate model-image correspondences (i, j) are determined by comparing the intensity encoding I_j of each extracted image feature to densities p(I_j|f_i) associated with model features. A candidate correspondence (i, j) exists if ||I_i − I_j|| ≤ ε_Ii. This procedure can be efficiently performed in O(MlogN) time complexity via approximate nearest neighbor techniques (Beis and Lowe, 1997), where N and M are the numbers of model and image features respectively, and by considering a small subset of the most probable model features as determined by p(f).

For each correspondence candidate (i, j), a model-image transform candidate T_ij is estimated via ML, i.e. $T_{ij}=\underset{T}{\text{argmax}}\{p(S_j\mid f_i,T)\}$. Transform candidates are then evaluated under p(T| ) in order to determine T_MAP, as follows. For each transform candidate T_ij, all image features {S_j} with model correspondences are transformed to normalized model space via T_ij. Image features whose transformed geometry falls within thresholds ε_x, ε_{ln σ} and ε_{cos θ} of their corresponding model features are considered to be inliers of T_i,j, as p(I_j, S_j|f_i, T)p(f_i) ≫ 0, and used to compute p(T| ) via Equations (4) and (5). Integral computation in Equation (5) is efficient, as p(I_j, S_j|f_i, T)p(f_i) ≈ 0 for non-inlier pairs (i, j) and these terms are discarded. The candidate transform maximizing p(T| ) is taken as T_MAP.

Note that T_MAP represents a global linear model-to-image transform, while inlier model-image correspondences within geometrical thresholds of T_MAP account for local deformations. Correspondences could be used in order to estimate deformable alignment solution throughout the image, for example as an interpolated deformation field (Arsigny et al., 2005). This is beyond the scope of this article and we leave this for future work, here least squares estimation (LSE) is used to derive a more accurate model-to-image similarity transform from correspondences associated with T_MAP. LSE is based on corresponding feature image location X, and thus requires a minimum of 3 non co-linear correspondences. Feature scale and orientation parameters could also be incorporated, however they tend to be more reflective of local image-specific variations, e.g. enlarged/reduced ventricle sizes in brain images, and less informative regarding the global model-to-image transform.

3. Results

Experiments here have two goals, the first is to demonstrate that FBA can be used to compute model-to-image alignment solutions in difficult cases with accuracy on par with state-of-the-art alignment approaches, at a fraction of the cost in terms of memory and computational time. The second is to demonstrate the ability of FBA to recover robust, globally optimal alignment solutions in scenarios where alignment approaches break down. Two distinct contexts are considered: T1-weighted MR images of the human brain in Section 3.2 and CT images of the human body in Section 3.3.

3.1. Experimental Details

Features are extracted from all images used in experiments as described in Section 2.1, our implementation is available online ³. DoG extrema in Equation (1) are identified using a 3D equivalent of the Gaussian pyramid method of Lowe (Lowe, 2004). Briefly, the range of X spans the image volume, scale is initialized at σ = 1.6 voxels and increased at a multiplicative rate of three samples per scale doubling or octave, i.e. κ = 2^1/3. The image is sub-sampled by a factor of two at each octave for efficiency, and feature extraction terminates once 2σ exceeds the minimum image dimension. DoG extrema within 2σ of the image border are discarded, as they are subject to border effects. Extrema arising from degenerate image structure whose 3D location is unstable are also identified and discarded, e.g. planar or tubular structures. This is done using the method of Rohr (Rohr, 1997), based on the 3×3 structure tensor or second moment matrix M generated from image gradient samples within the region (X, σ). Briefly, the ratio $\beta =\frac{\mathit{Det}(M)}{{(\frac{1}{3}Tr(M))}^3}$ calculated from the determinant Det(M) and the trace Tr(M) of M lies on the range [0, 1], where low β indicate degenerate image structure. Here, all extrema for which β < 0.2 are discarded, lower thresholds result in similar alignment solutions but increased processing requirements, higher thresholds begin to negatively impact alignment.

Cubical image patches of side length 4σ are rescaled to 11×11×11 voxels for orientation assignment and intensity encoding. A side length of 4σ allows inclusion of informative peripheral image structure into the encoding of intensity. The size of the volumetric histogram used in orientation assignment is determined such that the number of gradient orientation samples is sufficient to populate histogram bins. The image patch contains an inscribed sphere of integer radius $\frac{11}{5}=5$ voxels bearing $\frac{4}{3}\pi 5^3\approx 523$ gradient samples, and a volumetric histogram of size 11×11×11 bins is used. This results in greater than one vote per bin on average, as votes are accumulated on a spherical shell of radius 5 bins with a surface area of 4π5² ≈ 314 bins. The number of features extracted in an image is dependent on the content, here for example, a brain volume at 1mm voxel resolution produces approximately 2500 features.

Learning is applied as in Section 2.2.1 with geometrical thresholds empirically set to ε_{ln σ} = ln 1.5, ε_x = 0.5 and ε_{cos θ} = 0.8. These thresholds can be thought of as determining the maximum permissible geometrical variability of model features. Looser thresholds result in a smaller set of model features with higher geometrical variability, potentially grouping features arising from different underlying anatomical structures and leading to reduced alignment accuracy. Tighter thresholds result in a larger set of model features, with instances of the same anatomical structure potentially split into different clusters, resulting in reduced alignment efficiency. Here, geometrical thresholds are set to allow a high range of geometrical variability, as potential ambiguities in geometrical clustering are later resolved by appearance clustering. Fitting is performed as in Section 2.2.2, where the output is the optimal global 7-parameter similarity transform T_MAP, in addition to a set of probable model-image correspondences representing localized deformations. Alignment is relatively insensitive to the background feature constant α and 26 similar alignment solutions are achieved for a range of positive values, here α = 1 is used.

3.2. MR Brain Images

The experiments here demonstrate FBA in the context of model-to-subject alignment of T1-weighted MR brain images. A brain model, or atlas, is constructed from a set of 100 healthy training subject images from the OASIS data set which have been aligned into a standard reference space at resolution 176×208×176 (isotropic, 1.0mm voxel size) via a 12-parameter affine transform (Marcus et al., 2007). Note that learning is performed once off-line on a set of typical images of healthy subjects. A set of 12 difficult testing images (isotropic, voxel sizes 0.8–1.0mm) are used to demonstrate atlas-to-subject alignment, these are described in Figure 2.

Figure 2.

Axial slices of 12 test subject images. (1–5) exhibit significant anatomical abnormalities due to traumatic brain injury (NAMIC, 2011). Subjects (6,7) represent a healthy subject before and after skull-stripping. (8,9) exhibit large tumors (Archip et al., 2007). (10) is an intra-operative scan of subject (9) acquired at an unspecified oblique angle due to the surgical protocol (Archip et al., 2007). (11,12) exhibit non-uniformity and wrap-around artifacts.

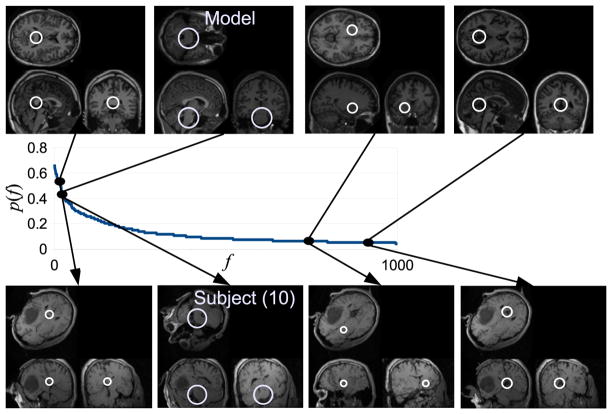
FBA alignment is generally successful, identifying reasonable global alignment solutions despite arbitrary initialization and significant abnormality. On average 40 atlas-to-subject correspondences are identified per alignment trial, Figure 3 illustrates examples identified in test subject (10) despite an unknown global orientation difference. These correspondences represent a locally linear alignment solution between distinctive, healthy anatomical structure shared by the atlas and subject. The probabilities of corresponding structures are quantified locally throughout the image from distribution p(f) estimated during learning, see the graph in Figure 3. Note that the tumor region produces no atlas-to-subject correspondences, as it bears no likeness to structure modeled in healthy training subjects, and thus does not impact alignment.

Figure 3.

Examples of model-to-subject brain image correspondences across global orientation changes. The central graph plots the probability distribution p(f) over model features, in descending order of probability. Images show a subset of 4 model features (upper row), their probabilities, and corresponding image features identified in subject 10 (lower row).

Alignment trials are also performed using three common robust image alignment algorithms: RBM (Ourselin et al., 2001) ⁴, FLIRT (Jenkinson and Smith, 2001) ⁵ and ELASTIX (Klein et al., 2010) ⁶ based on the open source ITK ⁷ project. RBM, FLIRT and ELASTIX are image-based techniques, that operate by determining a linear transform between test subjects and an average atlas template image constructed from the 100 training subjects. RBM, FLIRT and ELASTIX recover a 12-parameter affine transform commonly used in atlas-to-subject brain analysis (Klein et al., 2010), RBM and ELASTIX also recover a 6-parameter rigid transform, which may be more robust for the difficult test images used here. FBA alignment is the most efficient of the techniques, both in terms of computational resources and memory. The approximate running times for one alignment trial on a 2.5GHz Intel Core 2 processor are (in seconds) FBA: 20, ELASTIX: 33, RBM: 140 and FLIRT: 220. In terms of the memory, FBA requires approximately 0.5MB to store both model and image features, while image registration requires approximately 70MB to store floating point images. In contrast to image registration algorithms, FBA focuses computational resources primarily on feature extraction in individual images prior to alignment. Virtually all FBA running time is due to Gaussian convolution during feature extraction, this represents a one-time pre-processing step that could be significantly reduced via GPU optimization. With features extracted, FBA alignment requires less than 1 second.

Algorithms are compared in terms of approximate alignment error, which is quantified here by the average displacement error of 6 anatomical surfaces in aligned subject images relative to their locations in the atlas. The anatomical surfaces are shown by arrows in Figure 4 ‘Atlas Labels’, and consist of the inferior cortical surfaces of the left and right temporal lobes and the superior cortical surface (coronal slice) and the anterior, posterior and superior surfaces of the corpus callosum (sagittal slice). These structures are used as they are present in all testing images, they are manually labeled by a single rater. Note the goal here is not to quantify alignment error precisely, which in itself would be challenging for these images, but rather to provide an approximate error comparison and to identify alignment breakdown. The graph in Figure 4 plots the alignment error for the six methods tested here. All techniques achieve nominally low alignment error (i.e. less than 5mm) for nine of twelve subjects, three subjects (1, 7 and 10) represent difficult exceptions. Subject 1 is a difficult abnormal case that results in high error, particularly for ELASTIX. Subject 7 illustrates the tendency of the affine alignment to systematically stretch the cortex of the skull-stripped subject to match the atlas skull, highlighting how registration may be erroneously driven by overall object shape rather than distinctive image structure. Note that this problem is less pronounced for rigid RBM and ELASTIX alignment. Subject 10 illustrates the capacity of FBA to recover global orientation changes without initialization, while other registration techniques fail without correct initialization. FBA aligns all test cases here with error less than 5mm.

Figure 4.

A graph of alignment error for ELASTIX and RBM (affine and rigid), FLIRT (affine) and FBA over 12 test subject images. The image overlaying the graph shows sagittal and coronal slices of the average atlas, arrows illustrate labels used to quantify alignment error. Dashed lines indicate error measurements for difficult subjects 1,7 and 10. The upper left and right images illustrate alignment for subjects 7 and 10 where RBM, FLIRT and ELASTIX error is noticeably higher than FBA.

3.3. CT Body Images

This section demonstrates FBA in a context where existing image alignment techniques break down, inter-subject matching of human body scans. The American College of Radiology Imaging Network (ACRIN) (Johnson et al., 2008) data set consists of CT scans acquired for the study of colorectal neoplasia. The National Library of Medicine (NLM) Liver CT data set (Cleary, 2010) contains scans acquired for the analysis of liver tumors. It may be of interest to align these images for a joint study of structure common to all images, e.g. lower lung, liver or kidneys. While brain image alignment is relatively common, alignment of human body scans remains an open and difficult problem, for a number of reasons. The human body exhibits a high degree of variability from one person to the next due to myriad factors including age, sex, morphology (lean, obese), breathing state (inspiration/ expiration), body position (e.g. prone/supine), content of bowels, which influence the geometry of soft tissues. Body image alignment approaches in the literature typically assume images contain similar structure (Baiker et al., 2010; Jager and Hornegger, 2009), however this is generally not the case, as images acquired in studies focusing on different aspects may be cropped differently. This is particularly relevant in the case of the CT image modality, where truncated image acquisition reduces the exposure of the subject to harmful ionizing radiation.

Here, 20 random ACRIN subject images are chosen (isotropic, 1.56mm voxel size), aligned manually to a single subject according to major organ geometry, and used to train a feature-based model with identical parameters to those used in brain alignment. The 4 test subjects from the NLM liver CT data set are then aligned to this model (isotropic, 1.24–1.37mm voxel size). The result of FBA alignment is shown in Figure 5, note that all subjects are successfully aligned with respect to the atlas average, in particular subjects 1 and 4 with truncated abdominal regions. Approximate alignment error is quantified by the displacement of three anatomical landmarks that remain relatively stable across subjects, the superior aspect of the right and left hemidiaphram, and the location of the thoracic vertebrae, see arrows in Figure 5. An average error of 11 ± 3.2mm is obtained, which is reasonable considering the high degree of anatomical variability of the human body in the atlas.

Figure 5.

a) average ACRIN atlas, blurriness indicates the high degree of inter-subject variability. (b–e) NLM subjects (1–4) following successful FBA alignment, note inter-subject variability and image truncation. Arrows and lines across images indicate anatomical locations used to quantify alignment error.

Figure 6 illustrates example correspondences obtained in aligning truncated NLM subject 1 to the feature-based atlas, note the high degree of inter-subject variability. While it may be unrealistic to compute accurate alignment throughout the image due to inter-subject variability, truncation, etc, it may be possible within image regions associated with probable FBA correspondences. Figure 7 illustrates locally linear and deformable B-spline ⁸ alignment of corresponding feature regions identified in both a model and an NLM subject. The intensity difference |I1−I2| is noticeably less pronounced along tissue borders following deformable as opposed to linear alignment, indicating a more accurate alignment solution. The vertebrae of I2 are slightly stretched following deformation, however, and a more accurate alignment solution would account for bio-mechanical tissue properties such as rigid bone structure. This is a promising research direction that we leave for future work.

Figure 6.

Examples of model-subject correspondences in CT volumes. Each image consists of axial (upper) and sagittal (lower) volume slices. White circles illustrate the location and scale of features in the ACRIN model image (left) and in the new subject image (right), arrows indicate corresponding features.

Figure 7.

Deformable alignment of corresponding feature regions in CT volumes. The upper image pairs show axial and coronal slices of a feature identified in both an ACRIN model subject (left, I1) and an NLM subject (right, I2), white circles represent the location and scale of corresponding features. The lower images show fixed region I1 (left) and moving region I2 following local linear (center) and deformable (right) alignment in axial (upper row) and coronal (lower rows) views. Images |I1−I2| show the absolute difference between intensities in aligned regions, high intensity indicates alignment error.

To illustrate the difficulty of the task, alignment is also attempted using the FLIRT, RBM and ELASTIX algorithms. Trials are attempted using both the average ACRIN and individual ACRIN subjects as the atlas, with both subject-to-atlas and atlas-to-subject registration paradigms. Algorithm parameters are varied and the values resulting in the best alignment are considered. Alignment is generally unsuccessful, with all registration algorithms producing clearly incorrect, high error solutions. When manually initialized to the correct solution (translation, rotation, scaling), FLIRT remains unsuccessful, RBM and ELASTIX result in average errors of RBM: 13 ± 5.0mm, ELASTIX: 11 ± 3.1mm across the 4 NLM subjects. Figure 8 illustrates alignment error for FBA, RBM and ELASTIX as a function of initialization error in the form of vertical translation. ELASTIX and RBM both result in high error when initialized 80mm and 90mm from the correct solution, this poses a difficulty as protocols such as DICOM provide patient orientation but not translation within the volume. In contrast, FBA alignment is globally optimal and independent of initialization errors in location, orientation or scaling. Running times for alignment are approximately (in seconds) FBA: 28, ELASTIX: 36, RBM: 290.

Figure 8.

Alignment of NLM subject 1. The average atlas is shown in a). The graph shows average alignment error of FBA, RBM and ELASTIX associated with vertical initialization error. Images b) and c) show examples of successful and unsuccessful RBM alignment associated with vertical initialization errors of 0mm and 90mm, respectively.

4. Discussion

This article presents FBA, a method for efficient, robust and global model-to- image alignment of volumetric image data. FBA is based on a probabilistic model of 3D scale-invariant features, quantifying the appearance, geometry and occurrence probability of features in a set of training data. Novel techniques for assigning feature orientation and encoding intensity are developed. MAP estimation is used to identify a globally optimal, locally linear alignment solution from correspondences between features extracted in a new image and the model. Experiments demonstrate FBA in the contexts of difficult abnormal MR brain images and highly variable CT body scans, and compare with three state-of-the-art image alignment algorithms: FLIRT, RBM and ELASTIX. In the context of brain MRI, FBA achieves alignment accuracy similar to other approaches, while offering more robust, global solutions at a fraction of the cost in computation and memory. FBA leads to a system for general alignment of CT body scans, capable of coping with significant inter-subject variability and truncation, where other approaches break down without manual initialization. A number of model-to-image alignment techniques were investigated other than FLIRT, RBM and ELASTIX, however results were either poor or required a high degree of manual supervision, highlighting the difficulty of the experimental data.

The most immediate practical use of FBA is as a means of efficiently and robustly initializing registration or segmentation procedures in domains where training images are available. Memory requirements are reduced by more than an order of magnitude in comparison to standard image registration. For example a 256×256×176 brain volume of size 11MB (floating point) can be represented by a 0.4MB feature set, and a 0.1MB feature-based brain atlas containing the 1000 most frequently occurring features can be used to successfully align the set of testing images used in Section 3.2. Furthermore, while feature extraction imposes a one-time computational cost, e.g. approximately 20 seconds for brain images, the resulting feature set can be aligned extremely efficiently in sub-second time. This will be particularly important in applications in which images are aligned multiple times, e.g. group-wise registration (Wu et al., 2012) or content-based image retrieval.

FBA leads to a number of future research directions. Feature correspondences may be useful in computing more accurate deformable or articulated model-to-image transforms throughout the image. Neighborhood constraints may prove effective at modeling features arising from repeating image structures, e.g. vertebrae or airway structures. While 3D scale-invariant feature correspondences can be identified over a range of affine and non-linear deformations, 3D affine-invariant features (Mikolajczyk et al., 2005) may prove effective in coping with voxel anisotropy. Orientation-sensitive correspondences resulting from FBA could prove useful in analyzing and classifying subjects according to factors such as disease (Toews et al., 2010). FBA could be used to align complementary data sources, e.g. CT and positron emission tomography (PET) volumes (Camara et al., 2007), by developing inter-modality scale-invariant feature extraction and matching techniques. FBA could serve as a useful object detection framework for non-medical 3D scanning systems (Flitton et al., 2010). Finally, FBA could serve as an effective means of studying inter-species alignment or modeling growth in temporal image sequences, where one-to-one image correspondence may not exist throughout the image.

Highlights.

• A method is presented for efficient & robust model-subject alignment of 3D images.

• A probabilistic model represents images using 3D scale-invariant features.

• Alignment is achieved via max a-posteriori estimation, feature correspondences.

• Experiments involve difficult image alignment cases: disease, brain MRI, body CT.