On the role of hydrogel structure and degradation in controlling the transport of cell-secreted matrix molecules for engineered cartilage

Abstract

Damage to cartilage caused by injury or disease can lead to pain and loss of mobility, diminishing one’s quality of life. Because cartilage has a limited capacity for self-repair, tissue engineering strategies, such as cells encapsulated in synthetic hydrogels, are being investigated as a means to restore the damaged cartilage. However, strategies to date are suboptimal in part because designing degradable hydrogels is complicated by structural and temporal complexities of the gel and evolving tissue along multiple length scales. To address this problem, this study proposes a multi-scale mechanical model using a triphasic formulation (solid, fluid, unbound matrix molecules) based on a single chondrocyte releasing extracellular matrix molecules within a degrading hydrogel. This model describes the key players (cells, proteoglycans, collagen) of the biological system within the hydrogel encompassing different length scales. Two mechanisms are included: temporal changes of bulk properties due to hydrogel degradation, and matrix transport. Numerical results demonstrate that the temporal change of bulk properties is a decisive factor in the diffusion of unbound matrix molecules through the hydrogel. Transport of matrix molecules in the hydrogel contributes both to the development of the pericellular matrix and the extracellular matrix and is dependent on the relative size of matrix molecules and the hydrogel mesh. The numerical results also demonstrate that osmotic pressure, which leads to changes in mesh size, is a key parameter for achieving a larger diffusivity for matrix molecules in the hydrogel. The numerical model is confirmed with experimental results of matrix synthesis by chondrocytes in biodegradable poly(ethylene glycol)-based hydrogels. This model may ultimately be used to predict key hydrogel design parameters towards achieving optimal cartilage growth.

1 Introduction

It is well known that damage of articular cartilage due to injury, disease or genetic disorders can lead to joint pain and reduced mobility, drastically affecting one’s quality of life. With the prevalence of cartilage-related joint problems on the rise (Hootman & Helmick, 2006) and current surgical procedures offering imperfect solutions, new treatments are clearly warranted. Tissue engineering is one promising treatment option having the potential to yield living functional cartilage. Within this context, scaffolds are being developed to deliver chondrocytes (cartilage cells) to the damaged site and support new tissue deposition (Slaughter, 2009). However, engineering functionally competent and well-integrated cartilage remains a hurdle, limiting clinical translation of cartilage tissue engineering.

Encapsulation of cells in photopolymerizable and biodegradable hydrogels is one promising strategy being investigated for cartilage tissue engineering. This hydrogel platform can be injected and polymerized in situ for site-specific cell delivery and tailored to degrade over time, providing necessary space for new tissue growth. Poly(ethylene glycol) (PEG)-based hydrogels formed by photopolymerization hold promise because they recapitulate important aspects of the native tissue (e.g., maintaining the rounded chondrocyte morphology which is key to preserving the phenotype) (Bryant, 2003; Elisseeff, 1999) and are easily functionalized with degradable linkers (Sawhney, 1993) and bioactive molecules (Lee, 2005). For in situ cartilage tissue engineering, the scaffold must also withstand the in vivo physiological forces, a requirement that becomes even more important in large defects and joint resurfacing. In addition, hydrogel degradation must be incorporated to permit macroscopic tissue growth, but its rate should match tissue growth in order to maintain mechanical integrity and thus function throughout tissue development. While PEG hydrogels can be designed with mechanical properties similar to that of native cartilage (Bryant, 2004a; Villanueva, 2008), engineering mechanically competent cartilage remains a major challenge.

In optimizing the design of biodegradable hydrogels for cartilage tissue engineering, it is critical to understand how hydrogel structure, across multiple length scales, and its temporal changes with degradation support the production, transport and deposition of extracellular matrix (ECM). Hydrogels are crosslinked polymer networks with an average crosslink density that influences the mechanical properties, degree of swelling, mesh size, and subsequently transport properties. Because ECM molecules typically have high molecular weights, a large mesh size is often desirable to promote transport of these molecules through the gel for homogeneous tissue development. But, this leads to a mechanically inferior hydrogel. In contrast, a high crosslink density, which can conserve mechanical integrity similar to that of cartilage, is usually prohibitory to ECM transport (Nicodemus, 2011; Bryant, 2002). As a result, ECM transport is restricted to regions near chondrocytes (the pericellular region). This increased local matrix deposition may in turn further inhibit long-range ECM transport. While the introduction of degradation into the hydrogels can overcome many of these shortcomings, this strategy is only beneficial if degradation kinetics properly match matrix transport and deposition. The latter has not yet been achieved.

Designing the structure and degradation behavior of hydrogels for optimal tissue development is challenging due to the nonlinearity of the processes involved and the multiscale aspect of the problem. However, mathematical models can provide an important tool to guide hydrogel design as well as to provide a better understanding of the mechanisms controlling tissue production, transport and deposition. Theories of mixture and poro-elasticity have proven to be excellent frameworks onto which the deformation of tissues, such as cartilage, can be studied (Ateshian, 1997; Holmes & Mow, 1990; Kwan, 1990). In cartilage, the problem of matrix diffusion, transport and deposition has been addressed at cellular (Sengers, 2004) and tissue scales (Dimicco & Sah, 2003). More recently, mathematical models have been expanded to cartilage tissue engineering strategies, predicting matrix diffusion from cells within scaffolds (Trewenack, 2009). The problem of cell mediated gel degradation was also assessed with a triphasic mixture model (Vernerey, 2011) to better understand how degradation may affect both transport properties and gel mechanics. Finally, on a more global scale, a multiphasic model (made of linked ECM, scaffold and cells) was used to derive a steady-state solution for tissue growth as a function of scaffold properties (Haider et al., 2011). While the above studies have enabled a more quantitative understanding of the processes of synthesis, diffusion and deposition, few have considered the coupled physics of scaffold deformation, degradation and ECM transport for cells encapsulated in a degrading crosslinked hydrogel for which the size scale of porosity is of similar magnitude to that of many ECM molecules. Experimentally these processes have proven to be key in designing hydrogel scaffolds with encapsulated cells.

In the present work, we take an integrated experimental/modeling approach to further understand the role of hydrogel structure and degradation on the development of new tissue synthesized and deposited by chondrocytes (Fig. 1). The problem is described in terms of an ECM-producing chondrocyte surrounded by a triphasic mixture consisting of a degrading hydrogel, aqueous solvent and diffusing ECM molecules. The model shows, in agreement with experimental observations, how microstructural details such as crosslink density and degradation kinetics, lead to variations in matrix deposition and diffusion. In particular, we aim to develop a predictive model that accurately reflects the relationship between hydrogel structure and tissue development, and which will guide the design of hydrogels for successful engineered tissues.

Figure 1.

Mutiscale approach to modeling tissue production by cells encapsulated in hydrogels. Refer to the next sections for the parameters. Left: chondrocytes encapsulated within a PEG hydrogel, shown at day 3 after encapsulation. Cytosol of live cells fluoresce green showing the chondrocytic round morphology. Nuclei of dead cells fluoresce red. Scale bar indicates 100 microns. Right: chondroitin sulfate elaboration (red) by chondrocytes encapsulated within a degradable PEG hydrogel after 28 days in vitro. Cell nuclei are stained blue. Scale bar indicates 50 microns.

The paper is organized as follows. In section 2, the overall method to produce cell-encapsulated hydrogels is discussed with an introduction to the general modeling approach to describe hydrogel evolution. Section 3 describes the microscopic mechanisms of hydrogel deformation and degradation with a particular emphasis on the influence of processing parameters. We then discuss in section 4, how these mechanisms affect the diffusion of unbound ECM, and pay particular attention to the role of molecule size. We finally conclude the paper by presenting numerical simulations and experimental observations, which together illustrate the impact of hydrogel structure on the nature of tissue growth. Results are discussed in detail and recommendations for future tissue engineering strategies are given.

2 Hydrogel structure: processing and mathematical description

2.1 Processing of cell-laden hydrogels and control of initial hydrogel structure

The methods used to form biodegradable PEG hydrogels and encapsulate cells are described. Poly(ethylene glycol) (PEG) can be functionalized in numerous ways to add moieties for degradation and polymerization. Hydrolytically degradable lactides were reacted with PEG, MW 4600, to produce oligo(lactic acid)-PEG-oligo(lactic acid) (LA-PEG-LA) with an average of 2–3 lactic acid repeat units per side (Sawhney, 1993). PEG (MW 4600) and LA-PEG-LA were endcapped with polymerizable methacrylates by microwave methacrylation (Lin-Gibson et al., 2004) to produce PEG dimethacrylate (PEGDM) macromolecular monomers, which are essentially non-degrading on the time scale of the experiments, and degradable LA-PEG-LA dimethacrylate (PEG-LA-DM) macromolecular monomers or macromers. Primary bovine chondrocytes isolated from the femoral-patellar groove of a 1–3 week old calf (Research 87, Marlborough, MA) (Nicodemus, 2011) were used as the model cell type. Hydrogels with different initial crosslink densities were formed through photopolymerization (365 nm, 10 min) of PEGDM and/or PEG-LA-DM macromers at varying macromer concentrations (10, 15, or 20% w/w) with a photoinitiator (Irgacure 2959, 0.05% w/w) in chondrocyte culture medium. For cell encapsulations, chondrocytes were suspended in macromer solution at 50 million cells per mL macromer and photopolymerized. Cylindrical hydrogels (5mm height and 5 mm diameter) were cultured up to 4 weeks in a humid environment at 37 °C in 5% CO₂. The LIVE/DEAD® membrane integrity assay was used to qualitatively assess cell viability within hydrogel constructs. Images were acquired using a confocal laser scanning microscope (CLSM, Zeiss LSM 510, Thornwood, NY).

2.2 Overall modeling strategy of the macroscopic tissue evolution

Multiscale computational modeling was employed to understand key microscopic processes driving tissue growth in terms of hydrogel structure, degradation and cell density. At the tissue level, these processes may be entirely described by continuous field equations in terms of hydrogel displacement u, solvent pressure p and concentration of c^p ECM particles (e.g., glycoproteins or proteins), all functions of location X and time t. To reduce the complexity of the problem, a homogeneous cell distribution was considered such that the analysis of the entire tissue could be summarized by a model volume consisting of a single spherical chondrocyte of radius R_c embedded in a spherical hydrogel domain with radius R_g. Overall cell volume fraction, f_c, (Fig. 2) can then be described through the relation:

$$R_c/R_g={(f_c)}^{1/3}$$ (1)

Figure 2.

From real engineered tissues to an idealized mathematical model. Left picture shows cell nuclei (blue) and collagen (green). Scale bar represents 50 μm.

In spherical coordinates, the fields are functions of R, θ and ϕ. However, in this simplified system, under centro-symmetric assumption, the continuous fields only depend on the distance R from the center of the chondrocyte (in the initial, dry state). The macroscopic problem therefore consists of evaluating the evolution of the following three fields:

$$u(R,T),p(R,t),c^p(R,t)$$ (2)

These fields evolve as a result of the constant release of ECM molecules by chondrocytes from the cell membrane and changes in the osmotic swelling of the hydrogel resulting from bulk degradation. As we will see, the combination of degradation and ECM production that results in the growth and organization of the new tissue is highly dependent on the initial hydrogel structure and the design of its degradation through the number of degradable linkages.

The crosslinked polymer network of the hydrogel can be considered as a hydrated elastic solid whose mechanics highly depend on the underlying molecular structure (Peppas, 1986). To represent hydrogel degradation and tissue growth, the hydrogel was considered as a mixture (Vernerey, 2011; Vernerey, Foucard and Farsad, 2011; Vernerey and Farsad, 2011a) of three different phases that consist of the solid (or polymer) phase, the fluid (or solvent) phase, and the unbound ECM molecules (proteoglycans, collagens) phase. Consistent with mixture theory, each phase (denoted by α = s, f, p, respectively) is described with its volume fraction φ^α such that

$${\phi }^s+{\phi }^f+{\phi }^p=1\text{and}{\phi }^p\ll 1$$ (3)

This equation implies that each phase is saturated within the mixture. It is also reasonable to assume that each phase is incompresssible at the microscopic level due to the relatively low physiological pressure encountered in vivo. In other words, the true mass density ρ^αR of various phases remains constant during the growth process. Growth can however be measured by the change in effective mass density representing the mass of each phase per unit volume of mixture through the relation:

$${\rho }^{\alpha }(R)={\phi }^{\alpha }(R){\rho }^{\alpha R}(R)$$ (4)

Deformation and swelling

A particular feature of hydrogels, and soft tissue in general, is that they commonly undergo very large deformations (changes in volume can reach more than 1000% during swelling). Such deformable materials are usually described within finite deformation elasticity. In this context, the location x of a material point on the crosslinked polymer is related to its original position X before deformation through the deformation gradient tensor F:

$$\mathbf{F}=\frac{\mathbf{dx}}{\mathbf{dX}}=\left(\begin{array}{ccc}\partial r/\partial R& 0& 0\\ 0& r/R& 0\\ 0& 0& r/R\end{array}\right)\text{in}\text{centro}-\text{symmetric}\text{conditions}$$ (5)

where the current radius r is mapped to the initial radius R (before swelling). The determinant of F measures the change of volume between initial (dry polymer before swelling) and final configuration as follows:

$$dV={\mathit{JdV}}_0\text{where}J=det(\mathbf{F})=(\partial r/\partial R){(r/R)}^2$$ (6)

The value of J at equilibrium is denoted as the volumetric equilibrium swelling ratio Q, which can be determined from experiments. The volume fraction ${\phi }_{eq}^s$ of the polymer at swelling equilibrium is related to Q:

$${\phi }_{eq}^s=1/Q$$ (7)

where the volume fraction for the dry polymer is one.

Mechanical equilibrium

The hydrogel is subjected to a variety of mechanical forces which through hydrogel deformation, have strong effects on gel permeability and degradation as well as transport and deposition of unbound ECM molecules. These forces are accounted for through the balance of momentum of the hydrogel in the form (Li, 2004):

$${\nabla }_{\mathbf{X}}·({\mathbf{P}}^{\mathit{eff}}-J\pi {\mathbf{F}}^{-T})=0$$ (8)

where P^eff is the nominal effective stress tensor i.e. the stress acting on the crosslinked polymer only, and π is the interstitial fluid pressure. The notation ∇_X refers to the spatial differential operator with respect to the initial coordinates X. This equation clearly shows the effect of fluid pressure on the stress experienced by the polymer network.

3. The evolving structure and properties of degrading hydrogels

The solid phase of the gel (described as a crosslinked polymer) is mechanically represented as a rubber-like material, where polymethacrylate chains are linked together by PEG or PEG-LA crosslinks and swollen in an aqueous solvent. The mathematical model to describe its deformation and swelling is introduced below.

3.1 Physical model of the hydrogel

Free energy

The physical properties of a crosslinked polymer swollen with solvent (neglecting contributions from ECM molecules) are described by Flory-Rehner and rubber elasticity theories (Flory, 1953; Treloar, 1975). These theories are based on the description of the free energy of a swollen gel (Cowie, 2008) as the sum of contributions from elasticity/distortion ΔG^el and solvent mixing ΔG^mix.

$$\mathrm{\Delta }G=\mathrm{\Delta }{G}^{el}+\mathrm{\Delta }{G}^{\mathit{mix}}$$ (9)

where ΔG^mix is described by Flory-Huggins theory (Cowie, 2008) for two phases:

$$\mathrm{\Delta }{G}^{\mathit{mix}}=kT\left[N_{f}ln{\phi }^f+N_{s}ln{\phi }^s+N_{f}ln{\phi }^s\chi \right]$$ (10)

where N is the number of molecules and χ is the Flory-Huggins parameter (polymer-solvent interaction). The latter describes the thermodynamic interactions between solvent and polymer molecules where a higher positive value of χ denotes a repulsive interaction between the solvent and polymer molecules. Because the polymer network is one molecule, we assume a negligible contribution from term 2 (N_sln φ^s) in Eq. (10). The elastic contribution to the free energy ΔG is derived from Treloar (Treloar, 1975), neglecting the phantom network theory (Bell & Peppas, 1995) for simplicity. Denoting the quantities λ₁, λ₂ and λ₃ as the principal stretches in the principal directions of the right stretch tensor, the elastic free energy reads:

$$\mathrm{\Delta }{G}^{el}=\frac{1}{2}\left({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2-3-2ln({\lambda }_1{\lambda }_2{\lambda }_3)\right)\text{where}G=\rho \overline{\nu }{\rho }_{X}RT$$ (11)

where G is denoted as the shear modulus (Bell & Peppas, 1995; Treloar, 1975) and is a function of the specific volume ν̄ (inverse of density) of the solvent and the crosslink density ρ_X. We also note that that for isochoric deformation λ₁λ₂λ₃ = 1, ΔG^el becomes the strain density energy of a Neo-Hookean material. When the polymer interacts with water, however, significant volume change can be generated by osmotic pressure and the product λ₁λ₂λ₃ may become large enough to dominate the gel response.

Effective stress and osmotic pressure

The effective stress P^eff is thermodynamically defined as the energy conjugate of the deformation gradient F. It can therefore be defined in terms of the elastic free energy as:

$${\mathbf{P}}^{\mathit{eff}}=\partial \mathrm{\Delta }{G}^{el}/\partial \mathbf{F}$$ (12)

The osmotic pressure, based on the same idea as a Cauchy and Piola-Kirchhoff stress can be defined as

$$\mathbf{\Pi }=\partial \mathrm{\Delta }{G}^{\mathit{mix}}/\partial \mathbf{F}\text{where}\mathbf{\Pi }=J\pi {\mathbf{F}}^{-T}$$ (13)

where π is defined as a “Cauchy osmotic pressure” and Π is its associated “Piola-Kirchhoff osmotic pressure”. This equation, together with the mechanic equilibrium is defined as

$${\mathbf{P}}^{\mathit{eff}}-J\pi {\mathbf{F}}^{-T}=\partial \mathrm{\Delta }{G}^{el}/\partial \mathbf{F}-\partial \mathrm{\Delta }{G}^{\mathit{mix}}/\partial \mathbf{F}=0$$ (14)

The only unknown that the mechanic equilibrium equation contains is the Flory-Huggins parameter χ, which can be solved for by taking the derivatives of the elastic and mixing free energies with respect to the deformation gradient. Thus, Eq. (10), (11) and (14) gives a Flory-Huggins parameter χ = 0.464.

This relation enables the determination of osmotic pressure from free swelling experiments (described next). In particular, Eq. (14) can be used to relate the swelling ratio $Q=1/{\phi }_{eq}^s$ to crosslink density ρ_x at constant osmotic pressure as depicted in Fig. 4.

Figure 4.

(a) shows the nonlinear compressive/elastic modulus through the stress-strain curves for different crosslink densities. Experimental results and the model are compared. (b) shows the equilibrium swelling ratio as a function of crosslinking density for stable PEG hydrogels formed from PEGDM macromers obtained both experimentally and determined by the model. Error bars indicate standard deviation (n = 3).

3.2 Hydrolytic degradation

During degradation, the macroscopic properties of the hydrogel evolve dynamically. As a first approach, hydrolytic degradation is described by pseudo first-order kinetics (Metters, 2000), where crosslink density decreases with degradation time:

$$\frac{d{\rho }_x}{dt}=-k{\rho }_x$$ (15)

where k is the pseudo first order rate constant for hydrolytic degradation. Thus as time evolves, crosslinks degrade randomly within the gel, which leads to decreases in the shear elastic modulus G(Eq. (11)) but increases in swelling and mesh size, where the latter improves transport of ECM molecules through the gel. Solving Eq. (15) yields the evolution of crosslink density in time as:

$${\rho }_x(t)={\rho }_{x0}exp(-kt)$$ (16)

where ρ_x0 is the initial crosslink density of the swollen hydrogel. It is important to note that this model represents a simplified model for degradation kinetics. As such, it does not capture more subtle elements of degradation such as the phenomenon of reverse gelation. Reverse gelation refers to the point when there are fewer than two crosslinks per kinetic chain resulting in highly branched soluble polymer chains (Flory, 1953). The crosslink density at which reverse gelation occurs will depend largely on the length of the kinetic chain (Metters, 2000). Consequently for very short kinetic chains, reverse gelation can occur after only a few crosslinks have been broken. While not explicitly incorporated into this equation, the importance of this physical point should not be underestimated as it has the potential to dramatically influence how well macroscopic tissue can form prior to reverse gelation. It was shown that reverse gelation typically occurs when there is a 60%–80% mass loss for similar PEG-LA hydrogels (Metters, 2000).

3.3 Hydrogel processing and measurement of overall properties

In the above model, it can be seen that gel behavior is mainly described in terms of the structural quantity crosslink density ρ_x, which dictates shear modulus G, and the degradation behavior. Initial crosslinking density can be controlled experimentally by varying macromer length or the weight percent of PEG macromer in solution. While the rate of hydrolysis of the ester bond will not depend on hydrogel structure, the overall effective degradation rate can be altered by initial crosslink density and the number of ester bonds within the crosslink. Two macroscopic experiments were performed to indirectly measure these quantities. For stable hydrogels formed from PEGDM macromers, the equilibrium mass swelling ratio was measured and converted to volumetric swelling ratio Q, and direct unconfined compressive tests were performed. In addition bimodal degrading hydrogels were formed such that a fraction of the crosslinks would degrade (PEG-LA crosslinks), while the remaining crosslinks remain stable (PEG crosslinks) preventing the gel from undergoing rapid degradation and dissolution and loss of mechanical integrity (Bryant, 2004; Skaalure, 2012). For the bimodal degrading hydrogels, equilibrium volumetric swelling ratio Q was determined as a function of time. For the first experiment, hydrogels with varying crosslink density were made with 10, 15, and 20% PEGDM by weight, yielding 0.11, 0.22, and 0.38 M crosslinking densities, respectively, from Eq. (18). Swelling ratio and modulus were determined as a function of crosslink density and compared to theoretical prediction as shown in Fig. 4.

Crosslinking density

The equilibrium volumetric swelling ratio Q can be determined experimentally by measuring the equilibrium swollen mass M_s of hydrogels, and then lyophilizing to obtain the dry polymer mass, M_d (Peppas, 1986).

$$Q=J_{eq}=\frac{V}{V_0}=1+\frac{{\rho }_{\mathit{pegdm}}}{{\rho }_{\mathit{solv}}}\left(\frac{M_s}{M_d}-1\right)$$ (17)

In this relationship, ρ_pegdm and ρ_solv are the density of the PEGDM macromer and the solvent, and J_eq is the equilibrium jacobian, equivalent to Q. Therefore φ_eq^s is equal to the inverse of the swelling ratioQ.

At swelling equilibrium, considering the chemical equilibrium, we can assume that the change in chemical potential is zero, and we apply the definition that the partial derivative of ΔG (Eq. (9)) with respect to N_s is equal to the change in chemical potential. Applying this definition, simplifying and rearranging leads to the following definition for crosslinking density ρ_x (number of crosslinks per volume) of a polymer scaffold (see (Flory, 1953) chapter XIII 3 for more details). Neglecting the phantom network theory (no distinction between chain and chain-ends), one can show:

$${\rho }_x=\frac{-1}{V_1}\left(\frac{ln(1-{{\phi }_{eq}}^s)+{{\phi }_{eq}}^s+\chi {({{\phi }_{eq}}^s)}^2}{{({{\phi }_{eq}}^s)}^{1/3}-\frac{{{\phi }_{eq}}^s}{2}}\right)$$ (18)

where V₁ is the molar volume of the solvent. From this equation, experimental measurements of the swelling ratio Q are used to estimate hydrogel crosslinking density.

Gel Elastic modulus

To ensure consistency between model and experiments regarding the change of gel stiffness with crosslink density, the stress-strain response of the hydrogel in uniaxial, unconfined compression was assessed through two different routes. On the experimental side, unconfined cylindrical hydrogels were compressed to 15% strain at a constant rate of 0.5 mm per minute (MTS Synergie 100, 10 N) and the resulting stress was assessed by dividing the compressive force by the initial specimen cross-sectional area (nominal stress). On the theoretical side, these conditions were reproduced by evaluating the longitudinal stress and strains (subjected to zero transversal stress) of a hydrogel cylinder with varying crosslink densities using Eq. (8) and (11). Comparing numerical and experimental results provided in Fig. 4 (a) shows that the present model captures the key trends in gel behavior with a minimal number of material parameters. A more sophisticated model of the hydrogel mechanics may be able to provide a closer estimation of the results.

Rate of degradation

The measurement of degradation rate can be inferred by measuring the evolution of swelling ratio exhibited by a gel over time. Indeed, referring to the right side of (11), it can be seen that crosslink degradation is directly associated with a weakening of,the gel’s elastic modulus, which under the action of osmotic pressure, translates into swelling (or a decrease of the polymer volume fraction ${\phi }_{eq}^s$). This informs us about the evolution of the equilibrium volumetric swelling ratio $Q=1/{\phi }_{eq}^s$ over time. Using this method, it was possible to obtain a good match between the theoretical model and experimental measurements for a pseudo first-order degradation rate constant k equal to 0.11/day (Fig. 5). Swelling shows a general trend of an exponential increase with time (Mason, 2001), which was verified in a bimodally degradable system where 15 weight % macromer was used, where 95% of the macromer consisted of degradable PEG-LA-DM and 5% was non-degradable PEGDM.

Figure 5.

Swelling ratio Q over time in a bimodally degradable hydrogel consisting of a 95:5 weight ratio of PEG-LA-DM and PEGDM

4. Production and transport of ECM molecules within an evolving hydrogel structure

In vivo, chondrocytes produce all of the components of cartilage, which include the collagens and proteoglycans described in Table 1. Tissue deposition is typified initially by the formation of a protective pericellular matrix found immediately surrounding the cell, characterized by a meshwork of collagen VI as well as collagen II and aggrecan (Nicodemus, 2010). Macroscopic tissue deposition can only occur when matrix is secreted and retained throughout the surrounding extracellular matrix. When encapsulated in a hydrogel network, chondrocytes similarly secrete extracellular matrix molecules, which, in time, begin to recapitulate the structure and organization of native cartilage. However, in this case, the evolving nature of the scaffold structure strongly influences the way matrix molecules are transported and deposited to form a new tissue.

Table 1.

Composition of native cartilage.

	% by wet weight	Component	Size scale	Structure	Category
Collagens	20	Collagen II	400 nm	Linear fibers	Largemolecules
		Collagen VI	100 nm	Fibrillar
Aggrecan, proteoglycans, and their building blocks	5–7	Aggrecan aggregates	100 MDa	Highly branched
		Aggrecan	1–4 MDa	Branched
		Hyaluronan	MDa	Linear
		Link protein	45 kDa	Globular	Small molecules
		Glycosaminoglycans	5–30 kDa	Linear
		Decorin	40 kDa	Globular
		Biglycan	40 kDa	Globular
Other	70–75	Water	≪ ξ	-
		Salts	≪ ξ	-

Shaded part denotes the large matrix molecules. The symbol 3 represents the gel mesh size.

4.1. Classification of ECM molecules and experimental observation

At the molecular scale, the hydrogel is composed of a crosslinked network structure with a characteristic mesh size (varying with crosslinking density and degradation) that can permit or restrict diffusion of soluble molecules depending on their size relative to the average mesh size. As a first step, the proposed model treats matrix molecules as either ‘large’ or ‘small’ to demonstrate restricted vs. free diffusion through the hydrogel mesh. Future versions of the model will attempt to account for the wide variety of matrix molecules secreted by chondrocytes. For reference, a summary of the main ECM molecules that make up articular cartilage is presented in Table 1. Relative composition of components is expressed as a percentage of wet weight (Hardingham, 2006), and the size scale and structure of collagens (von der Mark, 2006) and proteoglycans (Hardingham, 2006) are presented.

For cell-laden photopolymerized hydrogels cultured for several weeks, deposition of matrix molecules can be characterized experimentally in a variety of ways. For this study, we present qualitative methods which demonstrate spatial deposition of specific matrix molecules via immunohistochemical techniques. Immunohistochemical staining for chondroitin sulfate was applied to dehydrated, paraffin-embedded 10 micron-thick sections of hydrogels as previously described (Nicodemus, 2011; Roberts, 2011). Briefly, sections were mounted onto slides and rehydrated, treated with chondroitinase ABC, and probed with a primary antibody against chondroitin-6-sulfate (Chemicon, Billerica, MA) followed by an AlexaFluor 546-conjugated secondary antibody and counterstained with DAPI. Images were acquired with a confocal laser scanning microscope at 40x magnification (Fig. 8 and 9).

Figure 8.

Figures (a), (b) and (c) show an experimental result and the model results for different crosslink densities of a stable hydrogel. Regarding the experimental pictures, chondroitin sulfate elaboration (red) by chondrocytes encapsulated within PEGDM hydrogels and cultured for 25 days in vitro with varied crosslinking density. Cell nuclei are stained blue. Scale bars indicate 50 microns. In the three-dimensional plots, the stress P_rr (kPa), strain E_rr, mesh size ξ (nm) and concentration c^p (mmol/mL) can be observed.

Figure 9.

(a) shows the results for a non-degradable stable hydrogel, while (b) shows it for a degradable hydrogel. First image is the experiment showing chondroitin sulfate elaboration (red) by chondrocytes at day 28 encapsulated within 10% w/w non-degradable PEGDM and degradable PEG-LA-DM hydrogels. Cell nuclei are stained blue. Scale bars indicate 50 microns. In the three-dimensional plots, the stress E_rr (kPa), strain P_rr, mesh size c^p (nm) and concentration c^p (mmol/mL) can be observed. Note that due to differences in image processing between experiments, chondroitin sulfate staining is of lower intensity than shown in Fig. (8).

4.2. Modeling molecular transport in deforming hydrogels

The transport of cell-secreted extracellular matrix molecules is a critical component of tissue growth, and tissue engineering strategies should aim to facilitate such processes. In the case of cells encapsulated in gels, controlled degradation of the gel crosslinks is required to achieve homogeneous distribution of cell-secreted matrix. Particularly, the rate and timing of this degradation are important factors. If degradation occurs too quickly, then major defects may develop that can have negative consequences on the macroscopic geometry and mechanical properties. If degradation occurs too slowly, the gel will prevent timely distribution of ECM molecules and tissue regeneration, entrapping the matrix molecules between cells and the gel, yielding only pericellular matrix tissue deposition. The ability to predict appropriate hydrogel degradation profiles coupled with cell-secreted matrix transport and tissue deposition requires a mathematical model that is able to capture the coupled physics between molecular transport, gel deformation and degradation. The theory of mixture provides an excellent framework in this context.

Mass transport

From a modeling point of view, transport of water (f) and unbound extracellular matrix molecules (p) can be described by their volumetric flux, taken with respect to polymer motion:

$${\mathbf{q}}^{\alpha }={\phi }^{\alpha }({\mathbf{v}}^{\alpha }-{\mathbf{v}}^s)$$ (19)

where α = f, p. Note that this definition of flux is consistent with an Eulerian approach, i.e., the flux is defined as the volume of constituent α per unit of time, passing through a unit surface S in the deformed configuration. When large deformations are considered, however, it is convenient to define the Lagrangian flux

$${\mathbf{Q}}^{\alpha }={J\mathbf{F}}^{-1}{\mathbf{q}}^a$$ (20)

as the amount of constituent α passing through a unit area in the reference gel configuration (defined in the dry state, i.e. initial configuration). Eq. (20) therefore shows the mapping of the flux from the current configuration to the dry polymer configuration. Using the assumption of incompressibility for all constituents, it is possible to derive the equation of mass balance in the form:

$$J\frac{D{\phi }^{\alpha }}{Dt}+{\nabla }_{\mathbf{X}}·{\mathbf{Q}}^{\alpha }=-{\phi }^{\alpha }\frac{DJ}{Dt}\text{where}\alpha =f,p$$ (21)

Here, the first equation quantifies the balance of mass of the fluid phase, while the second equation describes the balance of mass of the ECM molecules. Eq. (21) implies that the volumetric flux of the fluid phase (mapped back to the dry configuration) is directly linked to the swelling (or deswelling) J of the tissue.

Constitutive equation

An important aspect of the present study is the introduction of realistic constitutive relations governing the transport of ECM molecules and water through the gel and their relation to gel deformation and degradation. Assuming the effect of ECM molecules to be negligible on water flux, fluid flow can be expressed in terms of the pressure gradient ∇_x p as stated by Darcy’s law:

$${\mathbf{Q}}^f=-\kappa {J\mathbf{F}}^{-1}\left({\nabla }_{X}p\right),\text{where}\kappa =\frac{{\xi }^2(1-{\phi }^s)}{8{\overline{\mu }}_f\delta }$$ (22)

where κ is the isotropic gel permeability, δ is the tortuosity of the gel structure and μ̄_f is the fluid viscosity (see Table 2). We note that the gel permeability to water is a function of polymer mesh size ξ (Holmes & Mow, 1990), which is itself a function of gel crosslinking and can be related to swelling. This dependency was introduced by Bell and Peppas (Bell & Peppas, 1995) as follows:

$$\xi ={\xi }_0{({\phi }^s)}^{-1/3},\text{where}{\xi }_0={C_n}^{1/2}{n}^{1/2}l$$ (23)

where ξ₀ is the mesh size of the dry polymer, l is the average bond length, C_n is the polymer characteristic ratio, and n is the number of bonds between crosslinks, which is determined from the molecular weight between crosslinks and molecular weight of the polymer repeat unit (see Table 2). It is clear from Eq. (22) and (23) that gel swelling (through hydrolytic degradation for instance), by decreasing the value of φ^s, ultimately increases gel permeability and facilitates transport of water through the hydrogel. But also, the number of bonds between crosslinks n changes with changes in crosslink density (Flory, 1953), which means that the mesh size evolves with degradation.

Table 2.

Inputs used in the model.

Inputs	Value	Unit	Reference
V1	0.018	L/mol	Commonly known
ν̄	1	mL/g	Commonly known
ρpegdm	1.07	g/mL	Estimate
ρsolv	1	g/mL	Commonly known
Cn	4.0	-	(Merrill, 1993)
l	1.47	A	Commonly known
T	310	K	Physiologicaltemperature
δ	2	-	(Kestin, 1981)
μ̄f	0.65E-3	N.s/m2	(Thorne, 2005)
Mp	20	kDa	(Hardingham, 2006)

Because of their relatively small volume fraction, driving forces affecting the motion of unbound ECM molecules are of three types: an advection term (molecules tend to follow the solvent in its flow), a diffusion term within the solvent and thirdly, a term that describes resisting frictional forces from the hydrogel. To separate each contribution, we take the following approach. First, it is convenient to eliminate the friction force from the gel by considering the motion of ECM molecules in a pure solvent. In this case, the flux ${\mathbf{q}}_{\infty }^p$ can be readily decomposed into a component that follows the solvent flux given by Eq. (21) and a component representing the relative diffusion of the molecules in the solvent using Fick’s law. This leads to (Vernerey, 2011):

$${\mathbf{q}}_{\infty }^p=\left(D_{\infty }{\nabla }_x{c}^p-\frac{M^p}{{\rho }^{pR}}\kappa {\nabla }_{x}p\right)\text{where}{D}_{\infty }=\frac{k_{B}T}{6\pi {\overline{\mu }}_f{r}_s}$$ (24)

Here, M^p is the average molar mass of ECM molecules and D_∞ is the free solution diffusivity defined by the Stokes-Einstein relation (Rubinstein, 2003), r_s is the radius of gyration of small matrix molecules and k_B is the Boltzmann constant. The effect of the gel resistance on molecule transport can then be captured by realizing that when the ratio of radius of gyration r_s of ECM molecules is significantly smaller than the polymer mesh size (r_s/ξ ≪ 1), gel resistance is negligible and the ECM molecule flux q^p becomes ${\mathbf{q}}_{\infty }^p$. However, as r_s increases, we assume that gel resistance results in a decrease of q^p that is expressed in the form:

$${\mathbf{q}}^p={\mathbf{q}}_{\infty }^{p}g(\xi )\text{where}g(\xi )=\frac{1}{2}\left[1+\text{erf}\left(\frac{2}{\mathrm{\Delta }}(\xi -\delta -{\text{r}}_s)\right)\right]$$ (25)

where Δ is a parameter of the Gauss error function erf.

The function g used in this study attempts to capture the nonlinear relationship between ECM transport processes and the relative sizes of ECM molecules and hydrogel mesh. As shown in Fig. 6, this function clearly implies that (1) as ECM molecules become larger than the hydrogel mesh size, ECM transport is fully hindered (g → 0) and (2) as the hydrogel mesh size becomes significantly larger than ECM molecules size, gel resistance becomes negligible (g → 1). This expression was originally motivated by the work of Lustig and Peppas in (Lustig & Peppas, 1988) in their method to describe the change in diffusivity with the ratio r/ξ.

Figure 6.

Gauss error function used in the model to describe the constitutive relations. Δ is taken as 4r_s in the above figure.

Release of ECM molecules

As mentioned earlier (Table 1), chondrocytes produce different types of ECM molecules, which for our purposes may be distinguished by their size. “Small” molecules have a radius of gyration smaller than the initial hydrogel mesh size ξ and are therefore able to freely diffuse throughout the gel according to Eq. (25). “Large” molecules are distinguished by a radius that is larger than ξ and because they are unable to diffuse in the gel, they tend to accumulate between the cell and the scaffold, causing the gel to be pushed away from the cell. As depicted in Fig. 7, this behavior is modeled by prescribing appropriate “flux” boundary conditions at the cell membrane in the following fashion. We first introduce the normal ECM molecule flux release from the cell as ${\mathbf{Q}}_{\mathit{cell}}^p$ such that the release of large and small molecules can be split with the ratio f as:

$${\mathbf{Q}}_{\mathit{small}}^p={f\mathbf{Q}}^p\text{and}{\mathbf{Q}}_{\mathit{l}arge}^p=(1-f){\mathbf{Q}}^p$$ (26)

Figure 7.

Diffusivity of proteins through the hydrogel. How the size of a protein impacts the boundary conditions.

We note here that the value of f is entirely dependent on the cell metabolism and is not considered here as a tunable parameter. Considering the mass balance of the volume between the cell and the hydrogel, denoted by the pericellular matrix in Fig. 7, it can be shown that the above considerations translate into a two-fold boundary condition at the gel boundary R = R_c:

$$\begin{array}{l}\stackrel{.}{r}(R_c)=(1-f){\mathbf{Q}}_{\mathit{cell}}^p\\ c_{\mathit{gel}}^p={fc}_{\mathit{cell}}^p\end{array}$$ (27)

where a superimposed dot refers to a time derivative. Matrix molecule release is regulated by the cell itself, which is able to detect the surrounding ECM. Then, the small matrix molecule release is represented by a Dirichlet boundary condition. From these expressions, it is clear that if f = 1 all molecules released from chondrocytes get transported into the gel ( $c^p(R_c)=c_{\mathit{cell}}^p$). If f = 0, however, ECM molecule release translates into a deformation of the gel at the cell/gel boundary ( $\stackrel{.}{r}(R_c)={\mathbf{Q}}_{\mathit{cell}}^p$) and no diffusion of unbound ECM molecules into the hydrogel is observed (c^p(R_c) = 0). A more realistic situation is actually in an intermediate range with f ~ 0.8, which is a reasonable estimate, such that both gel deformation and unbound ECM molecule diffusion occur simultaneously.

5. Results and discussion

This section presents a combined modeling and experimental approach to investigate the dynamics of tissue transport and deposition in various hydrogel environments. Briefly, the computational model consists of numerically solving the balance of mass and momentum equations presented in Eq. (21) and (8), respectively, together with the constitutive equation describing the hydrogel. These nonlinear equations were discretized on a one-dimensional finite-element mesh using centro-symmetric assumptions and the resulting transient analysis was solved for three interacting fields (consisting of solid displacement u, fluid pressure π and ECM molecule concentration c^p) with an implicit Newton-Raphson scheme as described in (Farsad, 2012). In the experimental component of our study, tissue production is measured by the deposition of chondroitin sulfate, an abundant linear glycosaminoglycan with an average molecular weight of 20 kDa (Hardingham, 2006) and is most closely associated with proteoglycans, specifically aggrecan. This molecule is advantageous from a modeling perspective because it can exist as part of a smaller proteoglycan (1–4 MDa, Table 1), or as a part of a larger aggrecan aggregate (100 MDa, Table 1), which will exhibit more restricted diffusion. Chondroitin sulfate thus provides a good model molecule to demonstrate the deposition of an extracellular matrix composed of molecules of different size scales.

Model parameters were chosen in agreement with experimental observation, i.e., the initial volume fraction of cells was taken as f_cell = 0.01 and the cell radius was set to R_c = 10 μm. The true density of the polymer was fixed at ρ_pegdm = 1.07 g/cm³ and the true density of the matrix molecules was assumed to have the density of water i.e. ρ^pR = 1g/cm³. Other model inputs are described in Table 2.

5.1. Role of initial hydrogel mesh size on ECM distribution

We first aim to assess the effect of crosslink density on the diffusion of unbound ECM molecules throughout the gel in the absence of degradation. For this, gels were made with poly(ethylene glycol) dimethacrylate (PEGDM) with 10, 15, and 20% by weight compositions, yielding 0.11, 0.22, and 0.38 M crosslinking densities based on Eq (18).

The concentration of chondroitin sulfate throughout the gel was evaluated by immunohistochemical staining 25 days after encapsulation. As shown in Fig. 8, results show that higher crosslink densities (i.e., 0.22 and 0.38 M) reduce unbound ECM molecule diffusion and consequently lead to localized elaboration of ECM surrounding the chondrocytes within the hydrogel. To better understand these processes, the presented mixture model was used to assess the variation of various quantities (hydrogel stress, strain, unbound ECM molecule concentration and hydrogel mesh size) for the three crosslink densities considered in experiments. Model results are generally in agreement with experimental observations with respect to the spatial deposition of chondroitin sulfate (Fig. 8). Most notably, the numerical results capture the presence of matrix molecules that have diffused far from the cell into the extracellular space of the hydrogel for the low crosslink gel (0.11 M), where there is a distinct lack of these matrix molecules in the extracellular space of the higher crosslink gels (0.22 and 0.38 M). They also illustrate a few important mechanisms of ECM deposition in hydrogels.

First, the change in chondroitin sulfate deposition for different crosslink densities can be explained by the fact that ECM diffusivity is an increasing function of hydrogel mesh size (Eq. (25)), which is dependent on crosslink density. Indeed, lower crosslink densities are associated with a higher swelling ratio (Fig. 4), a lower polymer volume fraction and thus, a larger mesh size according to Eq. (23). This can be easily seen in the contour plots depicting mesh size distributions for the three considered crosslink densities in Fig. 8. This higher diffusivity enables ECM molecules to diffuse more homogeneously throughout the gel as seen in the concentration as a function of radial position plots in Fig. 8.

Second, the model clearly indicates the appearance of a pericellular matrix around the cell, consisting of large matrix molecules (MDa size scale, see Table 1) that accumulate between the chondrocyte and the surrounding gel due to their restricted diffusion. The growing pericellular matrix around the cell may result in compressive deformation of the gel near the cells, which is captured in the simulation results of Fig. 8. We note that this mechanism tends to decrease the mesh size immediately surrounding chondrocytes and may potentially hinder ECM diffusion in a local region around the cell.

5.2. Role of hydrolytic degradation on ECM transport

As observed in the previous section, homogeneous tissue deposition is difficult to achieve with non-degradable hydrogel systems. A solution to this problem therefore consists of introducing gels with crosslinks that can be cleaved over time and thus increase ECM molecule diffusivity over time. While this greatly improves ECM molecule transport, hydrogel degradation ultimately results in a weakening of the gel properties and if reverse gelation occurs before substantial tissue can be elaborated, complete loss of cells will occur. To investigate the effects of degradation, we compared the extent of ECM deposition after 28 days in (a) a non-degradable and (b) a degradable hydrogel, which both initially possess a crosslink density of 0.11M (Fig. 9). The degradable gel was characterized by the degradation kinetics discussed in section 3. Results presented in Fig. 9 show a dramatic increase of ECM molecule deposition and more homogeneous matrix deposition for the degradable system. Model predictions exhibit a similar trend and emphasize the underlying mechanisms of such behavior (Fig. 10a). As the hydrogel degrades, the radial stress decreases and swelling (or radial strain) increases under the effect of the osmotic pressure. These changes results in a significant increase in mesh size and, consequently, the enhancement of the diffusivity of ECM molecules (Fig. 11). In comparison, non-degradable hydrogels do not see any changes in swelling and diffusivity of ECM molecules. ECM molecule deposition in this system is therefore highly restricted.

Figure 10.

(a) shows the effect of swelling on the mesh size. And (b) shows the effect of the degradation rate k on the distribution of matrix molecules in the scaffold at day 25.

Figure 11.

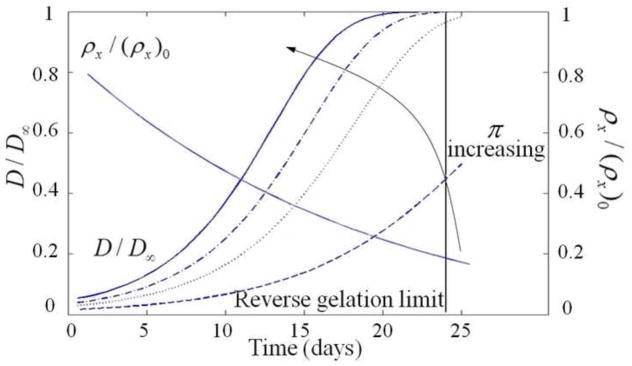
shows the different osmotic pressures (respectively 20, 200, 300, and 400 kPa) applied on the model to see the evolution of the diffusivity.

As can be seen in Fig. 10b, the rate of degradation also has a large influence on the diffusion of matrix molecules within the hydrogel. In the process of designing a degradable hydrogel, the hydrolytic pseudo first order rate constant (Eq. (15) and (16)) may be optimized to enable maximum ECM molecule deposition before the hydrogel scaffold reaches the reverse gelation point. From Eq. (18), it has been shown that for highly swollen gels (Q > 10) an estimate of the swelling can be found as Q ≃ ρ_x^−3/5 (Metters, 2001). Then, we can estimate the reverse gelation point from swelling properties just before reverse gelation occurs by ρ_x/ρ_x0(Q/Q₀)^−5/3. Using the values of Fig. 5 this happens when ρ_x/ρ_x0 becomes smaller than 20% (Fig. 10a and 11). In Fig. 9, macroscopic tissue deposition was observed at day 28, indicating that the evolution of ECM was able to maintain some level of three dimensional integrity after the hydrogel scaffold was fully degraded. However, a previous assessment of the overall mechanics of similar cell-laden hydrogels showed a significant drop in compressive modulus from the initial cell-laden hydrogel to the engineered tissue as a result of hydrogel degradation (Roberts, 2011). These findings indicate that additional optimizations are needed to better match hydrogel degradation with tissue elaboration. With this mathematical model, we will now be able to better predict optimal degradation parameters that support macroscopic tissue evolution in degradable hydrogels without losing mechanical integrity.

5.3. Role of osmotic pressure in diffusion of molecules and creation of tissue

Osmotic pressure is an important player in tissue transport as it is responsible for gel swelling and consequently controls hydrogel mesh size (and thus ECM molecule diffusivity). To investigate this aspect, we used the theoretical model to predict the effect of changing osmotic pressure on the evolution of ECM diffusivity through a degradable gel. Fig. 11 shows the obtained trends for four different osmotic pressures (π = 20, 200, 300 and 400 kPa). As expected, we observe that an increase in osmotic pressure precipitates a change in ECM molecule diffusivity through the gel. This observation is explained as follows: as a gel degrades, its bulk modulus decreases and its mechanical resistance to osmotic pressure becomes weaker; this results in significant gel swelling during degradation. Increasing the osmotic pressure tends to reinforce this swelling effect and thus enhance ECM molecule diffusivity due to the associated rise in mesh size. This mechanism is important as it could potentially enable a more homogeneous tissue distribution before a scaffold reaches the reverse gelation point.

5.4. Concluding remarks

The presented model provides a platform for better understanding the role of hydrogel scaffold structure on cartilage tissue engineering. It evaluates both degradable and non-degradable PEG-based hydrogels, which have shown promise in promoting neocartilage deposition. The developed model captures the limitations associated with tissue deposition in non-degradable PEGDM hydrogels and confirms the necessity of adding degradable units to hydrogels in order to enable the diffusion of ECM molecules throughout the scaffold. The model also demonstrates that very large ECM molecules will not diffuse throughout the hydrogel until after the reverse gelation point, a finding supported by experimental data. As an attempt to account for the existence of various ECM molecule sizes, the model splits these molecules in two categories, thus including the diffusion mechanism and the deposition of larger molecules forming the PCM. The model can accurately predict how crosslink density impacts ECM molecule diffusion. Moreover, the model is able to simulate the concentration distribution of molecules in the hydrogel, which is otherwise difficult to predict experimentally. The model also emphasizes that osmotic pressure is a key property for promoting diffusion through the gel.

However, there are several limitations to the current modeling approach and their acknowledgment is critical for improving mathematical models in the future. With regards to modeling the solvent, hydrogels are typically swollen in cell culture medium, consisting of proteins, growth factors, and salts. As opposed to water (as considered in our model), these components may interact with secreted ECM molecules, and can potentially affect both osmotic pressure and cell response. The model, while focusing on a single cell encapsulated in a spherical gel domain, accounts for the density of cells in the hydrogel through the cell volume fraction. Future work could consist of developing a three-dimensional model, which may show adhesion and inhomogeneous cell-cell interactions. Indeed, in order to create a macroscopic tissue, there must be overlap between the tissue being produced from different cells in order to create a homogeneous tissue structure. Finally, another component, which is ultimately difficult to model, is the dynamic nature of cells and the tissues they produce. Once matrix is deposited, it is not permanent, but is subject to reorganization or degradation by secreted enzymes. This process is necessary in vivo to transport newly synthesized ECM molecules from the pericellular region to the extracellular space (Mok, 1994). Similarly, modeling the secretion of matrix molecules from cells may be improved in further studies; cells can up-or down-regulate matrix synthesis in response to external cues, yet this process is not yet fully understood, meriting future investigation. Despite these limitations, this model captures the deposition of matrix molecules in non-degradable and degradable hydrogels, which is observed experimentally. Future directions of the model include considering mechano-transduction mechanisms to describe the regulation of ECM synthesis (Foucard, 2012; Foucard and Vernerey, 2012). In addition, accurate models of the membrane deformation and permeability (Vernerey and Farsad, 2011)(Vernerey, 2012) (Vernerey, 2011) will be critical in assessing the sensitivity of cells to mechanical loading and fluid flows, which are important in cartilage homeostasis and cartilage tissue engineering.

Overall, we have demonstrated that a computational triphasic model for tissue production by cells in hydrogels with varying structures and chemistries can generate simulations consistent with experimental observation. Despite the many assumptions and simplifications utilized, a powerful model has been developed that captures essential tissue dynamics in synthetic structures. The limitations serve to motivate future experimental work as well as eventually adding layers of complexity to the model. By validating the model in simple non-degradable and hydrolytically degradable systems, more complex chemistries and additives can feasibly be incorporated into the model in the future, such as incorporating physiological mechanical environments and some form of localized cell-mediated degradation (Vernerey et al., 2011). This increasing level of sophistication could aid in the design and characterization of novel tissue engineering environments. These models can be employed to both predict and understand successful tissue engineering structures, which could lead to more rapid development of clinically applied therapies.

Figure 3.

Schematics representing an idealized network structure formed from PEGDM or PEG-LA-DM macromers by radical chain polymerization. Left, non-degrading (based on experimental timescale) PEGDM hydrogels form a stable network structure. Right, hydrolytically degradable hydrogels made of PEG-LA-DM exhibit degradation and swelling with time.