A Robust Variational Approach for Simultaneous Smoothing and Estimation of DTI

Abstract

Estimating diffusion tensors is an essential step in many applications-such as diffusion tensor image (DTI) registration, segmentation and fiber tractography. Most of the methods proposed in the literature for this task are not simultaneously statistically robust and feature preserving techniques. In this paper, we propose a novel and robust variational framework for simultaneous smoothing and estimation of diffusion tensors from diffusion MRI. Our variational principle makes use of a recently introduced total Kullback-Leibler (tKL) divergence for DTI regularization. tKL is a statistically robust dissimilarity measure for diffusion tensors, and regularization using tKL ensures the symmetric positive definiteness of tensors automatically. Further, the regularization is weighted by a non-local factor adapted from the conventional nonlocal means filters. Finally, for the data fidelity, we use the nonlinear least-squares term derived from the Stejskal-Tanner model. We present experimental results depicting the positive performance of our method in comparison to competing methods on synthetic and real data examples.

1. Introduction

Diffusion weighted magnetic resonance imaging (MRI) is a very popular imaging technique that has been widely applied (Jones, 2010) in recent times. It uses diffusion sensitizing gradients to non-invasively capture the anisotropic properties of the tissue being imaged. Diffusion tensor imaging (DTI) approximates the diffusivity function by a symmetric positive definite tensor of order two (Basser et al., 1994). DTI is an MRI modality that provides information about the movement of water molecules in a tissue. DTI describes the diffusion direction of water molecules in the brain which is associated with the direction of fiber tracts in the white matter. When this movement is hindered by membranes and macromolecules, water diffusion becomes anisotropic. Therefore, in highly structured tissues such as nerve fibers, this anisotropy can be used to characterize local structure of the tissue. Consequently, many applications are based on the estimated diffusion tensor fields, such as registration (Gur and Sochen, 2007; Jia et al., 2011; Yang et al., 2008; Yeo et al., 2009; Wang et al., 2011), segmentation (Descoteaux et al., 2008; Hasan et al., 2007; Liu et al., 2007; Goh and Vidal, 2008; Savadjiev et al., 2008; Lenglet et al., 2006; Motwani et al., 2010; Wang and Vemuri, 2005; Vemuri et al., 2011), atlas construction (Assemlal et al., 2011; Mori et al., 2008; Barmpoutis and Vemuri, 2009; Xie et al., 2010), anatomy modeling (Faugeras et al., 2004), fiber tract related applications (Mori and van Zijl, 2002; Burgela et al., 2006; Durrleman et al., 2011; Lenglet et al., 2009; Savadjiev et al., 2008; Wang et al., 2010, 2012; Zhu et al., 2011) and so on. All of these latter tasks will benefit from the estimation of smooth diffusion tensors.

Estimating the diffusion tensors (DTs) from DWI is a challenging problem, since the DWI data are invariably affected by noise during its acquisition process (Poupon et al., 2008b; Tang et al., 2009; Tristan-Vega and Aja-Fernandez, 2010). Therefore, a robust DTI estimation method which is able to perform feature preserving de-noising is desired. For most of the existing methods, the DTs are estimated using the raw diffusion weighted echo intensity image (DWI). At each voxel of the 3D image lattice, the diffusion signal intensity S is related with its diffusion tensor D ∈ SPD(3) ¹ via the Stejskal-Tanner equation (Stejskal and Tanner, 1965)

$$S=S_{0}exp(-{b\mathbf{g}}^T\mathbf{Dg}),$$ (1)

where S₀ is the signal intensity without diffusion, b is the b-value and g is the direction of the diffusion sensitizing gradient.

There are various methods (Salvador et al., 2005; Batchelor et al., 2005; Fillard et al., 2007; Hamarneh and Hradsky, 2007; Pennec et al., 2006; Niethammer et al., 2006; Tang et al., 2009; Tristan-Vega and Aja-Fernandez, 2010; Wang et al., 2004; Vemuri et al., 2001; Wang et al., 2003; Chefd’hotel et al., 2004; Tschumperle and Deriche, 2003, 2005; Mishra et al., 2006; Poupon et al., 2008b; Barmpoutis et al., 2009a; Chang et al., 2005; Mangin et al., 2002) in existing literature, to estimate D from S. A very early one is direct tensor estimation (Westin et al., 2002), which gives an explicit solution for D and S₀. Though time efficient, it is sensitive to noise because only 7 gradient directions are used to estimate D and S₀. Another method is the minimum recovery error (MRE) estimation or least squares fitting (Basser et al., 1994) which minimizes the error when recovering the DTs from the DWI. MRE is better than direct estimation because it uses more gradient directions, which increases its reliability. However, it does not smooth the DWI or the DTI, and thus it is subject to noise in the input data.

With this in mind, many denoising frameworks (Gilboa et al., 2004; Spira et al., 2007) have been proposed to improve the signal to noise ratio (SNR). Some methods perform denoising on the DWI and then estimate the DTI. Typical approaches to DWI denoising are designed according to the statistical properties of the noise. Most of these approaches assume the noise follows the Rician distribution (Bennett A. Landman, 2007; Piurica et al., 2003; Koay and Basser, 2006; Descoteaux et al., 2008), and when denoising, they use the second order moment of Rician noise (McGibney and Smith, 1993), Maximum Likelihood (ML) (Sijbers and den Dekker, 2004) and Expectation Maximization (EM) approaches (Marzetta, 1995; DeVore et al., 2000), wavelets (Nowak, 1999), anisotropic Wiener filtering (Martin-Fernndez et al., 2007), total variation schemes (McGraw et al., 2004), Markov Random Fields (Zhang et al., 2001), nonparametric neighborhood statistics techniques like non-local means (NLM) (Awate and Whitaker, 2005; Coupe et al., 2008) and unbiased NLM (Manjon et al., 2008; Wiest-Daessle et al., 2008) algorithms, Perona-Malik-like smoothing (Basu et al., 2006) or linear minimum mean square error (LMMSE) scheme (Aja-Fernandez et al., 2008).

Alternatively, some methods first estimate the diffusion tensors from the raw DWI and then perform denoising on the tensor field (Moraga et al., 2007). One representative method is using the NLM framework incorporating a Log-Euclidean metric (Fillard et al., 2005). The drawback of such two-stage processes is that the errors might be accumulated from one stage to the other.

Bearing these deficiencies in mind, researchers developed variational framework (VF) based estimation (Tschumperle and Deriche, 2003; Chefd’hotel et al., 2004; Wang et al., 2003, 2004). These approaches take into account the SPD (symmetric positive definite) constraint on the diffusion tensors. The smoothing in all these approaches involves some kind of weighted averaging over neighborhoods which define the smoothing operators resulting from the variational principles. Some of these smoothing operators are locally defined and do not capture global geometric structure present in the image. Moreover, they are not statistically robust.

To overcome the aforementioned drawbacks, we propose a novel statistically robust variational non-local approach for simultaneous smoothing and tensor estimation from the raw DWI data. This approach combines the variational framework, non-local means and a statistically robust regularizer on the tensor field. The main contributions of this approach are three-fold. First, we use a statistically robust divergence measure total Bregman divergence to regularize the smoothness measure on the tensor field. Combined with the Cholesky decomposition of the diffusion tensors, this automatically ensures the positive definiteness of the estimated diffusion tensors, which overcomes the common problem for many techniques that manually force the tensor to be positive definite or resort to accuracy of finite precision arithmetic leading to the equivalence between testing for positive definiteness and positive semidefiniteness as in (Wang et al., 2003, 2004). Second, it uses an adaptation of the NLM to find the weight for the smoothness regularization terms. This preserves the global structure of the tensor field while denoising. Finally, it achieves simultaneous denoising and DTI estimation, which is able to avoid the error propagation of a two stage approach described earlier. Besides, this method can be easily extended to higher order tensor estimation. We will explain these points at length in the rest of the paper.

The rest of the paper is organized as follows. In Section 2, we introduce our proposed method, followed by the empirical validation in Section 3. Finally we conclude in Section 4.

2. Proposed method

Our proposed integrated variational non-local approach has three components, minimizing the data fidelity error, smoothing over S₀ and the tensor field. The proposed model is given by the following equation:

$$\begin{array}{l}\underset{S_0,\mathbf{D}\in \mathbf{SPD}}{min}\mathbf{E}(S_0,\mathbf{D})\\ =(1-\alpha -\beta ){\int }_{\mathrm{\Omega }}\sum _{i=1}^n{(S_i-S_{0}exp(-{b\mathbf{g}}_i^T{\mathbf{Dg}}_i))}^{2}d\mathbf{x}\\ +\alpha {\int }_{\mathrm{\Omega }}{\int }_{\mathcal{V}(\mathbf{x})}{w}_1(\mathbf{x},\mathbf{y}){(S_0-S_0(\mathbf{y}))}^{2}d\mathbf{y}d\mathbf{x}\\ +\beta {\int }_{\mathrm{\Omega }}{\int }_{\mathcal{V}(\mathbf{x})}{w}_2(\mathbf{x},\mathbf{y})\delta (\mathbf{D},\mathbf{D}(\mathbf{y}))d\mathbf{y}d\mathbf{x},\end{array}$$ (2)

where Ω is the domain of the image, n is the number of diffusion gradients, (x) is the search window at voxel x, and δ(D, D(y)) is the total Kullback-Leibler (tKL) divergence (Vemuri et al., 2011) between tensors D and D(y) which will be explained in detail later. The first term captures the non-linear data fitting error, the second and third terms are smoothness constraints on S₀ and D. α and β are constants balancing the fitting error and the smoothness ². w₁(x, y) and w₂(x, y) are the regularization weights for S₀ and D. Since S₀ and S are linearly related, while D and S are “logarithmically” related, so we use different methods to calculate w₁(x, y) and w₂(x, y). Note, S_i, S₀ and D by default represent the values at voxel x, unless specified otherwise.

The discrete case of (2) is

$$\begin{array}{l}\underset{S_0,\mathbf{D}\in \mathbf{SPD}}{min}\mathbf{E}(S_0,\mathbf{D})\\ =(1-\alpha -\beta )\sum _{\mathbf{x}\in \mathrm{\Omega }}\sum _{i=1}^n{(S_i-S_{0}exp(-{b\mathbf{g}}_i^T{\mathbf{Dg}}_i))}^2\\ +\alpha \sum _{\mathbf{x}\in \mathrm{\Omega }}\sum _{\mathbf{y}\in \mathcal{V}(\mathbf{x})}{w}_1(\mathbf{x},\mathbf{y}){(S_0-S_0(\mathbf{y}))}^2\\ +\beta \sum _{\mathbf{x}\in \mathrm{\Omega }}\sum _{\mathbf{y}\in \mathcal{V}(\mathbf{x})}{w}_2(\mathbf{x},\mathbf{y})\delta (\mathbf{D},\mathbf{D}(\mathbf{y})),\end{array}$$ (3)

Since most of the time, DTI estimation problems are in discrete case, we will focus on the discrete case in this work.

2.1. Computation of the weights w₁(x, y) and w₂(x, y)

w₁(x, y) and w₂(x, y) are the regularization weights of the smoothness terms. If w₁(x, y) is large, it requires S₀ and S₀(y) to be similar. Similarly, if w₂(x, y) is large, it requires D and D(y) to be similar. Usually, one requires S₀’s and D’s to be respectively similar only if the corresponding diffusion signals are similar. We will compute w₁(x, y) and w₂(x, y) according to the statistical properties of the diffusion weighted signals. It has been recognized that the diffusion signal S follows the Rician distribution (Piurica et al., 2003; Koay and Basser, 2006; Descoteaux et al., 2008), i.e.

$$p(S;\overline{S},{\sigma }^2)=\frac{S}{{\sigma }^2}exp\left(-\frac{S^2+{\overline{S}}^2}{2{\sigma }^2}\right)I_0\left(\frac{S\overline{S}}{{\sigma }^2}\right),$$ (4)

where S̄ is the signal without noise, σ is the variance of the Rician noise. Since S₀ is linearly related with S and D is “logarithmically” related with S, we set the regularization weights for S₀ and D to be

$$w_1(\mathbf{x},\mathbf{y})=\frac{1}{Z_1(\mathbf{x})}exp\left(\frac{-{\left|\right|S(\mathcal{N}(\mathbf{x}))-S(\mathcal{N}(\mathbf{y}))\left|\right|}^2}{h{\sigma }^2}\right),$$ (5)

$$w_2(\mathbf{x},\mathbf{y})=\frac{1}{Z_2(\mathbf{x})}exp\left(\frac{-{\left|\right|logS(\mathcal{N}(\mathbf{x}))-logS(\mathcal{N}(\mathbf{y}))\left|\right|}^2}{h{\sigma }^2}\right),$$ (6)

where Z₁ and Z₂ are normalizers, h is the filtering parameter (Coupe et al., 2006), and σ is the standard variation of the noise, which is estimated using the first mode of the background (Aja-Fernandez et al., 2009; Tristan-Vega and Aja-Fernandez, 2010). 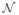(x) and 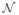(y) denote the neighborhoods of x and y respectively. The neighborhood of x can be viewed as the voxels around x or a square centered at x with a user defined radius. Furthermore,

$$\begin{array}{l}{\left|\right|S(\mathcal{N}(\mathbf{x}))-S(\mathcal{N}(\mathbf{y}))\left|\right|}^2=\sum _j^m{\left|\right|S({\mu }_j)-S({\nu }_j)\left|\right|}^2,\text{and}\\ {\left|\right|logS(\mathcal{N}(\mathbf{x}))-logS(\mathcal{N}(\mathbf{y}))\left|\right|}^2=\sum _j^m{\left|\right|logS({\mu }_j)-logS({\nu }_j)\left|\right|}^2,\end{array}$$

where μ_j and ν_j are the j^th voxels in the neighborhoods 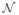(x) and 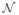(y) respectively, and m is the number of voxels in each neighborhood.

From (5), we can see that if the signal intensities for two voxels are similar, w₁(x, y) and w₂(x, y) are large. Consequently according to (3), S₀ and S₀(y), D and D(y) should be similar respectively.

NLM is known for its high accuracy and high computational complexity. To address the computational load problem, we use two methods. One is to decrease the number of computations performed by selecting voxels in the search window, and the other is to make use of parallel computing. Concretely, we will prefilter the voxels in the search window which are not similar to the voxel under consideration if their diffusion weighted signal intensities are not similar. This is specified as

$$\begin{array}{c}{w}_1(\mathbf{x},\mathbf{y})=\{\begin{array}{ll}\frac{1}{Z_1(\mathbf{x})}exp\left(\frac{-{\left|\right|S(\mathcal{N}(\mathbf{x}))-S(\mathcal{N}(\mathbf{y}))\left|\right|}^2}{h{\sigma }^2}\right),\hfill & \text{if}\frac{{\left|\right|S(\mathcal{N}(\mathbf{x}))\left|\right|}^2}{{\left|\right|S(\mathcal{N}(\mathbf{y}))\left|\right|}^2}\in [{\tau }_1,{\tau }_2]\hfill \\ 0,\hfill & \text{Otherwise}\hfill \end{array}.\\ w_2(\mathbf{x},\mathbf{y})=\{\begin{array}{ll}\frac{1}{Z_2(\mathbf{x})}exp\left(\frac{-{\left|\right|logS(\mathcal{N}(\mathbf{x}))-logS(\mathcal{N}(\mathbf{y}))\left|\right|}^2}{h{\sigma }^2}\right),\hfill & \text{if}\frac{{\left|\right|S(\mathcal{N}(\mathbf{x}))\left|\right|}^2}{{\left|\right|S(\mathcal{N}(\mathbf{y}))\left|\right|}^2}\in [{\tau }_1,{\tau }_2]\hfill \\ 0,\hfill & \text{Otherwise}\hfill \end{array}.\end{array}$$

τ₁ and τ₂ are the thresholds for prefiltering. We set τ₁ = 0.1 and τ₂ = 10 in our experiments.

In the context of parallel computing, we divide the computations into smaller parts and assign the computations to several processors. Since the smaller parts for NLM are not correlated, thus it can improve the efficiency a lot using parallel computing. In our case, we divide the volumes into 8 subvolumes, and assign each subvolume to one processor, and a desktop with 8 processors is used. This multi-threading technique greatly enhances the efficiency.

2.2. Computation of the tKL Divergence

tKL divergence is a special case of the recently proposed total Breman divergence (tBD) (Liu et al., 2010; Vemuri et al., 2011). This divergence measure is based on the orthogonal distance between the convex generating function of the divergence and its tangent approximation at the second argument of the divergence. The total Bregman divergence δ_f associated with a real valued strictly convex and differentiable function f defined on a convex set X between points x, y ∈ X is defined as,

$${\delta }_f(x,y)=\frac{f(x)-f(y)-\langle x-y,\nabla f(y)\rangle }{\sqrt{1+{\left|\right|\nabla f(y)\left|\right|}^2}},$$ (7)

where 〈·, ·〉 is inner product, and ||∇f(y)||² = 〈∇f(y), ∇f(y)〉 generally. tBD has been proven to have the property of being intrinsically robust to noise and outliers. Furthermore, it yields a closed form formula for computing the median (an ℓ₁-norm average) for a set of symmetric positive definite tensors. When f(x) = − log x and X is the set of probability density functions (pdf), Eq. (7) becomes the tKL divergence, which is

$${\delta }_f(x,y)=\frac{\int xlog\frac{x}{y}}{\sqrt{1+\int y{(1+logy)}^2}}.$$ (8)

Motivated by earlier use of tKL divergence as a dissimilarity measure between DTs for DTI segmentation (Vemuri et al., 2011), we use tKL to measure the dissimilarity between tensors and apply it in DTI regularization. It has been shown that the tKL divergence (Vemuri et al., 2011) based ℓ₁-norm average, termed by t-center, is invariant to special linear group transformations (denoted by SL(n))³. This is detailed in the following.

Since order-2 SPD tensors can be seen as covariance matrices of zero mean Gaussian pdf (Wang et al., 2004). Let P, Q ∈ SPD(l), then their corresponding pdf are

$$\begin{array}{l}p(\mathbf{t};\mathbf{P})=\frac{1}{\sqrt{{(2\pi )}^{l}det\mathbf{P}}}exp\left(-\frac{{\mathbf{t}}^T{\mathbf{P}}^{-1}\mathbf{t}}{2}\right),\\ q(\mathbf{t};\mathbf{Q})=\frac{1}{\sqrt{{(2\pi )}^{l}det\mathbf{Q}}}exp\left(-\frac{{\mathbf{t}}^T{\mathbf{Q}}^{-1}\mathbf{t}}{2}\right),\end{array}$$

and the tKL between them is explicitly given by,

$$\begin{array}{l}\delta (\mathbf{P},\mathbf{Q})=\frac{\int plog\frac{p}{q}d\mathbf{t}}{\sqrt{1+\int {(1+logq)}^{2}qd\mathbf{t}}}\\ =\frac{log(det({\mathbf{P}}^{-1}\mathbf{Q}))+tr({\mathbf{Q}}^{-1}\mathbf{P})-l}{2\sqrt{c_1+\frac{{(log(det\mathbf{Q}))}^2}{4}-c_{2}log(det\mathbf{Q})}},\end{array}$$

where $c_1=\frac{3l}{4}+\frac{l^{2}log2\pi }{2}+\frac{{(llog2\pi )}^2}{4}$ and $c_2=\frac{l(1+log2\pi )}{2}$.

Moreover, the partial minimization of the third term in (3)

$$\underset{\mathbf{D}}{min}\sum _{\mathbf{y}\in \mathbb{V}(\mathbf{x})}\delta (\mathbf{D},\mathbf{D}(\mathbf{y}))$$

leads to the t-center for the set of D(y). The t-center has been well studied in (Vemuri et al., 2011). Given a set of tensors {Q_i}, the t-center P^* minimizes the ℓ₁-norm divergence to all the tensors, i.e.,

$${\mathbf{P}}^{\ast }=arg\underset{\mathbf{P}}{min}\sum _i\delta (\mathbf{P},{\mathbf{Q}}_i),$$ (9)

and P^* is explicitly expressed as

$$\begin{array}{l}{\mathbf{P}}^{\ast }={\left(\sum _i\frac{a_i}{{\sum }_j{a}_j}{\mathbf{Q}}_i^{-1}\right)}^{-1},\\ a_i={\left(2\sqrt{c_1+\frac{{(log(det{\mathbf{Q}}_i))}^2}{4}-c_{2}log(det{\mathbf{Q}}_i)}\right)}^{-1}.\end{array}$$ (10)

The t-center for a set of DTs is the weighted harmonic mean, which is in closed form. Moreover, the weight is invariant to SL(n) transformations, i.e., a_i(Q_i) = a_i(A^T Q_iA), ∀A ∈ SL(n). The t-center after the transformation becomes

$${\widehat{\mathbf{P}}}^{\ast }={\left(\sum a_i{({\mathbf{A}}^T{\mathbf{Q}}_i\mathbf{A})}^{-1}\right)}^{-1}={\mathbf{A}}^T{\mathbf{P}}^{\ast }\mathbf{A}.$$ (11)

This means that if ${\{{\mathbf{Q}}_i\}}_{i=1}^m$ are transformed by some member of SL(n), the t-center will undergo the same transformation. It was also found that the t-center will be robust to noise in that the weight will be smaller if the tensor has more noise (Vemuri et al., 2011). These properties make it an appropriate tool for DTI applications.

2.3. The SPD Constraint

It is known that if a matrix D ∈ SPD, there exists a unique lower diagonal matrix L with its diagonal values all positive, and D = LL^T (Golub and Loan, 1996). This is the well known Cholesky factorization theorem. Wang et al. (Wang et al., 2003, 2004) were the first to use Cholesky factorization to enforce the positive definiteness condition on the estimated smooth diffusion tensors from the DWI data. They use the argument that testing for positive definiteness is equivalent to testing for positive semidefiniteness under finite precision arithmetic and hence their cost function minimization is set on the space of positive semidefinite matrices, which is a closed set that facilitates the existence of a solution within that space. Unlike Wang et al. (Wang et al., 2003, 2004), we use Cholesky decomposition and tKL divergence to regularize the smoothness of the tensor field, and this automatically ensures the diagonal values of L to be positive. This argument is validated as follows.

Substituting D = LL^T into (9), we get

$$\delta (\mathbf{L},\mathbf{L}(\mathbf{y}))=\frac{{\sum }_{i=1}^3(log{\mathbf{L}}_{ii}(\mathbf{y})-log{\mathbf{L}}_{ii})+tr({\mathbf{L}}^{-T}(\mathbf{y}){\mathbf{L}}^{-1}(\mathbf{y}){\mathbf{LL}}^T)-1.5}{\sqrt{c_1+\frac{{({\sum }_{i=1}^{3}log{\mathbf{L}}_{ii}(\mathbf{y}))}^2}{4}-c_2{\sum }_{i=1}^{3}log{\mathbf{L}}_{ii}(\mathbf{y})}}.$$ (12)

Because of using the “log” function in the computation, Eq. (12) automatically requires L_iis to be positive, therefore we do not need to manually force the tensor to be SPD. The detailed explanation is given in Appendix A.

2.4. Numerical Solution

In this section, we present the numerical solution to the variational principle (3). The partial derivative equations of (3) with respect to S₀ and L can be computed explicitly and are,

$$\begin{array}{l}\frac{\partial \mathbf{E}}{\partial S_0}=-2(1-\alpha -\beta )\sum _{i=1}^n{v}_i-2\alpha \sum _{\mathbf{y}\in \mathbb{V}(\mathbf{x})}{w}_1(\mathbf{x},\mathbf{y})(S_0-S_0(\mathbf{y})),\\ \frac{\partial \mathbf{E}}{\partial \mathbf{L}}=4(1-\alpha -\beta )\sum _{i=1}^{n}b{S}_0{v}_i{\mathbf{L}}^T{\mathbf{g}}_i{\mathbf{g}}_i^T-2\beta \sum _{\mathbf{y}\in \mathbb{V}(\mathbf{x})}\frac{w_2(\mathbf{x},\mathbf{y})({\mathbf{L}}^{-1}-{\mathbf{L}}^T{\mathbf{L}}^{-T}(y){\mathbf{L}}^{-1}(y))}{\sqrt{c_1+\frac{{({\sum }_{i=1}^{3}log{\mathbf{L}}_{ii}(\mathbf{y}))}^2}{4}-c_2{\sum }_{i=1}^{3}log{\mathbf{L}}_{ii}(\mathbf{y})}},\end{array}$$ (13)

where

$$v_i=(S_i-S_{0}exp(-{b\mathbf{g}}_i^T{\mathbf{LL}}^T{\mathbf{g}}_i))exp(-{b\mathbf{g}}_i^T{\mathbf{LL}}^T{\mathbf{g}}_i).$$ (14)

To solve (13), we use the limited memory quasi-Newton method described in (Nocedal and Wright, 2000). This method is useful for solving large problems with a lot of variables, as is in our case. This method maintains simple and compact approximations of Hessian matrices making them require, as the name suggests, modest storage, besides yielding linear rate of convergence. Specifically, we use linear Broyden-Fletcher-Goldfarb-Shanno (L-BFGS) method (Nocedal and Wright, 2000) to construct the Hessian approximation.

3. Experiments

We evaluated our method on synthetic datasets with various levels of noise, and real datasets, including rat spinal cord datasets and human brain datasets. Based on the estimated tensor fields using the technique presented in this paper, we achieved DTI segmentation for the rat spinal cord datasets, and some preliminary fiber tracking on human brain datasets. However, since the main thrust of this paper is estimation of smooth diffusion tensor fields, the segmentation and fiber tracking results are not presented here.

We compared our method with other state-of-the-art techniques including VF (Tschumperle and Deriche, 2003), NLM (Wiest-Daessle et al., 2008) and LMMSE (Tristan-Vega and Aja-Fernandez, 2010) respectively. We also presented the MRE method for comparison since several software packages (3DSlicer 3.6 ⁴ and fanDTasia (Barmpoutis et al., 2009b)) use this technique due to its simplicity. We implemented VF by ourselves since we did not find any open source versions on the web. For LMMSE, we used the implementation in 3DSlicer 3.6. For NLM, we used existing code ⁵ for DWI denoising and used our own implementation of the least squares fitting to estimate DTI from the denoised DWI. To ensure fairness, we tuned all the parameters of each method for every experiment, and chose the set of parameters yielding the best results. The visual and numerical results show that our method yields better results than competing methods.

3.1. DTI estimation from synthetic datasets

There are two groups of synthetic datasets. The first one is a 16 × 16 DTI with two homogeneous regions as shown in Fig. 1(a). Each region is a repetition of a tensor, and the two tensors are D₁ = [3.3, 1.8, 1.3, 0, 0, 1.2]′ and D₂ = [3, 2.2, 3, −1, 0, 0]′ ⁶. To generate the DWI based on this DTI, we let S₀ = 5, b = 1500s/mm², and g be 22 uniformly-spaced directions on the unit sphere starting from (1, 0, 0). Substituting the DTI, S₀, b, g into the Stejskal-Tanner equation, we generate a 16 × 16 × 22 DWI S. One representative slice of S is shown in Fig. 1(b). Then following the method proposed in (Koay and Basser, 2006), we add Rician noise to S and get S̃, using the formula $\stackrel{\sim }{S}(\mathbf{x})=\sqrt{{(S(\mathbf{x})+n_r)}^2+n_i^2}$, where n_r, n_i ~ N(0, σ²). By varying σ, we get different levels of noise and therefore a wide range of $\text{SNR}(\text{SNR}=\frac{\mathit{mean}(\mathbf{S})}{\sigma })$.

Figure 1.

(a) Ground truth synthetic DTI field, (b) the original DWI corresponding to g₁, (c) the Rician noise affected DWI, the DTI estimation using (d) MRE, (e) VF, (f) LMMSE, (g) NLM, and (h) the proposed technique.

In our experiments, we set α = 0.1 and β = 0.4. The search window size is set to be 25 and the neighborhood size is 9. Fig. 1(c) shows the slice in Fig. 1(b) after adding noise (SNR=60). The estimated DTI from using MRE, VF, NLM, LMMSE and the proposed method are shown in Fig. 1. The figure visually depicts that our method can estimate the tensor field more accurately.

To quantitatively assess the proposed variational unified model, we determine the accuracy of the computed principle eigenvectors of the tensors. Let ε_θ be the average angle between the principle eigenvectors of the estimated tensor field and the original known tensor field. Besides we compare the difference, denoted as ε_S0, between the estimated and ground truth S₀. The results are shown in Table 1, from which it is evident that our method outperforms others and the significance in performance is more evident at higher noise levels. Even though the accuracy of NLM and our proposed method is very similar at high SNR. however, our method is much more computationally efficient than NLM. The average CPU time taken to converge for our method on a desktop computer with Intel 8 Core 2.8GHz, 24GB of memory, GNU Linux and MAT-LAB (Version 2010a) is 3.51s, whereas, NLM requires 5.26s (note both methods are executed using multi-core processors).

Table 1.

Error in estimated DTI and S₀, using different methods, from synthetic DWI with different levels of noise.

SNR	error	MRE	VF	LMMSE	NLM	proposed	α = 0	β = 0
50	εθ	0.204 ± 0.064	0.107 ± 0.038	0.096 ± 0.060	0.085 ± 0.054	0.082 ± 0.045	0.112 ± 0.049	0.179 ± 0.062
	εS0	0.269 ± 0.138	0.217 ± 0.106	0.208 ± 0.080	0.191 ± 0.112	0.133 ± 0.103	0.171 ± 0.098	0.224 ± 0.082
40	εθ	0.550 ± 0.351	0.275 ± 0.312	0.203 ± 0.304	0.195 ± 0.301	0.108 ± 0.102	0.169 ± 0.192	0.539 ± 0.348
	εS0	0.584 ± 0.354	0.278 ± 0.359	0.215 ± 0.320	0.216 ± 0.328	0.140 ± 0.226	0.218 ± 0.225	0.542 ± 0.355
30	εθ	0.588 ± 0.359	0.434 ± 0.394	0.230 ± 0.363	0.217 ± 0.348	0.144 ± 0.130	0.214 ± 0.251	0.570 ± 0.359
	εS0	0.753 ± 0.441	0.485 ± 0.370	0.282 ± 0.401	0.275 ± 0.352	0.173 ± 0.231	0.286 ± 0.432	0.607 ± 0.451
15	εθ	0.727 ± 0.561	0.504 ± 0.388	0.396 ± 0.426	0.384 ± 0.422	0.218 ± 0.252	0.372 ± 0.283	0.711 ± 0.577
	εS0	0.968 ± 0.570	0.622 ± 0.517	0.479 ± 0.482	0.478 ± 0.457	0.235 ± 0.272	0.481 ± 0.474	0.921 ± 0.580
7	εθ	1.092 ± 0.595	0.688 ± 0.656	0.460 ± 0.526	0.519 ± 0.469	0.265 ± 0.276	0.457 ± 0.472	1.001 ± 0.591
	εS0	1.334 ± 1.094	0.827 ± 0.680	0.543 ± 0.583	0.562 ± 0.554	0.273 ± 0.283	0.592 ± 0.57	1.306 ± 1.095

We also evaluated the importance of the two regularization terms separately. α = 0 means removing the regularization on S₀, while β = 0 means removing the regularization on D. For these two cases, we evaluate the ε_θ and ε_S0, and the results are shown in the last two columns of Table 1. The results show that removing either regularization term will increase the DTI estimation error. This implies that both regularization terms are necessary in order to get accurate estimation results.

We also evaluated our method on the 64 × 64 fibercup dataset (Poupon et al., 2008a; Fillard et al., 2011) with a voxel size of 3 × 3 × 3mm³, a b-value of 1500s/mm² and 130 gradient directions. For the parameter settings in the proposed model, we chose α = 0.1 and β = 0.4. The search window size is 9 and the neighborhood size is 4. We showed the estimated S₀, D11, D12, D13, D22, D23, D33, FA and the visualization of the estimated DTI using fanDTasia (Barmpoutis et al., 2009a) in Fig. 2. The results depict that the proposed method can give a well smoothed and feature preserved tensor field.

Figure 2.

From left to right, top to bottom are the estimated S₀, D11, D12, D13, D22, D23, D33, FA and the visualization of the estimated DTI using fanDTasia.

3.2. DTI estimation from real datasets

We also did DTI estimation on a 100 × 80 × 32 × 52 3D rat brain DWI. The data was acquired using a PGSE technique with TR=1.5s, TE=28.3ms, bandwidth=35Khz, 52 diffusion weighted images with a b-value of 1334s/mm².

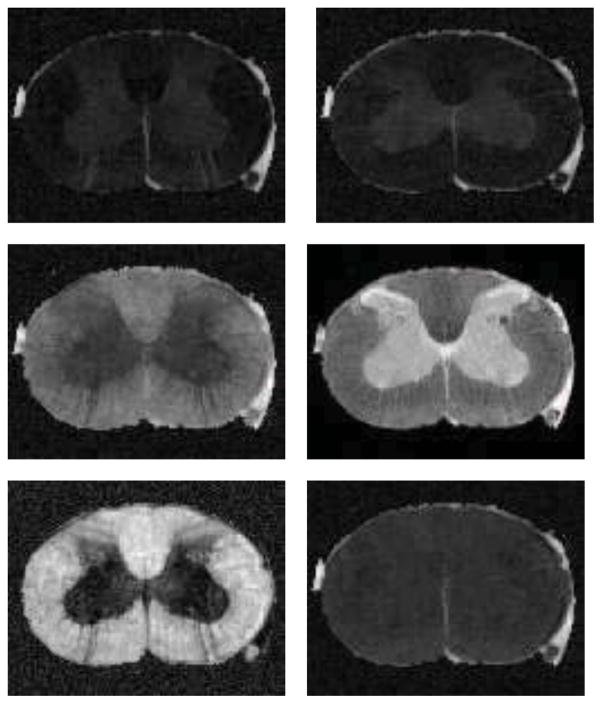
We compared with several other methods on the DTI estimation, however, to save space, we only show the results of MRE, LMMSE and our proposed method. We present D11, D22, D33, S₀, FA, and mean trace for each estimated result. The DTI estimation results of MRE, LMMSE and our proposed method are shown in Fig. 3, 4 and 5 respectively.

Figure 3.

From left to right, top to bottom are D11, D22, D33, S0, FA, and mean trace of the estimated tensor field using MRE on the rat cord data set.

Figure 4.

From left to right, top to bottom are D11, D22, D33, S0, FA, and mean trace of the estimated tensor field using LMMSE on the rat cord data set.

Figure 5.

From left to right, top to bottom are D11, D22, D33, S0, FA, and mean trace of the estimated tensor field using our proposed method on the rat cord data set.

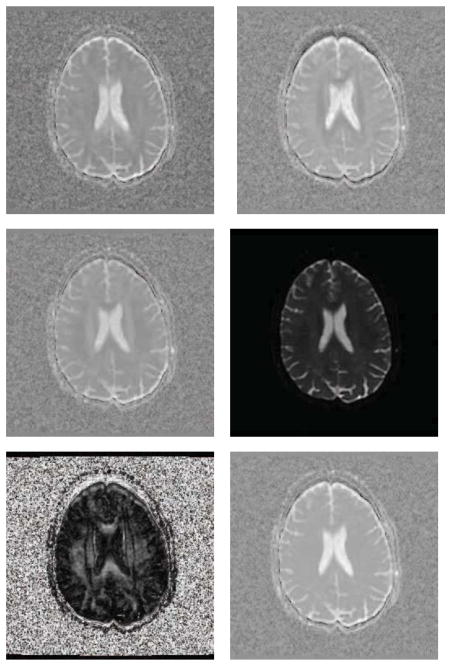
We used a human brain DWI dataset (256 × 256 × 72) provided by Alfred Anwander of the Max Planck Institute for Human Neuroscience (Makuuchi et al., 2009). The DWIs were acquired with a whole-body 3 Tesla Magnetom TRIO operating at 3T (Siemens Medical Solutions) equipped with an 8-channel head array coil. The twice-refocused spin-echo EPI sequence (TR = 12 s, TE = 100 ms) consists of 22 diffusion gradients with a b-value of 800s/mm².

For the parameters of our model, we chose α = 0.15 and β = 0.45. The search window size is 64 and the neighborhood size is 27. We compared with several other methods on the DTI estimation, however, to save space, we only show the results of MRE, LMMSE and our proposed method. We present D11, D22, D33, S₀, FA, and mean trace for each estimated result. The DTI estimation results of MRE, LMMSE and our proposed method are shown in Fig. 6, 7 and 8 respectively. The comparisons indicate that the proposed DTI estimation method generates better results.

Figure 6.

From left to right, top to bottom are D11, D22, D33, S0, FA, and mean trace of the estimated tensor field using MRE on the human brain dataset.

Figure 7.

From left to right, top to bottom are D11, D22, D13, S0, FA, and mean trace of the estimated tensor field using LMMSE on the human brain dataset.

Figure 8.

From left to right, top to bottom are D11, D22, D33, S0, FA, and mean trace of the estimated tensor field using our proposed method on the human brain dataset.

4. Conclusions

We proposed a robust variational non-local means based unified approach for simultaneous denoising and DTI estimation. The proposed method is a combination of a variational framework, non-local means and an intrinsically robust divergence measure to regularize the DTI estimation. In the variational principle, we used non-linear diffusion tensor fitting term, along with a combination of non-local means and the tKL based smoothness measure for denoising. To speed up the NLM method, we performed pre-filtering on the voxels in the search window to reduce the number of computations and made use of parallel computing to distribute the computational load. This variational non-local approach was validated with both synthetic and real datasets and was shown to be more accurate than competing methods in the literature. The results show that our method depicts better noise removal while preserving the structure information even at high levels of noise.

For future work, we plan to develop a GPU-based implementation to further reduce the computation time. After getting a more comprehensive tensor estimation technique, we will utilize it as a preprocessing step in applications to fiber tracking and DTI segmentation.

Highlights.

1. We use a statistically robust divergence-tBD to regularize the smoothness.

2. We use NLM as the weight for the regularization terms. This preserves the global structure.

3. This method enables simultaneous denoising and DTI estimation

Appendix A. Automatically ensuring the positivity of diag(L)

Since

$$\mathbf{L}=\left(\begin{array}{ccc}{\mathbf{L}}_{11}& 0& 0\\ {\mathbf{L}}_{21}& {\mathbf{L}}_{22}& 0\\ {\mathbf{L}}_{31}& {\mathbf{L}}_{32}& {\mathbf{L}}_{33}\end{array}\right),$$

and

$$\mathbf{D}={\mathbf{LL}}^T=\left(\begin{array}{ccc}{\mathbf{L}}_{11}^2& {\mathbf{L}}_{11}{\mathbf{L}}_{21}& {\mathbf{L}}_{11}{\mathbf{L}}_{31}\\ {\mathbf{L}}_{11}{\mathbf{L}}_{21}& {\mathbf{L}}_{21}^2+{\mathbf{L}}_{22}^2& {\mathbf{L}}_{21}{\mathbf{L}}_{31}+{\mathbf{L}}_{21}{\mathbf{L}}_{32}\\ {\mathbf{L}}_{11}{\mathbf{L}}_{31}& {\mathbf{L}}_{21}{\mathbf{L}}_{31}+{\mathbf{L}}_{21}{\mathbf{L}}_{32}& {\mathbf{L}}_{31}^2+{\mathbf{L}}_{32}^2+{\mathbf{L}}_{33}^2\end{array}\right)$$

Let L_ii = exp(a_i), i = 1, 2, 3, then by solving a_i, we can ensure the L_ii is positive. Therefore, the positiveness of the diagonal values of L is transferred to solve a_i.

Now L is converted to L̂:

$$\widehat{\mathbf{L}}=\left(\begin{array}{ccc}exp(a_1)& 0& 0\\ {\mathbf{L}}_{21}& exp(a_2)& 0\\ {\mathbf{L}}_{31}& {\mathbf{L}}_{32}& exp(a_3)\end{array}\right).$$

$$\begin{array}{l}\frac{\partial \mathbf{E}}{\partial \mathbf{L}}=4(1-\alpha -\beta )\sum _{i=1}^{n}b{S}_0{v}_i{\mathbf{L}}^T{\mathbf{g}}_i{\mathbf{g}}_i^T-2\beta \sum _{\mathbf{y}\in \mathbb{V}(\mathbf{x})}{w}_2(\mathbf{x},\mathbf{y})\frac{({\mathbf{L}}^{-1}-{\mathbf{L}}^T{\mathbf{L}}^{-T}(y){\mathbf{L}}^{-1}(y))}{\sqrt{c_1+\frac{{({\sum }_{i=1}^{3}log{\mathbf{L}}_{ii}(\mathbf{y}))}^2}{4}-c_2{\sum }_{i=1}^{3}log{\mathbf{L}}_{ii}(\mathbf{y})}},\\ \frac{\partial \mathbf{E}}{\partial \widehat{\mathbf{L}}}=\frac{\partial \mathbf{E}}{\partial \mathbf{L}}·\mathbf{J},\end{array}$$ (A.1)

where “·” is element-wise product, and

$$\mathbf{J}=\left(\begin{array}{ccc}exp(a_1)& 0& 0\\ 1& exp(a_2)& 0\\ 1& 1& exp(a_3)\end{array}\right).$$

Therefore, the partial derivative is in closed form. This can be solved using the L-BFGS method.