Abstract
According to the lipid raft hypothesis, biological lipid membranes are laterally heterogeneous and filled with nanoscale ordered “raft” domains, which are believed to play an important role for the organization of proteins in membranes. However, the mechanisms stabilizing such small rafts are not clear, and even their existence is sometimes questioned. Here, we report the observation of raft-like structures in a coarse-grained molecular model for multicomponent lipid bilayers. On small scales, our membranes demix into a liquid ordered (lo) phase and a liquid disordered (ld) phase. On large scales, phase separation is suppressed and gives way to a microemulsion-type state that contains nanometer-sized lo domains in an ld environment. Furthermore, we introduce a mechanism that generates rafts of finite size by a coupling between monolayer curvature and local composition. We show that mismatch between the spontaneous curvatures of monolayers in the lo and ld phases induces elastic interactions, which reduce the line tension between the lo and ld phases and can stabilize raft domains with a characteristic size of the order of a few nanometers. Our findings suggest that rafts in multicomponent bilayers might be closely related to the modulated ripple phase in one-component bilayers.
Keywords: coarse-grained simulations, phospholipids, cholesterol, Landau-Brazovskii model
Ever since its introduction some two decades ago (1, 2), the lipid raft concept has been discussed controversially (3–6). It rests on two established facts:
i) Biological membranes are laterally heterogeneous. Heterogeneity is necessary to achieve the functions of membrane proteins (e.g., in cellular signal transduction and trafficking, in endocytosis) (7).
ii) Lipid-lipid phase separation is observed in model multicomponent lipid bilayers. A variety of ternary mixtures containing cholesterol phase separate into a cholesterol-poor Lα or “liquid disordered” (ld) phase and a cholesterol-rich “liquid ordered” (lo) phase with a higher degree of chain order (8).
The lipid raft hypothesis states that lipid-lipid phase separation contributes to membrane heterogeneity and is exploited by nature to organize proteins (9–16). Preexisting “raft domains” supposedly provide a heterogeneous environment that sorts proteins and brings them close to each other, thus facilitating the protein–protein interaction needed for clustering. This concept provides an elegant picture for a number of experimental observations, including the reduced mobility of raft-associating proteins, which depends on cholesterol content (17); the submicroscopic local clustering of raft-associated proteins as observed by fluorescence resonance energy transfer (18); and the existence of detergent-resistant membrane fragments with a high content of cholesterol, sphingolipids, and raft-associated proteins (19).
All the experimental evidence is rather indirect, however, and the interpretation, in terms of lipid rafts, has been subject to debate (6). One problem with lipid rafts is that they cannot be observed in vivo with optical microscopic techniques; hence, they must be tiny. Diffusion experiments indicate that the domain sizes of rafts are probably in the range of a few tens of nanometers (17), and they have short lifetimes in the millisecond or microsecond regime. Thus, the current view is that rafts constitute dynamically changing nanoscale entities, which are collected to larger arrays on need by protein–protein interactions (5, 11, 16).
This naturally raises questions regarding the physical nature of rafts and the mechanisms stabilizing them. The first question is: If the physical basis of rafts is phase separation, why are they so small? A number of possible explanations have been pointed out. For example, it was argued that membranes in vivo are not at thermodynamic equilibrium, and the constant turnover of lipids may well disrupt the formation of large-phase separated domains (20). Alternatively, it was proposed that immobilized cytoplasm proteins generate disorder in the membrane, which prevents large-scale phase separation (21).
The second important question is whether biological membranes really do tend to phase-separate. Model multicomponent membranes may exhibit phase separation at physiological temperatures (22, 23). However, it is not clear whether this is also true for biological membranes. Veatch et al. (24) have isolated giant plasma vesicles directly from living rat cells and showed that they do undergo a demixing phase transition but that the demixing temperature is around T ∼ 15–25 °C. Hence, such membranes would be in a mixed state at physiological temperatures. Veatch et al. (25) and Honerkamp-Smith et al. (26) have argued that raft-like structures might emerge as a signature of critical fluctuations. This would restrict “rafts” to relatively small regions in parameter space, because critical clusters only become large close to critical points.
Alternatively, the membrane might be in the state of a 2D microemulsion, which is globally homogeneous but locally phase-separated with a characteristic length scale or domain size (27). Schick (28) has recently proposed a mechanism that would stabilize a microemulsion, which builds on a coupling between the local curvature of the bilayer and the local composition difference between the two leaflets (29). Such a coupling can generate modulated phases in mixed membranes under tension (30–33). Schick (28) argued that it could also stabilize a microemulsion-type state with a characteristic length scale of the order of 100 nm in membranes under tension, which would diverge in tensionless membranes, however.
A more traditional idea is that the membranes contain line-active agents (13) that reduce the line tension and eventually turn a phase-separated mixture into a microemulsion. Possible candidate agents are proteins (5) or minority lipids with a saturated tail and an unsaturated tail (34, 35). However, none of the lipids that are considered typical for lipid rafts (i.e., cholesterol, sphingolipids) has obvious line-active properties (28). Thus, this mechanism relies on additional assumptions regarding the composition of membranes containing rafts.
Typical model membranes for studying rafts (“raft mixtures”) contain cholesterol and at least two other lipid components. Three components seem necessary to bring about global lateral phase separation between liquid membrane phases (8). However, there is some evidence that nanoscopic domains may already be present in binary mixtures containing cholesterol, particularly in mixtures of cholesterol and a lipid with high main transition temperature (Tm). The literature on these mixtures is controversial. Whereas several authors have observed immiscible liquid phases, based on various techniques such as ESR, NMR, or diffusivity experiments (36–39), others claim that cholesterol and lipids are miscible in the whole high-temperature fluid range (ref. 8 and references therein). In particular, fluorescence microscopy images feature only one homogeneous phase (8). Feigenson (40) has introduced the notion of “type I” and “type II” mixtures, where the “type II mixtures” exhibit global phase separation, whereas the “type I mixtures” phase-separate on the nanoscale but are globally homogeneous, much like microemulsions. The experimental evidence suggests that binary lipid-cholesterol mixtures might be type I mixtures. Thus, bilayers of binary lipid-cholesterol mixtures already seem to have many of the intriguing properties attributed to lipid rafts, and a theoretical study of such binary systems should provide insight into the mechanisms stabilizing rafts.
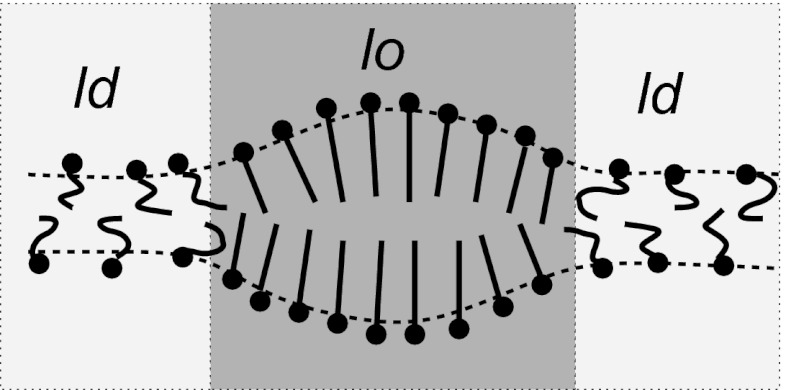
In the present paper, we contribute to the raft discussion with two main results. First, we present Monte Carlo simulations of a coarse-grained molecular model for binary lipid bilayers that demonstrate the existence of a thermodynamically stable heterogeneous membrane phase with raft-like lo nanodomains in an ld environment. Hence, raft formation is found to be a generic phenomenon that can already be observed in binary mixtures and does not require specific line-active agents. Second, we present a theory that rationalizes our results and explains raft formation by a coupling between local composition and monolayer curvature. The theoretical picture is illustrated in Fig. 1. Liquid ordered domains have a propensity to bend inward. If they oppose each other, as suggested by simulations, as well as by experiments (41), the bending competes with bilayer compression. This creates elastic tension, which reduces the line tension even for tensionless membranes and stabilizes domains with a well-defined diameter of the order of 10 nm.
Fig. 1.
Curvature mechanism generating rafts. The lo and ld regions in opposing monolayer leaflets are spatially correlated and have different spontaneous curvatures. This stabilizes domains of a finite size.
Thus, we identify a generic mechanism of raft formation in multicomponent membranes. It is different from the curvature-mediated mechanism proposed by Schick (28), which is based on bilayer curvature. Both the mechanism of Schick (28) and our own mechanism rely on a competition between bending and an opposing force. If the bilayer as a whole has a propensity to bend, the opposing force is the surface tension. Therefore, the surface tension sets the characteristic length scale, which thus diverges in tensionless membranes. In our monolayer curvature mechanism, the bending is opposed by bilayer compression, which results in a characteristic length scale of the order of the membrane thickness.
Coarse-Grained Simulations of Mixed Lipid Bilayers
Our generic coarse-grained simulation model is based on a successful model for one-component lipid bilayers (42), which reproduces the main phases of phospholipid membranes (liquid, tilted gel, and ripple phases) (43, 44) and the elastic properties of fluid dipalmitoylphosphatidylcholine (DPPC) bilayers at a semiquantitative level (45). Here, we introduce two types of lipids, “phospholipids” (P) and “cholesterol” (C), with interactions designed such that C is smaller and stiffer than P and has a special affinity to P, reflecting the experimental observation that sterols in lipid bilayers always tend to be solubilized with one or two other lipids (39). For the purpose of the present study, it is essential to design the model so that it captures those nonrandom mixing effects because they most likely drive the local segregation into ld and lo phases. Waheed (46) and Waheed et al. (47) recently studied the chemical potential of cholesterol in small systems of DPPC/cholesterol bilayers by atomistic (united atom) and coarse-grained simulations. In atomistic simulations, they found that the chemical potential drops with the cholesterol concentration, indicating a clear tendency of local segregation into a cholesterol-rich phase and a cholesterol-poor phase [about 0.3 thermal energy units (kBT) per lipid molecule]. This property was not reproduced by coarse-grained models that show no sign of random mixing (47). Our model is described in more detail in Materials and Methods.
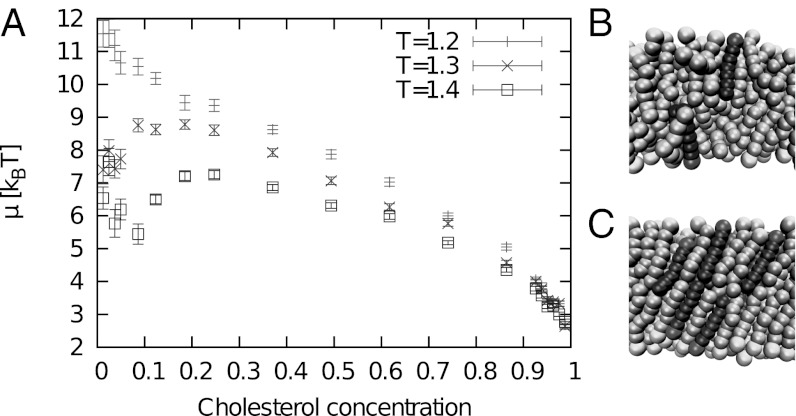
To examine whether the system phase-separates locally, we first consider small systems (162 lipids) at fixed composition. We find that such small systems almost always assume one of two states, either disordered (ld) or ordered (lo), or jump between the two, depending on the composition. Fig. 2 B and C shows sample configurations of these two states. For future reference, we have evaluated the pressure profiles across monolayers in the two states and computed the spontaneous curvature of monolayers c0 from the first moment (48). In the ld state, we obtain c0 = 0.2 ± 0.2σ−1, and in the lo state, c0 = 1.22 ± 0.09σ−1, using our simulation length unit σ ∼ 0.6 nm. Thus, monolayer regions in the lo state have a strong tendency to bend inward, whereas monolayer regions in the ld state tend to remain flat.
Fig. 2.
(A) Chemical potential difference in thermal energy units (kBT) vs. cholesterol content from canonical simulations of small, mixed bilayer systems (162 lipids). The corresponding snapshots show the system in the ld state (B) and in the lo state (C). The darker chains represent C lipids.
The free energy gain μ for replacing a P chain by a C chain (the chemical potential difference) is shown in Fig. 2A. For temperatures above the main transition of the pure P system (Tm = 1.2ɛ), the chemical potential curve has an upward slope in the region between ≈10% and ≈25% C chains. This indicates an unstable regime in which one would expect spontaneous demixing in larger systems.
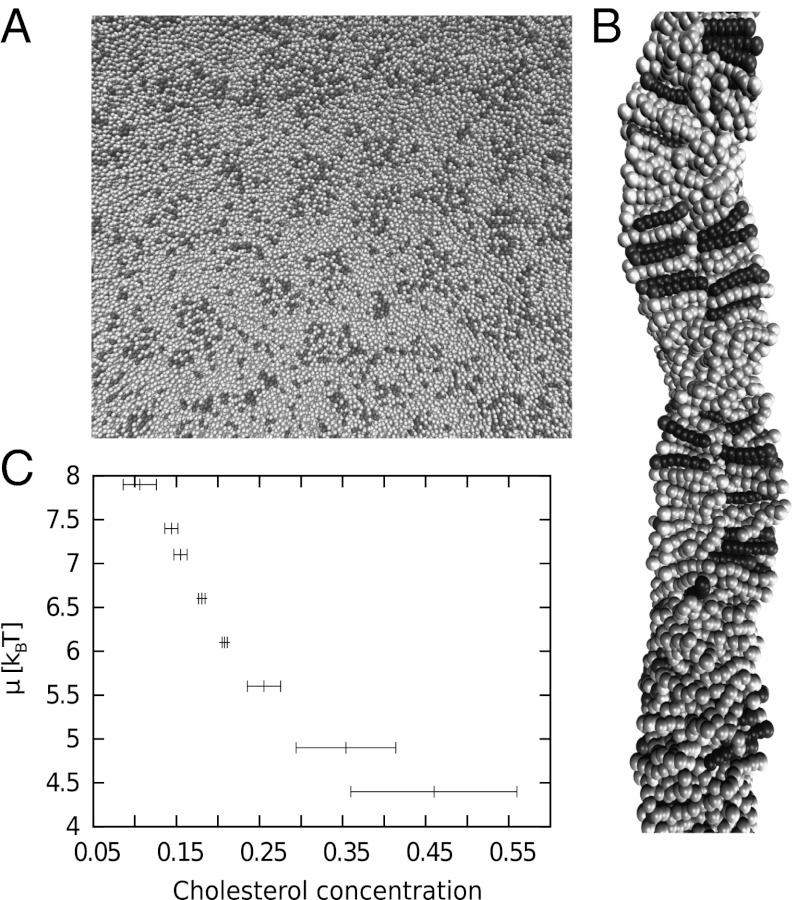
When looking at larger systems (20,000 lipids), however, we find that the system does not phase-separate globally. Instead, finite lo domains with a high concentration of C lipids appear, surrounded by the ld phase almost devoid of C lipids. To ensure that these domains are true equilibrium structures and not the result of incomplete phase separation, the simulations were conducted in the semigrandcanonical ensemble at fixed μ (i.e., lipids were allowed to switch their identities during the simulation). Fig. 3 A and B shows an example of an equilibrated configuration. One can see the raft-like structure of the membrane from the top view (Fig. 3A) and the structure of alternating lo and ld regions from the side view (Fig. 3B). Consistent with this observation, the behavior of the C concentration as a function of μ shows no sign of a phase transition (Fig. 3C).
Fig. 3.
Snapshots of a large bilayer system (20,000 lipids) featuring raft-like lo domains: top view (A) and an enlarged section of a side view (B). Parameters are kBT = 1.4, μ ≈ 6.6 kbT. (C) Chemical potential difference vs. C content from semigrandcanonical simulations of large systems.
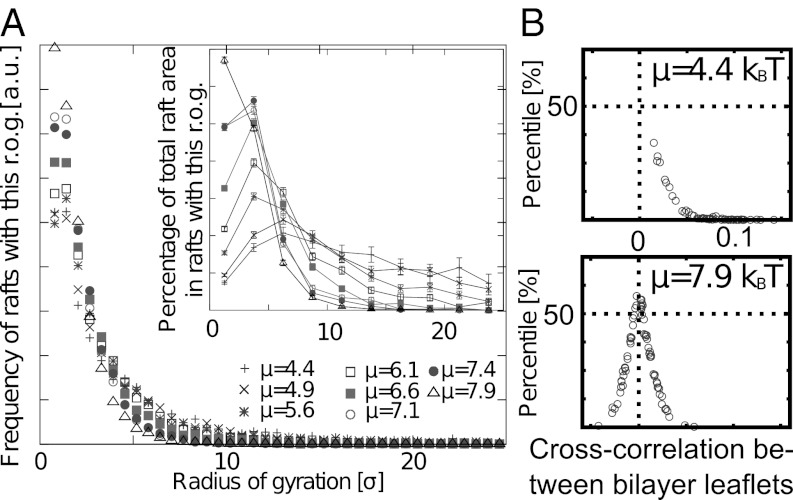
We analyze configurations such as shown in Fig. 3 following an algorithm described in Materials and Methods. This allows us to calculate the distribution of raft sizes (radii of gyration), as shown in Fig. 4A. Although the distributions look rather similar for different values of μ, the area fraction (Fig. 4A, Inset) clearly shows that in systems with larger μ (i.e., systems with a lower concentration of C), a greater fraction of the total raft area is present in the form of smaller rafts.
Fig. 4.
Characterization of raft domains. (A) Raft size distribution. The distribution of rafts with a given radius of gyration (r.o.g.) is shown. (Inset) Actual fraction of the raft area found in rafts of a given size. Lines are guides for the eye; μ is given in units of kBT. (B) Cross-correlation Ki of configuration i vs. percentile of conformations with randomly displaced monolayers, which have a higher correlation or anticorrelation 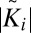 . Every point corresponds to an independent simulation configuration i. The more skewed a distribution is to the right side, the greater is the mean (positive) correlation between rafts on both sides. The lower the percentile of a point, the less likely it is that this particular value is coincidental. a.u., arbitrary units.
. Every point corresponds to an independent simulation configuration i. The more skewed a distribution is to the right side, the greater is the mean (positive) correlation between rafts on both sides. The lower the percentile of a point, the less likely it is that this particular value is coincidental. a.u., arbitrary units.
Next, we address the question of whether rafts in opposing monolayers are correlated. The normalized cross-correlation Ki (Materials and Methods) between monolayers of a configuration i tends to be positive, with values ranging from K = −0.05 to K = 0.15. To analyze whether a correlation Ki > 0 or anticorrelation Ki < 0 is significant, we generate a set of configurations with randomly shifted monolayers and determine the fraction of them having a higher (anti)correlation 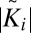 . At large μ (i.e., small C concentrations), the distribution of Ki is symmetrical around zero and shifting monolayers often enhances the correlation. Raft domains are thus uncorrelated in this regime. At large C concentrations, however, all values of Ki are positive and shifting monolayers almost always reduces the correlation. We conclude that the cross-correlation is significant at higher C concentrations and that rafts tend to oppose each other in the bilayer. This is compatible with experimental observations in membranes exhibiting global phase separation, where it was found that lo domains are strongly correlated across the membrane (41).
. At large μ (i.e., small C concentrations), the distribution of Ki is symmetrical around zero and shifting monolayers often enhances the correlation. Raft domains are thus uncorrelated in this regime. At large C concentrations, however, all values of Ki are positive and shifting monolayers almost always reduces the correlation. We conclude that the cross-correlation is significant at higher C concentrations and that rafts tend to oppose each other in the bilayer. This is compatible with experimental observations in membranes exhibiting global phase separation, where it was found that lo domains are strongly correlated across the membrane (41).
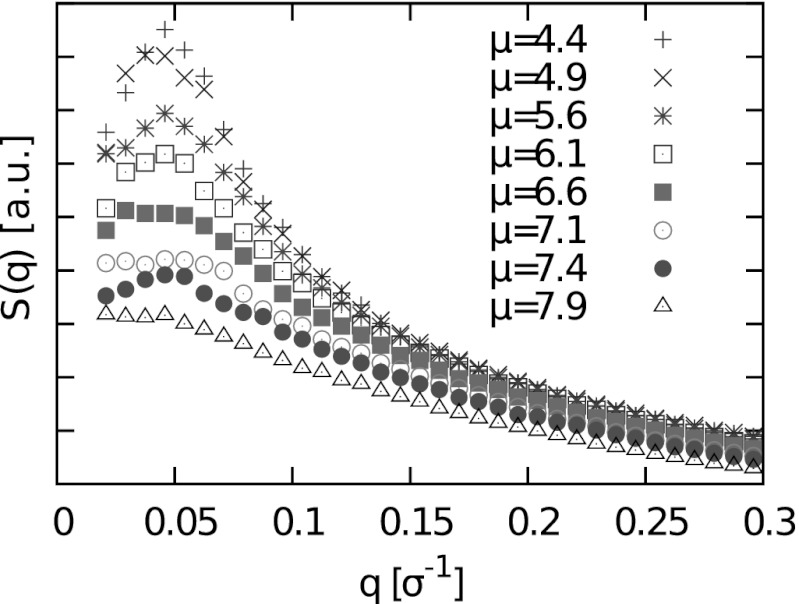
Finally, we consider the in-plane structure factor (Fig. 5). For small values of μ, we observe a peak at nonzero q ∼ 0.05σ−1, corresponding to a characteristic length scale of about 20σ ∼ 12 nm. Such a peak is a typical signature of a microemulsion (27).
Fig. 5.
Radially averaged structure factor of the raft conformations for different values of μ, with μ given in units of kBT. a.u., arbitrary units.
Elastic Theory of Raft Stabilization by Curvature
The main results of the simulations can be summarized as follows: (i) lo domains (rafts) of a finite nanoscale size are observed in two-component lipid bilayers, (ii) they are correlated across the membrane (i.e., rafts on the two leaflets tend to oppose each other), and (iii) the analysis of pressure profiles in small systems shows that lo monolayer domains have a propensity to bend inward (a spontaneous curvature). However, large-scale bending is prevented by the presence of the rafts on the opposing monolayer. These observations motivate the hypothesis that the elastic energy associated with the spontaneous curvature might be responsible for the finite size of the rafts (Fig. 1).
To analyze this possibility, we consider a simple elastic model for two coupled monolayers with composition-dependent spontaneous curvature, which combines a model for mixed films by Leibler and Andelman (30) with a bilayer model developed by Dan, Pincus, and coworkers (49–51) to describe bilayer deformations near inclusions. For simplicity, and in contrast to the model proposed by Schick (28), we assume that the local compositions on opposing monolayers are strictly equal and do not induce bilayer bending. Bending and thickness deformations then decouple, and for planar membranes, the elastic free energy of monolayer thickness deformations can be written as follows (45, 51–53):
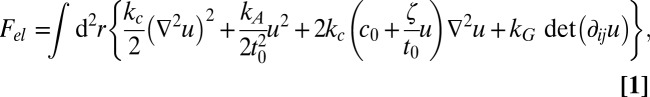 |
where u(r) denotes the local deviation from the mean monolayer thickness t0 and the other parameters represent material properties of the membrane: the bilayer bending and compressibility modulus kc and kA, the spontaneous monolayer curvature c0, an associated curvature-related parameter ζ (51), and the Gaussian rigidity of monolayers kG. Eq. 1 holds for tensionless membranes as well as for membranes under tension (54). We have used it in the past to fit deformation profiles of one-component membranes in the vicinity of inclusions, with good results even on molecular-length scales (45, 55).
We assume that the monolayer lateral phase separates into two phases, which are separated by narrow interfaces with a bare line tension λ0. In principle, all membrane parameters (t0, kc, kA, c0, ζ, and kG) should depend on the local composition. For simplicity, however, we will assume that only the spontaneous curvature c0 makes a jump from one phase to the other. In that case, the final elastic energy after minimization can be written in the simple form (Materials and Methods)
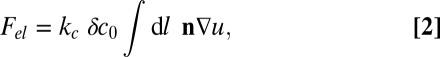 |
where the line integral 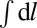 runs over all domain boundaries, n is the unit vector normal to the interface, and δc0 is the curvature mismatch (i.e., the difference of the spontaneous curvatures in the inner and outer phases).
runs over all domain boundaries, n is the unit vector normal to the interface, and δc0 is the curvature mismatch (i.e., the difference of the spontaneous curvatures in the inner and outer phases).
In many cases, this simple theory can be solved analytically. Details of the calculations are presented in Materials and Methods. For isolated plane interfaces, we obtain an elastic line energy (an elastic energy per boundary length L):
which acts as an additive contribution to the total line tension, 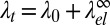 . Note that
. Note that 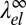 is negative. Here, we have introduced the in-plane correlation length
is negative. Here, we have introduced the in-plane correlation length 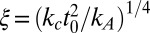 and the dimensionless membrane parameter b = 2ζξ2/t0. Because kc should be roughly proportional to
and the dimensionless membrane parameter b = 2ζξ2/t0. Because kc should be roughly proportional to 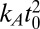 (56), ξ is of the order of the membrane thickness. Inserting actual numbers for the fluid phase of one-component DPPC bilayers from experiments, all-atom simulations, or simulations of our model (45), one consistently obtains values around ξ ∼ (0.9–1.4) nm. For the membrane parameter b, one obtains b = 0.65 for our DPPC model and b = 0.69 for all atom simulations of DPPC. Throughout this paper, we assume |b| < 1.
(56), ξ is of the order of the membrane thickness. Inserting actual numbers for the fluid phase of one-component DPPC bilayers from experiments, all-atom simulations, or simulations of our model (45), one consistently obtains values around ξ ∼ (0.9–1.4) nm. For the membrane parameter b, one obtains b = 0.65 for our DPPC model and b = 0.69 for all atom simulations of DPPC. Throughout this paper, we assume |b| < 1.
Because the elastic contribution 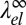 to the line tension is negative, the effect of elastic relaxation between two curvature-mismatched phases is similar to that of adding line-active surfactant agents. To assess its impact on the demixing transition, we analyze the scaling of λ0 and
to the line tension is negative, the effect of elastic relaxation between two curvature-mismatched phases is similar to that of adding line-active surfactant agents. To assess its impact on the demixing transition, we analyze the scaling of λ0 and 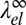 close to the critical demixing temperature Tc. The bare line tension vanishes according to λ0 ∼ (Tc − T)ν with the critical exponent ν = 1, corresponding to the universality class of the 2D Ising model (57). Likewise, the curvature mismatch δc0 will vanish on approaching Tc, and it seems reasonable to assume that δc0 is proportional to the composition difference of the two phases (i.e., the order parameter of the demixing transition). The elastic “line tension” should therefore scale as
close to the critical demixing temperature Tc. The bare line tension vanishes according to λ0 ∼ (Tc − T)ν with the critical exponent ν = 1, corresponding to the universality class of the 2D Ising model (57). Likewise, the curvature mismatch δc0 will vanish on approaching Tc, and it seems reasonable to assume that δc0 is proportional to the composition difference of the two phases (i.e., the order parameter of the demixing transition). The elastic “line tension” should therefore scale as 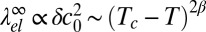 with the 2D Ising exponent β = 1/8. Comparing the exponents for λ0 and
with the 2D Ising exponent β = 1/8. Comparing the exponents for λ0 and 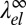 , we find that
, we find that 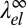 dominates close to Tc and the line tension becomes negative. Thus, macroscopic demixing is suppressed at Tc. The demixing transition is shifted to lower temperatures and gives way to a microemulsion or modulated phase.
dominates close to Tc and the line tension becomes negative. Thus, macroscopic demixing is suppressed at Tc. The demixing transition is shifted to lower temperatures and gives way to a microemulsion or modulated phase.
Next, we consider disks with a finite diameter D of one phase immersed in the other. In that case, the elastic line energy depends on D and we obtain (Materials and Methods)
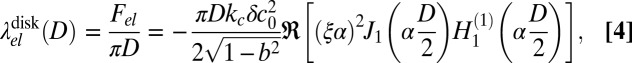 |
where Jn and 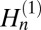 are Bessel and Hankel functions of the first kind. For comparison, we also consider the elastic line energy for isolated stripe domains of width D. It is given by
are Bessel and Hankel functions of the first kind. For comparison, we also consider the elastic line energy for isolated stripe domains of width D. It is given by
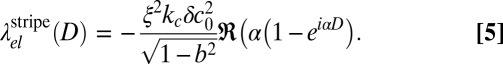 |
The functional dependence of 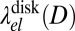 and
and 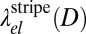 on the domain size D is illustrated in Fig. 6. As expected, both converge toward
on the domain size D is illustrated in Fig. 6. As expected, both converge toward 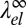 for a large D. At a finite D, the behavior is nonmonotonic: Both line energies exhibit a minimum of similar depth (equal within 3%), which is weak for negative b and becomes more pronounced as b approaches b → 1. The minimum is located at D ∼ 4ξ for disks and at D ∼ 2–4ξ for stripes. This result implies that domains of finite diameter become stable even before the asymptotic line tension vanishes; thus, the theory predicts a regime where the membrane is filled with small nanoscale domains (i.e., rafts). Because disk-shaped and stripe-shaped domains have similar line energies, the actual shape depends on the composition of the membrane. At low C concentrations, disks will dominate; using ξ ∼ 1 nm, the predicted characteristic raft size of around 4ξ corresponds to a few nanometers. This is compatible with typical raft sizes observed in the simulation (Fig. 4). Taking into account that σ ∼ 0.6 nm, our estimate is at the lower end of the values typically suggested in the literature (∼10–100 nm).
for a large D. At a finite D, the behavior is nonmonotonic: Both line energies exhibit a minimum of similar depth (equal within 3%), which is weak for negative b and becomes more pronounced as b approaches b → 1. The minimum is located at D ∼ 4ξ for disks and at D ∼ 2–4ξ for stripes. This result implies that domains of finite diameter become stable even before the asymptotic line tension vanishes; thus, the theory predicts a regime where the membrane is filled with small nanoscale domains (i.e., rafts). Because disk-shaped and stripe-shaped domains have similar line energies, the actual shape depends on the composition of the membrane. At low C concentrations, disks will dominate; using ξ ∼ 1 nm, the predicted characteristic raft size of around 4ξ corresponds to a few nanometers. This is compatible with typical raft sizes observed in the simulation (Fig. 4). Taking into account that σ ∼ 0.6 nm, our estimate is at the lower end of the values typically suggested in the literature (∼10–100 nm).
Fig. 6.
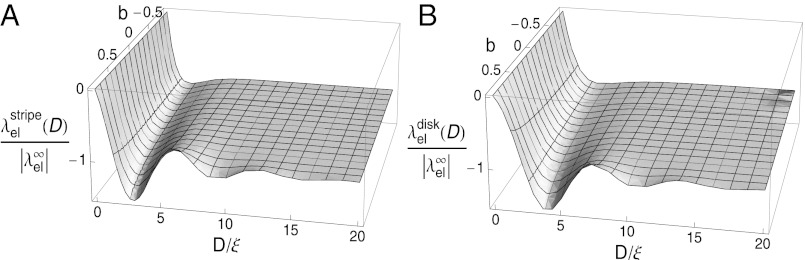
Rescaled elastic contribution to the line tension λel(D) for disk-shaped rafts of diameter D (A) and stripe-shaped rafts of thickness D vs. D (B) in units of in-plane correlation length ξ and membrane parameter b.
We should add that the raft domains interact with each other; hence, the theory actually predicts modulated phases with long-range order. Let us consider a system where the phase separation, described by a demixing order parameter Φ, is driven by a Ginzburg–Landau free energy functional of the form 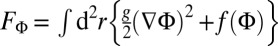 with
with 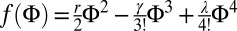 , and let the spontaneous curvature c0 depend linearly on Φ according to
, and let the spontaneous curvature c0 depend linearly on Φ according to 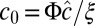 . As shown in Materials and Methods, a homogeneous phase in this model becomes unstable with respect to modulations with wavelength ξ at
. As shown in Materials and Methods, a homogeneous phase in this model becomes unstable with respect to modulations with wavelength ξ at 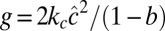 . Close to the spinodal, we recover the Landau–Brazovskii model, which provides a general framework for the description of phase transitions driven by short-wavelength instability between a disordered phase and ordered phases (58).
. Close to the spinodal, we recover the Landau–Brazovskii model, which provides a general framework for the description of phase transitions driven by short-wavelength instability between a disordered phase and ordered phases (58).
Because the same holds for the models for mixed membranes with bilayer curvature coupling mentioned in the introductory section (28, 30, 32), we expect the mean-field phase diagrams to be similar, with one important difference: In the bilayer coupling case, the characteristic wavelength 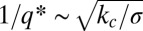 tends to be in the micrometer range and diverges for vanishing membrane tension σ, whereas here, the characteristic scale ξ is in the nanometer range and independent of membrane tension. Consequently, the effect of fluctuations is expected to be much bigger in the present case. Fluctuations are known to shift the order-disorder transition and to stabilize a locally structured disordered phase via the Brazovskii mechanism (58). The pattern formation then gives way to a microemulsion-type raft phase as observed in the simulations.
tends to be in the micrometer range and diverges for vanishing membrane tension σ, whereas here, the characteristic scale ξ is in the nanometer range and independent of membrane tension. Consequently, the effect of fluctuations is expected to be much bigger in the present case. Fluctuations are known to shift the order-disorder transition and to stabilize a locally structured disordered phase via the Brazovskii mechanism (58). The pattern formation then gives way to a microemulsion-type raft phase as observed in the simulations.
Discussion
To summarize, we have presented a coarse-grained simulation model for multicomponent lipid bilayer systems containing two types of lipids P and C with properties inspired by phospholipids and cholesterol. Our simulations show that this system forms thermodynamically stable nanoscale rafts of C-enriched lo domains surrounded by a sea of C-depleted ld phase. The in-plane structure factor features a peak at nonzero q; hence, we have a microemulsion-like structure with a characteristic wavelength of around 12 nm. Furthermore, we have suggested a mechanism that stabilizes rafts of finite size. The mechanism is based on the idea that the spontaneous curvature of monolayer regions in the lo and ld phases should differ. We have established this for our model, and it seems likely that it is also the case in real membranes. The curvature mismatch then generates elastic interactions that suppress global phase separation and stabilize nanoscale structures.
If rafts are a disordered modulated structure, one might ask whether the corresponding ordered modulated structure can be observed in nature as well. Indeed, modulated ordered structures with a very similar length scale are found in one-component membranes of phospholipids in the pretransition region between the fluid phase and the tilted gel phase  : the ripple phase
: the ripple phase 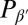 (59). It is generally observed in lipid bilayers that exhibit a tilted gel phase. It is also observed in our model (43), and the periodicity (∼10 nm) is comparable to the characteristic length scale of our raft state. The structure of rippled membranes is much more complicated than that of rafts. However, just like in rafts, it involves alternating stretches of gel-like and liquid-like domains, and simulations suggest that ripple formation is driven by lipid splay to a large extent (i.e., by monolayer curvature) (43). Thus, we may speculate that rafts and ripples represent just two sides of the same coin. Curvature-mediated rafts might be a generic phenomenon in multicomponent membranes, just like ripples are a generic phenomenon in one-component membranes.
(59). It is generally observed in lipid bilayers that exhibit a tilted gel phase. It is also observed in our model (43), and the periodicity (∼10 nm) is comparable to the characteristic length scale of our raft state. The structure of rippled membranes is much more complicated than that of rafts. However, just like in rafts, it involves alternating stretches of gel-like and liquid-like domains, and simulations suggest that ripple formation is driven by lipid splay to a large extent (i.e., by monolayer curvature) (43). Thus, we may speculate that rafts and ripples represent just two sides of the same coin. Curvature-mediated rafts might be a generic phenomenon in multicomponent membranes, just like ripples are a generic phenomenon in one-component membranes.
Unfortunately, rafts are much more difficult to study experimentally than ripples due to the lack of long-range order, as well as their subsecond lifetimes (60). The structure factor describing the distribution of domains on the nanoscale could possibly be measured by X-ray diffraction experiments on aligned multilamellar membranes (“membrane stacks”) of the relevant composition, either in reflection or transmission (61, 62). This would allow one to test whether the in-plane structure factor has a peak at nonzero wave vector in type I mixtures as predicted by our model (Fig. 5). In addition, recently developed superresolution microscopy techniques (63) might provide ways to visualize rafts in free membranes on the scale of a few nanometers.
Of course, the curvature mechanism proposed here does not exclude other mechanisms of raft formation, such as those discussed in the introductory section. Many mechanisms might compete in nature. In particular, it should be interesting to study the interplay of curvature-mediated rafts and lipid–protein interactions (21, 55) in future work.
Materials and Methods
Coarse-Grained Simulation Model.
The model is defined in terms of the length unit σ ≈ 0.6 nm and the energy unit ɛ ≈ 0.36⋅10−20 J (44). P molecules are represented by simple flexible chains of beads with a hydrophilic head and a hydrophobic tail, which self-assemble in the presence of structureless solvent beads (64). C molecules have the same basic structure, but they are shorter and stiffer except for one flexible end. All lipids are linear chains of six tail beads attached to one head bead, connected by finite extension nonlinear elastic (FENE) springs with the spring constant 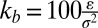 , equilibrium bond lengths r0 = 0.7σ (P lipid) and r = 0.6σ (C lipid), and logarithmic cutoffs at Δrmax = 0.2σ (P) and Δrmax = 0.15σ (C). Consecutive bonds in a chain with angle Θ are subject to a stiffness potential UBA(Θ) = kθ(1 − cos(Θ)) with stiffness constant kθ = 4.7ɛ (P lipids), kθ = 100ɛ (C lipids, first four angles), and kθ = 4.7ɛ (C lipid, last angle). Beads that are not directly bonded with each other interact via a Lennard–Jones potential
, equilibrium bond lengths r0 = 0.7σ (P lipid) and r = 0.6σ (C lipid), and logarithmic cutoffs at Δrmax = 0.2σ (P) and Δrmax = 0.15σ (C). Consecutive bonds in a chain with angle Θ are subject to a stiffness potential UBA(Θ) = kθ(1 − cos(Θ)) with stiffness constant kθ = 4.7ɛ (P lipids), kθ = 100ɛ (C lipids, first four angles), and kθ = 4.7ɛ (C lipid, last angle). Beads that are not directly bonded with each other interact via a Lennard–Jones potential 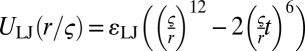 , which is truncated at a cutoff radius rc and shifted such that it remains continuous. At rc = 1, one recovers the purely repulsive Weeks-Chandler-Anderson potential (65). The interaction parameters for pairs of P or C beads (head or tail) and solvent beads are given by the following:
, which is truncated at a cutoff radius rc and shifted such that it remains continuous. At rc = 1, one recovers the purely repulsive Weeks-Chandler-Anderson potential (65). The interaction parameters for pairs of P or C beads (head or tail) and solvent beads are given by the following:
| Bead type-bead type | ɛ/ɛ | ζ/σ | rc/ζ |
| Head(any)-head(any) | 1.0 | 1.1 | 1.0 |
| Head(any)-tail(any) | 1.0 | 1.05 | 1.0 |
| Head(any)-solvent | 1.0 | 1.1 | 1.0 |
| Tail(P)-tail(P) | 1.0 | 1.0 | 2.0 |
| Tail(P)-tail(C) | 1.0 | 1.0 | 2.0 |
| Tail(C)-tail(C) | 0.9 | 1.0 | 2.0 |
| Tail(any)-solvent | 1.0 | 1.05 | 1.0 |
| Solvent-solvent | 0 |
Hence, all nonbonded interactions except the tail–tail interactions are repulsive, and the attraction between C tail beads is weaker than that between other tail beads.
The model was studied by Monte Carlo simulations at constant pressure P = 2ɛ/σ3 and constant zero surface tension in a fluctuating box of variable size and shape (42). The total number of lipids was kept fixed. The composition was sometimes allowed to fluctuate (semigrandcanonical ensemble). In that case, semigrandcanonical moves were implemented by means of configurational bias Monte Carlo moves (66), during which the identity of a lipid was switched between P and C. In the canonical simulations, the same moves can be used as virtual moves to determine the chemical potential difference μ for P and C chains.
Data Analysis.
To analyze configurations such as that shown in Fig. 3A, we map each monolayer onto a discrete grid χxy, where χ = 1 stands for “raft” and χ = 0 stands for “nonraft.” This is done with the following algorithm:
i) Assign chains to upper and lower bilayer leaflets according to their head-tail orientation.
ii) For each layer, sort chains into quadratic bins of side length 1.5σ according to the xy position of the head bead.
iii) Calculate the number density ρ, the C density ρc, and the nematic order S for each bin.
iv) At each vertex of the lattice, take the mean value of each observable in the surrounding bins.
v) If ρ⋅ρc⋅S > 0.15σ−4, the membrane at the vertex position is considered to be in the lo phase.
vi) Apply the Density Based Spatial Clustering of Applications with Noise (DBSCAN) cluster detection algorithm (67) with Eps = 3σ and minimum number of points (MinPts) = 3. The clusters are identified as lipid rafts.
The normalized cross-correlations Ki of opposing monolayers of a configuration i are calculated according to 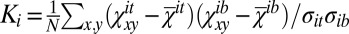 , where
, where 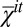 and
and 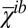 are the mean values of
are the mean values of 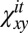 and
and 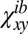 , respectively; σit and σib are their SDs, and N is the number of lattice points. To analyze whether a correlation Ki is significant, we take the same configuration i, displace one of the leaflets by a random offset with respect to the other
, respectively; σit and σib are their SDs, and N is the number of lattice points. To analyze whether a correlation Ki is significant, we take the same configuration i, displace one of the leaflets by a random offset with respect to the other 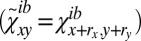 , and compare the new correlation
, and compare the new correlation 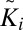 with Ki.
with Ki.
Solution of the Elastic Theory.
The elastic free energy Fel (Eq. 1) is minimized with respect to u(r) in the bulk (inside phase-separated domains) and to the boundary values of u and the normal derivative n∇u at the domain boundaries. We note that the latter must be continuous across the boundaries; otherwise, Fel diverges. This results in the Euler–Lagrange equation ξ4∇4u + 2bξ2∇2u + u = 0 in the bulk and in boundary conditions at the interfaces between domains: n∇(∇2u) must be continuous, and ∇2u jumps by 2δc0 at the boundaries. Inserting the Euler–Lagrange equations and the boundary condition in Eq. 1 gives the simplified expression in Eq. 2.
For stripe domains of width D with boundaries at z = ±D/2, the deformation profile u(z) satisfying the Euler–Lagrange equation and the boundary conditions is given by
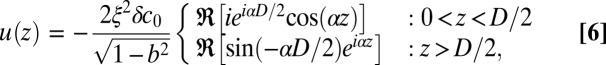 |
with 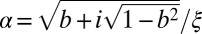 and u(−z) = u(z). Two isolated plane boundaries are obtained in the limit D → ∞. Finally, the radially symmetrical analytical solution for disk domains is
and u(−z) = u(z). Two isolated plane boundaries are obtained in the limit D → ∞. Finally, the radially symmetrical analytical solution for disk domains is
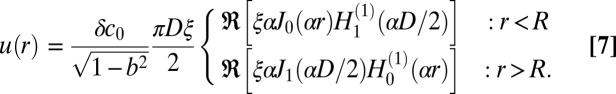 |
The profile of Eq. 7 satisfies the boundary conditions by virtue of the identity 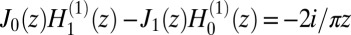 . Inserting Eqs. 6 and 7 into Eq. 2 gives Eqs. 5, 4, and 3 (in the limit D → ∞).
. Inserting Eqs. 6 and 7 into Eq. 2 gives Eqs. 5, 4, and 3 (in the limit D → ∞).
Derivation of the Landau–Brazovskii Model.
To analyze the situation close to the spinodal, we minimize F = Fel + FΦ for 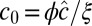 with respect to u. In wave-vector space q, this gives
with respect to u. In wave-vector space q, this gives 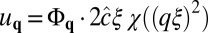 with χ(x) = x/(x2 − 2bx + 1). Inserting this in F and omitting boundary terms, we obtain
with χ(x) = x/(x2 − 2bx + 1). Inserting this in F and omitting boundary terms, we obtain 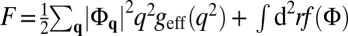 with
with  . The function geff(q2) has a minimum at
. The function geff(q2) has a minimum at 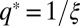 ; hence, a homogeneous phase (with Φ = constant) becomes unstable at geff(q*) = 0 [i.e.,
; hence, a homogeneous phase (with Φ = constant) becomes unstable at geff(q*) = 0 [i.e., 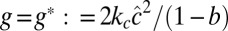 ]. Close to the spinodal, contributions q ∼ q* dominate; hence, we expand q2geff(q2) about q*2 up to second order. This finally gives a free energy expression of the Landau–Brazovskii form
]. Close to the spinodal, contributions q ∼ q* dominate; hence, we expand q2geff(q2) about q*2 up to second order. This finally gives a free energy expression of the Landau–Brazovskii form 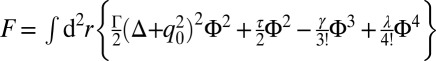 with
with 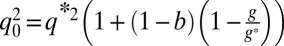 ,
, 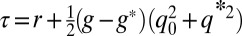 , and
, and 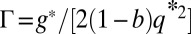 .
.
Acknowledgments
We thank S. Keller, T. Salditt, and M. Schick for valuable discussions. This work was supported by the German Science Foundation within the collaborative research center SFB-625. Simulations were carried out at the John von Neumann Institute for Computing (NIC) Jülich and the Mogon Cluster at Mainz University.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Simons K, van Meer G. Lipid sorting in epithelial cells. Biochemistry. 1988;27(17):6197–6202. doi: 10.1021/bi00417a001. [DOI] [PubMed] [Google Scholar]
- 2.Simons K, Ikonen E. Functional rafts in cell membranes. Nature. 1997;387(6633):569–572. doi: 10.1038/42408. [DOI] [PubMed] [Google Scholar]
- 3.Zurzolo C, van Meer G, Mayor S. The order of rafts. Conference on microdomains, lipid rafts and caveolae. EMBO Rep. 2003;4(12):1117–1121. doi: 10.1038/sj.embor.7400032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Pike LJ. Rafts defined: A report on the keystone symposium on lipid rafts and cell function. J Lipid Res. 2006;47(7):1597–1598. doi: 10.1194/jlr.E600002-JLR200. [DOI] [PubMed] [Google Scholar]
- 5.Hancock JF. Lipid rafts: Contentious only from simplistic standpoints. Nat Rev Mol Cell Biol. 2006;7(6):456–462. doi: 10.1038/nrm1925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Leslie M. Mysteries of the cell. Do lipid rafts exist? Science. 2011;334(6059):1046–1047. doi: 10.1126/science.334.6059.1046-b. [DOI] [PubMed] [Google Scholar]
- 7.Vereb G, et al. Dynamic, yet structured: The cell membrane three decades after the Singer-Nicolson model. Proc Natl Acad Sci USA. 2003;100(14):8053–8058. doi: 10.1073/pnas.1332550100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Veatch SL, Keller SL. Seeing spots: Complex phase behavior in simple membranes. Biochim Biophys Acta. 2005;1746(3):172–185. doi: 10.1016/j.bbamcr.2005.06.010. [DOI] [PubMed] [Google Scholar]
- 9.Brown DA, London E. Functions of lipid rafts in biological membranes. Annu Rev Cell Dev Biol. 1998;14:111–136. doi: 10.1146/annurev.cellbio.14.1.111. [DOI] [PubMed] [Google Scholar]
- 10.Jacobson K, Dietrich C. Looking at lipid rafts? Trends Cell Biol. 1999;9(3):87–91. doi: 10.1016/s0962-8924(98)01495-0. [DOI] [PubMed] [Google Scholar]
- 11.Edidin M. The state of lipid rafts: From model membranes to cells. Annu Rev Biophys Biomol Struct. 2003;32:257–283. doi: 10.1146/annurev.biophys.32.110601.142439. [DOI] [PubMed] [Google Scholar]
- 12.Pike LJ. Lipid rafts: Bringing order to chaos. J Lipid Res. 2003;44(4):655–667. doi: 10.1194/jlr.R200021-JLR200. [DOI] [PubMed] [Google Scholar]
- 13.Simons K, Vaz WLC. Model systems, lipid rafts, and cell membranes. Annu Rev Biophys Biomol Struct. 2004;33:269–295. doi: 10.1146/annurev.biophys.32.110601.141803. [DOI] [PubMed] [Google Scholar]
- 14.Zeyda M, Stulnig TM. Lipid Rafts & Co.: An integrated model of membrane organization in T cell activation. Prog Lipid Res. 2006;45(3):187–202. doi: 10.1016/j.plipres.2006.01.002. [DOI] [PubMed] [Google Scholar]
- 15.Hanzal-Bayer MF, Hancock JF. Lipid rafts and membrane traffic. FEBS Lett. 2007;581(11):2098–2104. doi: 10.1016/j.febslet.2007.03.019. [DOI] [PubMed] [Google Scholar]
- 16.Lingwood D, Simons K. Lipid rafts as a membrane-organizing principle. Science. 2010;327(5961):46–50. doi: 10.1126/science.1174621. [DOI] [PubMed] [Google Scholar]
- 17.Pralle A, Keller P, Florin EL, Simons K, Hörber JKH. Sphingolipid-cholesterol rafts diffuse as small entities in the plasma membrane of mammalian cells. J Cell Biol. 2000;148(5):997–1008. doi: 10.1083/jcb.148.5.997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zacharias DA, Violin JD, Newton AC, Tsien RY. Partitioning of lipid-modified monomeric GFPs into membrane microdomains of live cells. Science. 2002;296(5569):913–916. doi: 10.1126/science.1068539. [DOI] [PubMed] [Google Scholar]
- 19.Brown DA, Rose JK. Sorting of GPI-anchored proteins to glycolipid-enriched membrane subdomains during transport to the apical cell surface. Cell. 1992;68(3):533–544. doi: 10.1016/0092-8674(92)90189-j. [DOI] [PubMed] [Google Scholar]
- 20.Turner MS, Sens P, Socci ND. Nonequilibrium raftlike membrane domains under continuous recycling. Phys Rev Lett. 2005;95(16):168301. doi: 10.1103/PhysRevLett.95.168301. [DOI] [PubMed] [Google Scholar]
- 21.Yethiraj A, Weisshaar JC. Why are lipid rafts not observed in vivo? Biophys J. 2007;93(9):3113–3119. doi: 10.1529/biophysj.106.101931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Veatch SL, Keller SL. Separation of liquid phases in giant vesicles of ternary mixtures of phospholipids and cholesterol. Biophys J. 2003;85(5):3074–3083. doi: 10.1016/S0006-3495(03)74726-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Veatch SL, Keller SL. Miscibility phase diagrams of giant vesicles containing sphingomyelin. Phys Rev Lett. 2005;94(14):148101. doi: 10.1103/PhysRevLett.94.148101. [DOI] [PubMed] [Google Scholar]
- 24.Veatch SL, et al. Critical fluctuations in plasma membrane vesicles. ACS Chem Biol. 2008;3(5):287–293. doi: 10.1021/cb800012x. [DOI] [PubMed] [Google Scholar]
- 25.Veatch SL, Soubias O, Keller SL, Gawrisch K. Critical fluctuations in domain-forming lipid mixtures. Proc Natl Acad Sci USA. 2007;104(45):17650–17655. doi: 10.1073/pnas.0703513104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Honerkamp-Smith AR, Veatch SL, Keller SL. An introduction to critical points for biophysicists; Observations of compositional heterogeneity in lipid membranes. Biochim Biophys Acta. 2009;1788(1):53–63. doi: 10.1016/j.bbamem.2008.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Gompper G, Schick M. Phase Transitions and Critical Phenomena: Self-Assembling Amphiphilic Systems. Vol 16. Academic Press, London, UK; 1994. pp. 16–18. [Google Scholar]
- 28.Schick M. Membrane heterogeneity: Manifestation of a curvature-induced microemulsion. Phys Rev E Stat Nonlin Soft Matter Phys. 2012;85(3 Pt 1):031902. doi: 10.1103/PhysRevE.85.031902. [DOI] [PubMed] [Google Scholar]
- 29.Safran SA, Pincus P, Andelman D. Theory of spontaneous vesicle formation in surfactant mixtures. Science. 1990;248(4953):354–356. doi: 10.1126/science.248.4953.354. [DOI] [PubMed] [Google Scholar]
- 30.Leibler S, Andelman D. Ordered and curved meso-structures in membranes and amphiphilic films. J Phys. 1987;48:2013–2018. [Google Scholar]
- 31.Harden JL, MacKintosh FC. Shape transformations of domains in mixed-fluid films and bilayer membranes. Europhys Lett. 1994;28:495–500. [Google Scholar]
- 32.Sunil Kumar PB, Gompper G, Lipowsky R. Modulated phases in multicomponent fluid membranes. Phys Rev E Stat Phys Plasmas Fluids Relat Interdiscip Topics. 1999;60(4 Pt B):4610–4618. doi: 10.1103/physreve.60.4610. [DOI] [PubMed] [Google Scholar]
- 33.Baumgart T, Hess ST, Webb WW. Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature. 2003;425(6960):821–824. doi: 10.1038/nature02013. [DOI] [PubMed] [Google Scholar]
- 34.Brewster R, Pincus PA, Safran SA. Hybrid lipids as a biological surface-active component. Biophys J. 2009;97(4):1087–1094. doi: 10.1016/j.bpj.2009.05.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Yamamoto T, Brewseter R, Safran SA. Chain ordering of hybrid lipids can stabilize domains in saturated/hybrid/cholesterol lipid membranes. Europhysics Letters. 2010;91(2):28002-1-6. [Google Scholar]
- 36.Ipsen JH, Karlström G, Mouritsen OG, Wennerström H, Zuckermann MJ. Phase equilibria in the phosphatidylcholine-cholesterol system. Biochim Biophys Acta. 1987;905(1):162–172. doi: 10.1016/0005-2736(87)90020-4. [DOI] [PubMed] [Google Scholar]
- 37.Sankaram MB, Thompson TE. Cholesterol-induced fluid-phase immiscibility in membranes. Proc Natl Acad Sci USA. 1991;88(19):8686–8690. doi: 10.1073/pnas.88.19.8686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Almeida PFF, Vaz WLC, Thompson TE. Lateral diffusion in the liquid phases of dimyristoylphosphatidylcholine/cholesterol lipid bilayers: A free volume analysis. Biochemistry. 1992;31(29):6739–6747. doi: 10.1021/bi00144a013. [DOI] [PubMed] [Google Scholar]
- 39.Lindblom G, Orädd G. Lipid lateral diffusion and membrane heterogeneity. Biochim Biophys Acta. 2009;1788(1):234–244. doi: 10.1016/j.bbamem.2008.08.016. [DOI] [PubMed] [Google Scholar]
- 40.Feigenson GW. Phase diagrams and lipid domains in multicomponent lipid bilayer mixtures. Biochim Biophys Acta. 2009;1788(1):47–52. doi: 10.1016/j.bbamem.2008.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Collins MD, Keller SL. Tuning lipid mixtures to induce or suppress domain formation across leaflets of unsupported asymmetric bilayers. Proc Natl Acad Sci USA. 2008;105(1):124–128. doi: 10.1073/pnas.0702970105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schmid F, Düchs D, Lenz O, West B. A generic model for lipid monolayers, bilayers, and membranes. Comput Phys Commun. 2007;1177:168–171. [Google Scholar]
- 43.Lenz O, Schmid F. Structure of symmetric and asymmetric “ripple” phases in lipid bilayers. Phys Rev Lett. 2007;98(5):058104. doi: 10.1103/PhysRevLett.98.058104. [DOI] [PubMed] [Google Scholar]
- 44.West B, Schmid F. Fluctuations and elastic properties of lipid membranes in the fluid and gel state: A coarse-grained Monte Carlo study. Soft Matter. 2010;6:1275–1280. [Google Scholar]
- 45.West B, Brown FLH, Schmid F. Membrane-protein interactions in a generic coarse-grained model for lipid bilayers. Biophys J. 2009;96(1):101–115. doi: 10.1529/biophysj.108.138677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Waheed Q. 2012. Molecular Dynamics Simulations of Biological Membranes. Doctoral Thesis (Royal Institute of Technology, Stockholm, Sweden)
- 47.Waheed Q, Tjörnhammar R, Edholm O. Phase transitions in coarse-grained lipid bilayers containing cholesterol by molecular dynamics simulations. Biophys J. 2012;103(10):2125–2133. doi: 10.1016/j.bpj.2012.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Safran SA. Statistical Thermodynamics of Surfaces, Interfaces, and Membranes. Reading, MA: Addison–Wesley; 1994. pp. 193–200. [Google Scholar]
- 49.Dan N, Pincus P, Safran SA. Membrane induced interactions between inclusions. Langmuir. 1993;9:2768–2771. [Google Scholar]
- 50.Dan N, Berman A, Pincus P, Safran SA. Membrane induced interactions between inclusions. J Phys II. 1994;4:1713–1725. [Google Scholar]
- 51.Aranda-Espinoza H, Berman A, Dan N, Pincus P, Safran S. Interaction between inclusions embedded in membranes. Biophys J. 1996;71(2):648–656. doi: 10.1016/S0006-3495(96)79265-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Brannigan G, Brown FLH. A consistent model for thermal fluctuations and protein-induced deformations in lipid bilayers. Biophys J. 2006;90(5):1501–1520. doi: 10.1529/biophysj.105.075838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Brannigan G, Brown FLH. Contributions of Gaussian curvature and nonconstant lipid volume to protein deformation of lipid bilayers. Biophys J. 2007;92(3):864–876. doi: 10.1529/biophysj.106.094953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Neder J, West B, Nielaba P, Schmid F. Coarse-grained simulations of membranes under tension. J Chem Phys. 2010;132(11):115101. doi: 10.1063/1.3352583. [DOI] [PubMed] [Google Scholar]
- 55.Neder J, Nielaba P, West B, Schmid F. Interactions of membranes with coarse-grain proteins: A comparison. New J Phys. 2012;14:125017-1-24. [Google Scholar]
- 56.Rawicz W, Olbrich KC, McIntosh T, Needham D, Evans E. Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys J. 2000;79(1):328–339. doi: 10.1016/S0006-3495(00)76295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Honerkamp-Smith AR, et al. Line tensions, correlation lengths, and critical exponents in lipid membranes near critical points. Biophys J. 2008;95(1):236–246. doi: 10.1529/biophysj.107.128421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Brazovskii SA. Phase transitions of an isotropic system to a nonuniform state. Soviet Physics JETP. 1975;41(1):85–89. [Google Scholar]
- 59.Koynova R, Caffrey M. Phases and phase transitions of the phosphatidylcholines. Biochim Biophys Acta. 1998;1376(1):91–145. doi: 10.1016/s0304-4157(98)00006-9. [DOI] [PubMed] [Google Scholar]
- 60.Jacobson K, Mouritsen OG, Anderson RG. Lipid rafts: At a crossroad between cell biology and physics. Nat Cell Biol. 2007;9(1):7–14. doi: 10.1038/ncb0107-7. [DOI] [PubMed] [Google Scholar]
- 61.Salditt T. Thermal fluctuations and stability of solid-supported lipid membranes. J Phys Condens Matter. 2005;17:R287–R314. [Google Scholar]
- 62.Aeffner S, Reusch T, Weinhausen B, Salditt T. Energetics of stalk intermediates in membrane fusion are controlled by lipid composition. Proc Natl Acad Sci USA. 2012;109(25):E1609–E1618. doi: 10.1073/pnas.1119442109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Eggeling C, et al. Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature. 2009;457(7233):1159–1162. doi: 10.1038/nature07596. [DOI] [PubMed] [Google Scholar]
- 64.Lenz O, Schmid F. A simple computer model for liquid lipid bilayers. J Mol Liq. 2005;117:147–152. [Google Scholar]
- 65.Weeks JD, Chandler J, Andersen HC. Role of repulsive forces in forming the equilibrium structure of simple liquids. J Chem Phys. 1971;54:5237–5247. [Google Scholar]
- 66.Frenkel D, Smit B. Understanding Molecular Simulation: From Algorithms to Applications. 2nd Ed. Academic; 2001. pp. 336–350. [Google Scholar]
- 67.Ester M, Kriegel H, Sander J, Xu X. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (AAAI Press, Menlo Park, CA) 1996. A density-based algorithm for discovering clusters in large spatial databases with noise; pp. 226–231. [Google Scholar]