Ready-to-use food-allocation policy to reduce the effects of childhood undernutrition in developing countries

Abstract

Several aid groups have proposed strategies for allocating ready-to-use (therapeutic and supplementary) foods to children in developing countries. Analysis is needed to investigate whether there are better alternatives. We use a longitudinal dataset of 5,657 children from Bwamanda to construct a bivariate time-series model that tracks each child’s height-for-age z score (HAZ) and weight-for-height z score (WHZ) throughout the first 5 y of life. Our optimization model chooses which individual children should receive ready-to-use therapeutic or supplementary food based on a child’s sex, age, HAZ, and WHZ, to minimize the mean number of disability-adjusted life years (DALYs) per child during 6–60 mo of age [which includes childhood mortality calculated from a logistic regression and the lifelong effects of stunting (i.e., low HAZ)] subject to a budget constraint. Compared with the strategies proposed by the aid groups, which do not use HAZ information, the simple strategy arising from our analysis [which prioritizes children according to low values of a linear combination of HAZ, WHZ, and age and allocates the entire budget to therapeutic (i.e., 500 kcal/d) food for the prioritized children] reduces the number of DALYs by 9% (for the same budget) or alternatively incurs the same number of DALYs with a 61% reduction in cost. Whereas our qualitative conclusions appear to be robust, the quantitative results derived from our analysis should be treated with caution because of the lack of reliable data on the impact of supplementary food on HAZ and WHZ, the application of our model to a single cohort of children and the inclusion and exclusion errors related to imperfect food targeting.

Undernutrition is often measured by wasting [weight-for-height z score (WHZ) below −2 according to World Health Organization (WHO) child growth standards (1)] and stunting [height-for-age z score (HAZ) below −2]. Along with intrauterine growth restriction, wasting and stunting are estimated to account for over 21% of deaths and disability-adjusted life-years (DALYs) among the world’s children under 5 y old (2). The prevalences of stunting and wasting are particularly high in the least developed countries and are 9% and 38% in Sub-Saharan Africa and 19% and 47% in South Asia (3). Ready-to-use therapeutic food (RUTF) has revolutionized the treatment of severe wasting (WHZ < −3) (4), which is often attributable to the transient effects of disease or food shortages. In contrast, stunting is attributable to chronic undernutrition, is more difficult to reverse, and has lifelong health, education, and economic effects (5). Moreover, although children with severe undernutrition have the greatest risk, the majority of mortality and morbidity stems from the mild [WHZ or HAZ ∈(−2, −1)] and moderate [WHZ or HAZ ∈(−3, −2)] forms of undernutrition (6). The success of RUTF has led to the introduction of ready-to-use supplementary food (RUSF), which provides less energy at a lower cost than RUTF and enriches a child’s existing diet with the goal of treating mild or moderate undernutrition or preventing acute undernutrition (7, 8).

Consequently, in the face of restricted funds, it is not clear how limited food aid should be allocated to minimize the deleterious effects of undernutrition in the least developed countries. We construct a mathematical optimization model that allocates food to a cohort of children from 6 mo to 5 y old, with the goal of minimizing the DALYs attributable to early loss of life and years lost to disability, subject to a budget constraint on the amount of food aid. We optimize over a restricted class of policies that makes intervention decisions based on a child’s sex, age, HAZ, and WHZ and compare the performance of this policy to currently recommended policies (7, 8).

Model

Overview.

Details of the model formulation, statistical analysis, and optimization procedure are in SI Appendix and are briefly summarized here. We construct a time-series model for the evolution (in the absence of treatment) of each child’s WHZ and HAZ from 6 mo to 5 y using a longitudinal dataset of the weights and heights (up to six measurements at 3-mo intervals from October 1989 to February 1991) of a random cluster sample (16 villages out of a total of 52 villages) of 5,657 children from Bwamanda in the Democratic Republic of Congo (9). The effect of 3 mo of food intervention on subsequent HAZ and WHZ values is estimated using data from a cluster randomized trial (12 villages, with 6 receiving intervention) in Maradi, Niger, involving RUTF (10). We use logistic regression to estimate childhood mortality rates as a function of age, HAZ, and WHZ from data in ref. 9. Aggregating the individual time series for each child yields our system state equation, which tracks the evolution (over 3-mo intervals from 6 mo to 5 y) of the joint population-wide probability density function (PDF) of WHZ and HAZ for each sex. We optimize over a class of policies that allocates either RUTF, some supplementary food, or no food to each child based on the child’s sex, age, HAZ, and WHZ and compare the performance (DALYs for a fixed food aid budget) of this policy to currently recommended policies (7, 8).

Time-Series Model for Each Child’s HAZ and WHZ.

We fit the data in ref. 9 to a time-series model (separate models are developed for boys and girls) for the (HAZ,WHZ) dynamics in the absence of intervention (SI Appendix, Section 1). These data exhibit only modest seasonality, which is not inconsistent with the fact that malaria transmission was somewhat steady throughout the year (9); consequently, we do not incorporate seasonality into the model. To capture the nonstationarity, autocorrelation, and cross-correlation in these data, we model the dynamics of (HAZ,WHZ) for each individual (in 3-mo time intervals from 6 mo to 5 y) by a bivariate autoregressive integrated moving average process [ARIMA(2,1,0)] (11), i.e., the first-order differences are modeled by an autoregressive process of order 2, with the trend fit to a cubic function of age and the residuals modeled by a bivariate normal distribution.

Effect of Intervention.

We could find only one randomized clinical trial (10) that included a nontreatment control group, measured the impact of intervention on WHZ and HAZ values using the WHO standards (1) and had a sufficiently large sample size to produce reasonably accurate estimates. RUTF (500 kcal/d) was administered for 3 mo to 1,671 children ages 6–60 mo in ref. 10, and for lack of data, we assume that the change in HAZ or WHZ as a result of intervention is independent of age, sex, and pretreatment HAZ and WHZ levels. We model the effect of 3 mo of food intervention on HAZ and WHZ by independent lognormal distributions (SI Appendix, Section 2). Because of the lack of studies that reliably estimate the impact of supplementary food, we extrapolate the RUTF estimates to other intervention doses by making the key assumption that the mean treatment effect is linear in the amount of energy consumed. In a sensitivity analysis, we relax this key assumption.

Objective Function.

The mean number of DALYs associated with a child during ages 6–60 mo includes the number of years lost attributable to deaths during 6–60 mo plus the number of healthy life years lost attributable to disability (SI Appendix, Section 3). DALYs attributable to death are calculated using a total life expectancy of 46 y (12), a discount factor of 0.03, and uniform weighting of ages (13). We use logistic regression and data in ref. 9 to estimate the mortality rate in the following 3 mo as a function of a child’s age, HAZ, and WHZ. We discarded an attempt to incorporate HAZ and WHZ values from the previous 3 and 6 mo because multicolinearity drastically reduced the accuracy of the estimated regression coefficients.

The traditional approach to calculating DALYs in this setting is to assume that DALYs are incurred if and only if HAZ or WHZ is < −1. To avoid artificially inducing the optimal solution to maintain children at just above the HAZ = −1 and WHZ = −1 levels, we assume that the disability incurred is proportional to |1 + HAZ| or |1 + WHZ| for HAZ < −1 or WHZ < −1, and is 0 otherwise, and choose the proportionality constants, so that the expected DALYs is the same as under the traditional approach with DALY weights of 0.002 for HAZ < −1 and 0.0532 for WHZ < −1 (13). We follow the convention that stunting (ref. 14, p. 8), but not wasting (ref. 13, p. 269), has lifelong effects and make the simplifying assumption that people do not recover from stunting after age 5 y.

Policies.

The United States Agency for International Development (ref. 7, p. 48) recommends that RUTF should be given to children with WHZ < −3, blanket supplementary feeding should be used (assuming ample supply) if the probability P(WHZ < −2) ≥ 0.15 [or P(WHZ < −2) ∈ (0.1, 0.15) with aggravating factors], and targeted supplementary feeding should be used if P(WHZ < −2) ∈ (0.1, 0.15) [or P(WHZ < −2) ∈ (0.05, 0.1) with aggravating factors]. The World Food Program of the United Nations (ref. 8, p. 8) articulates a slightly different strategy: RUTF for children under age 5 y with WHZ < −2 should be targeted unless there are safety, accessibility, or health system capacity issues, blanket distribution of 50–100 kcal/d should go to <2-y olds if food insecurity is low and stunting is high, and blanket distribution of 250 kcal/d should be allocated to <3-y olds if food insecurity is high and malnutrition risk is high. For the basis of comparison, we consider seven benchmark policies inspired by these recommendations (Table 1). We assume RUTF is administered at a dose of 500 kcal/d. We allow supplementary food to be administered in various doses, although we use the term RUSF to correspond to a dose of 250 kcal/d. These policies include various combinations of three targeted treatments [RUTF for WHZ < −3, RUTF for WHZ < −2, or RUTF for WHZ < −3 plus RUSF for WHZ ∈ (−3, −2)] and three blanket distributions [no blanket distribution, RUSF to ≤3-y olds (and WHZ > −2), and 75 kcal/d to ≤2-y olds (and WHZ > −2)].

Table 1.

Seven benchmark policies listed according to increasing cost

Name of policy	Targeted		Blanket
	WHZ	Amount (kcal/d)	WHZ	Age (y)	Amount (kcal/d)
RUTF-SAM	<−3	500
RUTF-SAM + RUSF-MAM	<−3	500
	∈(−3, −2)	250
RUTF-MAM	<−2	500
RUTF-SAM + RUSF-MAM + blanket 75 kcal/d	<−3	500	>−2	≤2	75
	∈(−3, −2)	250
RUTF-MAM + blanket 75 kcal/d	<−2	500	>−2	≤2	75
RUTF-SAM + RUSF-MAM + blanket RUSF	<−3	500	>−2	≤3	250
	∈(−3, −2)	250
RUTF-MAM + blanket RUSF	<−2	500	>−2	≤3	250

Policies are defined by the amount of food given to children satisfying the WHZ and age specifications; targeted food applies to ages ≤5 y old. MAM, moderate acute malnutrition (i.e., WHZ < −2); SAM, severe acute malnutrition (i.e., WHZ < −3).

It is too difficult to compute an optimal solution to our problem, which would decide how many kilocalories per day to give each child based on sex, age, current (HAZ,WHZ), and (HAZ,WHZ) 3 and 6 mo previously. Instead, we consider a class of restricted (i.e., nonoptimal) policies and optimize within this class (SI Appendix, Section 4). This restricted class of policies bases its intervention decisions on a child’s score, S(HAZ_t, WHZ_t, t/3) in SI Appendix, Eq. 21. This score function, which varies by sex, represents the contribution (in DALYs) to the objective function by a child of age t months with current values (HAZ_t,WHZ_t), after accounting for the possibility that children under 5 y old might incur lifelong stunting effects. This class of policies has four parameters [two thresholds (θ_u, θ_l) and two dosage levels (x_l, x_u)] and is intended to be highly effective while still being computationally tractable and simple enough to implement in practice. It gives RUTF to children with S(HAZ_t,WHZ_t, t/3) > θ_u, gives x_u kcal/d to children with S(HAZ_t,WHZ_t, t/3) ∈ (θ_l, θ_u), and gives x_l kcal/d to children with S(HAZ_t,WHZ_t, t/3) ≤ θ_l. We assume that, for all policies, all food is consumed by its intended recipients.

Evolution of the Population-Wide PDF of (HAZ,WHZ).

To assess population-wide DALYs and costs, we aggregate the individual sample paths of (HAZ,WHZ) from the ARIMA model and incorporate the impact of intervention for our proposed class of policies to derive a transition equation that tracks the population-wide PDF of (HAZ,WHZ) from each age to the next, at 3-mo intervals (SI Appendix, Section 5). Due to the memory required in the ARIMA model, the state of the system at each age is given by a six-dimensional joint PDF of the population-wide HAZ and WHZ PDFs at the current age, at 3 mo younger and at 6 mo younger.

Optimization Problem.

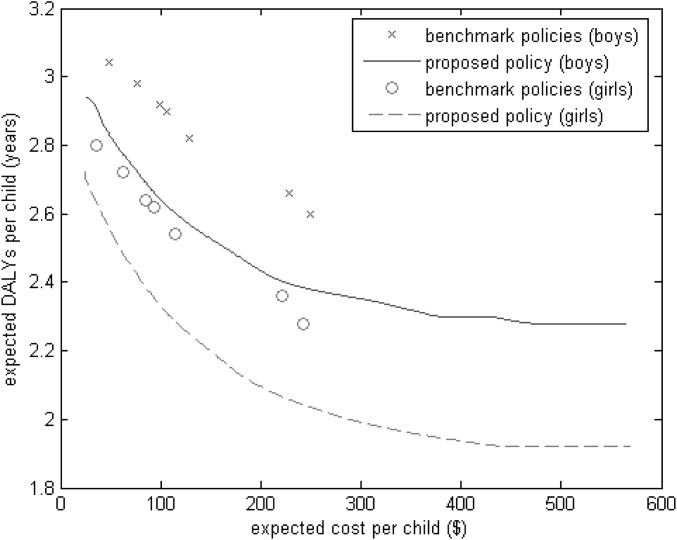
For the class of policies described above, we choose the parameter values (θ_u, θ_l, x_u, x_l) to minimize the mean number of DALYs per child during 6–60 mo subject to a budget constraint on the mean cost of food aid per child during 6–60 mo (SI Appendix, Section 6). We assume that RUTF costs $0.37/d×90 d=$33.30 per intervention per child for RUTF and $0.19/d × 90 d = $17.10 per intervention per child for RUSF (15). Costs for other daily dosages are assumed to vary linearly relative to these two cost estimates. By solving the optimization problem for many budget values, we generate a DALYs vs. cost tradeoff curve for our proposed class of policies. Because of the difficulties in computing the six-dimensional integral in the system state equation, we use simulation to evaluate the policies in Table 1 and to optimize and evaluate the proposed class of policies. We simulate 10⁶ children, which generates 95% confidence intervals in Fig. 1 of ±0.003 y for the mean DALYs and ±$0.16 for the mean cost.

Fig. 1.

Expected DALYs per child vs. expected cost per child for the seven benchmark policies in Table 1 and for the class of proposed policies.

Results

Parameter Estimates.

In the ARIMA model (SI Appendix, Section 1.7), the HAZ and WHZ values from 3, 6, and 9 mo earlier have a positive but progressively smaller effect on the current HAZ and WHZ. The cross-dependent coefficients from 3, 6, and 9 mo earlier sum to zero [as dictated by the form of ARIMA(2,1,0)] and consequently previous WHZ (HAZ, respectively) values have only a limited impact on the current HAZ (WHZ, respectively), although the effect of the most recent WHZ value on the current HAZ is larger than the effect of the most recent HAZ value on the current WHZ. Also, the variance of WHZ is considerably larger than the variance of HAZ (SI Appendix, Eqs. 9 and 12), consistent with the fact that wasting is transient and reversible, whereas stunting is due to long-term malnutrition.

Based on the treatment data in ref. 10, we estimate that 3 mo worth of RUTF increases HAZ by a random amount with mean 0.15 and SD 0.7, and increases WHZ by a random amount with mean 0.19 and SD 1.7.

The estimated 3-mo mortality rate is logit(−0.414HAZ − 0.236WHZ − 0.059t − 4.989) for boys and logit(−0.403HAZ − 0.431WHZ − 0.054t − 5.144) for girls. As expected, the death rate is higher for lower z scores and younger ages. The effects of wasting and stunting on mortality are roughly comparable for girls. The main difference between the sexes is that boys appear to be more likely to survive wasting than girls, although the difference is not statistically significant (SI Appendix, Table 7).

In the absence of treatment, we compute the portion of the mean DALYs per child attributable to each of the four components (SI Appendix, Eq. 18) and find that 91.4% is attributable to childhood mortality, 2.7% to childhood wasting, 1.0% to childhood stunting, and 4.9% to the lifelong effects of stunting (SI Appendix, Section 4).

Base-Case Results.

Fig. 1 plots mean DALYs vs. mean cost for each sex, where the proposed class of policies generates a tradeoff curve and each policy in Table 1 produces a point. The seven benchmark policies from Table 1 can also be viewed as generating a tradeoff curve, although not all seven policies, particularly the second-most costly policy, are on the lower-left envelope of these seven points. Averaged over the 14 points in Fig. 1, the proposed policy outperforms the seven benchmark policies, achieving a 9% reduction in mean DALYs for any given budget or achieving the same DALYs with a 61% reduction in the expected cost.

For all budget (i.e., expected cost) values in Fig. 1, the optimal parameter values satisfy θ_l = θ_u, x_l = 0 (SI Appendix, Section 7), and, hence, the optimal policy within our proposed class of policies takes a very simple form: give RUTF to children with S(HAZ_t,WHZ_t, t/3) > θ_u and give no food to children with S(HAZ_t,WHZ_t, t/3) < θ_u.

Sensitivity Analyses.

We perform four sensitivity analyses, where we recompute Fig. 1 after a change in some parameter values. Because >90% of the objective function is attributable to childhood mortality and the discount factor for childhood mortality varies little through the first 5 y (SI Appendix, Eq. 18), it seems likely that the proposed class of policies would perform nearly as well if we replace the score function S(HAZ_t,WHZ_t, t/3) by the much simpler argument in the logit function (e.g., −0.403HAZ − 0.431WHZ − 0.054t for girls). This is confirmed in the SI Appendix, Fig. 16, where the two tradeoff curves (one generated by the score function, the other generated by the logit function) are nearly indistinguishable (the average relative deviation is 0.5%).

Because our analysis is based on a specific longitudinal dataset (16), we explore another scenario that differs by the prevalence of wasting and stunting. For this dataset, the mean HAZ is −1.997, P(HAZ < −2) = 0.52, the mean WHZ is −0.580, P(WHZ < −3) = 0.029, and P(WHZ < −2) = 0.12 (16); these numbers are based on the outdated National Center for Health Statistics (NCHS) child growth standards, and the prevalence of stunting and wasting is 0.606 and 0.048 based on the WHO growth standards. In contrast, the current prevalence of stunting and wasting in Sub-Saharan Africa is 0.38 and 0.09 (ref. 3, p. 95). Hence, the ratio of stunting to wasting is higher in ref. 16 than the corresponding ratio for Sub-Saharan Africa or for most other studies (e.g., table 2 in ref. 17). Another dataset in ref. 16 is from Senegal, which has a lower stunting-to-wasting ratio than Sub-Saharan Africa: mean HAZ = −1.087, P(HAZ < −2) = 0.24, mean WHZ = −0.767, P(WHZ < −3) = 0.032 and P(WHZ < −2) = 0.16 (under the NCHS standards). We adapt our model to the Senegal scenario by changing only the trend terms in the ARIMA model. More specifically, we add the difference of the mean HAZs, −1.087 − (−1.997) = 0.910, to the right sides of SI Appendix, Eqs. 1 and 3 and add the difference of the mean WHZs, −0.767 − (−0.580) = −0.187, to the right sides of SI Appendix, Eqs. 2 and 4. Although the DALYs in the Senegal scenario are about half as much as in the base case, the qualitative results are very similar (SI Appendix, Fig. 17): relative to the benchmark policies, the proposed policy (which, again, is the “RUTF-or-nothing” policy) reduces expected DALYs by 7.5% and the expected cost by 55.5% (compared with 9% and 61% in the base case).

To assess the robustness of the optimality of the RUTF-or-nothing policy, we consider a scenario where P(WHZ < −2) = 0.15, which is the trigger for using blanket supplementary feeding in the absence of aggravating factors (7), and P(HAZ < −2) = 0.63, so that the stunting-to-wasting ratio is 4.2, which is the same as that in Sub-Saharan Africa (i.e., 0.38/0.09). As in the Senegal scenario, we change the trend terms in the ARIMA model but now further assume that HAZ and WHZ have normal distributions (SI Appendix, Table 12). The DALYs and costs under the benchmark policies are much higher in this scenario because of the large increase in wasting (SI Appendix, Fig. 18). The proposed policy is still the RUTF-or-nothing policy, and it reduces expected DALYs by 6.9% and the expected cost by 23.2% (compared with 9% and 61% in the base case).

To relax the key assumption that the mean and SD of the treatment effect is linear in the amount of energy consumed, we consider a simple concave function where the mean and SD of the treatment effect is proportional to the square root of the energy consumed. For example, the mean effect of RUSF (i.e., 250 kcal/d) would be 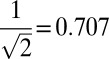times the mean effect of RUTF (500 kcal/d). As expected, the five policies in Table 1 that provide supplementary food perform better than they did in the base case (SI Appendix, Fig. 19). The simple policy that gives RUTF to some children and no food to the remaining children is still optimal among the class of proposed policies (under the additional assumption that, to prevent children from receiving impractically small amounts of food, the minimum nonzero amount of food given to a child is 50 kcal/d) and still dominates the benchmark policies, albeit by a smaller margin (the 9% and 61% reductions in the base case are now 5.6% and 43%).

Discussion

Food-Allocation Results.

Our main result is that, compared with the benchmark policies in Table 1, the proposed policy achieves either a 9% reduction in expected DALYs at the same expected cost, or a 61% reduction in expected cost at the same expected DALYs. There are three noteworthy aspects of this result. First, these improvements are attained by incorporating HAZ (and sex) into the food-allocation decision, rather than relying solely on WHZ (and age). The second and most surprising aspect is that, regardless of the budget, the optimal policy within the proposed class is very simple: even allowing for the possibility of dividing children into three groups every 3 mo, where one group receives RUTF and the other two groups receive arbitrary amounts of supplementary food, it is optimal to divide the children into two groups, with one receiving RUTF and the other receiving nothing. Although we have no rigorous mathematical proof, in SI Appendix, Section 8, we give a heuristic argument that provides some intuition for the optimality of the RUTF-or-nothing policy within the class of policies considered.

This policy stands in contrast to some existing proposals that use blanket supplementary feeding (7, 8); note that ref. 7 recommends blanket distribution if P(WHZ < −2) ≥ 0.15 or ∈ (0.1, 0.15) with aggravating conditions, which is in the range of our third sensitivity analysis. Indeed, this policy is as simple conceptually as the RUTF-SAM and RUTF-MAM policies in Table 1 and is simpler than the other five policies in Table 1, which place children into one of three (rather than two) categories and/or require an additional blanket distribution at a lower dose. Consequently, to the extent that simpler policies have lower screening costs, our omission of screening costs is a conservative assumption.

The third noteworthy aspect is that because >90% of the DALYs are attributable to childhood mortality, these reductions in expected DALYs or expected cost can be achieved with a much more transparent policy based on the logit function for the mortality rate; i.e., after dividing the argument in the logit function by the age coefficient, the policy gives RUTF to girls with the lowest values of 7.5HAZ + 8WHZ + age and to boys with the lowest values of 7HAZ + 4WHZ + age, where age is measured in months. Note that a switch from a benchmark policy to the proposed policy does not require any additional training or education: the benchmark policies and the proposed policy use the same raw data (weight, height, age, sex) from each child, and the most difficult part of computing, e.g., 7.5HAZ + 8WHZ + age, is the calculation of HAZ or WHZ, which is already required in all of the benchmark policies. However, one conceivable danger in using HAZ is that caretakers could overstate a child’s actual age in an attempt to reduce their HAZ score and receive food. If age was also incorporated into the allocation decision (as in our proposed policy), then the incentive to distort a child’s age may be more opaque.

The decision of where to reside on the optimal tradeoff curve (i.e., how much money should be spent) is very complex and depends on a variety of issues, including the amount of available funds, the background population-level risk, and the cost-effectiveness of competing interventions in health, education, and other areas of development. Because our model does not explicitly capture all of these factors, it is prudent to view our analysis as elucidating how best to allocate food under a specified budget constraint and not as providing explicit guidance on how much money to spend in a particular setting. Nonetheless, the marginal cost-effectiveness curve (in DALYs averted per dollar) for the proposed class of policies, which is the first derivative of the tradeoff curve in Fig. 1, is computed and discussed in SI Appendix, Section 9.

Our main qualitative result (that greater DALY reductions can be achieved by incorporating HAZ and WHZ information into food-allocation decisions) appears to be quite robust: even when the wasting-to-stunting ratio is unusually high (i.e., the Senegal sensitivity analysis), we still find significant improvements by incorporating HAZ. Our other main qualitative result (that the simple RUTF-or-nothing policy is optimal among all policies that allow for three energy levels of food) appears to be reasonably robust: even when RUSF (250 kcal/d) produces 0.707 times the mean effect of RUTF (500 kcal/d) or when the wasting prevalence is 0.15, the RUTF-or-nothing policy remains optimal within the proposed class of policies. Moreover, our omission of food sharing (at least to the extent that individual packets of RUTF are less apt to be shared than bulk RUSF), any fixed distribution costs per child that are independent of dose, and screening costs are all conservative assumptions in this regard, in that they all favor RUSF over RUTF. The insensitivity of the RUTF-or-nothing policy to the absolute and relative levels of stunting and wasting tentatively suggests that the use of blanket supplementary feeding would be outperformed by the RUTF-or-nothing policy, regardless of the background wasting prevalence and the severity of aggravating factors. However, unlike our main qualitative result, where good data exist, the robustness of this qualitative result remains uncertain until better data are produced regarding the relative efficacy of RUTF and RUSF.

Statistical Results.

Although our focus is on identifying and assessing food-allocation strategies, some of the statistical analyses required to construct our model are of independent interest. The ARIMA(2,1,0) model proposed here is consistent with a recent statistical analysis of 1,599 children from eight cohort studies (17). They find that HAZ in the first 6 mo has no effect on subsequent WHZ values up to 24 mo of age, which supports our choices to start the model at the age of 6 mo and to maintain 9 mo of memory in z values (i.e., two periods in the ARIMA model corresponds to three periods, or 9 mo, of memory). Our ARIMA coefficients, which imply that low WHZ values lead to a subsequent decrease in HAZ, are consistent with their observation that children with wasting or decreases in WHZ are at a higher risk for linear growth retardation (17, 18). Our model can also, but does not necessarily, satisfy their observation that greater WHZ variability causes lower subsequent HAZ. Moreover, in our model the effect of the previous WHZ value on the current HAZ is larger than the effect of the previous HAZ value on the current WHZ, which is consistent with the analysis in ref. 19.

Our logistic regression, by allowing the death rates to vary continuously with HAZ and WHZ, captures the fact that many deaths can be attributable to mild forms of undernutrition (20). The empirical mortality rates we derive from the data in ref. 9 exhibit a qualitative similarity to those derived from the odds ratios in table 2 of ref. 2 (SI Appendix, Section 3.2). In particular, in both sets of data, the mortality rate for HAZ < −3 is much smaller than the mortality rate for WHZ < −3, which appears to contradict the fact that the WHZ coefficient is smaller than the HAZ coefficient for boys in our logistic regression. However, this apparent contradiction is largely explained by an asymmetry in the joint distribution of HAZ and WHZ: for the data in ref. 9, 55.6% of children with WHZ < −3 have HAZ < −3, whereas only 1.8% of children with HAZ < −3 have WHZ < −3 (SI Appendix, Table 13), and, similarly, 68.8% of children with WHZ < −2 have HAZ < −2, whereas only 5.4% of children with HAZ < −2 have WHZ < −2 (SI Appendix, Table 14). That is, the mortality rate of children with low WHZ receives a compounding effect from low HAZ but not vice versa. This crucial asymmetry seems to have been overlooked, and the fact that univariate correlation with mortality is much larger for wasting than stunting may have led to an inadvertent focus on wasting. The identification of this asymmetry, if it can be reproduced in other datasets, should put stunting on an equal footing with wasting with respect to its importance in childhood undernutrition. Related studies using logistic regression models for childhood mortality are discussed in SI Appendix, Section 10.

Another statistical finding is that >90% of the DALYs associated with a cohort of children under age 5 y is attributable to early childhood mortality; in particular, the lifelong effect of stunting appears to be a second-order issue. Although DALYs do not incorporate productivity losses associated with cognitive impairment that is associated with stunting, the 3% discounting would cause this statistical finding to be largely unaffected if these productivity losses were included. With that said, stunting plays a significant role in early childhood mortality, and so food aid should focus on both low-HAZ and low-WHZ children.

Limitations of Our Study.

Our mathematical model captures only some of the issues surrounding food aid decisions. We take as given the food’s composition and implicitly assume that the food contains all of the relevant nutrients and minerals (21, 22) and is well accepted by caregivers and children. We believe that these are appropriate assumptions for the strategic questions being addressed here. We ignore the interaction of (HAZ,WHZ) values with various diseases such as HIV. This omission seems ethically appropriate because, e.g., if HIV status was incorporated into the model, the reduced impact of treatment and the higher death rate of HIV-positive children (26) may cause the optimization model to not allocate food to HIV-positive children; i.e., our omission of HIV status and other aggravating factors causes our current recommendations to be risk-averse in situations where there is high vulnerability, perhaps at the expense of some suboptimality. Although our time-series model could easily incorporate a seasonal component to capture the annual cycle of food shortages and malaria, the amount of seasonality in the data in ref. 9 does not appear to warrant this inclusion; however, our policy adapts well to a seasonal setting because it provides more aggressive intervention when (HAZ,WHZ) values are low. We ignore the possibility that a stunted child could develop obesity-related problems as an adult if given a high-energy, high-fat diet over long periods (24), although this would be a minor factor with a 3% discount rate. We also ignore any errors in measuring HAZ and WHZ. Height is more difficult to measure than weight and the variance in measurement error is likely negatively related to HAZ (although the noise impacts WHZ too), presumably leading to some attenuation bias with respect to the height coefficient estimates in our time-series model and logistic regression model.

Perhaps the most unrealistic assumption in our model is that all of the allocated food is consumed by its intended recipients. In practice, targeting inefficiency exists and can be caused by lack of access, screening errors, theft and spoilage during distribution, and food diversion via cultural practices of food-sharing within households and local communities. This issue is difficult to model because it requires the specification of how much food is lost, stolen, or shared with people over 5 y old, how much goes to untargeted children less than 5 y old (and the health of these untargeted children, given that sibling health is probably positively correlated), and the probability distribution of the fraction of targeted food that each targeted child consumes (e.g., if 80% of food is consumed by its intended recipients, do 80% of the targeted children receive all of their food and 20% receive none, do all targeted children receive 80% of their food, or, as is undoubtedly the case, is there a more complicated middle ground between these two extremes). Although this complex issue deserves to be studied (25), two things seem clear: imperfect targeting increases the number of DALYs and imperfect targeting occurs for all food-allocation policies, including the benchmark policies in Table 1 and the proposed class of policies. Hence, although imperfect targeting reduces the cost-effectiveness of various policies and, thus, might impact the total amount of food aid that is desirable, the most relevant question from a policy standpoint is whether the inclusion and exclusion error rates differ among various policies. Consequently, it would be valuable to gather data on, e.g., the relative amount of pilfering and food sharing for individual packets of RUTF vs. bulk RUSF.

In our view, the biggest shortcoming of the study is attributable to the paucity of data. The data include (HAZ,WHZ) evolution, the effect of treatment on (HAZ,WHZ), and the mortality rate, which we consider in turn. Although the dataset in ref. 9 is dated, it is one of the most comprehensive longitudinal datasets for children under 5 y [e.g., some studies have smaller sample sizes, have less frequent measurements (the Senegal data in ref. 16) or cover a smaller age span (19)]. It has a wasting-to-stunting ratio that is nearly the same as that in current Sub-Saharan Africa (3), and the growth pattern in SI Appendix, Figs. 7 and 8 is similar to those from other Sub-Saharan African datasets (e.g., figure 1 in ref. 19). Fitting an ARIMA model to data that had seasonality and more wasting would help assess the robustness of this approach (our crude sensitivity analysis uses the mean stunting and wasting from the Senegal dataset in ref. 16, but this dataset cannot be used directly because it has measurements at only 6-mo intervals). More generally, there is substantial heterogeneity among studies in terms of the sizes of their etiological effects (e.g., disease pressures, weather, potable water access, caregiving practices), and it is important to test this model in other cohorts.

Given that >90% of the DALYs are attributable to childhood mortality, it is important to understand how a child’s (HAZ,WHZ) history impacts his survival. Our estimates are derived from the data in ref. 9, and the mortality rate of those under 5 y in ref. 9 is similar to current estimates for the least developed countries (26). It is reassuring that our estimates are qualitatively similar to the odds ratios in ref. 2, which, in turn, are qualitatively similar to the relative risks in ref. 6, although the latter study used the outdated growth reference standards. However, further analysis is required to understand whether the different WHZ coefficient for boys vs. girls is real or an artifact of the data and whether this difference (if real) might be attributable to the possibility that boys received better care than girls. In addition, a much larger sample size would be needed to overcome the multicolinearity that naturally arises if one wants to understand the role of past (as opposed to only current) (HAZ,WHZ) values.

The weakest aspect of the data pertains to the effect of treatment. We found only one study (10) that was useful for our purposes: other studies either had small sample sizes, did not have a treatment-free control group, or did not measure HAZ and WHZ levels using the WHO growth standards. As a result, four key issues are not adequately addressed in our model. It would not be difficult to extend our model to allow the HAZ or WHZ increment attributable to treatment to depend on the pretreatment (HAZ,WHZ) levels, but this issue was not studied in ref. 10. The amount of interperson variability in the impact of treatment is very high, which makes it important to accurately model the entire probability distribution. For lack of distributional data, we assume a lognormal distribution; even if the raw data in ref. 10 were available, the distribution of the effect of treatment would need to be teased out from the distribution of the combined effects of treatment and natural evolution in the treatment arm and from the distribution of the natural evolution in the control group, both of which depend on pretreatment (HAZ,WHZ) levels. The third issue is our omission of the effect of food-intervention history on the size of the impact of the current food intervention. Indeed, for lack of data, we assume that the effects of each 3-mo course of treatment are independent and identically distributed, even for the same person. A marginal structural model (27), where (HAZ,WHZ) levels predict both survival and future food intervention and, hence, are influenced by prior food interventions, might be appropriate in this setting. Although prior food interventions appear to affect the performance of current food interventions (15), calibrating a marginal structural model would require longitudinal individual-level data on (HAZ,WHZ) and food intervention history. Finally, because ref. 10 only administered RUTF, the most glaring omission in the data is a reliable estimate of the effect of supplementary food. More generally, the fourth issue is to understand how the impact of treatment depends on the time duration of treatment and the daily dose, which dictates the relative attractiveness of various supplementary food strategies. Without data for guidance, we assume that the impact of treatment depends on the length of treatment and the daily dose only via their product, although the results of our sensitivity analysis suggest some insensitivity to this assumption. As with the third issue, data to understand the fourth issue will be difficult to gather (15). In addition to these four issues, a more subtle caveat about combining the Bwamanda data (9) and the RUTF trial data (10) is that mortality in ref. 9 is associated with free-living weights and heights, whereas the therapeutically induced gains in weight and height achieved in ref. 10 might have a smaller effect because of incomplete reversal of accumulated damage to immune function, internal organs, etc.

Conclusion

The development of a strategy to allocate ready-to-use foods in developing countries is a prime candidate for mathematical modeling and analysis: the problem is complex, the range of possible policies is immense, and it is difficult to run randomized controlled trials. Existing allocation policies have not been analyzed with respect to their suboptimality, and our study is intended to inform the debate on this topic. Although some of the data are sparse, our analysis suggests that the total number of DALYs attributable to childhood undernutrition could be reduced by basing food-allocation decisions on WHZ and HAZ rather than on WHZ alone. Indeed, our analysis exposes the pitfalls of relying solely on either WHZ (e.g., recommendations in refs. 7 and 8) or HAZ (e.g., the mathematical model in ref. 2), particularly given the asymmetric situation where many low-WHZ children have low HAZ but not vice versa. Moreover, we have derived a very simple policy that prioritizes children according to low values of a linear combination of HAZ, WHZ, and age and uses the entire budget on RUTF treatment for the highest priority children. This policy is at odds with, and appears to perform better than, some current proposals that include blanket supplementary feeding (7, 8). Because of the paucity of reliable data on the effect of treatment, the application of our model to only a single cohort of children, and our omission of some of the issues surrounding this complex problem (e.g., blanket distribution may provide helpful insurance against targeting errors, and may even be needed to make the targeting itself more effective by offering a cheap incentive for at-risk households to bring their children in for screening and feeding; targeted distribution may not be culturally, politically, or socially acceptable in all settings; and HAZ may suffer from incentive issues in the absence of birth records), we are precluded from making specific policy recommendations. Consequently, the main contribution of the study is not in the policy realm but in the problem-framing and -modeling: the bivariate ARIMA model for the evolution of a child’s (HAZ,WHZ), the aggregation of these individual sample paths to obtain the population-wide bivariate PDF at each age, the logistic regression for childhood mortality revealing a crucial asymmetry between HAZ and WHZ that makes HAZ just as important as WHZ for preventing childhood mortality, the formulation of the problem as a DALY-minimization problem subject to a budget constraint, the calculation that >90% of the DALYs are attributable to childhood mortality (and hence stunting is undesirable primarily because it leads to short-term death), and the development of policies that depend on a child’s sex, age, HAZ, and WHZ. Our analysis also reveals the pressing need for randomized control studies that allow for the estimation of the impact of supplementary food (e.g., RUSF at 250 kcal/d), as well as estimates for the probability distribution of the impact of treatment across individuals, the effect of pretreatment (HAZ,WHZ) levels on the effect of treatment, the manner in which daily dose and treatment duration influence the effect of treatment, the amount and nature of inclusion and exclusion errors (e.g., food sharing), and screening costs. Until such data become available, policymakers will need to make these strategic decisions in the face of incomplete information.