SMART Design Issues and the Consideration of Opposing Outcomes

1. INTRODUCTION

Sequential treatments, in which treatments are adapted over time based on the changing clinical status of the patient, are often necessary because treatment effects are heterogeneous across patients: not all patients will respond (similarly) to treatment, calling for changes in treatment in order to achieve an acute response or to place all patients on a positive health trajectory. Further, a treatment that is effective now for one patient may not work as well in the future for the same patient, again necessitating a sequence of treatments. Moreover, it is often necessary to balance benefits (e.g., symptom reduction) with burden (e.g., toxicity), a trade-off that may unfold over time. As a result, in clinical practice clinicians often find themselves implicitly or explicitly using a sequence of treatments with the goal of optimizing both short- and long-term outcomes, or, as may be the case in cancer treatment, to prevent death. Dynamic treatment regimes (DTRs) operationalize such sequential decision making. A DTR individualizes treatment over time via decision rules that specify whether, how, or when to alter the intensity, type, or delivery of treatment at critical clinical decision points. Sequential multiple assignment randomized trials (SMARTs) or equivalently, sequentially randomized trials, have been developed explicitly for the purpose of constructing proposals for high-quality DTRs.

In the “Evaluation of Viable Dynamic Treatment Regimes in a Sequentially Randomized Trial of Advanced Prostate Cancer,” Wang, Rotnitzky, Lin, Millikan, and Thall (2012, hereinafter, WRLMT) provide an excellent and lucid re-analysis of data from a SMART study and both motivate and encourage a discussion about design and analysis issues around SMARTs. In our comment, we focus on two important ideas raised by WRLMT: (1) the design of SMARTs (as opposed to the analysis of SMARTs), and (2) the analysis of, and presentation of results based on, multiple outcomes.

2. DESIGNING SMART STUDIES

2.1 Ensuring Viable Embedded DTRs in the Design of a SMART

It is critically important to ensure prior to the conduct of a SMART that the DTRs embedded within it are indeed viable.

A first step to ensure that the embedded DTRs are viable is a clear operationalization of the primary tailoring variable used to restrict subsequent treatment options within the SMART. Often the primary tailoring variable is a well-operationalized notion of early (or “in treatment”) response and non-response. WRLMT use the phrase “course-specific success or failure”. In this regard, the efforts of the prostate SMART study designers are commendable: As noted in WRLMT and in more detail in Thall et al. (2007), after an 8-week course of initial treatment, success (versus failure) was defined as a decline of at least 40% in prostate-specific antigen (PSA), no regression of any magnitude on any measurable disease dimension, no symptom increase in pain, anorexia, asthenia, or cachexia, and no new lesions or new cancer-related symptoms. Further, criteria for scoring success after being offered the second course of the same treatment were also clearly operationalized.

A second important step to ensure that the embedded DTRs are viable is a clear operationalization of how to treat patients in the event that additional common contingencies (e.g., beyond what is typically thought of as course-specific success or failure) arise during treatment. Such contingencies may include intolerable side effects (such as toxicity in the treatment of cancer, or weight gain in the treatment of schizophrenia), excessive treatment burden (such as is possible with preventive and behavioral interventions), and treatment drop-out or refusal to receive subsequent treatment (such as may happen with most any intervention). Indeed, in our experience, the clinical trial protocol (including the materials provided to either the Data Safety Monitoring Board and/or Institutional Review Boards), will detail a plan for what will happen in the event that any of these common contingencies arise. Often, the plan may be a transfer of the patient to “treatment as usual by patient’s clinician,” or in some settings, the plan may include a behavioral therapy aimed at re-engagement of the patient in treatment. The embedded DTRs are only viable if they incorporate the trial protocol plans for these commonly occurring contingencies.

In their re-analysis of the prostate SMART, WRLMT report that among the 47 participants who did not complete their therapy according to the 12 originally conceived DTRs embedded within the SMART, 35 of them did so due to severe toxicity or progressive disease (PD). WRLMT note that in actual oncology practice, severe toxicity or PD preclude further chemotherapy for patients with advanced prostate cancer and, instead, indicate a therapeutic or palliative treatment of some sort. They further note that this is precisely what was discovered to have happened during the conduct of the prostate SMART. Given the relatively large proportion (35/150 = 23%) of participants who were affected by PD or toxicity so severe as to preclude chemotherapy, we suspect that the trial protocol likely detailed a plan (i.e., the provision of therapeutic or palliative care for those with severe toxicity or PD) for these contingencies.

In other SMART studies, a common contingency is that a patient misses the clinic visit during which course-specific success or failure is assessed. If the patient returns to the clinic for treatment beyond the window of time during which subsequent (originally-planned) treatments are appropriate, a clear alternative treatment plan is necessary in order to make the embedded DTRs viable. This issue is particularly important in the design of SMARTs because the trial design depends on course-specific success or failure.

To summarize, common contingencies that may arise during treatment require a pre-specified treatment plan and the absence of such a plan may lead to the consideration of non-viable embedded DTRs. Of course, we do not mean to imply that the embedded DTRs need to be tailored to any and all contingencies that may arise.

The primary consequence of having non-viable DTRs in the design of a SMART is that it becomes unclear what DTRs the SMART is designed to make inferences about. As a result, the effects of the proposed DTRs resulting from the study will be less replicable as it will be unclear to future investigators how these contingencies were handled in the trial. Since the primary motivation to conduct a SMART in the first place is to inform decision making concerning the sequencing of treatments, this is a consequential omission in the design of SMARTs. Thus, the consideration of additional contingencies as part of the embedded DTRs is not merely a quality control measure or an ethical concern. Rather, the treatment plan following one of these contingencies is part of the definition of the embedded DTRs. Without accounting for these additional contingencies, as we learned from WRLMT, we do not have realistic DTRs that are applicable to the population of interest and, therefore, useful in informing sequential decision making.

Our message that it is critical to ensure that embedded DTRs are viable during the design phase of a SMART is not new. Indeed, as emphasized in the recent National Research Council’s study report on “The Prevention and Treatment of Missing Data in Clinical Trials” (2010), the consideration of viable interventions should be a basic tenet of all RCT designs. However, unlike standard RCTs, SMARTs force us to confront this issue. Since the primary focus of standard RCTs is often on initial treatment offerings, this means that even when there exist (or should exist) treatment plans for common contingencies that may arise, they are not always explicitly considered to be part of the definition of treatment. Instead, these common contingencies are often considered treatment outcomes. We note that while the rate at which these contingencies occur is a treatment outcome, the plan for how to treat participants in these situations is part of the definition of treatment, a subtle but important distinction. In contrast, since SMARTs are explicit in their aim to develop DTRs, the issue of what to do next given common contingencies that may arise (even beyond what is considered course-specific success or failure) is less easily “swept under the rug.”

2.2 Matching the Statistical Analysis to the Rationale for a SMART

In our experience designing SMART studies, the overarching goal of the study is to construct one or more proposals for high-quality DTRs. These proposals would then be combined with the results of other studies and emerging science to produce DTR(s) that would form one or more of the intervention arms in a future randomized confirmatory trial. Thus, the goal of a SMART is often quite different from the more “confirmatory” goal of most standard RCTs. This appears to be the case in the prostate SMART considered here, as WRLMT write “The ultimate goal was to use the results of the trial as a basis for generating hypotheses and planning a future, confirmatory trial.” This goal is quite similar to the goal of randomized factorial designs used in engineering (Box et al. 1978) and its emerging use in the development of behaviorial interventions (Collins et al. 2005; Collins et al. 2007; Collins et al. 2009; Collins et al. 2011; Strecher et al. 2008; Chakraborty and Murphy 2009). Indeed, SMARTs can be viewed as randomized factorial designs (Murphy and Bingham 2009). Similar to the use of factorial designs in engineering, SMARTs are intended to aid in the construction of a multi-component intervention (namely, a DTR) as opposed to confirm a best DTR. Accordingly, the statistical analysis of a SMART need not have a confirmatory flavor. For example, in these factorial designs, investigators might not conduct hypothesis tests. Instead, investigators might rank order the treatment/intervention factors in terms of estimated effect sizes and keep the x most highly ranked factors; similar “ranking and selection” ideas have been proposed in the clinical trial literature (Simon et al. 1985; Sargent and Goldberg 2001) as well. If hypothesis tests are used, the focus is on reducing the Type II error as opposed to controlling the Type I error rate. For example, scientists might test a small number of pre-specified hypothesis, each at a specified, marginal, significance level and then control the overall error rate of the remaining hypothesis (Collins et al. 2007; Chakraborty and Murphy 2009).

Despite the fact that the prostate SMART study discussed by WRLMT appears to be focused on constructing proposals for high quality DTRs, WRLMT control the experiment-wise error rate (i.e., they construct simultaneous confidence intervals). It is thus easy to misinterpret the use of simultaneous confidence intervals as implying that the trial was intended to be confirmatory. We maintain that regime-specific confidence intervals should and can be used to conduct inference in building a high quality DTR. Of course, these non-simultaneous confidence intervals will not confirm that one regime is best. In fact, much of the current work on sample size planning for SMARTs (Feng and Wahed 2008; Feng and Wahed 2009; Oetting et al. 2010; Li and Murphy 2011) does not focus on devising sample size formulae that control the experiment-wise error rate. Rather, the focus has been on formulae that control the Type I error of a pre-specified primary aim that aides in building an effective DTR. We acknowledge that SMARTs can be designed to confirm which of the embedded DTRs is best; indeed in some settings, such as in the development of internet based interventions where large sample sizes are inexpensively obtained, this approach may be desirable and is likely feasible.

3. COMPOSITE ENDPOINTS

Our second comment describes a new approach that can be used in addition to endpoints such as those considered by WRLMT to further quantify the trade-off between toxicity and efficacy. In Section 3.3, WRLMT discuss three composite endpoints (Y^binary, Y^ordinal, and Y^expert) of treatment efficacy and toxicity. These three composite endpoints, as well as log-survival time, were used in the re-analysis by WRLMT. The three endpoints exploit newly available toxicity and efficacy data (not available during the primary analysis of the trial) which the authors show serve as better surrogates for the overall health status of patients over the entire 32 week treatment period compared to the endpoints stipulated by the original study protocol.

The three new endpoints differ in terms of how they trade-off toxicity and efficacy during chemotherapy. We suspect this is important in oncology because the most efficacious chemotherapies are likely the treatments associated with high levels of toxicity and vice-versa, that is, some chemotherapies that are less effective may also be the ones that are also less toxic. This question, of how to trade-off opposing outcomes, also arises in other areas of clinical research such as in the treatment of schizophrenia where the trade-off is between symptom relief and weight gain.

As implied by the authors, the choice of the endpoint Y necessarily influences the conclusions drawn from the study, but the “correct” choice of the endpoint is often not obvious or even well-defined. The authors note that Y^ordinal is in a sense finer-grained than Y^binary because it “distinguishes therapies that produce transient efficacy benefits from therapies that don’t.” They further note that Y^expert “distinguishes not only regimes that provide transient efficacy benefits from those that don’t, but it also quantifies the clinical desirability of the different transient benefits.” In examining the results in WRLMT, we can see that using all-or-nothing “success” (i.e., Y^binary) as the desired outcome produces a different estimated optimal DTR than the result obtained when considering (possibly transient) efficacy benefits: the results show that the estimated optimal DTR according to Y^binary is (TEC, KA/VE), while the estimated optimal DTR according to Y^ordinal or Y^expert is (TEC, CVD).

As a possible adjunct to the high-quality analysis presented in the paper, we can conduct a sensitivity analysis with respect to the endpoint definition that provides further insight into how the results would change depending on the relative utilities of different joint outcomes. For example, this can be done by considering outcomes $Y_{(a,a\ast )}^{\ast }(\delta )=(1-\delta )·Y_{(a,a\ast )}^{\mathrm{bin}}+\delta ·Y_{(a,a\ast )}^{\mathrm{expert}}$, where δ ∈ [0, 1] is used to interpolate between the binary outcome score and the expert outcome score. Note that for δ = 0, we recover the binary outcome score, whereas for δ = 1 we recover the expert outcome score, and for intermediate values of δ, we define an outcome that is a combination of both. The different outcomes indexed by δ under this framework represent not just different levels of granularity, but different sets of preferences for $Y_{(a,a\ast )}^{\mathrm{expert}}$ vs $Y_{(a,a\ast )}^{\mathrm{bin}}$.

For this example, since the authors’ estimate of the DTR means, Ẽ[Y_(a,a*)], is linear in the observed outcome scores Y_i, we can use the estimates provided in the paper to compute DTR means for $Y_{(a,a\ast )}^{\ast }(\delta )$. Figure 1 illustrates how the estimated DTR means change as a function of δ.

Figure 1.

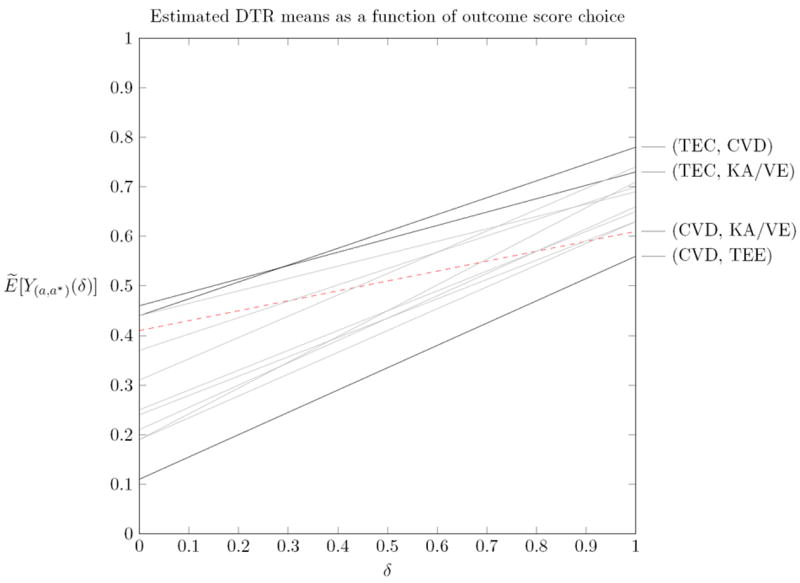
Estimated DTR means as a function of δ, where $Y_{(a,a\ast )}(\delta )=(1-\delta )·Y_{(a,a\ast )}^{\mathrm{bin}}+\delta ·Y_{(a,a\ast )}^{\mathrm{expert}}$.

As expected, we see that (TEC, KA/VE) is preferable for Y^bin (δ = 0), whereas (TEC,CVD) is preferable for Y^expert (δ = 1). The cross-over point, at δ ≈ 0.28, helps us understand at what preference point the results will differ. Such an analysis is useful since different patients or clinicians may have different preferences in how they trade-off Y^expert vs Y^bin. Figure 1 also shows that (CVD, TEE) appears the worse no matter what the trade-off. Further, we see that some DTRs change ranking substantially for different outcomes: for example, (CVD,KA/VE) goes from 4th for Y^bin to second-last for Y^expert.

One could also imagine doing a similar analysis that trades off two different expert scores, for example $Y_{(a,a\ast )}^{\mathrm{expert}-1}$ vs $Y_{(a,a\ast )}^{\mathrm{expert}-2}$, which may represent two opposing views (operationalized by different choices for C_j) on how to trade-off efficacy vs toxicity. Or one could imagine a similar analysis that trades off two continuous, direct measures of toxicity vs efficacy, such as Y_(a,a*) (δ) = (1 − δ) · T(a, a*) + δ · E(a, a*). The latter may only be possible if toxicity and efficacy can be placed on “similar footing” so that a linear convex trade-off of this sort is clinically meaningful. This could be done by first “calibrating” or “scaling” the measures of T and E to ensure the linear combination is meaningful so that, for example, δ = 0.5 represents a moderate or typical clinical preference for one outcome over the other. This last idea may not be possible in oncology research since, as noted by WRLMT, severe toxicity may be so highly undesirable that no level of efficacy (no matter how high) could trade-off with it.

This approach to trading-off two or more opposing outcomes is being developed further for use in data analyses that build optimal DTRs (say, using Q-Learning) from data arising from SMARTs (Lizotte et al. 2010).