Collective Enumeration

Abstract

Many joint decisions in everyday life (e.g., Which bar is less crowded?) depend on approximate enumeration, but very little is known about the psychological characteristics of counting together. Here we systematically investigated collective approximate enumeration. Pairs of participants made individual and collective enumeration judgments in a 2-alternative forced-choice task and when in disagreement, they negotiated joint decisions via verbal communication and received feedback about accuracy at the end of each trial. The results showed that two people could collectively count better than either one alone, but not as well as expected by previous models of collective sensory decision making in more basic perceptual domains (e.g., luminance contrast). Moreover, such collective enumeration benefited from prior, noninteractive practice showing that social learning of how to combine shared information about enumeration required substantial individual experience. Finally, the collective context had a positive but transient impact on an individual's enumeration sensitivity. This transient social influence may be explained as a motivational factor arising from the fact that members of a collective must take responsibility for their individual decisions and face the consequences of their judgments.

A rich history of behavioral and neurobiological investigations has characterized, in exquisite detail, our ability to enumerate (Butterworth, 2000). The bulk of this research is obtained from experiments in which people of different ages (Halberda, Mazzocco, & Feigenson, 2008), mental capacities (Butterworth, Varma, & Laurillard, 2011), and even cultural and ethnographical backgrounds (Butterworth, Reeve, Reynolds, & Lloyd, 2008; Gordon, 2004) are asked, on their own, to enumerate the number of items in a given set. An individual's ability to discriminate the numerosities of two sets of objects depends on a range of factors including the spatial frequency composition of the visual stimuli (Dakin, Tibber, Greenwood, Kingdom, & Morgan, 2011), immediate prior sensory experience (Burr & Ross, 2008), availability of attentional resources (Vetter, Butterworth, & Bahrami, 2008), and the observer's level of arithmetic competence (Halberda et al., 2008; Piazza et al., 2010). Accurate and exact enumeration is restricted to the subitizing range that is, fewer than five items (Jevons, 1871). In contrast, all the studies reviewed above generally involved rapid estimates of numerosities well beyond subitizing. It has been suggested that such approximate enumeration depends on approximate representations of numerosity mapped onto overlapping Gaussians on an internal analogue subjective scale compare (Izard & Dehaene, 2008).

In everyday life, however, very frequently such approximate enumeration is not a solitary but a collective endeavor. For example, on a night out with friends, deciding which bar is less crowded is a collective decision usually based on approximate enumeration. Many similar collective decisions depend on approximate enumeration, yet we know very little about the psychological characteristics of collective enumeration.

For simple visual luminance contrast discriminations, collective sensitivity can exceed the best individual sensitivity as long as the members of the collective are similarly sensitive and can communicate freely with one another (Bahrami et al., 2010). A “weighted confidence sharing” (WCS) model for collective perceptual decision making can account for these findings. This model makes an important assumption about the nature of perceptual representation of contrast within each individual, namely that such a representation can be thought of as a Gaussian distribution with a mean (corresponding to perceived contrast) and a standard deviation (corresponding to noise in the perceptual neuronal representation). To compare their percepts and make a joint decision, the model proposes that participants share their confidence (defined by the ratio of the distribution's mean to its standard deviation) with one another and the joint decision will agree with the individual whose shared confidence is higher. Given isolated individuals' sensitivities (which are separately estimated), this model makes an exact, parameter-free prediction for group sensitivity consistent with empirical findings (Bahrami et al., 2010) for visual contrast discrimination. The choice of a Gaussian assumption is reasonable for visual contrast discrimination, and such assumptions have also been claimed for numerosity discrimination (Dehaene, 2003; Piazza, Izard, Pinel, Le Bihan, & Dehaene, 2004). Therefore, empirical testing of collective enumeration against the predictions of the WCS model provides an opportunity for a rigorous examination of whether the Gaussian assumptions also apply to approximate enumeration and whether proposed mechanisms for collective contrast discrimination can be generalized to more abstract, higher level tasks such as enumeration.

When collaborating individuals communicate freely and have access to their decision outcomes, the benefit of collective decision for simple visual discriminations is stable across time (Bahrami et al., 2012a). In this case, optimal collective performance (i.e., behavior that is consistent with the predictions of the WCS model) does not require prior practice. Whether collective enumeration improves with practice or not is unknown. The implications of this possibility go beyond the realm of enumeration because currently fashionable models of social learning (Behrens, Hunt, & Rushworth, 2009; Behrens, Hunt, Woolrich, & Rushworth, 2008; Hampton, Bossaerts, & O'Doherty, 2008) invariably assume that the agents engaged in social interactions need only to learn about the “others” and so far have ignored the relevance of “know thyself” for effective social interaction. Any impact of private familiarization on joint behavior for enumeration would mean that learning about self may also constitute an important aspect of social learning.

Finally, we consider the impact of engaging in collective enumeration on the performance of each person. In the “two-person safety game,” two observers (akin to two guards patrolling a building) have to detect a rare alarm signal. They incur a cost only if both miss it. Game theoretic analysis and empirical results (Erev, 1998; Gopher, Itkin-Webman, Erev, Meyer, & Armony, 2000) show that in such situations, the more sensitive person will try even harder but the less sensitive person degenerates into even worse performance than when doing the task on their own. Another line of research in social psychology has highlighted a different situation where people “try less hard” when they have to perform a given task as part of a team. This phenomenon is called “social loafing,” the canonical example of which is the “tug of war” game where people apply substantially less force (than the maximum they are capable of) to the rope when they are part of a team (Karau & Williams, 1993). Finally, social identity theory (SIT; Tajfel, 1978) postulates that group membership increases motivation for achievement because individuals aspire to achieve and maintain a positive social identity that directly contributes to their self-esteem. For example, experimental manipulation of social identity modulates top-down attentional biases to visual stimuli at very early stages of visual processing (Montalan et al., 2011). Contrary to social loafing, SIT predicts that individual performance will be better in collaborative contexts. Thus, collaborative context may have complex and curious effects on individual behavior. Here we set out to investigate this question systematically by probing each person's enumeration sensitivity in interactive as well as in isolated contexts.

Method

Participants

All participants were recruited using the UCL Division of Psychology and Language Sciences' database of registered volunteers. In Experiment 1, a total of N = 30 individuals were recruited (mean age ± SD = 24.7 ± 6.2). All participants were healthy male adults with normal or corrected-to-normal visual acuity. Participants who were assigned to the same dyad were recruited independently and did not know each other in advance. To test the impact of familiarity, in Experiment 2, a separate group of participants (N = 14, i.e., 7 pairs of familiar participants—mean age ± SD = 23.6 ± 4.8) were recruited such that one member was recruited from the database and was asked to bring a friend along to participate in the experiment. No participant was recruited more than once. Both experiments were approved by the local ethics committee. Written informed consent was obtained from all participants. Participants received a fixed monetary compensation for their contribution.

Display Parameters and Response Mode

In both experiments, both dyad members sat in the same testing room. Each viewed his own display. Display screens were placed on separate tables at right angles to each other (Figure 1B). The two displays were connected to the same graphic card via a video amplifier splitter and controlled by the Cogent toolbox (http://www.vislab.ucl.ac.uk/cogent.php/) for MATLAB (Mathworks Inc).

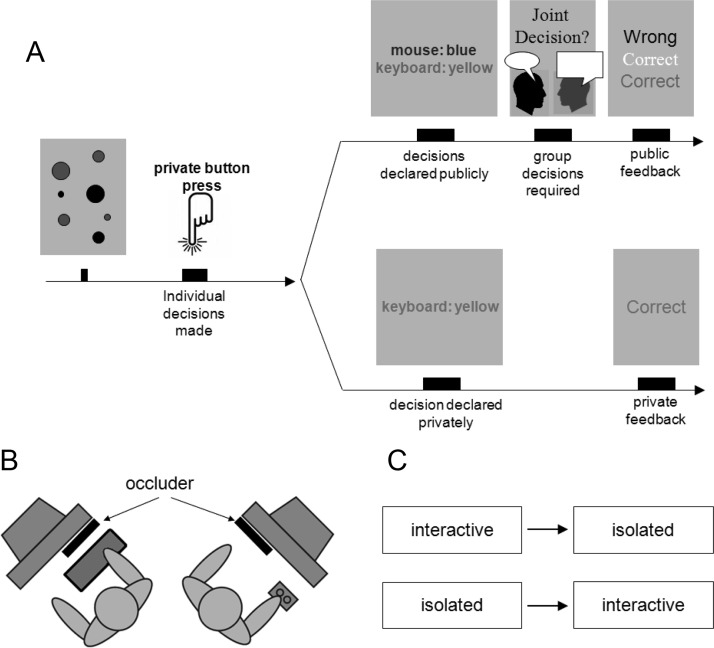
Figure 1. Experimental setup and design. (A) Sequence of events in a trial: Each trial started with a visual stimulus (gray and black dots are used here to represent yellow and blue, respectively). Participants then indicated their private decision by a button press without any communication. In the interactive condition (top panel), decisions were then publically shared and if there was a disagreement, participants negotiated a joint decision. The trial ended with public announcement of the decision outcomes (here the white color refers to group decision outcome). In the noninteractive condition (lower panel), decision and outcome were kept private and no communication was permitted. (B) Spatial organization of the participants, display, the occluder and the response instruments. (C) Experimental design. Dyads were randomly assigned to one of two orders.

Each participant viewed an LCD display at a distance of ∼57 cm (resolution = 800 × 600–Samsung SyncMaster 710, 22” and Dell Professional P2211H 22”). Using a look-up table, the output luminance of the displays was linearized. Background luminance was 55.0 Cd/m² in both displays. The displays were connected to a personal computer through an output splitter that sent identical outputs to both of them. Within each session of the experiment, one participant responded with the keyboard and the other with the mouse. Both participants used their right hand to respond.

Each participant viewed one-half of their screen (Figure 1B): the participant using the keyboard viewed the left half of one display, the participant responding with the mouse viewed right half of the other display. Thick black cardboard was placed on the occluded half of each display. By using the occluding cardboard, we segregated the dyad members display from one another (Figure 1B). This configuration provided a simple way to control the social aspect of the task (see Procedure). Participants always received identical stimuli (in terms of numerosity, retinal size, luminance, contrast, duration). In the interactive condition (Figure 1A, top row) the decisions and final outcomes were displayed on both participants' view. In the isolated condition (Figure 1A, bottom row), each participant only viewed his own decision and outcome. Thus, the occluding cardboard was used to display independent visual input to dyad members in the isolated condition only. It ensured that each participant only received feedback about the outcome of their own decision in the isolated condition. Although there was therefore no need for the occluding cardboard in the interactive condition, we retained it to ensure there were no visual stimulus confounds between conditions.

Design and Task

A 2-Alternative Forced Choice (2-AFC) task was employed (Figure 1A). One observation interval was provided. Participant viewed a dot array on the screen and privately decided whether the number of blue or yellow dots was larger in the display. Experiment 1 was conducted to disentangle the role of social interaction and prior isolated practice in enumeration sensitivity. We employed the design schematically displayed in Figure 1C. Half of our unfamiliar (N = 14 participants) dyads started the experiment with the interactive condition first (top row). The other half (N = 16 participants) started the experiment with the isolated condition (bottom row). Experiment 2 was conducted to address the role of familiarity between dyad members in collective enumeration. All dyads who participated in this experiment took the interactive condition without any prior isolated practice.

Stimuli

In each trial, an array of dots was presented on the screen. The array consisted of yellow and blue dots. These two sets of dots' numbers differed by one of the four ratios: 2:1, 4:3, 6:5, 8:7, and in each set the total number of dots varied between 5 and 16 elements. The color of the more numerous set was randomized. To avoid the confounding effects of irrelevant perceptual dimensions (luminance, hue, density), half of the trials were “dot-size controlled” (the average diameter of the dots in the two sets were equal) and the other half were “area controlled” (the total areas of the two sets were equal; Halberda et al., 2008). In the size controlled trials, dot diameter varied between 0.97 and 2.04 degrees of visual angle for both sets. In the area controlled trials, dot diameter varied between 0.97 and 2.04 degrees for the smaller set, and between 0.62 and 1.45, 0.8 and 1.77, 0.85 and 1.8, 0.87 and 1.9 degrees for the smaller set for the ratios 2:1, 4:3, 6:5, 8:7, respectively. Minimum center-to-center spacing between the dots was 1.57 degrees.

Procedure

Each trial was started by the participant responding with the keyboard. A black central fixation cross (width: 0.75 degrees visual angle) appeared on the screen for a variable period, drawn uniformly from the range 500–1000ms. The stimulus dot array was then presented for 200ms. The fixation cross turned into a question mark after the stimulus to prompt the participants to respond. The question mark stayed on the screen until both participants had responded. Each participant initially responded privately, that is, without consulting the other. The experimenter made sure that no communication took place at this stage. Participant using the keyboard responded by pressing “N” and “M” for the blue and yellow, respectively; the participant who used the mouse responded with a left and right click for the blue and yellow, respectively. Individual decisions were then displayed on the screen (Figure 1A).

In the interactive condition (Figure 1A, top row), these private decisions were then announced publicly to both participants. Response instruments (mouse and keyboard) were used to denote participants. To avoid spatial biasing, the relative vertical location of the mouse and keyboard were randomized. If the decisions of the two participants disagreed, they were instructed to talk to each other and arrive at a joint decision. Inputting the joint decision was delegated to keyboard and mouse in odd and even trials, respectively by the computer program. Individual and group decision outcomes were then provided publicly. Participants were also free to choose any strategy that they wished.

In the isolated condition (Figure 1A, bottom row), the decision was announced privately for each participant followed directly by decision outcome. In this condition, although the participants were sitting in the same testing room and went through the trials together (here too, all trials were initiated by the keyboard) they never discussed their opinions and did not receive any information about the other person's performance.

Participants started the experimental session with one practice block (16 trials) that was conducted in order to familiarize them with the tasks. The practice block was drawn from the same condition from which the group would start the experiment (Figure 1C). For example, if a group was supposed to start with the interactive condition then they practiced the interactive condition. This design ensured that the total number of trials each individual took was identical across experimental manipulations. Then, two main experimental sessions (one for each condition, 10 blocks of 32 trials in each session) were conducted. Halfway through each session, participants swapped places to counterbalance the use of the input device. There were no rewards or punishments (money or otherwise) for performing better or worse. Overall accuracy was not reported to the participants.

Data Analysis

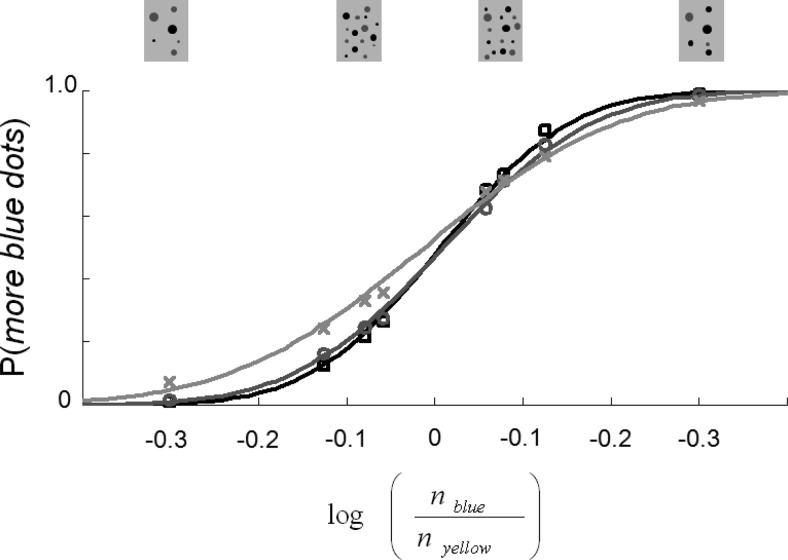
Enumeration sensitivity was quantified by estimating the slope of the psychometric function that related the log difference between numerosity of blue and yellow dots to choice of blue trials (Figure 2). Psychometric functions were estimated for individuals (Figure 2, gray symbols and lines) and dyad (Figure 2, black symbols and line) separately. A cumulative Gaussian function with parameters bias, b, and variance, σ² was fitted to each obtained psychometric function by a probit regression model employing the glmfit function in MATLAB (Mathworks Inc). A participant with bias b and variance σ² would have a psychometric curve, denoted P(Δn)

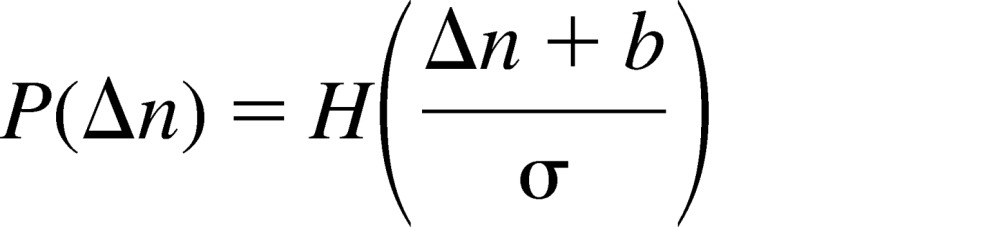1

where Δn = log(number of Blue dots) – log (number of Yellow dots) and H(z) is the cumulative normal function,

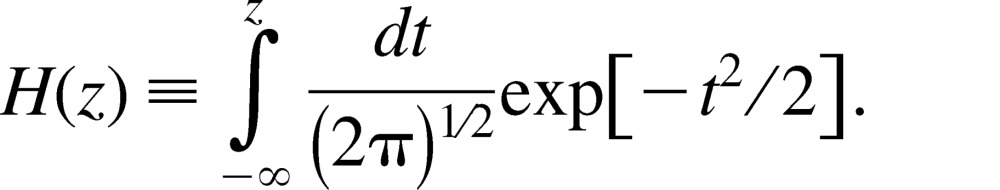2

Figure 2. The psychometric function relating the choice of “more blue dots” to the log of the ratio of number of blue to yellow dots (gray and black dots are used here to represent yellow and blue, respectively). Data points are the average across dyads (black, N = 15), the more sensitive members of dyads (dark gray curve and circles, N = 15) and less sensitive member members of dyads (light gray curve and circles, N = 15). The curves are best the fitting cumulative normal.

Here, the psychometric curve, P(Δn), corresponds to the probability of saying that there was more blue dots on the screen. Given this definitions for P(Δn), the variance is related to the maximum slope of the psychometric curve, denoted s, via

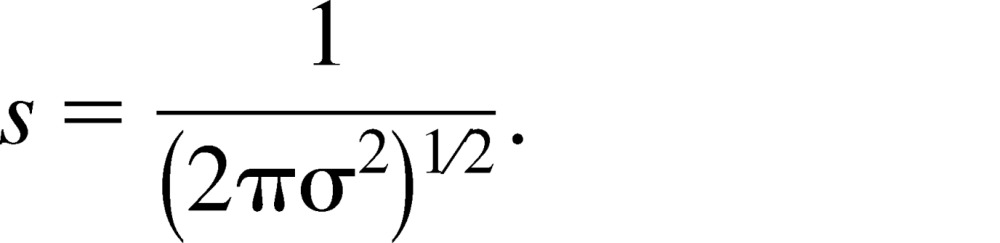3

This slope parameter quantifies the enumeration sensitivity.

Weighted Confidence Sharing (WCS) Model

If dyad members communicated their information to each other accurately and made best use of their shared confidences, how sensitive could they be given their individual sensitivities? We have recently developed (Bahrami et al., 2010) a “weighted confidence sharing” model to estimate this upper boundary for visual contrast sensitivity which is a far simpler visual feature than numerosity. Here we refer to confidence as the probability that the participant thinks his decision is the correct one. The collective decision is then reached by combining decisions of the participants weighted by their communicated confidence. The model assumes that (a) participants have access to their variance on the task; (b) they believe their private decisions are unbiased; and finally (c) they accurately communicate their confidence in their decision to each other.

Previous research in perception shows that observers can express their confidence in their judgments reliably: higher confidence ratings are associated with higher accuracy (Fleming, Weil, Nagy, Dolan, & Rees, 2010; Green & Swets, 1966; Morgan, Mason, & Solomon, 1997; Pierce & Jastrow, 1884; Song et al., 2011). Sandberg, Bibby, Timmermans, Cleeremans, and Overgaard (2011) recently showed that these metacognitive expressions of confidence are most accurate about the reliability of the underlying perceptual decision when participants are instructed to directly describe the vividness of their perceptual experience rather than use a numerical rating scale or postdecision wagering. Our research (Bahrami et al., 2012b) shows that when participants are allowed to freely discuss their perceptual decisions without imposing any particular communication strategy, they accrue significantly more collective benefit compared to if they were strictly instructed to use a numerical scale for sharing their confidence. Moreover, collective decisions are in accord with our WCS model only when people freely discuss decisions. Finally, quantitative analysis of conversations shows than specific linguistic indicators of shared confidence are predictive of variability in the collective benefit (Fusaroli et al., in press).

To describe the model briefly; we define the confidence communicated by participant i as the ratio Δn_i / σ_i (cf. eq. 1). Thus, the participant's confidence is mathematically expressed as a z-score which we denote z₁ and z₂ for the two participants in a dyad. We have previously shown (Bahrami et al., 2010) that for luminance contrast discrimination, the Bayes optimal decision boundary for joint decision is z₁+ z₂ = 0, that is, to choose the second interval (corresponding to Δn positive) if z₁+ z₂>0, and the first interval (corresponding to Δn negative) if z₁+ z₂<0. The upper boundary of the collective decision making by this weighted confidence sharing is given by

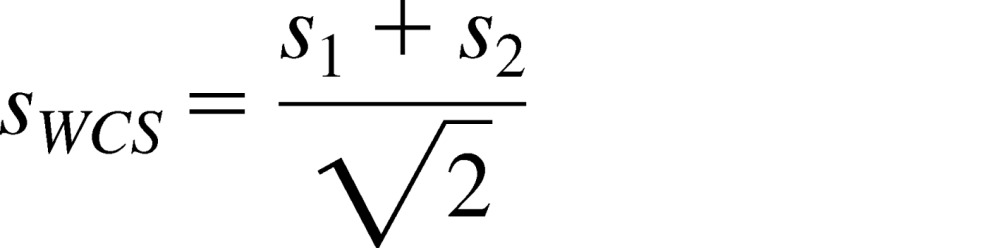4

where s₁ and s₂ are the individual slopes (defined according to Equation 3). Thus, the model identifies the dyad's potential for collective achievement under the assumption that the members can communicate their confidence to each other accurately. We compared the empirically obtained data to this potential upper bound to see whether the confidence sharing model can be generalized to the case of enumeration. We defined an “optimality index” (s_dyad /s_wcs) as the ratio of the dyad's slope (s_dyad) to that predicted by the weighted confidence sharing model, (s_wcs).

Results

Collective Benefit: Can Two Heads Count Better Than One?

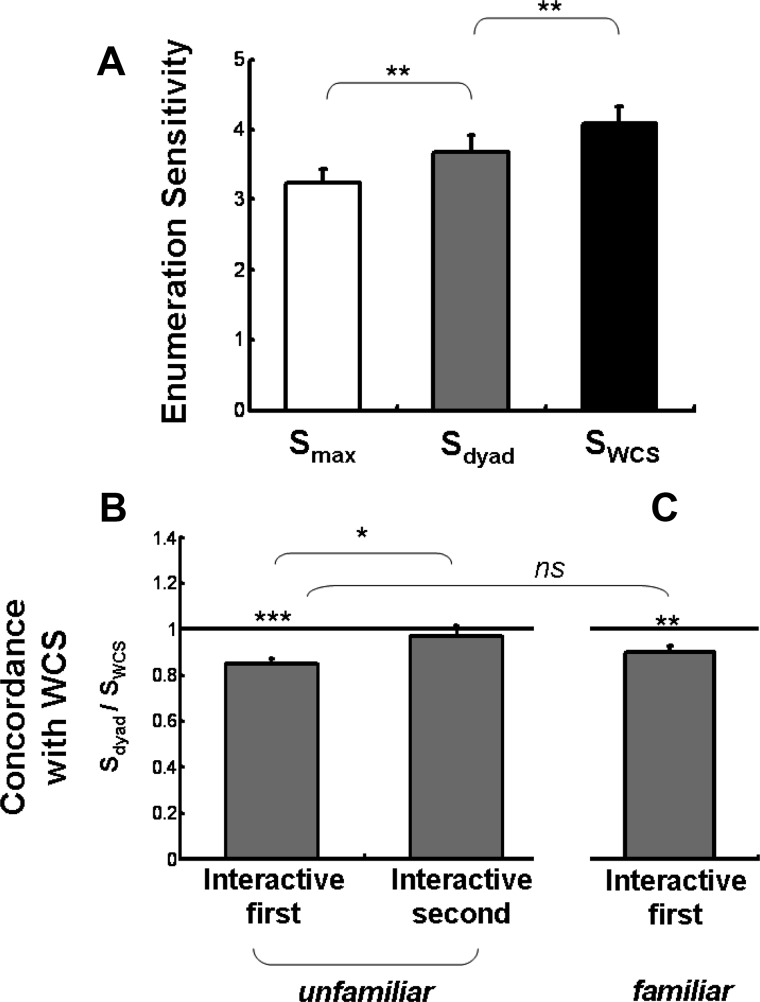
The collective was robustly more successful at enumeration than individuals. Figure 2 illustrates the average psychometric functions relating the probability of reporting larger number of blue dots versus log of the ratio of the number of blue to yellow dots. Two observations were apparent: the slope of the average dyad psychometric function (black, averaged across N = 15) was steeper than the best (i.e., more sensitive) members' (dark gray). Moreover, performance curves for the dyad and best member were much closer to each other than that of the lesser performing dyad member (light gray) suggesting that decision strategy employed by the dyads must have taken into account the difference between the member's sensitivity. Quantitative estimation of the slope of the psychometric functions showed that dyad slope (s_dyad) was significantly greater than the best (s_max) members (Figure 3A; t(14) = 2.93; p = .011) demonstrating for the first time that social interaction and collective decision making enhanced enumeration sensitivity.

Figure 3. The results of collective enumeration. (A) Average enumeration sensitivity (the slope of the psychometric function) is plotted for the best members of the dyads (white), as well as for the dyads (gray) and the corresponding sensitivity expected by the WCS model (black). Error bars = 1 SE. (B) Concordance with the WCS model is plotted for dyads who took the interactive session first (see Figure 1C) versus those who took the non-interactive session first. Horizontal line indicates agreement with the model. Values below the line indicate that the empirical performance was inferior to model prediction. ** p < .01. Error bars = 1 SE. (C) Familiarity control experiment: conventions are the same as panel B but the members of each dyad were familiar with one another.

Is Collective Enumeration Consistent With Weighted Confidence Sharing?

Based on the separately estimated individual member's enumeration sensitivity we could use the weighted confidence sharing model (see Methods) to draw a prediction for each dyad's sensitivity which marked the theoretical upper boundary, given the assumptions of the model about the content of the communication and nature of the decision rule applied by the dyad (Bahrami et al., 2010). Dyad sensitivity was significantly lower than the model predictions (Figure 3A) t(14) = 3.23; p = .006.

The Role of Prior Practice in the Task

Each dyad completed one interactive and another isolated session (in counterbalanced order—see Figure 1C and Methods). As a result, dyads who took the interactive task on the second session (Figure 1C, bottom row) had the chance to familiarize with the task in the preceding isolated session. Our design (Figure 1C) allowed us to test the possibility that prior, isolated practice could have helped dyads make better joint decisions. We split the dyads into two groups according to whether the dyad took the interactive test in the first or second session. In order to compare the success of collective decision making process, one has to bear in mind that dyads with more sensitive members are expected do well irrespective of how well the dyad members interacted. In order to see which dyads achieved better collective decisions, therefore, dyad performance should be normalized. To perform such normalization, we asked how well each dyad performed compared to what the WCS model expected them to do. As such, this optimality index (i.e., the ratio s_dyad /s_wcs; see Methods) gives a quantitative estimate of how well the dyad fulfilled its potential given its members' individual sensitivities. The closer concordance with the WCS model is associated with an optimality index that is closer to 1.

We compared the optimality index obtained from the dyads that participated in the interactive condition first (Figure 1C; top row) and those who participated the interactive session second (Figure 1C; bottom row). The results (Figure 3B) showed that indeed, the dyads who started with the interactive session performed significantly worse than expected by the confidence sharing model (one-sample t test), t(7) = −6.13; p = .0005, whereas those who took the interactive task after having had experience of the task in the isolated session performed nearly optimally (one-Sample t test), t(6) = −0.68; p = .52. Direct comparison of the two groups showed that the “interactive second” group of dyads showed a significantly higher concordance with the WCS model (independent sample t test), t(13) = −2.12; p = .045. Thus, prior individualized practice without any communication helped participants cooperate more effectively later and realize their collective potential.

The Impact of Familiarity Between Dyad Members

A recent study (Bahrami et al., 2012a) showed that dyads that performed a collective visual contrast discrimination task did not need much practice to achieve reliable collective benefit. Dyads tested in that study never had any prior, isolated practice yet displayed robust collective benefit consistent with the WCS model from a very early stage of the experiment. The dyads in that study (but not in the results described above) were familiar with one another. For each dyad, Bahrami and colleagues (2012a) had recruited only one of the participants and asked him to bring along a friend to sit for the experiment together. It is therefore possible that collective benefit reported by Bahrami et al. (2012a) was a consequence of personal acquaintance rather than task practice. To see whether mere familiarity, irrespective of practice in the task, was adequate for achieving optimal performance, in Experiment 2 we recruited another 7 dyads composed of friends who knew each other very well (see Methods) and conducted the exact same interactive experiment with them but all dyads were tested in the interactive session first. The results (Figure 3C), however, showed that familiarity per se did not help dyads achieve optimal collective performance. Collective enumeration sensitivity was significantly lower than the prediction of the weighted confidence sharing model (t(6) = −3.4; p = .014). Moreover, direct comparison of the “interactive first” group of nonfamiliar dyads from Experiment 1 and familiar dyads in Experiment 2 did not show any significant difference between them (Figure 3C; independent sample t test), t(13) = −1.3; p = .22.

The Impact of Social Interaction on Individual Performance

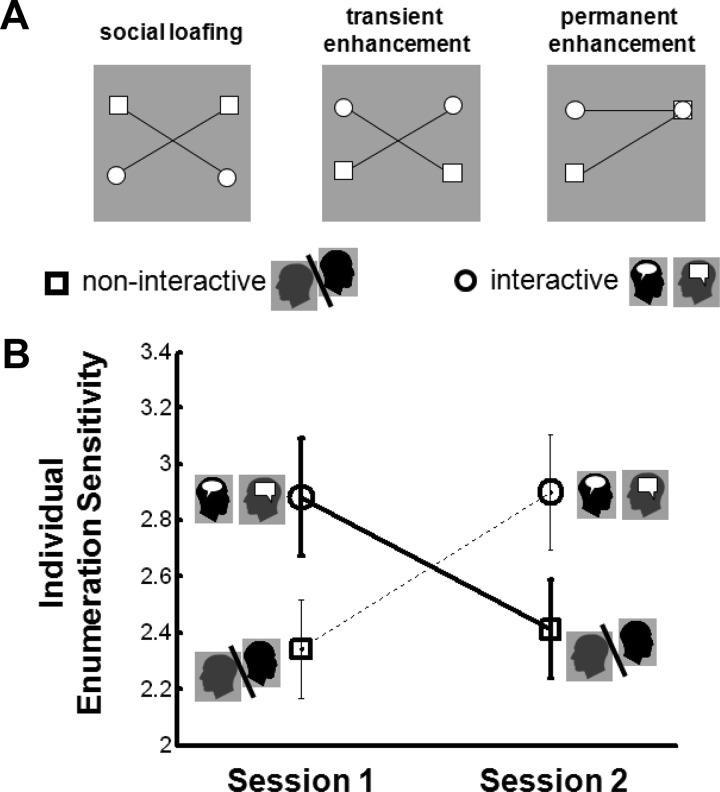
Our design allowed us to investigate the impact of social interaction and joint decision making on individual performance. Our participants performed the enumeration task in isolation or collectively (Figure 1C) in separate sessions. We employed a mixed 2-way analysis of variance (ANOVA; with order as the between subject factor: interactive followed by noninteractive and vice versa; and session as the within subject factor; see Figure 1C) to compare individual slopes. The results (Figure 4B) did not show a main effect for either factor (p > .2). However, a highly significant interaction was demonstrated, F(1, 28) = 24.51; p < .001, indicating the no matter in which order the dyads took the experiment, individual sensitivity was significantly superior in the interactive versus noninteractive sessions; post hoc stats for interactive vs. noninteractive overall: t(29) = 5.01; p < .001; post hoc stats for int vs. nonint for I-NI group: t(15) = 2.91; p = .0107; post hoc stats for int versus nonint for NI-I group: t(13) = 4.55; p < .001.

Figure 4. The impact of collective context on individual performance. (A) Graphical representation of 3 different predictions. (B) Enumeration sensitivity (slope of psychometric function) for individuals are plotted for when they undertook the task in isolation (squares) and when shared opinions and made collective decisions together (circles). Error bar = 1 SE.

Discussion

There were three principal findings from this work. First, we found that dyadic decisions were superior to individuals in approximate enumeration sensitivity. Second, the magnitude of collective benefit was, however, not consistent with the predictions of the weighted confidence sharing model (Bahrami et al., 2010) for dyads who had no prior practice with enumeration task, irrespective of their familiarity with one another. Prior individual practice enhanced collective performance. Finally, individual performance was strongly modulated by collaborative context. Individual enumeration sensitivity was much better in interactive versus isolated sessions. This benefit did not require prior practice and was transient and specific to the collaborative session. It is important to reemphasize here that, the collective benefit from interaction (Figure 3A, gray vs. white bar) and the higher individual sensitivity in the interactive sessions (Figure 4B, circles vs. squares) are two separate and independent findings.

Social interaction and information sharing allowed the dyads to achieve better enumeration sensitivity than their best member. This result shows that enumeration information can be effectively communicated, compared and aggregated across individuals to take advantage of multiple observations made by the dyad members. The information aggregated via shared observations is the sample of some (individual) perceptual signal corrupted by some variable level of noise. Assuming that the participants were not biased and the task structure (a balanced 2-alternative forced choice employed here) did not systematically bias them to any one decision, sharing the observations via interaction should increase sensitivity by cancelling out/reducing the impact of individual random noise. The quantitative amount of this collective benefit is critically useful for telling us about the content of and the decision rule applied in the interaction.

The WCS model (Bahrami et al., 2012b; Bahrami et al., 2010) makes a specific prediction about the magnitude of the collective benefit to be obtained from dyads with known individual sensitivities. This model has successfully characterized collective decision making in the case of visual luminance contrast discrimination (Bahrami et al., 2010). However, the findings reported here (Figure 3A) show that this model, with its current assumptions and decision rule, fails to capture collective enumeration under some conditions. A number of factors may be responsible for the difference between collective contrast discrimination (Bahrami et al., 2010) and enumeration. One possibility is that the assumptions of the WCS model may not apply to enumeration. An important assumption of the WCS model is that the individual perceptual representation employed in the decision process is well characterized by a Gaussian distribution with a given mean (corresponding to the percept strength or vividness) and standard deviation (corresponding to the perceptual noise). Whereas previous studies have confirmed the relevance of this assumption for luminance contrast (e.g., Carandini, 2004), the neuronal representation of approximate enumeration may not fit the characteristics of a Gaussian distribution, although this has been claimed (Nieder, 2005). The results depicted in Figure 3A, therefore, would raise some doubt concerning the Gaussian assumption for representation of approximate numerosity.

When the same results were examined depending on prior noninteractive practice with the enumeration task (Figure 3B), WCS turned out to be a good predictor of collective benefit for participants who had had prior practice. This result cautions against refuting the assumption of Gaussian distribution for approximate enumeration outright and suggests that the reason underlying disagreement with the model may be sought elsewhere.

As two distinct types of perceptual decision, approximate enumeration and contrast discrimination differ in a number of critical respects. Luminance contrast is an elementary feature of the visual environment and is processed at the earliest levels of the visual stream (e.g., primary visual cortex). In contrast, the abstract notion of approximate numerosity requires multiple levels of computational processing (Stoianov & Zorzi, 2012) and has neural correlates at much higher, association-levels of visual stream in the primate parietal cortex (Castelli, Glaser, & Butterworth, 2006; Hubbard, Piazza, Pinel, & Dehaene, 2005; Vetter, Butterworth, & Bahrami, 2011). However, these distinctions do not directly account for the difference that we found between collective enumeration and contrast discrimination.

Another assumption of the WCS model is that dyad members have an accurate account of their own confidence and communicate this confidence accurately. Perhaps an important missing link is that whereas the characteristics of decision confidence and metacognition have been studied in detail for contrast discrimination (Bahrami et al., 2012b; Fleming et al., 2010; Song et al., 2011), to our knowledge, little is known about decision confidence in approximate enumeration. Some very recent work (Fusaroli et al., in press) shows that collective decisions are principally based on shared confidence.

Our results raise the possibility that for luminance contrast, participants' decision confidence reflects the reliability of those decisions relatively stably across time. But for approximate enumeration, this may take time and practice to develop. This prediction can be directly tested in future studies. In other words, the dyads that had prior noninteractive practice had the opportunity to introspect and learn to express their confidence more accurately to one another and/or interpret their partner's expressed confidence more accurately. This possibility highlights the hitherto underexplored role of learning about oneself in effective social learning. Previous models of social learning have so far only been concerned with formation of an accurate representation of the “other's” mental state (Hampton et al., 2008) or reliability (Behrens et al., 2008). These results remind us that for successful social interaction, knowledge of one's own reliability is as important as having a correct understanding of others. Future computational models of social learning should therefore take this issue into account. It is important to note here that our control experiment with familiar dyads (Figure 3C) showed decisively that prior history of interpersonal familiarity does not contribute significantly to collective enumeration.

Conversations as a “Black Box”

We treated the conversations leading to joint decisions as a “black box” without specifically investigating the way in which the conversations led to a joint decision. We had two reasons for this choice. During data collection, we observed that there was a large variability between dyads in how well they seemed to collaborate, whether they seemed to have taken the collective aspect of the experiment to heart and whether they were entertained by the experimental procedure. Based on these observations, we rated the dyads on an impression scale between 0 and 5 for “quality of observed collaboration.” On this scale, groups that interacted sporadically and did not seem to enjoy it were rated 0 and those who paid a lot of attention and found the collective decisions amusing and enjoyable—for example, rejoicing in correct group decisions were rated 5. However, we found that this qualitative rating was a very poor predictor of the behavioral collective benefit quantified by the ratio S_dyad/S_max (Pearson r = .04, p = .55). This result suggested that perhaps (our) qualitative observations of interactions are not particularly relevant for telling us about what contributed to accuracy of the joint decisions.

Recently, Fusaroli and colleagues (in press) performed a comprehensive quantitative analysis of the conversations that took place in one of our earlier interactive experiments (Bahrami et al., 2010) that involved luminance contrast discrimination. We used the video footage of those experiments to transcribe all the conversations that took place in each experimental session. The transcriptions were then submitted to a double-blind analysis by expert linguists and a customized automated text processing program. We found that conversations predominantly concerned the participants' level of confidence in their decisions. Collective benefit was indeed predicted by the contents and style of communication of confidence. Specifically, we found that local linguistic alignment (LLA) and global linguistic convergence (GLC) were positively correlated with collective benefit. LLA designated the participants' propensity to flexibly and reciprocally adapt to each other's ways of talking on a trial by trial basis. GLC quantified the degree to which, across the entire session, participants of a dyad converged on a limited functional set of shared expressions of confidence rather than indecisively drifting between multiple sets of expressions.

A thorough understanding of the phenomenon of collective enumeration would require a similar analysis of conversations in the experiments reported here. Moreover, it would be very interesting to see if the same markers of interactive conversation content that we found for luminance contrast discrimination could generalize to the case of collective enumeration. It is worth mentioning here that our qualitative observations of the interactions in the current experiments agree with the findings reported by Fusaroli and colleagues. Interestingly, although here the decision involved comparing the number of items in the two sets, we did not observe any dyad that explicitly shared their estimates of the number of items; instead, they generally communicated their confidence in their decisions. However, both video transcription and expert linguistic analysis are very slow and time-consuming processes and such an analysis is therefore beyond the scope of this article.

Impact of Collective Context on Individual Sensitivity

Finally, our findings showed that individual enumeration sensitivity was enhanced under interactive context (Figure 4B). To interpret this finding, we first contrast several predictions depicted in Figure 4A. If social loafing was present (Figure 4A, left panel), individual performance should be superior under noninteractive condition (square symbols) irrespective of the order in which the interactive and noninteractive experiments were performed. The “two person safety game” (not illustrated here) would predict that compared to noninteractive session, the better participant should show improvement and the worse person should show decline and on average, there would be no change in sensitivity. If, for whatever reason, social interaction were to endow the participants with enhanced individual sensitivity, this enhancement could either be transient, meaning that the individual sensitivity declines in the group that perform the noninteractive task in the second session (Figure 4A, middle panel) or permanent (Figure 4A, right panel) meaning that the same group will continue to perform superiorly in the second, noninteractive session. The results (Figure 4B) clearly show that the interactive context had a positive but transient impact on individual sensitivity. These results are neither consistent with social loafing nor the “two-person safety game.”

How could the individual benefit from interaction be explained? The individuals who underwent the interactive session after having had ample practice in the isolated session (Figure 4B, dashed line) showed a significant rise in sensitivity. If the interaction benefit for individuals was due to perceptual learning (from ample individual practice) and/or developing a superior decision making strategy (e.g., from sharing introspections and discussing decision criteria in the interactive session), then we would expect the benefit to be (a) smaller if no prior practice as provided and (b) stable and sustained once it had been achieved. However, the results from interactive → noninteractive condition (Figure 4B, solid line) clearly showed that the benefit of interaction did not require prior (isolated) practice and was transient. Therefore, it is unlikely that individuals' benefits from interaction were because of perceptual learning or optimized decision strategies.

Comparing previous research on social loafing (Karau & Williams, 1993) and social identity (Tajfel, 1978) with our experiments reported here provides an interesting (admittedly speculative) clue for explaining our results. As could be observed in a game of “Tug of War,” social loafing often occurs in settings where it is not possible to attribute the responsibility for the collective's failure to any specific individual (Karau & Williams, 1993). In the experiments described here, however, individual and group decisions were clearly spelled out and decision outcomes were publicly shared. As a result, a participant who misled the team to the wrong decision had to face the dismal outcome at the end of the trial. We suggest that the transparent assignment of responsibility may have had a strong motivational impact on the participants. This suggestion is in line with previous work on social identity theory (Abrams & Hogg, 1988). SIT proposes that individuals are motivated to maintain and enhance their self-esteem, and a positive social identity contributes strongly to self-esteem (Tajfel, 1978). Membership of a group in a collaborative context with explicit assignment of responsibility—such as provided by our experiment—provides a situation where one's social identity depends critically on contribution to the group that, in turn depends on individual performance.

The transient nature of the benefit of collective context on individual sensitivity that we observed is also in line with this explanation. As such, performing the task together may not fundamentally change an participants' sensory and/or numerosity processing but instead motivate them to do much better, perhaps by sustaining the participants in a heightened attentive state for longer times (Montalan et al., 2011). Outside the collective context, the incentive for high performance (i.e., group membership) was no longer present and the dyads who took the noninteractive session second showed a significant decline in individual sensitivity. These results also have important implications for interpreting previous social psychological studies that probed collective and individual performance in separate, independent blocks (Hastie & Kameda, 2005; Sorkin, Hays, & West, 2001). Our findings suggest that by underestimating the individuals' true capacity, those previous studies may have overestimated the collective benefit. Future research on collective interactions should therefore take the motivational impact of interaction on individual performance into account. We acknowledge that the attribution of the interactive benefit for individuals to motivational factors is speculative, warranted here by exclusion of other possible factors. Our experimental manipulations did not involve direct manipulation of motivational factors and so this may be a fruitful avenue for future research.

Conclusion

Two heads can count better than one, but not as well as expected by previous models of collective sensory decision making about contrast if prior practice is not available. Moreover, unlike contrast discrimination, collective enumeration benefited from prior, noninteractive practice showing that social learning of combining shared information about enumeration requires substantial individual experience. Finally, the collective context had a positive but transient impact on individual's enumeration sensitivity. This social impact is best explained as a motivational factor arising from the fact that observers in a collective have to take responsibility for their individual decisions and face the consequences of their judgments.