Abstract
Diverse mechanical perturbations elicit arterial growth and remodeling responses that appear to optimize structure and function so as to achieve mechanical homeostasis. For example, it is well known that functional adaptations to sustained changes in transmural pressure and blood flow primarily affect wall thickness and caliber to restore circumferential and wall shear stresses toward normal. More recently, however, it has been shown that changes in axial extension similarly prompt dramatic cell and matrix reorganization and turnover, resulting in marked changes in unloaded geometry and mechanical behavior that presumably restore axial stress toward normal. Because of the inability to infer axial stress from in vivo measurements, simulations are needed to examine this hypothesis and to guide the design of future experiments. In this paper, we show that a constrained mixture model predicts salient features of observed responses to step increases in axial extension, including marked increases in fibrous constituent production, leading to a compensatory lengthening that restores original mechanical behavior. Because axial extension can be modified via diverse surgical procedures, including bypass operations and exploited in tissue regeneration research, there is a need for increased attention to this important aspect of arterial biomechanics and mechanobiology.
Keywords: vascular adaptation, axial stretch, collagen, elastin, elongation
1 Introduction
Considerable evidence now suggests a fundamental role for axial wall stress in compensatory arterial adaptations to genetic defects and diverse perturbations in mechanical loading. It has been suggested, for example, that an artery may have more control over its local axial force than it does over local blood flow and pressure, which are dictated largely by proximal cardiac output and distal resistance vessels, and that it may exploit this local capability to regulate stress-mediated changes in geometry or structure that tend to achieve or restore mechanical homeostasis [15]. Much of the renewed interest in axial behaviors was motivated by the provocative finding reported by Jackson et al. [16]†. Briefly, they showed, in a rabbit model, that extending common carotid arteries well beyond their in vivo length causes them to grow lengthwise and remodel rapidly because “arterial tissue, especially extracellular matrix, accumulated at a nearly unprecedented rate after axial strain was imposed.” Moreover, they suggested that this remodeling appeared to be stimulated primarily by the imposed change in axial stress or stretch, not related changes in pressure-induced circumferential stress or flow-induced wall shear stress. In other words, changes in axial stress or stretch appear to be strong stimuli for significant arterial growth and remodeling (G&R); they even appear to affect the orientation of the mitotic axis of the smooth muscle cells, which in turn likely affects the orientation at which newly produced collagen is incorporated within extant matrix [4].
Gleason and Humphrey [7] used both a standard stress analysis and a simple model of arterial G&R to study numerically the experiment reported by Jackson and colleagues. Briefly, using a 3-D analysis that included complexities related to residual stresses and nonlinearly anisotropic material behaviors, they con-firmed that imposed axial extensions at physiologic pressures affect primarily the axial, not circumferential, stress and that the transmural distributions of stress remain nearly uniform. This finding motivated the use of a 2-D constrained mixture model that accounted for different material properties, natural (stress-free) configurations, and constant rates of turnover of structurally significant passive constituents at constant rates. It appears, however, that rates of turnover - both for constituent production and removal - can change throughout stress-mediated adaptations [e.g., 30, 31, 39] and vasoactivity plays an important complementary role in many cases [4, 13, 35].
In this paper, therefore, we revisit the class of experiments reported by Jackson and colleagues and employ an extended constrained mixture model that includes potentially complementary effects of vasoactivity and matrix turnover as well as functions for mass production and removal that depend on changing differences in biaxial intramural and wall shear stresses from homeostatic targets [33]. Moreover, rather than study the carotid artery, we consider a model intracranial (basilar) artery, which has a much lower percentage of elastin than central arteries such as the carotids and aorta and consequently a lower value of homeostatic axial prestretch. Although structurally significant elastin does not turnover in maturity, it nonetheless appears to play a key role in governing axial mechanical properties, including axial prestretch [3]. Flow-induced changes in axial stretch have also been reported in the basilar artery [21], again emphasizing the potentially fundamental role of axial behaviors in many different cases of arterial adaptation.
2 Methods
Following Baek et al. [2] and Valentín et al. [35], we model the basilar artery as a thin walled axisymmetric cylindrical pressure vessel. Hence, mean circumferential and axial Cauchy stresses are
| (1) |
| (2) |
where P is the transmural pressure, a is the current inner radius, h is the current thickness, and f is the applied axial force at G&R time s. These equilibrium equations can be combined with constitutive relations for the principal Cauchy stress resultants Ti = σi h, where i = z, θ and, by the rule of mixtures, the stored energy function for the artery W = ΣWk for k = 1, 2,…n families of structurally significant constituents. Hence, we have at any G&R time s [11, 25]
| (3) |
| (4) |
where λθ and λz are stretches for the artery and is the stress actively generated by smooth muscle, which is prescribed as a function of vasoactive molecule concentration C and muscle fiber stretch [2, 33–35], namely
| (5) |
where Tmax is a scaling parameter with units kPa, φm is the evolving mass fraction of active smooth muscle, λM is the stretch at which the active force generating capability is maximum, λ0 is the stretch at which muscle cannot generate any force, and is the current active muscle fiber stretch.
With regard to passive properties, structurally significant collagen and smooth muscle turnover continuously, that is, they are continuously produced (via synthesis or proliferation) and removed (via degradation or apoptosis). Noting that constitutuents only carry load as long as they exist, we let the evolving strain energy function for constituent k be written as [35]
| (6) |
where Mk(0) are initial mass densities, Qk(s) ∈ [0, 1] are fractions of material produced at or before time s = 0 that survive to current time s, mk(τ) are mass density production rate functions, and qk(s, τ) ∈ [0, 1] are fractions of material produced at any past time τ ∈ [0, s] that survive to current time s. Note, therefore, that prior to G&R (i.e., at s = 0), the standard mass-averaged rule of mixtures is recovered as it should be. Note, too, that the individual stored energy functions depend on individual, constituent dependent deformations, namely , the 2-D deformation gradient tensor for constituent k, subject to the kinematic constraint xk(s) = x(s) that all constituents deform together despite individual natural (stress-free) configurations Xk(τ) being allowed to evolve separately.
The membrane assumption and assumed loading allows us to write all deformations in terms of stretches. The total stretch experienced at G&R time s by a fibrillar constituent k deposited at time τ is
| (7) |
with
| (8) |
where denotes the angle between a fiber and the the artery’s axial (z) direction. These kinematic relations represent a series of multiplicative deformations and are discussed in detail by Baek et al. [1]. Note, too, that is the deposition stretch for the kth; it represents the fundamental hypothesis that synthetic cells produce and deposit new constituents within the existing extracellular matrix at preferred mechanical states [33].
As in previous constrained mixture implementations [2, 35], we modeled the passive mechanical response of elastin using a neo-Hookean strain energy function [5, 10]
| (9) |
where and are the stretches experienced by elastin, which can be determined from arterial stretches (λθ (s), λz(s)) and “growth-induced” prestretches . Note that the total stretches experienced by elastin do not depend on deposition time τ. This assumption reflects the observation that elastin is not continually produced in maturity as are collagen and smooth muscle. In contrast, functional elastin is produced and cross-linked exclusively during the perinatal period, and subsequently stretched elastically throughout normal development and maturation [3]. Finally, we employed Fung exponential strain energy functions for both collagen [10, 20]
| (10) |
and passive smooth muscle [8]
| (11) |
The stretch experienced by each of these constituents depends on its deposition stretch, and the stretch experienced by the arterial wall from deposition time τ to current G&R time s, as described by equation (7). We allow four fiber families of collagen, oriented axially, circumferentially, and helically [2, 10, 35]. Table 1 lists values of the associated material parameters.
Table 1.
Important parameter values used to model a representative mature basilar artery, before any perturbation.
| Role | Value | ||
|---|---|---|---|
| Geometry/Loads |
ah = 1.42 mm, hh = 0.176 mm P = 93 mmHg, Q = 3.075 ml/s, |
||
| Mass Kinetics |
|
||
| Vasoactivity |
Tmax = 150 kPa λM = 1.1, λ0 = 0.4 CB = 0.68, CS = 20 CB |
||
| Passive Elasticity |
c = 588.3 kPa,
|
It is well known that vascular smooth muscle cells and fibroblasts actively produce and organize new extracellular matrix proteins and glycoproteins in response to altered stretch and/or stress [22]. Moreover, endothelial cells change their production of vasoactive molecules in response to changes in wall shear stress [23], which in turn affects rates of matrix production [28, 29]. Hence, we prescribe the following constitutive relation for mass density productions [35]
| (12) |
where Δσ and ΔC are normalized changes in constituent fiber stresses and the net ratio of constrictors to dilators from their homeostatic values, respectively. The former vary with changes in transmural pressure and vasoactivity whereas the latter are functions of wall shear stress [cf. 32], namely
| (13) |
where τw(s) and are current and homeostatic wall shear stresses, respectively, with τw(s) = 4 μ Q/π a3(s), where μ is viscosity and Q is blood flow, and CB is the basal concentration and CS is a shear stress sensitivity factor. Equation (12) recovers basal rates of mass production under homeostatic conditions (Δσ = ΔC = 0) as it should.
It is generally accepted that degradation of extracellular matrix follows a first order type kinetics [24]. Hence, removal rates are prescribed herein as [cf. 2, 35]
| (14) |
where are rate-type parameters for mass removal having units of days−1. Among others, Willett et al. [37] show that degradation rates depend on stress level. Hence, these rate parameters, in turn, are prescribed as , where is a basal value, Δζ(τ̃) is the difference in fiber tension from its homeostatic value, and ζk(τ) is the level of tension on constituent k that was produced at time τ [35]. This formulation results in accelerated constituent removal (degradation) for altered levels of tension. Table 1 lists values for these and many other parameters, including constituent prestretches and homeostatic mass fractions and half-lives.
By prescribing in vivo axial length l, transmural pressure P, and volumetric flowrate Q at all G&R times s, we can calculate the evolving inner radius via equation (3); we can also calculate evolving wall thickness given the assumption that overall mass density ρ(s) = ρ(0) ∀s. Additional details of the implementation and associated fundamental assumptions are discussed elsewhere [2, 33–35]. Herein, we prescribe step increases in in vivo axial length l = δ lh, where lh is the homeostatic length, and investigate subsequent G&R-governed evolution of the wall.
3 Illustrative Results
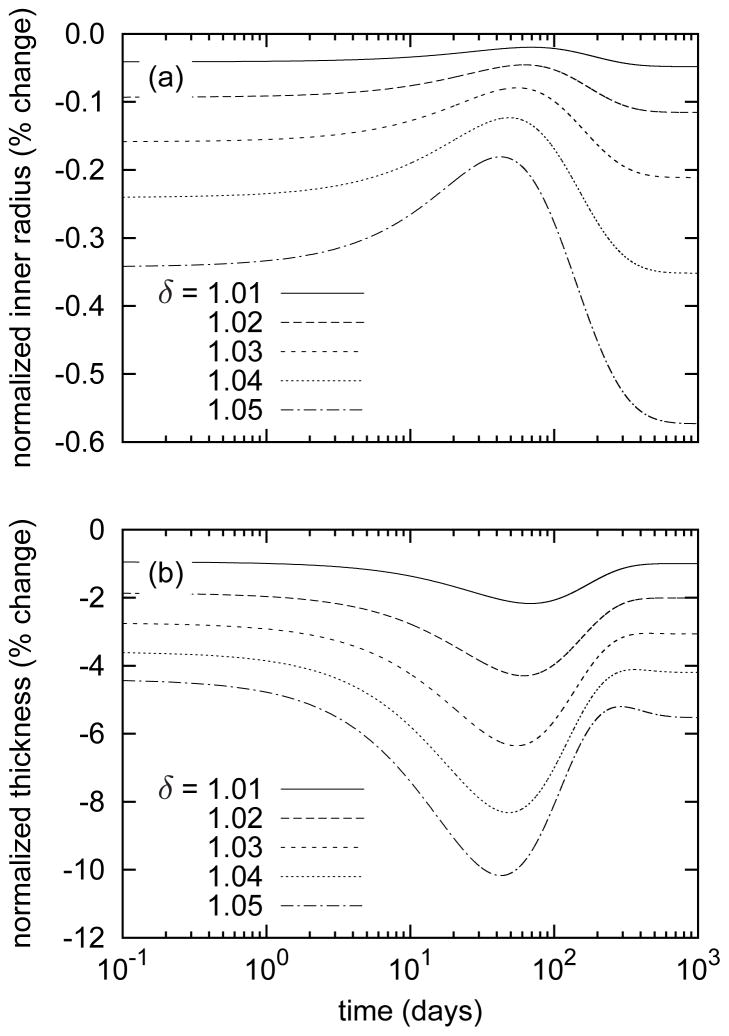
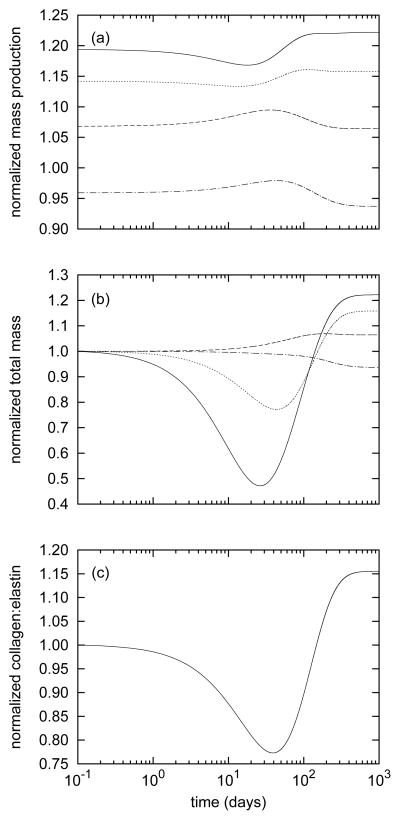
Consistent with values reported by Wicker et al. [36], the model basilar artery (at s = 0) exhibited an in vivo axial stretch lh/L(0) = 1.24 and an associated axial force of 3.68 mN at homeostatic conditions. While maintaining constant (homeostatic) transmural pressure (P = 93mmHg) and flow (Q = 3.075ml/s), we prescribed 1 to 5 percent step increases in in vivo axial extension at G&R time s = 0 (with , see equation (12)) to initiate the evolution of arterial geometry and properties. Instantaneous reductions in caliber and thickness due to isochoric motion were small, and thereafter the artery maintained its inner radius to within 1% of its preferred value despite non-monotonic changes that peaked near day 40 (figure 1, panel a). This negligible (i.e., not measurable clinically) change in inner radius and thus wall shear stress suggests that axial stretch-induced G&R is primarily an intramural stress-dominated process consistent with the original interpretation of Jackson et al. [16]. Changes in wall thickness (figure 1, panel b) were more pronounced, however. The wall instantaneously thinned isochorically and continued to thin as original material, deposited before time s = 0, degraded under the higher axial fiber tensions (see equation (14)). This atrophy resulted in a slight distending trend (due to decreased structural stiffness at constant pressure) until approximately day 40 (figure 1, panel a). After day 40, the model predicted increasing thicknesses, indicating that mass production outpaced mass removal. Indeed, despite sustained elevated rates of collagen production (figure 2, panel a), total axial and helical collagen masses decreased until approximately day 40 (figure 2, panel b). The evolving collagen to elastin ratio (figure 2, panel c) further revealed a biphasic evolution process, that is, competition between altered production and removal.
Figure 1.
Time courses of evolving inner radii (panel a) and thicknesses (panel b), each normalized with respect to values for the unperturbed artery, for indicated step changes in in vivo axial length l(s) = δ lh. Note the decreased inner radii and wall thicknesses at the instant of elongation due to isochoric motion. The evolution is characterized by a two-phased G&R process in which the first phase (s ∈ [0, ~ 40] days) is dominated by stretch-induced mass removal and atrophy, followed by a second phase characterized by a gradual thickening that causes slight luminal encroachment(s ∈ [~ 40, 1000] days).
Figure 2.
Time courses of mass production rates per unit area (panel a) and total masses per unit area (panel b) for axially- (solid), helically- (dashed), and circumferentially- (dotted) aligned collagen and smooth muscle (dash-dotted) for a 5% step increase in in vivo axial length. Panel (c) shows the evolving total collagen to elastin ratio. All quantities are normalized with respect to homeostatic values. Note the elevated and sustained increases in axial and helical collagen production. Circumferential collagen saw more modest increases in production, while smooth muscle production diminished. Although mass production rates remained relatively stable, the effects of stretch-induced degradation (see equation (14)) can be appreciated by the substantial reductions in total axial and helical collagen (panel b). This considerable atrophy was chiefly responsible for the predicted reductions of thickness up to day 40 (figure 1, panel b) and the associated reduction of the collagen to elastin ratio (panel c). After approximately 40 days, total axial and helical collagen masses began to increase, suggesting that mass production outpaced mass removal.
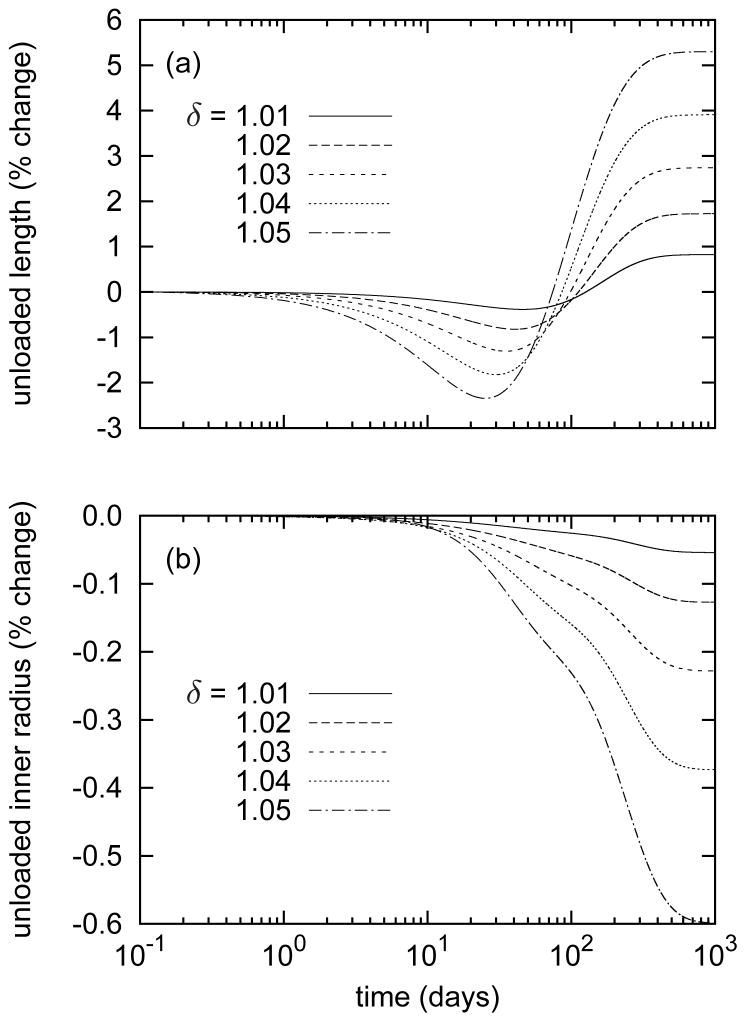
Evolving changes in unloaded geometry also revealed salient G&R trends and illustrated the important biaxial effects of comparatively highly prestretched and biologically stable elastin. Predicted unloaded axial lengths (figure 3, panel a) followed the evolving collagen to elastin ratios. The predicted initial losses of collagen, particularly with axial orientation, allowed the elastin to retract the artery further upon unloading; that is, reduced axial and helical collagen mass provided reduced compressive resistance to the elastin. The opposite was true after the collagen to elastin ratio rose above the baseline value (Mc(0)/Me(s) = 11.0). The additional collagen, much of it oriented axially and helically, provided higher compressive resistance to elastin, resulting in larger unloaded lengths. Also, this new collagen was deposited in the new (elongated) configuration, thereby entrenching the artery in the elongated state, again consistent qualitatively with the interpretation of Jackson et al. [16]. In contrast, unloaded inner radii experienced slight monotonic decreases (figure 3, panel b) as circumferential collagen production increased only modestly and (circumferentially aligned) smooth muscle production decreased. This slight net reduction of stiff circumferential constituents resulted in a reduced compressive resistance to elastin.
Figure 3.
Time courses of evolving unloaded lengths (panel a) and inner radii (panel b), normalized with respect to those of the unperturbed artery, for indicated step changes in in vivo axial length l = δ lh. The model predicted decreasing unloaded lengths up to day 40, followed by an increase and asymptotic stabilization. Note that this behavior follows the evolving collagen to elastin ratio (figure 2, panel c). The decreased unloaded inner radii resulted from a loss of smooth muscle.
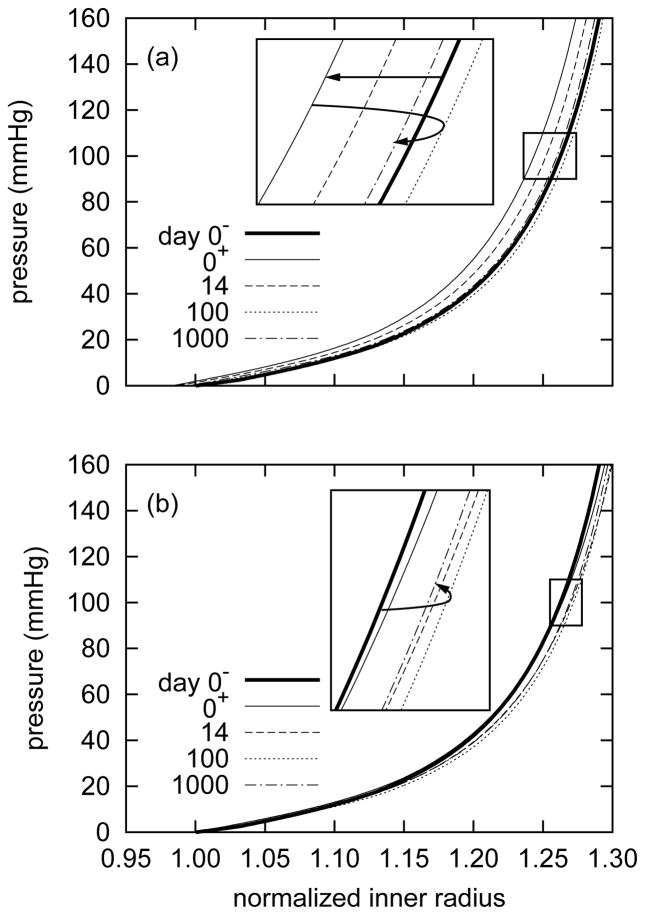
Passive “pressure-diameter” behaviors (figure 4) revealed small evolving G&R-governed changes in overall mechanical properties. Nevertheless, these responses suggested superficially different trends depending on the normalizing value for inner radius. For example, by normalizing the current pressurized inner radius a(s) by the original unpressurized inner radius before extension A(0−) (figure 4, panel a), the response curve shifted to the left at the instant of extension at time s = 0+. As the artery remodeled around the new (elongated) configuration, the response curves eventually shifted to the right. Notwithstanding some “overshoot,” the artery’s passive response at 1000 days approached the original (day 0−) response. This suggested an instantaneous slight circumferential stiffening resulting from a coupled biaxial behavior and isochoric motion following the step axial extension, with a subsequent gradual return to the homeostatic response.
Figure 4.
Evolving passive “pressure-diameter” responses due to G&R for a 5% step increase in in vivo axial length, where the abscissa ‘normalized inner radius’ is expressed as the ratio of the current deformed inner radii to the original unpressurized inner radius before elongation a(s)/A(0−) (panel a) or the current unpressurized inner radius a(s)/A(s) (panel b). Results are for the current in vivo axial length l = δ lh. The solid bold curve represents the response before the extension at time s = 0−. The light solid curve represents the response at the instant of the step increase in length at time s = 0+. Note the instantaneous leftward shift indicating a stiffer response as a consequence of coupled biaxial behavior and isochoric motion, followed by a gradual rightward shift as the artery remodeled towards its original compliance (inset, panel a). The model predicted some “overshoot” at day 100 followed by a slight reversal. Normalizing with respect to the current unpressurized configuration obscures the instantaneous effect of elongation and suggests that the artery became more compliant (inset, panel b). This result highlights the importance of choosing appropriate and consistent reference configurations, which affect substantially data interpretation.
On the other hand, by normalizing the current pressurized inner radius a(s) by the the current unpres-surized inner radius after extension A(s) (figure 4, panel b), the response curve exhibited no leftward shift at the instant of extension. Rather, the response curves shifted to the right, suggesting a progressive increase in compliance with time. Eventually, and after some “overshoot”, the response curve settled on a slightly more compliant behavior, one that would likely not be discernible experimentally. This interpretation is consistent with the prediction that the artery loses (stiff) circumferential smooth muscle (figure 2, panels a and b and figure 3, panel b), thereby reducing effective circumferential stiffness. These two interpretations of the same results emphasize the importance of choosing appropriate and consistent measures of stretch, particularly when comparing experimental findings and numerical predictions.
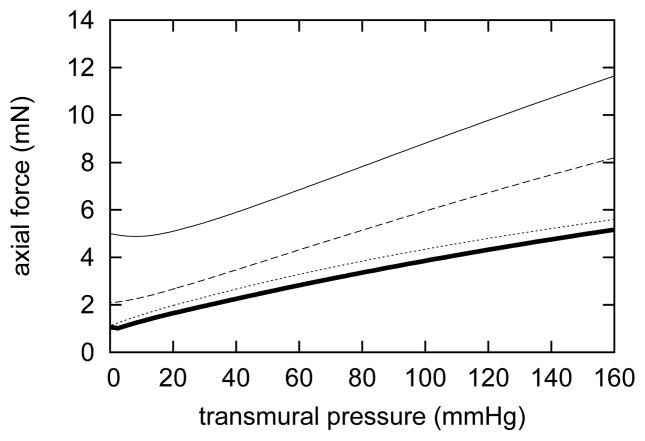
Gleason et al. [9] observed evolving passive axial “force-pressure” behavior in arteries following sustained increases in axial extension. Our model predicted similar trends (figure 5) in response to a sustained 5% increase in axial stretch; applied axial forces gradually decreased for any given pressure. By day 1000, the axial force-pressure response at l = δ lh was nearly equal to that at day 0 and l = lh, further suggesting that the artery remodeled around its new increased length so as to recover its original behavior. The evolving axial “force-pressure” behavior depends primarily on the natural configurations of axial and helical collagen. The gradual shift by nearly 5% corresponds closely to the change in natural configurations for axially and helically oriented collagen. Note, too, that the artery was able to closely match its original axial “force-pressure” behavior despite elastin not turning over. This suggests that the passive effects of axial and helical collagen dominate axial tensile behavior in basilar arteries.
Figure 5.
Evolving passive axial “force-pressure” responses due to G&R for a 5% step increase in in vivo axial extension at days 0 (solid), 14 (dashed), and 1000 (dotted). The original “force-pressure” response is indicated by the solid bold curve. Response curves shifted down as the artery remodeled around its new axial length [cf. 9]. Note that by 1000 days, the passive response nearly equaled the original response, indicating a near complete recovery of the artery’s original axial “force-pressure” behavior at the new in vivo axial length.
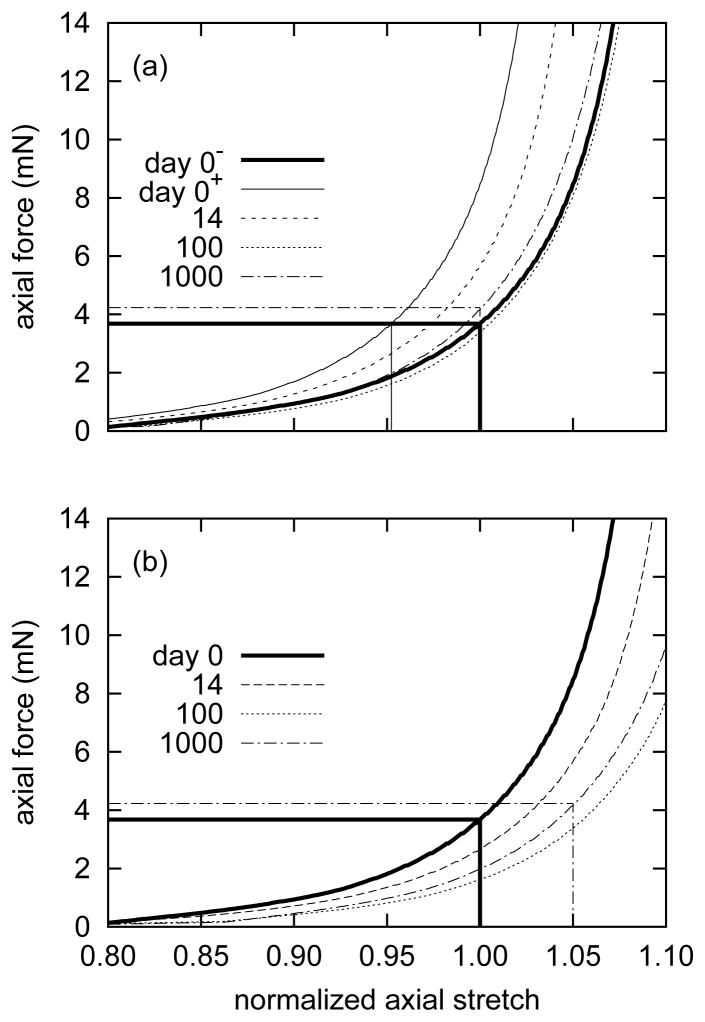
Predicted passive axial “force-length” behavior also evolved as a result of a sustained 5% increase in axial extension. By measuring overall axial stretch with respect to the current in vivo axial length l = δ lh (figure 6, panel a), the model suggested an instantaneous axial stiffening as a result of biaxial behavior at the new in vivo axial length with a gradual return to its original behavior. The instantaneous stiffening is an artifact of shifting the normalizing axial stretch by 1 −1/δ. As the artery remodeled around its new axial extension, it almost completely recovered its original axial “force-length” behavior. By measuring stretch with respect to the original in vivo axial length lh (figure 6, panel b), the model revealed a gradual rightward shift as the artery remodeled. After 1000 days, the axial “force-length” behavior shifted to the right by approximately 5%, indicating gradual G&R driven compliance. As in the case of evolving “pressure-diameter” behavior, the two different axial “force-length” interpretations depend upon the normalizing measure of stretch used.
Figure 6.
Evolving passive axial “force-length” responses due to G&R for a 5% step increase in in vivo axial length, where the abscissæ ‘normalized axial length’ are expressed as the ratios of the current axial length to the current in vivo axial length l(s)/δ lh (panel a) and the original in vivo axial length l(s)/lh (panel b). Results shown are for constant transmural pressure P = Ph. Panel (a) reveals an instantaneous initial leftward shift of 1 − 1/δ in response to the axial extension, followed by a gradual rightward shift as the artery remodeled around the new (extended) in vivo axial length. The axial force-length response at day 1000 approached that of day 0−. The same results, when normalized with respect to lh (panel b), revealed a gradual rightward shift. By day 1000, the axial force at l(s)/lh = 1.05 was nearly equal to that at day 0 and l(s)/lh = 1. Note the slight “overshoot” at day 100. This behavior at time s = 0+, when normalized with respect to lh, is identical to that at time s = 0−.
4 Discussion
It has long been known that sustained alterations in blood pressure and flow induce significant arterial adaptations that appear to restore circumferential and wall shear stress to homeostatic values [e.g., 4, 8, 11–13, 17, 19, 26, 30, 32, 38, 39]. More recently, however, it has become apparent that arteries similarly adapt to sustained changes in axial stretch or stress [7, 9, 15, 16]. The goal of this paper was to explore, via computational modeling, possible means by which such adaptations occur.
4.1 Ubiquitous G&R Mechanisms
Because of the highly nonlinear axial stress-stretch behavior exhibited by most arteries, even modest step changes in axial extension can cause dramatic increases in intramural stress as compared to those induced by typical in vivo changes in transmural pressure or volumetric flow. That is, a restricted vasoactive range can limit initial changes in caliber in response to abrupt changes in flow and the passive circumferential stiffness of the artery can limit the severity of its distension in response to abrupt changes in transmural pressure. In contrast, an imposed increase in axial extension represents a different type of perturbation since dimensions are changed directly, thus resulting in marked changes in stress. Nevertheless, despite differences in perturbations (changing flow, pressure, or axial extension), we posit that the associated G&R responses occur via similar fundamental mechanisms: mechanically-mediated rates of constituent turnover, changes in vasoactivity, and deposition of new matrix that is prestretched to preferred values. Hence, the time-dependent nature of G&R results primarily the type and severity of the perturbation.
4.2 Predicted Mechanisms
The most obvious consequence of axial extension-induced arterial G&R is an increase in unloaded length, which is consistent with Jackson et al. [16] noting that “the stretched artery grew into its new length.” The present simulations suggest that this response results primarily from an increased deposition of axially and helically-oriented collagen at its preferred value of deposition stretch within the new stretched configuration, which provides greater compressive resistance to the highly prestretched elastin. The model arteries were predicted to almost completely recover their original in vivo axial force-length and force-pressure responses by essentially shifting the response curves. This remarkable ability is due to the predicted sustained changes in mass fractions and production rates in response to the dramatically altered state of intramural axial stress, not changes in circumferential or wall shear stress. Predicted changes in pressure-diameter behavior were less pronounced, but were consistent with expected behavior.
The model also predicted competing effects of mass removal and production, resulting in biphasic evolutions in geometry and properties. As the collagen to elastin ratio decreased during the first phase, unloaded lengths decreased; then, as collagen deposition outpaced removal and the collagen to elastin ratio increased, the unloaded length increased. Changes in unloaded length manifest in vivo as changes in axial stretch, which in turn affect the biaxial state of stress since σθ = σ̂θ (λθ, λz) and σz = σ̂z(λθ, λz). This association between in vivo axial stretch and collagen to elastin ratio was recently seen to explain, in part, normal species-to-species differences in the former [12], thus it should not be surprising that changing axial stretches manifest in normal adaptations to altered loading. Indeed, for this reason, axial mechanics likely plays a strong role in all aspects of arterial health and disease progression, including hypertension, development of aneurysms, Marfan syndrome, and aging to name a few.
4.3 Clinical Relevance
Jackson et al. [16] observed that significant axial unloading can result in tortuosity, which was not resolved experimentally over periods usually sufficient for arterial G&R. Although the case of a sustained decrease in axial stretch was not investigated numerically herein, we can consider some possible reasons based on intuition gleaned from our simulations. Irreversible tortuosity may result, in part, from a much lower rate of degradation and particularly synthesis of collagen fibers when they experience a dramatic decrease in tension as compared to when they experience an increase in tension. Also, because functional elastin is not produced in mature arteries, an artery subjected to a stretch less than its original in vivo stretch would continue to have much less stressed elastin, noting that stressed elastin appears to be fundamental in mechanical homeostasis; its loss results in aneurysmal dilatation and/or tortuousity [cf., 27].
Recognition of the importance of axial stress in arterial homeostasis and adaptations is clearly much more recent (ca. 2002) than the longstanding knowledge of the importance of pressure-induced circumferential stress and flow-induced wall shear stress. Consequently, there is a pressing need for increased attention to its clinical importance. Given that axial stress appears to be such a strong regulator of arterial G&R, there is a need to study effects of bypass procedures, using either native or synthetic grafts, on the host vessel response. Similarly, there is a need to consider potential effects of axial extension on construct development in tissue engineering of blood vessels.
4.4 Conclusion
The present constrained mixture model appears to capture salient features of arterial G&R in response to increased axial extension similar to prior results for altered pressure and flow [35]. Nevertheless, it is important to note that the present simulations were found to be much more sensitive to prescribed values of the rate parameters in the relations for matrix production. It is possible that this increased numerical sensitivity reflects, in part, the increased biological sensitivity in responses observed experimentally by Jackson et al. [16]. Alternatively, this observation may also serve as an important reminder that there is a pressing need for more biological data to formulate improved constitutive relations for the stress mediated production and removal, including their dependence on perturbations in all stresses from homeostatic values. That is, we currently do not know the best functional forms for mk(τ) and qk(s, τ) - recall equations (12) and (14) - and we do not know the best metric of stress on which they depend. Nevertheless, the present results are encouraging and suggest that a single theory of arterial growth and remodeling, containing a single set of material parameters, should be able to describe and predict responses to diverse perturbations in the chemomechan-ical environment once we have refined the requisite constitutive relations and material parameters based on improved data, particularly on stress-mediated constituent turnover rates. Together, therefore, continued parallel advances in vascular mechanobiology, medical imaging, biomechanical modeling, and computational methods promise to increase significantly our understanding of vascular physiology, pathophysiology, injury, and clinical intervention, and thus to improve clinical care via more personalized and pre-emptive treatments [14, 18].
Acknowledgments
This work was supported, in part, via NIH grants HL-64372, HL-80415, and HL-86418.
Footnotes
We are saddened to acknowledge the untimely passing of Prof. B. L. Langille (October 29th, 2008), a true pioneer in studies of arterial adaptation.
References
- 1.Baek S, Rajagopal KR, Humphrey JD. A theoretical model of enlarging intracranial fusiform aneurysms. J Biomech Eng. 2006;128(1):142–9. doi: 10.1115/1.2132374. (Print) [DOI] [PubMed] [Google Scholar]
- 2.Baek S, Valentín A, Humphrey JD. Biochemomechanics of cerebral vasospasm and its resolution: II. constitutive relations and model simulations. Ann Biomed Eng. 2007;35(9):1498–1509. doi: 10.1007/s10439-007-9322-x. (Print) [DOI] [PubMed] [Google Scholar]
- 3.Cardamone L, Valentín A, Eberth J, Humphrey J. Origin of axial prestretch and residual stress in arteries. Biomech Model Mechanobiol. 2009 doi: 10.1007/s10237-008-0146-x. (in press) [DOI] [PMC free article] [PubMed]
- 4.Dajnowiec D, Langille BL. Arterial adaptations to chronic changes in haemodynamic function: coupling vasomotor tone to structural remodelling. Clin Sci (Lond) 2007;113(1):15–23. doi: 10.1042/CS20060337. (Electronic) [DOI] [PubMed] [Google Scholar]
- 5.Dorrington K, McCrum N. Elastin as a rubber. Biopolymers. 1977;16(6):1201–1222. doi: 10.1002/bip.1977.360160604. [DOI] [PubMed] [Google Scholar]
- 6.Figueroa CA, Baek S, Taylor CA, Humphrey JD. A computational framework for fluid-solid-growth modeling in cardiovascular simulations. Comput Meth Appl Mech Eng. 2009 doi: 10.1016/j.cma.2008.09.013. URL http://www.sciencedirect.com/science/article/B6V29-4TPPDXD-1/2/469bea93997eede01638392fc8fc8157. (inpress) [DOI] [PMC free article] [PubMed]
- 7.Gleason RL, Humphrey JD. Effects of a sustained extension on arterial growth and remodeling: a theoretical study. J Biomech. 2005:38. 1255–61. doi: 10.1016/j.jbiomech.2004.06.017. Print. [DOI] [PubMed] [Google Scholar]
- 8.Gleason RL, Taber LA, Humphrey JD. A 2-d model of flow-induced alterations in the geometry, structure, and properties of carotid arteries. J Biomech Eng. 2004;126(3):371–81. doi: 10.1115/1.1762899. [DOI] [PubMed] [Google Scholar]
- 9.Gleason RL, Wilson E, Humphrey JD. Biaxial biomechanical adaptations of mouse carotid arteries cultured at altered axial extension. J Biomech. 2007;40(4):766–776. doi: 10.1016/j.jbiomech.2006.03.018. (Print) [DOI] [PubMed] [Google Scholar]
- 10.Holzapfel GA, Gasser TC, Ogden RW. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J Elasticity. 2000;61(1–3):1–48. [Google Scholar]
- 11.Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer-Verlag; New York: 2002. [Google Scholar]
- 12.Humphrey JD. Vascular adaptation and mechanical homeostasis at tissue, cellular, and sub-cellular levels. Cell Biochem Biophys. 2008;50(2):53–78. doi: 10.1007/s12013-007-9002-3. (Print) [DOI] [PubMed] [Google Scholar]
- 13.Humphrey JD. Mechanisms of arterial remodeling in hypertension. coupled roles of wall shear and intramural stress. Hypertension. 2008;52(2):195–200. doi: 10.1161/HYPERTENSIONAHA.107.103440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Humphrey JD, Taylor CA. Intracranial and abdominal aortic aneurysms: Similarities, differ-ences, and need for a new class of computational models. Annu Rev Biomed Eng. 2008;10(1):221–246. doi: 10.1146/annurev.bioeng.10.061807.160439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Humphrey JD, Eberth JF, Dye WW, Gleason RL. Fundamental role of axial stress in compensatory adaptations by arteries. J Biomech. 2009;42:1–8. doi: 10.1016/j.jbiomech.2008.11.011. URL http://www.sciencedirect.com/science/article/B6T82-4V4M307-1/2/fba97bb02818f814b8e9fc17e3ed3458. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jackson ZS, Gotlieb AI, Langille BL. Wall tissue remodeling regulates longitudinal tension in arteries. Circ Res. 2002;90(8):918–25. doi: 10.1161/01.RES.0000016481.87703.CC. [DOI] [PubMed] [Google Scholar]
- 17.Kamiya A, Togawa T. Adaptive regulation of wall shear stress to flow change in the canine carotid artery. Am J Physiol. 1980;239(1):H14–21. doi: 10.1152/ajpheart.1980.239.1.H14. [DOI] [PubMed] [Google Scholar]
- 18.Krams R, Breeuwer M, van de Vosse F. Personalised imaging and biomechanical modelling of large vessels. Med Biol Eng Comput. 2008;46(11):1057–1058. 11. doi: 10.1007/s11517-008-0417-9. URL http://dx.doi.org/10.1007/s11517-008-0417-9. [DOI] [PubMed] [Google Scholar]
- 19.Langille BL. Arterial remodeling: relation to hemodynamics. Can J Physiol Pharmacol. 1996;74(7):834–41. [PubMed] [Google Scholar]
- 20.Lanir Y. Constitutive equations for fibrous connective tissues. J Biomech. 1983;16(1):1–12. doi: 10.1016/0021-9290(83)90041-6. (Print) [DOI] [PubMed] [Google Scholar]
- 21.Lehman RM, Owens GK, Kassell NF, Hongo K. Mechanism of enlargement of major cerebral collateral arteries in rabbits. Stroke. 1991;22(4):499–504. doi: 10.1161/01.str.22.4.499. (Print) [DOI] [PubMed] [Google Scholar]
- 22.Lehoux S, Castier Y, Tedgui A. Molecular mechanisms of the vascular responses to haemodynamic forces. J Intern Med. 2006;259(4):381–392. doi: 10.1111/j.1365-2796.2006. 01624.x. (Print) [DOI] [PubMed] [Google Scholar]
- 23.Li YSJ, Haga JH, Chien S. Molecular basis of the effects of shear stress on vascular endothelial cells. J Biomech. 2005/10;38(10):1949–1971. doi: 10.1016/j.jbiomech.2004.09.030. URL http://www.sciencedirect.com/science/article/B6T82-4DTBRNS-7/2/a2d95ae45562de5a4f70e0f425fd6121. [DOI] [PubMed] [Google Scholar]
- 24.Niedermüller H, Skalicky M, Hofecker G, Kment A. Investigations on the kinetics of collagen-metabolism in young and old rats. Exp Gerontol. 1977;12(5–6):159–68. doi: 10.1016/0531-5565(77)90001-8. (Print) [DOI] [PubMed] [Google Scholar]
- 25.Pipkin AC. Integration of an equation in membrane theory. Z Angew Math Phys. 1968;19(5):818–819. URL http://dx.doi.org/10.1007/BF01591012. [Google Scholar]
- 26.Reneman R, Hoeks A. Wall shear stress as measured in vivo: consequences for the design of the arterial system. Med Biol Eng Comput. 2008;46(5):499–507. 05. doi: 10.1007/s11517-008-0330-2. URL http://dx.doi.org/10.1007/s11517-008-0330-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rigamonti D, Saleh J, Liu AM, Hsu FP, Mergner WJ, Humphrey JD. Dolichoectatic aneurysm of common carotid artery: an animal model with histological correlation. Pathobiology. 1994;62(1):8–13. doi: 10.1159/000163872. (Print) [DOI] [PubMed] [Google Scholar]
- 28.Rizvi MAD, Myers PR. Nitric oxide modulates basal and endothelin-induced coronary artery vascular smooth muscle cell proliferation and collagen levels. J Mol Cell Cardiol. 1997;29(7):1779–1789. doi: 10.1006/jmcc.1996.0480. [DOI] [PubMed] [Google Scholar]
- 29.Rizvi MAD, Katwa L, Spadone DP, Myers PR. The effects of endothelin-1 on collagen type I and type III synthesis in cultured porcine coronary artery vascular smooth muscle cells. J Mol Cell Cardiol. 1996;28(2):243–252. doi: 10.1006/jmcc.1996.0023. [DOI] [PubMed] [Google Scholar]
- 30.Sluijter JPG, Smeets MB, Velema E, Pasterkamp G, de Kleijn DPV. Increase in collagen turnover but not in collagen fiber content is associated with flow-induced arterial remodeling. J Vasc Res. 2004;41(6):546–55. doi: 10.1159/000081972. (Print) [DOI] [PubMed] [Google Scholar]
- 31.Strauss BH, Robinson R, Batchelor WB, Chisholm RJ, Ravi G, Natarajan MK, Logan RA, Mehta SR, Levy DE, Ezrin AM, Keeley FW. In vivo collagen turnover following experimental balloon angioplasty injury and the role of matrix metalloproteinases. Circ Res. 1996;79(3):541–50. doi: 10.1161/01.res.79.3.541. (Print) [DOI] [PubMed] [Google Scholar]
- 32.Taber LA. A model for aortic growth based on fluid shear and fiber stresses. J Biomech Eng. 1998;120(3):348–54. doi: 10.1115/1.2798001. [DOI] [PubMed] [Google Scholar]
- 33.Valentín A, Humphrey JD. Evaluation of fundamental hypotheses underlying constrained mixture models of arterial growth and remodeling. Phil Trans R Soc Lond A. 2009 doi: 10.1098/rsta.2009.0113. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Valentín A, Humphrey JD. Parameter sensitivity study of a constrained mixture model of arterial growth and remodeling. J Biomech Eng. 2009 doi: 10.1115/1.3192144. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Valentín A, Cardamone L, Baek S, Humphrey JD. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J R Soc Interface. 2009;6(32):293–306. doi: 10.1098/rsif.2008.0254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wicker BK, Hutchens HP, Wu Q, Yeh AT, Humphrey JD. Normal basilar artery structure and biaxial mechanical behaviour. Comput Meth Biomech Biomed Eng. 2008;11(5):539–551. doi: 10.1080/10255840801949793. URL http://www.informaworld.com/10.1080/10255840801949793. [DOI] [PubMed] [Google Scholar]
- 37.Willett TL, Labow RS, Avery NC, Lee JM. Increased proteolysis of collagen in an in vitro tensile overload tendon model. Ann Biomed Eng. 2007;35(11):1961–1972. doi: 10.1007/s10439-007-9375-x. (Print) [DOI] [PubMed] [Google Scholar]
- 38.Wolinsky H. Response of the rat aortic media to hypertension. Morphological and chemical studies. Circ Res. 1970;26(4):507–522. doi: 10.1161/01.res.26.4.507. (Print) [DOI] [PubMed] [Google Scholar]
- 39.Xu C, Zarins CK, Bassiouny HS, Briggs WH, Reardon C, Glagov S. Differential transmural distribution of gene expression for collagen types I and III proximal to aortic coarctation in the rabbit. J Vasc Res. 2000;37(3):170–82. doi: 10.1159/000025728. (Print) [DOI] [PubMed] [Google Scholar]