Adaptive role switching promotes fairness in networked ultimatum game

Abstract

In recent years, mechanisms favoring fair split in the ultimatum game have attracted growing interests because of its practical implications for international bargains. In this game, two players are randomly assigned two different roles respectively to split an offer: the proposer suggests how to split and the responder decides whether or not to accept it. Only when both agree is the offer successfully split; otherwise both get nothing. It is of importance and interest to break the symmetry in role assignment especially when the game is repeatedly played in a heterogeneous population. Here we consider an adaptive role assignment: whenever the split fails, the two players switch their roles probabilistically. The results show that this simple feedback mechanism proves much more effective at promoting fairness than other alternatives (where, for example, the role assignment is based on the number of neighbors).

The Ultimatum Game has been catching up with the Prisoner's Dilemma in characterizing and elucidating the issues surrounding the emergence and persistence of altruistic behavior. In a typical ultimatum game, two players are asked to divide a sum of money. Of the two players, one acts as the proposer and the other as the responder. The proposer proposes a portion of the money to give to the responder, whose reaction shall decide their own incomes. If the responder accepts the offered money, the remaining money flows into the proposer's account. Otherwise, they each get nothing. Obviously, a rational responder should accept any amount of the money, however small the amount is, as the opposite choice leaves him with zero income. The backward induction leads to the subgame perfect equilibrium prediction¹ that the proposer should claim almost all of the money and leave the remaining to the responder. However, deluging experimental findings are at odds with this purely analytical reasoning. These experiments evidence that most individuals do give 40 to 50% of the total money, and around half of their co-players reject offers below 30%²,³,⁴,⁵,⁶.

Mounting effort has been devoted to probe the origins of this behavior²,³,⁴,⁵,⁷,⁸,⁹,¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³. In one pioneering work, two types of the game structure were designed to study the ultimatum bargaining behavior². In the easy game, two subjects are asked to complete the division of a sum of money c by the two-stage decisions. In the complicated game, the money is replaced by black and white chips. Ensuing this work several important experiments were conducted. Ref. 8 came to conclude that the subgame-perfect equilibrium, if not fail, at least poorly predicts the observed results, which can be approximated by incorporating the distributional concerns into the utility functions. Inexperienced players tend to adhere to the equal division while experienced players behave more like the gamesmen⁷. Bolton found that a comparative model fits well with the qualitative regularities observed in these experiments²,⁴,⁷,⁸. Later, several studies consistently replicated these regularities in the ultimatum game with complete information, whereas players tend to accept the possible smallest fraction of the amount if they have no information of the amount to be divided (i.e., incomplete information)²⁴,²⁵. A uniform similarity is that games usually involve more than one period, and if a game does not end in period one, the two subjects alternate the roles of proposer and responder in period two, and so on in later periods²,⁴,⁵,⁷,⁸.

In the context of evolutionary game theory, Nowak and his coauthors have demonstrated that fairness evolves by virtue of reputation. In this work, the reputation is related to what deals the responders have accepted in the past²⁶. Empathy can also drive the population to a state in which players demand and offer a fair share of the money¹⁶,²⁷,²⁸. Apart from the well-mixed culture¹⁶,²⁶,²⁷,²⁸, population structure was also found to play a key role in the evolution of altruistic behavior¹⁰,¹¹,¹²,¹³,¹⁴,¹⁵,¹⁶,¹⁷,¹⁸,¹⁹,²⁰,²¹,²²,²³,²⁹. In these spatial games, population structures are characterized by some specific networks. Nodes of these networks denote individuals, and the edges define the interaction relationship. Iranzo et al. have studied the spatial ultimatum game in detail³⁰. They found that the quasiempathetic individuals can frequently emerge and fixate spontaneously. These individuals tend to offer close to their acceptance thresholds. Later, they have reported that whenever individuals are restricted to interact with a fraction of the total population, the empathy itself may be selected, and this empathy can lead to the establishment of non-rational large offers significantly above the smallest possible ones³¹. Ref. 16 has reported that unfair allocation scheme is favored in the well-mixed population while relatively fair split evolves in spatial settings. The authors¹⁰ have found that increases in the neighborhood size and in the degree of disorder engender similar effect, driving the population towards the state where responders increase the levels of “rationality”. Interestingly, fairness behavior can emerge and persist on the condition that agents update their strategies just based on the payoff signals of previous ultimatum game¹⁴. Very recently Sinatra et al. have also added the relevant literature by probing the evolution of fairness behavior in the context of categorizing players into three cases¹¹.

It should be noted that most experimental studies have considered multistage ultimatum game, without the complication of population structure. On the contrary, most spatial ultimatum games have assumed that either a pair of linked neighbors play the ultimatum game twice, both as responders and proposers, or the two players are assigned as proposer and responder with equal probability. However, because of the difference in individuals' social ties, status, prestige and reputation, individuals may have different initiative to allocate resource. Putting another way, paired neighbors may enjoy asymmetrical likelihood to be the first mover. Actually, a large body of experimental studies have concentrated on the effects of alternating roles on the giving behavior in the multistage ultimatum game. What the population dynamics shall result remains unclear when the assignment of game roles is subject to these realistic factors such as social ties or the efficiency of resource utility.

Here we constructed a minimal model, combining the two aspects, the spatial structure and the role assignment mechanism, to investigate the evolution of the giving and asking strategies in the framework of evolutionary game theory. The absolute symmetry for individuals to act as the proposer is broken up. Between role switches comes the natural selection, under which the strategies acquiring larger payoffs are more likely to propagate. As for the role assignment, we consider two regimes. In one regime, of two connected neighbors, the probabilities for whom to be chosen as the proposer are dependent on their degrees when playing the ultimatum game (for convenience, we shall call this case the degree-based role assignment regime hereafter). In the other regime, the game role depends on the outcome of the previous ultimatum game (feedbackbased role assignment regime). If two protagonists have arrived at an agreement on how to split the money, the proposer would still act as proposer in next round with the same probability γ (≥0.5) as in the present round. Otherwise, the responder would act as proposer with the probability γ in next round. Our results show that whenever individuals of small degree have more chances to be proposers, the population evolves towards a state deviate from the game-theoretic prediction, and even equilibrates at a modest giving and asking level. More optimistically, sufficiently swift role switching can stabilize the population at a state of fair split.

Results

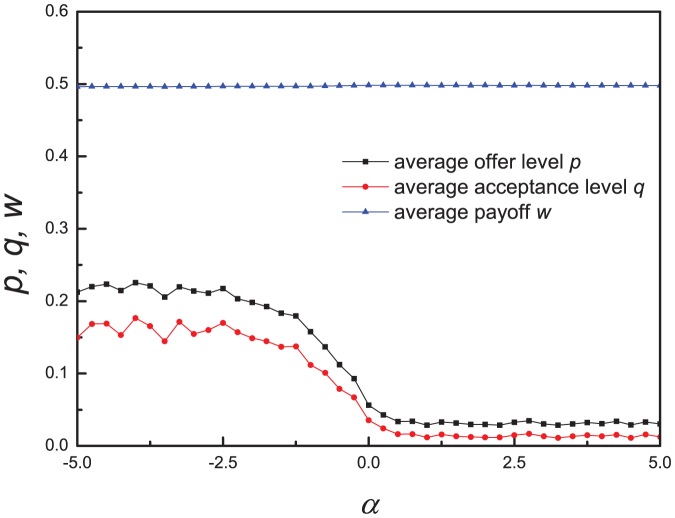
We first go with the results of the population dynamics under the degree-based role assignment regime. Fig. 1 shows that as α increases from −5 to +5, both the offer and acceptance levels in the population monotonically decrease, while the average payoff per person always approaches a little less than 0.5 whatever α is. What these observations imply is the following. Whenever individuals of low degree acquire a greater chance to be the proposer, they are willing to provision a considerable fraction of the money to their responders. As these responders have more partners to interact with, they tentatively and gradually enhance their minimal acceptance level. On the contrary, whenever individuals of large degree are endowed with the larger likelihood to act as the proposers, they are inclined to give their responders a parsimonious part of the money. Since these responders have just a few partners to interact with, they are coerced to lower their acceptance threshold. It is worth noting that whenever the role assignment goes independent of the degree (i.e., α = 0), the population is equilibrated at very low offer and acceptance level, indicating the scale-free network itself is unable to induce the evolution of the fair split and egalitarian asking rate, which is different from the remarkably positive effect of the heterogeneity in promoting cooperation³²,³³.

Figure 1. The average offer level p, acceptance level q, and the average payoff w of the population as functions of the parameter α at the equilibrium state.

The population is structured by the scale-free networks. The degree-based role assignment regime is invoked to determine whoever acts as the proposer. The larger the α is, the more likely the individuals of larger degrees serve as the proposers. Moderate fairness and gentle asking rate stabilize whenever low-degree individuals gain more chances to be proposers. However, the Nash Equilibrium solution of the Ultimatum game is recovered whenever advantage skews towards the large-degree individuals. Other parameter: m = 3, m₀ = 3, the population size N = 1000, selection intensity β = 10, δ = 0.005.

We can further elaborate these results on the degree-based role assignment. Large-degree individuals have more neighbors to interact. Once enjoying the dominance in the role assignment, they can gradually bring down their offer levels. Of all their neighbors, those who decline these offers would receive nothing, whereas those who accept the offers get none-zero payoffs. Generally speaking, hub individuals accumulate much larger payoff than individuals of small degrees. Through social learning, these hub individuals can disseminate their offer levels to their neighbors. As for the acceptance level, hub individuals imitate those who acquire larger payoff among their neighbors (i.e., those who have accepted the offers). Of intrigue is that whenever individuals of low degree are preferentially chosen to propose in the ultimatum game, they compete to be altruistic towards their neighbors. This competition should be limited to a certain extent. In other words, individuals sticking to the absolutely fair split cannot survive the evolutionary race. This is straightforward to understand. Most large-degree individuals act at responders. There is a tradeoff for them between sticking to the high acceptance levels and accepting more offers by appropriately lowering their acceptance levels. Proposers of low degree are able to obtain more payoff by reducing their proposed fractions, provided that these offers are accepted. Once declined, these proposers incur great loss. This occasionally happens because of the mutation. However, those who attempt to satisfy these slightly waxing demands still enjoy the dominance in accruing payoff comparing to other proposers who are declined and the responders. Therefore, these offers can be learned by the hub individuals. And hub individual's acceptance levels also spread to the leaf neighbors slowly. Most of the time the population resides at this equilibrium. From time to time, some individuals with low offer and acceptance can prevail in the population, but this is just transient (see Fig. 2a). Whenever large-degree individuals are placed more frequently in the role of proposers, the evolutionary process sees different property. These proposers can tentatively down-regulate their offers by just satisfying such neighbors whose acceptance levels are among the lowest. As for loss owing to the decline of the high-demanding responders, it plays a negligible role in the hub individuals' spreading their strategies (see Fig. 2b). We thus come to the conclusion that enduing low degree individuals with more chance to divide the money, fairness can be induced in a modest extent.

Figure 2. The average offer level p, acceptance level q, and the average payoff w of the population in a typical evolutionary process for different α.

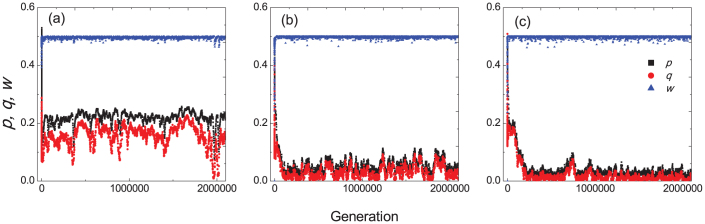
The left plot α = −5 and the middle plot α = 0, and the right plot α = 5. The population is structured by the scale-free networks. The degree-based role assignment regime is invoked to determine whoever acts as the proposer. Other parameter: m = 3, m₀ = 3, the population size N = 1000, selection intensity β = 10, δ = 0.005.

Further comparison between Figs. 2a, 2b and 2c reveals that the average offer and acceptance levels of the population oscillate around their respective intermediate levels. Measured by the magnitude of oscillation, stability of the population varies with α. Specifically, the population is more stable for α = 5 than for α = 0, which is still more stable than for α = −5. The gradual weakening in stability with α's decrease suggests that large-degree individuals, when provided with more chance to be proposers, are able to inhibit the spreading of high acceptance levels generated by mutation (see Fig. 2c). Whenever low degree individuals enjoy the role advantage, they also attempt to degrade their offer levels. Their responders, especially those with large social ties, can selectively accept the higher offers, which naturally leads to the competition between the proposers. As a consequence, the attempt very seldom ends up with success. Most of the time, the proposers are ‘coerced' to maintain intermediate offer levels. In between the two extremes is the case of random role assignment. The offer and acceptance levels oscillate in a modest way.

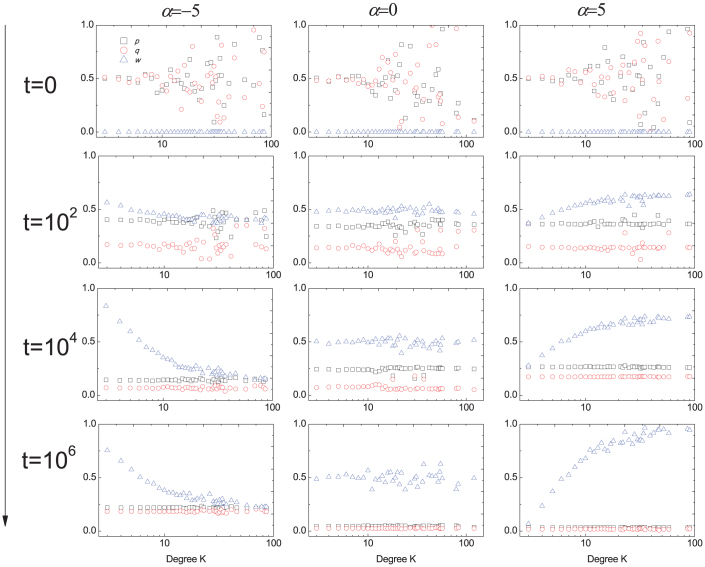
To further understand the role of individuals of varying degree on the evolution of fairness, the distributions of the individuals' offer, acceptance levels and average payoff as a function of degree are illustrated at several specific time points for three typical values of α. Comparing plots related to the cases α = −5, 0, and 5 in Fig. 3 shows that whoever, independent of their degree, acts as proposers more frequently obtains higher payoffs. Whenever assigned as the proposer by flipping the coin, the payoffs for large-degree and low-degree individuals are approximately equal. They also share the property that after a long time period of transition, the acceptance level always tightly ties with the offer level. Differences arise between hub individuals and leaf individuals in terms of the stable level of offer, acceptance level, and the extent to which the proposers exploit the recipients as α varies. α = 5 renders the large degree individuals ruthlessly exploit the leaf nodes just as above analyzed. Interestingly, randomly assigning the roles does not lead to marked payoff difference for individuals of varying degree. Whenever the advantage as first proposer skews towards low degree individuals, they also exploit their recipients but to an extent not so strong as when α = 5.

Figure 3. The average offer level p, acceptance level q, and the average payoff w of the population as functions of the degree k in a typical evolutionary process.

The population is structured by the scale-free networks. The degree-based role assignment regime is invoked to determine whoever acts as the proposer. The larger the α is, the more likely the individuals of larger degrees serve as the proposers. The individuals standing in the role of proposers averagely enjoy great advantage in accruing payoffs. However, low-degree individuals still offer fairly high fraction of the money to others, while high-degree individuals ruthlessly squeeze the low-degree individuals. Other parameter: m = 3, m₀ = 3, the population size N = 1000, selection intensity β = 10, δ = 0.005.

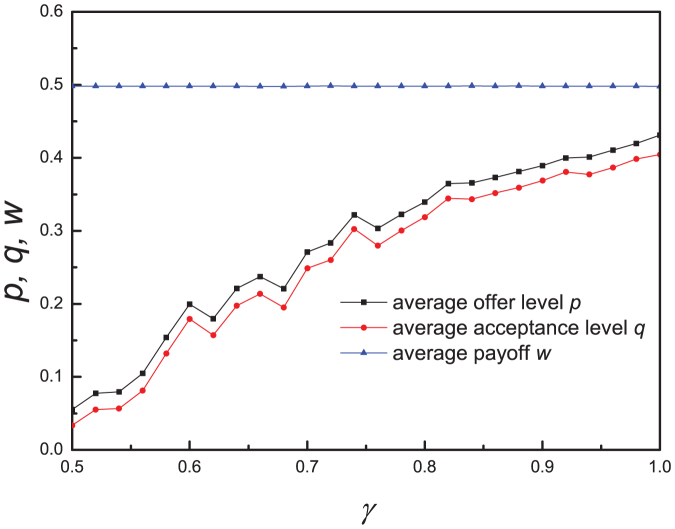
Failure to reach an agreement is detrimental for both the proposer and the responder, which is obviously a waste of resource. To surmount this potential waste, the proposers who had been rejected should conceal in future interactions by letting the responder have a chance to take a turn. There is no lack of regulatory institutions enforcing the role switching or maintaining on the basis of resource allocation. To characterize this realistic scenario, we let a proposer still be the proposer with the probability γ in next round if he has succeeded in splitting the money. However, if his proposal has been rejected, the proposer still takes the role of proposer just with the complementary probability 1 − γ. Obviously, γ = 0.5 means that both players are offered equal chance to be the proposer independent of their social ties. In this case, the population converges into a state, in which the average offer and acceptance levels are as low as 0.05, and 0.03 respectively. This once again confirms the inefficiency of the scale-free property alone in promoting the fairness. However, as γ increases, these proposers who have succeeded in splitting the money shall be more likely to be the proposers in the next round. Results show that the level of fairness increases as γ increases from 0.5 to 1 (see Fig. 4). The acceptance level also follows up these offer levels. Therefore, the adaptive role switching favors the evolution of fairness. One would ask what is the underlying reason for the emergence of the fair split and accompanying fair asking rate?

Figure 4. The average offer level p, acceptance level q, and the average payoff w of the population as functions of the parameter γ at the equilibrium state.

The population is structured by the scale-free networks. The feedback-based role assignment regime is invoked to determine whoever acts as the proposer. The larger the γ is, the more strong whoever acts as the proposer in next round depends on the outcome of previous round. Strong fairness and demanding asking rate emerge and persist whenever the outcome of current round uniquely decides the role of next round. However, individuals almost adhere to the reasonable solution when they are stochastically appointed as the proposer. Other parameter: m = 3, m₀ = 3, the population size N = 1000, selection intensity β = 10, δ = 0.005.

The evolutionary process corresponding to γ = 0.5 is equivalent to that in α = 0 in the degree-based role assignment regime. In this case, individuals of large degree actually own double advantages in competing to survive. On the one hand, they afford to be rejected by a fraction of their neighbors. Therefore, they would tentatively reduce their offers to the extent that most of the neighbors still accept. Large-degree individuals, on average, still accrue higher payoff than the responders. On the other hand, large-degree individuals are more likely followed by the periphery nodes. These two factors cause the population to linger most time in the state of low offer and acceptance levels. At some time point, some individuals do increase their offers by mutation. Before spreading out, they are quickly replaced by those who still stick to the low offers, quickly pulling the population back (see Fig. 5a).

Figure 5. The average offer level p, acceptance level q, and the average payoff w of the population in a typical evolutionary process for different γ.

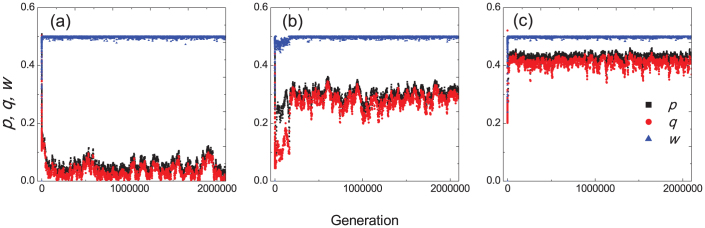
The left plot γ = 0.5 and the middle plot γ = 0.75, and the right plot γ = 1.0. The population is structured by the scale-free networks. The feedback-based role assignment regime is invoked to determine whoever acts as the proposer. Other parameter: m = 3, m₀ = 3, the population size N = 1000, selection intensity β = 10, δ = 0.005.

For another extreme case γ = 1 (see Fig. 5c), attempting to increase one's own payoff by reducing the offer is actually a risky action, since the opponent's acceptable minimum is unknown and the role adaptively switches so quickly. Once the proposed allocation is denied, the proposer advantage would be transferred to the responder in the next round. Therefore, a proposer must be cautionary enough to lower his proposed fraction in order to stand in the place of proposer for future. As for the individuals acting as the responders, they can risk to maintain their minimal acceptance at a level near the fair split. If all proposers have failed in meeting the level, they all each get nothing. Only if some proposers have offered higher factions than those the responders have required, then other proposers are put in a disadvantageous place in competition. These are the rationales for the emergence of fair split and the follow-up acceptance level for this quickly adaptive role switching. For case γ = 0.75, the positive effect on the evolution of fairness is compromised, leading to that the average offer and acceptance are kept around intermediate levels of p₀ = 0.31 and q₀ = 0.33 (see Fig. 5b).

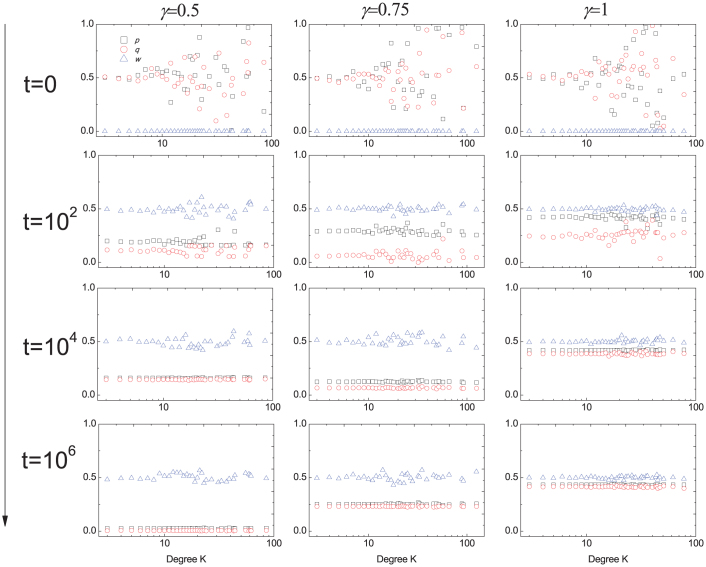
Similarly, we here exhibit the distribution of the individuals' offer, acceptance levels and average payoff as a function of degree at several specific time points for three typical values of γ (see Fig. 6a, 6b and 6c). One can find that there is no remarkable difference in terms of payoff (slightly less than 0.5) between individuals of varying degree independent of γ. That is to say, in this adaptive role assignment regime, no proposers can continually exploit the responders. When attempting to obtain higher payoff by reducing the proposed fractions, proposers must at the same time take into account whether these fractions would be refused. Once refused, they not only lose the potential payoff advantage relative to their responders in the current round, but also have to transfer the role advantage to their responders for future interactions. As a consequence, proposers tend to satisfy the responders' demand to stand in the place of proposers.

Figure 6. The average offer level p, acceptance level q, and the average payoff w of the population as functions of the parameter γ in a typical evolutionary process.

The population is structured by the scale-free networks. The feedback-based role assignment regime is invoked to determine whoever acts as the proposer. The larger the γ is, the more strong whoever acts as the proposer in next round depends on the outcome of previous round. The population dynamics exhibit no significant difference in terms of p, q and w for individuals of varying degree for γ = 1. Other parameter: m = 3, m₀ = 3, the population size N = 1000, selection intensity β = 10, δ = 0.005.

Discussion

We have instituted a minimal model to investigate how different role assignments affects the evolution of fairness in the ultimatum game. The population is structured by the scale free network. We proposed two role assignment regimes. In the degree-based role assignment regime, the parameter α defines the dependence of the chance to be proposers on individuals' degrees. The larger α, the more chances the large degree individuals have. And α = 0 corresponds to random role assignment. The results show that whenever large degree individuals are more likely to propose (i.e., α > 0), the population evolves towards to states of very low offer and acceptance level. In contrast, α < 0 makes the population deviate from the Nash solution of the classic ultimatum game. Whenever low degree individuals have absolute dominance over hubs in role allocation, intermediate offer and acceptance levels can be maintained. We have also found that further lowering α is unable to induce higher offer and acceptance levels. Especially for the extreme case α = −∞, the individuals of smaller degrees are deterministically assigned as the proposer. Under this extreme, the offer and acceptance levels are very similar to those obtained for the case α = −5. As a conclusion, giving more chance for low degree individuals to act as proposers favors the establishment of fairness but to a modest extent. In the feedback-based role assignment regime, proposers who have succeeded in splitting the money still act as proposes with a larger likelihood. Otherwise, the role advantage would be transferred to their responders in next round. If the role switching proceeds quickly enough (γ = 1), proposers tend to make fair proposal, and responders have egalitarian asking rate of the money to allocate.

Previous experimental studies⁴,⁵,⁸,²⁵ have assumed that the amount of the money to be divided would decay over round before an agreement is achieved. Here we keep the amount unchanged over time as the players seek the feasible split schemes, as we concentrate on the effects of the role assignment itself on the evolution of fairness. The two regimes well characterize the variation of individuals in getting the priority to divide the money. The degree-based regime is uniquely determined by their degrees. Once the population structure is fixed, the chance of each individual being the proposer is constant. From the perspective of statistics, this regime is actually a static assignment. However, we cannot neglect the importance of this symmetry-breaking regime on the evolution of fairness just as the formation of a valley usually starts with a small gully in the floor. In the feedback-based regime, the role alternation can be spontaneously or forcefully executed by the third-party supervisor. It is adaptive. This regime proves very effective in inducing the emergence and persistence of the fairness behavior in the ultimatum game.

Methods

Model

The population is structured by the Barabasi-Albert scale free network³⁴,³⁵,³⁶,³⁷. Each site of the network represents an individual. Individuals interact along the network edges. To generate such a network, we start with a ring of m₀ nodes. At each time step, a new node accompanying m edges are added into the current network. Each edge attaches to extant nodes with probabilities proportional to their degrees. Duplicate links are prohibited. Repeating this growth-preference attachment mechanism, until there are N nodes in the network²³. Throughout we assume that the amount of the money to be divided is 1. At the start of the evolution, each individual's strategy pairs (p, q) are randomly and independently assigned in the interval of [0, 1]. p means that an individual is willing to allocate out a portion of p whenever acting as the proposer, and q the threshold below which the individual would decline when in role of the responder.

During the evolutionary process, all individuals play the ultimatum game with all their directly connected neighbors. Different from¹⁴,²⁰, we here assume that a pair of connected individuals just play the ultimatum game once in one generation. A natural question arises: who shall be the proposer? We propose two different regimes for assigning the role: the degree-based role assignment regime and the feedback-based role assignment regime. In the degree-based role assignment regime, whoever acts as the proposer just depends on the pairs' degrees. Suppose there are two neighboring individuals, say A and B. The probability that individual A serves as the proposer is assigned as 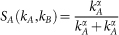, where k_A and k_B are individuals A and B's degree, respectively. The parameter is employed to measure how the degree is correlated with the role assignment. Obviously, positive α means that individuals with larger degrees are more likely to be the proposers. Negative α corresponds to the inverse side. And the random role allocation is recovered for α = 0, which is independent of the degree. In this regime, the role allocation is non-adaptive, the likelihood of whoever is the proposer remains constant during the evolutionary process as the population structure remains unchanged.

Different from the degree-based regime, the feedback-based role assignment regime is adaptive. In this adaptive regime, the outcome of the previous round determines the probability of whoever would be the proposer in next round. Specifically, the proposer who have split the money successfully would still, otherwise the responder, act as the proposer with a large probability in the next round. Still say two individuals A and B. If A proposes to divide the money and B agrees to accept in step t, A still acts as the proposer with probability γ(≥0.5) in step t + 1. Otherwise B acts as the proposer with probability γ in step t + 1. The rationale behind this assignment is as follows. Whenever the allocation gets done, both are satisfactory. Once the proposed fraction is below the responder's minimal acceptance level, the latter is dissatisfied. The resource drives away. Therefore, the proposer should make a compromise to let the responder divide the money in future. Even sometimes the realization of this role switching can be accomplished by the third party's enforcement.

In the end of each generation, all individuals have accumulated the payoff and they would experience the strategy updating synchronously. Following common practice, individuals of better performance are more likely to disseminate their strategies. Each individual randomly chooses a neighbor to learn. Whenever B serves as A's model, A adopts B's strategy with the probability given by the Fermi function W(s_A → s_B) = [1 + exp(β(P_A − P_B))]⁻¹, where P_A, P_B are A, B's payoff respectively, and β the selection intensity. The parameter β weighs how much role the payoff difference plays in the strategy updating process. Specifically, the intensity determines the level of uncertainty, which can be ascribed to errors in judgment owing to mistakes and external influences. The experimental findings³⁸ have verified that this function can well characterize the human's imitation behavior. Parameter β = 0 means the neutral drift while β = +∞ means the deterministic learning. As the strategies are continuous, precisely imitating the model's strategy is almost impossible. We thus introduce a small perturbation in strategy updating. That is, after learning, A's strategy is (p_A + δ₁, q_A + δ₂) with δ₁ and δ₂ being randomly picked up from a small interval [−δ, δ].

We would like to concentrate on whether the fairness can emerge under the role-allocation regimes. However, because of the strong heterogeneity in degree distribution, the individuals occupying the hubs enjoy remarkable dominance in enhancing their proposed offers, and the reduction in the remaining money can be compensated by rendering more neighbors accept the offers¹¹. To decouple this effect from the role-allocation regimes, we normalize individuals' payoffs by dividing the number of their social ties²⁹. This also has the implication that individuals, though possessing different social ties, just are able to experience the same number of games in the same time period.

Numerical simulation

The simulations are conducted on scale-free networks, with each node accommodating one individual. Each network consists of 1000 nodes (i.e., population size = 1000). The two entries (p, q) of each individual's strategy are randomly initialized in the interval [0, 1] independently. After a transition stage of 10⁶ generations, the offer level, the acceptance level, the payoff per person of the population are averaged over another 10⁶ generations as the equilibrium values. The parameter related to the mutation is set to be δ = 0.005.

Author Contributions

T.W., F.F., Y.L.Z. and L.W. performed analyses, discussed the results, and contributed to the text of the manuscript.