Abstract
We adopted a novel method to tune the terrace width of Si(111) substrate by varying the direction of heating current. It was observed that the uniaxial magnetic anisotropy (UMA) of Fe films grown on the Si(111) substrate enhanced with decreasing the terrace width and superimposed on the weak six-fold magnetocrystalline anisotropy. Furthermore, on the basis of the scanning tunneling microscopy (STM) images, self-correlation function calculations confirmed that the UMA was attributed mainly from the long-range dipolar interaction between the spins on the surface. Our work opens a new avenue to manipulate the magnetic anisotropy of magnetic structures on the stepped substrate by the decoration of its atomic steps.
The structure and magnetic properties of magnetic nanostructures on vicinal substrates have been widely investigated for decades1,2,3,4,5. The atomically flat terraces separated by steps are generally used as templates for preparing various self-organized nanostructures, including regular arrays of nanodots1, nanostripes2,3, atomic wires4 and ultrathin films5. Furthermore, the terraces can be employed to confine magnetic nanodot assemblies and form one dimensional (1D) quantum-well states6,7,8,9,10. For these low-dimensional magnetic materials, the interplay between quantum confinement and broken symmetry often emerges novel electronic structures and magnetic properties. As a result, the magnetic anisotropy of the magnetic nanostructures, which is vital for magnetoelectronic technology, can be drastically manipulated by the stepped surfaces2,3,4,5. Recently, we observed the tunability in both the magnetic anisotropy and magnetic coupling of Fe nanodots on a curved Cu(111) substrate with varying the terrace width11.
Si(111) substrate has been often selected to obtain different stepped surfaces12,13. Compared to metallic substrates, Si substrate is convenient to get a clean surface, and the surface morphology can be manipulated by different treating processes14,15,16. Moreover, the magnetic nanostructures grown on the atomically flat Si(111) terraces have advantages in spintronic applications as a natural integration with Si-based semiconductor devices. The obstacle resulted from the interdiffusion between the magnetic metals and Si substrates can be overcome via inserting a buffer layer of copper or iron silicides17,18. In our previous work19,20,21,22, quasi 1D magnetic nanodot assemblies were fabricated on vicinal Si(111) surface with relatively large miscut angles (~4°). Unfortunately, the terrace width of these stepped substrates cannot be tuned easily once the miscut angle is fixed, which causes difficulty in investigating the effect of terrace width on magnetic properties by using identical substrates. Here, we adopted a novel method to tailor the terrace width of Si(111) substrates via controlling the direction of direct heating current passing through the sample. The magnetic anisotropy of the corresponding epitaxial Fe films grown on these Si(111) surfaces was continuously tuned. The six-fold magnetocrystalline anisotropy superimposed on a weak UMA can be characterized in the sample with the widest terrace, and the UMA will be enhanced with decreasing the terrace width. The magnetic anisotropy constants and the origin of UMA were determined via the magnetic hysteresis curves simulation and self-correlation function calculation. This work not only advances the understanding of the magnetic anisotropy in nanostructures, but also enriches our capacity of fabricating magnetic nanostructures and manipulating the magnetic properties for potential applications.
Results
Fig. 1(a) illustrates the schematic configuration of the substrate treatment and preparation process for these Cu/Fe/FeSi2/Si(111) samples. During this direct current heating treatment19,23, the current passed through the substrate, and the direction of current changed from parallel to perpendicular to the step. Fig. 1(b) shows a coordinate system used in the magneto-optical Kerr effect (MOKE) measurements and the latter data simulation. The ex-situ magnetization hysteresis curves were determined in the longitudinal MOKE geometry at different sample azimuthal angles, φ. The azimuthal angle φ denotes the angle of external magnetic field with respect to the surface step (Si [1–10]).
Figure 1. The schematic configuration of the sample preparation and MOKE measurement, and STM images of sample surface.
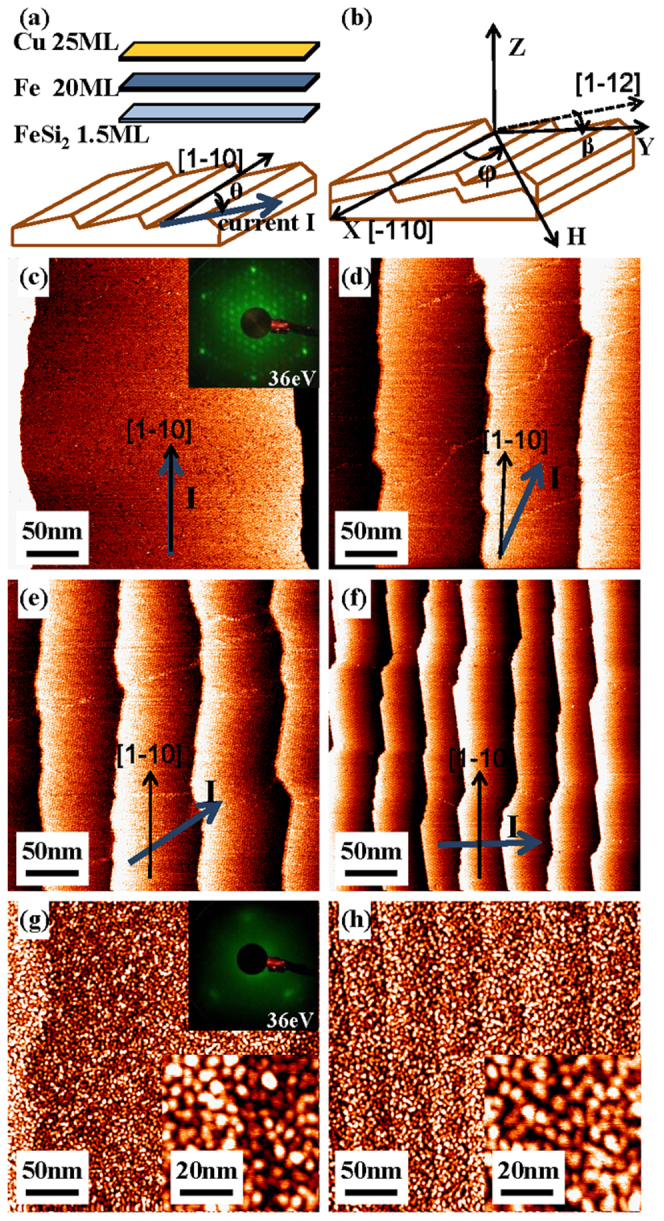
(a) The schematic configuration of the substrate treating with controllable heating current and film preparation process. (b) The coordinate system used in the MOKE measurements and the latter data simulation. (c)–(f) STM images of clean surfaces on four Si(111) substrates I–IV with different width of the terrace. The arrows indicate that the direction of the heating current changes continuously on each sample, which induce the vibration of the width of surface step. (g)–(h) STM images of 20 ML Fe films on p( 2 × 2 )/Si (111) of Sample I and IV with the corresponding small scale images in the lower right corner. The typical LEED patterns are illustrated in the insets of (c) and (g).
The large scale STM images as indicated in Figs. 1 (c)–(f) demonstrate the atomically flat Si(111) surfaces of four samples I–IV with different terrace widths. The direction of heating current for each sample was denoted by the arrows in these images. The substrate of sample I was heated with the current parallel to the surface steps. The Si(111)-7 × 7 reconstructured surface with the terrace width of 230 ± 30 nm was obtained as shown in Fig. 1 (c). The Si(111)-7 × 7 reconstructured surfaces for all the four samples are proved by LEED measurements. For samples II–IV, the angles between the heating current and the steps vary from 30° to 90°, resulting in a decrease of the terrace width. The corresponding terrace widths are dII = 100 ± 20 nm, dIII = 80 ± 20 nm, dIV = 45 ± 15 nm, respectively (Figs. 1 (d)–(f)).
The phenomenon that the variation of terrace width of Si(111) substrate with heating current direction can be explained by the surface electromigration of Si adatoms15,16. The step bunching due to heating by direct current has been well documented on the Si(111) surface with 1° miscut angle15,16. It was observed that the step bunching was influenced by either annealing temperature or the direction of current flow. However, the effect of heating current direction either parallel or perpendicular to the step on the terrace width is not well understood yet. Here, we tuned the step morphologies by annealing vicinal Si(111) at a fixed temperature while adjusting the applied electric field 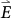 from parallel to perpendicular to the step. When the Si(111) substrates was treated by direct current heating, in addition to the heating temperature, the electric field also influences the surface morphology. The Si adatoms would be driven by an electromigration force
from parallel to perpendicular to the step. When the Si(111) substrates was treated by direct current heating, in addition to the heating temperature, the electric field also influences the surface morphology. The Si adatoms would be driven by an electromigration force 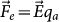 , where
, where 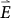 is the electric field applied on the Si adatoms, and qa is the effective charge of Si adatoms. The electromigration force could drive the Si adatoms to flow on the surface along the direction of electric field. When the direct current was applied parallel to the step (θ = 0°), the Si adatoms would flow along the edge without changing the step density. Therefore, the widest terrace was achieved (Fig. 1(c)). On the other hand, when the direct current was applied perpendicular to the step (θ = 90°), Si adatoms driven by the largest electromigration force perpendicular to the terrace edge would diffuse along the electric field and form the narrowest terrace width, as shown in Fig. 1 (f).
is the electric field applied on the Si adatoms, and qa is the effective charge of Si adatoms. The electromigration force could drive the Si adatoms to flow on the surface along the direction of electric field. When the direct current was applied parallel to the step (θ = 0°), the Si adatoms would flow along the edge without changing the step density. Therefore, the widest terrace was achieved (Fig. 1(c)). On the other hand, when the direct current was applied perpendicular to the step (θ = 90°), Si adatoms driven by the largest electromigration force perpendicular to the terrace edge would diffuse along the electric field and form the narrowest terrace width, as shown in Fig. 1 (f).
In the framework of the surface electromigration model, a scaling law was derived16
where l is the average terrace width. N is the number of atoms in one step height, and F is the electromigration force perpendicular to the steps. Parameters α and q are positive exponents which vary for different systems and heating methods. For our samples with single atomic steps, Eq. (1) was simplified as 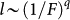 . Using the experimental data of sample II–IV, the value of parameter q = 1.1 was obtained. For sample I, when the electromigration force F perpendicular to the step is smaller than a critical value, the surface terrace will be stable and not become wider16.
. Using the experimental data of sample II–IV, the value of parameter q = 1.1 was obtained. For sample I, when the electromigration force F perpendicular to the step is smaller than a critical value, the surface terrace will be stable and not become wider16.
Figs. 1(g) and (h) display the surface morphology of 20 monolayer (ML) iron film deposited on the FeSi2 p(2 × 2)(111)/Si(111) surface of samples I and IV, respectively. The epitaxial growth of bcc α-Fe film is verified by the LEED pattern (Inset of Fig. 1(g)). Due to the small grains of Fe with the surface fluctuation of 2.4 ± 0.3 nm, the single atomic steps become hardly visible. From the high resolution STM images in the lower right corner of Figs. 1(g) and (h), we can observe that the terrace width has no obvious influence on the grain size and shape.
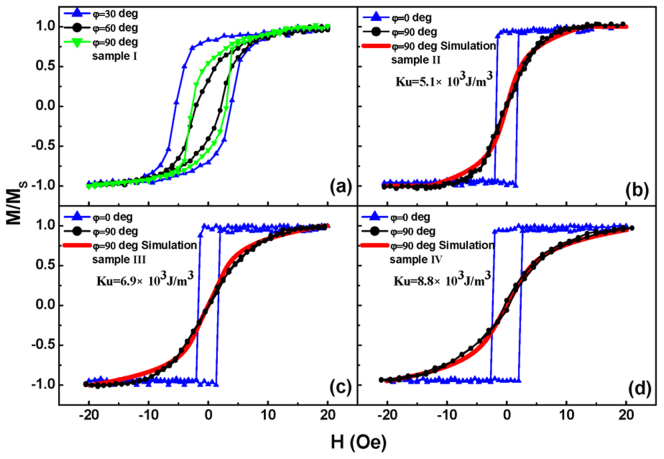
The longitudinal MOKE measurements were performed with applied magnetic field at various orientation φ for each sample as illustrated by Fig. 1(b). The representative magnetic hysteresis loops measured by ex situ MOKE were displayed in Fig. 2. The variation of hysteresis loops with φ indicated in-plane magnetic anisotropy. For sample I, the hysteresis loops varied significantly. However no loops with the normalized remanence close to 1 or 0 were found at any azimuthal angle φ. As shown in Fig. 2 (a), the hysteresis loop with the largest and the smallest normalized remanence Mr/Ms = 0.782, and Mr/Ms = 0.365 appear at φ = 30° and φ = 60°, respectively, indicating that a six-fold magnetic anisotropy exists in this sample. The difference in hysteresis loops for φ = 30° and φ = 90° suggests that an additional magnetic anisotropy is superimposed. For the other three samples, the rectangular hysteresis loops with Mr/Ms≈1 and the sheared loops without remanence were found at φ = 0° and 90°, respectively (Figs. 2(b)–(d)).
Figure 2. Experimental and simulated magnetic hysteresis loops.
Typical in-plane magnetic hysteresis loops at different azimuthal angles of Sample I–IV ((a)–(d)) characterized by MOKE. Except for Sample I, Sample II–IV ((b)–(d)) exhibited standard easy and hard hysteresis loops at φ = 0° and 90°. The corresponding simulated hysteresis loops at hard axis (red lines) are displayed in (b)–(d).
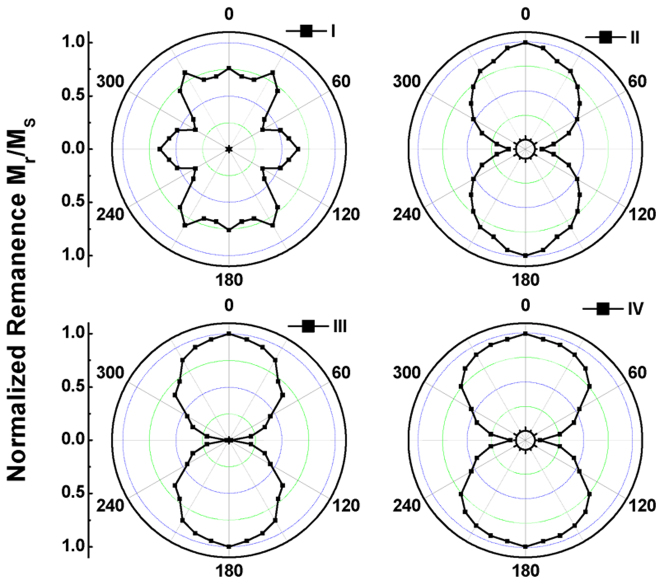
For a comprehensive description of the in-plane magnetic anisotropy of these four samples, the normalized remanence Mr/Ms as a function of azimuthal angle φ of each sample is demonstrated in Fig. 3. The complicated symmetry of magnetic anisotropy is observed in sample I from Fig. 3 (a). The angular dependence of the normalized remanence with eight maxima can be well explained by the superposition of a six-fold and a UMA contribution. The UMA with the easy axis parallel to the steps makes the values of the normalized remanence nearby φ = 0° generally larger than that around φ = 90°. Moreover, the six-fold magnetocrystalline anisotropy of Fe(111) film modifies the UMA to generate other six peaks at φ = 30°, 90°, 150°, 210°, 270°, 330°, respectively. As displayed in Figs. 3 (b)–(d), the other three samples exhibit similar two-fold symmetric curves of the angular dependence of the normalized remanence. The peak width of the curves at φ = 0° increases with decreasing the terrace width, suggesting that the UMA enhances and consequently conceals the weak six-fold magnetocrystalline anisotropy.
Figure 3. The angular dependence of the normalized remanence Mr/Ms obtained from the experimental hysteresis loops.
Sample I shows a UMA superimposed on a weak six-fold anisotropy, and Sample II–IV display a gradually enhanced UMA with the six-fold anisotropy almost concealed.
To quantitatively analysis the various magnetic anisotropies, especially the UMA, the coherent rotation model is introduced to simulate the hysteresis loops. Besides the UMA energy with the easy axis along the steps, the magnetocrystalline anisotropy energy with first- and second-order terms, the surface magnetic anisotropy energy, the demagnetization energy and the Zeeman energy are taken into account. Thus, the total free energy density of the Fe/Si(111) film under an external magnetic field H can be written as24
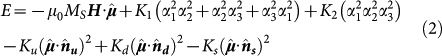 |
where 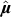 is the unit vector of the magnetic moment and MS is the saturation magnetization. K1 and K2 are the first two cubic magnetocrystalline anisotropy constants, with αi denoting the directional cosines of the vector
is the unit vector of the magnetic moment and MS is the saturation magnetization. K1 and K2 are the first two cubic magnetocrystalline anisotropy constants, with αi denoting the directional cosines of the vector 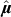 with respect to [100], [010], and [001]. Ku, Ks and Kd represent the anisotropy constants of UMA energy, the surface magnetic anisotropy energy and the demagnetization energy, with the corresponding unit vector of the easy axis in the anisotropy
with respect to [100], [010], and [001]. Ku, Ks and Kd represent the anisotropy constants of UMA energy, the surface magnetic anisotropy energy and the demagnetization energy, with the corresponding unit vector of the easy axis in the anisotropy 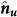 ,
, 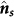 and
and 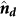 . It is noteworthy that the directions of
. It is noteworthy that the directions of 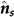 and
and 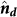 are normal to the Fe(111) plane and the film plane, respectively. Therefore, a small angle β exists between
are normal to the Fe(111) plane and the film plane, respectively. Therefore, a small angle β exists between 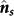 and
and 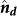 , which equals to the dip angle of surface steps (for the four samples,
, which equals to the dip angle of surface steps (for the four samples, 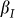 = 0.07°,
= 0.07°, 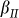 = 0.17°,
= 0.17°, 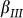 = 0.21°,
= 0.21°, 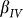 = 0.38°). Our modification to Eq. (2) with this small angle β is vital to obtain accurate simulation results in these samples with complicated and weak anisotropies. The bulk value MS = 1.7 × 106 A/m is used, while K1 = 4.5 × 104 J/m3 and Ks/Kd = 0.2 are adopted from our previous ferromagnetic resonance (FMR) analysis for the Fe/Si(111) system20. By using K2 and Ku as the fitting parameters, various hysteresis loops can be simulated based on Eq.(2). The enhancement of UMA with decreasing the terrace width can be confirmed by the following fitted results of the other three samples: KuII = 5.1 × 103 J/m3, KuIII = 6.9 × 103 J/m3, KuIV = 8.8 × 103 J/m3. Unfortunately, due to the limit of this simulation based on the coherent rotation model, only the simulation results of the sheared loops nearby the hard axis can be well fitted with the experimental loops. Therefore, the accurate values of K2 and Ku in sample I cannot be obtained by this method.
= 0.38°). Our modification to Eq. (2) with this small angle β is vital to obtain accurate simulation results in these samples with complicated and weak anisotropies. The bulk value MS = 1.7 × 106 A/m is used, while K1 = 4.5 × 104 J/m3 and Ks/Kd = 0.2 are adopted from our previous ferromagnetic resonance (FMR) analysis for the Fe/Si(111) system20. By using K2 and Ku as the fitting parameters, various hysteresis loops can be simulated based on Eq.(2). The enhancement of UMA with decreasing the terrace width can be confirmed by the following fitted results of the other three samples: KuII = 5.1 × 103 J/m3, KuIII = 6.9 × 103 J/m3, KuIV = 8.8 × 103 J/m3. Unfortunately, due to the limit of this simulation based on the coherent rotation model, only the simulation results of the sheared loops nearby the hard axis can be well fitted with the experimental loops. Therefore, the accurate values of K2 and Ku in sample I cannot be obtained by this method.
In order to further explore the contribution of the surface morphology to the UMA, the surface morphology induced in-plane magnetic shape anisotropy is estimated by means of the self-correlation function method19. According to this method, the UMA originated from the long-range dipolar interactions can be calculated by using the surface profile data extracted from the STM images.
The self-correlation function 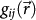 described the surface roughness as25
described the surface roughness as25
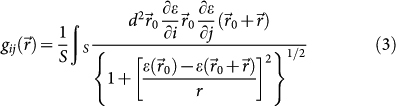 |
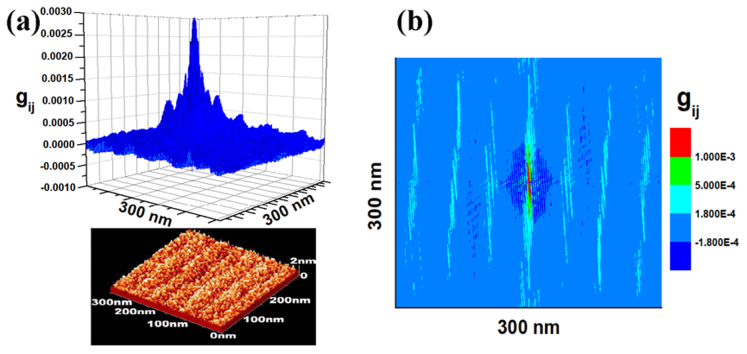
where S is the film surface adopted in the calculation, and 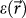 is the height distribution of the surface, which can be obtained from the STM images. Fig. 4 (a) shows the spatial distribution of
is the height distribution of the surface, which can be obtained from the STM images. Fig. 4 (a) shows the spatial distribution of 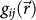 calculated from the STM image. The data of
calculated from the STM image. The data of 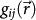 in the plane of the film surface display obviously striped structure along the direction of the step as shown in Fig. 4(b).
in the plane of the film surface display obviously striped structure along the direction of the step as shown in Fig. 4(b).
Figure 4. The typical spatial and in-plane distribution of the self-correlation function 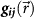 .
.
The spatial distribution of 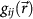 with the corresponding calculated STM image (a), and in-plane arrangement (b) of
with the corresponding calculated STM image (a), and in-plane arrangement (b) of 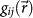 . The value of
. The value of 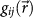 in the plane of the film surface display obviously striped structure along the direction of the step.
in the plane of the film surface display obviously striped structure along the direction of the step.
Then, the shape tensor [N] is defined by the distribution of 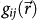 25,
25,
where d is the thickness of the magnetic film, and the constant of magnetic shape anisotropy induced by the surface morphology can be directly given by [N]25,
Consequently, the calculated results for the four samples yield the following magnetic shape anisotropy constants: 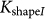 = 5.2 × 103 J/m3,
= 5.2 × 103 J/m3, 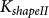 = 7.1 × 103 J/m3,
= 7.1 × 103 J/m3, 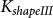 = 9.3 × 103 J/m3 and
= 9.3 × 103 J/m3 and 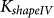 = 1.2 × 104 J/m3.
= 1.2 × 104 J/m3.
Discussion
STM images exhibited that the terrace width of stepped Si(111) substrate can be continuously tuned by the direction of heating current. The MOKE magnetic hysteresis loops revealed that the terrace width has a significant influence on magnetic anisotropy of the epitaxial Fe films grown on these Si(111) substrate. The self-correlation function calculations demonstrated that the magnetic anisotropy resulted from the surface morphology is in good agreement with the experimental one (as summarized in Table I). The good agreement proves that the tunable UMA in this Fe/Si(111) system is mainly originated from the long-range dipolar interaction between the spins on the surface with different terrace widths.
Table 1. The uniaxial magnetic anisotropy Ku fitted based on the experimental and simulated hysteresis loops, and the magnetic shape anisotropy Kshape calculated from the surface morphology for every sample.
| Samples | I | II | III | IV |
|---|---|---|---|---|
| Ku (103 J/m3) | —— | 5.1 | 6.9 | 8.8 |
| Kshape (103 J/m3) | 5.2 | 7.1 | 9.3 | 12 |
Our work suggests that the magnetic anisotropy of Fe film on Si(111) substrate can be flexibly tuned by direct heating current. To our knowledge, the tunability in magnetic anisotropies of Fe ultrathin films on Si(111) substrate via direction variation of heating current was not commonly seen in literature. This finding opens a new avenue to manipulate the magnetic anisotropy via decorating the atomic step of substrates, which can enriches our capacity of fabricating magnetic nanostructures and manipulating the magnetic properties for potential applications.
Methods
The samples were deposited by molecular-beam epitaxy in an ultrahigh vacuum (UHV) system with a base pressure of 2.0×10−10 mbar. We used the phosphorus-doped Si(111) substrate with a small miscut angle of 0.1° towards the [11-2] direction. The substrates were cut from the identical Si wafer along different orientations to control the angle θ between the atomic step and the heating current in the following substrate treating procedure. After the substrates were introduced into the UHV chamber, they were degassed at 600°C, followed by a standard direct current flashing procedure at 1250°C to obtain the atomically flat Si(111)-7 × 7 reconstructured surfaces with different terrace widths19,23. During this flashing process, the heating current was directly passed through the substrate. The Fe films were grown using an 99.999% pure iron wire heated through e-beam evaporation at room temperature with a deposition rate of 1.5 ML(monolayer)/min20. In order to avoid the Fe-Si intermixing, an atomically flat ultrathin p(2 × 2) iron silicide template was first prepared through 1.5 monolayer (ML) of iron annealed for 10 min at 400°C. The deposition of 20 ML Fe was subsequently performed, at which thickness the step of iron films was still visible. The evolution of surface morphology and structure of the samples were characterized by scanning tunneling microscope (STM) and low energy electron diffraction (LEED) equipped in this UHV system. Before ex situ measurements, 25 ML of Cu was capped to avoid the samples oxidization, and the in situ surface magneto-optical Kerr effect (SMOKE) measurements confirmed the magnetic properties did not change due to the capping layer. The ex-situ MOKE measurements were carried out to investigate the in-plane magnetic anisotropy of the samples.
Author Contributions
Z.H.C., Q.W., W.H. and H.-L.L. planned the experiments. Q.W. and H.L.L. carried out the experiments. All the co-authors contributed to the analysis and discussion for the results. Z.-H.C. and Q.W. wrote the paper with the input from all the co-authors.
Acknowledgments
This work was supported by the National Basic Research Program of China (973 program, Grant Nos. 2009CB929201, 2011CB921801, and 2012CB933102) and the National Natural Sciences Foundation of China (50931006, 11034004, and 51021061).
References
- Weiss N. et al. Uniform Magnetic Properties for an Ultrahigh-Density Lattice of Noninteracting Co Nanostructures. Phys. Rev. Lett. 95, 157204 (2005). [DOI] [PubMed] [Google Scholar]
- Hauschild J. et al. Dipolar superferromagnetism in monolayer nanostripes of Fe(110) on vicinal W(110) surfaces. Phys. Rev. B 57, R677 (1998). [Google Scholar]
- Shen J. et al. Magnetism in one dimension: Fe on Cu(111). Phys. Rev. B 56, 2340 (1997). [Google Scholar]
- Gambardella P. et al. Oscillatory Magnetic Anisotropy in One-Dimensional Atomic Wires. Phys. Rev. Lett. 93, 077203 (2004). [DOI] [PubMed] [Google Scholar]
- Shen J. et al. Structural and magnetic phase transitions of Fe on stepped Cu(111). Phys. Rev. B 56, 11134 (1997). [Google Scholar]
- Bürgi L. et al. Confinement of Surface State Electrons in Fabry-Pérot Resonators. Phys. Rev. Lett. 81, 5370 (1998). [Google Scholar]
- Zhitenev N. B. et al. Localization of Surface States in Disordered Step Lattices. Phys. Rev. Lett. 92, 196805 (2004). [DOI] [PubMed] [Google Scholar]
- Mugarza A. et al. Modelling nanostructures with vicinal surfaces. J. Phys. Condensed Matter 18, S27 (2006). [Google Scholar]
- Ortega J. E. et al. Electron Wave Function at a Vicinal Surface: Switch from Terrace to Step Modulation. Phys. Rev. Lett. 84, 6110 (2000). [DOI] [PubMed] [Google Scholar]
- Baumberger F. et al. Step-Lattice-Induced Band-Gap Opening at the Fermi Level. Phys. Rev. Lett. 92, 016803 (2004). [DOI] [PubMed] [Google Scholar]
- Yin L. F. et al. Tuning the Ferromagnetic Coupling of Fe Nanodots on Cu(111) via Dimensionality Variation of the Mediating Electrons. Phys. Rev. Lett. 104, 167202(2010) [DOI] [PubMed] [Google Scholar]
- Men F. K. et al. Self-Organized Nanoscale Pattern Formation on Vicinal Si(111) Surfaces via a Two-Stage Faceting Transition. Phys. Rev. Lett. 88, 096105 (2002). [DOI] [PubMed] [Google Scholar]
- Kirakosian A. et al. Atomically accurate Si grating with 5.73 nm period. Appl. Phys. Lett. 79, 1608 (2001). [Google Scholar]
- Viernow J. et al. Regular step arrays on silicon. Appl. Phys. Lett. 72, 948 (1998). [Google Scholar]
- Yang Y. N. et al. An STM study of current-induced step bunching on Si(111). Surf. Sci. 356, 101 (1996). [Google Scholar]
- Usov V. et al. Experimental quantitative study into the effects of electromigration field moderation on step bunching instability development on Si(111). Phys. Rev. B 83, 155321(2011). [Google Scholar]
- Kak M. et al. Sixth-order contribution to the cubic anisotropy in Fe(111) thin films on Si(111). Surf. Sci. 566–568, 278 (2004). [Google Scholar]
- Castrucci P. et al. Magnetic force microscopy study of perpendicular magnetization reorientation for Fe grown on Cu/Si(111). Phys. Rev. B 65, 235435 (2002). [Google Scholar]
- Sun D. L. et al. Uniaxial magnetic anisotropy of quasi-one-dimensional Fe chains on Pb/Si. Appl. Phys. Lett. 94, 012504 (2009). [Google Scholar]
- Du H. F. et al. Determination of magnetic anisotropies in ultrathin iron films on vicinal Si(111) substrate by the ferromagnetic resonance. Appl. Phys. Lett. 96, 142511 (2010). [Google Scholar]
- Fang Y. P. et al. Surface morphology and magnetic anisotropy of obliquely deposited Co/Si(111) films. Appl. Phys. Lett. 97, 022507 (2010). [Google Scholar]
- Fang Y. P. et al. Improvement of the uniformity and dipole ferromagnetism in Co nanodots assemblies on Pb/Si(111) via step tuned dimensionality variation. Nanotechnology 21, 465703 (2010). [DOI] [PubMed] [Google Scholar]
- Li J. L. et al. Spontaneous Assembly of Perfectly Ordered Identical-Size Nanocluster Arrays. Phys. Rev. Lett. 88, 066101 (2002). [DOI] [PubMed] [Google Scholar]
- Rezende S. M. et al. Ferromagnetic resonance of Fe(111) thin films and Fe(111)/Cu(111) multilayers. Phys. Rev. B 49, 15105 (1994). [DOI] [PubMed] [Google Scholar]
- Bubendorff J. L. et al. Origin of the magnetic anisotropy in ferromagnetic layers deposited at oblique incidence. Europhys. Lett. 75, 119 (2006). [Google Scholar]