Theoretical implications of incorporating relative biological effectiveness into radiobiological equivalence relationships

Abstract

Objective:

Earlier radiobiological equivalence relationships as derived for low-linear energy transfer (LET) radiations are revisited in the light of newer radiobiological models that incorporate an allowance for relative biological effectiveness (RBE).

Methods:

Linear-quadratic (LQ) radiobiological equations for calculating biologically effective dose at both low- and high-LET radiations are used to derive new conditions of equivalence between a variety of radiation delivery techniques. The theoretical implications are discussed.

Results:

The original (pre-LQ) concept of equivalence between fractionated and continuous radiotherapy schedules, in which the same physical dose is delivered in each schedule, inherently assumed that low-LET radiation would be used in both schedules. LQ-based equivalence relationships that allow for RBE and are derived assuming equal total physical dose between schedules are shown to be valid only in limited circumstances. Removing the constraint of equality of total physical dose allows the identification of more general (and more practical) relationships.

Conclusion:

If the respective schedules under consideration for equivalence both involve radiations of identical LET, then the original equivalence relationships remain valid. However, if the compared schedules involve radiations of differing LET, then new (and more restrictive) equivalence relationships are found to apply.

Advances in knowledge:

Theoretically derived equivalence relationships based on the LQ model provide a framework for the design and intercomparison of a wide range of clinical techniques including those involving high- and/or low-LET radiations. They also provide a means of testing for the validity of variously assumed tissue repair kinetics.

Radiobiological equivalence relationships continue to play an important role in radiation oncology, providing a means of intercomparing alternative radiotherapy treatment schedules in terms of their biological effectiveness and, in principle, allowing the fine-tuning and optimisation of treatments. Such relationships allow any treatment schedule to be converted into a therapeutically equivalent (or improved) alternative through manipulation of various schedule parameters (fraction size, dose rate etc.) or through the consideration of different physical methods of dose delivery (brachytherapy, targeted therapy, permanent implants etc.).

In this paper, the original concept of radiobiological equivalence (the so-called Liversage equivalence, applicable only to intercomparisons between fractionated and continuous schedules) is revisited and re-assessed in the light of more recent advances in radiobiological modelling. In doing so, we demonstrate that Liversage-type equivalence is a special and restricted case of a much wider range of possible equivalence relationships, including, for example, those involving radiations with increased linear energy transfer (LET). High-LET therapies such as those using protons or light ions have been the subject of much interest in recent years because of the therapeutically advantageous dose distributions afforded by the Bragg-peak phenomenon and (especially in the case of light ions) on account of their improved radiobiological effectiveness [1]. Updating equivalence relationships to include allowance for relative biological effectiveness (RBE) is therefore timely. In the same way that the concept of equivalence currently assists in assessing low-LET therapies, it is expected that this will become increasingly relevant in the high-LET domain as these therapies emerge and mature, especially in relation to clinical trials where comparisons will inevitably need to be made with low-LET treatment outcomes. This article does not attempt to provide a clinical evaluation of these equivalence relationships but rather seeks to update the theoretical model by incorporating what is now known about RBE and to discuss some important implications.

Methods and materials

Systematic investigation of the concept of equivalence between fractionated high dose rate (FHDR) treatments and continuous low dose rate (CLDR) treatments was first undertaken by Liversage [2] at a time when FHDR brachytherapy treatments using high-activity cobalt-60 sources were being introduced to replace earlier CLDR treatments using low-activity radium-226 or caesium-137. As long as cellular repopulation during treatment is insignificant (as is the case with late-responding normal tissues), the number, n, of FHDR brachytherapy fractions required to replace an existing CLDR treatment, provided that the physical dose delivered in each case is identical, was found to be defined by the relationship

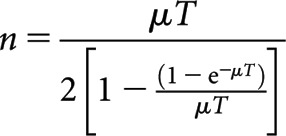(1)

where T is the overall CLDR treatment time and μ is the tissue-specific mono-exponential repair rate constant given by μ=0.693/τ, where τ is the cellular repair half-time for the tissue concerned. Equation (1) was derived by development of an earlier idea by Lajtha and Oliver [3] and involved equating the respective slopes of the assumed “single-target/two-hit” survival curves associated with CLDR and FHDR treatments. When the slopes were equal, it was assumed that an approximate iso-effect existed between the schedules. In cases where the CLDR treatment time is relatively large compared with τ, then Equation (1) reduces to the simpler relationship

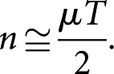(2)

Noting that nd=RT, where R is the dose rate, Equation (2) may be alternatively written as follows:

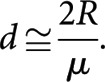(3)

Equations (2) and (3) have been extensively tested in large-scale experiments on a non-mammalian system and have been found to be accurate to within 10% over a wide range of comparisons [4]. In this paper, the type of equivalence defined by these equations will be referred to as “Liversage equivalence”. There are several points that should be noted in relation to Liversage equivalence. Firstly, the relationship only holds when it is assumed that the same physical dose is given in the two cases. Secondly, and provided the assumption of mono-exponential repair kinetics is valid, the relationship between n and T involves only one radiobiological parameter (µ). Since µ is solely a measure of sublethal damage repair rates and is unrelated to the shape of the dose–response curve, then it follows that the equivalence relationship is also independent of the dose–response parameters describing the survival curve. It is important to emphasise at this point that in cases where the repair kinetics are more complex (e.g. those exhibiting multiexponential characteristics) although more repair parameters would be involved in the equivalence relationship, it would nevertheless remain independent of the dose–response characteristic. Thirdly, the equations above inherently assume that the radiations being used possess low LET, i.e. there is no mechanism for incorporating an allowance for RBE. Finally, and as noted earlier, the relationships ignore the effects of any concurrent repopulation that may occur in either the FHDR treatment or the CLDR treatment, although this omission is likely to be of little or no consequence when considering equivalence conditions for late-responding normal tissues or slow-growing tumours.

The Liversage relationship, although derived to address specific questions relating to the safe clinical use of FHDR brachytherapy, need not, in principle, be restricted solely to brachytherapy applications. Liversage equivalence was developed around a single-target/two-hit model of cell survival associated with a cell-survival curve possessing an initial slope of zero and an a symptotic straight line slope at high dose. However, subsequent developments in the linear-quadratic (LQ) formulation [5–7] paved the way for a more general examination of the concept of iso-effectiveness in which different radiation schedules could be equated in terms of their biologically effective dose (BED). By following this approach, Dale [8] showed that the Liversage equivalence relationship could be derived directly as a consequence of the LQ model and that other equivalence relationships could also be identified, e.g. between FHDR and permanent implant treatments or between CLDR and permanent implant treatments. In all cases, the equations were independent of the tissue α/β ratio, i.e. as with the original Liversage derivation, the specific nature of the dose–response relationship did not feature in the equivalence relationships.

In the remainder of this article, we demonstrate how the introduction of RBE effects changes the nature of equivalence and discuss their implications. No attempt is made here to evaluate the clinical applications; rather we highlight and discuss the implications that logically follow from bringing the theoretical model up to date.

Radiations of different LETs are distinguished by their RBE, the ratio of the doses required by a reference radiation and a test radiation to produce the same biological effect. In practice, RBE varies between a maximum (RBE_max) at zero dose to a minimum (RBE_min) at infinite dose [9]; RBE_max and RBE_min correspond, respectively, to the ratio of the high- to low-LET α (linear) radiosensitivity parameter and the square root of the ratio of the high- to low-LET β (quadratic) radiosensitivity parameter. The incorporation of RBE into the BED equation for fractionated radiotherapy leads to the following previously published expression for the high-LET BED of a fractionated schedule [9–14]:

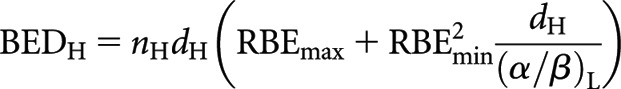(4)

where n is the number of fractions and d the dose fraction size. Subscripts H and L refer to high and low LET, respectively. By analogy, the respective low-LET BED equations for CLDR (when treatment time, T, is long) and permanent implant (decaying source) (from [8]) are re-expressed in high-LET form as follows:

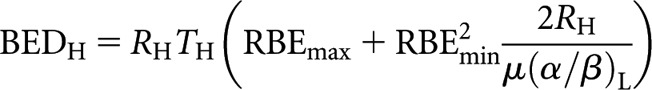(5)

and

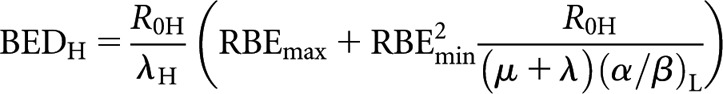(6)

where R_0H is the initial dose rate and λ is the radioactive repair constant, equal to 0.693/T_½, where T_½ is the radioactive half-life.

With these high-LET BED equations (4–6) and their low-LET counterparts, it is possible to derive revised relationships for equivalence between high- and low-LET schedules or, in fact, between any of these schedules regardless of LET. For example, to define a high-LET fractionated schedule to replace a low-LET CLDR schedule first involves equating the high-LET fractionated BED equation with the low-LET CLDR BED equation

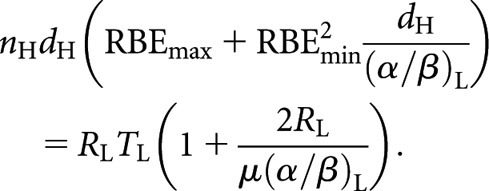(7)

The Liversage interpretation of equivalence requires the delivery of equal total physical doses, n_Hd_H = R_LT_L, so that

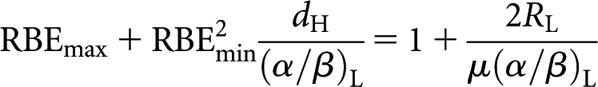(8)

and solving for dose per fraction d_H

(9)

It will be noted that Equation (8) is identical to the Liversage relationship [Equation (3)] in the special case where RBE_max and RBE_min are equal to unity. Following the same procedure, the relationship for equivalence between high-LET fractionated and low-LET permanent implant (decaying source) is

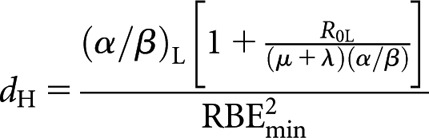(10)

and between high- and low-LET fractionated schedules it is

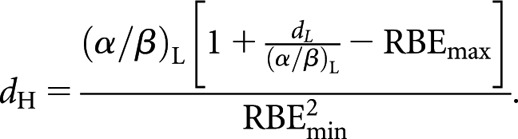(11)

However, in relation to the specific characteristics of Liversage equivalence as discussed above, the inclusion of the RBE effect now raises some difficulties. Firstly, regarding equality of total physical dose, Equation (9) (for example) reveals that for this to be even feasible with the high-LET schedule requires the term in square brackets to be >0, i.e.

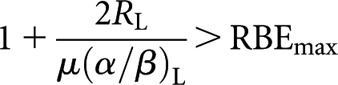(12)

since otherwise a positive value of d_H will not be found. This condition of course represents a theoretical limit since, in practice, d_H also needs to be large enough to be clinically realistic. In terms of LQ methodology, the left-hand side of condition (12) is the low-LET relative effectiveness (RE_low) factor for a continuous low dose rate delivery (in the LQ model, RE is the factor by which the physical dose must be multiplied to obtain the BED measure of biological effect). It is a function that incorporates dose delivery factors, e.g. dose rate or fraction size, and tissue-specific radiobiological parameters. For fractionated therapy delivered in acute doses, the associated low-LET expression is RE=(1 + d/[α/β]) [6]. Thus, the secondary requirement to maintain Liversage equivalence can be expressed in more general terms as RE_low>RBE_max (of interest is the fact that the RBE_min parameter does not feature in this general requirement). Other specific restrictions also apply to relationships (10) and (11) from which the same general requirement that RE_low>RBE_max can be seen to arise. A simple numerical analysis indicates that, while this condition might be satisfied for proton therapy (RBE_max≈1.1), it seems increasingly unachievable for higher values of RBE_max, such as that which would apply to carbon ions (RBE_max≈3). Secondly, the inclusion of RBE now means that, except in the case where the two schedules under comparison each involve identical radiation types, the α/β ratio no longer cancels. Significantly therefore, since it remains in the derived relationships (9–11), knowledge of this tissue-specific parameter is required. Consequently, there can be no Liversage-type equivalence for all tissues in situations where respective schedules involve radiations of differing LET.

If the radiations used in the compared schedules are each of high LET, then (for example) Equation (7) becomes

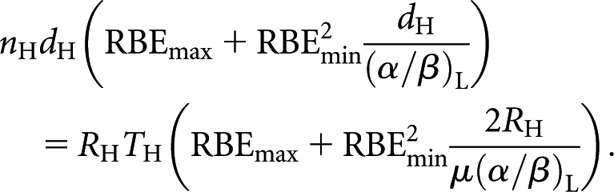(13)

In the special case where the physical doses are identical and where the two schedules under comparison each involve identical radiation types, then the dose, the RBE factors and the α/β ratios all cancel out of Equation (13), leading back to the original Liversage relationships [Equations (2) and (3)]. This independence of RBE holds in all cases of Liversage-type (same dose) equivalence when the LET is the same in both the schedules being compared, i.e. in such cases the original (simple) Liversage equations remain valid for all LET radiations.

In nearly all practical circumstances, there is no pre-requisite for wishing to deliver the same total physical dose when changing schedules—indeed, a prime attraction of high-LET radiation is the potential to achieve good clinical results using fewer fractions. Thus, when considering equivalence in such cases, a generally applicable relationship that is not constrained by equality of total physical dose can be more useful. This is simply illustrated by examining equivalence between high- and low-LET fractionated schedules by equating the low- and high-LET BED equations

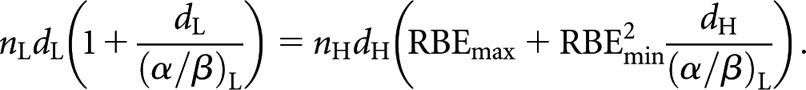(14)

Since equal total dose is no longer a prerequisite (i.e. n_Ld_L ≠ n_Hd_H), this leaves a choice of whether to retain an equal number of fractions or an equal dose per fraction in the respective low- and high-LET schedules. For an equal number of fractions, n_L and n_H simply cancel, leaving the new equivalence relationship

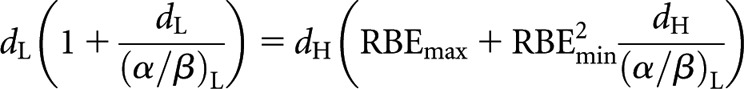(15)

which can be arranged as the following quadratic equation:

and solved for positive values of d_H

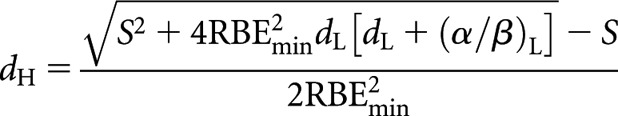(16)

where

Alternatively, for an equal dose per fraction (d_L = d_H = d), from Equation (14)

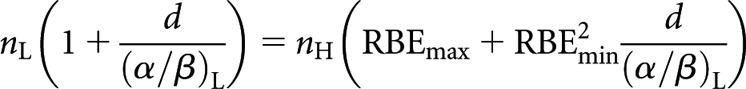(17)

which can then be solved for n_H

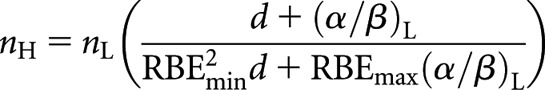(18)

Since it is generally economically advantageous to deliver high LET in fewer fractions, Equation (18) would appear to be more clinically useful than Equation (16).

It will be noted that the corrections involved are not simple multiples of an assumed RBE factor; rather, they are functions of RBE_max, RBE_min and tissue α/β ratio. As pointed out previously by Carabe-Fernandez et al [9] and by Dale and Jones [10], more complex equations are necessary as they inherently take account of the variation of RBE with fraction size and with tissue type.

Discussion

In the comparison between FHDR and CLDR treatments, Liversage-type equivalence (because it is independent of the nature of the underlying dose–response relationship) involves only the assumed repair kinetic parameters (in the case of mono-exponential repair, just µ). If two tissue types are being considered (e.g. tumour and late-responding normal tissue), and if the repair kinetics are the same for both these tissues, then Liversage equivalence represents the condition whereby the therapeutic index can be maintained by delivering the same physical dose in the new schedule as in the old schedule. Once a consideration for any RBE change between the schedules is included, the equivalence relationship is found to depend additionally upon RBE_max, RBE_min and the tissue α/β ratio.

The assumption of mono-exponential repair is also inherent in the new equations presented in this paper. However, the likelihood of there being identical repair characteristics in the two key tissues is very questionable, a point particularly relevant in cases involving CLDR or permanent implants in one of the schedules under comparison. This could be easily overcome by simply replacing the mono-exponential repair term in the original relevant BED equation with the required repair kinetics (if known) and rederiving the equivalence relationship.

Additionally, neither the Liversage relationships nor those derived here take any account of concurrent cellular repopulation in any of the tissues being irradiated. This should not be a significant problem if the overall treatment times of the respective schedules being considered are similar. However, if the treatment times are significantly different, then the equivalence relationships should be regarded as being most reliable for slowly dividing tissues only, i.e. late responding normal tissues. This can be illustrated by considering two schedules, 1 and 2, which can be any combination of low and high LET. In the presence of repopulation, their respective BEDs are given by BED₁=TD₁×RE₁ − RF₁ and BED₂=TD₂×RE₂ − RF₂, where TD is the total physical dose, RE is relative effectiveness and RF is the repopulation BED. Thus, for equivalence in the presence of repopulation, it follows that

If Schedules 1 and 2 are of identical duration, then RF₁ = RF₂, and since, by definition, TD₁ = TD₂ in the special case of Liversage equivalence, then RE₁ = RE₂ [this equality between RE₁ and RE₂ provides the basis of the equivalence relationship between, for example, overall treatment time (T) in CLDR and fraction number (n) in FHDR, as discussed above]. However, if Schedules 1 and 2 are of different duration, as may well be the case, then RF₁ and RF₂ are not equal. Suppose that RF is a fraction, f, of the uncorrected BED (TD × RE), then

and for Liversage equivalence

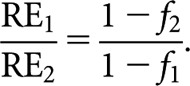Thus any subsequent relationship between, say, n and T is changed by this magnitude. For example, if RF₁ and RF₂ are, respectively, 1% and 10% of the uncorrected BED (because Schedule 2 is much longer), then the derived equivalence relationship is changed by a factor of (1 − 0.1)/(1 − 0.01)=0.91. A fairly secure extreme limit for this factor is 0.75, since in practice the value of RF rarely exceeds about 25% of the uncorrected BED.

None of the observations discussed above undermine the principles of equivalence but rather serve to reinforce the point that extrapolation of low-LET clinical experience to high-LET situations, with a view to improving outcome, will be heavily reliant upon a wider knowledge of the relevant radiobiological parameters.

The relationships derived above along with further relationships derived following the same methods are listed in the appendices. It should be noted that the relationships presented here are expressed in terms of RBE_max, RBE_min and tissue (low-LET) α/β ratio simply to maintain the convention utilised in the earlier work from which they are derived. They could equally be expressed solely in terms of low- and high-LET α and β values, and there may well be situations where this approach is preferable, in which case the relationships can be easily reformulated as required.

Conclusions

General equivalence relationships that are applicable for low- and high-LET radiotherapy situations have been derived through the use of previously derived extensions to the LQ model. An important observation is that an earlier interpretation of equivalence (Liversage equivalence) only holds in the case where the radiation type is the same in the two schedules under consideration. In the case where the radiations in two schedules x and y are of different LET, such that RBE_(y)>RBE_(x), then

• (1)a second condition [RE_(x)>RBE_max(y)] must be satisfied for the higher-LET (y) schedule to be feasible using the same total physical dose
• (2)RBE_min(y) plays no role in determining whether this condition can be met and
• (3)the inclusion of RBE means that knowledge of the tissue-specific α/β ratio is required and in consequence there is no universal equivalence for all tissues in such cases.

Appendices

In the appendices that follow we present the revised equivalence relationships incorporating RBE. Liversage-type equivalence relationships, i.e. those requiring equal total physical dose, are presented in Appendix A. The more generally applicable relationships that do not require equal total physical dose are presented in Appendix B. For ease of reference the equations are summarised in Table A1.

Table A1.

Summary of revised equivalence relationships with equation references

Schedule x	Schedule y	Liversage equivalence (equal total dose)	Equal total dose not required
Low-LET fractionated	High-LET fractionated	A1	B1-1, B1-2
Low-LET fractionated	High-LET CLDR	A2	B2
Low-LET fractionated	High-LET permanent implant (decaying source)	A3	B3
Low-LET CLDR	High-LET fractionated	A4	B4
Low-LET permanent implant (decaying source)	High-LET fractionated	A5	B5
High-LET fractionated	High-LET fractionated	A6	B6-1, B6-2
High-LET fractionated	High-LET CLDR	A7	B7
High-LET fractionated	High-LET permanent implant (decaying source)	A8	B8
High-LET CLDR	High-LET fractionated	A9	B9
High-LET permanent implant (decaying source)	High-LET fractionated	A10	B10

CLDR, continuous low dose rate; LET, linear energy transfer.

Appendix A

Liversage-type equivalence relationships (those requiring equal total physical dose) are presented in this appendix. Equations (A1–A5) convert from low LET to high LET, whereas Equations (A6–A10) convert between high-LET schedules of different LETs. To be feasible, Equations (A1–A10) require the following condition to be satisfied:

Low-LET fractionated (x) to high-LET fractionated (y)

High-LET dose per fraction, d_y

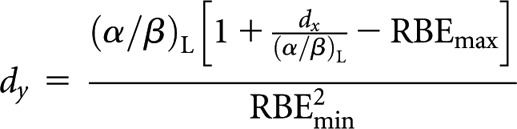(A1)

Low-LET fractionated (x) to high-LET CLDR (y)

High-LET dose rate, R_y

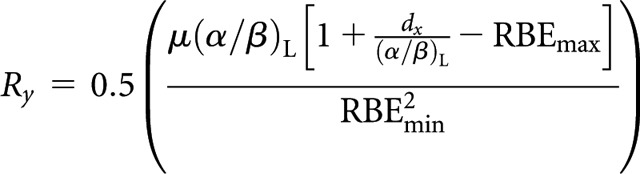(A2)

Low-LET fractionated (x) to high-LET permanent implant (decaying source) (y)

High-LET initial dose rate, R_0(y)

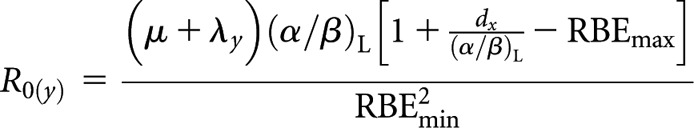(A3)

Low-LET CLDR (x) to high-LET fractionated (y)

High-LET dose per fraction, d_y

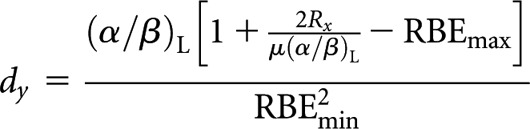(A4)

Low-LET permanent implant (decaying source) (x) to high-LET fractionated (y)

High-LET dose per fraction, d_y

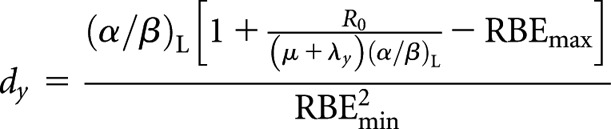(A5)

High-LET fractionated (x) to higher-LET fractionated (y)

High(er)-LET dose per fraction, d_y

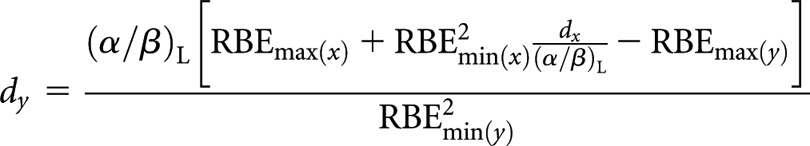(A6)

High-LET fractionated (x) to higher-LET CLDR (y)

High(er)-LET dose rate, R_y

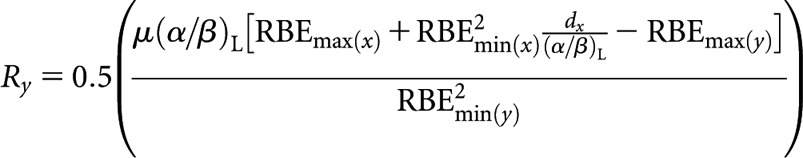(A7)

High-LET fractionated (x) to higher-LET permanent implant (decaying source) (y)

High(er)-LET initial dose rate, R_0(y)

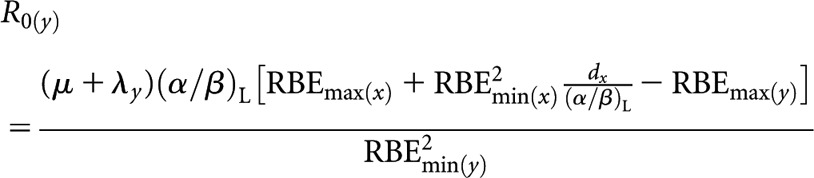(A8)

High-LET CLDR (x) to higher-LET fractionated (y)

High(er)-LET dose per fraction, d_y

(A9)

High-LET permanent implant (decaying source) (x) to higher-LET fractionated (y)

High(er)-LET dose per fraction, d_y

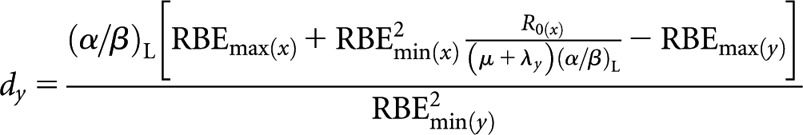(A10)

Appendix B

The more generally applicable equivalence relationships (those not requiring equal total physical dose) are presented in this appendix. Equations (B1-1–B5) convert from low to high LET, whereas Equations (B6–B10) convert between high-LET schedules of different LET.

Low-LET fractionated (x) to high-LET fractionated (y)

High-LET dose per fraction, d_y

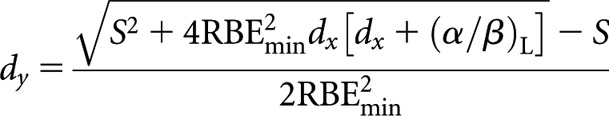(B1-1)

where S = RBE_max(α/β)_L or for high-LET number of fractions, n_y

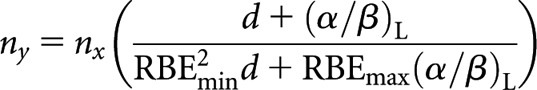(B1-2)

Low-LET fractionated (x) to high-LET CLDR (y)

High-LET dose rate, R_y

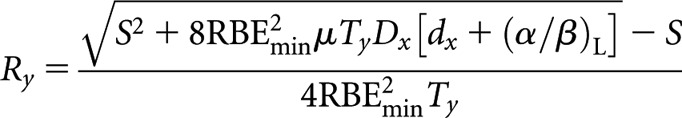(B2)

where S = RBE_max μT_y(α/β)_L.

Low-LET fractionated (x) to high-LET permanent implant (decaying source) (y)

High-LET initial dose rate, R_0(y)

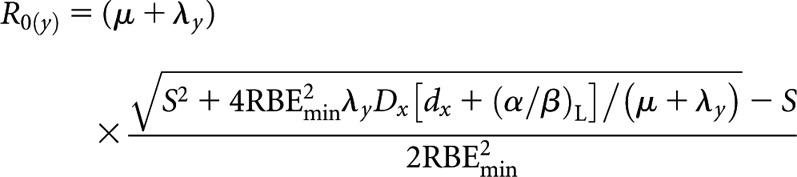(B3)

where S = RBE_max(α/β)_L.

Low-LET CLDR (x) to high-LET fractionated (y)

High-LET dose per fraction, d_y

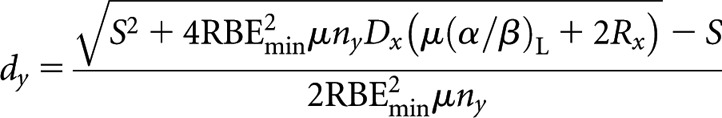(B4)

where S = RBE_max μn_y(α/β)_L.

Low-LET permanent implant (decaying source) (x) to high-LET fractionated (y)

High-LET dose per fraction, d_y

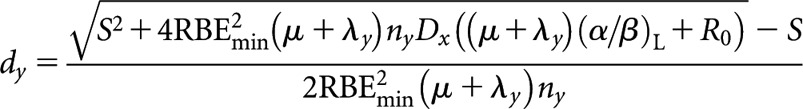(B5)

where S = RBE_maxn_y(μ +λ_y)(α/β)_L.

High-LET fractionated (x) to higher-LET fractionated (y)

High(er)-LET dose per fraction, d_y

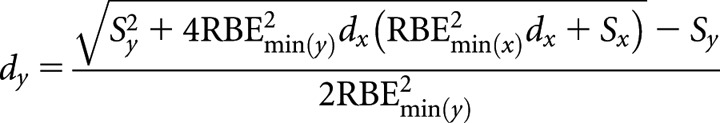(B6-1)

where S_x = RBE_max(x)(α/β)_L and S_y = RBE_max(y)(α/β)_L or for high(er)-LET number of fractions, n_y

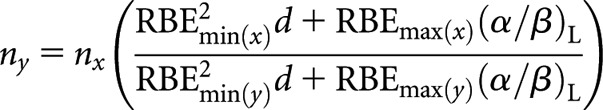(B6-2)

High-LET fractionated (x) to higher-LET CLDR (y)

High(er)-LET dose rate, R_y

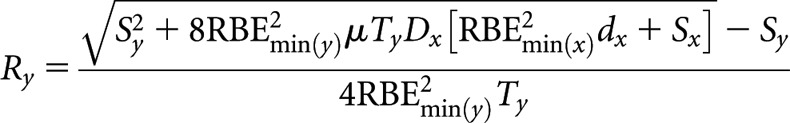(B7)

where S_x = RBE_max(x)(α/β)_L and S_y = RBE_max(y)μT_y(α/β)_L.

High-LET fractionated (x) to higher-LET permanent implant (decaying source) (y)

High(er)-LET initial dose rate, R_0(y)

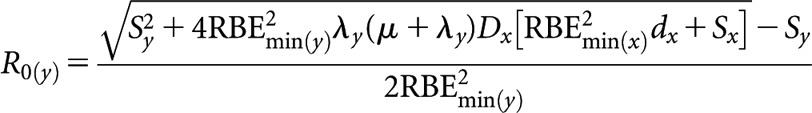(B8)

where S_x = RBE_max(x)(α/β)_L and S_y = RBE_max(y)(μ + λ_y)(α/β)_L.

High-LET CLDR (x) to higher-LET fractionated (y)

High(er)-LET dose per fraction, d_y

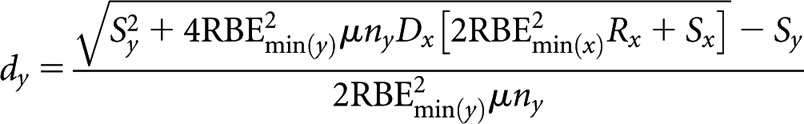(B9)

where S_x = RBE_max(x)μ(α/β)_L and S_y = RBE_max(y)μn_y(α/β)_L.

High-LET permanent implant (decaying source) (x) to higher-LET fractionated (y)

High(er)-LET dose per fraction, d_y

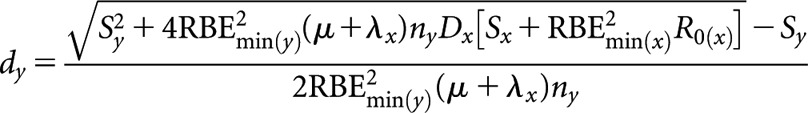(B10)

where S_x = RBE_max(x)(μ + λ_x)(α/β)_L and S_y = RBE_max(y)n_y(μ + λ_x)(α/β)_L.