A two-component nonlinear mixed effects model for longitudinal data, with application to gastric emptying studies

Abstract

Gastric emptying studies are of great interest in human and veterinary medical research to evaluate effects of medications or diets for promoting gastrointestinal motility and to examine unintended side-effects of new or existing medications, diets, or procedures. Summarizing gastric emptying data is important to allow easier comparison between treatments or groups of subjects and comparisons of results among studies. The standard method for assessing gastric emptying is by using scintigraphy and summarizing the nonlinear emptying of the radioisotope. A popular model for fitting gastric emptying data is the power exponential model. This model can only describes a globally decreasing pattern and thus has the limitation of poorly describing localized intragastric events that can occur during emptying. Hence, we develop a new model for gastric emptying studies to improve population and individual inferences using a mixture of nonlinear mixed effects models. One mixture component is based on a power exponential model which captures globally decreasing patterns. The other is based on a locally extended power exponential model which captures both local bumping and rapid decay. We refer to this mixture model as a two-component nonlinear mixed effects model. The parameters in our model have clear graphical interpretations that provide a more accurate representation and summary of the curves of gastric emptying pattern. Two methods are developed to fit our proposed model: one is the mixture of an Expectation Maximization algorithm and a global two-stage method and the other is the mixture of an Expectation Maximization algorithm and the Monte Carlo Expectation Maximization algorithm. We compare our methods using simulation, showing that the two approaches are comparable to one another. For estimating the variance and covariance matrix, the second approach appears approximately more efficient and is also numerically more stable in some cases. Our new model and approaches are applicable for assessing gastric emptying in human and veterinary medical research and in many other biomedical fields such as pharmacokinetics, toxicokinetics, and physiological research. An example of gastric emptying data from equine medicine is used to demonstrate the advantage of our approaches.

1. Introduction

Gastric emptying studies are important in human and veterinary medical research to evaluate medications or diets for promoting gastrointestinal motility and to examine unintended side-effects of new or existing medications, diets, and other procedures or interventions. Examples of this clinical importance include studying the impact on gastric emptying of the composition and size of diets or medications in a wide range of diseases such as diabetes mellitus, scleroderma, and AIDS as well as studying gastric emptying during the post-operative period [1–9]. The way in which gastric emptying data are summarized is therefore important for establishing the validity of gastric emptying studies, and for allowing easier comparison between treatments or between groups of subjects and comparisons of results among studies.

There are numerous studies evaluating gastric emptying in human medicine. Meyer et al. [1] studied the impact of size of liver particles emptied from the human stomach. Meyer et al. [2] reported that the physical characteristics other than size and shape affected gastric emptying of indigestible particles which may be of importance in the design of drugs. Camilleri et al. [3] studied motility disorders of the gastrointestinal tract to characterize patterns of human gastric emptying and colonic filling of radiolabeled solid residue and the influence of the oral intake of subsequent meals on ileocolonic transfer of chyme. Akkermans et al. [4] applied standardized dual-isotope radionuclide gastric emptying techniques to quantify gastric motor function scintigraphically and to study the pathophysiology of gastric emptying in various motor disorders. The rationale for standardization was that many factors can affect gastric emptying, including the duration of the pretest fast (e.g. overnight), elimination of anxiety, venipuncture, abstinence from smoking and various medications. Debrecebi et al. [5] reported the role of capsacin-sensitive primary afferent sensory nerves in the regulation of gastrointestinal motility in humans on the basis of reports indicating that capsacin-sensitive primary afferent sensory nerves have an important role in many gastrointestinal processes in the stomach, intestine, and gallbladder of animals. Hyett et al. [9] evaluated the prognostic value of gastric emptying studies in the morbidity associated with diabetic gastroparesis by comparing diabetic patients with classic symptoms of gastroparesis (including early satiety, postprandial fullness, bloating, abdominal swelling, nausea, vomiting, and retching) and delay in a radionucleotide gastric emptying study. This delayed radionucleotide gastric emptying study predicted negative health outcomes in diabetic patients with symptoms of gastroparesis.

Evaluation of gastric emptying in animals also has been widely reported. Parkman et al. [6] investigated cholinergic effects on gastric motility by studying the effects of the cholinergic antagonist, atropinem, and the cholinergic agonist, bethanechol, using simultaneous measurement of gastric myoelectric activity, antral contractility, and regional gastric emptying. They described an animal model for studying of gastric physiology and evaluation of gastrointestinal prokinetic drugs, and pharmacoscintigraphic studies of new drug formulations with associated absorption studies. El-Salhy [7] determined that gastric emptying of diabetic female mice was significantly slower than that of a control group of mice. Anderson et al. [8] developed a model of gastric emptying in pigs, which are anatomically and physiologically similar to humans.

There have been many approaches to analysis of gastric emptying data for making comparisons between emptying patterns after different meals, between different groups of subjects, or between treatments [1, 4, 5, 7]. The standard method for assessing gastric emptying in humans and animals is scintigraphy [4, 5, 7, 10, 11], where the total number of scintigraphic counts of a radioisotope-labeled meal remaining in the stomach is measured repeatedly at specified time intervals in humans and animals [4, 5, 11–14]. It was reported that the nonnutrient liquid emptying rate from the stomach is rapid and exponential, whereas solids empty at a relatively constant rate determined by the nutrient content of the food and by small intestinal feedback mechanisms. The lag phase is the initial period, during which emptying of the solid meal is delayed. The delay is a finite time determined by the nature of the solid meal. Semi-solid meals and nutrient liquids empty in an intermediate pattern. For the analysis of data from gastric emptying studies, several models were proposed based on an exponential, a double exponential, a power exponential, and a modified power exponential models [15–17]. The power exponential and modified power exponential models are currently the most popular models. A modified power exponential model is especially useful for studying the fractional meal retention value, whereas the power exponential model can be applicable for any type of outcome value including the fraction of a meal and the total number of scintigraphic counts of meal remaining in the stomach. Both models can be easily be used to calculate a lag phase time, which is defined as the time when the second derivative of the function is equal to zero, because the lag phase time has a closed form in both models.

A limitation of these models is that they only describe a globally decreasing pattern of scintigraphic counts, which may not always be the case during some stages of emptying in some individuals. Variation in the globally decreasing pattern may occur because of physiological reasons (e.g. shifting of the labeled meal within the stomach or reflux of emptied material from the duodenum into the stomach) or because of other causes of measurement error. A nondecreasing gastric emptying pattern was shown in the previous studies [5, 6] as well as in our study. Debrecebi et al. [5] calculated four values to summarize gastric emptying curves: maximum value of the curve, time belonging to this maximum, slope of the rising part of the curve which was the maximum value divided by time belonging to it, and time belonging to the 50 per cent of the area under the curve. These values were not estimated but were obtained directly from a scatter plot. Statistical comparisons between medications, treatments or groups of subjects have been made using t-tests at each time point. Because a comparison of t-tests between groups or diets for every time point has inconsistent results, t-tests based on plots of the mean curves are not a good way for making statistical comparisons.

In our study from equine medicine, we also observed a nondecreasing gastric emptying pattern in some horses. The horses were evaluated for purposes of validating an alternative method (breath-testing using C13-labeled octanoic acid) for assessing gastric emptying by comparing the results of that method with scintigraphic results [12, 13]. We note that a similar study was performed using human subject [5]. All horses received a solid-phase meal; 14 horses received only the test meal (octanoic acid with egg), whereas seven horses received the test meal along with atropine, administered to prolong gastric emptying. The rationale for prolonging gastric emptying was to determine whether the breath-testing was correlated with scintigraphy in horses with prolonged emptying, as this might occur with pathologic conditions inducing ileus and delayed gastric emptying, such as post-operative ileus. The total number of scintigraphic counts of the test meal remaining in the stomach was measured repeatedly at specified time intervals in each horse. We first fitted the data using the power exponential model. When the count data were plotted as a function of time, some of the data showed either a dramatic drop in the counts remaining in the stomach or a local upward bump in the graph, suggesting filling rather than emptying. These observations illustrated the aforementioned limitations with regards to individuals of the power exponential model as applied to individuals to obtain a summary statistic that could subsequently be compared among individuals.

The limitations of the power exponential model may result from the fact that only one or two parameters are used to summarize the data from an individual subject. Thus, one cannot obtain information when the local upward bump or rapid decay occurs, and what amount of local change occurs. To our knowledge, the methods for addressing these limitations of commonly used methods for analysis of gastric emptying are yet to be developed and we do so here by using a mixture of mixed effects models.

While the power exponential model may provide an adequate summary of the gastric emptying for an individual subject, one loses information and statistical power by not using all of the observations made for an individual. This is particularly important for the relatively common situation in which studies involve a relatively small number of subjects to evaluate the effects of diets or medications in patients with diseases such as diabetes. Therefore, we considered the application of a random coefficient regression model [18, 19] which accommodates both variation among measurements within individuals and individual-to-individual variation. In addition, because individuals studied may not be derived from a homogeneous sub-population, a single regression model likely cannot adequately fit data from heterogeneous sub-populations.

Our goal for this paper is to develop a new model that provides a more accurate representation and summary of the curves of gastric emptying data, thereby allowing for improved comparisons between treatments or between groups of subjects. A new model should be able to capture both a globally decreasing pattern and a local nondecreasing pattern, using as few parameters as possible. The parameters should have clear graphical interpretations. Specifically, we are interested in a new model which gives us additional information regarding when the local upward bump or rapid decay occurs and what amount of local change occurs. Our new model is based on a mixture of nonlinear mixed effects models. We refer to this mixture model as a two-component nonlinear mixed effects model (two-component NLME). Using our new model, we are also able to estimate the proportion of individuals fit by either model. The estimation of the mixture proportions gives a clear indication of whether the potential deviation from the power exponential model exists, and, if so, whether the proportions of deviation differ for different diet treatments. Another goal is to develop methods for fitting the two-component NLME. In this paper, we have develop two methods based on the frequentist approach for fitting the new model: one is the mixture of an Expectation Maximization (EM) algorithm [20] and a global two-stage (GTS) method [21, 22] and the other is the mixture of an EM algorithm and the Monte Carlo Expectation Maximization (MCEM) algorithm [23, 24]. The GTS is an iterative EM-type algorithm to compute the normal theory maximum likelihood estimates and is the most common approach for a mixed model. The MCEM is another possible approach for a mixed model. Unlike GTS, it is used to directly calculate the likelihood by integrating out random variables using Markov Chain Monte Carlo (MCMC) methods and to then obtain the maximum likelihood estimates for fixed parameters.

The paper is organized as follows. In Section 2, we review the power exponential model and explain the limitation of this model. In Section 3, we describe a two-component NLME and illustrate how we derive it. Our proposed model allows each individual gastric emptying process to be from one of the two mixture components; one component contains a local bump or decay and the other does not. In Section 4, we discuss two methods to fit our proposed model: one is the mixture of an EM algorithm and a GTS method and the other is the mixture of an EM algorithm and the MCEM algorithm. In Section 5, we report the results of simulations comparing our methods. In Section 6, we apply our approaches to data from an equine gastric emptying study. Section 7 contains concluding remarks.

2. Power exponential model

The power exponential model is one of the most popular models for analyzing and summarizing gastric emptying data [15–17]. The model is

$$y_{jk}=A_{0j}{2}^{-{\left(\frac{t_{jk}}{t_{50j}}\right)}^{{\beta }_j}}+\sigma {\epsilon }_{jk}.$$

The y_jk represents the meal, drug, or other types remaining in the stomach at the kth time point of the jth subject where k = 1, …, n_j and j = 1, …, h. The t_jk is the corresponding sampling time and A_0j stands for the amount of meal, drug, or other types remaining in the stomach at time 0. The t_50j represents the parameter of time at which one-half of the meal or other types present at time 0 remain in the stomach of the jth subject. The β_j is the shape parameter of the lag phase of the decreasing curve of the jth subject. The intraindividual error ε_jk is assumed to be independent and identically distributed with zero mean and unit variance. The intraindividual variance is accounted for by the scale parameter σ.

For β_j = 1, the power exponential is the same as the exponential model. A value of β_j >1 describes a curve with an initial lag in emptying the gastric content. This type of curve is often seen for gastric emptying of a solid meal emptying (solid-phase emptying), where the initial lag phase may represent the time required to grind the food or treatment into smaller particles [1]. A value of β_j <1 describes a curve with a very rapid initial emptying, followed by a second slower emptying phase. Such a pattern is often seen for liquid-phase emptying (i.e. the emptying of a liquid meal).

We note that the log-transformation of this model resulted in a poor fit; If we normalize y_jk as $y_{jk}^{\ast }=y_{jk}/A_{0j}$, some data points $y_{jk}^{\ast }$ are larger than 1 when an initial emptying is slow. Points with $y_{jk}^{\ast }$ near 1 as well as those with $y_{jk}^{\ast }$ near 0 are spreads out in comparison with the rest of the data points and may have a large influence on the parameter estimates. Points inconsistent with the curve or with a monotone emptying pattern will affect parameters estimated using the linearized form post the log-transformation more seriously than those estimated using a nonlinear least-squares approach. It has been reported that the curve obtained using nonlinear least squares (NLS) provided a better fit [15].

3. Two-component nonlinear mixed effects model

Let f(t_jk, θ_j) represent the mixture of two nonlinear functions characterizing the relationship between y_jk and t_jk, with θ_j (h × 1) being the subject-specific regression parameters. The kth amount of meal remaining in the stomach for subject j follows the model

$$y_{jk}=f(t_{jk},{\mathit{\theta }}_j)+\sigma {\epsilon }_{jk},$$

where ε_jk denotes the random error and is assumed to be independent and identically distributed with zero mean and unit variance, independently of θ_j. The intraindividual variance is accounted for by the scale parameter σ.

We propose a suitable candidate for f(t_jk, θ_j) by following these rules:

• The mathematical curve should capture both a global decreasing pattern and a local nondecreasing pattern with as few parameters as possible.

• The parameters should have graphical interpretations; changes in the value of a parameter should have a graphical relationship to changes in the shapes of the observed emptying curves.

• The individual model should accommodate all observed emptying curves.

Based on these rules, our proposed model f(t_jk, θ_j) is developed using the mixture of two nonlinear functions, m₁(t_jk) and m₂(t_jk). We first explain these two functions. Let θ_1j = (t_50j, β_j)^T and define m₁(t_jk; θ_1j) as the mean function of the power exponential model

$$m_1(t_{jk};{\mathit{\theta }}_{1j})=A_{0j}{2}^{-{\left(\frac{t_{jk}}{t_{50j}}\right)}^{{\beta }_j}},$$

which describes a global decreasing pattern.

Since we are interested in a new model that gives us information regarding when the local upward bump or decay occurs and what amount of local change occurs, we enrich the power exponential model by allowing two additional parameters (γ_j, η_j) that describe a local bumping or decay. We let γ_j represent the amount of local change, where γ_j >0 means a local bumping and γ_j <0 indicates a local rapid decay. The η_j stands for the position when the local maximal change occurs and its range is (0,1] so that the local maximum or minimum occurs at time η_j t_50j. Defining θ_2j = (γ_j, η_j), we define

$$m_2(t_{jk};{\mathit{\theta }}_{1j},{\mathit{\theta }}_{2j})=A_{0j}{2}^{-{\left(\frac{t_{jk}}{t_{50j}}\right)}^{{\beta }_j}+B(t_{jk};t_{50j},{\gamma }_j,{\eta }_j)},$$

where B(t_jk; t_50j, γ_j, η_j) is a nonlinear function which satisfy the following conditions:

• C1: B(t_50j; t_50j, γ_j, η_j) = 0 by the definition of t_50j;

• C2: lim_tjk→0 B(t_jk; t_50j, γ_j, η_j) = lim_tjk→∞B(t_jk; t_50j, γ_j, η_j)= a constant C; the decay rate is of the order o{−(t_jk/t_50j)^βj} as t_jk → ∞;

• C3:B(t_jk; t_50j, γ_j, η_j) has a local maximum or minimum at η_j t_50j;

• C4:|B(t_jk; t_50j, γ_j, η_j)− C| is a logconcave function.

We consider these four conditions by the following reasons. The C1 is necessary to ensure that the new function m₂(t_jk) has the same t_50j as m₁(t_jk). For C2, we determine that the effect of bumping decays as t_jk → ∞. In other words, B(t_jk) is of lower order than −(t_jk/t_50j)^β_j. Therefore, we can impose the equality lim_tjk→∞B(t_jk) = C = lim_tjk→0 B(t_jk). C3 is by our definition of η_j t_50j. C4 warrants that the effect of bumping or decay is localized near the local maximum or minimum point.

Some examples of B(t_jk) are t_jk exp(−t_jk) or $t_{jk}^{a}exp(-{bt}_{jk})$ for any a>0 and b>0. We can show that the general _jk exp(−function B(t_jk), satisfying C1–C4, has the following asymptotic expansion under some conditions.

Theorem 3.1

Let B(t_jk) be any analytic function, satisfying C1–C4, B′(0) ≠ 0, and $B(t_{jk})=o(t_{jk}^{{\beta }_j})$ as t_jk → ∞. Then we have

$$B(t_{jk})=\{\begin{array}{ll}C+{\gamma }_j{t}_{jk}exp(-t_{jk})+o(t_{jk})\hfill & \text{as}{t}_{jk}\to 0,\hfill \\ C+{\gamma }_j{t}_{jk}exp(-t_{jk})+o(t_{jk}^{{\beta }_j})\hfill & \text{as}{t}_{jk}\to \infty .\hfill \end{array}$$

The proof of this result is shown in Appendix.

The characteristic of t_jk exp(−t_jk) reflects that of the data as well. Using our data we observe that the local bumping happen before t_50j and that the effect of local bump decays rapidly along time. We also observe that there is no effect of bumping at the beginning and that the effect shows up for some time interval. We note that the function t_jk exp(−t_jk) has such characteristics. The term B(t_jk) under the conditions of Theorem 1 can be approximated by C + γ_j t_jk exp(−t_jk). To implement this function, we normalize the time by t_50j so that B(t_jk) has its upward bump or decay at η_j t_50j.

Therefore, we have B(t_jk) = C + γ_j (t_jk/t_50j)exp(−t_jk/η_j t_50j), which decays exponentially and has its maximum or minimum value η_j t_50j. Since B(t_50j) = 0, C is −γ_j exp(−1/η_j). Consequently, B(t_jk) = −γ_j exp(−1/η_j) + γ_j (t_jk/t_50j)exp(−t_jk/η_j t_50j). The function m₂(·) can be rewritten as the following:

$$m_2(t_{jk};{\mathit{\theta }}_{1j},{\mathit{\theta }}_{2j})=A_{0j}{2}^{-{(\frac{t_{jk}}{t_{50j}})}^{{\beta }_j}-{\gamma }_{j}exp(-\frac{1}{{\eta }_j})+{\gamma }_j(\frac{t_{jk}}{t_{50j}})exp(-\frac{t_{jk}}{{\eta }_j{t}_{50j}})}.$$

We refer to this function as a ‘locally extended power exponential model’. We note that this function is the same as the power exponential function when γ_j is zero.

Let i represent the indicator of the ith sub-population; i = 1 means that the sub-population of subjects follows the power exponential model; i = 2 means that the sub-population of subjects follows the locally extended power exponential model. Define z_ij = 1 if the true mean function for subject j is m_i (t_jk), and 0 otherwise. The distribution of z_ij is Ber(π_i), where π₁ = Pr(z_1j = 1) represents the proportion of subjects following the power exponential model, π₂ = Pr(z_2j = 1) stands for the proportion of subjects following the locally extended power exponential model that can capture local bump or rapid decay, and z_1j + z_2j = 1.

Our proposed model for f(t_jk; θ_j) is

$$\begin{array}{l}f(t_{jk};{\mathit{\theta }}_j)=z_{1j}{A}_{0j}{2}^{-{(\frac{t_{jk}}{t_{50j}})}^{{\beta }_j}}+(1-z_{1j})A_{0j}{2}^{-{(\frac{t_{jk}}{t_{50j}})}^{{\beta }_j}+B(t_{jk};t_{50j},{\gamma }_j,{\eta }_j)}\\ =z_{1j}{m}_1(t_{jk};{\mathit{\theta }}_{1j})+(1-z_{1j})m_2(t_{jk};{\mathit{\theta }}_{1j},{\mathit{\theta }}_{2j}).\end{array}$$

This two-component nonlinear model allows us to estimate the proportion of individuals from different sub-populations as well as give more accurate summaries of gastric emptying pattern. To account for variation in the population behavior, we assume that θ_j = (θ_1j, θ_2j) are random variables from a distribution with mean θ and covariance Σ, θ_j ~ [θ, Σ]; the usual specification is that of multivariate normal distribution. We refer to this model as a two-component NLME.

4. Methods

4.1. Introduction

This section describes two methods to fit the two-component NLME. Section 4.2 describes the method using both EM and GTS, whereas Section 4.3 develops the method based on the both EM and MCEM approach.

4.2. The mixture of EM and GTS

We use two EM algorithms; the one algorithm is to estimate parameters including π_i and the other is to update a set of random coefficients θ_j = (θ_1j, θ_2j) in the GTS step.

Let Y_obs = (Y_jk), Y_miss = (Z_ij, θ_j), Y_complete = (Y_obs, Y_miss) = Y_c. For estimating parameters using the first EM, we can use the Newton–Raphson method, which requires the gradient of the expectation of the log-likelihood for complete data with respect to each of the parameters. However, when η_j → 0, the first derivative of the mean function of the locally extended power exponential model with respect to γ_j is the same as that of η_j. Because |B(t_jk; t_50j, γ_j, η_j)|<C^* exp(−1/η_j), for some constant C^*, B(t_jk; t_50j, γ_j, η_j) → 0 as η_j → 0. Therefore, when η_j is close to zero, it is difficult to estimate γ_j and η_j simultaneously. To overcome this problem, we estimate η_j using a grid search with 0.1 increments in the range [0.1, 0.9].

We define the following functions, g_1j (·) and g_2j (·) as

$$\begin{array}{l}{g}_{1j}({\mathit{\theta }}_{1j},{\sigma }^2)=\prod _{k=1}^{n_j}\frac{1}{\sqrt{2{\sigma }^2}}exp\left[-\frac{{\{y_{jk}-m_1(t_{jk};{\mathit{\theta }}_{1j})\}}^2}{2{\sigma }^2}\right]=\prod _{k=1}^{n_j}{g}_{1j·1}(y_{ij}\mid {\mathit{\theta }}_{1j},{\sigma }^2),\\ g_{2j}({\mathit{\theta }}_{1j},{\mathit{\theta }}_{2j},{\sigma }^2)=\prod _{k=1}^{n_j}\frac{1}{\sqrt{2{\sigma }^2}}exp\left[-\frac{{\{y_{jk}-m_2(t_{jk};{\mathit{\theta }}_{1j},{\mathit{\theta }}_{2j})\}}^2}{2{\sigma }^2}\right]=\prod _{k=1}^{n_j}{g}_{2j·1}(y_{ij}\mid {\mathit{\theta }}_{1j},{\mathit{\theta }}_{2j},{\sigma }^2).\end{array}$$

Let gθ_j (θ_j |θ, Σ) be the probability density function of a multivariate normal distribution with a mean vector θ and variance and covariance matrix Σ, which is the distribution of θ_j. Let θ̄_1j = (θ_1j) and θ̄_2j = (θ_1j, θ_2j). Then the log-likelihood of the complete data Y_c is

$$log(L_c)=\sum _{i=1}^2\sum _{j=1}^h{z}_{ij}\{log{\pi }_i+log{g}_{ij}({\overline{\mathit{\theta }}}_{ij},{\sigma }^2)\}+log{g}_{{\mathit{\theta }}_j}({\mathit{\theta }}_j\mid \mathit{\theta },\mathbf{\sum }).$$

Define Ψ = (π₁, ε², θ_1j, θ_2j) and let Ψ^(l) be the estimates of Ψ obtained from the lth step of EM. For a given ${\eta }_j^{(l)}\in [0.1,0.9]$, other parameters are estimated by the procedures shown in Steps 1 and 2. Then the optimal ${\eta }_j^{(l)}$ is selected to maximize the log-likelihood and Ψ^(l) is obtained for a given optimal ${\eta }_j^{(l)}$. We then update the random coefficients of (θ_1j, γ_j) in GTS shown in Steps 3–5 and also update the random coefficient of η_j using the standard two-stage method (STS) shown in Step 6. Each step is described below.

• Step 1 (E-step):

  $$\begin{array}{l}E(Z_{ij}\mid {\mathbf{Y}}_j={\mathbf{y}}_j)={Pr}_{{\mathrm{\Psi }}^{(l)}}\{Z_{ij}=1\mid {\mathbf{Y}}_j={\mathbf{y}}_j\}\\ =\frac{{\pi }_i^{(l)}{g}_{ij}({\overline{\mathit{\theta }}}_{ij}^{(l)},{\sigma }^{{(l)}^2})}{{\sum }_{i=1}^2{\pi }_i^{(l)}{g}_{ij}({\overline{\mathit{\theta }}}_{ij}^{(l)},{\sigma }^{{(l)}^2})}\\ ={\tau }_{ij}({\mathrm{\Psi }}^{(l)}).\end{array}$$

  Hence, we have

  $${\pi }_i^{(l+1)}=\frac{{\sum }_{j=1}^h{\tau }_{ij}({\mathrm{\Psi }}^{(l)})}{h}.$$

  The E-step can then be computed as

  $$Q(\mathrm{\Psi }\mid {\mathrm{\Psi }}^{(l)})=E_{{\mathrm{\Psi }}^{(l)}}\{(log(L_c)\mid {\mathbf{Y}}_{\text{obs}})\}=\sum _{i=1}^2\sum _{j=1}^h{\tau }_{ij}({\mathrm{\Psi }}^{(l)})\{log{\pi }_i^{(l)}+log{g}_{ij}({\overline{\mathit{\theta }}}_{ij}^{(l)},{\sigma }^{{(l)}^2})\}.$$

• Step 2 (M-step): Using Q(Ψ^(l)), we calculate maximum likelihood estimates of ${\mathit{\theta }}_j^{(-{\eta }_j)}=({\mathit{\theta }}_{1j},{\gamma }_j)$ and σ². These estimates are obtained from the following equations:

  $$\sum _{i=1}^2\sum _{j=1}^h{\tau }_{ij}({\mathrm{\Psi }}^{(l)})\left\{\frac{\partial log{g}_{ij}({\overline{\mathit{\theta }}}_{ij}^{(l)},{\sigma }^{{(l)}^2})}{\partial {\mathit{\theta }}_j^{(-\eta )}}\right\}=\mathbf{0}$$

  and

  $${\widehat{\sigma }}^{{(l+1)}^2}=\frac{{\sum }_{i=1}^2{\sum }_{j=1}^h{\tau }_{ij}({\mathrm{\Psi }}^{(l)}){\sum }_k{\{y_{jk}-m_i({\overline{\mathit{\theta }}}_{ij}^{(l)})\}}^2}{{\sum }_{i=1}^2{\sum }_{j=1}^h{n}_j{\tau }_{ij}({\mathrm{\Psi }}^{(l)})}.$$

  These estimates are used in Ψ^(l+1).

• Step 3: We repeat Steps 1–2 by varying η_j in the range [0.1, 0.9] by increments of 0.1 and then obtain Ψ^(l) for a given η_j = argmax_ηj Q(Ψ^(l)).

• Step 4 (E-step for GTS): This step updates the parameters of ${\mathit{\theta }}_j^{(-{\eta }_j)}$. Let ${\mathit{\theta }}_j^{(-{\eta }_j)\ast }$ be an estimate of ${\mathit{\theta }}_j^{(-{\eta }_j)}$. Using the gradient matrix (X) of the mean function with respect to ${\mathit{\theta }}_j^{(-{\eta }_j)}$, we obtain an estimate of the asymptotic covariance matrix $V_j^{(-{\eta }_j)}={\sigma }^2{({\mathbf{X}}^{\prime }\mathbf{X})}^{-1}$. So, we have ${\mathit{\theta }}_j^{(-{\eta }_j)\ast }\mid {\mathit{\theta }}_j^{(-{\eta }_j)}\sim \mathit{MVN}({\mathit{\theta }}_j^{(-{\eta }_j)},V_j^{(-{\eta }_j)})$. This implies

  $${\mathit{\theta }}_j^{(-{\eta }_j)\ast }\sim \mathit{MVN}({\mathit{\theta }}_j^{(-{\eta }_j)},V_j^{(-{\eta }_j)}+{\mathrm{\sum }}^{(-{\eta }_j)}),$$

  where Σ^(−η_j) is the subset of Σ and does not contain both the variance of η_j and the covariance among η_j and ${\mathit{\theta }}_j^{(-{\eta }_j)}$. At the (m +1)th GTS iteration within the lth EM step,

  $${({\widehat{\mathit{\theta }}}_j^{(-{\eta }_j)})}_{(l,m+1)}={\{{(V_j^{(-{\eta }_j)})}_{(l)}^{-1}+{({\widehat{\mathrm{\sum }}}^{(-{\eta }_j)})}_{(m)}^{-1}\}}^{-1}\{{(V_j^{(-{\eta }_j)})}_{(l)}^{-1}{\mathit{\theta }}_j^{(-{\eta }_j)\ast }+{({\widehat{\mathrm{\sum }}}^{(-{\eta }_j)})}_{(l,m)}^{-1}{\widehat{\mathit{\theta }}}_{(l,m)}^{(-{\eta }_j)}\}.$$

• Step 5 (M-step for GTS): We obtain the following:

  $$\begin{array}{l}{\widehat{\mathit{\theta }}}_{(m+1)}^{(l)}=h^{-1}\sum _{j=1}^h{({\widehat{\mathit{\theta }}}_j^{(-{\eta }_j)})}_{(l,m+1)},\\ {\widehat{\mathrm{\sum }}}_{(l,m+1)}^{(-{\eta }_j)}=h^{-1}\sum _{j=1}^h\{{({\widehat{\mathit{\theta }}}_j^{(-{\eta }_j)})}_{(l,m+1)}-{\widehat{\mathit{\theta }}}_{(l,m+1)}^{(-{\eta }_j)}\}{\{{({\widehat{\mathit{\theta }}}_j^{(-{\eta }_j)})}_{(l,m+1)}-{\widehat{\mathit{\theta }}}_{(l,m+1)}^{(-{\eta }_j)}\}}^{\text{T}}+h^{-1}\sum _{j=1}^h{\{{(V_j^{(-{\eta }_j)})}_{(l)}^{-1}+{({\widehat{\mathrm{\sum }}}^{(-{\eta }_j)})}_{(l,m)}^{-1}\}}^{-1}.\end{array}$$

• Step 6: We estimate the population mean and variance of η_j using STS as follows:

  $$\begin{array}{l}{\widehat{\eta }}_{(l,m+1)}=h^{-1}\sum _{j=1}^h{({\widehat{\eta }}_j)}_{(l)},\\ {\widehat{\sigma }}_{{\eta }_{(l,m+1)}}^2=h^{-1}\sum _{j=1}^h{\{{({\widehat{\eta }}_j)}_{(l)}-{\widehat{\eta }}_{(l,m+1)}\}}^2,\\ \widehat{\mathit{cov}}\{{({\eta }_j)}_{(l)},{({\mathit{\theta }}_j^{-({\eta }_j)})}_{(l,m+1)}\}=h^{-1}\sum _{j=1}^h\{{({\widehat{\eta }}_j)}_{(l)}-{\widehat{\eta }}_{(l,m+1)}\}{\{{({\widehat{\mathit{\theta }}}_j^{(-{\eta }_j)})}_{(l,m+1)}-{\widehat{\mathit{\theta }}}_{(l,m+1)}^{(-{\eta }_j)}\}}^{\text{T}}.\end{array}$$

• Step 7: Repeat Steps 1–6 until (π₁, σ², θ, Σ) converge.

For initial values of parameters, we chose π₁ as 0.5. NLS estimators were selected for σ², θ_1j, and θ_2j. The initial values of θ and Σ were chosen using the estimates of STS. The selection of initial values was not sensitive when the values were selected within 2 standard deviation of our initial values.

4.3. The mixture of EM and MCEM

Instead of using the GTS procedure to update random coefficients, we use MCEM. Unlike the GTS, it allows one to directly calculate the marginal likelihood by integrating out the random variables using MCMC, and to then obtain the maximum likelihood estimates for fixed parameters. The MCEM is used to samples θ_j from the complete conditional distribution [θ_j |data, π₁, σ², θ, Σ] and then EM is used to estimate fixed parameters. Although this approach needs more computation time than the previous method, it is numerically more stable when η_j is small because there is no calculation requirement of the first and second derivative of likelihood with respect to η_j.

We generate ${\mathit{\theta }}_j^M$, M = 1, …, T, where T is the total number of iterations of MCMC, from the complete conditional distribution [θ_j |data, π₁, σ², θ, Σ] using the Metropolis–Hastings algorithm [25]. The complete conditional distribution is

$$\begin{array}{l}[{\mathit{\theta }}_j\mid \text{d}\mathit{ata},{\pi }_1,{\sigma }^2,\mathit{\theta },\mathrm{\sum }]\propto \prod _{i=1}^2{\pi }_i\prod _{j=1}^h{g}_{ij}({\mathit{\theta }}_j,{\sigma }^2)\times g_{{\mathit{\theta }}_j}({\mathit{\theta }}_j\mid \mathit{\theta },\mathrm{\sum })\\ \propto \prod _{i=1}^2{\pi }_i\prod _{k=1}^{n_j}{g}_{ij·1}(y_{jk}\mid {\mathit{\theta }}_j,{\sigma }^2)\times g_{{\mathit{\theta }}_j}({\mathit{\theta }}_j\mid \mathit{\theta },\mathrm{\sum }).\end{array}$$

• Step 1a (MC step): We generate ${\mathit{\theta }}_j^M$ using a Metropolis–Hastings algorithm. The choice of our proposal distribution is a multivariate normal distribution with mean vector ${\mathit{\mu }}_{j.p}={\mathit{\theta }}_j^{M-1}$ and covariance matrix C_j·p = C₀Σ̂_EMGTS, where C₀ is a constant such that C₀>1 and Σ̂_EMGTS is the estimator obtained by the method of the mixture of EM and GTS. Choosing this proposal distribution is based on the works of Carlin and Gelfand [26] and Chip and Greenberg [27]. We choose the initial values ${\mathit{\theta }}_j^0$ as the values of EMGTS and we change C0 from 2 to 5. We note that in our study our estimated values were not significantly different when we varied C₀ from 2 to 5. Hence we set C₀ = 2. We find that this proposal distribution gives faster convergence in the Metropolis–Hasting algorithm than does another proposal distribution with diagonal covariance matrix. We then implement the Metropolis–Hasting algorithm. By comparing the current values ${\mathit{\theta }}_j^{\text{current}}$ with the new sample ${\mathit{\theta }}_j^{\text{new}}$ from proposal distribution, we accept the new sample ${\mathit{\theta }}_j^{\text{new}}$ with the probability

  $$min\left\{1,\frac{{\prod }_{i=1}^2{\pi }_i{\prod }_{k=1}^{n_j}{g}_{ij·1}(y_{jk}\mid {\mathit{\theta }}_j^{\text{new}},{\sigma }^2)\times g_{{\mathit{\theta }}_j}({\mathit{\theta }}_j^{\text{new}}\mid {\mathit{\theta }}^{\text{current}},\mathrm{\sum })}{{\prod }_{i=1}^2{\pi }_i{\prod }_{k=1}^{n_j}{g}_{ij·1}(y_{jk}\mid {\mathit{\theta }}_j^{\text{current}},{\sigma }^2)\times g_{{\mathit{\theta }}_j}({\mathit{\theta }}_j^{\text{current}}\mid {\mathit{\theta }}^{\text{new}},\mathrm{\sum })}\right\}.$$

  Since our proposal distribution is a symmetric distribution, gθ_j (•|•) is the same in both the numerator and denominator. Hence gθ_j (•|•) is cancelled out. We select N_M samples after a burn-in time iterations, e.g. N_M = 2000 after a burn in time of 10 000 iteration.

• Step 2a (MCEM step): For given M and ${\mathrm{\Psi }}^{(l)}=({\pi }_1^l,{\sigma }^{2l},{\mathit{\theta }}^l,{\mathrm{\sum }}^l)$, which are defined as the estimators obtained from the lth EM iteration, we calculate the following:

  $${\tau }_{\mathit{ijM}}({\mathrm{\Psi }}^{(l)})=\frac{{\pi }_1{\prod }_{k=1}^{n_j}{g}_{1j·1}(y_{jk}\mid {\overline{\mathit{\theta }}}_{ij}^M)}{{\pi }_1{\prod }_{k=1}^{n_j}{g}_{1j·1}(y_{jk}\mid {\overline{\mathit{\theta }}}_{ij}^M)+{\pi }_2{\prod }_{k=1}^{n_j}{g}_{2j·1}(y_{jk}\mid {\overline{\mathit{\theta }}}_{2j}^M)}.$$

  Then we obtain τ̂_ij(Ψ^(l)) and ${\pi }_i^{(l+1)}$ using the sample mean:

  $$\begin{array}{c}{\widehat{\tau }}_{ij}({\mathrm{\Psi }}^{(l)})=\frac{{\sum }_{M=1}^{N_M}{\tau }_{\mathit{ijM}}({\mathrm{\Psi }}^{(l)})}{N_M},\\ {\widehat{\pi }}_i^{(l+1)}=\frac{{\sum }_{j=1}^h{\widehat{\tau }}_{ij}({\mathrm{\Psi }}^{(l)})}{h},\end{array}$$

• Step 3a (E-step): The E-step can then easily be computed as

  $$\begin{array}{l}Q(\mathrm{\Psi }\mid {\mathrm{\Psi }}^{(l)})=E_{{\mathrm{\Psi }}^{(l)}}\{(log(L_c)\mid Y_{\mathit{obs}})\}\\ =\frac{1}{N_M}\sum _{i=1}^2\sum _{j=1}^h\sum _{M=1}^{N_M}{\tau }_{\mathit{ijM}}({\mathrm{\Psi }}^{(l)})\{log{\pi }_i^{(l)}+log{g}_{ij}({\overline{\mathit{\theta }}}_{ij}^{(l)},{\sigma }^{{(l)}^2})\}+log{g}_{{\mathit{\theta }}_j}({\mathit{\theta }}_j^M\mid {\mathit{\theta }}^l,{\mathrm{\sum }}^l).\end{array}$$

• Step 4a (M-step): Using Q(Ψ^(l)), the M-step consists of estimating σ²,

  $${\sigma }^{{(l+1)}^2}=\frac{{\sum }_{i=1}^2{\sum }_{j=1}^h{\sum }_{M=1}^{N_M}{\tau }_{\mathit{ijM}}({\mathrm{\Psi }}^{(l)}){\sum }_{k=1}^{n_j}{\{y_{jk}-m_i({\overline{\mathit{\theta }}}_{ij}^{(l)})\}}^2}{{\sum }_i^2{\sum }_j^h{n}_j{\sum }_{M=1}^{N_M}{\tau }_{\mathit{ijM}}({\mathrm{\Psi }}^{(l)})},$$

  and estimating (θ, Σ) which are solutions of the following equations:

  $$\begin{array}{l}\frac{1}{N_M}\sum _{i=1}^2\sum _{j=1}^h\sum _{M=1}^{N_M}\frac{\partial log{g}_{{\mathit{\theta }}_j}({\mathit{\theta }}_j^M\mid \mathit{\theta },\mathrm{\sum })}{\partial \mathit{\theta }}=\mathbf{0},\\ \frac{1}{N_M}\sum _{i=1}^2\sum _{j=1}^h\sum _{M=1}^{N_M}\frac{\partial log{g}_{{\mathit{\theta }}_j}({\mathit{\theta }}_j^M\mid \mathit{\theta },\mathrm{\sum })}{\partial \mathbf{\sum }}=\mathbf{0}.\end{array}$$

  Hence, θ^l+1 and Σ^l+1 are the sample mean and the variance and covariance matrix of posterior samples, respectively.

• Step 5a: Repeat Steps 1a–4a until (π₁, σ², θ, Σ) converge.

Initial values of π₁ and σ² were chosen as 0.5 and the NLS estimator, respectively. The initial values of θ and Σ were chosen using the estimators of a STS.

5. Simulation study

We performed a simulation study to compare the following two methods:

• EMGTS: a method based on the mixture of EM and GTS;

• EMMCEM: a method based on the mixture of EM and MCEM.

For our gastric emptying data, 21 individuals were simulated with 50 observations points per individual at (1500) min with 10 increments. The individuals θ_j = (θ_1j, θ_2j) were generated from multivariate normal distributions with mean (100, 2, 1.5, 0.5)^T and covariance matrix Σ, a profile generated for individual j by adding independent normal errors with variance ${\sigma }_{\epsilon }^2$. The following five cases were simulated, with each case involving 100 simulations.

• Case 1: The mixing proportions are ${\pi }_1=\frac{14}{21}$ and ${\pi }_2=\frac{7}{21}$ and Σ has a compound-symmetric structure with a correlation coefficient of ρ = 0.1. The standard deviations are fixed as σ_t50 = σ_β = σ_γ = 1, σ_η = 0.15, and σ_ε = 0.1.

  Case 2: The same setting as Case 1, except the correlation coefficient ρ = 0.5.

  Case 3: The same setting as Case 2, except σ_ε = 1.5.

  Case 4: The same setting as Case 2, except that Σ has a AR(1) structure with corr(θ_l1, θ_l2) = 0.6^{|l₁−l₂|}.

  Case 5: The same setting as Case 2, except π₁ = 1 and π₂ = 0.

  Case 6: The same setting as Case 1, except σ_t50 = 60.

Case 1 is based on the two-component NLME with the covariance matrix of random variables having a small correlation coefficient. Case 2 is based on the same model with the covariance matrix of random variables having a relatively larger correlation coefficient than that of Case 1. These cases are chosen to investigate how accurately the two methods capture these two cases as the correlations increase. Case 3 is the same setting as Case 2 with relative large measurement error to explore how the methods performed for a data set with more noise. Case 4 is the same setting of Case 2 with a different covariance structure. It is considered in order to better understand how the two methods perform based on a different dependence structure. Case 5 is chosen to investigate the performances for the proposed estimators under the power exponential model. Case 6 is considered to make simulation data that are more similar to our example.

For each case and simulated data, individual estimates were obtained for each of our approaches. The population mean and covariance matrix of θ_j were also estimated for each method. We computed the average mean values and MSEs of the parameters. The average MSEs values for Cases 1–3 are given in Table I. In both methods, the MSEs of π₂ were less than 0.004, meaning both methods capture the mixing proportion well. Using EMGTS, the estimated values of t₅₀, β, γ, η, and ${\sigma }_{\epsilon }^2$ in Case 1 were (99.53, 1.92, 1.02, 0.76, 0.1) which were quite close to the true values (100, 2, 1.5, 0.5, 0.1). By comparing these results, the estimated η was less accurate than those of other estimated parameters. Using EMMCEM, the estimated values of t₅₀, β, γ, η, and ${\sigma }_{\epsilon }^2$ in Case 1 were (99.78, 1.99, 0.88, 0.75, 0.1) which were also close to the true values. We also note that the estimated η was less accurate than other parameters. For estimating the variance and covariance matrix, EMMCEM has a smaller MSE than EMGTS in Case 1. For Case 2, we have similar results. By comparing the performance of each method between two cases, we notice that the MSEs of both methods in Case 2 are larger than those in Case 1 which implies that both methods perform worse as correlation increases. For estimating the variance and covariance matrix, EMMCEM also has smaller MSE than EMGTS. By comparing the performance between the two methods in Cases 1 and 2, the simulation results suggest that EMMCEM performs better than EMGTS when the correlation increases. In addition, we also observe that EMMCEM is numerically more stable when η_j is small, but it requires more computation time than EMGTS. However, in Case 3 where there is more noise in the simulated data, the MSEs of both methods increase two times more than those of Case 2, indicating that both methods perform worse as noise increases. For estimating the variance and covariance matrix, like Cases 1 and 2, EMMCEM has a smaller MSE than EMGTS. On the other hand, when we consider an AR(1) covariance structure in Case 4 instead of a compound symmetric structure, the MSEs of most parameters were decreased in both methods, while the MSEs of γ, the covariances between β and γ, between β and η, and between γ and η were increased, meaning that the performance of both methods depends on the covariance structure of random effects. The average MSE values for Cases 4–5 are given in Table II. For Case 5, where the simulated data are obtained from power exponential model, the MSE value of the mixing proportion is 0.002 in both methods. This indicates that our approaches perform relatively well. For Case 6, the MSEs of most parameters are larger than those of Case 1. However, we notice that the MSEs of some parameters including τ are smaller than those of Case 1. The average MSE values for Case 6 are given in Table III.

Table I.

Average mean square error value of parameters for each method.

	True value		Case 1 EMGTS	EMMCEM	Case 2 EMGTS	EMMCEM	Case 3 EMGTS	EMMCEM
π2	0.3333	est.	0.314	0.338	0.305	0.343	0.326	0.314
		mse	0.002	0.001	0.003	0.002	0.003	0.003
t50	100	est.	99.537	99.786	100.430	100.781	102.306	102.055
		mse	2.352	2.379	4.092	3.178	6.101	5.985
σt50	1	est	2.446	2.123	1.951	1.964	2.958	2.940
		mse	3.375	3.197	2.588	2.541	5.661	5.528
β	2	est.	1.921	1.991	1.925	2.056	1.751	1.752
		mse	0.065	0.038	0.081	0.056	0.103	0.110
σβ	1	est.	0.926	0.951	0.947	0.957	0.758	0.730
		mse	0.028	0.023	0.043	0.039	0.067	0.049
γ	1.5	est.	1.022	0.882	0.932	0.808	0.804	0.864
		mse	0.591	0.454	0.454	0.511	0.619	0.618
σγ	1	est.	0.960	1.129	1.399	1.038	1.529	1.459
		mse	0.222	0.087	0.292	0.097	0.316	0.272
η	0.5	est.	0.760	0.746	0.810	0.723	0.844	0.793
		mse	0.594	0.576	0.644	0.488	0.721	0.588
ση	0.15	est.	0.346	0.327	0.325	0.308	0.353	0.336
		mse	0.042	0.033	0.034	0.028	0.056	0.049
σε	0.1/1.5	est.	0.101	0.102	0.099	0.099	1.661	1.645
		mse	0.00003	0.00002	0.00001	0.00001	0.035	0.034
cov(t50, β)	ρ	est.	0.163	0.166	−0.099	−0.106	−0.275	−0.276
		mse	0.038	0.038	0.387	0.377	0.683	0.685
cov(t50, γ)	ρ	est.	−0.303	−0.272	−0.328	−0.313	−0.408	−0.403
		mse	0.115	0.100	0.711	0.682	0.875	0.858
cov(t50, η)	0.15ρ	est.	−0.029	−0.022	−0.028	−0.028	−0.064	−0.056
		mse	0.002	0.001	0.022	0.012	0.043	0.038
cov(β, γ)	ρ	est.	−0.021	−0.018	0.0081	0.0078	0.094	0.093
		mse	0.001	0.001	0.251	0.243	0.268	0.253
cov(β, η)	0.15ρ	est.	0.007	0.007	0.008	0.008	0.004	0.004
		mse	0.0001	0.0001	0.005	0.005	0.006	0.005
cov(γ, η)	0.15ρ	est.	0.008	0.008	0.014	0.015	0.010	0.013
		mse	0.0001	0.0001	0.004	0.004	0.004	0.004

In this simulation, we generate 14 individuals following the power exponential model and seven individuals following the locally extended power exponential model, that is ${\pi }_1=\frac{14}{21}$ and ${\pi }_2=\frac{7}{21}$. The individuals θj = (t_50j, β_j, γ_j, η_j) were generated from the multivariate normal distributions with mean (100, 2, 1.5, 0.5)^T and covariance matrix Σ with a compound-symmetric structure using three cases; Case 1: ρ = 0.1 and σ_ε = 0.1, Case 2: ρ = 0.5 and σ_ε = 0.1, and Case 3: ρ = 0.5 and σ_ε = 1.5. EMGTS= a method based on the mixture of EM and GTS; EMMCEM= a method based on the mixture of EM and MCEM.

Table II.

Average mean square error value of parameters for each method.

	True value		Case 4 EMGTS	EMMCEM	Case 5 EMGTS	EMMCEM	True value
π2	0.3333	est.	0.305	0.310	0.033	0.038	0
		mse	0.003	0.003	0.002	0.002
t50	100	est.	100.079	100.286	100.029	100.043	100
		mse	1.750	1.902	0.413	0.465
σt50	1	est.	1.405	1.503	2.411	2.369	1
		mse	1.267	1.3048	3.709	3.764
β	2	est.	1.844	1.722	1.715	1.876	2
		mse	0.084	0.051	0.081	0.063
σβ	1	est.	0.831	0.893	0.732	0.807	1
		mse	0.057	0.055	0.071	0.063
γ	1.5	est.	1.814	1.782	0.231	0.219	0
		mse	0.167	0.140	0.081	0.076
σγ	1	est.	1.026	0.996	0.097	0.064	0
		mse	0.113	0.076	0.010	0.009
η	0.5	est.	0.790	0.713	0.1	0.129	0
		mse	0.616	0.474	0.019	0.018
ση	0.15	est.	0.337	0.302	0.016	0.014	0
		mse	0.036	0.023	0.008	0.008
σε	0.1	est.	0.093	0.099	0.095	0.094	0.1
		mse	0.00001	0.00001	0.00005	0.00006
cov(t50, β)	ρ	est.	0.470	0.509	0.233	0.203	ρ
		mse	0.318	0.314	0.060	0.059
cov(t50, γ)	ρ2	est.	0.339	0.348	−0.121	−0.134	0
		mse	0.218	0.218	0.067	0.060
cov(t50, η)	ρ3	est.	0.175	0.189	0.043	0.048	0
		mse	0.114	0.109	0.013	0.013
cov(β, γ)	ρ	est.	0.527	0.539	0.005	0.006	0
		mse	0.295	0.223	0.0003	0.0004
cov(β, η)	ρ2	est.	0.382	0.375	0.002	0.003	0
		mse	0.0210	0.0209	0.0004	0.0004
cov(γ, η)	ρ	est.	0.532	0.529	0.002	0.002	0
		mse	0.035	0.033	0.0003	0.0002

In this simulation, the individuals θ_j = (t_{50 j}, β_j, γ_j, η_j) were generated from the multivariate normal distributions with mean (100, 2, 1.5, 0.5)^T and covariance matrix Σ with two cases; Case 4: ${\pi }_1=\frac{14}{21},{\pi }_2=\frac{7}{21}$, σ_ε = 0.1, and AR(1) covariance matrix Σ and Case 5: π₁ = 1, π₂ = 0, σ_ε = 0.1, and a compound symmetric covariance matrix Σ with ρ = 0.5. EMGTS is a method based on the mixture of EM and GTS; EMMCEM is a method based on the mixture of EM and MCEM.

Table III.

Average mean square error value of parameters for each method.

	True value		Case 6 EMGTS	EMMCEM
π2	0.3333	est.	0.321	0.334
		mse	0.002	0.002
t50	100	est.	100.294	99.270
		mse	4.371	4.391
σt50	60	est.	67.842	68.433
		mse	128.657	137.873
β	2	est.	1.804	1.736
		mse	0.130	0.164
σβ	1	est.	0.826	0.814
		mse	0.059	0.0580
γ	1.5	est.	1.731	1.761
		mse	0.168	0.135
σγ	1	est.	0.972	0.959
		mse	0.111	0.109
η	0.5	est.	0.711	0.720
		mse	0.273	0.275
ση	0.15	est.	0.211	0.232
		mse	0.037	0.036
σε	0.1	est.	0.099	0.098
		mse	0.00006	0.00005
cov(t50, β)	ρ	est.	0.075	0.072
		mse	1.041	1.030
cov(t50, γ)	ρ	est.	−0.045	−0.047
		mse	0.040	0.0398
cov(t50, η)	0.15ρ	est.	−0.010	−0.011
		mse	0.009	0.009
cov(β, γ)	ρ	est.	0.315	0.141
		mse	0.566	0.578
cov(β, η)	0.15ρ	est.	0.151	0.153
		mse	0.025	0.023
cov(γ, η)	0.15ρ	est.	0.121	0.130
		mse	0.026	0.032

In this simulation, the individuals θ_j = (t_50j, β_j, γ_j, η_j) were generated from the multivariate normal distributions with mean (100, 2, 1.5, 0.5)^T and covariance matrix Σ; Case 6: ${\pi }_1=\frac{14}{21},{\pi }_2=\frac{7}{21}$, σ_t50 = 60, σ_ε = 0.1, and a compound symmetric covariance matrix Σ with ρ = 0.1. EMGTS is a method based on the mixture of EM and GTS; EMMCEM is a method based on the mixture of EM and MCEM.

Overall our simulation studies, the MSEs of τ are relative large compared with other parameters. The MSEs of τ are large in Cases 1–3 and Case 5 and their values are similar in each case. But, the MSEs of τ in Cases 4 and 6 are smaller than those of the other cases. This is because the estimation of τ is sensitive to the expectation of B^*(t_ij), where B(t_jk) = τ_j B^*(t_jk) and B^*(t_jk) = − exp(−1/η_j)+ (t_jk/t_50j). In Case 1, where σ_t50 is small, B^*(t_jk; t_50j, γ_j, η_j) is more likely to be zero. The average expected value of B^*(t_jk) is 0.05. In this case, τ does not play an important role. The estimated value is different from true value. Thus, the bias of γ is large so that the MSEs are large. On the contrary, when σ_t50 is large such as Case 6, B^*(t_jk; t_50j, γ_j, η_j) is more likely not to be zero. The average expected value is 0.12. The estimated value of τ is close to the true value so that the bias is not large. Hence, the MSEs of Case 6 are smaller than those of Case 1. In Case 4, the average expected value of B^*(t_jk) is 0.11, whereas it is 0.05 in Case 2. The MSEs of τ are affected by both correlation between t₅₀ and τ and correlation between t₅₀ and γ. This result is based on simulation result but it is not proved theoretically.

6. Example of a gastric emptying study in equine medicine

For the purposes of illustrating the relative performance of the models, Elashoff et al. [15] defined the following formulae ‘ $R_{NL}^2$’ to determine whether or not a nonlinear curve provides a good fit to the data:

$$R_{NL}^2=1-\frac{\text{Residual}\text{sum}\text{of}\text{squares}}{\text{Total}\text{sum}\text{of}\text{squares}},$$

where the total sum of squares is n − 1 times the square of the standard deviation of the observed fractions. $R_{NL}^2$ can be less than 0 when the data are better fit by a horizontal line than they can be by the estimated nonlinear curves.

The motivating example for our study, which was described in Section 1, is from equine medicine. We first normalize y_jk as $y_{jk}^{\ast }=y_{jk}/A_{0j}$ and then fit the model using a NLS. For each horse and model, the $R_{NL}^2$ value was obtained. For the 14 horses (those that received the test meal without atropine treatment), the means of the $R_{NL}^2$ values for the power exponential model and the locally extended power exponential model were 0.95 and 0.97, respectively. For the seven horses that received the test meal along with atropine-induced prolongation of gastric emptying, the means of the $R_{NL}^2$ values for the power exponential model and the locally extended power exponential model were 0.94 and 0.98, respectively. In particular, the locally extended power exponential model outperformed the power exponential model in both horse 1936 and 1944. For horse 1936, $R_{NL}^2$ of the power exponential model and the locally extended power exponential model were 0.89 and 0.98, respectively; for horse 1944, the $R_{NL}^2$ of the two models were 0.86 and 0.97, respectively. We then fitted the two-component NLME model and noticed that the mean of the complete conditional distribution [θ_j |data, π₁, σ², θ, Σ] obtained from EMMCEM is similar to the estimated value of EMGTS. The two approaches based on EMGTS and EMMCEM took about 15 and 60 min to run, using a Mac Pro with two 3.0 GHz Quad-Core Intel Xeon processors, and 10 GB of memory. Our code is written in Matlab and is available upon request.

We found evidence that the estimates of parameter, t₅₀, between the two treatment groups (one with 14 untreated horses and the other with seven atropine-treated horses) were significantly different using conditional t-test which is conditional on the estimates of the random effects variance–covariance parameters (p–value= 0.0001). The estimates of β between the two treatments were also significantly different (p–value= 0.0001) using conditional t-test. However, the γ and η were not significantly different with p-values 0.304 and 0.767, respectively. The 95 per cent approximate confidence interval for the difference in parameter t₅₀, β, γ, and η between the treatments are [79.24, 207.08], [0.21,1.81], [−1.37, 4.39], and [−0.012, 0.004], respectively. These approximate confidence intervals on the variance–covariance components and the fixed effects are obtained using the approximate distributions for the maximum likelihood estimates.

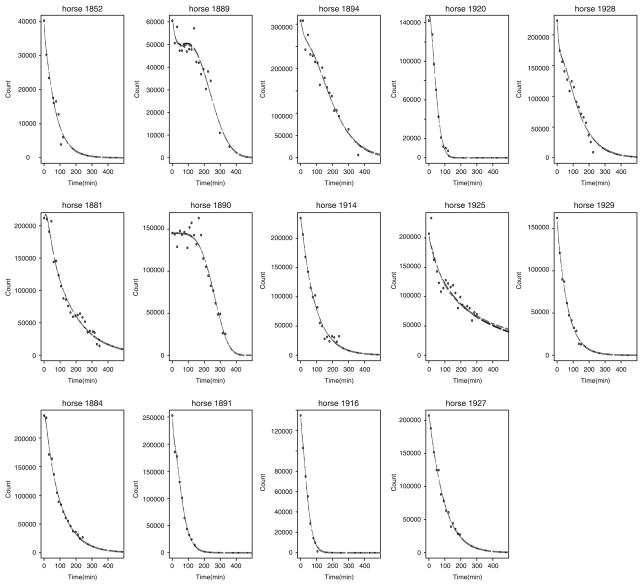
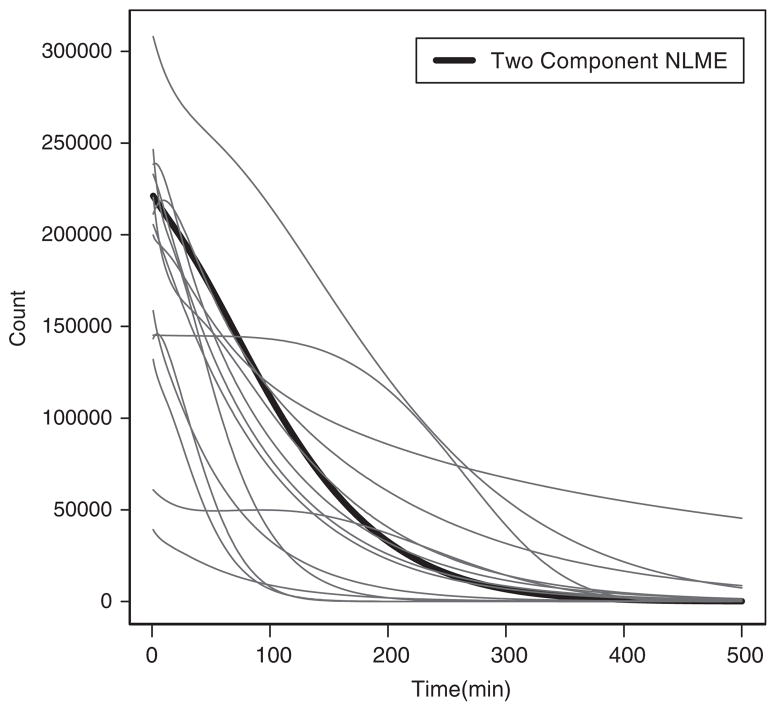
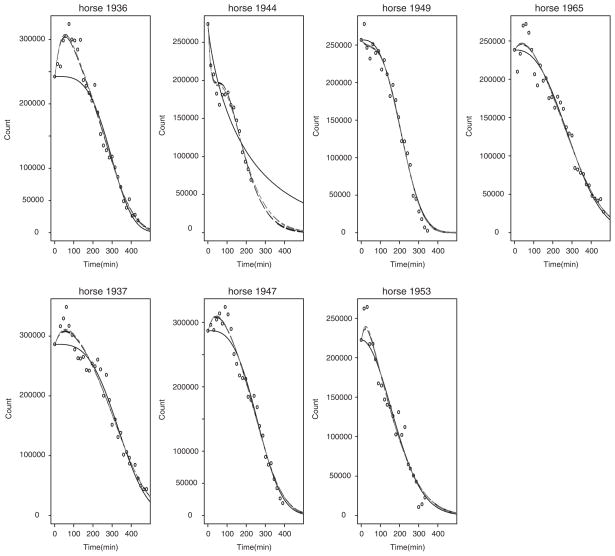
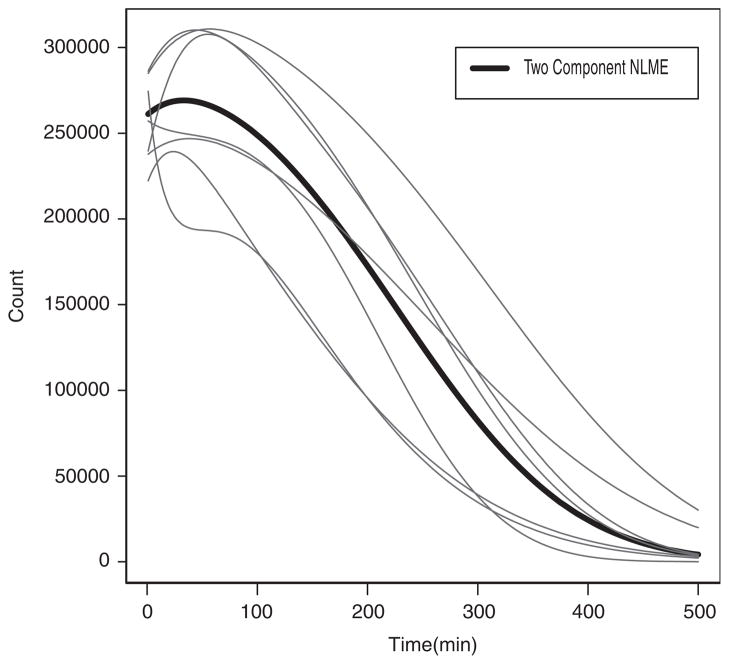
The estimated and individual and population parameters are summarized in Tables IV and V, respectively. The fitted individual curve and the population curve for the 14 untreated horses are plotted in Figures 1 and 2, respectively. The fitted individual curve and population curve for the seven atropine-treated horses are plotted in Figures 3 and 4, respectively. From Figures 1 and 3, we note that the fitted individual curves from EMGTS and EMMCEM are very close to each other. The proportions following either the power exponential model or the locally extended power exponential model were estimated. For the 14 untreated horses that received the test meal, the 6 out of 14 horses (43 per cent) were estimated to follow a power exponential model and 8 out of them (57 per cent) were deemed to follow a locally extended power exponential model. The estimated means of γ and η are −0.54 and 0.204, which correspond to the local rapid decay occurs at time 0.20t₅₀ and the amount of local rapid decay is 0.54. For the seven atropine-treated horses, only two horses (1949 and 1965) out of them (29 per cent) followed the power exponential model, whereas the other five horses (71 per cent) followed the locally extended power exponential model, respectively. The estimated means of γ and η are 0.78 and 0.198, which implied that the local upward bump was maximized at time 0.198t₅₀ and the amount of bump is 0.78. We also note that the 95 per cent confidence interval for σ_γ is [1.43, 4.06] using the data from the 14 untreated horses and is [1.84, 5.82] using the data from the seven atropine-treated horses, respectively. The lower bound of latter interval is 1.3 times larger and its range is 1.5 times wider than the first interval. These results show that our model captures the local bumping (Figures 1 and 3 for horses 1889, 1936, 1937, 1944, 1947) as well as the rapid decays (Figures 1 and 3 for horses 1881, 1894, 1884, 1916, 1944, 1920). Therefore, our model can give more accurate representation and summary of the curves of gastric emptying data, thereby allowing more accurate comparison between emptying patterns for the two different treatment groups.

Table IV.

The estimated individual parameters in the two-component nonlinear mixed effects model.

Treatment (i)	Horse id	j	t50j	βj	γj	ηj	πi	Subpop
1	1852	1	45.850	0.995	−1.241	0.249		1
	1881	2	112.646	1.023	2.606	0.259		2
	1884	3	70.926	1.021	1.401	0.099		2
	1889	4	229.182	2.748	−4.155	0.220		2
	1890	5	260.501	4.188	−0.061	0.481		1
	1891	6	47.263	1.346	−2.473	0.099		2
	1894	7	164.463	1.515	−1.922	0.280	0.429	2
	1914	8	63.415	1.008	0.371	0.120		1
	1916	9	35.119	1.399	−1.328	0.190		2
	1920	10	44.308	1.742	1.045	0.099		2
	1925	11	135.465	0.594	0.336	0.100		1
	1927	12	68.023	1.070	0.007	0.200		1
	1928	13	91.471	1.163	−3.453	0.249		2
	1929	14	43.055	0.984	−0.745	0.240		1
2	1936	1	288.673	3.188	5.215	0.270		2
	1937	2	330.415	2.833	1.894	0.101		2
	1944	3	153.152	1.645	−6.019	0.161		2
	1947	4	258.805	2.789	1.785	0.239	0.714	2
	1949	5	212.499	2.933	−0.552	0.359		1
	1953	6	179.184	1.774	2.126	0.099		2
	1965	7	288.372	2.315	0.977	0.159		1

The estimates were obtained by EMMCEM. The 14 horses received the test meal without atropine (treatment = 1) and seven horses received the test meal along with atropine (treatment = 2); ‘Subpop = 1’ means that horse has the mean function of power exponential model and ‘Subpop = 2’ means that the horse has the mean function of locally extended power exponential model.

Table V.

The estimated population parameters and 95 per cent confidence intervals of them in the two component nonlinear mixed effects model.

Treatment	Parameter	95 Per cent lower bound	est.	95 Per cent upper bound
1	σ	0.076	0.085	0.094
	t50	64.027	100.835	137.642
	β	0.996	1.485	1.975
	γ	−2.105	−0.544	1.018
	η	0.154	0.204	0.267
	σt50	48.090	69.649	100.872
	σβ	0.606	0.911	1.368
	σγ	1.432	2.412	4.062
	ση	0.058	0.102	0.152
	cov(t50, β)	0.407	0.751	0.909
	cov(t50, γ)	−0.642	−0.146	0.435
	cov(t50, η)	0.140	0.594	0.892
	cov(β, γ)	−0.688	−0.268	0.287
	cov(β, η)	−0.091	0.521	0.912
	cov(γ, ρ)	−0.668	−0.215	0.148
2	σ	0.054	0.061	0.068
	t50	199.452	244.443	289.44
	β	2.033	2.497	2.961
	γ	−1.722	0.775	3.272
	η	0.141	0.198	0.272
	σt50	35.519	60.099	101.690
	σβ	0.322	0.585	1.062
	σγ	1.836	3.269	5.823
	ση	0.048	0.087	0.121
	cov(t50, β)	0.012	0.687	0.932
	cov(t50, γ)	−0.014	0.643	0.912
	cov(t50, η)	−0.973	−0.028	0.614
	cov(β, γ)	−0.221	0.569	0.908
	cov(β, η)	−0.064	0.596	0.942
	cov(γ, η)	−0.910	0.041	0.838

The estimates were obtained by EMMCEM using the 14 horses which received the test meal without atropine (treatment = 1) and seven horses which received the test meal along with atropine (treatment = 2).

Figure 1.

The estimated individual curves obtained from fitting the two-component nonlinear mixed effects model using 14 horses that received the test meal without atropine: the solid line curve of power exponential random effects model using GTS (black), the dashed-dotted line curves of mixture model using EMGTS (gray), and the dashed line curves of mixture model using EMMCEM (black).

Figure 2.

The estimated population curve (solid thick line) and individual curves (thin lines) of the two-component nonlinear mixed effects model (two-component NLME) which is obtained from EMMCEM using 14 horses that received the test meal without atropine.

Figure 3.

The estimated individual curves obtained from fitting the two-component nonlinear mixed effects model using seven horses that received the test meal with atropine: the solid line curve of power exponential random effects model using GTS (black), the dashed-dotted line curves of mixture model using EMGTS (gray), and the dashed line curves of mixture model using EMMCEM (black).

Figure 4.

The estimated population curve (solid thick line) and individual curves (thin lines) of the two-component nonlinear mixed effects model (two-component NLME) which is obtained from EMMCEM using seven horses that received the test meal with atropine.

7. Discussion

In this article, we have proposed a two-component NLME to describe a more accurate representation and summary of the curves of gastric emptying patterns between treatments or groups of subjects that will facilitate comparisons of results within and among individual studies. Our proposed model is developed by the mixture of two nonlinear mixed effects models: one component is based on the power exponential model which captures the globally decreasing pattern, and the other is based on the locally extended power exponential model, which captures local bump or rapid decay. Therefore, our model can capture both a globally decreasing pattern and a local nondecreasing pattern simultaneously. In addition, this model captures the variation from measurements within each individuals and the variation across individuals. We can also adequately fit data from heterogeneous sub-populations so that we are able to estimate and compare the proportion of individuals from different sub-populations. When the data are homogeneous, we can use a locally extended power exponential model to understand gastric emptying behavior.

We have developed two methods in order to fit the two-component NLME. One is the mixture of EM and GTS and the other is the mixture of EM and MCEM. We compared the two approaches using simulation studies. The results of these simulations suggest that the two approaches are comparable to each other. For estimating the variance and covariance matrix, the second approach appears approximately more efficient and is numerically more stable in some cases. However, it requires more computation time than the first approach.

In Debrecebi et al. [5], four values of gastric emptying curves were taken into consideration: maximum value of the curve, time belonging to this maximum, slope of the rising part of the curve which was maximum value divided by time belonging to it, and the time associated with 50 per cent of the area under the curve. Our model can be useful to scientists to model data from disciplines such as pharmacokinetics and toxicokinetics. In our example from equine medicine, the two-component NLME provided a good fit to the data points observed from individual subjects of heterogeneous sub-populations. The parameters from this model have clear graphical interpretations. Thus, our model provides a more accurate representation and summary of curves of scintigraphic gastric emptying data than the standard approach.

We note that, for our example, we additionally fit a one component random effects model using a locally extended power exponential model and compare the fitted curves with those using the two-components mixture model. The fitted curves are very similar to each other although the estimated parameter values are somewhat different. This is because a locally extended power exponential model is a more general model than a power exponential model. This implies that if we do not consider the two-component mixture model, we can always only consider a locally exponential model. Part of the contribution of this article is to propose a locally exponential model. During the exploratory stage, the mixture modeling strategy provides an easy and systematic way to understand whether the additional component in a locally exponential model is needed for a particular horse or the traditional power exponential model is sufficient. A sub-population that has more Z_1j = 0 implies a higher level of heterogeneity within that sub-population. This is a piece of helpful information even though the exact proportion may not be of interest.

We point out that the estimation of τ is sensitive to the expectation of B^*(t_ij) as we have described in Section 5. If the expectation of B^*(t_ij) is close to zero, γ does not play an important role in the model. In our simulation, we observed that this expectation value is closer to zero when the variance of t₅₀ is large and it is also closer to zero when the variance–covariance of the random effect has an AR(1) structure than compound symmetry structure. This is based on simulation results, not theoretical justification. Developing theoretical property of τ will help us to understand the model better. We will do this in the future work.

We note that the A_0j, which is the amount of meal, drug, or other substance remaining in the stomach at time 0, is defined as the amount fed at time 0. We treat this as a fixed constant number. However, it is an interesting idea to treat A_0j as a parameter considering measurement errors. Since the measurement error model [28] has been well applied in many epidemiological studies, developing our approach to allow measurement error model will be worthwhile future research.

Our approaches are based on frequentist methods for fitting the two-component NLME. A fully Bayesian approach can be also used to fit the model. We assume that the distribution of the random coefficients have a multivariate normal distribution. We note that, as stated in Section 3.3.2 of [29], even though we make the normal random effect assumption in the GTS and related EM algorithm, because they are convenient tools to model the first and second moments of random effects, the normal random effect assumption is not essential here. When the number of subjects and within-subject sample sizes is sufficiently large, it may be worthwhile to consider a nonparametric prior such as the Dirichlet process [30, 31] as an effort to precisely model the distribution of the random effects. For the errors within each subject, we checked the residual plots which are not displayed in the paper but are available upon request. We would like to point out that, for most of the horses, the points are roughly scattered around zero in a random fashion without special patterns. There are some exceptions, such as horse 1937 and 1965, which show a certain level of heteroscedasticity. We have not pursued further in relaxing the constant variance assumption. This and the direction of considering the semiparametric Bayesian approach [30–34] could be future research topics for the data sets with larger sample sizes.

Appendix A: Proof of Theorem 1

For ease of notation, we write B(t) instead of B(t_jk). Since B(t) is analytic, it has a Taylor expansion in a neighborhood of t = 0. That is, B(t) = C +γt + γ₂t² +· · · + γ_n tⁿ + · · · for γ ≠ 0. Since we know that {t exp(−t)} ≈ t as t → 0, B(t) = C + γ{t exp(−t)} + γ₂{t exp(−t)}² + … + γ_n {t exp(−t)}ⁿ +· · · = C +γt exp(−t)+o(t) as t → 0. When t → ∞, B(t) = o(t^β) = C +γt exp(−t)+o(t^−β) as t → ∞ because γt exp(−t)+o(t^−β). We note that for any a>0 and b>0, {t^a exp(−bt)} = {t exp(−t)}+o(t^β) as t → ∞. We remark that if B(t) = C + γϕ (t)+ γ₂ϕ(t)+· · · + γ_nϕ(t)ⁿ +· · · for any function ϕ(t) such that ϕ(t) ≈ t as t → 0 and ϕ(t) ≈ 0 in order of o(t^β) as t → ∞, then ϕ(t) ≈ t exp(−t) in order of o(t) as t → 0 of o(t^β) as t → ∞.