A Spatial Poisson Hurdle Model for Exploring Geographic Variation in Emergency Department Visits

Summary

We develop a spatial Poisson hurdle model to explore geographic variation in emergency department (ED) visits while accounting for zero inflation. The model consists of two components: a Bernoulli component that models the probability of any ED use (i.e., at least one ED visit per year), and a truncated Poisson component that models the number of ED visits given use. Together, these components address both the abundance of zeros and the right-skewed nature of the nonzero counts. The model has a hierarchical structure that incorporates patient- and area-level covariates, as well as spatially correlated random effects for each areal unit. Because regions with high rates of ED use are likely to have high expected counts among users, we model the spatial random effects via a bivariate conditionally autoregressive (CAR) prior, which introduces dependence between the components and provides spatial smoothing and sharing of information across neighboring regions. Using a simulation study, we show that modeling the between-component correlation reduces bias in parameter estimates. We adopt a Bayesian estimation approach, and the model can be fit using standard Bayesian software. We apply the model to a study of patient and neighborhood factors influencing emergency department use in Durham County, North Carolina.

1. Introduction

Visits to hospital emergency departments (EDs) have been rising steadily in the U.S. for the past two decades. Between 1997 and 2007, ED visits increased 23%, to about 125 million visits annually (Owens and Mutter, 2010). Many of these visits could be treated in non-ED settings. For example, Weinick et al. (2010) found that up to 27% of ED visits could be handled at a retail or urgent care clinic, saving approximately $4.4 billion in health care costs annually. This continued use of EDs for routine care not only increases health costs, it impedes access to services and reduces patients’ satisfaction with care (Jayaprakash et al., 2009).

There are a number of potential reasons for the rise in ED use. Demographic changes, such as the aging U.S. population, have increased demand for EDs (Weber et al., 2008). Rising numbers of uninsured patients, who lack access to alternative sources of care, may also be a contributing factor (U.S. Government Accountability Office, 2003). Moreover, because ED use is most common among Medicare and Medicaid participants, burgeoning enrollment in federally subsidized health care programs may also contribute to increased ED use (McCaig and Burt, 2005). Finally, growing demand for medical care has placed excess burden on clinical practices, making appointments difficult to obtain (Trude, 2002; Cunningham, 2006). As a result, EDs may have become more attractive due to their convenience and accessibility without an appointment (Guttman et al., 2003; Cunningham, 2006).

As with other health services, there is considerable community-level variation in ED use. Availability of outpatient clinics often varies at a local level, and communities also differ greatly with respect to population characteristics associated with ED use, including median household income and percent uninsured (Cunningham, 2006). ED rates can also vary substantially within a small geographic region. Everage et al. (2010) found that ED visits for asthma in Rhode Island were affected by neighborhood factors such as air quality and poor housing conditions. Li et al. (2003) found that lower home ownership rates were associated with increased ED use. More recently, Dulin et al. (2009) used a geographic information systems (GIS) analysis to show that Hispanic neighborhoods in Charlotte, North Carolina, differed with respect to their primary and urgent-care needs. These results have prompted health officials and policymakers to seek targeted interventions to identify and address community-level disparities in ED use.

With these goals in mind, investigators at Duke University in Durham, North Carolina, recently reviewed hospital admission records from the Duke Decision Support Repository (DSR), a data warehouse containing demographic, diagnostic and treatment information on over 3.6 million patients seen at Duke University Health System hospitals and clinics. The review was restricted to Durham County residents seen at either a Duke-affiliated ED or non-ED clinic during the 2009 calendar year. As part of the study, the investigators sought to identify spatial patterns in ED use within Durham County and to examine patient- and neighborhood-level factors influencing such usage.

From a statistical standpoint, several important features of the DSR data must be considered. First, the data are potentially zero inflated: nearly 70% of the DSR patients made no ED visits in 2009, while others made regular visits due to lack of insurance or other resource limitations. Second, because the probability of ED use is likely correlated with the expected number of ED visits among users, a suitable model should account for this correlation. This is especially important in zero-inflated models, as failing to account this dependence may produce biased parameter estimates (Su et al., 2009). Third, because the data are clustered by neighborhood, within-cluster correlation should be addressed. And finally, because adjacent regions are likely to have similar ED counts, the model should provide spatial smoothing and borrowing of information across neighboring areas.

In this paper, we present a spatial Poisson hurdle model to address these aspects of the data. The model consists of two components: a Bernoulli component that models the probability of any ED use (i.e., at least one ED visit annually) and a truncated Poisson component that models the number of repeat visits among users. Together, these components accommodate both the high proportion of zeros and the right-skewness of the nonzero counts. For each component, we include patient- and area-level covariates, as well as spatially dependent random effects which account for correlation between neighboring areas. The spatial effects are modeled via a bivariate conditionally autoregressive (CAR) prior, which induces dependence between the model components.

Our approach builds on recent work on spatial models for zero-inflated data. Agarwal et al. (2002) proposed a spatial zero-inflated Poisson (ZIP) model that incorporated spatial effects into the Poisson component. Rathbun and Fei (2006) developed a similar model in which the “structural” (i.e., extra-Poisson) zeros were modeled via a spatial probit model. Ver Hoef and Jansen (2007) introduced spatio-temporal ZIP and hurdle models that included distinct spatial random effects for the model components. Gschlößl and Gzado (2008) developed a spatial generalized-Poisson model to study the incidence of meningococcal disease. However, these models assume independent random effects for the two components, which may lead to biased inferences. To address this potential drawback, Recta et al. (2011) recently proposed a correlated spatial hurdle Poisson model for point-referenced (e.g., latitude-longitude) zero-inflated data.

The model described here can be regarded as an areal-data counterpart to the model proposed by Recta et al. (2011) for point-referenced data. In our case, the spatial units are aggregated regions of space—specifically, groups of residential blocks—rather than point-specific locations defined by a set of x–y coordinates. In this setting, area-level spatial models are needed to account for the potential association between bordering regions. To accommodate this association, we introduce a set of random effects linked by a bivariate CAR prior that induces correlation between the Bernoulli and Poisson components of the hurdle model and allows spatial units to “borrow information” from their neighbors, thereby improving inferences. Through a simulation study, we show that addressing these sources of correlation can improve inferences on model parameters. We adopt a Bayesian estimation approach, and the models can be easily fit in standard Bayesian software such as WinBUGS (Spiegelhalter et al., 2007).

The remainder of the paper is organized as follows: Section 2 describes the DSR data; Section 3 outlines the proposed model; Section 4 discusses posterior computation and model assessment; Section 5 details the simulation study; Section 6 applies the model to the DSR data; and Section 7 provides a discussion and outlines directions for future research.

2. The DSR Data

The Duke University Decision Support Repository (DSR) has been in existence for over a decade. Originally built as an administrative and financial database, the DSR holds 14 years of demographic, diagnostic and procedure data on over 3.8 million patients seen at Duke Medical Hospital, Durham Regional Hospital, and over 100 outpatient clinics in the Duke University Health System. The data have been deployed for secondary use in numerous research studies and quality improvement initiatives (Horvath et al., 2011).

As part of a ongoing study exploring contributors to ED use, university investigators recently reviewed hospital admission records for non-Hispanic white, non-Hispanic black, and Hispanic residents of Durham County who were seen at either an ED or non-ED clinic during the 2009 calendar year. The DSR data were geo-referenced by residential address and subsequently linked at the Census block group level to data from the 2005–2009 American Community Survey (U.S. Census Bureau, 2010). The final dataset contained over 137,000 records from the 129 Census block groups in Durham County, and included information on the annual number of ED visits for each patient, patient-level demographics (age, race, gender and insurance status), and selected block group characteristics (percent of residents below the federal poverty level and percent of housing units currently occupied by residents).

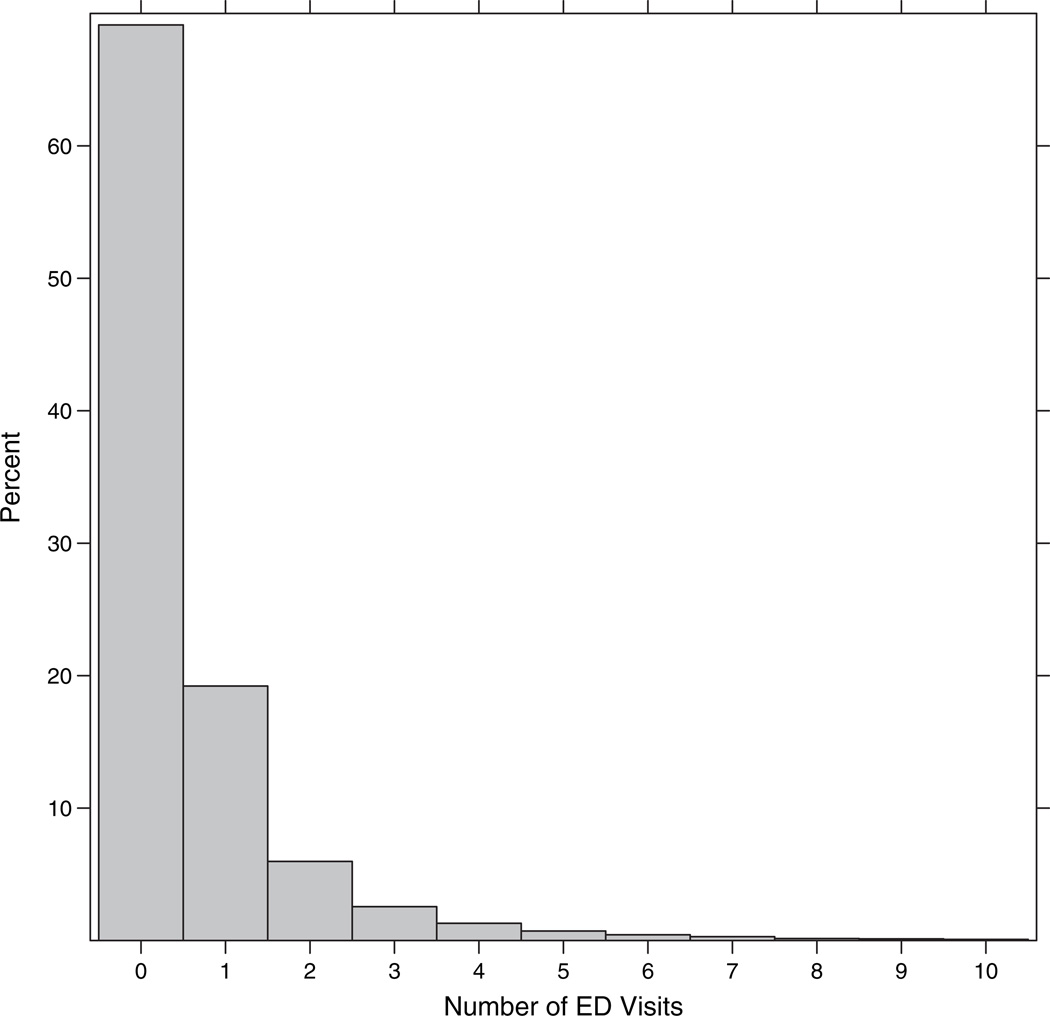
Figure 1 presents a partial histogram of the number of ED visits in 2009. Nearly 70% of the patients made no ED visits in 2009; among those who did use the ED, the number of visits ranged from 1 to 95, with 95% of the patients having fewer than six visits annually. The high proportion of zeros coupled with the right-skewed nonzero counts suggests potential zero inflation relative to the ordinary Poisson. As a simple illustration, suppose that the data were generated under an independent and identically distributed (i.i.d.) Poisson model with mean parameter μ = 0.65, the average number of ED visits among DSR patients (and hence the MLE of μ). Under this basic model, we would expect 52% zeros and 34% 1’s—far fewer zeros and more 1’s than actually observed. In the presence of such zero inflation, special distributions are needed to provide adequate fit to the data, as we describe in the following section.

Fig. 1.

Partial histogram of ED visits (up to 10 visits).

Table 1 provides summary statistics on patient and block group characteristics. Most patients were female, of non-Hispanic white or non-Hispanic black race, with a median age of 36 years. About 60% had private medical insurance as opposed to federal or self-paid insurance. Most of the 129 block groups in Durham County had low poverty levels and high rates of occupied housing: the median percent below poverty was 13.42 (range = 0 to 91.73%), which is nearly identical to the national average of 13.5%; the median percent occupancy was 91.15 (range = 30.49 to 100%), which is just above the national average of 88.2% (U.S. Census Bureau, 2010). The median block group size was 882 (range = 64 to 3604).

Table 1.

Summary statistics for DSR Study.

Patient Characteristics (N = 137, 504)
Variable	n	%
One or more ED visits in 2009	42,760	31
Male Gender	55764	41
Race
Non-Hispanic White	65,021	47
Non-Hispanic Black	62,371	46
Hispanic	10,112	7
Private Insurance	80,517	59
	Median	Range
Age (years)	36	(0.50, 109)
Number of ED Visits in 2009 among ED users	1	(1, 95)
Block-Group Characteristics (n = 129)
	Median	Range
Block Group Size	882	(64, 3604)
% Below Poverty	13	(0, 92)
% Occupied Housing	91	(30, 100)

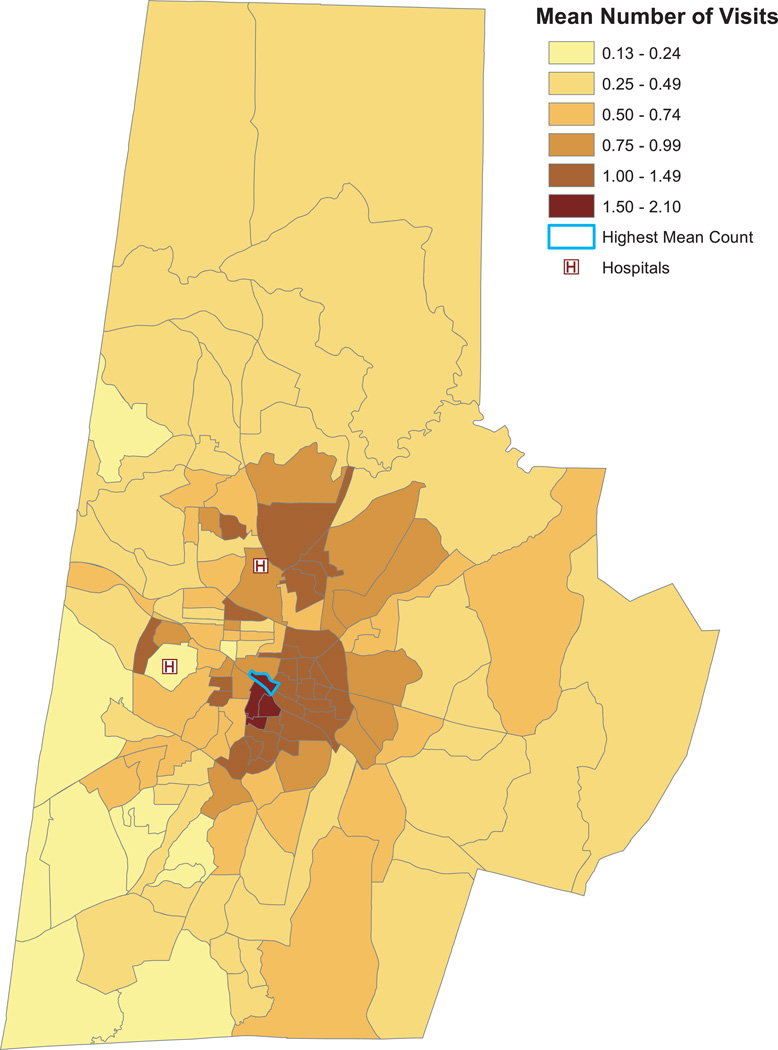
Figure 2 presents the average number of ED visits per patient for each block group in Durham County. The locations of the two EDs are denoted by “H”. The color shades correspond to sextiles of the average count distribution rounded at the second decimal place, with the pale yellow shade denoting the lowest sextile and dark red shade denoting the uppermost sextile. The average number of visits per patient ranged from 0.13 to 2.10 across the county. There is also substantial spatial clustering of the counts. Patients in the pale yellow block groups—for example, those in the southwest corner of the county—averaged between 0.13 and 0.24 visits in 2009. In contrast, patients in the darkest red regions (e.g., southeast of the two hospitals) averaged between 1.50 to just over two ED visits during the year. This south central portion of the county includes several low income, under-insured, and minority neighborhoods, all of which are associated with increased ED use (Cunningham, 2006). The block group outlined in blue has the highest mean count, with an average of 2.10 visits annually per patient.

Fig. 2.

Mean number of ED visits in 2009 by block group. The locations of Duke University Medical Center and Durham Regional Hospital are represented by \H". Color shades correspond to sextiles of the count distribution rounded to the second decimal place. The block group outlined in blue has the highest average count (2.10 visits annually per patient).

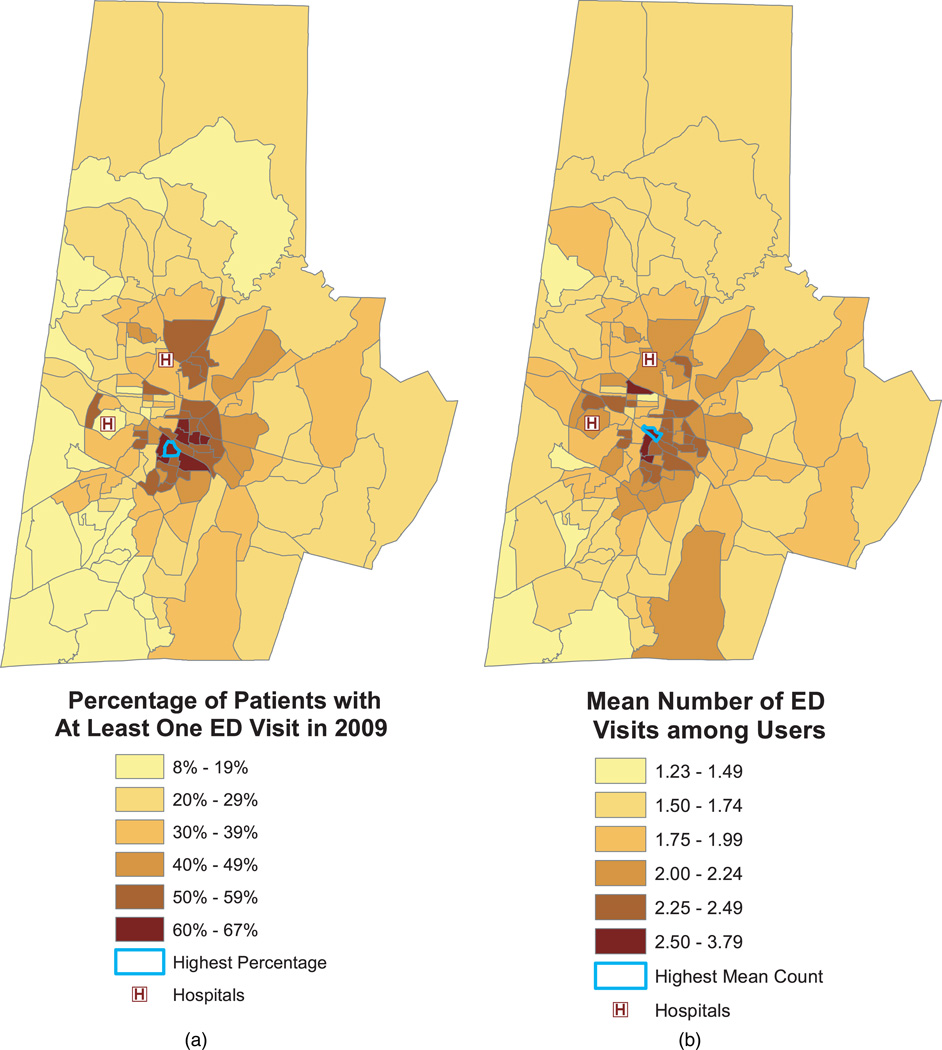
Figure 3 displays the percent of ED users (left panel) and the mean number of ED visits among such users (right panel). These figures are the sample-based counterparts to the two components of the Poisson hurdle model put forth in the following section. The outlined block groups have the highest percentage of ED users (67%, left panel) and mean count among users (3.79 annual visits per patient, right panel). Not surprisingly, percent ED use was highly correlated with the average number of visits among users (biserial correlation = 0.81). Consequently, the two maps show similar spatial patterns in which block groups with high rates of ED use tend have high mean counts among users. An exception is the block group that includes Duke University Medical Center (lower left “H”); this block group has a low percentage of users but relatively high average counts among users. However, this block group also has one of the lowest sample sizes among the 129 block groups (n = 96), which may account for this reversal in trend.

Fig. 3.

Percentage of patients with at least one ED visit in 2009 (left panel) and mean number of ED visits among those with at least one ED visit (right panel). The outlined block groups have the highest percentage of users (left panel) and mean count among users (right panel).

3. Spatial Poisson Hurdle Model

The Poisson hurdle model (Mullahy, 1986) is a two-component mixture model consisting of a point mass at zero followed by a truncated Poisson distribution for the nonzero observations. For i.i.d. responses, the hurdle model is given by

$$\begin{array}{cc}\text{Pr}(Y_i=0)\hfill & =1-p,0\le p\le 1\hfill \\ \text{Pr}(Y_i=k)\hfill & =p\frac{{\mu }^k{e}^{-\mu }}{k!(1-{\mathrm{e}}^{-\mu })},k=1,\dots ,\mathrm{\infty },0<\mu <\mathrm{\infty },\hfill \end{array}$$ (1)

where Y_i denotes the response for subject i = 1, …, n, and μ is the mean for an untruncated Poisson distribution. Alternative count distributions, such as the negative binomial or power series distribution (Ghosh et al., 2006), can also be used. Because the zeros and nonzero counts are modeled uniquely, the hurdle model can accommodate both the large proportion of zeros and a right-skewed distribution for the positive counts. By comparison, a standard Poisson regression would have to compromise between these two competing features of the data, since the large proportion of zeros would tend to lower the Poisson mean while large nonzero values would tend to increase it.

In health services research, p is known as the utilization probability—i.e., the probability of using services at least once. When (1 − p) > e^−μ, the data are zero inflated relative to an ordinary Poisson; when (1 − p) < e^−μ there is zero deflation (i.e., fewer than expected zeros). In the extremes, p = 0 or 1. When p = 1, there are no zero counts and the model reduces to a truncated Poisson, and when p = 0, there are no users (i.e., all counts equal zero), and the model is degenerate at zero. Typically, one assumes that p is strictly between 0 and 1, so that all subjects have a nonzero probability of usage and are therefore considered “potential” users even if they do not actually use services during the study period. The parameter μ measures the frequency of repeat visits; as μ increases, the average number of repeat visits among users also increases. The expected count under the Poisson hurdle model is given by E(Y) = pμ/ (1 − e^−μ).

A special case of (1) is the zero-inflated Poisson (ZIP) model (Lambert, 1992), which consists of a degenerate distribution at zero mixed with an untruncated Poisson distribution:

$$\begin{array}{cc}P(Y_i=0)\hfill & =(1-p)+p{\mathrm{e}}^{-\mu },0<p<1\hfill \\ P(Y_i=k)\hfill & =p\frac{{\mu }^k{\mathrm{e}}^{-\mu }}{k!},k=1,\dots ,\mathrm{\infty },0<\mu <\mathrm{\infty }.\hfill \end{array}$$ (2)

Note that the ZIP model can be rewritten as a hurdle model with utilization probability p(1 − e^−μ). Unlike the hurdle model, which accommodates zero deflation as well as zero inflation, the ZIP allows only for zero inflation. For recent discussions of zero-inflated count models, see Ridout et al. (1998) and Neelon et al. (2010).

The hurdle model can be extended to accommodate aggregated spatial data by introducing covariates and spatial random effects:

$$\begin{array}{cc}\hfill p(y_{\mathit{\text{ij}}}|{\varphi }_i)& =(1-p_{\mathit{\text{ij}}})1_{(y_{\mathit{\text{ij}}}=0)}+p_{\mathit{\text{ij}}}\text{Tpois}(y_{\mathit{\text{ij}}};{\mu }_{\mathit{\text{ij}}})1_{(y_{\mathit{\text{ij}}}>0)}\hfill \\ \hfill g^{-1}(p_{\mathit{\text{ij}}})& ={\mathit{x}}_{1\mathit{\text{ij}}}^{\prime }{\mathit{\beta }}_1+{\mathit{w}}_{1i}^{\prime }{\mathit{\alpha }}_1+f_1(z_{\mathit{\text{ij}}})+{\varphi }_{1i}\hfill \\ \hfill \text{log}({\mu }_{\mathit{\text{ij}}})& ={\mathit{x}}_{2\mathit{\text{ij}}}^{\prime }{\mathit{\beta }}_2+{\mathit{w}}_{2i}^{\prime }{\mathit{\alpha }}_2+f_2(z_{\mathit{\text{ij}}})+{\varphi }_{2i},j=1,\dots ,n_i;i=1,\dots ,n,\hfill \end{array}$$ (3)

where y_ij denotes the observed response for patient j in block group i; p_ij = Pr(Y_ij > 0); Tpois(y_ij ; μ_ij) denotes a truncated Poisson distribution with parameter μ_ij; g denotes a link function such as the logit or probit; x_kij is a vector of patient-level fixed-effect predictors for component k (k = 1, 2); β_k denotes the corresponding vector of patient-level, fixed-effect regression coefficients; w_ki and α_k denote block-group–level fixed-effect predictors and regression parameters for the k-th component; f₁(z_ij) and f₂(z_ij) are optional smooth functions of a continuous predictor z_ij (e.g., patient age) to be modeled via splines; and ϕ_i = (ϕ_1i, ϕ_2i)′ is a vector of spatially dependent random effects specific to the i-th block group. In what follows, we assume that the fixed effect covariates are identical for the two components (i.e., x_1ij = x_2ij = x_ij and w_1i = w_2i = w_i), but in general this is not necessary.

Intuitively, ϕ_1i is a latent variable contributing to the propensity to use ED services for patients living in block group i; likewise, ϕ_2i is a latent block group effect contributing to the expected number of visits given use. Controlling for observed covariates, larger values of ϕ_1i imply that patients living in block group i are more likely to use the ED at least once compared to patients in block groups with lower ϕ_1i values. That is, a larger ϕ_1i value implies a higher rate of ED use for block group i relative to other block groups. Similarly, larger values of ϕ_2i imply, on average, more repeat visits among ED users in the i-th block group compared to other block groups.

In a sense, these random effects account for unmeasured block group characteristics, which likely affect the propensity to use services and the mean number of repeat visits in related ways. For example, block groups with a high proportion of ED users may also have a high frequency of repeat usage. To accommodate this potential association, and to provide spatial smoothing and sharing of information across neighboring areas, we assume a bivariate intrinsic CAR (bICAR) prior distribution for ϕ_i (Mardia, 1988; Carlin and Banerjee, 2003; Gelfand and Vounatsou, 2003):

$${\varphi }_i|{\varphi }_{(-i)},\mathbf{\Sigma }~{\mathrm{N}}_2\left(\frac{1}{m_i}{\displaystyle \sum _{l\in {\partial }_i}}{\varphi }_l,\frac{1}{m_i}\mathbf{\Sigma }\right),$$ (4)

where m_i is the number of neighbors of block group i, ∂_i is the set of neighbors for block group i, and Σ is a 2×2 variance-covariance matrix. If a fixed-effect intercept is included in the model, a sum-to-zero constraint must be applied to {ϕ₁, …,ϕ_n} to ensure an identifiable model.

Prior (4) states that the conditional mean of ϕ_i is an average of the neighboring spatial effects, with covariance matrix Σ scaled by the number of neighbors for block group i. The prior incorporates information from neighbors through the conditional mean, thus allowing adjacent block groups to effectively “borrow information” from one another. This information sharing can yield more reliable random effect predictions for block groups with small sample sizes. Further, the scaled variance-covariance matrix implies that, as the number of neighbors m_i increases, the more information there is to borrow in predicting ϕ_i, and hence the more prior confidence we have that ϕ_i is (conditionally) similar to the average of its neighbors. In this way, the scaled covariance provides a degree of spatial smoothing.

The off-diagonal element of Σ, Σ₁₂, denotes the within–block-group covariance between ϕ_1i and ϕ_2i; it controls the association between the two model components. When Σ₁₂ > 0, block groups with a higher proportion of ED users tend to have higher mean counts among users. When Σ₁₂ = 0, the two components of the hurdle model are uncorrelated and governed by distinct spatial processes. In this case, the propensity to use ED services is unrelated to the mean number of repeat visits within a block group, and the model components can be estimated by fitting two separate regressions—one for the probability of any use and another for the number of visits given use. As we discuss in the following section, it is advisable to start by fitting the bICAR prior, obtain and estimate of Σ₁₂, and if there is insufficient evidence to conclude Σ₁₂ ≠ 0, one can then proceed with fitting a reduced model that assumes independent model components.

As it turns out, prior (4) gives rise to an improper joint prior distribution for $\mathbf{\Phi }=({\varphi }_1^{\prime },\dots ,{\varphi }_n^{\prime })\prime$ (Banerjee et al., 2004):

$$\mathbf{\Phi }|\mathbf{\Sigma }\propto \text{exp }\left(-\frac{1}{2}\mathbf{\Phi }\prime \left[(M-A)\otimes {\mathbf{\Sigma }}^{-1}\right]\mathbf{\Phi }\right),$$ (5)

where M = diag(m₁,m₂, …, m_n) and A is taken to be an adjacency matrix with a_ii = 0, a_ij = 1 if block groups i and j are neighbors, and a_ij = 0 otherwise. Because (M − A) is singular, the joint distribution in (5) is improper, although the posterior of Φ is itself proper. To ensure a proper prior, one can introduce a spatial smoothing parameter, s < |1|, that multiplies the adjacency matrix A (Cressie, 1993). However, as Banerjee et al. (2004) note, this entails somewhat counter-intuitively that the conditional mean of ϕ_i in (4) is a proportion of the average neighboring effects. Moreover, in practice, the posterior mode of s tends to be close to 1, essentially resulting in a bICAR model. We therefore restrict our attention to the intrinsic bivariate CAR throughout and consider extensions to proper CAR models in the Discussion section.

Note that the bICAR prior accommodates two potential sources of correlation in the data. The first is the within–block-group correlation between ED use and the intensity of repeat use. As noted above, this correlation is controlled by Σ₁₂: when Σ₁₂ > 0, block groups with a higher proportion of ED users tend to have more repeat visits among users. This within–block-group correlation can also be accommodated via non-spatial, bivariate normal random effects, since it arises simply from the bivariate nature of the prior and not from the additional spatial structure imposed by the CAR distribution.

The second source of correlation is the between–block-group association induced by the CAR prior. The CAR prior implies that adjacent block groups are more strongly correlated than block groups situated farther apart in space. Thus, the CAR prior behaves somewhat like a two-dimensional version of an AR(1) prior for temporally correlated data. In the temporal setting, measurements occurring close in time are highly correlated, and this association decays as observations move farther apart in time. Likewise, for the CAR prior, adjacent block groups have more influence on one another than do block groups separated farther apart in space.

These two sources of correlation make intuitive sense in our application: it is reasonable to assume, a priori, that ED use and intensity of repeat use are correlated within block groups and that block groups in close proximity to one another behave in similar ways with respect to their ED counts. Indeed, the former feature was depicted in Figure 3, which showed similar spatial patterns for ED use (Figure 3[a]) and the frequency of visits given use (Figure 3[b]), and the latter feature was evidenced in Figure 2, which showed substantial spatial clustering of the ED counts.

4. Bayesian Estimation, Posterior Computation and Model Assessment

We adopt a fully Bayesian approach for model estimation. This approach offers several potential advantages over classical (e.g., maximum likelihood) estimation procedures. First, Bayesian inference allows one to express uncertainty about model parameters through prior distributions. These prior distributions are then combined with the current data via Bayes’ Theorem to obtain updated posterior distributions. In this way, Bayesian methodology provides a natural scheme for learning from prior experience. Second, by incorporating recent developments in Markov chain Monte Carlo (MCMC) methods (Gelfand and Smith, 1990), including Gibbs sampling, Bayesian models provide a flexible way to handle complex nonlinear regressions such as ours. At convergence, the MCMC draws form a Monte Carlo sample from the joint posterior distribution of the model parameters, which can then be used to obtain parameter estimates and corresponding uncertainty intervals, thus avoiding the need for asymptotic assumptions when assessing the sampling variability of parameter estimates. Finally, because we obtain draws from the entire joint posterior distribution of the model parameters, estimation of complex parameter functions is straightforward. For example, the Bayesian framework is ideal for estimating and obtaining uncertainty intervals for functions such as the expected count in model (1), given by E(Y) = pμ/ (1 − e^−μ). In a frequentist setting, one would have to perform bootstrapping or perhaps derive a delta-method approximation to obtain standard errors and confidence intervals for such quantities.

To complete the model specification, we assign weakly informative proper priors for the remaining model parameters. For β₁, β₂, α₁, and α₂, we assume exchangeable normal priors. For the spatial covariance matrix, Σ, we assume an inverse-Wishart prior with 2 or more degrees of freedom. As an alternative to the inverse-Wishart prior, one can rewrite ϕ_i as a linear combination of independent univariate CARs (Gelfand et al., 2004); however, given the low dimension of Σ in our case, the inverse-Wishart prior is easily accommodated.

Posterior computation proceeds via Gibbs sampling, which draws iteratively from the full conditional distributions of the model parameters. For the most part, the full conditionals for the spatial Poisson hurdle model do not have convenient closed forms; however, we can take advantage of the sampling routines in WinBUGS to implement the algorithm. Although WinBUGS has no pre-designated truncated Poisson distribution, which is needed to specify the hurdle model likelihood, one can use the “zeros trick” in WinBUGS to explicitly define the hurdle likelihood. For details on the use of the zeros trick, see “Tricks: Advanced Use of the Bugs Language” in the WinBUGS User Manual (Spiegelhalter et al., 2007). The bICAR prior can be specified in WinBUGS version 1.4.3 via the mv.car function.

Convergence of the MCMC chains can be monitored using standard Bayesian diagnostic procedures, such as trace plots and the Brooks-Gelman-Rubin scale-reduction statistic, R̂, which compares the total within- and between-chain variation to the within-chain variation (Gelman et al., 2004). At convergence, R̂ = 1, indicating that the initially dispersed chains have converged to a stationary distribution. As a practical guide, a 0.975 quantile for R̂ less than 1.2 is indicative of convergence. These diagnostics can be performed in WinBUGS or in R (R Development Core Team, 2010) using the coda or boa packages (Plummer et al., 2010; Smith, 2007).

For model comparison, we adopt the deviance information criterion (DIC) proposed by Spiegelhalter et al. (2002). DIC is defined as D̅(θ) + p_D, where D̅(θ) = E[D(θ)|y] is the posterior mean of the deviance, D(θ), and p_D = D̅(θ) − D(E[θ|y]) is the difference in the posterior mean of the deviance and the deviance evaluated at the posterior mean of the parameters. D̅(θ) is a measure of the model’s relative fit, while p_D provides a penalty for the model’s complexity. Models with smaller DIC are considered preferable.

To assess the adequacy of the final model, we apply posterior predictive assessments, whereby the observed data are compared to data replicated from the posterior predictive distribution (Gelman et al., 1996). If the model fits well, the replicated data, y^rep, should resemble the observed data y. To quantify the similarity, one can choose a discrepancy measure, T = T(y, θ), that takes an extreme value if the model conflicts with the observed data. Popular choices for T include sample quantiles and residual-based measures. The Bayesian predictive p-value denotes the probability that the discrepancy measure based on the predictive sample, T^rep = T(y^rep, θ), is more extreme than the observed measure T. A Monte Carlo estimate of the predictive p-value can be computed by evaluating the proportion of draws in which T^rep > T. A p-value close to 0.50 represents adequate model fit, while p-values near 0 or 1 indicate lack of fit. The cut-off for determining lack of fit is subjective, although by analogy to the classical p-value, a Bayesian predictive p-value between 0.05 and 0.95 suggests adequate fit with respect to T^rep.

To evaluate the fit of our model, we adopt two discrepancy measures: the proportion of zero observations and the mean count among the nonzero observations. For each measure, we plot posterior predictive distributions and present predictive p-values. We also present histograms comparing the observed and posterior-predictive counts of ED visits.

5. Simulation Study

To better understand the properties of the proposed model, we conducted a small simulation study comparing a model with correlated spatial effects (the “correlated” model) to a model that included separate spatial effects for the two components (the “separate model”). The aim of the simulation was to determine how parameter bias and precision changed as the correlation between ϕ_1i and ϕ_2i increased.

We simulated 100 data sets under four correlation values: ρ = 0, ρ = 0.25, ρ = 0.50, and ρ = 0.75. To emulate the case study below, we used the Durham County adjacency matrix for the simulation. This matrix contains 129 block groups and 768 total adjacencies. Because the (M − A) matrix in (5) is singular, the spatial random effects cannot be simulated directly. To avoid this limitation, we introduced the spatial smoothing parameter, s, mentioned above and set it equal to 1 − 1E-6, which closely approximates the ICAR model. We then generated spatial random effects $\mathbf{\Phi }=({\varphi }_1^{\prime },\dots ,{\varphi }_n^{\prime })\prime$ from the joint prior (5) with $\mathbf{\Sigma }=\left(\begin{array}{cc}\hfill 4\hfill & \hfill {\mathbf{\Sigma }}_{12}\hfill \\ \hfill {\mathbf{\Sigma }}_{12}\hfill & \hfill 6\hfill \end{array}\right)$ and Σ₁₂ taking the values 0, 2, 4, and 6 corresponding to the four ρ values above. Next, we simulated 25 response values for each block group under the following Poisson hurdle model:

$$\begin{array}{cc}\hfill \text{logit}(p_{\mathit{\text{ij}}})& ={\beta }_{11}+{\beta }_{12}{x}_{\mathit{\text{ij}}}+{\varphi }_{1i}\hfill \\ \hfill \text{log}({\mu }_{\mathit{\text{ij}}})& ={\beta }_{21}+{\beta }_{22}{x}_{\mathit{\text{ij}}}+{\varphi }_{2i},j=1,\dots ,25;i=1,\dots ,129,\hfill \end{array}$$ (6)

where (β₁₁, β₁₂) = (−1, 1), (β₂₁, β₂₂) = (2, 1), and covariate x_ij generated from a discrete uniform distribution on the interval (0,4).

We conducted the simulations in WinBUGS 1.4.3, which we called from R via the package R2WinBUGS (Sturtz et al., 2005). For each ρ value, we ran the bivariate and separate models for 30,000 iterations each with a burn-in of 10,000, which was sufficient to ensure convergence based on trace plots and Gelman-Rubin statistics. We retained every 20th observation to reduce autocorrelation. The intercept terms (β₁₁ and β₂₁) were assigned flat priors, and the slope parameters, β₁₂ and β₂₂, were assigned weakly informative normal priors centered at their true values. For the correlated model, we assigned a bICAR prior to ϕ_i using the mv.car function, with a 5-df inverse-Wishart prior for Σ. For the separate model, we assigned ϕ_1i and ϕ_2i independent univariate CAR priors using the car.normal function in WinBUGS, with U(0,10) and U(0,20) priors for the respective standard deviations terms.

The results are detailed in Table 2. The columns present the true parameter values, the posterior mean estimates, and the estimated bias and MSE across the 100 simulations. Parameters estimates, biases, and MSEs were generally similar for two models, with exception of β₂₁, the intercept for the Poisson component, where the separate model showed increased bias as ρ increased. The separate model also showed increased bias for the variance components (Σ₁₁ and Σ₂₂) when ρ ≥ 0.50, but less bias when ρ < 0.50. These results support previous findings by Su et al. (2009), who investigated non-spatial two-part models for “semi-continuous” data and likewise found bias in the intercept term of the nonzero component. Essentially, when the random effects are truly correlated but assumed to be independent, the binomial component does not contribute enough information to the second component, resulting in positive bias in the intercept term of this component (Su et al., 2009).

Table 2.

Results from simulation study comparing bivariate CAR and separate CAR Poisson hurdle models (n = 100 simulated datasets). Parameter estimates and biases for β₂₁ are highlighted in bold.

			Posterior estimates
			Correlated model			Separate model
ρ	Model Parameter	True Value	Posterior Mean	Bias	MSE	Posterior Mean	Bias	MSE
0	β11	−1	−1.01	−0.01	0.007	−1.004	−0.004	0.007
	β12	1	1.01	0.01	0.002	1.01	0.01	0.002
	β21	2	2.004	0.004	0.004	1.996	−0.004	0.004
	β22	−1	−1.001	−0.001	<0.001	−1.001	−0.001	<0.001
	Σ11	4	3.996	−0.004	0.46	4.17	0.17	0.54
	Σ12	0	−0.013	−0.013	0.85	—	—	—
	Σ22	16	15.60	−0.40	4.59	16.04	0.04	4.87
0.25	β11	−1	−1.01	−0.01	0.005	−1.01	−0.01	0.005
	β12	1	1.01	0.01	0.002	1.01	0.01	0.002
	β21	2	2.01	0.01	0.004	2.02	0.02	0.004
	β22	−1	−0.999	0.001	<0.001	−0.999	0.001	<0.001
	Σ11	4	3.996	−0.004	0.52	4.18	0.18	0.62
	Σ12	2	1.92	−0.08	0.92	—	—	—
	Σ22	16	15.75	−0.25	3.72	15.91	−0.09	3.86
0.50	β11	−1	−1.01	−0.01	0.006	−1.002	−0.002	0.006
	β12	1	1.01	0.01	0.002	1.01	0.01	0.002
	β21	2	2.03	0.01	0.005	2.05	0.05	0.008
	β22	−1	−1.002	−0.002	<0.001	−1.002	−0.002	<0.001
	Σ11	4	4.06	0.06	0.70	4.18	0.18	0.86
	Σ12	4	4.02	0.02	0.84	—	—	—
	Σ22	16	15.65	−0.35	4.56	15.45	−0.55	4.97
0.75	β11	−1	−1.01	− 0.01	0.007	−0.99	0.01	0.007
	β12	1	1.01	0.01	0.002	0.99	−0.01	0.002
	β21	2	2.01	0.01	0.006	2.09	0.09	0.01
	β22	−1	−1.001	−0.001	<0.001	−1.001	−0.001	<0.001
	Σ11	4	4.11	0.11	0.68	4.31	0.31	0.93
	Σ12	6	6.16	0.16	1.70	—	—	—
	Σ22	16	15.92	−0.08	7.03	14.67	−1.33	6.69

Generally speaking, while the results for the two models are not drastically different, they do support the use of correlated spatial hurdle model, particularly when the true correlation is high (e.g., ρ ≥ 0.50). We also expect the correlated model to provide more precise random effect predictions, leading in turn to improved predictions of expected counts and other quantities of interest.

6. Analysis of the DSR Data

To analyze the DSR data, we fit the following spatial hurdle model:

$$\begin{array}{cc}\hfill \text{logit}(p_{\mathit{\text{ij}}})& ={\beta }_{11}+{\beta }_{12}{\text{Male}}_{\mathit{\text{ij}}}+{\beta }_{13}{\text{NHB}}_{\mathit{\text{ij}}}+{\beta }_{14}{\text{Hisp}}_{\mathit{\text{ij}}}+{\beta }_{15}{\text{Priv}}_{\mathit{\text{ij}}}+{\alpha }_{11}{\text{PctOcc}}_i+{\alpha }_{12}{\text{PctBelow}}_i+f_1({\text{Age}}_{\mathit{\text{ij}}})+{\varphi }_{1i}\hfill \\ \hfill \text{log}({\mu }_{\mathit{\text{ij}}})& ={\beta }_{21}+{\beta }_{22}+{\text{Male}}_{\mathit{\text{ij}}}+{\beta }_{23}{\text{NHB}}_{\mathit{\text{ij}}}+{\beta }_{24}{\text{Hisp}}_{\mathit{\text{ij}}}+{\beta }_{25}{\text{Priv}}_{\mathit{\text{ij}}}+{\alpha }_{21}{\text{PctOcc}}_i+{\alpha }_{22}{\text{PctBelow}}_i+f_2({\text{Age}}_{\mathit{\text{ij}}})+{\varphi }_{2i},\hfill \end{array}$$ (7)

where Male denotes male gender; NHB and Hisp are indicators of non-Hispanic black and Hispanic race (with non-Hispanic white serving as the reference category); Priv denotes private insurance; Pctocc is the percent of occupied homes in block group i; and Pctbelow denotes the percent of residents below poverty level for block group i. Since previous studies have suggested a nonlinear effect for patient age (Niska et al., 2010), we model age as a smooth function, f_k(Age_ij) (k = 1, 2), which we approximate by cubic B-splines with interior knots at the first, second and third quartiles of the age distribution (18.33, 35.50 and 54.34 years, respectively). Specifically, we let

$$f_k({\text{Age}}_{\mathit{\text{ij}}})={\displaystyle \sum _{h=1}^6}{\gamma }_{\mathit{\text{kh}}}{B}_h({\text{Age}}_{\mathit{\text{ij}}}),k=1,2,$$ (8)

where γ_k = (γ_k1, …, γ_k6)′ is a vector of regression coefficients specific to component k and {B_h} is the set of corresponding basis functions (excluding an intercept).

As in Section 5, we assigned improper uniform priors to the intercept parameters, β₁₁ and β₂₁, and weakly informative N(0,10) priors to the remaining regression coefficients, including the spline parameters. We assumed a bICAR prior for ϕ_i with an IW(2,I₂) prior for the spatial covariance Σ, where I₂ denotes the two-dimensional identity matrix. The models were fit again in WinBUGS 1.4.3 via R2WinBUGS. We ran three initially dispersed chains for 30,000 iterations each, discarding the first 10,000 as burn-in. Model diagnostics such as trace plots and Gelman-Rubin statistics indicated rapid convergence of the chains. WinBUGS code for this analysis is provided in the Appendix.

For comparison, we also ran the model with separate CAR priors for ϕ_1i and ϕ_2i. As in the simulation study, we assigned U(0,10) and U(0,20) priors to the standard deviations terms of ϕ_1i and ϕ_2i, respectively. We then used the DIC criterion to compare the fit of the bivariate and separate CAR models. The DIC for the separate model was 277,494 (D̅ = 277, 277, p_D = 217), whereas the DIC for the bivariate spatial model was 277,479 (D̅ = 277, 267, p_D = 212), indicating superior fit for the bivariate model. Not surprisingly, both hurdle models vastly outperformed the standard (single-component) Poisson model, which had a DIC value of 297,931.

Table 3 presents the posterior summaries from the bivariate model for all parameters except the the B-spline coefficients, γ_kh, which are difficult to interpret in raw form. The estimates for percent home occupancy and percent below poverty level are presented in terms of a 10-unit change. Male gender, black and Hispanic race, and block group poverty were positively associated with increased probability of one or more ED visits, while private insurance reduced the likelihood of an ED visit. Based on a predictive marginal calculations (c.f., Graubard and Korn, 1999; Neelon et al., 2010), we found that patients without private insurance averaged 4.29 (95% posterior interval = [4.26, 4.43]) times more ED visits annually than those with private insurance.

Table 3.

Posterior mean estimates and 95% posterior intervals (PIs) from the bivariate CAR Poisson hurdle model (excluding age parameters). Estimates for percent occupied housing and percent below poverty are given for a 10-unit change.

Model Component	Variable	Parameter	Posterior Mean	95% PI
Bernoulli	Intercept	β11	−0.65	(−0.73, −0.58)
	Male	β12	0.20	(0.17, 0.22)
	Non-Hispanic black	β13	0.68	(0.65, 0.71)
	Hispanic	β14	0.56	(0.50, 0.61)
	Private Insurance	β15	−1.32	(−1.35, −1.30)
	% Occupied Housing	α11	0.02	(−0.02, 0.06)
	% Below Poverty	α12	0.10	(0.07, 0.12)
Poisson	Intercept	β21	0.70	(0.64, 0.77)
	Male	β22	−0.13	(−0.15, −0.11)
	Non-Hispanic black	β23	0.05	(0.03, 0.08)
	Hispanic	β24	−0.57	(−0.62, −0.54)
	Private Insurance	β25	−0.60	(−0.62, −0.58)
	% Occupied Housing	α21	0.01	(−0.03, 0.05)
	% Below Poverty	α22	0.04	(0.02, 0.07)
Variance Components	Var(ϕ1i)	Σ11	0.22	(0.16, 0.31)
	Cov(ϕ1i, ϕ2i)	Σ12	0.10	(0.06, 0.15)
	Var(ϕ2i)	Σ22	0.14	(0.10, 0.19)
	Corr(ϕ1i, ϕ2i)	ρ	0.57	(0.42, 0.70)

The variance component estimates indicate more between–block-group variability in ED use (as measured by Σ₁₁) than in intensity of repeat visits (as measured by Σ₂₂). In both cases, the posterior intervals were quite narrow and bounded away from zero, suggesting that the variance components were well identified. The estimate of the random-effect correlation ρ was 0.57 (95% posterior interval = [0.42, 0.70]), providing additional evidence for the appropriateness of the bivariate model.

Interestingly, the estimates for male gender and Hispanic race reversed direction between the Bernoulli and Poisson components. For example, compared to non-Hispanic whites, Hispanics are estimated to have 1.75 (95% posterior interval = [1.65, 1.84]) higher adjusted odds of visiting and ED at least once. However, among ED users, Hispanics make on average 21% (95% posterior interval = [18%, 24%]) fewer visits than non-Hispanic whites, based on a predictive marginal calculation. Thus, while Hispanics are more likely than non-Hispanic whites to visit the ED at least once, Hispanic ED users make fewer repeat visits on average than white users. This points to a potential difference between the way Hispanics and non-Hispanic whites use ED services. In particular, although modest ED use seems to be more ubiquitous among Hispanics, they are disinclined to use EDs repeatedly; in contrast, there may be a small minority of white patients who use ED services for their routine care. Note that on the whole, Hispanic and non-Hispanic white patients make similar numbers of visits annually, with Hispanics averaging 0.51 visits to the ED per year and non-Hispanic whites averaging 0.48 visits annually (risk ratio = 1.05 [1.00, 1.09]). However, when we look at the two components of the hurdle model separately, we see strikingly different patterns in ED use between these two cohorts: occasional ED use is more prevalent among Hispanics, but white users tend to make more return visits. This is a relatively new finding, and one that would likely have been missed in a standard, single-component Poisson regression analysis.

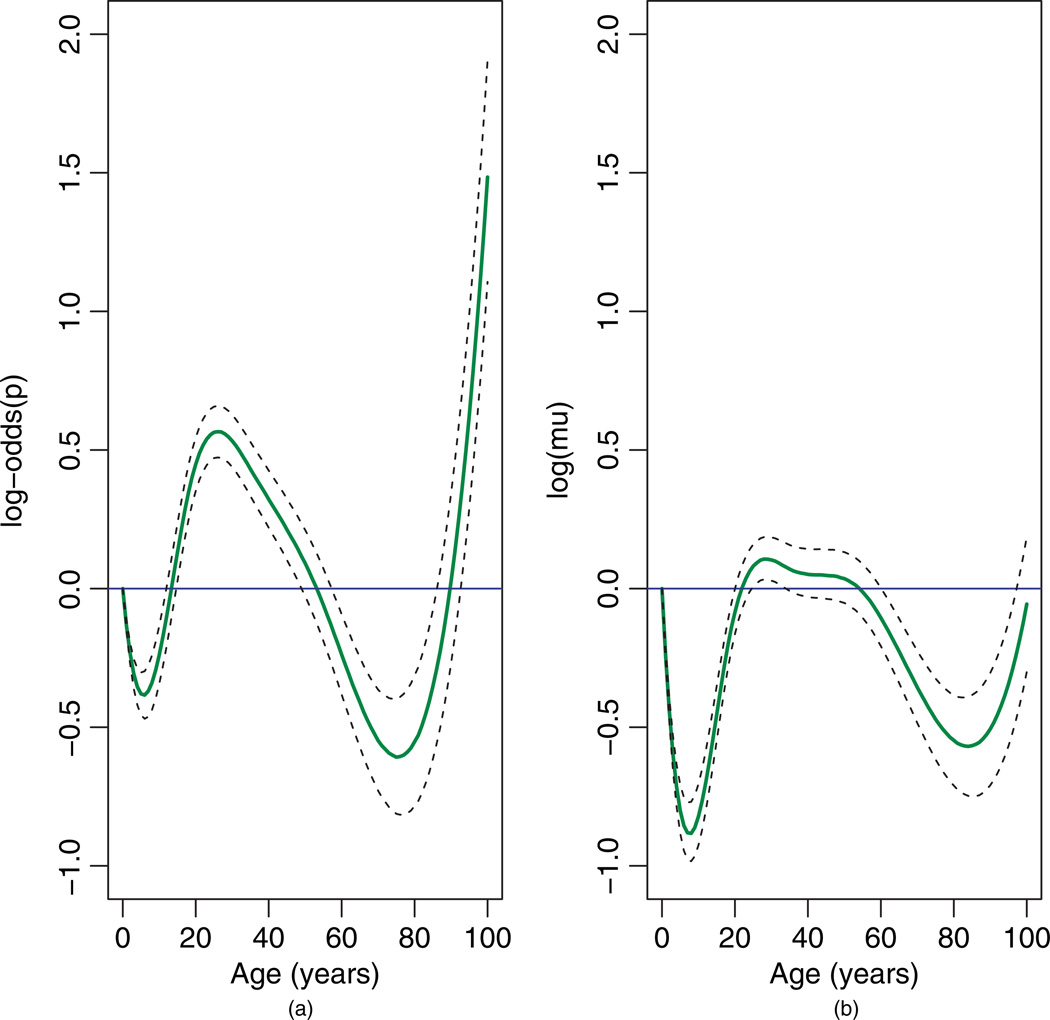
Figure 4 displays the age trends on the linear-predictor scale for the two model components. The horizontal lines at zero correspond to no age effect. In Figure 4(a), the log-odds of ED use decreases during the first decade of life, increases steadily until the late 20s, and then declines until age 75 before a final upswing. This bimodal pattern has been documented by previous studies (Niska et al., 2010; LaCalle and Rabin, 2010). The peak in usage during the late 20s may be due to higher rates of injury, violence, or motor vehicle accidents among this age group. The steepness of the curve in the later years may be due in part to sparseness of the data: only 4% of patients (n = 5166) are over age 75. In Figure 4(b), there is a “protective” effect of age during the early and later years, indicating that ED users in these extreme age ranges tend to make fewer visits than those aged 20–50.

Fig. 4.

Age effect on linear-predictor scale for (a) the Bernoulli component and (b) the Poisson component of the spatial hurdle model. Horizontal lines denote no age effect. Dashed lines denote 95% posterior intervals.

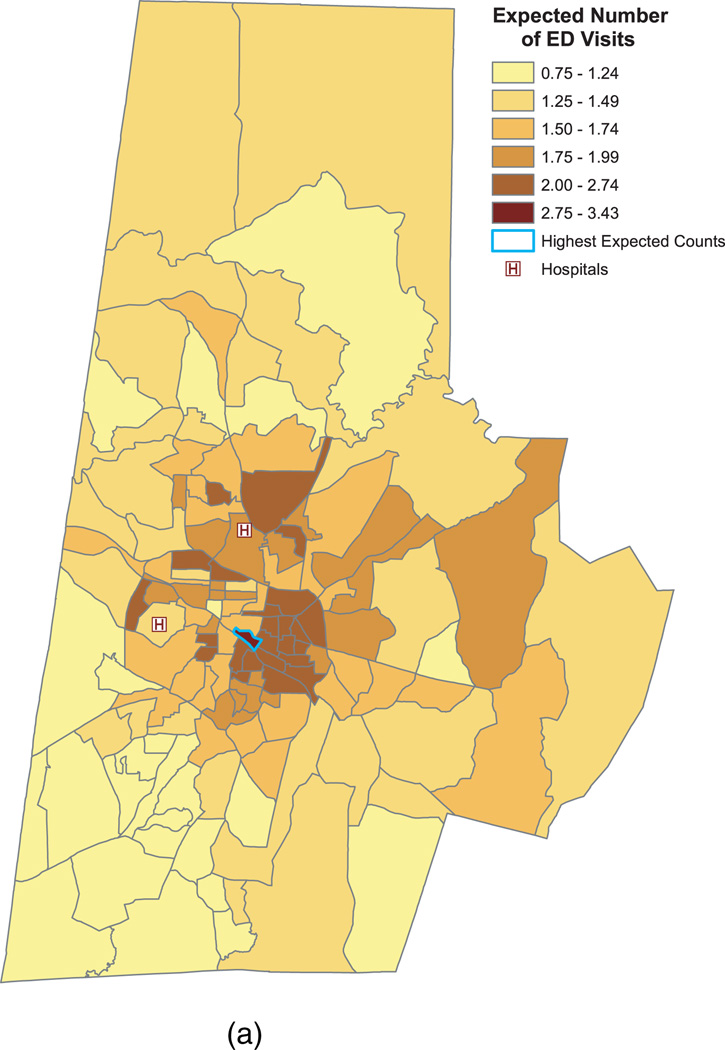
Figure 5(a) presents the estimated number of ED visits for a “high-risk” cohort comprising non-Hispanic black males, aged 36, who lack private insurance. The expected counts for these patients ranged from 0.75 to 3.43 with a median of 1.64 and an IQR of (1.33, 1.93). The spatial pattern is similar to the pattern for the raw average counts presented earlier in Figure 2. (For illustrative purposes, we reproduce these raw counts in Figure 5(b).) As panel (a) indicates, southeast central Durham again shows the highest average number of visits per year. In these neighborhoods, non-Hispanic black males, aged 36, who lack private insurance are expected to make between 2 and 3.43 visits to the ED annually. As before, the block group outlined in blue has the highest expected counts at 3.43 visits per patient (95% posterior interval = [3.18, 3.73]). Note that the estimates in Figure 5(a) are higher than those in Figure 5(b), since in panel (a) we are plotting the expected counts for a high-risk patient cohort, whereas in panel (b) we present the average counts for all patients.

Fig. 5.

Predicted and observed ED visits by block group. Panel (a) shows the predicted number of annual ED visits for non-Hispanic black males, 36 years of age, without private insurance. The outlined block group has the maximum expected counts (3.43 visits per patient per year). Panel (b) reproduces the raw counts from Figure (2) in order to highlight the similarity in spatial patterns between the predicted and observed counts.

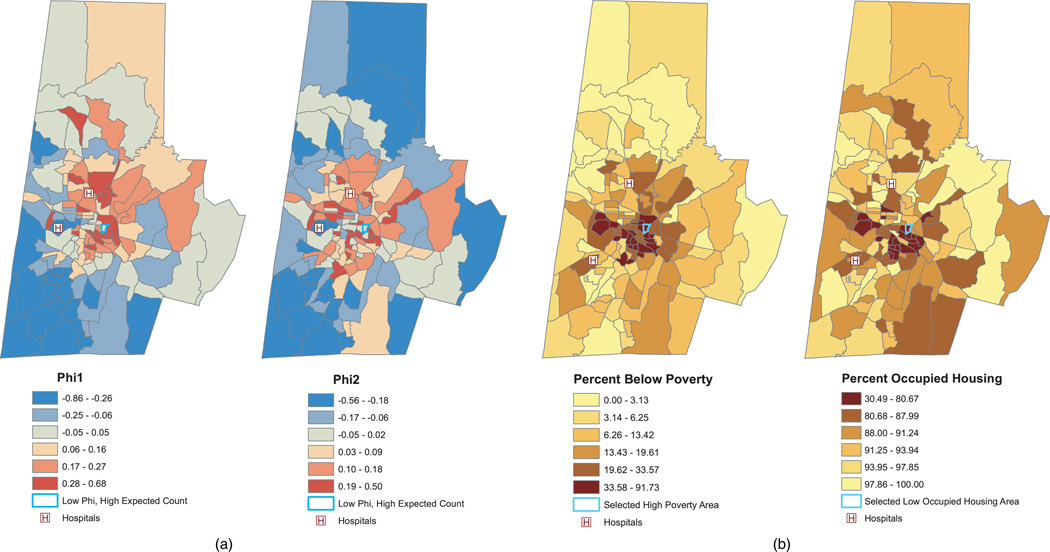
Figures 6(a) presents the model-based predictions of the random effects, ϕ_1i and ϕ_2i. As the figure suggests, there is substantial spatial variation in the random effects. Block groups in red have increased expected counts compared to “typical” (i.e., ϕ_i = 0) block groups with similar poverty and occupied housing levels, while those in blue have lower expected counts after adjusting for poverty and home occupancy. The dark blue cluster in the southwest corner consists of block groups with particularly low expected counts after adjusting for poverty and occupancy level. This area may include several local urgent-care clinics that provide an alternative to the ED, thereby lowering the expected count in this area relative to other block groups. The block group outlined in blue exemplifies one with a high estimated count per patient (2.32 annual visits per patient, Figure 5[a]), but with random effects near zero, suggesting that the high count for this block group is mainly due to its high poverty and low occupied housing rates. Indeed, as Figure 6(b) shows, this block group is in the upper sextile of the poverty distribution, with 65% of its residents below poverty level; it is also in the lowest sextile of the housing occupancy distribution, with only 61% of its homes occupied.

Fig. 6.

Figure (a) presents the model-based predictions of spatial random effects ϕ_1i and ϕ_2i. Figure (b) shows the observed block group characteristics of percent below poverty and percent occupied housing. The block group outlined in blue in represents one with high expected counts (as depicted in Figure 5), but with ϕ_i ≈ 0. Note that the legend for percent occupancy in panel (b) is inverted so that red corresponds to lower occupancy levels.

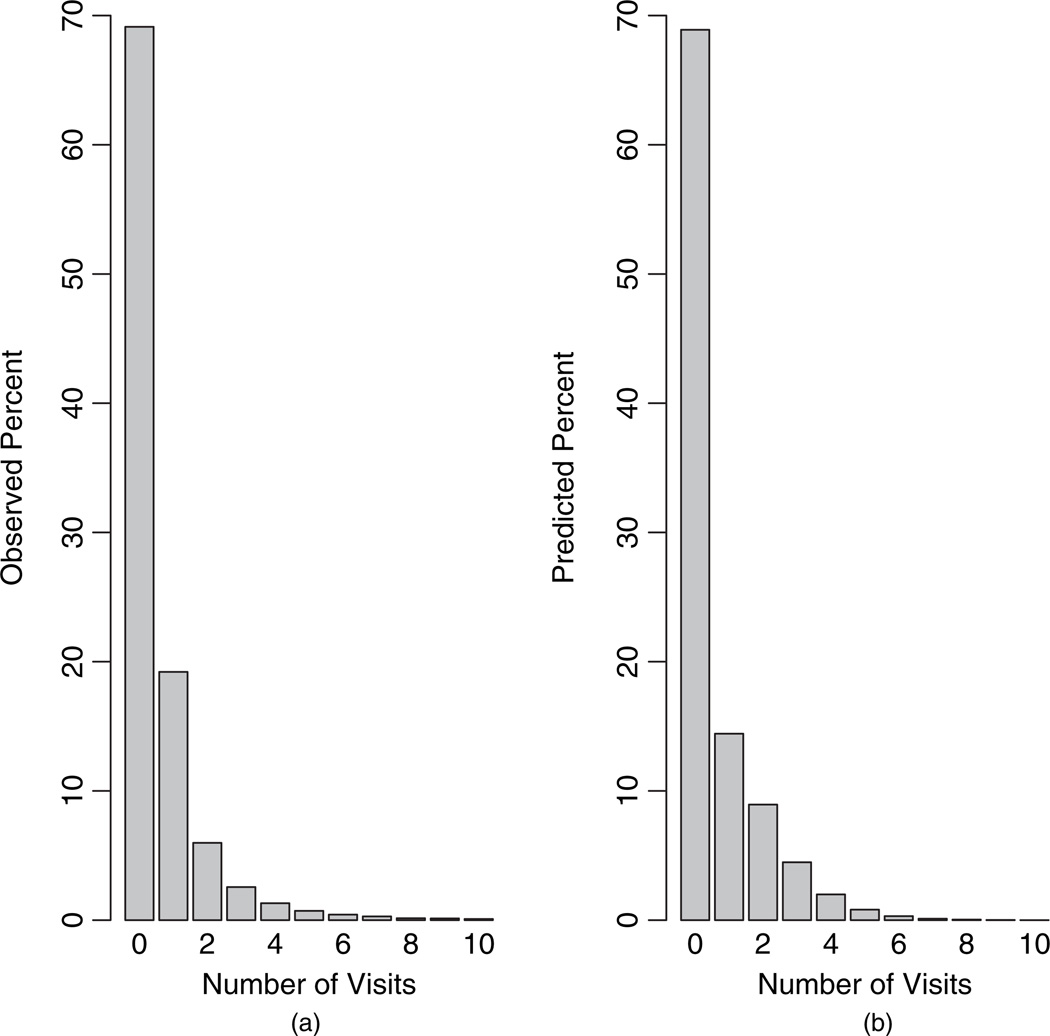
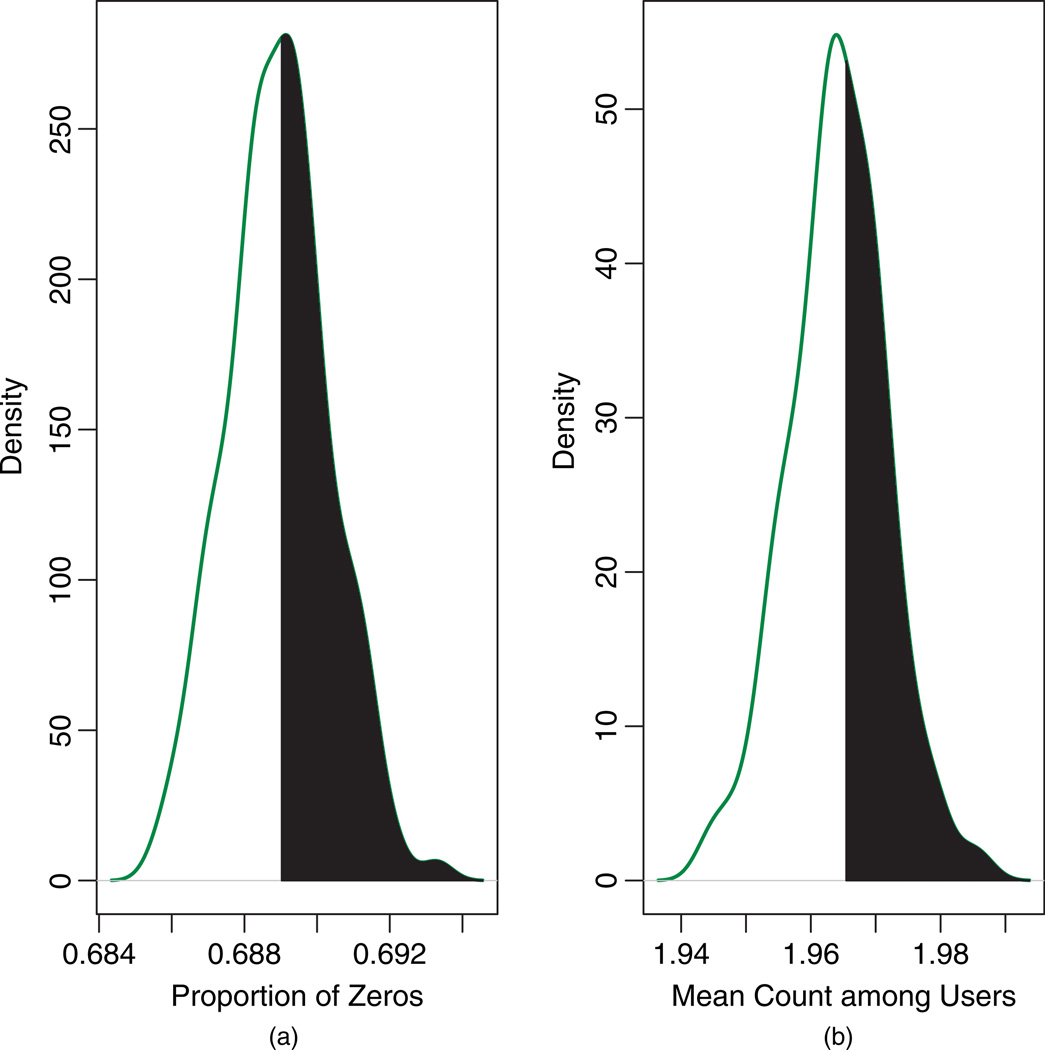
As a final check of model fit, we compared histograms of the observed counts and the posterior-predictive counts based on our model (Figure 7). Overall, the model provided reasonable fit, reproducing the correct percentage of zeros (69%), but slightly under-predicting the percentage of ones (observed = 19.21%; predicted = 14.43%), while slightly over-predicting counts two through four. Figure 8 presents the posterior predictive distributions for the proportion of zeros and the mean nonzero count. The Bayesian predictive p-values were 0.47 and 0.42 respectively, indicating adequate fit based on these two discrepancy measures.

Fig. 7.

Histograms of (a) observed counts and (b) posterior-predictive counts based on the proposed model.

Fig. 8.

Posterior-predictive distributions for (a) the proportion of zeros and (b) the mean count given y > 0. The vertical lines denote the observed values, and the shaded regions correspond to the Bayesian predictive p-values (0.47 and 0.42, respectively).

7. Discussion

This paper proposed a spatial Poisson hurdle model for exploring geographic variation in ED visits. The model consists of binary and truncated Poisson components, each including patient- and area-level predictors, as well as spatially dependent random effects. The random effects are modeled via a bivariate CAR prior, which induces correlation between the two components—an appealing feature if regions with high rates of ED use also exhibit high mean counts among users. Our simulation study suggests that modeling this correlation reduces bias in the spatial covariance parameters and in the intercept of the Poisson component, a finding supported by previous work on non-spatial two-component models (Su et al., 2009).

Overall, the model has several attractive features: 1) it addresses potential zero inflation relative to ordinary Poisson; 2) it models both ED use and the frequency of repeat use; 3) it accommodates dependence between model components, which can lead to less biased inferences; 4) it accounts for between-patient and within-block group correlation; and 5) it provides spatial smoothing and sharing of information across neighboring blocks groups.

The DSR analysis revealed several important findings. First, patients without private insurance make, on average, 4.29 times more trips to the ED per year than patients with private insurance. While the direction of this effect is not surprising, this analysis is among the first to use hierarchical models to quantify the extent to which lack of private insurance influences ED use. Our analysis also indicated that Hispanic and non-Hispanic white patients tend to make similar numbers of visits annually, with Hispanics making an average of 0.51 visits per year and non-Hispanic whites making approximately 0.48 visits annually. However, when one examines the two components of the hurdle model separately, different patterns in ED use emerge: modest ED use is more prevalent among Hispanics, but white users tend to make more return visits. The net result is that the expected counts are similar for the two groups. This is a relatively new finding, and one that might be overlooked in a standard, single-component Poisson regression analysis. We also found a bimodal effect for age, with peak ED use occurring around age 30 and after age 75. This bimodality has been reported in earlier studies (Niska, 2010; LaCalle and Rabin, 2010). And finally, southeast central Durham, an area comprising several low-income and underinsured neighborhoods, had the highest average number of visits per patient.

The results from this study could be used to guide a number of community-based initiatives to alleviate ED overcrowding. First, by identifying areas with high ED use, health officials can establish community health centers and local urgent care clinics to provide alternative outlets for primary medical, dental, and behavioral health care (Roby et al., 2011; Grumbach and Grundy, 2010). To reduce ED use during non-peak hours, these centers should have flexible hours, allowing patients to arrive after work and on weekends (GAO Report, 2011). Mobile health clinics can also be deployed in underserved communities to improve access to basic medical services.

Second, community outreach teams could be deployed in high-risk neighborhoods to promote health education, assist in chronic care management, and provide information about local health resources (Niska, 2010). Community “health ambassadors” could organize health fairs and disseminate information through neighborhood social hubs such as barber shops, beauty salons, laundromats, tiendas, and faith-based organizations (Pullen-Smith et al., 2008).

And finally, communities can establish more effective modes of transportation to and from local clinics, including evening and weekend bus, van, and carpool services. Directed community-level efforts such as these are essential to alleviating ED burden, since many residents may not actively seek or have access to health services through traditional channels.

Future work could explore spatial patterns among subgroups of patients with different medical diagnoses. This would allow investigators to identify the etiology behind ED use in a particular community and establish targeted interventions to address residents’ specific health needs. For example, if ED use is mainly due to mental health issues, local health officials could work to improve community behavioral health services. Future studies should also examine the relationship between ED use and concurrent use of other health services, since several studies have shown that high ED users frequently utilize other sources of health care as well (LaCalle and Rabin, 2010). In this way, health officials can determine whether ED use in a particular community is due to lack of alternative resources, or if there are other root causes for ED use in the community.

Our analysis also points to areas for further statistical development. First, additional patient and block group variables, such as patient education and median household income, could be included. Moreover, since it is well documented that Medicare and Medicaid patients use services differently from those paying out of pocket (LaCalle and Rabin, 2010), future geospatial analyses should investigate patterns of use among various insurance cohorts. One could also allow the age effect to vary spatially by introducing random effects for the spline coefficients, as in MacNab and Gustafson (2007). This would induce an age by block group interaction, enabling one to determine, for example, whether peak use in the late 20s occurs primarily in areas with high rates of motor vehicle accidents or violent crime. Next, to control the extent of spatial smoothing, one could fit the generalized MCAR model proposed by Jin et al. (2005), which would introduce a unique spatial smoothing parameter, s_k, for each component. And finally, the model could be generalized to accommodate semi-continuous data characterized by a point mass at zero and a continuous, right-skewed distribution, such as a log-normal, for the nonzero values. This model could be used to explore geographical variation in semi-continuous outcomes such as hospital length of stay. For a review of non-spatial semi-continuous models, see Olsen and Shafer (2001), Tooze et al. (2002), and Neelon et al. (2011).

In general, the spatial Poisson hurdle model should prove useful to investigators confronting spatially dependent count data characterized by an abundance of zeros. The Bayesian approach described here provides a practical method for fitting such models.

Appendix A

WinBUGS code for spatial Poisson hurdle model

model {
K←10000    * Constant for implementing zeros trick
for (i in 1:N) {
  ** Likelihood **
  p[i]← max(0.001, min(0.999,q[i]))
  logit(q[i])←beta1[1]+ beta1[2]*male[i]+beta1[3]*black[i]+beta1[4]*hisp[i]+beta1[5]*private[i]+
              alpha1[1]*pctoccup[i]+alpha1[2]*pctbelow[i]+gamma1[1]*b1[i]+gamma1[2]*b2[i]+
              gamma1[3]*b3[i]+gamma1[4]*b4[i]+gamma1[5]*b5[i]+gamma1[6]*b6[i]+Phi[1,id[i]]
                                     ** Note: b1–b6 are spline basis functions imported from R
  log(mu[i])←beta2[1]+ beta2[2]*male[i]+beta2[3]*black[i]+beta2[4]*hisp[i]+ beta2[5]*private[i]+
             alpha2[1]*pctoccup[i]+alpha2[2]*pctbelow[i]+gamma2[1]*b1[i]+gamma2[2]*b2[i]+
             gamma2[3]*b3[i]+gamma2[4]*b4[i]+ gamma2[5]*b5[i]+gamma2[6]*b6[i]+Phi[2,id[i]]

  z[i]←step(y[i]-1)             ** I(y>0)
  ll[i]←(1-z[i])*log(1-p[i]) + z[i]*(log(p[i]) + y[i]*log(mu[i]) - mu[i] - loggam(y[i]+1) - log(1-exp(-mu[i]))) ** Log-likelihood
  zeros[i]←0
  zeros[i] ~ dpois(phi[i])      ** Zeros trick
  phi[i]← - ll[i]+K
 }
 ** Priors **
  beta1[1] ~ dflat()             ** Intercepts
  beta2[1] ~ dflat()
  for (j in 2:5) {
    beta1[j] ~ dnorm(0,.1)       ** Patient-level fixed-effect parameters
    beta2[j] ~ dnorm(0,.1)
  }
  for (j in 1:2) {
    alpha1[j] ~ dnorm(0,.1)      ** Block-level fixed-effect parameters
    alpha2[j] ~ dnorm(0,.1)
  }
  for (j in 1:6) {
    gamma1[j] ~ dnorm(0,.1)      ** B-Spline coefficients
    gamma2[j] ~ dnorm(0,.1)
  }
 ** Bivariate CAR Prior for Phi
    Phi[1:2,1:n] ~ mv.car(adj[],weights[],m[],R[,])   ** m specifies no. of neighbors
    for(i in 1:M){weights[i] ← 1}                     ** M is the sum of the vector m
 ** Spatial Precision and Covariance
    R[1:2, 1:2] ~ dwish(Omega[ , ], 2)                ** Omega = diag(2) and included as part of data
    Sigma.phi[1:2,1:2]←inverse(R[, ])
    rho←Sigma.phi[1,2]/sqrt(Sigma.phi[1,1]*Sigma.phi[2,2])
 }