Metabolic Fluxes in an Illuminated Arabidopsis Rosette^,

Kinetic flux profiling has been extensively used in unicellular bacterial systems to study primary metabolism. We present a framework for its use in estimating photosynthetic fluxes in land plants. The resulting flux estimates are benchmarked against published flux estimates.

Abstract

Photosynthesis is the basis for life, and its optimization is a key biotechnological aim given the problems of population explosion and environmental deterioration. We describe a method to resolve intracellular fluxes in intact Arabidopsis thaliana rosettes based on time-dependent labeling patterns in the metabolome. Plants photosynthesizing under limiting irradiance and ambient CO₂ in a custom-built chamber were transferred into a ¹³CO₂-enriched environment. The isotope labeling patterns of 40 metabolites were obtained using liquid or gas chromatography coupled to mass spectrometry. Labeling kinetics revealed striking differences between metabolites. At a qualitative level, they matched expectations in terms of pathway topology and stoichiometry, but some unexpected features point to the complexity of subcellular and cellular compartmentation. To achieve quantitative insights, the data set was used for estimating fluxes in the framework of kinetic flux profiling. We benchmarked flux estimates to four classically determined flux signatures of photosynthesis and assessed the robustness of the estimates with respect to different features of the underlying metabolic model and the time-resolved data set.

INTRODUCTION

Photosynthetic CO₂ assimilation is central to life, and understanding its regulation and integration with end-product synthesis is a major challenge in plant biochemistry. Existing studies in plants mainly focused on defining metabolic pathways and their subcellular compartmentation and studying the regulation of component enzymes (Bauwe et al., 2010; Hibberd and Covshoff, 2010; Stitt et al., 2010). In the past decade, high-throughput methods have been applied to measure metabolites involved in photosynthetic C metabolism (Cruz et al., 2008; Timm et al., 2008; Arrivault et al., 2009; Suzuki et al., 2012), to study the relation between enzyme activities and steady state metabolite levels (Sulpice et al., 2010), to analyze gene expression (Biehl et al., 2005), to relate transcript levels to in vitro activities of the encoded enzymes (Gibon et al., 2004), and to estimate rates of turnover of individual enzymes (Piques et al., 2009). An emerging picture is that in vitro activities of enzymes only partly reflect the levels of transcripts, that many enzymes exhibit slow turnover rates, and that there is little relation between in vitro activities of enzymes and the levels of individual metabolites in photosynthetic C metabolism.

The most biologically important description of metabolism is the set of metabolic fluxes that it generates. This represents the integrated output of the molecular machinery and biochemical characteristics studied by other high-throughput technologies. It is also a key determinant of cellular physiology and growth (Blank and Sauer, 2004). The goal of this study is to use stable isotope labeling with ¹³CO₂ to estimate fluxes in the well-characterized photosynthetic metabolism in a land plant leaf. This is a challenging task given the complex topology and subcellular compartmentation of the pathways and the wide range of fluxes and turnover times of the metabolites that are involved in them.

Ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco) catalyzes the initial carboxylation reaction, in which CO₂ is added to the 5C carbon acceptor ribulose-1,5-bisphosphate (RuBP) to form two molecules of 3-phosphoglycerate (3PGA). Most of the 3PGA is used to regenerate RuBP in the Calvin-Benson cycle (CBC). This involves the reduction of PGA to triose-phosphates, a process that consumes the vast majority of the NADPH and ATP generated in the light reactions, followed by a series of condensation, cleaving, and phosphatase and phosphorylation reactions that rearrange 3C triose-phosphate skeletons into the 5C carbon acceptor RuBP. The net C gain (in the ideal case, one-sixth of fixed C) is used to synthesize end products: mainly Suc and starch. Some C is converted to organic acids and amino acids. This requires the assimilation of additional CO₂ in the anaplerotic reaction catalyzed by phosphoenolpyruvate carboxylase (PEPc).

Rubisco catalyzes a side reaction in which RuBP reacts with O₂ to form one molecule of 3PGA and one molecule of 2-phosphoglycollate. Under current atmospheric conditions, in organisms without a C concentrating mechanism, this side reaction occurs at 25% of the rate of the reaction with CO₂ (Sharkey, 1988). 2-Phosphoglycollate is salvaged via a complex pathway termed photorespiration, in which it is converted via glycolate to glyoxylate, transaminated to Gly, decarboxylated to Ser, and converted back via hydroxypyruvate and glycerate to 3PGA. This process results in a 25 to 30% decrease in the net rate of C fixation and a 20% decrease in quantum yield (Foyer et al., 2009; Bauwe et al., 2010).

In eukaryotic algae and plants, a further major complication is introduced by subcellular compartmentation. Briefly, the CBC and starch synthesis occur in the chloroplast, while triose-phosphates are exported to the cytosol for conversion to Suc. Photorespiration occurs in the chloroplast, peroxisome, cytosol, and mitochondria. Organic acid and amino acid metabolism occurs in the plastid, cytosol, and mitochondria, and large amounts of these metabolites accumulate in the vacuole (for details, see Supplemental Methods 1 online).

Pioneering isotope labeling experiments with ¹⁴CO₂, which were performed almost 60 years ago (Calvin, 1956), played a key role in the discovery of the CBC (Benson, 2002). Since then, isolated studies have analyzed ¹⁴C labeling kinetics at the subcellular level and used this information to estimate fluxes at selected reaction steps (Stitt et al., 1983). However, technical challenges meant that most ¹⁴C labeling studies were restricted to analyses of the rate of carboxylation and the distribution of fixed C between end products. In the last 10 years, new analytical chemistry tools, like metabolomics, have increased our knowledge of metabolism (Nunes-Nesi et al., 2005; Arrivault et al., 2009; Stitt et al., 2010). The use of stable isotopes (Schaefer et al., 1980; MacLeod et al., 2001; Schwender et al., 2004a; Römisch-Margl et al., 2007), coupled with improvements in analytical methods, has opened new possibilities for metabolism research (DellaPenna and Last, 2008; Saito and Matsuda, 2010).

Successful applications of ¹³C-labeling and gas chromatography–time-of-flight–mass spectrometry (GC-TOF-MS) have been reported for a range of species and tissues, including Escherichia coli (Yuan et al., 2006; Haverkorn van Rijsewijk et al., 2011), Saccharomyces cerevisiae (Birkemeyer et al., 2005), photoautotrophic cyanobacteria, Synechocystis sp (Huege et al., 2011; Young et al., 2011), Arabidopsis thaliana (Huege et al., 2007; Williams et al., 2010), soybean (Glycine max) embryos (Sriram et al., 2004), Brassica napus (Schwender et al., 2004b, 2006), and potato (Solanum tuberosum) tubers (Roessner-Tunali et al., 2004). However, to date, there are relatively few reports that use ¹³CO₂ to study metabolism in photosynthesizing plant tissue. Furthermore, these studies usually analyzed individual leaves that were harvested from the plant following incubation of part of the leaf with ¹³CO₂ and could be compromised by export of enriched compounds to other parts of the leaf or the remainder of the plant. Ito and Mitsumori (1992) measured ¹³C incorporation into photorespiratory intermediates, several amino acids, and sugars in intact sunflower (Helianthus annuus) leaves, while Hasunuma et al. (2010) investigated labeling of CBC intermediates and sugar phosphates in tobacco (Nicotiana tabacum) leaf discs. Huege et al. (2007) demonstrated a method for the full labeling of Arabidopsis rosettes by growing plants from germination onwards in a sealed chamber in a ¹³CO₂ atmosphere and subsequently used GC-TOF-MS to study the decay of ¹³C in a set of metabolites. Eisenreich and Bacher (2007) suggested using ¹³CO₂ as a universal precursor for in vivo experiments in photosynthesizing plant tissues; however, these authors focused their research on NMR analysis of pathways of secondary metabolism.

The topology of photosynthetic C fixation pathways poses a particular challenge for flux studies. Most methods for analyzing ¹³C enrichment patterns and estimating fluxes assume steady state metabolic states and steady state labeling states (reviewed in Ratcliffe and Shachar-Hill, 2006). Very little information about fluxes can be extracted from data obtained at isotopic steady state following the feeding of ¹³CO₂. On the other hand, qualitative analysis of non–steady state labeling kinetics with ¹³C is extremely challenging due to the large number of isotopomers (Antoniewicz et al., 2007; Young et al., 2008). Such analyses are further complicated by the large range of turnover times of metabolite pools, which span between <1 s for many metabolites in the CBC to ∼1 min for intermediates in Suc synthesis to several minutes for intermediates of photorespiration (Stitt et al., 1983; Arrivault et al., 2009; for details, see Supplemental Methods 2 online).

In this study, we used a custom-designed labeling chamber to carry out short-term ¹³CO₂ labeling of intact Arabidopsis rosettes under ambient steady state conditions. Several complementary analytical platforms were applied, including GC-TOF-MS and two recently developed liquid chromatography–tandem mass spectrometry (LC-MS/MS) platforms (Lunn et al., 2006; Arrivault et al., 2009), allowing quantitative determination and ¹³C enrichment calculation of 40 metabolites from the CBC, Suc and starch synthesis, glycolysis, amino acid and organic acid metabolism, as well as trehalose-6-phosphate (Tre6P) metabolism. The main aims of this study were as follows: (1) to qualitatively test expectations about the labeling kinetics of metabolites in photosynthetic metabolism in a higher plant, (2) to use labeling kinetics to provide information about what proportion of the metabolite pool is likely to be involved in photosynthetic metabolism, and (3) to use this information to estimate a selected set of fluxes through photosynthetic end products, which can be compared with independent measurements to benchmark the data and model.

RESULTS

Construction of the ¹³C Labeling System

Several aspects had to be reconciled in the design of a chamber to perform ¹³CO₂ labeling of whole Arabidopsis rosettes under physiological conditions (see Supplemental Figure 1 online): (1) The volume had to be as small as possible to minimize the time lag after introducing ¹³CO₂ but large enough to hold a 5-week-old Arabidopsis plant in a pot; (2) the chamber had to be built from transparent material that did not drastically alter light quality; and (3) the rosette has to be quenched in ambient light and without allowing entry of ¹²CO₂ due to the rapid turnover of CBC metabolites (see Introduction). We used commercially available 380-mL in vitro plant culture boxes (Magenta GA-7). While rapid quenching in large-leaved species is best performed by freeze clamping the leaf between two liquid N₂ precooled metal blocks (Badger et al., 1984; Quick et al., 1991), this is not practical for Arabidopsis rosettes. Instead, the plants were grown with plastic foil under the rosette and quenched by flooding them with a large volume of liquid N₂ poured down a funnel inserted through a small inlet in the side of the box. This allowed quenching without shading the plants or opening the box.

Arabidopsis Rosette Labeling Experiment

Five-week-old plants were rapidly transferred from growth chambers to the labeling chamber, which was continuously washed through the whole experiment by a stream of air (5 liters min⁻¹) prepared from cylinders containing pure N₂, O₂, and ¹³CO₂ that had been mixed in a gas blender (see Methods). Plants were harvested 5 and 10 s and 1, 3, 10, 20, and 60 min after the start of labeling. Shorter pulses were not possible due to the dead space of the chamber and the CO₂ inside the plant leaf. Due to the small size and rapid turnover of pools in the CBC, these treatments do not allow resolution of individual fluxes in the CBC (see below) but do facilitate estimation of overall flux in the CBC and the fluxes in photorespiration as well as starch and Suc synthesis.

Analysis of Isotopomers of 40 Metabolites

Samples were analyzed using three analytical platforms, namely, GC-TOF-MS, ion exchange LC-MS/MS, and reverse-phase LC-MS/MS. This allowed quantification of 40 metabolites from the CBC, starch and Suc biosynthesis, the photorespiratory pathway, amino acid metabolism, glycolysis, the tricarboxylic acid cycle (TCAC), and Tre6P metabolism. The mass distribution of all metabolites determined shifted to a higher mass-to-charge ratio with increasing labeling time, as illustrated for 3PGA, which is the first product of CO₂ fixation (see Supplemental Figure 2 online). Labeling kinetics were reproducible between three biological replicates (e.g., average ¹³C enrichment and sd were 65.8 and 4.9% for RuBP isotopomer, corresponding to the fully labeled molecule after 1 h of labeling and 40.8 and 3.5% for Ala). The total content of the measured metabolites did not change significantly between different labeling times (see Supplemental Table 1 online).

The Pattern of Labeling Can Be Separated by k-Means Clustering

To obtain an overview of the labeling kinetics, the average ¹³C enrichment profiles over the three biological replicates for all measured metabolites were subjected to k-means clustering based on Euclidian distance. To determine number of clusters, k, the crude rule of thumb by Mardia et al. (1979), was used, whereby

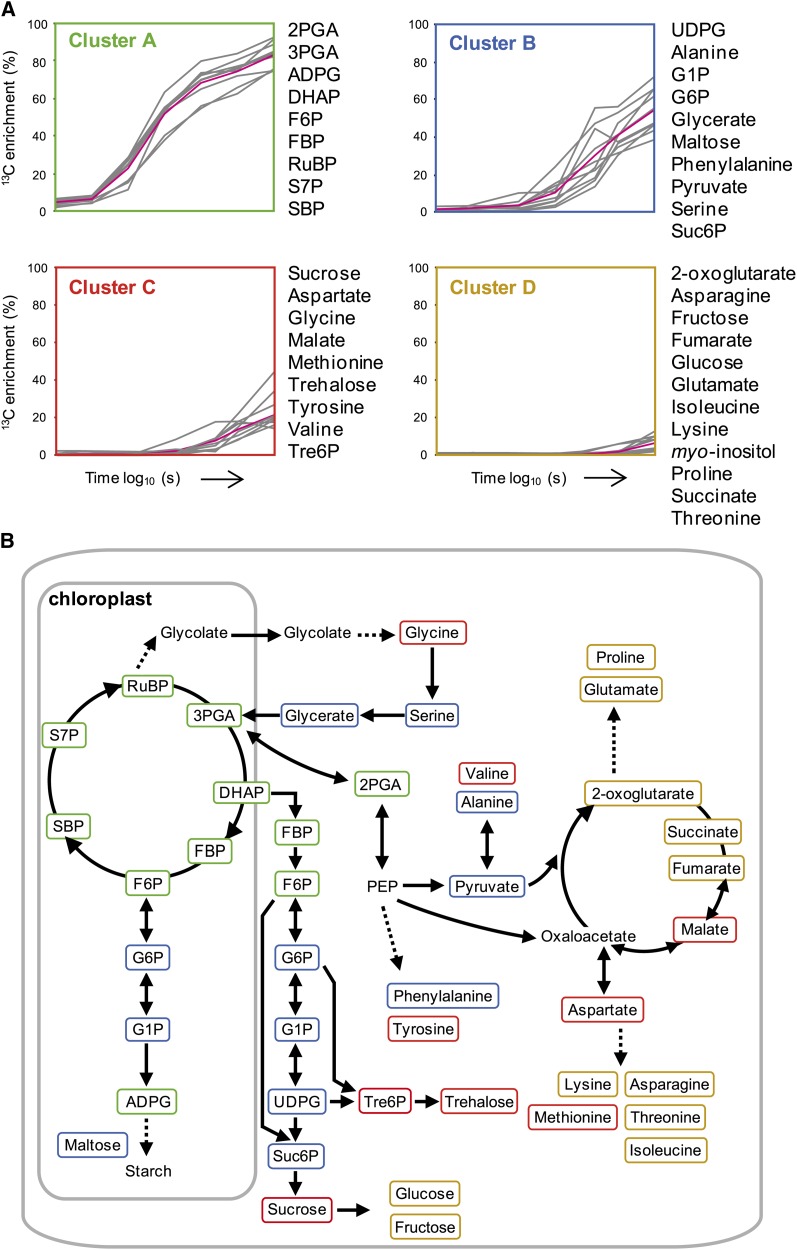
and 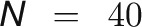is the number of metabolites. This analysis resulted in four clusters with very different labeling patterns (Figure 1A). The abbreviations used in the following text are defined in the legend of Figure 1. The first cluster, which was labeled the fastest, comprises all the CBC intermediates, together with ADP-Glc (ADPG) and 2-phosphoglyceric acid (2PGA). The second cluster consists of Glc-1-phosphate (G1P), Glc-6-phosphate (G6P), UDP-Glc (UDPG), and Suc-6-phosphate (Suc6P), which are intermediates in Suc synthesis, two photorespiratory intermediates (glycerate and Ser), maltose, pyruvate, and Ala. Gly is assigned to the third cluster, but this may be because a large proportion of the pool is not labeled at all (see below). The third and fourth clusters comprise slowly labeled metabolites (hexose sugars, organic acids, other amino acids, Tre6P, and trehalose).

Figure 1.

Overview of ¹³C Labeling Kinetics from Primary C Metabolism.

(A) k-means clustering. Gray lines show the ¹³C enrichment (calculated as in Methods) of individual metabolites, and magenta lines show average ¹³C enrichment of all metabolites in the cluster.

(B) Schematic representation of labeling kinetics. The scheme distinguishes the plastidic compartment but not the cytosol, peroxisomes, mitochondria, and vacuole. Metabolites are highlighted according to cluster following the color scheme in (A). Solid and double-headed arrows represent irreversible and reversible reactions, respectively. Dashed arrows represent conversions involving several steps.

Visualization of the clusters on a simplified scheme of photosynthetic metabolism revealed that metabolites in a given pathway usually show similar labeling kinetics (Figure 1B). Similar labeling kinetics for two metabolites implies that the metabolites are in, or are close to, isotopic equilibrium. All CBC intermediates are in close isotopic equilibrium with each other and with ADPG, which is an intermediate in the starch synthesis pathway, and 2PGA, which is located exclusively in the cytosol and is a precursor for organic acid synthesis. Similarly, G6P, G1P, UDPG, and Suc6P, which are predominantly located in the cytosol and are intermediates of Suc synthesis, cluster together, as do pyruvate and Ala, which is synthesized from pyruvate, and Tre6P and trehalose. It is reassuring that the known topology of the metabolic pathways can be broadly recapitulated by an analysis of the labeling kinetics. However, it should be noted that this analysis does not provide information about the magnitude of fluxes. Isotopic equilibrium can be established by a rapid interconversion of two metabolites, even if there is negligible net flux. Even if labeling kinetics do reflect net flux between two metabolites, the absolute value of the flux will depend on the pool sizes.

Pool Sizes and Compartmentation of Metabolites

The absolute levels of the metabolites are shown in Table 1. There is a large dynamic range, even for metabolites in the same pathway (e.g., 11.7 and 173 nmol g fresh weight [FW]⁻¹ for G1P and G6P, respectively), with the extremes being 0.55 (ADPG) and >1000 (Suc, Ser, Fru, and Glc) nmol g FW⁻¹.

Table 1. Amount and Subcellular Distribution of Compounds in Arabidopsis.

Compounds	Amount (nmol g FW−1)	Plastid (%)	Cytosol (%)	Vacuole (%)
3PGAa	200 ± 45	44	56	0
2PGAa	20 ± 4.5	0	100	0
ADPGa	0.55 ± 0.05	100	0	0
DHAPa	2.7 ± 0.6	23	77	0
F6Pa	86.4 ± 14.6	34	66	0
FBPa	8.9 ± 2.3	70	30	0
G1Pa	11.7 ± 2.4	8	92	0
G6Pa	173 ± 51	17	83	0
RuBPa	46.7 ± 8.2	83	17	0
S7Pa	28.0 ± 5.4	82	18	0
SBPa	9.6 ± 3.0	75	25	0
UDPGa	35.7 ± 5.7	0	100	0
R5Pa	1.2 ± 0.2	49	51	0
X5P+Ru5Pa	8.7 ± 2.6	100	0	0
Suc6Pa	0.82 ± 0.36	0	100	0
PEPa	52.5 ± 9.9	6	94	0
Gly	543 ± 59	28	33	39
Glycerate	169 ± 65	31	47	22
Ser	4,265 ± 326	36	22	42
myo-inositol	922 ± 108	66	0	34
Suc	3,432 ± 167	19	31	50
Trehalose	20.8 ± 3.0	50	0	50
Glu	3,682 ± 1,042	30	42	28
Malate	1,820 ± 547	0	0	100
2-Oxoglutarate	63.1 ± 18.8	6	35	59
Pyruvate	99.2 ± 35.6	24	31	45
Val	139 ± 16	32	0	68
Ile	38.9 ± 4.5	33	0	67
Pro	641 ± 90	31	24	45
Thr	459 ± 58	42	0	58
Fumarate	1,154 ± 47	0	0	100
Asp	1,050 ± 346	19	46	35
Phe	53.1 ± 6.9	48	0	52
Asn	380 ± 25	30	17	53
Fru	1,458 ± 30	0	12	88
Glc	2,669 ± 475	12	23	65
Arg	164 ± 18	42	0	58
Tyr	9.8 ± 1.2	45	0	55
Citrate	1,916 ± 505	0	0	100
Shikimate	35.9 ± 7.6	37	22	41
Succinate	84.0 ± 48.2	4	17	79
Ala	228 ± 24	16	14	70
Gln	2,349 ± 177	11	0	89
Nitrate	224,000 ± 4,100	0	0	100
Aconitate	14.5 ± 5.5	0	0	100
Isocitrate	33.5 ± 3.6	0	0	100
Lys	n.d.	n.d.	n.d.	n.d.
Maltose	n.d.	n.d.	n.d.	n.d.
Met	9.9 ± 1.4	42	13	45

Data are from three independent nonaqueous gradients. 2PGA is assumed to be only in the cytosol and its amount to be 10% of the 3PGA amount. Subcellular distributions (%) were calculated using a three-compartment model (plastid, cytosol, and vacuole). For metabolites marked with an “^a,” a two-compartment model was used (plastid and cytosol). n.d., not determined.

Pool sizes in the vacuole, plastid, and cytosol were estimated using nonaqueous fractionation (Gerhardt et al., 1987). Nonaqueous fractionation does not generate pure organelle preparations, but instead, a set of fractions that are partially enriched in different subcellular compartments. The subcellular distribution of metabolites of interest is estimated by (multidimensional) regression against marker traits (usually enzyme activities) that are specific for a particular compartment. However, it is not possible to accurately determine the subcellular level in a compartment that contains only a small proportion of the total pool (Gerhardt et al., 1987). There were large differences between metabolites in their subcellular distributions (Table 1). Some metabolites, such as RuBP, sedoheptulose-1,7-bisphosphate (SBP), Fru-1,6-bisphosphate (FBP), ADPG, UDPG, malate, fumarate, and isocitrate were largely in a single compartment, while others like dihydroxyacetone phosphate (DHAP), 3PGA, hexose phosphates, hexoses, most amino acids, and organic acids were present in two or more compartments. This resembles results from earlier studies in spinach (Spinacia oleracea) (Gerhardt et al., 1987; Riens et al., 1991; Winter et al., 1994), maize (Zea mays) (Weiner and Heldt, 1992), barley (Hordeum vulgare) (Winter et al., 1993), and Arabidopsis (Krueger et al., 2011) leaves.

The Labeling Kinetics for CBC Intermediates and Glycolytic Intermediates Follow Similar Patterns

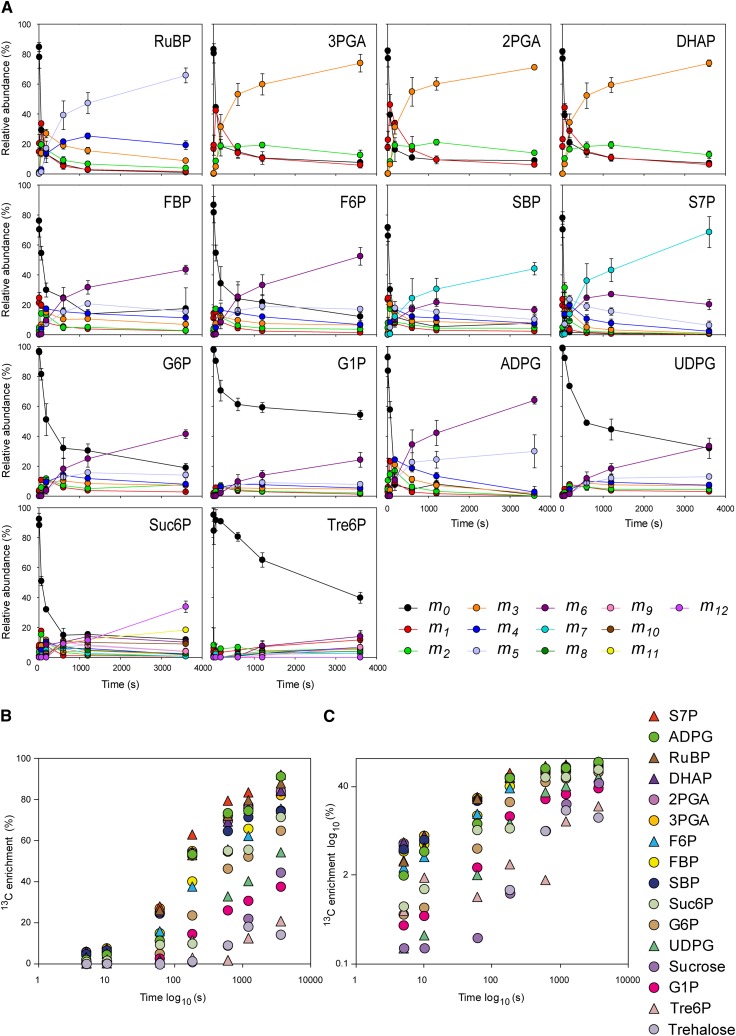
Figure 2A provides detailed information about the labeling kinetics of individual CBC intermediates. Label was incorporated at the earliest time points, leading to a rapid decrease in the proportion of the metabolite present as the ¹²C isotopomer, a progressive increase and then decline of intermediate forms, and a steady increase in the ¹³C isotopomer in which all C atoms are labeled. In Figures 2B and 2C, the average ¹³C enrichment is plotted on a log scale to better illustrate the enrichment kinetics. Even at the earliest time points, all CBC intermediates displayed similar relative labeling (see Supplemental Figure 3A online for additional plots). When ¹³C enrichment of CBC intermediates was plotted against ¹³C enrichment of 3PGA, which is the first product of the CO₂ assimilation, very high values were obtained for the Pearson correlation coefficient (see Supplemental Figure 3B online). This parallel labeling is in accordance with the very short half-times estimated from pool size and pathway stoichiometry (Arrivault et al., 2009). One exception was FBP, which was labeled more slowly than DHAP, from which FBP is formed, and more slowly than metabolites located further downstream in the CBC, like SBP, sedoheptulose-7-phosphate (S7P), and RuBP. This indicates that a significant part of the FBP pool is not directly involved in the CBC.

Figure 2.

¹³C Labeling Kinetics of Metabolites from CBC, Starch, Suc, and Trehalose Biosynthesis Pathways.

(A) Time course of mass distribution. The relative abundance of each isotopomer (m_n) for a given metabolite is represented; n is the number of ¹³C atoms incorporated.

(B) and (C) ¹³C enrichment. The x axis corresponds to the labeling time on a log₁₀ scale. In (C), the y axis corresponds to ¹³C enrichments on a log₁₀ scale.

Values (%) are average of three biological replicates ± sd, with the exception of Suc6P and Tre6P at time 180 s (n = 1). For clarity, sds are not shown in (B) and (C).

Another unexpected finding was that CBC intermediates do not rapidly become fully labeled (Figure 2; see Supplemental Figure 3A online). After 10 min, the average ¹³C enrichment was ∼70% for RuBP, 3PGA, DHAP, and S7P, 65% for SBP, and 55% for FBP and F6P. Even after 60 min, the most highly labeled metabolite, S7P, was only enriched to 92%, while the other CBC intermediates showed labeling around 70% (see Supplemental Table 2 online). One explanation for this behavior might be internal recycling of ¹²C isotope from unlabeled pools (see Discussion).

Labeling Kinetics for Intermediates in Starch and Suc Synthesis

Starch is synthesized from F6P via G6P, G1P, and ADPG in the chloroplast, while Suc is synthesized from triose-phosphates that are exported to the cytosol and converted via FBP, F6P, G6P, G1P, UDPG, and Suc6P to Suc. The labeling kinetic of ADPG was only slightly slower than labeling kinetics for CBC metabolites (Figure 2; see Supplemental Figure 3A online). It should be noted that the ADPG pool is very small, with the result that ADPG will turn over rapidly even though flux through it is much smaller than in the CBC (see later). Slower labeling was observed for F6P, followed by G6P, G1P, UDPG, Suc6P, and even slower labeling for Suc (Figure 2 and see below). These results confirm that the intermediates in Suc synthesis have a much shorter turnover time than those in the CBC (Stitt et al., 1983). Some of the F6P, G6P, and G1P are located in the chloroplast (Stitt et al., 1983; Gerhardt et al., 1987). These plastid pools are expected to label rapidly; labeling kinetics of plastid F6P should resemble those of other CBC intermediates, while those of ADPG provide a minimum estimate for the labeling kinetics of plastid G6P and G1P pools. Therefore, the labeling kinetics of the cytosolic F6P, G6P, and G1P pools would be anticipated to be even slower than those of the total pools of these metabolites.

Surprisingly, there was a marked difference between the labeling kinetics of G1P and G6P (Figure 2A; see Supplemental Figure 3A and Supplemental Table 2 online). These two metabolites are interconverted via a reversible reaction catalyzed by phosphoglucomutase. The ¹²C isotopomer decay of G1P was much slower than that of G6P. After 20 min, it almost reached a plateau in which over half of the pool still consisted of nonlabeled isotopomer. When the ¹³C isotopomers are inspected, the intermediate isotopomers rise and fall, and the fully labeled form is dominant at 20 and 60 min of G1P (Figure 2A). This isotopomer labeling pattern indicates that there are two pools of G1P, of which one is subject to labeling and the other is effectively unlabeled. This labeling pattern is unlikely to be generated by an influx of unlabeled ¹²C into G1P because this would lead to a slower but monophasic decrease of the ¹²C isotopomer and the accumulation of incompletely labeled ¹³C isotopomers. UDPG showed a similar, though not so marked, response. This contrasts with Suc6P, which after 20 to 60 min was almost as heavily labeled as the CBC intermediates and more heavily labeled than G6P, G1P, and UDPG, despite being located downstream of the latter metabolites in the pathway of Suc synthesis (Figure 2; see Supplemental Figure 3A, Supplemental Table 2, and Supplemental Data Set 1 online).

The incomplete labeling of G1P might potentially be due to another molecule that is not involved in photosynthetic metabolism but coelutes with G1P from the liquid chromatography and has the same mass and fragment ion as G1P. We checked the specificity of the G1P measurements by showing that two different enzymatic reactions that use G1P completely remove the corresponding signal (see Supplemental Figure 4 online). This behavior could not be explained by differences in pool sizes, since the G1P pool is 14 times smaller than G6P (Table 1), or subcellular compartmentation, as G1P and G6P showed a similar distribution between the cytosol and chloroplasts when Arabidopsis tissue was fractionated on nonpolar density gradients (Table 1). We also checked if the deviant response of G1P was due to a large proportion being located in cells that did not perform photosynthesis. The petiole and major veins were dissected from leaf lamina and the cut material was analyzed by LC-MS/MS. The small difference observed in the distribution of G1P and G6P (55 and 44% in petiole and 45 and 56% in leaf lamina for G1P and G6P, respectively) could not explain the incomplete labeling kinetic of G1P.

Labeling Kinetics of Sugars

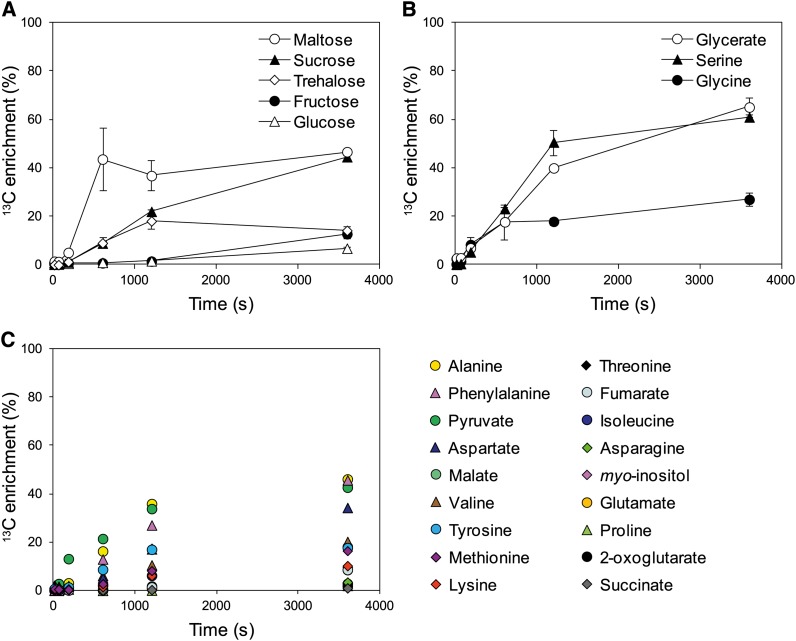
Suc was gradually labeled over the entire 60-min period, while Glc and Fru were only very slowly labeled (Figure 3A). This confirms results from earlier studies with ¹⁴CO₂ labeling (Jensen and Bassham, 1966; King et al., 1967; Stitt et al., 1980), which established that Suc is the major product of photosynthesis. Glc and Fru are formed by hydrolysis of Suc by invertase, which is evidently a slow process in Arabidopsis, at least under the experimental conditions used here.

Figure 3.

¹³C Enrichment of Sugars, Organic Acids, and Amino Acids.

Sugars (A), photorespiration cycle intermediates (B), and organic acids and amino acids (C). Values (%) are average of three biological replicates ± sd.

Maltose showed faster labeling than Suc. While ¹³C enrichment in Suc rose gradually through the entire time course (1, 9, 22, and 45% at 3, 10, 20, and 60 min), the equivalent values for maltose were 5, 44, 37, and 47% (Figure 3A; see Supplemental Table 2 online). The labeling kinetics of individual isotopomers indicates that about half the maltose pool is subject to labeling, while the other half is effectively unlabeled (see Supplemental Figure 5 and Supplemental Data Set 1 online). As the absolute pool size of Suc is much larger than that of maltose (Table 1), this does not alter the conclusion that Suc is the main product of photosynthesis. Nevertheless, it raises questions with respect to the source of the maltose.

Labeling Kinetics of Photorespiratory Intermediates

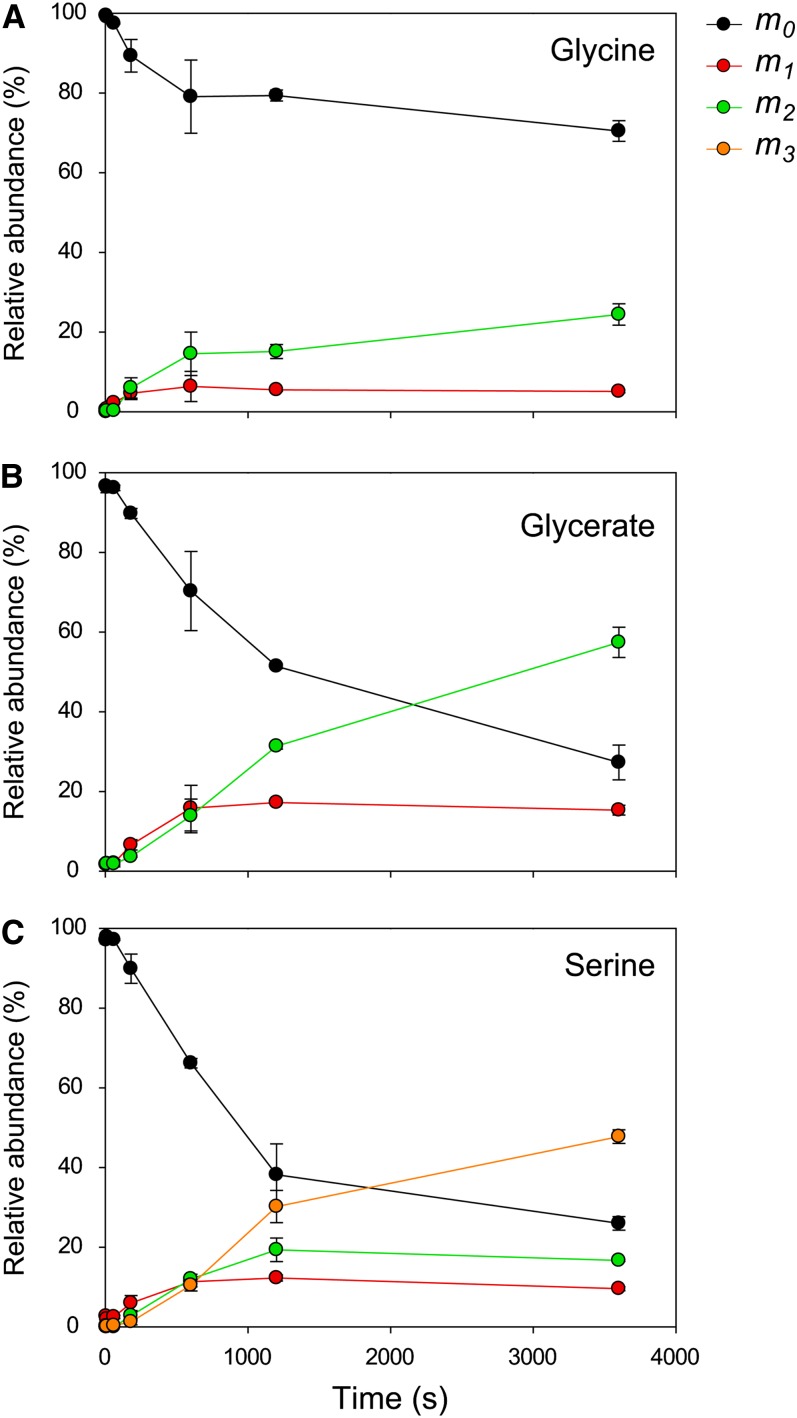
The three metabolites from photorespiration detected by our analysis (Gly, Ser, and glycerate) showed moderately rapid labeling (Figure 3B). ¹³C enrichment of Gly displayed different kinetics compared with that in Ser and glycerate. After a short lag, Gly labels rapidly for 10 min, but the speed of labeling then abruptly slows down, whereas labeling of glycerate and Ser continues to increase. The ¹²C isotopomer of Gly decreases to ∼80% of the total Gly pool in the first 10 min and remains at this value for the remainder of the experiment (Figure 4A). Furthermore, by 10 min, most of the ∼20% decrease of the ¹²C isotopomer can be accounted for by an increase of the isotopomer containing two ¹³C atoms. As for G1P, this labeling pattern strongly indicates that there are two pools of Gly in the rosette, with one (∼20% of the total pool) being involved in photorespiration, and another pool (∼80% of the total) not participating in this process. A similar but less marked response was seen for Ser and glycerate (Figures 4B and 4C).

Figure 4.

Time Course of Mass Distribution of Photorespiration Cycle Intermediates.

Gly (A), glycerate (B), and Ser (C). The relative abundance of each isotopomer (m_n) for a given metabolite is represented, and n corresponds to the number of ¹³C atoms incorporated in the metabolite. Values (%) are average of three biological replicates ± sd.

Labeling of Amino Acids and Organic Acids

Photosynthetic chloroplasts lack a complete glycolytic sequence (Stitt and Rees, 1980; Andriotis et al., 2010). Synthesis of organic acids and amino acids therefore starts with the conversion of 3PGA to 2PGA and phosphoenolpyruvate (PEP) in the cytosol. PEP is then further metabolized via pyruvate kinase (PK) and PEPc.

The labeling kinetics of 3PGA, which is present at equivalent levels in the chloroplast and cytosol (Table 1), and 2PGA, which is exclusively located in the cytosol (Stitt et al., 1980), are almost identical (see Supplemental Table 2 and Supplemental Data Set 1 online), suggesting a high exchange rate between the plastid and the cytosol (Stitt et al., 1983). PEP could not be analyzed due to the instability of this metabolite during extraction.

Pyruvate showed progressive labeling for the first 10 to 20 min but then slowed down such that only about half the total pool was labeled at all, but this part was mainly the isotopomer containing three ¹³C. As already discussed, this response indicates the presence of two pools: one that is labeled with a half-time of 10 to 20 min and one that is still effectively unlabeled even after 60 min and is presumably not involved in the pathways that use newly fixed C. The rate of labeling in the first 10 to 20 min is slower than for 3PGA but still marked, especially if the enrichment is normalized by subtracting the proportion that remains as the ¹²C isotopomer after 60 min.

Labeling of organic acids and amino acids varied with respect to the speed of labeling and the proportion labeled (Figure 3C; see Supplemental Figure 6 online). Organic acids involved in the TCAC, like isocitrate, 2-oxoglutarate, succinate, fumarate, and malate, were labeled relatively slowly, with only a small proportion being labeled at 60 min, as previously demonstrated (Tcherkez et al., 2005, 2009). As previously shown (Gauthier et al., 2010; Tcherkez et al., 2012a) the labeling of 2-oxoglutarate and Glu was also very slow. Many other metabolites downstream of PK and PEPc were also only weakly labeled, including malate, fumarate, and succinate (Figure 3C; see Supplemental Figure 6 online; see also Discussion). Some amino acids showed more rapid labeling. This included Ala and Asp, which are formed by transamination reactions from pyruvate and oxaloacetate. Ile and Val, which are synthesized from pyruvate, also displayed quite rapid labeling of a subpool, representing ∼20% of the total pool in the rosette. The relatively rapid labeling of aromatic amino acids is consistent with them being synthesized from E4P, which is an intermediate in the CBC, and PEP. Asn, Thr, Lys, and Met, which are derived from Asp, were labeled only slowly and partially.

Labeling of Tre6P, Trehalose, and Myo-Inositol

The ¹²C isotopomer decay of Tre6P was slow and almost linear over the time course of the experiment (Figure 2A; see Supplemental Figure 3A online), and, after 60 min of labeling, the unlabeled form still represented the predominant Tre6P isotopomer (∼40%). Tre6P showed mild ¹³C enrichment, with up to 21% at 60 min (Figures 2B and 2C). Trehalose also showed only mild ¹³C enrichment (i.e., up to 9, 18, and 14% at 10, 20, and 60 min, respectively) (Figures 2B and 2C; see Supplemental Table 2 online). As the trehalose pool is 370-fold smaller than the Suc pool and is much less weakly labeled, it is only a very minor product. Based on their enrichment, Tre6P and trehalose clustered in the same group (Figure 1).

Labeling of myo-inositol was very slow (see Supplemental Figure 6A online), with ¹³C enrichment of ∼3% after 60 min of labeling (see Supplemental Table 2 online).

Utilization of Experimental Data for Flux Estimation by Kinetic Flux Profiling

Methods available to model fluxes from labeling data are outlined in Supplemental Methods 2 online. To model fluxes from our data set, we chose to use kinetic flux profiling (KFP) (Yuan et al., 2006, 2008). While some of the existing approaches allow usage of different fragments and, thus, potentially more informative data sets, KFP facilitates the computation of individual reaction fluxes in complex networks from incomplete data sets. KPF uses a mass action–like differential equation model for the washout of the unlabeled fraction of metabolic pools (compare Methods and Supplemental Methods 3 online). In the original formulation, KFP was used to fit fluxes locally, using prior knowledge of the reactions that take place in the vicinity of a metabolite (see example 3 in Supplemental Methods 3 online). Here, we extend the applicability of KFP by providing a global fit to the labeling data. The global fit is performed via a simulated annealing, the results of which are then used in gradient descent, both with respect to a variance-weighted mean squared error function (see Supplemental Methods 4 online), and confidence intervals are estimated by standard procedure (see Supplemental Methods 5 online).

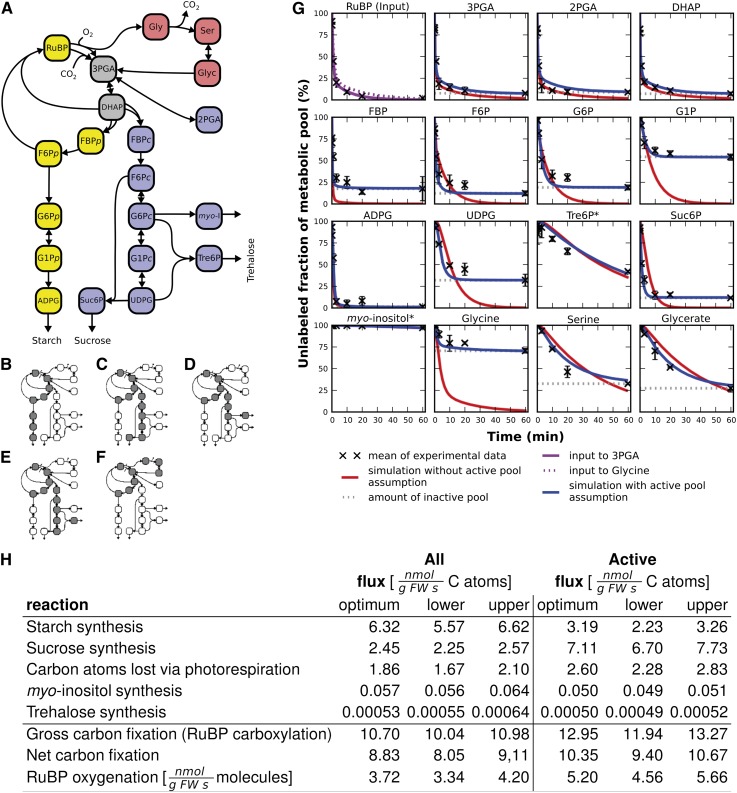
The metabolic model used in our calculations (Figure 5A; see Supplemental Methods 6 online) comprises the CBC, photorespiration, and starch, Suc, trehalose, and myo-inositol biosynthesis. Fluxes from PEP to organic acids and amino acids were omitted because inherent features of the pathway topology prevent accurate estimation of flux from the ¹³CO₂ labeling kinetics in this part of metabolism (see Discussion). As we later show, the overall flux is low, and its omission does not introduce a large error into estimates of fluxes in the remainder of photosynthetic metabolism. CBC intermediates were assumed to be located exclusively in the plastid (Table 1) except for DHAP, 3PGA, F6P, and FBP. As the plastidic and cytosolic pools of 3PGA and DHAP are in rapid isotopic equilibrium (Stitt et al., 1983), they were modeled as a single pool. Further evidence for this assumption is provided by the observation that 2PGA, which is exclusively in the cytosol, showed similar labeling kinetics to 3PGA and DHAP, which are distributed between the plastid and cytosol (Table 1, Figure 2A; see Supplemental Figure 3 online). Starch and Suc biosynthesis are known to be exclusively located in the plastid and cytosol, respectively (Stitt et al., 1980), with the plastidic and cytosolic pools showing different labeling kinetics (Stitt et al., 1983). Nonaqueous fractionation data were therefore used to explicitly measure the plastid and cytosolic pools of F6P, G6P, and G1P in our material (Table 1; see Supplemental Table 3 online) and to provide experimental evidence that Suc6P is almost exclusively located in the cytosol. Tre6P was assumed to be cytosolic. Compartmentation of the photorespiratory intermediates Gly, Ser, and glycerate was initially neglected (i.e., we assumed isotopic equilibrium between pools in different subcellular compartments). Reactions were classified as irreversible or in rapid isotopic equilibrium (Figure 5A; see Supplemental Methods 6 online) based on experimental knowledge about their in vivo reversibility (Stitt et al., 1980, 2010). To simplify the fitting procedure, RuBP labeling dynamics were used as a proxy for input to the system (see Methods) with the correction for the possibility of spawning unlabeled molecules (see Supplemental Methods 6 online) under the assumption of random label distribution in each mass isotopomer. We included Suc6P and Tre6P in the model but omitted Suc and trehalose because we could not obtain labeling information for their complete C backbone (see Supplemental Table 4 online). However, this does not affect the reliability of the model. Indeed, it means that these products are treated in the same manner as starch, for which ¹³C enrichment data were not available.

Figure 5.

Pathway Model, Elementary Flux Modes, and Flux Estimates.

(A) Pathway model. The model includes the CBC, photorespiration, and Suc, starch synthesis, myo-inositol, and trehalose synthesis. There is explicit separation of cytosolic (blue, subscript c) and plastidic pools (yellow, subscript p) that are not equilibrated by transporters. Plastidic and cytosolic pools of 3PGA and DHAP are treated as a single pool (gray) that is in isotopic equilibrium (Stitt et al., 1983) due to rapid exchange via the triose-phosphate phosphate transporter. Metabolite pools involved in photorespiration are shown in pink. Reactions are set as irreversible (single-headed arrow) or reversible (double-headed arrow), based on experimental data (Bassham and Krause, 1969; Stitt et al., 1980).

(B) to (F) Elementary flux modes of the model: synthesis of starch (B), synthesis of Suc (C), synthesis of myo-inositol (D), synthesis of trehalose (E), and photorespiration (F).

(G) Simulation of best fit. Measured data for the proportion of the total pool present as the ¹²C isotopomer are shown as crosses (±sd) and the predicted decay dynamics of the ¹²C isotopomer modeled using the unadjusted data set (red line) and after excluding the inactive pool (blue line). Gray dotted lines indicate the inactive pool. For Tre6P and myo-inositol (asterisks), which have a small total pool size, the active pool assumption is not applied. The RuBP panel shows the input models for the influx to the pool of 3PGA (purple solid line) and Gly (purple dotted line). The corresponding crosses indicate the data used for parameter estimation.

(H) Selected fluxes and rates for the two scenarios included that were used for benchmarking. The rates of Rubisco carboxylation and oxygenation are given as RuBP consumption (i.e., use of CO₂ or O₂, respectively). Fluxes were estimated for two scenarios (1) All, using unadjusted ¹²C isotopomer decay and metabolite content data sets. (2) Active, using the pool of each metabolite that is actively involved in photosynthetic fluxes. The inactive pool was nominally defined as the proportion that remains as ¹²C isotopomer at 60 min. It was subtracted from the ¹²C isotope kinetic (i.e., the 60-min value is set as zero). The absolute pool (Table 1) was also decreased in the same proportion. For each scenario, flux estimates are denoted by the optimal value obtained with the fit “optimum” and the “lower” and “upper” 95% confidence limits obtained from the Monte-Carlo simulation.

The distribution of net fluxes in the entire network can be described as a non-negative linear combination of five flux modes (Figures 5B to 5F), which are themselves in metabolic steady state. Each mode comprises the CBC, including the C fixation by Rubisco and the pathway to one of the five out-fluxes of the system (loss of CO₂ in photorespiration and the biosynthesis of starch, Suc, trehalose, and myo-inositol). The CBC is included in all five flux modes because part of the fixed C is used for RuBP regeneration to maintain the steady state. The calculations require three assumptions: (1) the labeling data are obtained from a metabolic system that is in steady state (i.e., all concentrations of metabolites and fluxes are constant) (see Supplemental Table 2 online), (2) enzymes do not display isotope discrimination, and (3) the metabolic pools are well mixed (i.e., there is negligible channeling).

Application of the extended KFP method to the metabolic model provided estimates of intracellular fluxes that provide the best overall variance-weighted fit (Press et al., 2007) to the experimentally determined pool sizes and the labeling kinetics for depletion of the ¹²C isotopomer (Figure 5; see Supplemental Table 3 and Supplemental Data Set 1 online). These reference flux estimates were benchmarked by comparing them with those expected during photosynthesis in a C₃ plant like Arabidopsis. Based on the substrate specificities of Rubisco, the rate of carboxylation should be fourfold higher than oxygenation (see Introduction and values in Sharkey, 1988). Also, Suc synthesis is approximately twofold faster than starch synthesis in Arabidopsis in the conditions used in our study (Gibon et al., 2009), while Tre6P synthesis is an order of 1000 slower (Lunn et al., 2006).

Modeled Fluxes

We first modeled fluxes assuming that the entire pool of each metabolite is involved in photosynthetic flux (Figure 5H, case All; full results are presented in Supplemental Tables 5 and 6 online). The value of the variance-weighted mean squared error of the best fit was much larger than one (the variance-weighted mean square error of 8035 and 12 estimated parameters), suggesting unreliable goodness of fit. The estimated rate of RuBP oxygenation was about a third of the rate of carboxylation (3.72:10.70), and the rate of starch synthesis was ∼2.6 times higher than the rate of Suc synthesis (6.32:2.45). While the relation between carboxylation and oxygenation is close to expectations, the model seriously overestimates the rate of starch synthesis and underestimates the rate of Suc synthesis. The 95% confidence intervals for the estimated fluxes are given in Figure 5H; interestingly, the data enforce a small and left-skewed estimate of the trehalose synthesis rate, causing it to fall out of its confidence interval. Furthermore, the fitted curves for the washout of ¹²C showed very poor agreement to measured data for Gly, UDPG, and G1P and relatively poor agreement for G6P, F6P, FBP, and Suc (Figure 5G, red lines). This analysis indicated that the poor performance of the model might be associated with the attempt to fit, in particular, the modeled fluxes to the experimental data for Gly, G1P, and UDPG. Significantly, the washout curve for the ¹²C isotopomer for each of these metabolites plateaued before 60 min, and a substantial proportion of the pool that had become labeled was present as the fully labeled ¹³C isotopomer (Figure 2; see Supplemental Figures 3 and 6 online). As already discussed, this pattern may arise due to the presence of two pools, of which only one is involved in photosynthetic metabolism.

The assumption was made that part of the total metabolite pool in the rosette does not participate in photosynthesis because it is located in the vacuole and/or nonphotosynthetic cells. The model was reimplemented after adjusting the pool sizes to only include pools that are likely to be involved in photosynthesis. In the following, this is termed “the active pool assumption.” The active pool was set as the difference between the total pool and the nominal value of the ¹²C isotopomer after 60 min. The proportion of the metabolite that was not labeled at this time was subtracted from the ¹²C isotopomer content at each time point (Figures 2 and 4; see Supplemental Figures 3 and 6 online) for the purpose of defining the washout kinetics and from the total pool (Table 1) for the purpose of defining the absolute pool size. Metabolites for which this led to a major correction include Gly, G1P, and UDPG (active pool equivalent to ∼25, 40, and 63% of the total pool, respectively; Figures 2 and 4). As already explained, the isotopomer labeling pattern for these metabolites is in agreement with the existence of two separate pools, rather than incomplete labeling of one pool. The active pool assumption was not applied to Tre6P and myo-inositol because their ¹²C isotopomers had not reached a plateau in the time span of our experiment.

As shown in Figure 5H, case Active, the modeled flux for RuBP carboxylation (12.95 nmol g FW⁻¹ s⁻¹ RuBP) was ∼2.49-fold higher than the rate of oxygenation (5.20 nmol g FW⁻¹ s⁻¹ RuBP), and the modeled rate of Suc synthesis (7.11 nmol g FW⁻¹ s⁻¹ C atoms) was ∼2.2-fold higher than the rate of starch synthesis (3.19 nmol g FW⁻¹ s⁻¹ C atoms). The modeled fluxes to myo-inositol and to trehalose via Tre6P were very low with values of 0.05 and 0.0005 nmol g FW⁻¹ s⁻¹ C atoms, respectively. The modeled curves for washout of ¹²C isotopomers closely matched the experimental data (Figure 5G, blue lines), leading to values for the variance-weighted mean squared error of 2145, which is fourfold smaller than in the previously examined scenario without the active pool assumption.

The goodness-of-fit value reflects the extent to which the model of photosynthetic metabolism matches the gathered data. The current relatively high values for goodness of fit are probably due to aspects of compartmentation, which are not yet accounted for in our underlying metabolic model. We chose to restrict the representation of compartmentation in the model to parameters for which experimental evidence was available and not to seek to improve fit by adding additional untested assumptions.

However, we note that the relatively high goodness of fit would not result from the choice of excluding fluxes from PEP to organic acids and amino acids due to the complexity of modeling these pathways. This might lead to unreliable flux estimates from our model if the excluded fluxes were high. We summed the ¹³C detected at 60 min in organic acids and amino acids downstream of PEP (Figure 1B) and compared it to the summed ¹³C found in all measured metabolites. The organic acids and amino acids accounted for only 2.6% of the total ¹³C. This is probably an overestimate, since this comparison omits ¹³C in starch and because some of the ¹³C in organic acids and amino acids is incorporated by PEPc (see Discussion for flux estimates).

Estimation of Unlabeled Influx

The model still does not address the observed incomplete labeling of the CBC intermediates, many of which are thought to be unique to photosynthesis. To address this issue, we treated the C atoms of all the CBC intermediates as one well-mixed pool to which there is an unlabeled influx of C atoms and simulated the dynamics of enrichment. This is justified by the short turnover times and near-isotopic equilibration of the intermediates (see Supplemental Figure 3B online). The labeling behavior of the CBC intermediates corresponds to that of RuBP. In this simplified model (see Supplemental Figure 7 and Supplemental Table 7 online), the labeling dynamics of this single pool is governed by five fluxes: gross fixation, net fixation (equivalent to net out-flux from the cycle), photorespiration out-flux, photorespiration influx, and an unlabeled influx (see Supplemental Figure 7A online). This model was fitted to the washout of RuBP and the enrichment of the influx to the CBC from photorespiration, described by an exponential function (see Supplemental Figures 7B and 7C online). We again used the variance-weighted mean squared error function. We note that while the influx from photorespiration to the CBC in the full flux model relied on the pool sizes of the metabolites participating in photorespiration, here, this is no longer the case as we directly used the fit to the washout dynamics of glycerate. The best fit to the experimental data for RuBP is obtained by including an additional unlabeled influx of 0.0017 nmol g FW⁻¹ s⁻¹ C atoms. This is equivalent to ∼0.02% of gross C fixation (see Supplemental Figure 7F online). This indicates that the incomplete labeling kinetics of CBC intermediates can be almost fully attributed to the influx of incompletely labeled C from photorespiration (see Supplemental Figures 7D and 7E online). This simplified model also provides an estimated ratio of carboxylation to oxygenation, with the latter being approximately threefold higher. This is in good agreement with the expectation (between three and four; see above) but is somewhat higher than the prediction from the full model implemented with the active pool assumption (only 2.49-fold higher; see above).

Robustness of the Full Model to Alterations in Experimental Values

We further examined these differences in the modeled ratio of carboxylation to oxygenation by considering further modifications of the full model in which, in addition to Tre6P and myo-inositol, we did not apply the active pool assumption to the following: (1) the two photorespiratory intermediates glycerate and Ser and (2) glycerate, Ser, and (as an example of for many possible CBC intermediates) triose-phosphates, denoted by Active 2 and 3, respectively, in Supplemental Table 8 online. The modeled ratio of carboxylation to oxygenation rose to 3.0 in Active 2, whereas it remained fairly low (2.68) in Active 3. These results show, not unexpectedly, that the modeled fluxes are sensitive to the model used, and the experimental data values that are supplied to the model.

We also investigated the robustness of the full model to other changes in experimental values. This is an alternative approach to that of Antoniewicz et al. (2006), who established the relative importance of measurements by linking flux variances with the variances of measurements (see Discussion). Supplemental Figure 8 online shows the log-fold change of the relative difference of flux estimates with respect to the reference flux estimates (given in Figure 5) for each changed input. Successive alterations of the PGA pool size between 50 and 125% of the reference values resulted in little change in CBC flux until PGA was decreased to 50%, with little effect on photorespiration and a shift to increased Suc synthesis at 125% PGA. In addition, there was a more pronounced decrease of the flux to starch at 50% PGA and only slight changes in flux to myo-inositol and photorespiration (see Supplemental Figure 8 online). Changing the pool size of ADPG to either 50 or 125% of the nominal value had little effect on CBC and photorespiration, but it resulted in an increase of flux to Suc and a decrease of flux to starch. Changes in the pool size of UDPG decreased the modeled flux through the CBC and, especially, photorespiration and also decreased starch synthesis but had little effect on the flux to Suc. Decreasing the Gly pool to 50% resulted in a decrease of all flux estimates, while decreasing it to 75 or increasing it to 125% lead to a decrease in the flux to starch and a slight increase of flux through photorespiration and to Suc. A progressive increase of the pool size of Ser from 50 to 125% of its nominal value led to a marked decrease of the modeled flux through CBC and photorespiration, with a mixture of effects on the starch and Suc synthesis. We also conducted robustness analysis to quantify the stability of the estimated flux to a simulated dramatic change in subcellular compartmentation of G6P (see Supplemental Figure 9 online). Successive alterations of the compartmentation of the G6P pool between the cytosol and chloroplast from 99:1, 80:20, 60:40, 40:60, to 1:99 resulted in only a mild decrease in flux through the CBC, negligible effects on photorespiration, an increase of fluxes to Suc, a decrease of flux to starch, and negligible effects on trehalose and myo-inositol synthesis.

DISCUSSION

We modeled photosynthetic fluxes by exposing the rosette of an intact Arabidopsis plant to ¹³CO₂, determining kinetic changes in isotope patterns of 40 metabolites of primary metabolism and analyzing the data using an extended KFP approach. Our approach to flux estimation differs from that used previously in plants (Rontein et al., 2002; Schwender et al., 2004a). These studies used steady state labeling to address a series of important biological questions, including the role of Rubisco in developing seeds, the regulation of oil seed metabolism, and the interaction between primary metabolism and biosynthetic pathways. However, steady state labeling is not applicable to photosynthesis because CO₂ is the only substrate, and the isotopic steady state will not provide an informative labeling pattern for the purpose of estimating fluxes. In a recent elegant study, Young et al. (2011) modified the formulation to facilitate modeling of isotopic nonstationary pools in Synechocystis and provide the first metabolic flux model of a photoauxotroph. Their study provided a comprehensive flux map for all CBC reactions and some side reactions, including those catalyzed by Glc-6-phosphate dehydrogenase, malic enzyme, and the photorespiratory pathway. It also identified pathways that might compromise cyanobacterial productivity. We used an extension of the KFP approach, as it allowed us to estimate fluxes through photosynthetic end products and to benchmark them against classically determined flux signatures of photosynthesis. Unlike the approach of Young et al. (2011), in which metabolic pool sizes are fitted as free parameters, we constrained the model with measured pool sizes obtained by mass spectrometry, including the use of nonaqueous fractionation, to provide information on subcellular pool sizes.

Before we discuss the model, some features of the experimental data per se should be addressed. Using k-means clustering analysis, we were able to demonstrate a clear temporal sequence of labeling, with CBC intermediates, ADPG, and 2PGA labeling rapidly, followed by metabolites in Suc synthesis and photorespiration, then pyruvate, Ala, and aromatic amino acids, with organic and other amino acids being labeled very slowly or even negligibly. These clusters closely reflect known pathway topologies. The labeling dynamics also fit those expected from pathway stoichiometry and pool sizes (Stitt et al., 1983; Gerhardt et al., 1987; Benson, 2002; Arrivault et al., 2009). In contrast with the situation in cyanobacteria (Young et al., 2011), the labeling kinetics of the CBC intermediates were not clearly discriminated. Labeling of all measured CBC intermediates closely followed that of 3PGA. The estimated half-lives of CBC intermediates are almost all <1 s in Arabidopsis leaves (Arrivault et al., 2009). Resolution of fluxes within the CBC in leaves will require even earlier harvests after introducing ¹³CO₂, which is hardly possible due to the time needed to exchange the CO₂ in the chamber and within the leaf or the use of conditions in which the rate of photosynthesis is far lower than that used in this study.

Our data set contain some rather unexpected features. These include (1) the slow labeling kinetics of FBP, (2) the rapid labeling kinetics of maltose, (3) the very incomplete labeling of UDPG and G1P compared with metabolites upstream (F6P and G6P) and downstream (Suc6P) of them in the pathway of Suc synthesis, (4) the very slow and incomplete labeling of many organic acids and especially the Gln 2-oxoglutarate aminotransferase (GOGAT) pathway intermediates Gln, Glu, and 2-oxoglutarate, and (5) the incomplete labeling of all pools including the CBC intermediates. Another important feature is the differential dynamics of labeling of the various pools, which raises the question as to which time scale is the most appropriate for modeling. In their study of ¹³C labeling of tobacco plants, Hasunuma et al. (2010) reported similar labeling kinetics for many metabolites to those reported here. However, their data analysis was restricted to estimating turnover rates.

We implemented an extension to the KFP approach that allows us to estimate photosynthetic fluxes from the ¹²C-isotopomer washout kinetics of 16 metabolites. The underlying metabolic model includes prior knowledge about pathways, the reversibility of reactions (Gerhardt et al., 1987; Arrivault et al., 2009), topology, compartmentation (Gerhardt et al., 1987; Table 1), rate of equilibration of label between compartments by the triose-phosphate transporter (Stitt et al., 1983), and experimental information about total pool sizes and their distribution between the plastid and cytosol (Table 1; see Supplemental Table 3 online). The flux estimates were benchmarked against signature flux ratios of photosynthesis previously defined by gas exchange and ¹⁴C labeling. For this purpose, we used the ratio of the carboxylation and oxygenation reactions of Rubisco and ratio of the fluxes to Suc and starch. In Arabidopsis at ambient CO₂, these should be approximately (2.5 to 3):1 and 2:1, respectively (Häusler et al., 2000; Cegelski and Schaefer, 2006; Gibon et al., 2009; Bauwe et al., 2010). It should be noted that although the photorespiratory flux estimate in Synechocystis (Young et al., 2011) was even lower than the value cited above, this is likely to be explained by an efficient C concentrating mechanism in this species that suppresses the oxygenase reaction of Rubisco (Kaplan and Reinhold, 1999).

Flux modeling using unadjusted experimental data returned flux ratios that were far from the expected ratios. Furthermore, for many metabolites, the modeled washout kinetics showed a poor fit to the experimental data. Inspection of the full labeling kinetics of individual metabolites revealed that in many cases only part of the total metabolite pool is involved in photosynthesis. Flux modeling using pool sizes that had been corrected to consider only pools actively participating in photosynthetic metabolism gave values of 2.5:1 and 2.2:1 for the carboxylation/oxygenation ratio and the Suc/starch ratio, respectively, a good agreement between the modeled washout kinetics and the experimental data. A further flux, which modeled to trehalose via Tre6P, was very low (0.0005 nmol g FW⁻¹ s⁻¹ C atoms). This corresponds to 0.15 nmol Tre6P g FW⁻¹ h⁻¹, which is in agreement with the synthesis rate of Tre6P measured by Lunn et al. (2006) after the addition of Suc to starved seedlings. Interestingly, realistic estimates for the carboxylation/oxygenation ratio were obtained without information about labeling of the initial photorespiratory intermediate 2-phosphoglycolate. While it will be important to extend our technical platform to include this metabolite, among others, this points to the robustness of our approach and also shows that flux estimates can be obtained using larger and more slowly labeled pools like Gly, Ser, and glycerate.

The correction of pool sizes to exclude pools that do not participate in photosynthesis is supported by the labeling kinetics and, in the case of Suc synthesis, by a comparison of the labeling kinetics of metabolites located further downstream in the pathway. Nevertheless, this analysis begs the question how active and inactive metabolite pools are discriminated. The most likely explanation is spatial compartmentation, which could occur at various levels, including cellular, subcellular, and within-organellar microcompartmentation. For Gly, Ser, glycerate, and many organic acids, nonaqueous fractionation indicated that a large part of the total pool is indeed located in the vacuole. For UDPG and G1P, we evaluated subcellular distribution and whether the pool sizes of these metabolites were different in parts of the leaf that are not photosynthetically active, namely, the venal tissues. Neither approach pinpointed the location of an inactive pool; nevertheless, two other possibilities remain. First, bioinformatic analysis of Arabidopsis metabolite profiles revealed patterns suggestive of microcompartmentation of metabolism within organelles (Krueger et al., 2011), as previously postulated for a pool of UDPG that is involved in cellulose synthesis (Amor et al., 1995). Secondly, recent studies in Arabidopsis and potato implicate the presence of as yet unidentified G1P transporters at the plastid and plasma membranes (Fettke et al., 2011). Further analyses will be required to fully understand the exact mechanisms by which the active and inactive pools of these metabolites are separated. Given the rapid advance of techniques for spatial resolution of metabolism (Aharoni and Brandizzi, 2012), it is likely that the exact reason underlying the unexpected labeling may become apparent in future experiments.

Returning to other unexpected features of our data, the slow labeling of FBP indicates that a substantial part of the total FBP pool is not directly involved in the CBC. This is unlikely to be explained by slower labeling of a cytosolic pool because the latter is small (Table 1) and is in isotopic equilibrium with the triose-phosphates (Stitt et al., 1983). One possible explanation might be binding of FBP on Rubisco active sites (Von Caemmerer and Quick, 2004).

Another noteworthy feature is the rapid labeling of maltose. Maltose is produced during starch degradation at night (Stitt et al., 2010). However, it is unlikely that rapid labeling of maltose is a result of transient starch degradation, since the labeling is very fast, meaning that starch granules would have to be rapidly degraded in the light, which has not been observed (Zeeman et al., 2002) except under special atypical conditions (Stitt and Heldt, 1981). A more likely hypothesis is de novo biosynthesis of maltose in the light, possibly in the chloroplasts. Mutagenesis of AGPase to promote in vivo activity led to an increase in maltose levels in the light (Hädrich et al., 2012). ¹⁴CO₂ labeling studies of spinach chloroplasts detected very-short-term labeling of maltose from ¹⁴CO₂ (Linden et al., 1975; Schilling, 1982; Linden and Schilling, 1984). As this molecule was asymmetrically labeled, its formation cannot be attributed to the action of β-amylase on starch. This mechanism would also explain why the maltose is not completely labeled in our experiments.

The labeling kinetics of organic acids are extremely slow. Until recently (Zell et al., 2010), these had been considered to be minor products of photosynthesis, although net synthesis is required to provide C skeletons for amino acid synthesis. It was also surprising that GOGAT pathway intermediates like Glu and 2-oxoglutarate show very slow labeling. Fluxes through the GOGAT pathway include the refixation of ammonium released by Gly decarboxylase and are therefore of the same order as the rate of photorespiration (Foyer et al., 2009). Indeed, we estimated that <2.6% of the fixed ¹³C moved into organic acids and amino acids that lie downstream of pyruvate, supporting the small flux through amino acids of negligible effect to the other flux estimates (see Supplemental Table 9 online).

Net synthesis of organic acids and organic acids requires an anaplerotic reaction, which is catalyzed by PEPc in plants. PEPc incorporates ¹³CO₂ into the C1 position of oxaloacetate. As a result of rapid equilibration with malate and fumarate, the label is rapidly randomized between the C1 and C4 positions (Tcherkez et al., 2005). This label will then be converted to other organic acids via the TCAC. It should be noted that total ¹³C incorporation into organic acids and amino acids will therefore overestimate the flow of ¹³C from the CBC. Pyruvate can be formed via PK or from malate via NADP- or NAD-malic enzyme or via a direct side product of Rubisco, in which pyruvate is produced at ∼0.7% of the rate of 3PGA (Pearce and Andrews, 2003). It is not facile to use mass spectrometric data to discriminate between the fluxes toward organic acid and amino acid formation via PEPc, malic enzyme, the side reaction of Rubisco, PK, and pyruvate dehydrogenase. This would require site-specific labeling data, which could only be obtained by a suite of enzymatic cleavage reactions, resulting in a massive increase in sample number and data complexity. For this reason, we did not attempt to model fluxes from the CBC to organic acids and amino acids.

One potential way to circumvent this problem in the future may be to attempt simultaneous ¹³C and ¹⁵N feeding studies. Another perhaps simpler approach would be to extend the mass spectrometry analysis platform using NMR to evaluate positional isotopomers at the atomic level (Tcherkez et al., 2011, 2012b). However, it is important to note that such analyses are currently technically restricted for two reasons. First, due to sensitivity issues, NMR experiments still require large sample sizes (Kruger et al., 2008); to perform such experiments would thus necessitate the growth of a massive number of plants and require a huge acquisition time. Second, to date, a method for efficient and rapid ¹⁵N labeling of leaf material is not available. These hurdles notwithstanding, such an experiment remains an exciting future prospect, as is the extension of modeling strategies to further characterize the fluxes in these pathways.

At a qualitative level, the low level of label in GOGAT intermediates implies that 2-oxoglutarate is internally recycled, with very little de novo synthesis and/or is obtained from a preexisting unlabeled pool. In agreement with this notion, it has been proposed that 2-oxoglutarate is synthesized in the light from a preexisting pool of citrate (Tcherkez et al., 2012a, 2012b). More generally, the slow labeling of organic acids and amino acids derived from them is consistent with the idea that glycolysis and the TCAC are inhibited in the light, when the TCAC operates in a noncyclic manner (Tcherkez et al., 2009, 2012a; Sweetlove et al., 2010). The very low enrichment in organic acids like isocitrate, fumarate, and malate can also be explained because the vast majority of these metabolites are located in the vacuole (Table 1; Lips and Beevers, 1966a, 1966b; Steer and Beevers, 1967).

Another interesting feature of our data set is the incomplete labeling of the CBC intermediates, including metabolites that are unique to the CBC like SBP and RuBP. A similar finding was reported in a recent study in tobacco leaves (Hasunuma et al., 2010) as well as an earlier, more focused study that determined the ¹³C labeling of the 3PGA pool in Quercus rubra (Delwiche and Sharkey, 1993). Incomplete labeling of CBC intermediates indicates the presence of an unlabeled influx that dilutes the ¹³CO₂ that is fixed by Rubisco and/or dilutes metabolic pools involved in regeneration of RuBP. Our computational analysis demonstrates that the incomplete labeling of CBC intermediates can be almost completely explained by the incomplete labeling of the C that returns to the CBC from photorespiration. It is likely that this is the result of a slow exchange of labeled C in the pools of Gly, Ser, and glycerate that are directly involved in photorespiration with pools of Gly, Ser, and glycerate that are not directly involved in photorespiration and act as a temporary reservoir of unlabeled C that is slowly introduced into the CBC (see above). A best fit of the simplified model was obtained by adding a further very small additional influx of unlabeled C, equivalent to ∼0.02% of the gross fixation. This could derive from a variety of sources, including very slow degradation of starch (Weise et al., 2006) and refixation of CO₂ that is respired from unlabeled substrates in nonphotosynthetic cells in the leaf.

The simplified model yielded a slight increase in the value for the rate of carboxylation relative to oxygenation (to 3.02, compared with 2.87 and 2.49 in the full model implemented with total pools and with active pools, respectively). The estimate from the simplified model is closest to the expected range of 3 to 4 (Sharkey, 1988; Cegelski and Schaefer, 2006), while when the full model is used, a better fit for this output, but not for other outputs, was obtained when it was implemented with total pools rather than the active pool assumption. We interpret this as indicating that these models represent approximations that do not fully represent a more complex situation, where there is probably partial label exchange between two or more pools of various intermediates. Nevertheless, the relation between the modeled rates of carboxylation and oxygenation are relatively robust against these changes in the model and experimental inputs. The same held for tests in which the levels and compartmentation of other metabolites were altered. This is an alternative approach to robustness to that used by Antoniewicz et al. (2006), who established the relative importance of measurements by linking flux variances with the variances of measurements. However, in the context of a plant leaf, which contains many cell types and subcellular compartments, sources, or errors may not be fully captured by just considering the variance of the data. It also requires consideration of the potential impact of multiple metabolite pools, which may participate to differing degrees in the flux in question.

In summary, we were able to establish an experimental setup to perform short-term ¹³CO₂ labeling of Arabidopsis rosettes, in a manner that allowed rapid quenching of metabolism, to determine the labeling kinetics of 40 metabolites of primary C metabolism and to model the major fluxes during photosynthesis via kinetic flux profiling. Implementation of an approach that discriminates between active and inactive metabolite pools and only takes the active pools into consideration returned flux ratio estimates in keeping with those canonically reported. This finding demonstrates that it is possible to use stable isotope feeding alongside mass spectrometry profiling to gain insights into the dynamics and fluxes in a metabolic system as complex as photosynthesis in a C₃ leaf. Our study also indicates the importance of information about metabolite compartmentation and suggests that its use will be a prerequisite for modeling of photosynthetic, and probably other metabolic processes, in multicellular eukaryotic tissues. Future application of the response of the metabolic network of photosynthesis to environmental or genetic perturbation will be essential to deepen our understanding of the metabolic regulation of this key process and may have implications for the improvement of crop yield and ultimately the redirection of C to high value natural products. In addition, utilization of this approach to study the even more complex photosynthesis pathways, like that exhibited in C₄ plants such as maize, may provide important enabling insights into harnessing this pathway in synthetic biology approaches to enhance the efficiency of photosynthesis of C₃ species.

METHODS

Chemicals

¹³CO₂ (isotopic purity 99 atom percentage) was purchased from Campro Scientific. All other chemicals were purchased from Sigma-Aldrich, Roche, or Merck.

Plant Growth

Arabidopsis thaliana, accession Columbia-0, was grown under 8/16-h day/night cycles at an average irradiance of 120 µmol m⁻² s⁻¹, temperatures of 22/20°C, and 50% relative humidity. Plants were grown in individual 6-cm-diameter pots, with water/gas-permeable plastic foil (Aquafol) between the rosette and the soil. Plants with fully expanded 5-week-old rosettes (stage 3.90; Boyes et al., 2001) were used for ¹³CO₂ feeding experiments and subcellular metabolite level determination.

¹³CO₂ Feeding Experiments

The gas mixture was prepared using mass flow controllers (Brooks Instrument), one controller per gas type. Each gas type was supplied separately at a fixed flow rate and mixed in a single PVC tube, resulting to a final concentration of 78% N₂, 21% O₂, 400 ppm ¹³CO₂, and a final flow of 5 liters min⁻¹. After passing through a humidifier, the gas mixture was supplied to the inside of the transparent labeling chamber (Magenta GA-7 plant culture box), of volume 380 mL, by three transparent PVC pipes placed on the top rear of the box in such a way that the gas stream was directed to the plant rosette. These highly transparent boxes allow the transmission of 97% of the irradiance. Therefore, a photon flux density of 115 µmol m⁻² s⁻¹ (as measured in the box with a LI-250A light meter; Li-Cor) was provided by a FL-460 lighting unit from Walz. The labeling chamber was continuously washed with this mixture through the whole experiment.

Within a maximum of a few seconds, it is possible to completely remove ¹²CO₂ from the atmosphere in the labeling chamber and maintain this state throughout the entire experiment. To estimate the removal rate of ¹²CO₂, an empty labeling chamber was washed with the same gas mixture as during the experiment (flow 5 liters min⁻¹), and the ¹²CO₂ concentration was tracked using an infrared CO₂ gas analyzer (Li-Cor LI-800). After 3 to 5 s, the ¹²CO₂ concentration was negligible, approximating 0 ppm. In addition, we estimated the time of the exchange of gases in the chamber by constructing a mathematical model: Given that the volume of the chamber (V) and the gas flow (F) are known, the influx and efflux are the same, and unlabeled CO₂ is rapidly mixing with ¹³CO₂ inside the chamber, the time course of the ¹²CO₂ content inside the chamber can be described by an exponential function, whose half-life-period is given by 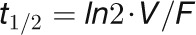. The estimated 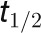for the gas in the chamber with volume of 380 mL is 3 s. In addition, we calculated the residence time (volume/flow rate) in the humidifier to be 6 s (flow rate of 5 liters min⁻¹ and volume of 500 mL). Since the gas flow was constant during the entire experiment, the residence time of the humidifier should not affect the ¹²C wash out time in the box.

The experiment was started 2 h after the onset of light in the growth chamber, and the last labeled plant was harvested 1 h before the offset of lights. Individual plants in their pot were quickly moved from the growth chamber to the labeling chamber (<5 s) and quenched 5 or 10 s and 1, 3, 10, 20, or 60 min after the start of labeling in a random manner. Three biological replicates were obtained for each labeling condition. Metabolism was quenched directly in the chamber by pouring a large volume of liquid nitrogen over the rosette through a funnel that was placed through a small outlet in the side of the box and held just above and slightly to the side of the plant in such a way as to avoid shading the rosette. All frozen plant material above the plastic foil was collected and stored at −80°C.

Determination of Metabolite Levels and Isotope Distributions

Prior to utilization, plant material was ground to a fine powder using a Retsch ball-mill. For GC-TOF-MS, the levels of all metabolites were quantified essentially as described by Roessner et al. (2001). Metabolites were extracted from 100 mg (fresh weight) of frozen plant powder, and derivatization was performed as described by Fiehn et al. (2000). The GC-TOF-MS was run using the same settings as detailed by Lisec et al. (2006). The resulting chromatograms were processed using TagFinder software. Analytes were manually identified using the TagFinder plug-in of the TagFinder software (Luedemann et al., 2008) and the reference library mass spectra and retention indices housed in the Golm Metabolome Database (http://gmd.mpimp-golm.mpg.de; Kopka et al., 2005). Interpretation of gas chromatography–electron impact fragments derived in GC-TOF-MS analysis were performed based on previously published detailed EI fragmentation pattern of trimethylsilylated and methoxiaminated carbohydrates (DeJongh et al., 1969; Laine and Sweeley, 1973; MacLeod et al., 2001; Sanz et al., 2002) and amino acids (Abramson et al., 1974; Leimer et al., 1977). Furthermore, interpretation was supported by the mass shifts observed upon in vivo ¹³C labeling (Huege et al., 2007). Since mass fragments comprising the full metabolite C backbone, such as M⁺ (molecular ion) or M-15⁺ (mass fragment generated by the loss of CH₃⁺ group), were often mostly present at low intensities or even below their detection limit, alternative fragment ions for mass isotopomer analysis, proposed by Huege et al. (2007), were used (see Supplemental Table 4 online).

For LC-MS/MS quantification, metabolites were extracted from 15 mg (fresh weight) of frozen plant powder as described by Lunn et al. (2006) and Arrivault et al. (2009). Suc6P and Tre6P were measured as described by Lunn et al. (2006). Other measurements were performed as described previously (Arrivault et al., 2009), but mass spectrometry settings were adapted for the quantification of all isotopomers of the compounds as shown in Supplemental Table 10 online. The run was divided into four segments with dwell times of 100 ms or less, adapted to obtain a minimum of 15 scans per chromatogram. For the nucleotide sugars ADPG and UDPG, the isotopomers were restricted to labeling occurring in the hexose, but the fully labeled isotopomers were also monitored. For the partially labeled isotopomers of 2-oxoglutarate and succinate, two labeling alternatives were possible and monitored, considering the label being present in the product ion or not. For these isotopomers, signal peak areas from both alternatives were summed. In the case of 2PGA and 3PGA, which could be separated by the liquid chromatography condition used, the chromatograms obtained with the standards were of poor quality compared with the ones observed in plant extract. Consequently, quantification was not performed for these compounds, and the data presented are solely based on signal peak areas obtained in extracts. The obtained peaks were integrated using the Thermo Finnigan processing software package LCQuan-2.5.

The electron impact fragmentation of trimethylsilylated and methoxiaminated metabolite derivatives (analytes), which are observed in routine metabolite profiles using gas chromatography–mass spectrometry (GC-MS) technology (see for example Fiehn et al., 2000; Lisec et al., 2006), require thorough interpretation of gas chromatography–electron impact fragmentation patterns and knowledge concerning the sum formula of each analyzed mass fragment when using ¹³C-isotope labeling. By contrast, the LC-MS/MS method allows the quantification of the whole C backbone of the metabolites, which is highly beneficial when calculating ¹³C fractional enrichment. Since mass spectrometry detects ionized compounds separated by their mass-to-charge ratio, the mass-to-charge ratio of ¹³C-labeled compounds increases by an amount that equals the number of incorporated ¹³C atoms (see the example in Supplemental Figure 2 online). Therefore, by determining the ratio of intensity of the monoisotopic ion and its isotopic ions, the ratio of stable isotope labeling can be quantified (Hasunuma et al., 2010).

Both GC-TOF-MS and LC-MS/MS matrices were subsequently processed using the Corrector software tool (http://www-en.mpimp-golm.mpg.de/03-research/researchGroups/01-dept1/Root_Metabolism/smp/CORRECTOR/index.html). After correction, quantification of the metabolites was performed based on calibration curves obtained with authentic standards whose matrices were also corrected. Relative isotopomer abundance (m_n) for each metabolite in which n¹³C atoms are incorporated is calculated in mass fragments (Wittmann and Heinzle, 1999; van Winden et al., 2002; Huege et al., 2007) from GC-MS analysis and in whole molecules from LC-MS/MS analysis by the following equation:

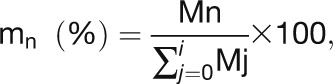where M_n represents the isotopomer abundance for each metabolite. The ¹³C enrichment of the metabolite possessing i C atoms is calculated as follows:

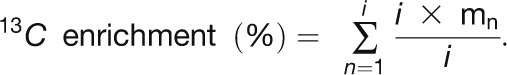Removal of G1P by Enzymatic Reactions

All reactions (final reaction volume 165 µL) contained 150 μL of plant extract (corresponding to 10 mg FW material), 20 mM HEPES-KOH, pH 8, and 5 mM MgCl₂. To remove G1P from the extracts, either 0.4 units of phosphoglucomutase, 0.7 units of glucose 6-phosphate dehydrogenase and 0.75 mM NADP, or 0.5 units of UGPase, 0.2 units of PPase, and 0.75 mM UTP were added to the reaction mixtures. Control reactions were performed as described above, but enzymes were omitted. Mixtures were incubated at 30°C for 1.5 h, heated at 100°C for 2 min, and precipitated proteins removed by centrifugation (14,000 rpm, 5 min). For LC-MS/MS measurements, 10 μL of the mixtures was analyzed.

Nonaqueous Fractionation

For determination of subcellular metabolite levels, cellular compartments were separated using density gradient centrifugation under nonaqueous condition as described in Krueger et al. (2011). Metabolites were extracted from dried fraction aliquots and quantified by GC-TOF-MS (Roessner et al., 2001) and LC-MS/MS (Lunn et al., 2006; Arrivault et al., 2009). Based on enzymatic markers, subcellular metabolite distributions were computed using the BestFit command line tool (Krueger et al., 2011).

Extended KFP and Robustness Analysis

KFP allows for determining reaction fluxes based on a mass-action-like differential equation model for the washout of the unlabeled fraction of metabolic pools, whereby

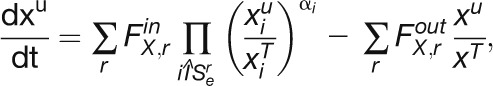where is the unlabeled content of metabolite 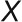, 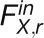is the influx to metabolite 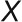from reaction 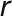, and 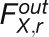denotes the out-flux from . The model of central C metabolism is comprised of 30 mass-action-like differential equations, shown in Supplemental Methods 6 online. The net fluxes of each reaction can be expressed as a positive linear combination of six independent modes, which describe the way of a fixated C atom to an out-flux of the system. Since each of these out-fluxes is normalized to one C atom per second, the coefficients of the positive linear combination are the parameters to be estimated. Unlike the original KFP approach whereby local fits are conducted for each reaction in the model, we provide a global fit of the model to the experimental data. We use the time-resolved washout of the unlabeled fraction for all pools as well as nonaqueous fractionation data for the compartmentalized pools (see Supplemental Data Set 1 and Supplemental Tables 3 and 7 online). Double-exponential function is fitted to the washout kinetics of RuBP for the purpose of estimating individual fluxes (see Supplemental Table 3 online), while an exponential function with an offset is fitted to the washout kinetics of glycerate (see Supplemental Table 7 online) to estimate the unlabeled influx to explain the incomplete labeling of CBC intermediates. In the case of RuBP, the input function is corrected for the possibility of spawning unlabeled molecules (see Supplemental Methods 6 online). For compartmentalized pools, the weighted sum according to the nonaqueous fractionation data is fitted. Simulated annealing approach, followed by quasi-Newton optimization, are used to estimate the model parameters with variance-weighted mean squared error function (see Supplemental Methods 4 online). The correspondence between the reactions and fluxes is given in Supplemental Table 8 online. For each fit, 30 repetitions are performed and the best result is reported. The estimated net flux of a reaction is given in of C atoms entering or leaving a particular pool participating in the reaction, except for carboxylation and oxygenation, for which the unit is RuBP. The active pool for each metabolite is given by the fraction of the pool that labeled 60 min into the experiment, termed active pool assumption. For compartmentalized pools, the weighted sum according to the nonaqueous fractionation data is fitted only to the active pool. Confidence intervals for the flux estimates are obtained from Monte Carlo sampling (see Supplemental Methods 5 online).

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure 1. Schematic Visualization of the Chamber Used for Arabidopsis Rosette Labeling.

• Supplemental Figure 2. Exemplary Mass Distribution of 3PGA.

• Supplemental Figure 3. ¹³CO₂ Labeling Kinetics of Metabolites from Calvin-Benson Cycle, Starch, Sucrose, and Trehalose Biosynthesis Pathways.

• Supplemental Figure 4. Removal of G1P by Enzymatic Reactions.

• Supplemental Figure 5. Time Course of Mass Distribution of Maltose and Sucrose.

• Supplemental Figure 6. Time Course of Mass Distribution of Sugars, Amino Acids, and Organic Acids.

• Supplemental Figure 7. Simplified Model for Estimating Unlabeled Influx.

• Supplemental Figure 8. Variation of Pool Sizes.

• Supplemental Figure 9. Variation in Compartmentalization Data for G6P.

• Supplemental Table 1. Metabolic Content of ¹³CO₂-Labeled Arabidopsis Rosettes.

• Supplemental Table 2. ¹³CO₂ Enrichment of Metabolites.

• Supplemental Table 3. Parameters and Data Used for Flux Estimates.

• Supplemental Table 4. Gas Chromatography–Electron Impact Fragmentation Patterns.

• Supplemental Table 5. Reactions, Flux Notation, and Flux Estimates.

• Supplemental Table 6. Reactions, Flux Notation, and Exchange Flux Estimates.

• Supplemental Table 7. Parameters and Data Used for the Simplified Model.

• Supplemental Table 8. Comparison of Flux Estimates Regarding the Different Model Assumption.

• Supplemental Table 9. Comparison of Flux Estimates Regarding the Influence of an Additional Flux Mode toward Amino Acid Synthesis.

• Supplemental Table 10. Specific Isotopomer-Dependent MS Parameters Used in Selected Reaction Monitoring.

• Supplemental Methods 1. Compartmentalization and Major Pathways of Carbon Metabolism in a Photosynthetically Active Leaf.

• Supplemental Methods 2. Labeling Strategies.

• Supplemental Methods 3. Introduction to Extended Kinetic Flux Profiling.

• Supplemental Methods 4. Optimization Fit to the Mass Spectrometric Data.

• Supplemental Methods 5. Estimation of Confidence Interval by Monte Carlo Simulation.

• Supplemental Methods 6. Application to Central Carbon Metabolism.

• Supplemental Data Set 1. Relative Isotopomer Abundance.

Glossary

Rubisco

ribulose-1,5-bisphosphate carboxylase/oxygenase

RuBP

ribulose-1,5-bisphosphate

3PGA

3-phosphoglycerate

2PGA

2-phosphoglyceric acid

CBC

Calvin-Benson cycle

PEPc

phosphoenolpyruvate carboxylase

GC-TOF-MS

gas chromatography–time-of-flight–mass spectrometry

LC-MS/MS

liquid chromatography–tandem mass spectrometry

TCAC

tricarboxylic acid cycle

ADPG

ADP-Glc

G1P

Glc-1-phosphate

G6P

Glc-6-phosphate

UDPG

UDP-Glc

Suc6P

Suc-6-phosphate

FW

fresh weight

SBP

sedoheptulose-1,7-bisphosphate

FBP

Fru-1,6-bisphosphate

DHAP

dihydroxyacetone phosphate

S7P

sedoheptulose-7-phosphate

PK

pyruvate kinase

Tre6P

trehalose-6-phosphate

KFP

kinetic flux profiling

GOGAT

Gln 2-oxoglutarate aminotransferase

GC-MS

gas chromatography–mass spectrometry