Assessing the Comparative-Effectiveness of Antidepressants Commonly Prescribed for Depression in the US Medicare Population

Abstract

Background

Depression is among the most common chronic illnesses in the US elderly Medicare population, affecting approximately 11.5% of beneficiaries with estimated costs of about US$65 billion annually. Patients with depression are typically treated with antidepressants - most commonly the Selective Serotonin Reuptake Inhibitors (SSRIs). SSRIs vary substantially in their costs, side effect profiles and convenience of use. All these factors might affect medication adherence and subsequently down-stream medical costs.

Aims of Study

To assess the comparative-effectiveness of three antidepressants (escitalopram, citalopram, sertraline) commonly-prescribed for depression in Medicare.

Methods

We used pharmacy and medical claims data for a 5 percent national random sample of Medicare beneficiaries who were diagnosed with depression in 2008 and followed until 12/31/2009. Key measures included drug spending, medication adherence to antidepressants, down-stream non-drug medical costs at three levels: all, psychiatric and depression related costs. Three methods were conducted to test robustness: generalized linear regression (GLM), propensity score matching, and instrumental variables (IV) approach. For the instrumental variables approach, we used a two-stage residual inclusion model, using geographic variation in the use of the various drugs as instruments. Specifically, we calculated the ratio of the number of individuals who used each drug to the total number of individuals using any antidepressants at the 306 Dartmouth hospital-referral regions.

Results

The regression and the propensity score matching method each showed that patients using escitalopram had significantly worse adherence, higher drug costs, and higher medical costs than patients using either citalopram or sertraline. However, our IV analysis yielded different results. While drug costs remained significantly higher for escitalopram patients, we found that escitalopram users had lower non-drug medical spending than patients who used citalopram, which was enough to offset the higher drug costs. The instrumental variables results also suggested that sertraline users had lower non-drug medical costs than citalopram users. The differences between sertraline and escitalopram were not statistically significant for medical spending, but sertraline users had lower drug costs and better adherence than escitalopram users.

Discussion

The IV method yielded somewhat different results than the GLM regressions and the propensity score matching methods. Once we controlled for selection bias using the instrumental variables, we found that escitalopram is actually associated with lower medical spending. One interpretation is that the IV approach mitigates selection biases due to unobserved factors that are not controlled in regular regressions. However, one conclusion remains the same: in every model, we found that sertraline was at least as cost-effective as or more cost-effective than the other drugs.

Limitations

Potential unobserved factors affecting the choice of three antidepressants are possible.

Implications for Health Policies

All methods indicated that sertraline is the most cost-effective drug to treat depression. Substantial savings to Medicare could be realized by using more cost-effective antidepressants such as sertraline.

Implications for Further Research

Geographic variation in the use of prescription drugs has been underutilized as an instrumental variable in comparative-effectiveness research. Our study demonstrates that it can help to control for selection biases in observational data.

INTRODUCTION

Depression is among the most commonly diagnosed chronic illnesses in the elderly Medicare population, affecting approximately 11.5% of beneficiaries with estimated costs of about $65 billion annually.^1,2 According to the US National Institute of Mental Health, in any given year, an estimated two million Americans over the age of 65 (out of about 35 million) have a significant depressive illness, and another five million may be struggling with depressive symptoms.³ Depression is also associated with higher medical comorbidities and co-morbid depression has a negative effect on self-care among patients, worsening their social and physical functioning, their health status, and increasing total medical expenditures.^4–7

Patients with depression are typically treated with antidepressants. Maintenance treatment using antidepressants in older adults has been shown to reduce relapse and the recurrence of depressive episodes.⁸ The most widely used antidepressants are the Selective Serotonin Reuptake Inhibitors (SSRIs), which have similar therapeutic effects but varying costs. For example, costs differ substantially among three most commonly prescribed SSRIs among US Medicare beneficiaries: escitalopram (Lexapro) is still on patent and costs $119 for 30 20mg tablets (according to drugstore.com); an equivalent therapeutic dosage of citalopram costs $27 for 30 40mg tablets) and sertraline costs $16 for 30 100mg tablets).

One recent meta-analysis of randomized control trials found that escitalopram was more effective than citalopram (measured by response and dropout rates), but that sertraline was not significantly different from either escitalopram or citalopram.⁹ In addition, some clinicians think escitalopram has better titration than sertraline, so patients on escitalopram might be more likely to get a true antidepressant dosage than those on sertraline. This might lead to better adherence and lower downstream medical costs. Thus, the higher drug costs might be offset by the lower medical costs. However, this has not been rigorously tested using real world data, especially among Medicare population who are often excluded in clinical trials.¹⁰

Our study takes advantage of the most recently available Medicare Part D data (2008–2009) to compare the three most commonly prescribed SSRIs among US Medicare beneficiaries: escitalopram (Lexapro), citalopram (Celexa), and sertraline (Zoloft). We test three statistical approaches – generalized linear models (GLM), propensity score matching and instrumental variables (IV) – to examine medication adherence and down-stream non-drug medical spending among three groups of patients on each of three antidepressants.

METHODS

Study Population

We obtained a 5 percent national random sample of Medicare beneficiaries who were diagnosed with depression in 2008, enrolled in a stand-alone Part D plan (PDP), and not simultaneously enrolled in Medicaid. Data were provided by the US Centers for Medicare & Medicaid Services Chronic Condition Warehouse (CMS-CCW). Based on their definition, beneficiaries who had at least one claim in 2008 with the ICD-9 diagnosis code from 296.20–296.26, 296.30–296.36, 296.50–296.56, 296.60–296.66, 296.89, 298.0, 300.4, 309.1, and 311 were identified as having depression. We obtained 2008–2009 enrollment information, pharmacy and medical data for this population.

We identified the three most frequently-prescribed antidepressants from our 2008 Part D event data: citalopram (Celexa), sertraline (Zoloft), and escitalopram (Lexapro). They are all in the Selective Serotonin Reuptake Inhibitors (SSRIs) therapeutic class. Both sertraline and citalopram have been available in generic form since the mid-2000s. Escitalopram, which is the pure S-enantiomer of citalopram, is only available under the brand-name Lexapro, and hence is substantially more expensive than either citalopram or sertraline.

We identified three study cohorts depending on whether they used: 1) escitalopram (10mg, 20mg, tablets), 2) sertraline HCL (50mg, 100mg, tablets), or 3) citalopram HBR (10mg, 20mg, 40mg, tablets) for at least 90 continuous days in 2008. We focused on these relatively high dosages because they are usually the final therapeutic dosages. The first day of the 90-day period was identified as the index day, and the three cohorts were followed up for one year from the index date. We also defined a wash-out period as not using any antidepressant for at least 60 days prior to the index date. In order to define the 60-day wash-out period, we excluded patients who were not enrolled in a PDP during the 60 days prior to the index date. In addition, we excluded patients who were treated with two or more of the three drugs.

Outcome Measures

We focused on four outcome measures: 1) average monthly prescription drug spending (total and antidepressant spending) 2) medication adherence for antidepressants; 3) non-drug total medical spending, and 4) non-drug spending only for services related to depression. These outcomes were all measured during the one-year follow-up period.

The medication adherence was assessed by the medication possession ratio (MPR), defined as the proportion of days covered by antidepressants during the study period. Because the current clinical guidelines recommend antidepressant treatment for at least 6 months, we also measured MPR during the first 6 months of treatment.

Data Analytic Procedures

We conducted three approaches to assess each of the outcome measures: GLM, propensity score matching, and IV.

Generalized Linear Model

We conducted generalized linear regression models for each possible drug comparison (citalopram vs. sertraline, escitalopram vs. sertraline, and escitalopram vs citalopram). We used a log link and a gamma distribution. Each model included controls for gender, race, age, Zip-Code level income, disability status, number of Elixhauser comorbidities, prescriber specialty (psychiatry, family medicine, internal medicine, physician's assistant, or other), dummies for whether the patient was diagnosed with depression, rheumatoid/osteoarthritis (RA/OA), Alzheimer’s disease, chronic heart failure (CHF), chronic obstructive pulmonary disease (COPD), and diabetes in 2007 or earlier, and Dartmouth Atlas hospital-referral region (HRR) level average drug spending and non-drug medical spending. All models with drug related outcomes also control for the patient’s Prescription Drug Hierarchical Condition Category (RxHCC) risk score in the prior year, and models with non-drug spending outcomes control for the patient’s Hierarchical Condition Category (HCC) risk score in the prior year.^11,12 The HCC and RxHCC risk scores are used by Medicare to adjust payments for medical services and prescription drugs, respectively, based on a patient’s comorbidities.

For psychiatric-related spending and depression-related spending, there were a large number of individuals with zero spending. For these outcomes we ran a two-part model.. Both one-part and two-part GLM models have been shown to perform well in cases with a large number of zeros in medical spending.¹³

Finally, in order to correct the standard errors for possible correlation between drug spending and non-drug medical spending within individuals, we used a seemingly unrelated estimation model that included the total drug spending, antidepressant spending, and total non-drug medical spending outcomes (“suest” command approach in Stata).

Propensity score matching

Propensity score methods were conducted using a two-step process. First, we calculated a propensity score for each individual by calculating the predicted probability of using each drug from three separate logistic regressions comparing each drug pair. The logistic models included the same covariates as the generalized linear model as described above. Second, we used the kernel matching algorithm whereby each case in the treatment is matched to every case in the control group,¹ and the difference in outcomes is weighted by the distance between the propensity scores using the epanechnikov kernel function.¹⁴

Instrumental Variables

Even after adjusting for the covariates in the regression or propensity score models, there still may be unobserved differences between the groups, which could cause bias. For example, patients that use escitalopram (Lexapro), the newest and most expensive of the three drugs, may also have a preference for higher medical spending. In order to control for unobserved heterogeneity between the three groups, we used geographic variations in prescribing patterns as instrumental variables. There is a substantial literature on the large geographic differences in utilization of medical technologies including drugs, after controlling for patient characteristics.¹⁵ Because these differences exist, a patient’s location may act similar to random assignment. Patients living in areas with higher than average utilization of sertraline, for example, might be more likely to use that drug than a similar patient in an area with low utilization of the drug.

Using a 5% random sample of all Medicare beneficiaries in 2008, we calculated the proportion of antidepressant patients using each of the three antidepressants at the HRR level.¹⁶ For example, we calculated the proportion of escitalopram users by dividing the total number of patients in the region that received at least one prescription for escitalopram by the total number of patients in the region that received any antidepressant. We then assigned the regional average to each patient based on their Zip Code of residence.

In order for instrumental variables to be valid, they must be correlated with the treatment assignment and uncorrelated with the stochastic error term in the regression. Although the second assumption is untestable, geographic variation in antidepressant utilization is likely to be an effective instrument because it is unlikely that unobserved variables such as individual preferences are correlated with which drugs are most prevalent in the region. However, in order to control for the possibility that regional level medical spending was correlated with the instruments, each regression controls for the regional average medical spending as well as the regional average drug spending.

We used a Two Stage Residual Inclusion (2SRI) model with a GLM second stage regression.¹⁷ For each drug comparison, our first stage was a linear regression to predict the probability that the individual was in the treatment group. Each regression controlled for all of the same covariates as in the standard regression analysis, in addition to the HRR-level utilization ratios of the comparison drugs. Linear models were used in the first stage despite the fact that the outcome was binary, because linear first stage regressions have been shown to produce consistent estimators, even when the first stage regression is misspecified.¹⁸ In the second stage, a GLM regression was run following the same procedure as above, but each regression also included the residuals from the first stage regression.

RESULTS

The study cohort included 4,435 individuals, of whom 1,520 (34%) were taking escitalopram, 1,559 (35%) were taking citalopram, and 1,356 (31%) were taking sertraline. Table 1 compares the unadjusted baseline characteristics of each of the three study groups.

Table 1.

Unadjusted Characteristics of the Study Population ^*

Variable
	Escitalopram	Citalopram	Sertraline	P Value
	(n=1,520)	(n=1,559)	(n=1,356)
Female, %	73.2	68.7	72.1	0.015
Race, %
Non-Hispanic    White	92.8	92.8	92.1	0.727
Black	3.3	3.5	3.6	0.893
Other Races	3.9	3.7	4.3	0.744
Age	75.0±0.3	74.3±0.3	74.2±0.3	0.100
LIS, %	19.7	21.7	21.0	0.353
Prescription drug risk score, mean	0.70±0	0.71±0	0.71±0	0.191
No. Elixhauser comorbidities, mean	3.17±0.07	2.90±0.06	3.05±0.07	0.015
Diagnosed chronic conditions in prior year, %
Depression	46.6	36.7	40.4	<0.01
Alzheimer's	11.2	9.8	9.1	0.150
Heart Failure	22.5	20.4	22.3	0.288
COPD	12.3	12.9	15.9	0.011
Diabetes	26.2	27.2	28.1	0.539
RA/OA	29.3	27.3	28.2	0.459

^*Plus-minus values are means±SE.

Abbreviations: LIS = low income subsidies, this group includes duals and non-duals with low-income subsides for Part D; COPD = Chronic obstructive pulmonary disease; RA/OA = Rheumatoid arthritis/osteoarthritis.

The groups did not differ significantly in age, race, receipt of low income subsidies, prescription drug risk score, or in the prevalence of Alzheimer’s disease, heart failure, diabetes, COPD, or arthritis. However, citalopram patients were less likely to be female than both escitalopram patients (68.7% vs. 73.2%; p<0.01) and sertraline patients (68.7% vs. 72.1%; p=0.04). Citalopram patients had fewer Elixhauser comorbidities than escitalopram patients (2.90 vs. 3.17; p<0.01), but did not differ significantly from sertraline patients. The three groups also differed in measures of previous diagnosis of depression. Escitalopram patients were most likely to have been diagnosed with depression in the previous year (46.6%), followed by sertraline patients (40.4%), and citalopram patients (36.7%).

Table 2 compares the results of the three different methods (multiple regression, propensity score matching, and instrumental variables). Panel A presents the multiple regression results. Not surprisingly, escitalopram, which was only available as the brand name drug, Lexapro, was associated with higher total antidepressant spending as well as higher total drug spending than either of the other two drugs which each had several available generic substitutes. Sertraline users also had marginally higher drug costs than citalopram users, but only the difference in antidepressant spending was statistically significant at the 5% level. In addition to the substantial difference in drug costs, escitalopram users spent approximately $150 more per month on total non-drug claims than citalopram users. Escitalopram patients also had higher spending on claims where a psychiatric condition was indicated as a primary or secondary diagnosis than either citalopram or sertraline users. Finally, adherence, as measured by MPR, was lower in the escitalopram group both at the 6 month follow-up and the one year follow-up as compared with either of the alternative treatments.

Table 2.

Three Methods for Comparing Outcomes across Antidepressant Treatment Groups

Panel A. Generalized Linear Model Regressions
	[1]		[2]		[3]
Outcome	Escitalopram - Citalopram		Citalopram - Sertraline		Escitalopram - Sertraline
	Difference	P-value	Difference	P-value	Difference	P-value
Total Drug Spendinga	104.18***	<0.01	−19.54*	0.057	86.33***	<0.01
Antidepressant Spendinga	55.67***	<0.01	−3.10***	<0.01	53.17***	<0.01
6-Month MPRb	−3.17***	<0.01	0.801	0.200	−2.26***	<0.01
1-year MPRb	−5.62***	<0.01	0.467	0.613	−5.09***	<0.01
Total Non-Drug Spendinga	150.02**	0.043	−0.947	0.990	148.23*	0.055
Two-Part Models
	Difference	Confidence Interval	Difference	Confidence Interval	Difference	Confidence Interval
Psychiatric- Related Spendingc	75.94***	21.24 To 138.22	11.69	−43.61 To 64.51	86.36***	28.45 To 149.17
Depression- Related Spendingc	25.55	−12.62 To 64.22	10.15	−26.04 To 46.28	28.59	−12.79 To 70.78
Observations	3,052		2,893		2,853

Panel B. Propensity Score Matching
	[1]		[2]		[3]
Ourcome	Escitalopram - Citalopram		Citalopram - Sertraline		Escitalopram - Sertraline
	Difference	P-value	Difference	P-value	Difference	P-value
Total Drug Spending	98.41***	<0.01	−18.33	0.110	77.53***	<0.01
Antidepressant Spending	54.81***	<0.01	−3.07***	<0.01	51.77***	<0.01
6-Month MPR	−3.31***	<0.01	0.78	0.219	−2.27***	<0.01
1-year MPR	−5.65***	<0.01	0.53	0.569	−5.06***	<0.01
Total Non- Drug Spending	177.05**	0.038	1.41	0.984	120.57	0.165
Psychiatric- Related Spending	77.20**	0.017	5.20	0.849	68.79**	0.043
Depression- Related Spending	35.83	0.093	−1.95	0.920	17.22	0.4593
Observations	3,052		2,893		2,853

Panel C. Instrumental Variables
	[1]		[2]		[3]
Outcome	Escitalopram - Citalopram		Citalopram - Sertraline		Escitalopram - Sertraline
	Difference	P-value	Difference	P-value	Difference	P-value
Total Drug Spending	62.47	0.261	−136.71*	0.082	226.47**	0.040
Antidepressant Spending	68.45***	<0.01	−8.50	0.171	57.24***	<0.01
6-Month MPR	−9.26***	<0.01	3.97	0.382	−2.56	0.658
1-year MPR	−12.81***	<0.01	2.43	0.717	−8.59	0.310
Total Non- Drug Spending	−260.00	0.523	1898.78***	<0.01	462.50	0.522
Psychiatric- Related Spending	−308.77*	0.083	351.38	0.100	−39.03	0.887
Depression- Related Spending	−283.77**	0.026	314.78*	0.075	−164.58	0.426
First Stage F- Statistic	56.50		27.44		18.15
Observations	3,052		2,893		2,853

^aindicates standard errors were obtained from seemingly unrelated equations including total drug spending, antidepressant spending, and total non-drug spending, and corrected for heteroskedasticity (“suest” command approach in Stata)

^bindicates heteroskedasticity robust standard errors were used

^cindicates that the marginal effects from a two-part model are presented with bootstrapped confidence intervals.

Note:

^***denotes p-value<0.01;

^**denotes p-value<0.05; and

^*denotes p-value<0.1.

The results from the propensity score analysis (Table 2, Panel B) show very similar results to the regression. Both models show that drug spending and adherence differ significantly among the three groups, and that non-drug psychiatric spending is the highest among the escitalopram group.

Instrumental Variables

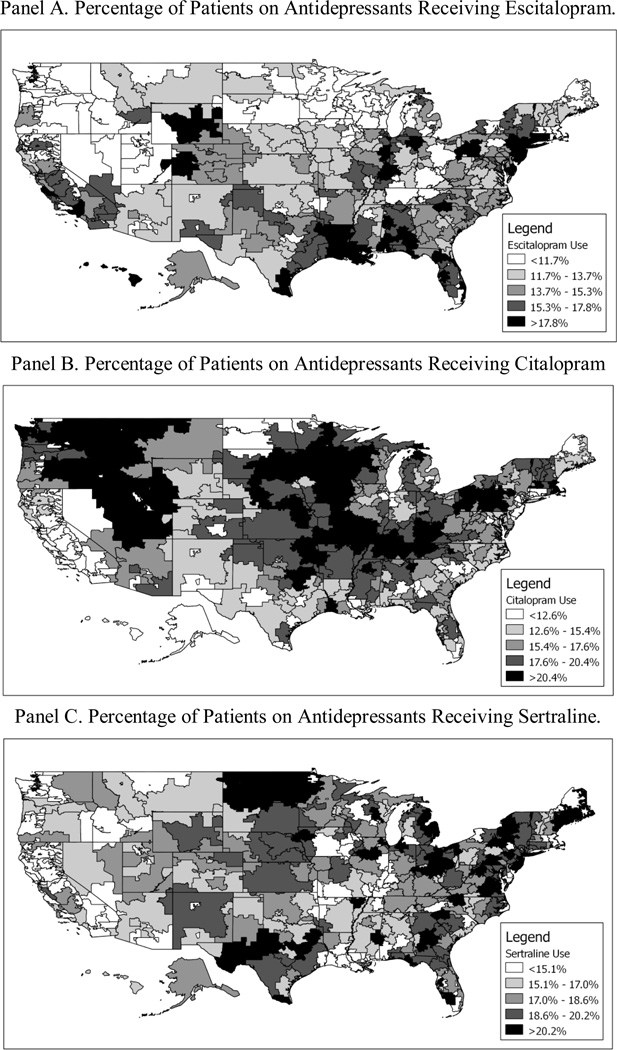
Figure 1 shows the geographic variation in utilization of the three drugs. The degree of variation is remarkably high. For example, in Newark, NJ, 24.8% percent of antidepressant patients received a prescription for escitalopram, 6.7% received a prescription for citalopram, and 21.2% received a prescription for sertraline. By contrast, in St. Cloud, MN, only 4.6% of patients used escitalopram, while 29.8% used citalopram, and 18.8% used sertraline.

Figure 1.

Geographic Variation in Antidepressant Use.

Panel C of Table 2 shows the 2SRI results. Many of the key results are similar to the regression and propensity score matching results. Not surprisingly, for example, spending on antidepressants for escitalopram users was significantly higher than spending for either citalopram or sertraline users. Additionally, escitalopram users had worse adherence than citalopram users. However, unlike in the regression results, we did not observe a significant difference in adherence between escitalopram and sertraline users. Most strikingly, the sign of the difference in all three of the non-drug spending outcome flips for the escitalopram vs. citalopram comparison. The IV results suggest that depression related spending is lower in the escitalopram group than in the citalopram group. Additionally, while the conventional regression results show that non-drug spending is nearly identical between the citalopram and sertraline groups, the IV results imply that non-drug spending is significantly lower among sertraline users.

The F-test for the significance of the excluded instruments in the first stage shows that the instruments may be stronger in some of the drug comparisons than others. For the escitalopram vs. citalopram comparison, the F-statistic is 56.50, which suggests that the instruments are quite strong. The F-statistics for the citalopram-sertraline comparison and the escitalopram-sertraline comparisons are 27.44 and 18.15, respectively. Although there is not much concern that the instruments are weak, they are relatively weaker in the sertraline comparisons, which could explain why the standard errors are higher in these regressions.

In order to compare the results from IV method and the GLM regression, we used an F-test to examine the joint significance of the first stage residuals in the second stage regressions (Table 3).This is equivalent to the Hausman specification test. Under the null hypothesis, the standard regression model is consistent and efficient, so it should be superior to the IV model. The results show that the GLM results are consistent in most of the comparisons. However, several results differ significantly between the IV and GLM models, including depression and psychiatric spending in the escitalopram-citalopram comparison, and total medical spending in the citalopram-sertraline comparison. This implies that the IV model is the preferred specification for these outcomes.

Table 3.

Specification Tests Comparing GLM to Instrumental Variables Methods

	[1]		[2]		[3]
Outcome	Escitalopram - Citalopram		Citalopram - Sertraline		Escitalopram - Sertraline
	Chi square	P-value	Chi square	P-value	Chi square	P-value
Total Drug Spending	0.58	0.4451	2.24	0.1343	1.59	0.2074
Antidepressant Spending	1.68	0.1951	0.74	0.3887	0.12	0.7309
6-Month MPR	3.53	0.0602	0.50	0.4813	0.00	0.9581
1-year MPR	2.30	0.1294	0.09	0.7675	0.17	0.6778
Total Non- Drug Spending	1.06	0.3028	8.72***	0.0031	0.19	0.6620
Psychiatric- Related Spending	5.32***	0.0210	2.52	0.1126	0.24	0.6218
Depression- Related Spending	6.42***	0.0113	3.02*	0.0821	0.91	0.3403

Note:

^***denotes p-value<0.01;

^**denotes p-value<0.05; and

^*denotes p-value<0.1.

COMMENT

Overall, we found that patients who used escitalopram had substantially higher drug costs and worse medication adherence compared to patients who used either citalopram or sertraline. However, despite these differences, our instrumental variables model suggested that escitalopram patients had lower costs for depression-related non-drug treatment compared with citalopram patients. Sertraline patients also had lower total medical spending than citalopram patients, but, with the exception of drug costs, we did not find any differences between escitalopram and sertraline patients. These findings suggest that escitalopram or sertraline may be more effective choices than citalopram for Medicare patients. Additionally, because sertraline was associated with lower drug costs than escitalopram, but not with worse outcomes, sertraline appears to be the most cost-effective drug for treating depression.

The IV methods yielded somewhat different results than the GLM regressions and the propensity score matching methods. In the regression and propensity score matching methods, we found that both sertraline and citalopram were associated with lower costs (both drug and non-drug) than escitalopram. One possible explanation for the different results is that there is some unobserved patient selection into the different treatment groups. It is possible that patients who used escitalopram, which is the most expensive drug, also preferred higher medical spending. Once we focus on the part of the treatment selection that is essentially random (i.e. the part associated with geographic differences) using the instrumental variables, we see that escitalopram is actually negatively associated with medical costs. Despite the very different results of the different methods, one conclusion remains the same: in every model, we found that sertraline was at least as cost-effective as or more cost-effective than the other drugs.

Our study could be the first evaluating the comparative-effectiveness of these three commonly prescribed SSRIs using national Medicare data. Such observational studies have several advantages over clinical trials. We studied the Medicare population, who are often excluded in trials yet have different treatment profiles due to polypharmacy and adverse drug reactions ¹⁰. In addition, we studied the real-world effects regarding medication costs and adherence, which is difficult to study in clinical trials. Significant price differences between the different medications could affect adherence.¹⁹

One potential problem using observational design to study comparative-effectiveness is the heterogeneity of patients on different treatments. We compared three approaches to test robustness of the results: multiple regression, propensity score, and instrumental variables. We used the wide geographic variation in the utilization of the different medications for depression as instrumental variables. Since Zip Code of residence is highly predictive of treatment, these local area differences act similar to random assignment. This approach has been used in a number of studies,^20–22 but has been underutilized in pharmaceutical comparative effectiveness studies. We explored this approach using Part D data.

In sum, we found that patients using sertraline had outcomes that were at least as good as or better than patients using escitalopram or citalopram in terms of adherence, drug costs, medical spending. In our instrumental variables regression, which is our preferred specification, we also concluded that escitalopram may also lead to lower down-stream medical costs that more than offset its higher cost, as compared to citalopram. Overall, however, the combination of lower drug costs, better adherence, and lower down-stream medical costs seem to indicate that sertraline is the most cost-effective drug to treat depression. Substantial savings to Medicare could be realized by using more cost-effective antidepressants such as sertraline.