Least Squares Estimation Without Priors or Supervision

Abstract

Selection of an optimal estimator typically relies on either supervised training samples (pairs of measurements and their associated true values) or a prior probability model for the true values. Here, we consider the problem of obtaining a least squares estimator given a measurement process with known statistics (i.e., a likelihood function) and a set of unsupervised measurements, each arising from a corresponding true value drawn randomly from an unknown distribution. We develop a general expression for a nonparametric empirical Bayes least squares (NEBLS) estimator, which expresses the optimal least squares estimator in terms of the measurement density, with no explicit reference to the unknown (prior) density. We study the conditions under which such estimators exist and derive specific forms for a variety of different measurement processes. We further show that each of these NEBLS estimators may be used to express the mean squared estimation error as an expectation over the measurement density alone, thus generalizing Stein’s unbiased risk estimator (SURE), which provides such an expression for the additive gaussian noise case. This error expression may then be optimized over noisy measurement samples, in the absence of supervised training data, yielding a generalized SURE-optimized parametric least squares (SURE2PLS) estimator. In the special case of a linear parameterization (i.e., a sum of nonlinear kernel functions), the objective function is quadratic, and we derive an incremental form for learning this estimator from data. We also show that combining the NEBLS form with its corresponding generalized SURE expression produces a generalization of the score-matching procedure for parametric density estimation. Finally, we have implemented several examples of such estimators, and we show that their performance is comparable to their optimal Bayesian or supervised regression counterparts for moderate to large amounts of data.

1 Introduction

The problem of estimating signals based on partial, corrupted measurements arises whenever a machine or biological organism interacts with an environment that it observes through sensors. Optimal estimation has a long history, documented in the published literature of a variety of communities: statistics, signal processing, sensory perception, motor control, and machine learning, to name just a few. The two most commonly used methods of obtaining an optimal estimator are Bayesian inference, in which the estimator is chosen to minimize the expected error over a posterior distribution, obtained by combining a prior distribution with a model of the measurement process, and supervised regression, in which the estimator is selected from a parametric family by minimizing the error over a training set containing pairs of corrupted measurements and their correct values. Here, we consider the problem of obtaining a least squares (also known as minimum mean squared error) estimator, in the absence of either supervised training examples or a prior model. Specifically, we assume a known measurement process (i.e., the probability distribution of measurements conditioned on true values), and we assume that we have access to a large set of measurement samples, each arising from a corresponding true value drawn from an unknown signal distribution. The goal, then, is to obtain a least squares estimator given these two ingredients.

The statistics literature describes a framework for handling this situation, generally known as empirical Bayes estimation, in which the estimator is learned from observed (noisy) samples. More specifically, in the parametric empirical Bayes approach, one typically assumes a parametric form for the density of the clean signal, and then learns the parameters of this density from the noisy observations. This is usually achieved by maximizing likelihood or matching moments (Morris, 1983; Casella, 1985; Berger, 1985), both of which are inconsistent with our goal of minimizing mean squared estimation error. In addition, if one assumes a parametric form for the density of the clean signal, which cannot give a good fit to the true distribution, performance is likely to suffer. For the case of Poisson observations, Robbins introduced a nonparametric empirical Bayesian least squares (NEBLS) estimator that is expressed directly in terms of the measurement density, without explicit reference to the prior (Robbins, 1956). This remarkable result was subsequently extended to cases of additive gaussian noise (Miyasawa, 1961) and to general exponential measurements (Maritz & Lwin, 1989), where it was referred to as a simple empirical Bayes estimator.

Here, we develop a general expression for this type of NEBLS estimator, written in terms of a linear functional of the density of noisy measurements. The NEBLS estimators previously developed for Poisson, gaussian, and exponential measurement processes are each special cases of this general form. We provide a complete characterization of observation models for which such an estimator exists, develop a methodology for obtaining the estimators in these cases, and derive specific solutions for a variety of corruption processes, including the general additive case and various scale mixtures. We also show that any of these NEBLS estimators can be used to derive an expression for the mean squared error (MSE) of an arbitrary estimator that is written as an expectation over the measurement density (again, without reference to the prior). These expressions provide a generalization of Stein’s unbiased risk estimate (SURE), which corresponds to the special case of additive gaussian noise (Stein, 1981)), and analogous expressions that have been developed for the cases of continuous and discrete exponential families (Berger, 1980; Hwang, 1982). In addition to unifying and generalizing these previous examples, our derivation ties them directly to the seemingly unrelated NEBLS methodology.

In practice, approximating the reformulated MSE with a sample average allows one to optimize a parametric estimator based entirely on a set of corrupted measurements, without the need for the corresponding true values that would be used for regression. This has been done with SURE (Donoho & Johnstone, 1995; Pesquet & Leporini, 1997; Benazza-Benyahia & Pesquet, 2005; Luisier, Blu, & Unser, 2006; Raphan & Simoncelli, 2007b, 2008; Blu & Luisier, 2007; Chaux, Duval, Benazza-Benyahia, & Pesquet, 2008), and recently with the analogous exponential case (Eldar, 2009). We refer to this as a generalized SURE-optimized parametric least squares estimator (since the generalized SURE estimate is used to obtain the parameters of the least squares estimator, we use the acronym gSURE2PLS, with mnemonic pronunciation “generalized sure to please”). For the special case of an estimator parameterized as a linear combination of nonlinear kernel functions, we develop an incremental algorithm that simultaneously optimizes and applies the estimator to a stream of incoming data samples. We also show that the NEBLS solution may be combined with the generalized SURE expression to yield an objective function for fitting a parametric density to observed data, which provides a generalization of the recently developed score matching procedure (Hyvärinen, 2005, 2008). Finally, we compare the empirical convergence of several example gSURE2PLS estimators with that of their Bayesian counterparts. Preliminary versions of this work have been presented in Raphan and Simoncelli (2007b, 2009) and Raphan (2007).¹

2 Introductory Example: Additive Gaussian Noise

We begin by illustrating the two forms of estimator for the scalar case of additive gaussian noise (the vector case is derived in section 6.1). Suppose random variable Y represents a noisy observation of an underlying random variable, X. It is well known that given a particular observation Y = y, the estimate that minimizes the expected squared error (sometimes called the Bayes least squares estimator) is the conditional mean:

$$\begin{array}{cc}\hfill \widehat{x}=& {\mathbf{E}}_{X\mid Y}(X\mid Y=y)\hfill \\ \hfill =& \int x{P}_{X\mid Y}(x\mid y)dx\hfill \\ \hfill =& \int x\frac{P(X,Y)(x,y)}{P_Y\left(y\right)}dx,\hfill \end{array}$$ (2.1)

where the denominator contains the distribution of the observed data, which we refer to as the measurement density (sometimes called the prior predictive density). This can be obtained by marginalizing the joint density, which in turn can be written in terms of the prior on X using Bayes’ rule:

$$P_Y\left(y\right)=\int P_{X,Y}(x,y)dx=\int P_{Y\mid X}(y\mid x)P_X\left(x\right)dx.$$ (2.2)

2.1 Nonparametric Empirical Bayes Least Squares Estimator

The NEBLS estimation paradigm, in which the least squares estimator is written entirely in terms of the measurement density, was introduced by Robbins (1956) and was extended to the case of gaussian additive noise by Miyasawa (1961). The derivation for the gaussian case is relatively simple. First, note that the conditional density of the measurement given the true value is

$$P_{Y\mid X}(y\mid x)=\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-{(y-x)}^2∕2{\sigma }^2},$$

and thus, substituting into equation 2.2,

$$P_Y\left(y\right)=\int \frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-{(y-x)}^2∕2{\sigma }^2}{P}_X\left(x\right)dx.$$ (2.3)

Differentiating this with respect to y and multiplying by σ² on both sides gives

$$\begin{array}{cc}\hfill {\sigma }^2{P}_Y^{\prime }\left(y\right)=& \int (x-y)\frac{1}{\sqrt{2\pi {\sigma }^2}}{e}^{-{(y-x)}^2∕2{\sigma }^2}{P}_X\left(x\right)dx\hfill \\ \hfill =& \int (x-y)P_{X,Y}(x,y)dx\hfill \\ \hfill =& \int x{P}_{X,Y}(x,y)dx-y{P}_Y\left(y\right).\hfill \end{array}$$

Finally, dividing through by P_Y(y) and combining with equation 2.1 gives

$$\begin{array}{cc}\hfill \widehat{x}\left(y\right)=& y+{\sigma }^2\frac{P_Y^{\prime }\left(y\right)}{P_Y\left(y\right)}\hfill \\ \hfill =& y+{\sigma }^2\frac{d}{dy}\log P_Y\left(y\right).\hfill \end{array}$$ (2.4)

The important feature of the NEBLS estimator is its expression as a direct function of the measurement density, with no explicit reference to the prior. This means that the estimator can be approximated by estimating the measurement density from a set of observed samples. The derivation relies on only the assumptions of squared loss function and additive gaussian measurement noise, but is independent of the prior. We will assume squared loss throughout this article, but in section 3, we describe an NEBLS form for more general measurement conditions.

We can gain some intuition for the solution by considering an example in which the prior distribution for x consists of three isolated point masses (delta functions). The measurement density may be obtained by convolving this prior with a gaussian (see Figure 1, top). And, according to equation 2.4, the optimal estimator is obtained by adding the log derivative of the measurement density (see Figure 1, bottom), to the measurement. This is a form of gradient ascent, in which the estimator “shrinks” the observations toward the local maxima of the log density. In the vicinity of the most isolated (left) delta function, this shrinkage function is antisymmetric with a slope of negative one, resulting in essentially perfect recovery of the true value of x. Note that this optimal shrinkage is accomplished in a single step, unlike methods such as the mean-shift algorithm (Comaniciu & Meer, 2002), which uses iterative gradient ascent on the logarithm of a density to perform nonparametric clustering.

Figure 1.

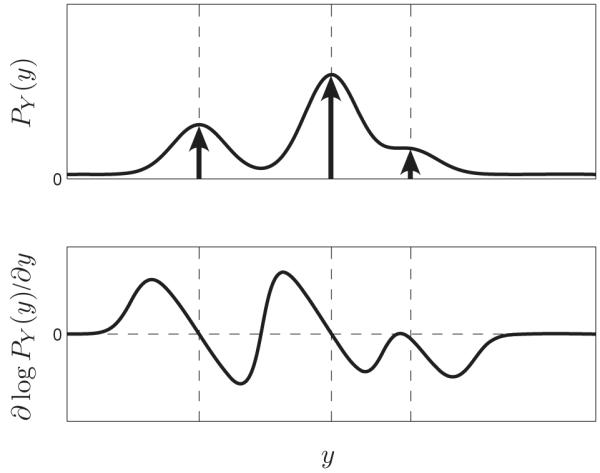
Illustration of the NEBLS estimator for a one-dimensional value with additive gaussian noise. (Top) Measurement density, P_Y(y), arising from a signal with prior consisting of three point masses (indicated by upward arrows) corrupted by additive gaussian noise. (Bottom) Derivative of the log measurement density, which, when added to the measurement, gives the NEBLS estimator (see equation 2.4).

2.2 Dual Formulation: SURE-Optimized Parametric Least Squares Estimation

Next, as an alternative to the BLS estimator, consider the parametric regression formulation of the optimal estimation problem. Given a family of estimators, f_θ, parameterized by vector θ, we wish to select the one that minimizes the expected squared error:

$$\widehat{\theta }=\arg \underset{\theta }{\min }{\mathbf{E}}_{X,Y}\left({\left(f_{\theta }\right(Y)-X)}^2\right),$$

where the subscripts on the expectation indicate that it is taken over the joint density of measurements and correct values. In practice, the optimal parameters are obtained by approximating the expectation with a sum over clean/noisy pairs of data, {x_k, y_k}:

$$\widehat{\theta }=\arg \underset{\theta }{\min }\frac{1}{N}\sum _{k=1}^N{\left(f_{\theta }\right(y_k)-x_k)}^2.$$ (2.5)

Although this regression expression is written in terms of a supervised training set (i.e., one that includes the true values, x_k), the NEBLS formula of equation 2.4 may be used to derive an expression for the mean squared error that relies on only the noisy measurements, y_k. To see this, we rewrite the parametric estimator as f_θ (y) = y + g_θ (y) and expand the mean squared error:

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X,Y}\left({\left(f_{\theta }\right(Y)-X)}^2\right)=& {\mathbf{E}}_{X,Y}\left({(Y+g_{\theta }(Y)-X)}^2\right)\hfill \\ \hfill =& {\mathbf{E}}_{X,Y}\left(g_{\theta }^2\left(Y\right)\right)+2{\mathbf{E}}_{X,Y}\left(g_{\theta }\right(Y)\cdot (Y-X\left)\right)\hfill \\ \hfill & +{\mathbf{E}}_{X,Y}\left({(Y-X)}^2\right)\hfill \\ \hfill =& {\mathbf{E}}_Y\left(g_{\theta }^2\left(Y\right)\right)+2{\mathbf{E}}_{X,Y}\left(g_{\theta }\right(Y)\cdot (Y-X\left)\right)+{\sigma }^2.\hfill \end{array}$$ (2.6)

The middle term can be written as an expectation over Y alone by substituting the NEBLS estimator from equation 2.4, and then integrating by parts:

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X,Y}\left(g_{\theta }\right(Y)\cdot (Y-X\left)\right)=& {\mathbf{E}}_Y\left(g_{\theta }\right(Y)\cdot (Y-{\mathbf{E}}_{X\mid Y}(X\mid Y)\left)\right)\hfill \\ \hfill =& {\mathbf{E}}_Y\left(g_{\theta }\left(Y\right)\cdot \left(Y-Y-{\sigma }^2\frac{P_Y^{\prime }\left(Y\right)}{P_Y\left(Y\right)}\right)\right)\hfill \\ \hfill =& {\sigma }^2{\mathbf{E}}_Y\left(g_{\theta }\left(Y\right)\cdot \frac{P_Y^{\prime }\left(Y\right)}{P_Y\left(Y\right)}\right)\hfill \\ \hfill =& -{\sigma }^2\int \left(g_{\theta }\left(y\right)\cdot \frac{P_Y^{\prime }\left(y\right)}{P_Y\left(y\right)}\right)P_Y\left(y\right)dy\hfill \\ \hfill =& -{\sigma }^2\int g_{\theta }\left(y\right)\cdot P_Y^{\prime }\left(y\right)dy\hfill \\ \hfill =& {\sigma }^2\int g_{\theta }^{\prime }\left(y\right)\cdot P_Y\left(y\right)dy\hfill \\ \hfill =& {\sigma }^2{\mathbf{E}}_Y\left(g_{\theta }^{\prime }\left(Y\right)\right),\hfill \end{array}$$

where we have assumed that the term ${\phantom{\mid }{P}_Y\left(y\right)g_{\theta }\left(y\right)\mid }_{-\infty }^{\infty }$ that arises when integrating by parts is zero (as y goes to ±∞, we assume P_Y(y) dies off faster than g_θ(y) grows).

Finally, substituting this back into equation 2.6 gives an expression for estimation error:

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X,Y}\left({(X-f_{\theta }(Y\left)\right)}^2\right)=& {\mathbf{E}}_Y\left(g_{\theta }^2\right(Y\left)\right)+2{\sigma }^2{\mathbf{E}}_Y\left(g_{\theta }^{\prime }\left(Y\right)\right)+{\sigma }^2\hfill \\ \hfill =& {\mathbf{E}}_Y\left(g_{\theta }^2\right(Y)+2{\sigma }^2{g}_{\theta }^{\prime }(Y)+{\sigma }^2).\hfill \end{array}$$ (2.7)

This remarkable equation expresses the mean squared error over the joint distribution of values and measurements as an expected value over the measurements alone. It is known as Stein’s unbiased risk estimator (SURE), after Charles Stein, who derived it and used it as a means of comparing the quality of different estimators (Stein, 1981).² In section 4, we derive a much more general form of this expression that does not assume additive gaussian noise.

In practice, SURE can be approximated as an average over an unsupervised set of noisy measurements, and this approximation can then be minimized over the parameters, θ, to select an estimator:

$$\widehat{\theta }=\arg \underset{\theta }{\min }\frac{1}{N}\sum _{k=1}^N\left(g_{\theta }^2\left(y_k\right)+2{\sigma }^2{g}_{\theta }^{\prime }\left(y_k\right)\right),$$ (2.8)

where we have dropped the last term (σ²) because it does not depend on the parameter vector, θ. Note that unlike the supervised regression form of equation 2.5, this optimization does not rely on access to true signal values, {x_k}. We refer to the function associated with the optimized parameter, $g_{\widehat{\theta }}\left(y\right)$, as a SURE-optimized parametric least squares (SURE2PLS) estimator. This type of estimator was first developed for removal of additive gaussian noise by Donoho and Johnstone (1995), who used it to estimate an optimal threshold shrinkage function (the resulting estimator is named SUREshrink). These results have been generalized to other shrinkage estimators (Benazza-Benyahia and Pesquet, 2005; Chaux et al., 2008), as well as linear families of estimators (Pesquet and Leporini, 1997; Luisier et al., 2006; Raphan and Simoncelli, 2007b, 2008; Blu and Luisier, 2007), which we discuss in section 5.

Intuitively, the objective function in equation 2.8 favors functions g(·) that have both a small squared magnitude and a large negative derivative in locations where the measurements, y_k, are concentrated. As such, a good estimator will “shrink” the data toward regions of high probability, as can be seen in the optimal solution shown in Figure 1. Note also that the noise parameter σ² acts as a weighting factor on the derivative term, effectively controlling the smoothness of the solution.

2.3 Combining NEBLS with SURE Yields the Score Matching Density Estimator

The SURE2PLS solution developed in the previous section can be applied to any parametric estimator. Consider a specific estimator that is derived by starting with a parametric form for the prior, $P_X^{\left(\varphi \right)}\left(x\right)$. Combining this with the likelihood (using equation 2.3, which specifies a convolution of the gaussian noise density with the prior) generates a parametric form for the measurement density, $P_Y^{\left(\varphi \right)}\left(y\right)$. And given this, the expression of equation 2.4 gives the BLS estimator associated with this prior: $g_{\varphi }\left(y\right)={\sigma }^2\frac{d}{dy}\log P_Y^{\left(\varphi \right)}\left(y\right)$. Finally, substituting this estimator into equation 2.8 and eliminating common factors of σ yields an objective function for the density parameters ϕ given samples {y_k}:

$$\widehat{\varphi }=\arg \underset{\theta }{\min }\frac{1}{N}\sum _{k=1}^N\left[{\left(\frac{d}{dy}\log P_Y^{\left(\varphi \right)}\left(y_k\right)\right)}^2+2\frac{d^2}{d{y}^2}\log P_Y^{\left(\varphi \right)}\left(y_k\right)\right].$$ (2.9)

This objective function allows one to choose density parameters that are optimal for solving the least-squares estimation problem. By comparison, most parametric empirical Bayes procedures select parameters for the prior density by optimizing some other criterion (e.g., maximizing likelihood of the data, or matching moments; Casella, 1985), which are inconsistent with the estimation goal.³

Outside the estimation context, equation 2.9 provides an objective function that can be used for estimating the parameters of the density $P_Y^{\left(\varphi \right)}\left(y\right)$ from samples. This general methodology, dubbed score matching, was originally proposed by Hyvärinen (2005), who developed it by noting that differentiating the log of a density eliminates the normalization constant (known in physics as the “partition function”). This constant is generally a complicated function of the parameters, and thus an obstacle to solving the density estimation problem. In a subsequent publication, Hyvärinen (2008) showed a relationship of score matching to SURE by assuming the density to be estimated is the prior (i.e., the density of the clean signal), and taking the limit as the variance of the gaussian noise goes to zero. Here (and previously, in Raphan & Simoncelli, 2007b), we have interpreted score matching as a means of estimating the density of the noisy measurements, with the objective function expressing the MSE achieved by an estimator that is optimal for removing finite-variance gaussian noise when the measurements are drawn from $P_Y^{\left(\varphi \right)}\left(y\right)$. Notice that in this context, although σ² does not appear in the objective function of equation 2.9, it provides a means of controlling the smoothness of the parametric density family, $P_Y^{\left(\varphi \right)}\left(y\right)$, by equation 2.3. Of course, just as maximum likelihood (ML) has been used to estimate parametric densities outside the context in which it is optimal (i.e., compression), the score matching methodology has been used in contexts for which squared estimation error is not relevant and with parametric families that cannot have arisen from an additive gaussian noise process.

3 General Formulation: NEBLS Estimator

We now develop a generalized form for the NEBLS estimator of equation 2.4. Suppose we make a vector observation, y, that is a corrupted version of an unknown vector x (these need not have the same dimensionality). The BLS estimate is again the conditional expectation of the posterior density, which we can express using Bayes’ rule as⁴

$$\begin{array}{cc}\hfill \widehat{\mathit{x}}\left(\mathit{y}\right)=& \int \mathit{x}{P}_{X\mid Y}(\mathit{x}\mid \mathit{y})d\mathit{x}\hfill \\ \hfill =& \frac{\int \mathit{x}{P}_{Y\mid X}(\mathit{y}\mid \mathit{x})P_X\left(\mathit{x}\right)d\mathit{x}}{P_Y\left(\mathit{y}\right)}.\hfill \end{array}$$ (3.1)

Now define linear operator A to perform an inner product with the likelihood function

$$\mathbf{A}\left\{f\right\}\left(\mathit{y}\right)\equiv \int P_{Y\mid X}(\mathit{y}\mid \mathit{x})f\left(\mathit{x}\right)d\mathit{x},$$

and rewrite the measurement density in terms of this operator:

$$\begin{array}{cc}\hfill P_Y\left(\mathit{y}\right)=& \int P_{Y\mid X}(\mathit{y}\mid \mathit{x})P_X\left(\mathit{x}\right)d\mathit{x}\hfill \\ \hfill =& \mathbf{A}\left\{P_X\right\}\left(\mathit{y}\right).\hfill \end{array}$$ (3.2)

Similarly, the numerator of the BLS estimator, equation 3.1, may be rewritten as a composition of linear transformations applied to P_X(x):

$$\begin{array}{cc}\hfill N\left(\mathit{y}\right)=& \int P_{Y\mid X}(\mathit{y}\mid \mathit{x})\mathit{x}{P}_X\left(\mathit{x}\right)d\mathit{x}\hfill \\ \hfill =& (\mathbf{A}\circ \mathbf{X})\left\{P_X\right\}\left(\mathit{y}\right),\hfill \end{array}$$ (3.3)

where operator X is defined as

$$\mathbf{X}\left\{f\right\}\left(\mathit{x}\right)\equiv \mathit{x}f\left(\mathit{x}\right).$$

Note that equation 3.2 implies that P_Y always lies in the range of A. Assuming for the moment that A is invertible, we can define A⁻¹, an operator that inverts the observation process, recovering P_X from P_Y. The numerator can then be written as

$$\begin{array}{cc}\hfill N\left(\mathit{y}\right)=& (\mathbf{A}\circ \mathbf{X}\circ {\mathbf{A}}^{-1})\left\{P_Y\right\}\left(\mathit{y}\right)\hfill \\ \hfill =& \mathbf{L}\left\{P_Y\right\}\left(\mathit{y}\right),\hfill \end{array}$$ (3.4)

with linear operator L ≡ A ∘ X ∘ A⁻¹. In general, this operator maps a scalar-valued function of a vector, P_Y(y), to a vector-valued function. In the discrete scalar case, P_Y(y) and N(y) are each vectors, the argument yselects a particular index, A is a matrix containing P_Y|X, X is a diagonal matrix containing values of x, and ∘ is simply matrix multiplication. Combining all of these, we arrive at a general NEBLS form of the estimator:

$$\widehat{\mathit{x}}\left(\mathit{y}\right)=\frac{\mathbf{L}\left\{P_Y\right\}\left(\mathit{y}\right)}{\left\{P_Y\right\}\left(\mathit{y}\right)}.$$ (3.5)

That is, the BLS estimator may be computed by applying a linear operator to the measurement density and dividing this by the measurement density. This linear operator is determined solely by the observation process (as specified by the density P_Y|X), and thus the estimator does not require any knowledge of or assumption about the prior P_X.

The derivation above may seem like sleight of hand, given that we assumed that the prior could be recovered exactly from the measurement density using A⁻¹. But in section 6.2, we show that while the operator A⁻¹ may be ill conditioned (e.g., a deconvolution in our introductory example of section 2), it is often the case that the composite operator L is more stable (e.g., a derivative in the introductory example). More surprising, even when A is strictly non invertible, it may still be possible to find an operator L that generates a NEBLS estimator. In section 6 and appendix B, we use equation 3.5 to derive NEBLS estimators for specific observation models, including those that have appeared in previous literature.

The NEBLS expression of equation 3.5 may be used to rewrite other expectations over X in terms of expectations over Y. For example, if we wish to calculate E_X|Y{Xⁿ | Y = y}, then equation 3.4 would be replaced by (A ∘ Xⁿ ∘ A⁻¹){P_Y} = (A ∘ Xⁿ ∘ A⁻¹)ⁿ{P_Y} = Lⁿ{P_Y}.⁵ Exploiting the linearity of the conditional expectation, we may extend this to any polynomial function, g(x) = ∑c_kx^k:

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X\mid Y}\left(g\right(X)\mid Y=y)\approx & {\mathbf{E}}_{X\mid Y}\left(\sum _k{c}_k{X}^k\mid Y=y\right)\hfill \\ \hfill =& \frac{\sum _k{c}_k{\mathbf{L}}^k\left\{P_Y\right\}\left(\mathit{y}\right)}{\left\{P_Y\right\}\left(\mathit{y}\right)}\hfill \\ \hfill =& \frac{g\left(\mathbf{L}\right)\left\{P_Y\right\}\left(\mathit{y}\right)}{\left\{P_Y\right\}\left(\mathit{y}\right)}.\hfill \end{array}$$ (3.6)

And finally, consider the problem of finding the BLS estimator of X given Z where

$$Z=r\left(Y\right),$$

with r an invertible, differentiable, transformation. Using the known properties of change of variables for densities, we can write P_Y(Y) = J_r P_Z(r(Y)), where J_r is the Jacobian of the transformation r(·). From this, we obtain

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X\mid Z}(X\mid Z=z)=& {\mathbf{E}}_{X\mid Y}\left(X\mid Y=r^{-1}\left(z\right)\right)\hfill \\ \hfill =& \frac{\mathbf{L}\left\{P_Y\right\}\left(r^{-1}\right(z\left)\right)}{P_Y\left(r^{-1}\right(z\left)\right)}\hfill \\ \hfill =& \frac{\mathbf{L}\left\{J_r(P_Z\circ r)\right\}\left(r^{-1}\right(z\left)\right)}{J_r{P}_Z\left(z\right)}.\hfill \end{array}$$ (3.7)

4 Dual Formulation: SURE2PLS Estimation

As in the scalar gaussian case, the NEBLS estimator may be used to develop an expression for the mean squared error that does not depend explicitly on the prior, and this may be used to select an optimal estimator from a parametric family. This form is particularly useful in cases where it proves difficult to develop a stable nonparametric approximation of the ratio in equation 3.5 (Carlin & Louis, 2009).

Consider an estimator f_θ(Y) parameterized by vector θ, and expand the mean squared error as

$${\mathbf{E}}_{X,Y}\left({\mid {\mathit{f}}_{\theta }\left(Y\right)-X\mid }^2\right)={\mathbf{E}}_{X,Y}({\mid {\mathit{f}}_{\theta }\left(Y\right)\mid }^2-2{\mathit{f}}_{\theta }(Y)\cdot X+{\mid X\mid }^2).$$ (4.1)

Using the NEBLS estimator of equation 3.5, the second term of the expectation may be written as

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X,Y}\left({\mathit{f}}_{\theta }\right(Y)\cdot X)=& {\mathbf{E}}_Y\left({\mathit{f}}_{\theta }\left(Y\right)\cdot {\mathbf{E}}_{X\mid Y}(X\mid Y)\right)\hfill \\ \hfill =& {\mathbf{E}}_Y\left({\mathit{f}}_{\theta }\left(Y\right)\cdot \frac{\mathbf{L}\left\{P_Y\right\}\left(Y\right)}{P_Y\left(Y\right)}\right)\hfill \\ \hfill =& \int {\mathit{f}}_{\theta }\left(\mathit{y}\right)\cdot \frac{\mathbf{L}\left\{P_Y\right\}\left(\mathit{y}\right)}{P_Y\left(\mathit{y}\right)}{P}_Y\left(\mathit{y}\right)d\mathit{y}\hfill \\ \hfill =& \int {\mathit{f}}_{\theta }\left(\mathit{y}\right)\cdot \mathbf{L}\left\{P_Y\right\}\left(\mathit{y}\right)d\mathit{y}\hfill \end{array}$$ (4.2a)

$$=\int {\mathbf{L}}^{\ast }\left\{{\mathit{f}}_{\theta }\right\}\left(\mathit{y}\right)\cdot \left\{P_Y\right\}\left(\mathit{y}\right)d\mathit{y}$$ (4.2b)

$$={\mathbf{E}}_Y\left({\mathbf{L}}^{\ast }\right\{{\mathit{f}}_{\theta }\left\}\right(\mathit{Y}\left)\right),$$ (4.2c)

where L* is the dual operator of L, defined by the equality of lines 4.2a and 4.2b. In general, L* maps a vector-valued function of y into a scalar-valued function of y. In the discrete scalar case, L* is simply the matrix transpose of L. Substituting this for the second term of equation 4.1, and dropping the last term (since it does not depend on θ), gives a prior-free expression for the optimal parameter vector:

$$\begin{array}{cc}\hfill \widehat{\theta }=& \arg \underset{\theta }{\min }{\mathbf{E}}_{X,Y}\left({\mid f_{\theta }\left(Y\right)-X\mid }^2\right)\hfill \\ \hfill =& \arg \underset{\theta }{\min }{\mathbf{E}}_Y({\mid \left\{{\mathit{f}}_{\theta }\right\}\left(Y\right)\mid }^2-2{\mathbf{L}}^{\ast }\{{\mathit{f}}_{\theta }\left\}\right(Y\left)\right).\hfill \end{array}$$ (4.3)

This generalized SURE (gSURE) form includes as special cases those formulations that have appeared in previous literature (see section 1, and Table 1 for specific citations).⁶ Our approach thus serves to unify and generalize these results, and to show that they can be derived from the corresponding NEBLS estimators. Conversely, it is relatively straightforward to show that the estimator of equation 3.5 can be derived from the gSURE expression of equation 4.3 (see Raphan, 2007, for a proof).

Table 1.

NEBLS Estimation Formulas for a Variety of Observation Processes, as Listed in the Left Column.

Observation Process	Observation Density: PY|X(y|x)	Numerator of Estimator: L{PY}(y)
General discrete	A (matrix)	(A ∘ X ∘ A−1)PY(y)
Additive:
General (section 6.1)	PW(y − x)	$\mathit{y}{P}_Y\left(\mathit{y}\right)-{\mathcal{F}}^{-1}\left\{i{\nabla }_w\ln \left(\widehat{P_W}\left(\omega \right)\right)\widehat{P_Y}\right(\omega \left)\right\}\left(\mathit{y}\right)$
Gaussian (Miyasawa, 1961; Stein, 1981*)	$\frac{\exp -\frac{1}{2}{(\mathbf{y}-\mathbf{x}-\mu )}^T{\wedge }^{-1}(\mathbf{y}-\mathbf{x}-\mu )}{\sqrt{\mid 2\pi \wedge \mid }}$	(y − μ)PY(y) + Λ ∇y(y)
Laplacian	$\frac{1}{2\alpha }{e}^{-\mid (y-x)∕\alpha \mid }$	$y{P}_Y\left(y\right)+2{\alpha }^2\{P_W^{\prime }\star P_Y\}\left(y\right)$
Poisson	$\sum \frac{{\lambda }^k{e}^{-\lambda }}{k!}\delta (y-x-ks)$	yPY(y) − λs PY(y − s)
Cauchy	$\frac{1}{\pi }\left(\frac{\alpha }{{\left(\alpha \right(y-x\left)\right)}^2+1}\right)$	$y{P}_Y\left(y\right)-\{\frac{1}{2\pi \alpha y}\star P_Y\}\left(y\right)$
Uniform	$\{\begin{array}{cc}\frac{1}{2a},\hfill & \mid y-x\mid \le a\hfill \\ 0,\hfill & \mid y-x\mid >a\hfill \end{array}\phantom{\}}$	$y{P}_Y\left(y\right)+a{\sum }_k\mathrm{sgn}\left(k\right)P_Y(y-ak)-\frac{1}{2}\int P_Y\left(\tilde{y}\right)\mathrm{sgn}(y-\tilde{y})d\tilde{y}$
Random number of components	PW(y − x), where:  $W\sim {\sum }_{k=0}^K{W}_k$,  Wk i.i.d. (Pc), K ~ Poiss(λ)	yPY(y) − λ{(yPc) ⋆ PY}(y)
Gaussian scale mixture	$\mathit{Y}=\mathit{x}+\sqrt{Z}\mathit{U}$, U ~ N(0, Λ), Z ~ pZ	$\mathit{y}{P}_Y\left(\mathit{y}\right)+\left({\mathcal{F}}^{-1}\left\{\frac{{\int }_0^{\infty }z{p}_z\left(z\right)e^{-z\frac{1}{2}{\omega }^T\wedge \omega }dz}{{\int }_0^{\infty }{p}_z\left(z\right)e^{-z\frac{1}{2}{\omega }^T\wedge \omega }dz}\right\}\star \wedge {\nabla }_{\mathit{y}}{P}_Y\right)\left(y\right)$
Discrete exponential:
General (section B.1)   (Maritz & Lwin, 1989; Hwang, 1982*)	h(x)g(n)xn	$\frac{g\left(n\right)}{g(n+1)}{P}_Y(n+1)$
Inverse (Hwang, 1982)	h(x)g(n)x−n	$\frac{g\left(n\right)}{g(n-1)}{P}_Y(n-1)$
Poisson (section 6.1)   (Robbins, 1956; Hwang, 1982*)	$\frac{x^n{e}^{-x}}{n!}$	(n + 1)PY(n + 1)
Continuous exponential:
General (section B.3)  (Maritz & Lwin, 1989; Berger, 1980*)	h(x)g(y)eT(y)x	$\frac{g\left(y\right)}{T^{\prime }\left(y\right)}\frac{d}{dy}\left(\frac{P_Y\left(y\right)}{g\left(y\right)}\right)$
Inverse (Berger, 1980*)	h(x)g(y)eT(y)/x	$-g\left(y\right){\int }_y^{\infty }\frac{T^{\prime }\left(\tilde{y}\right)}{g\left(\tilde{y}\right)}{P}_Y\left(\tilde{y}\right)d\tilde{y}$
Laplacian scale mixture	$\frac{1}{x}{e}^{-\frac{y}{x}}$, x, y > 0	Pr{Y > y}
Power of fixed:
General (section B.3)	$\widehat{P_{Y\mid X}}(\omega \mid x)={\left[\widehat{P_W}\right(\omega \left)\right]}^x$	$\left({\mathcal{F}}^{-1}\left\{\frac{1}{i\frac{d}{dw}\ln \left(\widehat{P_W}\right(\omega \left)\right)}\right\}\star \left(y{P}_Y\right)\right)\left(y\right)$
Gaussian scale mixture	$\frac{1}{\sqrt{2\pi x}}{e}^{-\frac{y^2}{2x}}$	EY{Y; Y > y}
Signal-dependent AWGN	$Y=ax+\sqrt{x}W$, $W\sim \mathcal{N}(0,1)$	$\mathrm{sgn}\left(a\right)\left(\left(e^{ax}{I}_{\{ax<0\}}\right)\star \left(y{P}_Y\right)\right)\left(y\right)$
Multiplicative α-stable	$Y=x^{\frac{1}{\alpha }}W$,  W α-stable	$\left({\mathcal{F}}^{-1}\left\{\frac{i}{\mathrm{sgn}\left(\omega \right){\mid \omega \mid }^{\alpha -1}}\right\}\star \left(y{P}_Y\right)\right)\left(y\right)$
Multiplicative lognormal (section B.4)	Y = xeW, W Gaussian	$e^{\frac{3}{2}{\sigma }^2}{P}_Y\left(e^{{\sigma }^2}y\right)y$
Uniform mixture (section B.5)	$\begin{array}{cc}\hfill \frac{1}{2x},\hfill & \hfill \mid y\mid \le x\hfill \\ \hfill 0,\hfill & \hfill \mid y\mid >x\hfill \end{array}$	∣y∣PY(y) + Pr{Y > ∣y∣}

Notes: Expressions in parentheses indicate the section containing the derivation and brackets contain the bibliographical references for operators L, with the asterisk denoting references for the parametric dual operator, L*. Middle column gives the measurement density (note that variable n replaces y for discrete measurements). Right column gives the numerator of the NEBLS estimator, L{P_Y}(y). The symbol * indicates convolution, a hat (e.g., $\widehat{P_W}$) indicates a Fourier transform, and ${\mathcal{F}}^{-1}$ is the inverse Fourier transform.

In practice, we can solve for the optimal θ by minimizing the sample mean of this quantity:

$$\widehat{\theta }=\arg \underset{\theta }{\min }\frac{1}{N}\sum _{k=1}^N\{{\mid \left\{{\mathit{f}}_{\theta }\right\}\left({\mathit{y}}_k\right)\mid }^2-2{\mathbf{L}}^{\ast }\{{\mathit{f}}_{\theta }\left({\mathit{y}}_k\right)\}.$$ (4.4)

where {y_k} is a set of observed data. This optimization does not require any knowledge of (or samples drawn from) the prior P_X, and so we think of it as the unsupervised counterpart of the standard (supervised) regression solution of equation 2.5. When trained on insufficient data, this estimator can still exhibit errors analogous to overfitting errors seen in supervised training. This is because the sample mean in equation 4.4 is only asymptotically equal to the MSE. As with supervised regression, cross-validation or other resampling methods can be used to limit the dimensionality or complexity of the parameterization so that it is appropriate for the available data.

The resulting generalized SURE-optimized parametric least squares (gSURE2PLS) estimator, ${\mathit{f}}_{\widehat{\theta }}$, may be applied to the same data set used to optimize $\widehat{\theta }$. This may seem odd when compared to supervised regression, for which such a statement makes no sense (since the supervised training set already includes the correct answers). But in the unsupervised context, each newly acquired measurement can be used for both estimation and learning, and it would be wasteful not to take advantage of this fact. In cases where one also has access to some supervised data $\{\mathit{x},{\mathit{y}}_n\mid n\in \mathcal{S}\}$, in addition to unsupervised data $\{{\mathit{y}}_n\mid n\in \mathcal{U}\}$, the corresponding objective functions may be combined additively (since they both represent squared errors) to obtain a semisupervised solution:

$$\begin{array}{cc}\hfill \widehat{\theta }=& \arg \underset{\theta }{\min }\sum _{k\in \mathcal{S}}{\mid \left\{{\mathit{f}}_{\theta }\right\}\left({\mathit{y}}_k\right)-{\mathit{x}}_k\mid }^2+\sum _{k\in \mathcal{u}}\{{\mid {\mathit{f}}_{\theta }\left({\mathit{y}}_k\right)\mid }^2-2{\mathbf{L}}^{\ast }\{{\mathit{f}}_{\theta }\left({\mathit{y}}_k\right)\}\hfill \\ \hfill =& \arg \underset{\theta }{\min }\sum _{k\in \mathcal{S}\cup \mathcal{U}}{\mid \left\{{\mathit{f}}_{\theta }\right\}\left({\mathit{y}}_k\right)\mid }^2-2\sum _{k\in \mathcal{S}}{x}_k{\mathit{f}}_{\theta }\left({\mathit{y}}_k\right)-2\sum _{k\in \mathcal{U}}{\mathbf{L}}^{\ast }\left\{{\mathit{f}}_{\theta }\right\}\left({\mathit{y}}_k\right),\hfill \end{array}$$

where we have again discarded a term that does not depend on θ. Again, the gSURE2PLS methodology allows the estimator to be initialized with some supervised training data, but then to continue to adapt its estimator while performing the estimation task.

The operator L* extracts that information from a function on Y that is relevant for estimating X and may be used in more general settings than the one considered here. For example, the derivation in equation 4.2c can be generalized, using the result in equation 3.6, to give

$${\mathbf{E}}_{X,Y}\left(f\right(X\left)g\right(Y\left)\right)={\mathbf{E}}_Y\left(f\right({\mathbf{L}}^{\ast }\left)\right\{g\left\}\right(Y\left)\right),$$

for arbitrary polynomials f and g (and hence functions that are well approximated by polynomials). And this may be further generalized to any joint polynomial, which can be written as a sum of pairwise products of polynomials in each variable. As a particular example, this means that we can recover any statistic of X (e.g., any moment of the prior) through an expectation over Y:

$${\mathbf{E}}_X\left(f\right(X\left)\right)={\mathbf{E}}_Y\left(f\right({\mathbf{L}}^{\ast }\left)\right\{1\left\}\right(Y\left)\right),$$ (4.5)

where 1 indicates a function whose value is (or vector whose components are) always one.

Finally, for a parametric prior density, the NEBLS estimator of equation 3.5 may be substituted into the gSURE objective function of equation 4.4 to obtain a generalized form of the score matching density estimator of equation 2.9. Specifically, a parametric density $P_Y^{\left(\varphi \right)}$ may be fit to data {y_k} by solving

$$\widehat{\varphi }=\arg \underset{\varphi }{\min }\frac{1}{N}\sum _{k=1}^N\left[{\mid \frac{\mathbf{L}\left\{P_Y^{\left(\varphi \right)}\right\}}{P_Y^{\left(\varphi \right)}}\left({\mathit{y}}_k\right)\mid }^2-2{\mathbf{L}}^{\ast }\left\{\frac{\mathbf{L}\left\{P_Y^{\left(\varphi \right)}\right\}}{P_Y^{\left(\varphi \right)}}\right\}\left({\mathit{y}}_k\right)\right].$$ (4.6)

Recall that the operator L is determined by the observation process that governs the relationship between the true signal and the measurements in the original estimation problem. When used in this parametric density estimation context, different choices of operator will lead to different density estimators, in which the density is selected from a family “smoothed” by the measurement process underlying L. In all cases, the density estimation problem can be solved without computing the normalization factor, which is eliminated in the quotient $\mathbf{L}\left\{P_Y^{\left(\varphi \right)}\right\}∕P_Y^{\left(\varphi \right)}$.

As a specific example, assume the observations are positive integers, n, sampled from a mixture of Poisson densities, $P_Y^{\left(\varphi \right)}\left(n\right)$, where the rate variable X is distributed according to a parametric prior density, $P_Y^{\left(\varphi \right)}\left(x\right)$. Using the form of L for Poisson observations (see section 6.1), we obtain an estimator for parameter ϕ from data {n_k}:

$$\widehat{\varphi }=\arg \underset{\varphi }{\min }\frac{1}{N}\sum _k\left\{{\left(\frac{(n_k+1)P_Y^{\left(\varphi \right)}(n_k+1)}{P_Y^{\left(\varphi \right)}\left(n_k\right)}\right)}^2-2\left(\frac{{\left(n_k\right)}^2{P}_Y^{\left(\varphi \right)}\left(n_k\right)}{P_y^{\left(\varphi \right)}\left(n_{k-1}\right)}\right)\right\}.$$

5 Incremental gSURE2PLS Optimization for Kernel Estimators

The gSURE2PLS methodology introduced in section 4 requires us to minimize an expression that is quadratic in the estimation function. This makes it particularly appealing for use with estimators that are linear in their parameters, and several authors have exploited this in developing estimators for the additive gaussian noise case (Pesquet and Leporini, 1997; Luisier et al., 2006; Raphan and Simoncelli, 2007b, 2008; Blu & Luisier, 2007). Here, we show that this advantage holds for the general case, and we use it to develop an incremental algorithm for optimizing the estimator.

Consider a scalar estimator that is formed as a weighted sum of fixed nonlinear kernel functions:

$$f_{\theta }\left(y\right)=\sum _j{\theta }_j{h}_j\left(y\right)={\theta }^T\mathit{h}\left(y\right),$$

where h(y) is a vector with components containing the kernel functions, h_j(y). Substituting this into equation 4.4, and using the linearity of the operator L* gives a gSURE expression for unsupervised parameter optimization from n samples:

$${\widehat{\theta }}_n=\arg \underset{\theta }{\min }\frac{1}{n}\left\{{\theta }^T\left(\sum _{k=1}^n\mathit{h}\left(y_k\right)\mathit{h}{\left(y_k\right)}^T\right)\theta -2{\theta }^T\sum _{k=1}^n{\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_k\right)\right\},$$ (5.1)

where L*{h}(y) is a vector whose jth component is L*{h_j}(y). The quadratic form of the objective function allows us to write the solution as a familiar closed-form expression:

$${\widehat{\theta }}_n={\mathbf{C}}_n^{-1}{\mathit{m}}_n,$$ (5.2)

where we define

$${\mathbf{C}}_n\equiv \sum _{k=1}^n\mathit{h}\left(y_k\right)\mathit{h}{\left(y_k\right)}^T$$ (5.3a)

$${\mathit{m}}_n\equiv \sum _{k=1}^n{\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_k\right).$$ (5.3b)

Note that the quantity m_n is (n times) an n-sample estimate of E_Y(L*{h}(Y)), which by equation 4.2c provides an unsupervised estimate of E_X,Y(h(Y) · X).

In addition to allowing a direct solution, the quadratic form of this objective function lends itself to an incremental algorithm, in which the estimator is both applied to and updated by each measurement as it is acquired sequentially over time. The advantage of such a formulation is that the estimator can be updated gradually, based on all previous observations, but without needing to store and access those observations for each update. To see this, we rewrite the expressions in equation 5.3 as

$${\mathbf{C}}_n={\mathbf{C}}_{n-1}+\mathit{h}\left(y_n\right)\mathit{h}{\left(y_n\right)}^T$$ (5.4a)

$${\mathit{m}}_n={\mathit{m}}_{n-1}+{\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_n\right).$$ (5.4b)

These equations, combined with equation 5.2, imply that the optimal parameter vector can be computed by combining the most recent data observation y_n with summary information stored in an accumulated matrix C_n−1 and vector m_n−1. The basic algorithm is illustrated in a flow diagram in Figure 2. For each iteration of the algorithm, an incoming data value y_n is used to incrementally update the estimator, and the same estimator is then used to compute the estimate ${\widehat{x}}_n$. The diagram also includes an optional path for supervised data x_n, which may be used to improve the estimator.

Figure 2.

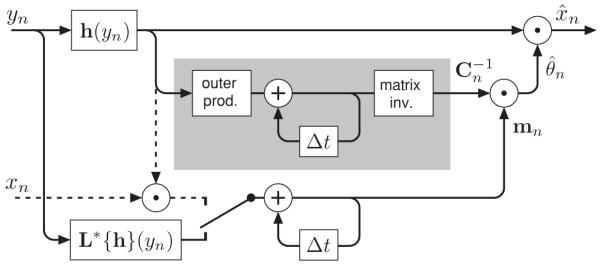
Circuit diagram for an incremental gSURE2PLS kernel estimator, as specified by equation 5.2 and 5.4b. The quantities m_n and C_n must be accumulated and stored internally. The gray box encloses the portion of the diagram in which ${\mathbf{C}}_n^{-1}$ is computed and may be replaced by a circuit that directly accumulates the inverse matrix, ${\mathbf{S}}_n={\mathbf{C}}_n^{-1}$ (see appendix A). The entire diagram can also be formulated in terms of the parameter vector, ${\widehat{\theta }}_n$, in place of the vector m_n (also shown in appendix A). If supervised data (i.e., clean values x_n) are available for some n, they may be incorporated by flipping the switch to activate the dashed-line portion of the circuit (effectively replacing the right-hand side of equation 4.2c by the left-hand side).

This incremental formulation bears some similarity to the well-known Kalman filter (Kalman, 1960), which provides an incremental estimate of a state variable that is observed through additive gaussian measurements. But note that the standard Kalman filter is based on a state model with known linear or gaussian dynamics and known gaussian noise observations, whereas our formulation allows a more general (although still assumed known) observation model that is applied to independent state values drawn independently from an unknown prior.

In practice, this algorithm may be made more efficient and flexible in a number of ways. Specifically, the equations may be rewritten so as to accumulate the inverse covariance matrix, thus avoiding the costly matrix inversion on each iteration. They may also be written so as to directly accumulate the estimator parameter vector $\widehat{\theta }$ instead of m. Finally, the accumulation of data can be weighted (e.g., exponentially) over time so as to emphasize the most recent data and “forget” older data. This is particularly useful in a case where the distribution of the state variable is changing over time. These variations are described in appendix A.

6 Derivation of NEBLS Estimators

In section 2, we developed the NEBLS estimator for the scalar case of additive gaussian noise. The formulation of section 3 is much more general and can be used to obtain NEBLS estimators for a variety of other corruption processes. But in many cases, it is difficult to obtain the operator L directly from the expression in equation 3.4, because inversion of the operator A is unstable or undefined. This issue is addressed in detail in section 6.2. But we first note that it is necessary and sufficient that applying L to the measurement density produces the numerator of the BLS estimator in equation 3.1:

$$(\mathbf{L}\circ \mathbf{A})\left\{P_X\right\}=(\mathbf{A}\circ \mathbf{X})\left\{P_X\right\},$$

where we have used equations 3.2 and 3.3 to express both numerator and measurement density as linear functions of the prior. This expression must hold for every prior density, P_X. From the definition of A, this means that it is sufficient to find an operator L such that

$$\mathbf{L}\left\{P_{Y\mid X}\right(\mathit{y}\mid \mathit{x}\left)\right\}=\mathit{x}{P}_{Y\mid X}(\mathit{y}\mid \mathit{x}).$$ (6.1)

Cressie (1982) noted previously that if an operator could be found that satisfied this relationship, then it could be used to define a corresponding NEBLS estimator. Here we note that in the scalar case, this equation implies that for each value of x, the conditional density P_Y|X(y|x) must be an eigenfunction (or eigenvector, for discrete variables) of operator L, with associated eigenvalue x.⁷ We have used this eigenfunction property to obtain a variety of NEBLS estimators by direct inspection of the observation density P_Y|X. Table 1 provides a listing of these, including examples that appear previously in the nonparametric empirical Bayes and SURE-optimized estimator literatures.

6.1 Derivation of Specific NEBLS Estimators

In this section, we provide a derivation for a few specific NEBLS estimators and their gSURE2PLS counterparts. Derivations of the remainder of the estimators given in Table 1 are provided in appendix B.

6.1.1 Additive Noise: General Case

Consider the case in which a vector-valued variable of interest is corrupted by independent additive noise: Y = X + W, with the noise drawn from some distribution, P_W(w). The conditional density may then be written as

$$P_{Y\mid X}(\mathit{y}\mid \mathit{x})=P_W(\mathit{y}-\mathit{x}).$$

We seek an operator that, when applied to this conditional density (viewed as a function of y), will obey

$$\mathbf{L}\left\{P_W\right(\mathit{y}-\mathit{x}\left)\right\}=\mathit{x}{P}_W(\mathit{y}-\mathit{x}).$$ (6.2)

Subtracting y P_W(y − x) from both sides of equation 6.2 gives

$$\mathbf{M}\left\{P_W\right(\mathit{y}-\mathit{x}\left)\right\}=-(\mathit{y}-\mathit{x})P_W(\mathit{y}-\mathit{x}),$$

where we have defined linear operator M{f}(y) ≡ L{P_Y}(y) − y P_Y(y). Since this equation must hold for all x, it implies is a linear shift-invariant operator (acting in y) and can be represented as convolution with a kernel m(y). Taking the Fourier transform of both sides and using the convolution and differentiation properties gives

$$\begin{array}{cc}\hfill \widehat{\mathit{m}}\left(\omega \right)\widehat{P_W}\left(\omega \right)=& -\left(\widehat{\mathit{y}{P}_W}\right)\left(\omega \right)\hfill \\ \hfill =& -i{\nabla }_{\omega }\widehat{P_W}\left(\omega \right),\hfill \end{array}$$

so that

$$\begin{array}{cc}\hfill \widehat{\mathit{m}}\left(\omega \right)=& -i\frac{{\nabla }_{\omega }\widehat{P_W}\left(\omega \right)}{\widehat{P_W}\left(\omega \right)}\hfill \\ \hfill =& -i{\nabla }_{\omega }\ln \left(\widehat{P_W}\left(\omega \right)\right).\hfill \end{array}$$ (6.3)

Thus, the linear operator is

$$\mathbf{L}\left\{P_Y\right\}\left(\mathit{y}\right)=\mathit{y}{P}_Y\left(\mathit{y}\right)+{\mathcal{F}}^{-1}\left\{\widehat{\mathit{m}}\left(\omega \right)\widehat{P_Y}\left(\omega \right)\right\}\left(\mathit{y}\right),$$ (6.4)

where ${\mathcal{F}}^{-1}$ denotes the inverse Fourier transform. The dual operator (consistent with equations 4.2a and 4.2b), is then:

$${\mathbf{L}}^{\ast }\left\{\mathit{f}\right\}\left(\mathit{y}\right)={\mathit{y}}^T\mathit{f}\left(\mathit{y}\right)+{\mathcal{F}}^{-1}\left\{\widetilde{\widehat{\mathit{m}}}\right(\omega \left)\widehat{\mathit{f}}\right(\omega \left)\right\}\left(\mathit{y}\right),$$ (6.5)

where f is the vector-valued estimator and a tilde indicates the Hermitian transpose (i.e., conjugation and transpose).

Note that throughout this discussion, X and W play symmetric roles. Thus, we can solve for the BLS estimator if we know the density of either the noise or the signal. We also note that if the additive noise is such that the observation process is not invertible (e.g., if the Fourier transform of P_W is band-limited), the proof of equation 6.4 implies that this operator is still valid if we define

$${\nabla }_{\omega }\ln \left(\widehat{P_W}\right(\omega \left)\right)=0$$

whenever $\widehat{P_W}\left(\omega \right)=0$. As examples, we consider the following specific cases of additive noise.

6.1.2 Additive Gaussian Noise (Vector Case)

The expression in equation 6.4 can be used to derive the solution for the full vector-valued generalization of the scalar gaussian additive noise case given in section 2. The noise model is

$$P_W\left(x\right)=\frac{1}{{(2\pi \mid \Lambda \mid )}^{n∕2}}{e}^{-\frac{1}{2}{(\mathit{x}-\mu )}^T{\Lambda }^{-1}(\mathit{x}-\mu )},$$

with covariance matrix Λ and mean vector μ. In this case, the Fourier transform of the density is

$$\widehat{P_W}\left(\omega \right)\propto e^{-i{\omega }^T\mu -\frac{1}{2}{\omega }^T\Lambda \omega },$$

which, on substitution into equation 6.3 yields

$$\widehat{m}\left(\omega \right)=[i\Lambda \omega -\mu ].$$

Substituting into equation 6.4, and then into equation 3.5 yields the NEBLS estimator:

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X\mid Y}(\mathit{x}\mid Y=\mathit{y})=& \mathit{y}-\mu +\frac{\Lambda {\nabla }_{\mathit{y}}{P}_Y\left(\mathit{y}\right)}{P_Y\left(\mathit{y}\right)}\hfill \\ \hfill =& \mathit{y}-\mu +\Lambda {\nabla }_{\mathit{y}}\ln \left(P_Y\right(\mathit{y}\left)\right).\hfill \end{array}$$ (6.6)

And substituting into equation 6.5 yields the dual operator:

$${\mathbf{L}}^{\ast }\left\{\mathit{f}\right\}\left(\mathit{y}\right)={(\mathit{y}-\mu )}^T\mathit{f}\left(\mathit{y}\right)-{\nabla }_{\mathit{y}}\cdot \left(\Lambda \mathit{f}\right(\mathit{y}\left)\right).$$

In Raphan and Simoncelli (2007a, 2010), we have developed a practical implementation of this NEBLS estimator, based on a local exponential approximation of the gradient of the log of the measurement density P_Y.

6.1.3 Additive Laplacian Noise (Scalar Case)

When the additive noise is drawn from a Laplacian distribution, we have

$$P_W\left(x\right)=\frac{1}{2\alpha }{e}^{-\mid x∕\alpha \mid },$$

with Fourier transform

$$\widehat{P_W}\left(\omega \right)=\frac{1}{1+{\left(\alpha \omega \right)}^2},$$

which gives

$$\widehat{m}\left(\omega \right)=2i{\alpha }^2\omega \widehat{P_W}\left(\omega \right).$$

The resulting BLS estimator is then

$${\mathbf{E}}_{X\mid Y}(x\mid Y=y)=y+\frac{2{\alpha }^2{P}_W^{\prime }\left(y\right)\star P_Y\left(y\right)}{P_Y\left(y\right)},$$ (6.7)

where ⋆ denotes convolution and

$$P_W^{\prime }\left(y\right)=-\left(\frac{1}{\alpha }\right)\mathrm{sgn}\left(y\right)P_W\left(y\right),$$

with

$$\mathrm{sgn}\left(y\right)=\{\begin{array}{cc}-1,\hfill & y<0\hfill \\ 0,\hfill & y=0\hfill \\ 1,\hfill & y>0.\hfill \end{array}\phantom{\}}$$

This solution uses a convolutional operator, as compared to the differentiation found in the gaussian case. There are a variety of noise densities (e.g., the family of generalized gaussian distributions) for which the operator will be a convolution with a kernel that depends on the form of the noise. In these cases, the kernel may be used directly to approximate the convolutional operator from observed samples {y_k}:

$$K\star P_Y\left(y\right)\approx \frac{1}{N}\sum _{k=1}^{N}K(y-y_k).$$

Note that this has the form of a kernel density estimator. While such density estimators are generally biased (Scott, 1992), in our situation this approximation is unbiased and converges to the desired convolution K ⋆ P_Y as the number of samples (N) increases, since

$${\mathbf{E}}_Y\left(\frac{1}{N}\sum _{k=1}^{N}K(y-y_k)\right)=\int K(y-\tilde{y})P_Y\left(\tilde{y}\right)d\tilde{y}.$$

Of course, the denominator of equation 6.7 still needs to be approximated using some choice of density estimator (see Scott, 1992, for a review and further references).

Finally, substituting into equation 6.5 yields the dual operator

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(y\right)=yf\left(y\right)-2{\alpha }^2(P_W^{\prime }\star f)\left(y\right),$$

where the ⋆ indicates convolution.

6.1.4 Poisson Process with Random Rate

Assume the hidden value, X, is positive and continuous, while the observation, Y, is discrete and has Poisson distribution with rate X:

$$P_{Y\mid X}(n\mid x)=\frac{e^{-x}{x}^n}{n!}.$$

It is easy to verify that

$$(n+1)P_{Y\mid X}(n+1\mid x)=x{P}_{Y\mid X}(n\mid x),$$

and from this that

$$\mathbf{L}\left\{P_Y\right\}\left(n\right)=(n+1)P_Y(n+1).$$

As a result, the NEBLS estimator is

$${\mathbf{E}}_{X\mid Y}(X\mid Y=n)=\frac{(n+1)P_Y(n+1)}{P_Y\left(n\right)},$$

which matches the original result derived by Robbins (1956).

Finally, the dual operator, L*, is readily derived from L by writing equations 4.2a and 4.2b, and replacing the integral by a sum

$$\begin{array}{cc}\hfill \sum _{n=0}^{\infty }f\left(n\right)\mathbf{L}\left\{P_Y\right\}\left(n\right)=& \sum _{n=0}^{\infty }f\left(n\right)(n+1)P_Y(n+1)\hfill \\ \hfill =& \sum _{k=1}^{\infty }f(k-1)k{P}_Y\left(k\right)\hfill \\ \hfill =& \sum _{k=1}^{\infty }{\mathbf{L}}^{\ast }\left\{f\right\}\left(k\right)P_Y\left(k\right),\hfill \end{array}$$

from which we see that L*{f}(n) = nf(n − 1).

6.2 Noninvertible Observations

An NEBLS estimator always exists when the observation process, A, is invertible, as can be seen from equation 3.4. In some cases (including some of those derived in this article), the estimator exists even when A⁻¹ is not defined. On the other hand, it is clear that some estimation problems do not allow an NEBLS form. Consider the extreme situation in which the observation contains no information about the quantity to be estimated: the optimal estimator is simply the mean of the prior density, which must be known in advance (i.e., it cannot be estimated from the data). In this section, we examine the conditions under which an NEBLS estimator may be defined for a noninvertible observation process.

We first decompose the prior into a sum of three orthogonal components, P_X(x) = P₁(x) + P₂(x) + P₃(x), with

$$\begin{array}{cc}\hfill P_1\in & \mathcal{N}{\left(\mathbf{A}\right)}^{\perp }\hfill \\ \hfill P_2\in & \mathcal{N}\left(\mathbf{A}\right)\cap \mathcal{N}{(\mathbf{A}\circ \mathbf{X})}^{\perp }\hfill \\ \hfill P_3\in & \mathcal{N}\left(\mathbf{A}\right)\cap \mathcal{N}(\mathbf{A}\circ \mathbf{X}),\hfill \end{array}$$

where $\mathcal{N}(\cdot )$ denotes the nullspace of an operator and ()^⊥ the orthogonal complement of a subspace. The measurement density may now be expressed as

$$P_Y=\mathbf{A}\circ P_X=\mathbf{A}\circ P_1,$$

since the second and third density components lie in the nullspace of A. And since the first component of the prior is orthogonal to the nullspace, it may be recovered from the measurement density: P₁ = A^#{P_Y}, where ()^# indicates the pseudo-inverse. Note that P₁ is guaranteed to integrate to one as long as P_Y does, since

$$\begin{array}{cc}\hfill \int P_Y\left(\mathit{y}\right)d\mathit{y}=& \int \mathbf{A}\left\{P_1\right\}\left(\mathit{y}\right)d\mathit{y}\hfill \\ \hfill =& \int \int P_{Y\mid X}(\mathit{y}\mid \mathit{x})P_1\left(\mathit{x}\right)d\mathit{x}d\mathit{y}\hfill \\ \hfill =& \int \left[\int P_{Y\mid X}(\mathit{y}\mid \mathit{x})d\mathit{y}\right]P_1\left(\mathit{x}\right)d\mathit{x}\hfill \\ \hfill =& \int P_1\left(\mathit{x}\right)d\mathit{x}.\hfill \end{array}$$

Substituting the decomposed prior into the numerator of the BLS estimator, as given by equation 3.3, produces

$$\begin{array}{cc}\hfill (\mathbf{A}\circ \mathbf{X})\left\{P_X\right\}=& (\mathbf{A}\circ \mathbf{X})\left\{P_1\right\}+(\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\hfill \\ \hfill =& (\mathbf{A}\circ \mathbf{X}\circ {\mathbf{A}}^{\#})\left\{P_Y\right\}+(\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\hfill \\ \hfill =& \mathbf{L}\left\{P_Y\right\}+(\mathbf{A}\circ \mathbf{X})\left\{P_2\right\},\hfill \end{array}$$ (6.8)

where we have discarded the term containing P₃ (since it lies in the nullspace of operator A ∘ X, and replaced the term containing P₁ with its NEBLS equivalent. The second term depends on P₂, the component of the prior that cannot be recovered from the observation density but is nevertheless required to construct the BLS estimator. Thus, we can express the optimal estimator in NEBLS form if and only if the subspace containing this second component is zero (as is true of all solutions derived in this article). If not, then obtaining an optimal estimator requires a priori knowledge of that term.

Consider a simple example. Suppose we randomly select a coin with probability of heads X ∈ [0, 1], where X has prior density P_X. We then perform a binomial experiment, flipping the chosen coin n times and observing the number of heads, so that

$$P_{Y\mid X}\{k\mid x\}=\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)x^k{(1-x)}^{n-k},$$

where $\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)=\frac{n!}{(n-k)!k!}$. From this, we see that for each number of observed heads, k, the measurement probability consists of an inner product of P_X with a particular polynomial of degree n:

$$\begin{array}{cc}\hfill P_Y\left(k\right)=& \mathbf{A}\left\{P_X\right\}\left(k\right)\hfill \\ \hfill =& \left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right){\int }_0^1{P}_X\left(x\right)x^k{(1-x)}^{n-k}dx.\hfill \end{array}$$ (6.9)

Since the measurement process maps an arbitrary continuous prior density on the unit interval to a discrete measurement distribution, a simple dimensionality argument tells us that this process cannot be invertible. In particular, the measurement distribution contains the inner product of the prior density with n + 1 linearly independent polynomials of degree n, so we can recover the inner product of our prior with any polynomial of degree n but not with polynomials of higher degree. Define ${\left\{q_k\right(x\left)\right\}}_{k=0}^{\infty }$ as the set of orthogonal polynomials of ascending degree (obtained by} starting with monomials and using Gram-Schmidt orthogonalization over the unit interval). Then $\mathcal{N}{\left(\mathbf{A}\right)}^{\perp }$ is the space of polynomials of degree up to n, spanned by ${\left\{q_k\right(x\left)\right\}}_{k=0}^n$, and $\mathcal{N}\left(\mathbf{A}\right)$ is spanned by ${\left\{q_k\right(x\left)\right\}}_{k=n+1}^{\infty }$. From the observation distribution, we may reconstruct P₁, the projection of the prior density onto $\mathcal{N}{\left(\mathbf{A}\right)}^{\perp }$, but no component of the prior in $\mathcal{N}\left(\mathbf{A}\right)$.

It might seem natural at this point to Nsimply constrain the prior to be an nth-order polynomial in X, which would allow recovery of the entire prior from the observation distribution. Although this constraint would certainly allow construction of an NEBLS estimator, it is far more restrictive than necessary. To construct the BLS estimator, we must be able to calculate its numerator, which is the inner product of the prior with a polynomial of degree n + 1:

$$\begin{array}{cc}\hfill N\left(k\right)=& (\mathbf{A}\circ \mathbf{X})\left\{P_X\right\}\left(k\right)\hfill \\ \hfill =& \left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right){\int }_0^1{P}_X\left(x\right)x^{k+1}{(1-x)}^{n-k}dx\hfill \\ \hfill =& \left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right){\mathbf{E}}_X\left(x^{k+1}{(1-x)}^{n-k}\right).\hfill \end{array}$$

This does not depend on the prior component P₃, which lies in the space spanned by ${\left\{q_k\right(x\left)\right\}}_{k=n+2}^{\infty }$, and therefore there is no need to place any restrictions on this component of the prior (e.g., by assuming it is equal to zero). The prior component P₂, on the other hand, which lies in the space spanned by q_n+1(x) (i.e., P₂(x) = cq_n+1(x), for some constant c), cannot be recovered from the observation density and is required to derive the BLS estimator. Thus, the BLS estimator may be written as a sum of a prior-free term and a second term,

$$(\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\left(k\right)=c\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right){\int }_0^1{q}_{n+1}\left(x\right)x^{k+1}{(1-x)}^{n-k}dx.$$

The value of c must be assumed a priori.

It is worth pointing out that this behavior is tied to the parameterization used. If, for example, we choose X ∈ [0, ∞) with density P_X and then perform the Bernoulli experiment with probability of heads $\frac{X}{X+1}$, then

$$\begin{array}{cc}\hfill P_Y\left(k\right)=& \left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)\int P_X\left(x\right){\left(\frac{x}{x+1}\right)}^k{\left(\frac{1}{x+1}\right)}^{n-k}dx\hfill \\ \hfill =& \left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)\int P_X\left(x\right)x^k{\left(\frac{1}{x+1}\right)}^{n}dx.\hfill \end{array}$$

In order to obtain the BLS estimator of X, we need to know

$$N\left(k\right)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)\int P_X\left(x\right)x^{k+1}{\left(\frac{1}{x+1}\right)}^{n}dx.$$

Now it is easy to see that for k < n,

$$N\left(k\right)=\frac{\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n\hfill \\ \hfill k+1\hfill \end{array}\right)}{P}_Y(k+1).$$

Knowing P_Y(k) gives the inner product of P_X, using weighting function ${\left(\frac{1}{x+1}\right)}^n$, with all polynomials up to degree n. However, in order to know N(n), we need to know the inner product of P_X with xⁿ⁺¹. Therefore, in general, we cannot solve for N(n). Again, we can get around this by making assumptions about the missing (but necessary) portion of the prior.

Now consider the problem of developing a gSURE formula when the observation process is noninvertible. In this case, the constraints on the operator involve an interaction between the observation process and the family of estimators over which optimization occurs. From equation 4.2c, we see that the gSURE expression for the MSE relies on finding an operator M* satisfying

$${\mathbf{E}}_Y\left({\mathbf{M}}^{\ast }\right\{{\mathit{f}}_{\theta }\left\}\right(Y\left)\right)={\mathbf{E}}_Y\left({\mathbf{E}}_X\right(X\mid Y\left){\mathit{f}}_{\theta }\right(Y\left)\right),\forall {\mathit{f}}_{\theta }\in \mathcal{F},$$ (6.10)

which must hold for any observation density that could have arisen through the measurement process (i.e., P_Y = A ∘ P_X, for some density P_X). Decomposing the prior into orthogonal components as in equation 6.8, allows us to write

$${\mathbf{E}}_{X\mid Y}(X\mid Y=\mathit{y})=\frac{\mathbf{L}\left\{P_Y\right\}\left(\mathit{y}\right)}{P_Y\left(\mathit{y}\right)}+\frac{(\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\left(\mathit{y}\right)}{P_Y\left(\mathit{y}\right)}.$$

Substituting this back into equation 6.10 and integrating by parts, we see that

$$\begin{array}{cc}\hfill \int {\mathbf{M}}^{\ast }\left\{{\mathit{f}}_{\theta }\right\}\left(\mathit{y}\right)P_Y\left(\mathit{y}\right)d\mathit{y}=& {\mathbf{E}}_Y\left(\frac{\mathbf{L}\left\{P_Y\right\}\left(Y\right)}{P_Y\left(Y\right)}{\mathit{f}}_{\theta }\left(Y\right)\right)\hfill \\ \hfill & +{\mathbf{E}}_Y\left(\frac{(\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\left(Y\right)}{P_Y\left(Y\right)}{\mathit{f}}_{\theta }\left(Y\right)\right)\hfill \\ \hfill =& \int {\mathbf{L}}^{\ast }\left\{{\mathit{f}}_{\theta }\right\}\left(\mathit{y}\right)P_Y\left(\mathit{y}\right)d\mathit{y}\hfill \\ \hfill & +\int (\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\left(\mathit{y}\right){\mathit{f}}_{\theta }\left(\mathit{y}\right)d\mathit{y},\forall {\mathit{f}}_{\theta }\in \mathcal{F},\hfill \end{array}$$

or, equivalently,

$$\begin{array}{cc}\hfill \int & ({\mathbf{M}}^{\ast }-{\mathbf{L}}^{\ast })\left\{{\mathit{f}}_{\theta }\right\}\left(\mathit{y}\right)P_Y\left(\mathit{y}\right)d\mathit{y}\hfill \\ \hfill & =\int (\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\left(\mathit{y}\right){\mathit{f}}_{\theta }\left(\mathit{y}\right)d\mathit{y},\forall {\mathit{f}}_{\theta }\in \mathcal{F},\hfill \end{array}$$ (6.11)

which must hold for P_Y = A{P_X}, for any prior P_X = P₁ + P₂ + P₃. Note that P_Y does not depend on the prior component P₂ since it lies in the nullspace of A). Thus, if we vary this component of the prior, the left side of equation 6.11 will stay the same while the right side will change, which implies that

$$\begin{array}{cc}\hfill \int & (\mathbf{A}\circ \mathbf{X})\left\{P_2\right\}\left(\mathit{y}\right){\mathit{f}}_{\theta }\left(\mathit{y}\right)d\mathit{y}=0,\forall {\mathit{f}}_{\theta }\in \mathcal{F},\hfill \\ \hfill & \forall P_2\in \mathcal{N}\left(\mathbf{A}\right)\cap \mathcal{N}{(\mathbf{A}\circ \mathbf{X})}^{\perp },\hfill \end{array}$$

or, equivalently,

$$\mathcal{F}\subseteq (\mathbf{A}\circ \mathbf{X}){\left\{P_2\right\}}^{\perp },\forall P_2\in \mathcal{N}\left(\mathbf{A}\right)\cap \mathcal{N}{(\mathbf{A}\circ \mathbf{X})}^{\perp }.$$ (6.12)

This is therefore a necessary condition for the operator M* to exist. It is also a sufficient condition, since if equation 6.12 is satisfied, then the operator M = L will satisfy equation 6.11. Thus, selecting a family of estimators that satisfies the constraint of equation 6.12 guarantees that the optimal solution may be found through gSURE2PLS even when an NEBLS solution does not exist. Note that for overly restricted families of estimators, the choice of operator, M, may not be unique.

In our coin tossing example, since the subspace of functions that are in the nullspace of A but orthogonal to the nullspace of A ∘ X is spanned by q_n+1(x), equation 6.12 requires that

$$\sum _{k=0}^n\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)f_{\theta }\left(k\right)\int q_{n+1}\left(x\right)x^{k+1}{(1-x)}^{n-k}dx=0,\forall f_{\theta }\in \mathcal{F}$$

(note that integral over y is replaced by a sum over k). Since, q_n+1(x) is orthogonal to polynomials of degree less than n + 1, this is equivalent to requiring that

$$\sum _{k=0}^n\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)f_{\theta }\left(k\right)\int q_{n+1}\left(x\right)x^{n+1}dx=0,\forall f_{\theta }\in \mathcal{F},$$

which in turn implies that

$$\sum _{k=0}^n\left(\begin{array}{c}\hfill n\hfill \\ \hfill k\hfill \end{array}\right)f_{\theta }\left(k\right)=0,\forall f_{\theta }\in \mathcal{F}.$$

7 Empirical Convergence Properties

In this section, we implement several scalar NEBLS and gSURE2PLS estimators and examine their convergence properties.

7.1 NEBLS Examples

In practice, the NEBLS estimators rely on approximating the density of the observed data, P_Y(Y), and the estimator quality depends critically on the choice of density estimator. If the density estimate converges to the true measurement density, then the associated NEBLS estimator should approach the BLS estimator as the number of data samples grows. In Figure 3, we examine the behavior of three estimators based on equation 3.5. The first case corresponds to data drawn independently from a binary source, which are observed through a process in which bits are switched with probability $\frac{1}{4}$. The estimator does not know the binary distribution of the source (which was a “fair coin” for our simulation) but does know the bit-switching probability. For this estimator, we use the observations to approximate P_Y using a simple histogram and then use the matrix version of the linear operator in equation 3.4 to construct the estimator. We then apply the constructed estimator to the same observed data to estimate the uncorrupted value associated with each observation. We measure the behavior of the estimator, $\widehat{x}\left(y\right)$, using the empirical MSE,

$$\frac{1}{N}\sum _{k=1}^N{\left(\widehat{x}\right(y_k)-x_k)}^2,$$ (7.1)

where {x_k} are the underlying true values and $\left\{\widehat{x}\right(y_k\left)\right\}$ are the corresponding estimates based on the observations. We characterize the behavior of this estimator as a function of the number of data points, N, by running many Monte Carlo simulations for each N, constructing the estimator using the N observations, applying the constructed estimator to these observations, and recording the empirical MSE. Figure 3 indicates the mean improvement in empirical MSE (measured by the increase in empirical MSE compared with using the ML estimator, which, in this case, is the identity function) over the Monte Carlo simulations, the mean improvement using the conventional BLS estimation function, $\widehat{x}\left(y\right)={\mathbf{E}}_{X\mid Y}(X\mid Y=y)$, assuming the prior density is known, and the standard deviations of the improvements taken over our simulations. Note that the large variance in the BLS estimator for small numbers of data points arises from fluctuations of the empirical MSE.

Figure 3.

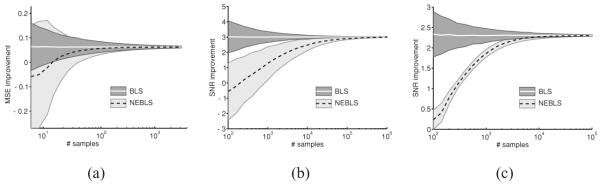
Empirical convergence of NEBLS estimator to conventional BLS solution, as a function of number of observed samples of Y. For each number of observations, each estimator is simulated many times. Black dashed lines show the improvement of the NEBLS estimator, averaged over simulations, relative to the ML estimator. The white line shows the mean improvement using the conventional BLS solution, E_X|Y(X | Y = y), assuming the prior density is known. Gray regions denote ±1 standard deviation. (a) Binary noise (10,000 simulations for each number of samples). (b) Poisson noise (1000 simulations). (c) Additive gaussian noise (1000 simulations).

Figure 3b shows the case of estimating a randomly varying rate parameter that governs an inhomogeneous Poisson process. The prior on the rate (unknown to the estimator) is exponential. The observed values Y are the (integer) values drawn from the Poisson process. In this case, the histogram of observed data was used to obtain a naive approximation of P_Y(n), the appropriate operator from Table 1 was used to convert this into an estimator, and this estimator was then applied to the observed data. It should be noted that improved performance for this estimator is expected if we were to use a more sophisticated approximation of the ratio of densities.

Figure 3c shows similar results for additive gaussian noise, with the empirical MSE being replaced by the empirical signal-to-noise-ratio (SNR), which is defined as

$$\mathit{SNR}\left(dB\right)=20{\log }_{10}\left(\frac{\sum _{k=1}^N{x}_k^2}{\sum _{k=1}^N{\left(\widehat{x}\right(y_k)-x_k)}^2}\right).$$ (7.2)

The signal density is a generalized gaussian with exponent 0.5, and the noisy SNR is 4.8 dB. In this case, we compute equation 3.5 using a more sophisticated approximation method, as described in Raphan and Simoncelli (2007a). We fit a local exponential model similar to that used in Loader (1996) to the data in bins, with bin width adaptively selected so that the product of the number of points in the bin and the squared bin width is constant. This bin width selection procedure, analogous to adaptive binning procedures developed in the density estimation literature (Scott, 1992), provides a reasonable trade-off between bias and variance and converges to the correct answer for any well-behaved density (Raphan & Simoncelli, 2007a). Note that in this case, convergence is substantially slower than for the binary case, as might be expected given that we are dealing with a continuous density rather than a single scalar probability. But the variance of the estimates is quite low, even for relatively small amounts of data.

7.2 gSURE2PLS Examples

Now consider the empirical behavior of the gSURE2PLS methodology in the additive gaussian case, as developed in section 2.2. The estimator is written as

$$f_{\theta }\left(y\right)=y+g_{\theta }\left(y\right),$$

and the parameter vector, θ, may be optimized over the observed data using the expression given by equation 2.8. As in the parameterization of section 5, we write the function g_θ(y) as a linear combination of nonlinear kernels

$$g_{\theta }\left(y\right)=\sum _j{\theta }_j{h}_j\left(y\right)={\theta }^T\mathit{h}\left(y\right),$$ (7.3)

where h(y) is a vector with jth component equal to kernel function h_j(y). We define these kernels as

$$h_j\left(y\right)=y{\cos }^2\left(\frac{1}{\alpha }\mathrm{sgn}\left(y\right){\log }_2(\mid y\mid ∕\sigma +1)-\frac{j\pi }{2}\right),$$

as illustrated in Figure 4. Then, as in section 5, substituting this into equation 2.7 yields a quadratic objective function with optimal solution

$${\widehat{\theta }}_n={\mathbf{C}}_n^{-1}{\mathit{m}}_n,$$ (7.4)

where

$$\begin{array}{cc}\hfill & {\mathbf{C}}_n=\sum _{k=1}^n\mathit{h}\left(y_k\right)\mathit{h}{\left(y_k\right)}^T\hfill \\ \hfill & {\mathit{m}}_n=-{\sigma }^2\sum _{k=1}^n{\mathit{h}}^{\prime }\left(y_k\right).\hfill \end{array}$$

We apply this estimator to the same data that were used to obtain ${\widehat{\theta }}_n$ and measure the empirical SNR.

Figure 4.

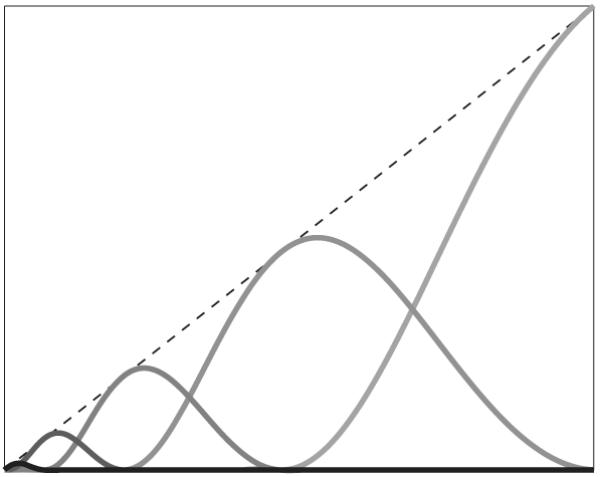
Example “bump” kernel functions, as used for linear parameterization of “SUREbumps” estimators in Figures 5a and 5b. The sum of these functions is the identity (indicated by the dashed black line).

For our simulations, we used a generalized gaussian prior, with exponent 0.5. The noisy SNR was 4.8 dB. Figure 5 shows the empirical behavior of these “SUREbumps” estimators when using 3 bumps (see Figure 5a) and 15 bumps (Figure 5b), illustrating the bias-variance trade-off inherent in the fixed parameterization. Three bumps behaves fairly well for small amounts of data, but the asymptotic behavior for large amounts of data is biased and thus falls short of ideal. Fifteen bumps asymptotes correctly but has very large variance for small amounts of data (i.e., it is overfitting). A more sophisticated method might use cross validation or some other resampling method to appropriately set the number of bumps to minimize both these effects. For comparison purposes, we have included the behavior of SUREshrink (Donoho & Johnstone, 1995), in which equation 2.7 is used to choose an optimal threshold, θ, for the function

$$f_{\theta }\left(y\right)=\mathrm{sgn}\left(y\right){(\mid y\mid -\theta )}^{+}.$$

As can be seen, SUREshrink shows significant asymptotic bias, although the variance behavior is nearly ideal.

Figure 5.

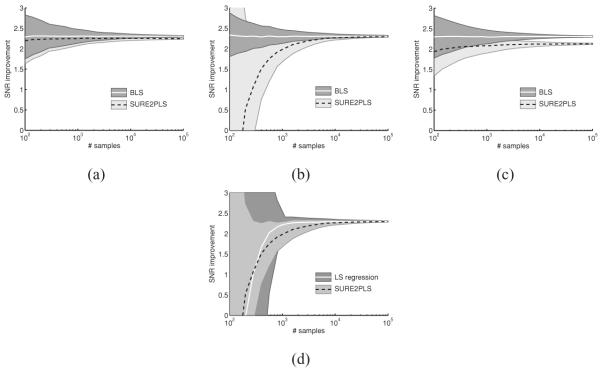
Empirical convergence of gSURE2PLS methods compared to optimal BLS solution, as a function number of data observations, for three different parameterized estimators. (a) Three-bump kernel estimator. (b) Fifteen-bump kernel estimator. (c) Soft thresholding (SUREshrink). (d) Comparisons of gSURE2PLS and supervised regression, for the 15-bump kernel estimator. All simulations use a generalized gaussian prior (exponent 0.5) and additive gaussian noise. Noisy SNR is 4.8 dB.

Figure 5d shows a comparison of the gSURE2PLS method to a supervised method, for the 15-bump kernel estimator (we find that the performance of the gSURE2PLS solution in the 3-bump and soft thresholding cases is nearly identical to that of the corresponding supervised regression solution). For each number of samples, N, the supervised method is trained on N pairs of state or measurement data and then tested on a separate set of N measurements. Compared with the gSURE2PLS method, we see that theaverage performance of the supervised method converges slightly faster, but the variance is slightly worse.

8 Discussion

We have developed two general (and related) reformulations of the least squares estimation problem for the setting in which one knows the observation process and has access to corrupted observations of many data samples. We do not assume knowledge of the prior density or assume access to samples from the prior.

The NEBLS form expresses the estimator in terms of a linear operator that depends on only the observation model. This unifies and generalizes those cases found in the literature (Robbins, 1956; Miyasawa, 1961; Maritz & Lwin, 1989). We discussed the conditions on measurement densities under which such NEBLS estimators may be obtained, provided a methodology for deriving them, and used it to derive solutions for a variety of specific observation situations. These estimators require estimating the observation density from observed data, and this may limit their usefulness, especially in high-dimensional cases. It is worth noting, however, that the NEBLS form can be employed successfully for the problem of denoising local blocks of signal or image data (Raphan & Simoncelli, 2010), where it provides an asymptotic correction of the recently developed “nonlocal means” estimator (Buades, Coll, & Morel, 2005).

We also used the NEBLS form to express the MSE as an expectation over the measurement density. This provides a generalization of SURE and related methods for exponential cases (Stein, 1981; Berger, 1980; Hwang, 1982), as well as providing a new means of deriving them from their seemingly unrelated NEBLS counterparts. The generalized risk estimate may then be used to optimize a parametric estimator (dubbed the gSURE2PLS estimator), as has been done with SURE for the gaussian noise case (Donoho & Johnstone, 1995; Pesquet & Leporini, 1997; Benazza-Benyahia & Pesquet, 2005; Luisier et al. 2006; Raphan & Simoncelli, 2007b, 2008; Blu & Luisier, 2007; Chaux et al., 2008). In cases where a NEBLS operator does not exist, we have shown how a parametric estimator family can be chosen so that gSURE2PLS is still valid. For any gSURE2PLS estimator that is parameterized as a sum of kernel functions, the gSURE optimization may be computed in closed form, and this leads naturally to an incremental algorithm in which the estimator is simultaneously refined by and applied to an incoming stream of measurements. Note that this incremental solution is general and not limited to the case of additive gaussian observations. We also showed that the two forms may be combined to yield a new form of parametric density estimation that is equivalent to score matching when the observation process is additive gaussian noise.

Finally, we have implemented several NEBLS and SURE2PLS estimators and examined their empirical convergence properties, showing that these estimators can perform as well as their full Bayesian or supervised regression counterparts. The implementation of NEBLS estimators must be handled on a case-by-case basis and can be tricky since it requires the estimation of the measurement density from observed samples. The gSURE2PLS case is generally more straightforward, with success depending primarily on selection of a parametric family that can provide a good approximation to the optimal estimator and for which optimization of the gSURE2PLS objective function is feasible. More generally, one could imagine adjusting the complexity of the estimator family depending on the amount of data available (for example, using cross-validation methods) or incorporating prior information about a particular problem to regularize the solution.

We believe it should be possible to generalize and extend these methods further. For example, we have assumed squared error loss throughout, but it is worth considering whether other loss functions might allow some form of nonparametric empirical Bayes solution. Note that equation 3.6 implies that our formulation is easily extended to any loss function that can be expressed as MSE in a nonlinearly transformed signal space. The advantage of the BLS solutions is that they effectively smooth the prior with the likelihood before integrating, whereas other estimators (such as MAP) will not generally have this property. A recent methodology, known as the discrete universal denoiser (DUDe) (Weissman, Ordentlich, Seroussi, Verdú, & Weinberger, 2005), provides a method for computing an optimal unsupervised denoiser with arbitrary loss functions. But the algorithm relies on recovery of the entire prior from the observed data and is thus restricted to discrete priors. Our other main assumption has been that the observation model is fully known, and we have not studied the effect of errors in this model on the performance of the resulting NEBLS and gSURE2PLS estimators. We believe it may also be possible to learn the dual operator L* satisfying equation 4.2c from supervised data (e.g., for a scenario in which the measurement process is unknown but stable, and the statistics of the environment are drifting, thus precluding the use of supervised regression). Note that in this case, it is only necessary to learn the operator L* in terms of its action on members of the parametric estimator family.

More generally, we think that the framework described here could be relevant for the design and construction of machines that need to optimize their estimation behavior in an environmentally adaptive way. On the biological side, Bayesian inference has been used to explain a variety of phenomena in human sensory and motor behavior, but very little has been said about how these estimators can be implemented, and even less about how these estimators can be learned without supervision or built-in priors. The estimators discussed here may offer a promising avenue for resolving these issues.

Appendix A. Incremental Forms for gSURE2PLS Estimators

In section 5, we showed a simple incremental form of gSURE2PLS for an estimator written as a linear combination of kernel functions. Here, we expand on this, providing a more efficient and more general form.

First, we note that it may be desirable to weight the incremental update rule in equation 5.4:

$$\begin{array}{cc}\hfill & {\mathbf{C}}_n=a_n{\mathbf{C}}_{n-1}+(1-a_n){\mathit{h}}_n{\mathit{h}}_n^T\hfill \\ \hfill & {\mathit{m}}_n=b_n{\mathit{m}}_{n-1}+(1-b_n){\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_n\right),\hfill \end{array}$$

where the weights, a_n and b_n, are scalars in the range (0, 1) and h_n is an abbreviation for h(y_n). The weighting can provide numerical stability (so that the stored quantities do not continue to grow indefinitely) and allow the estimator to adapt to slowly time-varying statistics. A value of $\frac{n-1}{n}$ will equally weight all past data, while smaller weights will weight recent data more heavily. The choice of weighting allows a compromise between including more data (which reduces the variance of the estimation error) and adapting more rapidly (which reduces bias). The former depends on the complexity or dimensionality of the parameterization, and the latter depends on the rate at which the environmental statistics change.

Second, note that the incremental solution as provided in section 5 requires the inversion of a matrix, which can be expensive, depending on the number of parameters. As is common in the derivation of the Kalman filter, we can use the Woodbury matrix identity (Hager, 1989) to rewrite the incremental form directly in terms of the inverse matrix:

$$\begin{array}{cc}\hfill {\mathbf{C}}_n^{-1}=& {\left(a_n{\mathbf{C}}_{n-1}+(1-a_n){\mathit{h}}_n{\mathit{h}}_n^T\right)}^{-1}\hfill \\ \hfill =& a_n^{-1}{\mathbf{C}}_{n-1}^{-1}-a_n^{-1}{\mathbf{C}}_{n-1}^{-1}{\mathit{h}}_n{({(1-a_n)}^{-1}+{\mathit{h}}_n^T{a}_n^{-1}{\mathbf{C}}_{n-1}^{-1}{\mathit{h}}_n)}^{-1}{\mathit{h}}_n^T{a}_n^{-1}{\mathbf{C}}_{n-1}^{-1}\hfill \\ \hfill =& a_n^{-1}\left[{\mathbf{C}}_{n-1}^{-1}-{\left(\frac{a_n}{1-a_n}+{\mathit{h}}_n^T{\mathit{v}}_n\right)}^{-1}{\mathit{v}}_n{\mathit{v}}_n^T\right],\hfill \end{array}$$

where we have defined

$${\mathit{v}}_n\equiv {\mathbf{C}}_{n-1}^{-1}{\mathit{h}}_n.$$

Note that since ${\mathit{h}}_n^T{\mathit{v}}_n$ is a scalar, computation of this expression does not require matrix inversion. Putting all of this together and letting S_n denote ${\mathbf{C}}_n^{-1}$, the incremental algorithm is defined by the following set of equations:

$${\mathit{v}}_n={\mathbf{S}}_{n-1}{\mathit{h}}_n$$ (A.1a)

$${\mathbf{S}}_n=a_n^{-1}\left[{\mathbf{S}}_{n-1}-{\left(\frac{a_n}{1-a_n}+{\mathit{h}}_n^T{\mathit{v}}_n\right)}^{-1}{\mathit{v}}_n{\mathit{v}}_n^T\right]$$ (A.1b)

$${\mathit{m}}_n=b_n{\mathit{m}}_{n-1}+(1-b_n){\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_n\right)$$ (A.1c)

$${\widehat{\theta }}_n={\mathbf{S}}_n{\mathit{m}}_n$$ (A.1d)

$${\widehat{x}}_n={\mathit{h}}_n^T{\widehat{\theta }}_n.$$ (A.1e)

The matrix S_n and the vector m_n constitute the stored state variables, and v_n, ${\widehat{\theta }}_n$, and ${\widehat{x}}_n$ are calculated based on this state and the observed data, y_n (or, more specifically, the observed data processed by the kernels, h(y_n) and L*{h}(y_n)).

Finally, it is also possible to rewrite these equations so that the parameter vector, ${\widehat{\theta }}_n$, takes the role of the stored state variable, in place of m_n. Specifically, we can substitute equation A.1c into A.1d to obtain:

$$\begin{array}{cc}\hfill {\widehat{\theta }}_n=& b_n{\mathbf{S}}_n{\mathit{m}}_{n-1}+(1-b_n){\mathbf{S}}_n{\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_n\right)\hfill \\ \hfill =& \frac{b^n}{a^n}\left[{\mathbf{S}}_{n-1}-{\left(\frac{a_n}{1-a_n}+{\mathit{h}}_n^T{\mathit{v}}_n\right)}^{-1}{\mathit{v}}_n{\mathit{v}}_n^T\right]{\mathit{m}}_{n-1}+(1-b_n){\mathbf{S}}_n{\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_n\right)\hfill \\ \hfill =& \frac{b_n}{a_n}\left[{\widehat{\theta }}_{n-1}-{\left(\frac{a_n}{1-a_n}+{\mathit{h}}_n^T{\mathit{v}}_n\right)}^{-1}{\mathit{v}}_n{\mathit{h}}_n^T{\widehat{\theta }}_{n-1}\right]+(1-b_n){\mathbf{S}}_n{\mathbf{L}}^{\ast }\left\{\mathit{h}\right\}\left(y_n\right).\hfill \end{array}$$

Appendix B. Derivations of Additional NEBLS Estimators

In this section, we provide derivations of the remainder of the NEBLS estimators and their dual operators, as listed in Table 1 (derivations for general additive noise and Poisson noise are in section 6.1).

B.1 Discrete Exponential Families

First, consider the discrete exponential family of the form

$$P_{Y\mid X}(n\mid x)=h\left(x\right)g\left(n\right)x^n,$$ (B.1)

where h is chosen to normalize the density (i.e., so that summing over n gives one). This case includes the Poisson case discussed in the previous section, among others. Noting that

$$P_{Y\mid X}(n+1\mid x)=h\left(x\right)g(n+1)x^{n+1},$$

we see by inspection that an operator satisfying the eigenfunction relationship of equation 6.1 is

$$\mathbf{L}\left\{P_Y\right\}\left(n\right)=\frac{g\left(n\right)}{g(n+1)}{P}_Y(n+1),$$

which tells us that

$${\mathbf{E}}_{X\mid Y}(X\mid Y=n)=\frac{g\left(n\right)}{g(n+1)}\cdot \frac{P_Y(n+1)}{P_Y\left(n\right)},$$

as found in Maritz and Lwin (1989). The dual form is readily obtained from equations 4.2a–b,

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(n\right)=\frac{g(n-1)}{g\left(n\right)}f(n-1).$$

Also, we note from equation 3.6 that the appropriate linear operator for ${\mathbf{E}}_{X\mid Y}\left(\frac{1}{X}\mid Y=n\right)$ will be

$$\mathbf{L}\left\{P_Y\right\}\left(n\right)=\frac{g\left(n\right)}{g(n-1)}{P}_Y(n-1).$$ (B.2)

This means that if P_Y|X is instead parameterized as

$$P_{Y\mid X}(n\mid X)=h\left(x\right)g\left(n\right)x^{-n},$$ (B.3)

we will have

$${\mathbf{E}}_{X\mid Y}(X\mid Y=n)=\frac{g\left(n\right)}{g(n-1)}\cdot \frac{P_Y(n-1)}{P_Y\left(n\right)}.$$

The dual form is then

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(n\right)=\frac{g(n+1)}{g\left(n\right)}f(n+1).$$

B.2 Continuous Exponential Families

Now consider the continuous exponential family of the form

$$P_{Y\mid X}(y\mid x)=h\left(x\right)g\left(y\right)e^{T\left(y\right)x},$$

where we assume that T is differentiable. By inspection, we obtain

$$\mathbf{L}\left\{P_{Y\mid X}\right(y\mid x\left)\right\}=\frac{g\left(y\right)}{T^{\prime }\left(y\right)}\frac{d}{dy}\left\{\frac{P_{Y\mid X}(y\mid X)}{g\left(y\right)}\right\}=x{P}_{Y\mid X}(y\mid x),$$

which gives the NEBLS estimator

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X\mid Y}(X\mid Y=y)=& \frac{g\left(y\right)\frac{d}{dy}\left\{\frac{P_Y\left(y\right)}{g\left(y\right)}\right\}}{T^{\prime }\left(y\right)P_Y\left(y\right)}\hfill \\ \hfill =& \frac{1}{T^{\prime }\left(y\right)}\frac{d}{dy}\ln \left(\frac{P_Y\left(y\right)}{g\left(y\right)}\right).\hfill \end{array}$$

The dual operator is

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(y\right)=\frac{-1}{g\left(y\right)}\cdot \frac{d}{dy}\left(\frac{f\left(y\right)g\left(y\right)}{T^{\prime }\left(y\right)}\right).$$

As before, we may also deduce that if the likelihood is instead parameterized as

$$P_{Y\mid X}(y\mid x)=h\left(x\right)g\left(y\right)e^{T\left(y\right)∕x},$$

we then have⁸

$$\mathbf{L}\left\{P_Y\right\}\left(y\right)=-g\left(y\right){\int }_y^{\infty }\frac{T^{\prime }\left(\tilde{y}\right)}{g\left(\tilde{y}\right)}{P}_Y\left(\tilde{y}\right)d\tilde{y},$$

and so

$${\mathbf{E}}_{X\mid Y}\left(\frac{1}{X}\mid Y=y\right)=\frac{-g\left(y\right){\int }_y^{\infty }\frac{T^{\prime }\left(\tilde{y}\right)}{g\left(\tilde{y}\right)}{P}_Y\left(\tilde{y}\right)d\tilde{y}}{P_Y\left(y\right)}.$$

The dual operator is then

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(y\right)=-\frac{T^{\prime }\left(y\right)}{g\left(y\right)}{\int }_0^{y}g\left(\tilde{y}\right)f\left(\tilde{y}\right)d\tilde{y}.$$

A particular case is that of a Laplacian scale mixture, for which

$$P_{Y\mid X}(y\mid x)=\frac{1}{x}{e}^{-\frac{y}{x}};x,y>0,$$

so that

$$\mathbf{L}\left\{P_Y\right\}\left(y\right)=P_Y\{Y>y\}$$

and

$${\mathbf{E}}_{X\mid Y}(X\mid Y=y)=\frac{P_Y\{Y>y\}}{P_Y\left(y\right)}.$$

B.3 Power of Fixed Density

An interesting family of observation processes are those for which

$$\widehat{P_{Y\mid X}}(\omega \mid x)={\left[\widehat{P_W}\right(\omega \left)\right]}^x,$$ (B.4)

for some density P_W. This occurs, for example, when X takes on integer values, and Y is a sum of X i.i.d. random variables with distribution P_W. Taking the derivative of equation B.4 gives

$$\begin{array}{cc}\hfill {\widehat{P_{Y\mid X}}}^{\prime }(\omega \mid x)=& {\widehat{P_W}}^{\prime }\left(\omega \right)x\widehat{P_W}{\left(\omega \right)}^{x-1}\hfill \\ \hfill =& \frac{{\widehat{P_W}}^{\prime }\left(\omega \right)}{\widehat{P_W}\left(\omega \right)}x\widehat{P_W}{\left(\omega \right)}^x\hfill \\ \hfill =& \frac{d}{d\omega }\ln \left(\widehat{P_W}\right(\omega \left)\right)x\widehat{P_{Y\mid X}}(\omega \mid x).\hfill \end{array}$$

Rearranging this equality and using the fact that differentiation in the Fourier domain is multiplication by an imaginary ramp in the signal domain gives

$$\begin{array}{cc}\hfill x\widehat{P_{Y\mid X}}(\omega \mid x)=& \frac{1}{\frac{d}{d\omega }\ln \left(\widehat{P_W}\right(\omega \left)\right)}{\widehat{P_{Y\mid X}}}^{\prime }(\omega \mid x)\hfill \\ \hfill =& \frac{1}{i\frac{d}{d\omega }\ln \left(\widehat{P_W}\right(\omega \left)\right)}y\widehat{P_{X\mid Y}}(\omega \mid x),\hfill \end{array}$$

and comparing to the desired eigenfunction relationship of equation 6.1 allows us to define the operator

$$\begin{array}{cc}\hfill \mathbf{L}\left\{P_Y\right\}\left(y\right)=& {\mathcal{F}}^{-1}\left\{\frac{1}{i\frac{d}{d\omega }\ln \left(\widehat{P_W}\right(\omega \left)\right)}\widehat{y{P}_Y}\left(\omega \right)\right\}\left(y\right)\hfill \\ \hfill =& (m\star (y{P}_Y\left)\right)\left(y\right),\hfill \end{array}$$ (B.6)

where

$$m\left(y\right)={\mathcal{F}}^{-1}\left\{\frac{1}{i\frac{d}{d\omega }\ln \left(\widehat{P_W}\right(\omega \left)\right)}\right\}.$$ (B.7)

Thus, the linear operation first multiplies P_Y by y and then convolves with m(y). The corresponding dual operator must first convolve f (y) with the dual of m(y) and then multiply by y, which we can express in the Fourier domain as

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(y\right)=y\cdot {\mathcal{F}}^{-1}\{\widetilde{\widehat{m}\left(\omega \right)}\cdot \widehat{f}(\omega \left)\right\}.$$

Four special cases are of particular interest. The first occurs when X is a positive variable and Y is a Poisson random variable with rate X. This corresponds to equation B.4 with

$$\widehat{P_W}\left(\omega \right)=e^{(e^{-i\omega }-1)}.$$

Substituting into equation B.7 gives

$$\widehat{m}\left(\omega \right)=e^{i\omega }.$$ (B.8)

Substituting this into equation B.6, taking the inverse Fourier transform, and substituting into equation 3.1 gives the estimator

$${\mathbf{E}}_{X\mid Y}(X\mid Y=n)=\frac{(n+1)P_Y(n+1)}{P_Y\left(n\right)},$$ (B.9)

consistent with the result derived in section 6.1.

The second example arises when X is a positive random variable and Y is a zero mean gaussian with variance X, a case known as the gaussian scale mixture (GSM) (Andrews & Mallows, 1974). In this case equation B.4 holds for

$$\widehat{P_W}\left(\omega \right)=e^{-\frac{1}{2}{\omega }^2},$$

and the operator will be

$$\widehat{m}\left(\omega \right)=\frac{-1}{i\omega },$$ (B.10)

which gives

$${\mathbf{E}}_{X\mid Y}(X\mid Y=y)=\frac{-\left(H\left(y\right)-\frac{1}{2}\right)\star \left(y{P}_Y\right(y\left)\right)}{P_Y\left(y\right)},$$ (B.11)

where H is the Heaviside step function. Since yP_Y(y) is odd, this is equal to

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X\mid Y}(X\mid Y=y)=& \frac{-\left(H\right(y\left)\right)\star \left(y{P}_Y\right(y\left)\right)}{P_Y\left(y\right)}\hfill \\ \hfill =& \frac{-{\int }_{-\infty }^y\tilde{y}{P}_Y\left(\tilde{y}\right)d\tilde{y}}{P_Y\left(y\right)}\hfill \\ \hfill =& \frac{-E_Y\{Y;Y<y\}}{P_Y\left(y\right)},\hfill \end{array}$$ (B.12)

where the numerator is now the mean of the density to the left of y and may be approximated in an unbiased way by the average of data less than y. Note that since E_Y{Y}= 0, this may also be written as⁹

$${\mathbf{E}}_{X\mid Y}(X\mid Y=y)=\frac{E_Y\{Y;Y>y\}}{P_Y\left(y\right)},$$ (B.13)

in agreement with our results in section B.2.

A third special case occurs when $Y\sim \mathcal{N}(aX,X)$. That is, Y is aX corrupted by by zero mean additive gaussian noise, with variance equal to X (we can trivially generalize to variance, which is linear in X). In this case equation B.4 will hold for

$$\widehat{P_W}\left(\omega \right)=e^{-\frac{1}{2}{\omega }^2-ia\omega }.$$

In this case, the NEBLS operator is

$$\mathbf{L}\left\{P_Y\right\}\left(y\right)=\left({\mathcal{F}}^{-1}\left\{\frac{1}{a-i\omega }\right\}\star \left(y{P}_Y\right)\right)\left(y\right),$$

where

$${\mathcal{F}}^{-1}\left\{\frac{1}{a-i\omega }\right\}\left(y\right)=\mathrm{sgn}\left(a\right)e^{ay}{I}_{\{ay<0\}},$$

so that

$${\mathbf{E}}_{X\mid Y}(X\mid Y=y)=\frac{\left(\right(\mathrm{sgn}\left(a\right)e^{ay}{I}_{\{ay<0\}})\star (y{P}_Y\left)\right)\left(y\right)}{P_Y\left(y\right)}.$$

A fourth special case is when X is a random positive value, W is an independent variable drawn from an α-stable distribution (Feller, 1970) with Fourier transform

$$\widehat{P_W}\left(\omega \right)=e^{-\frac{1}{\alpha }{\mid \omega \mid }^{\alpha }},$$

and

$$Y=X^{\frac{1}{\alpha }}W.$$

Generally, if P_W is an infinitely divisible distribution and X is an arbitrary positive real number, then the right side of equation B.4 will be the Fourier transform of some density, which can be used as the observation process. In the particular case of the alpha-stable distribution, the NEBLS operator is

$$\mathbf{L}\left\{P_Y\right\}\left(y\right)=\left({\mathcal{F}}^{-1}\left\{\frac{i}{\mathrm{sgn}\left(\omega \right){\mid \omega \mid }^{\alpha -1}}\right\}\star \left(y{P}_Y\right)\right)\left(y\right),$$

so that

$${\mathbf{E}}_{X\mid Y}(X\mid Y=y)=\frac{\left({\mathcal{F}}^{-1}\left\{\frac{i}{\mathrm{sgn}\left(\omega \right){\mid \omega \mid }^{\alpha -1}}\right\}\star \left(y{P}_Y\right)\right)\left(y\right)}{P_Y\left(y\right)}.$$

B.4 Multiplicative Lognormal Noise

Now consider the case of multiplicative lognormal noise,

$$Y=X{e}^W,$$

where W is gaussian noise of variance σ², and independent of X. In this case, taking logarithms gives

$$\ln \left(Y\right)=\ln \left(X\right)+W,$$

yielding an additive gaussian noise model. From the NEBLS solution for additive gaussian noise (see equation 6.6), we have

$${\mathbf{E}}_{X\mid Z}\left(\ln \right(X)\mid Z=z)=\frac{(z+{\sigma }^2{D}_z)\left\{P_Z\right\}\left(z\right)}{P_Z\left(z\right)},$$

where Z = ln(Y) and D_z represents the derivative operator with respect to z. However, we wish to find E_X|Y(X | Y) so we need to use the change of variables formula in equation 3.7. Since X = e^ln(X), we have

$${\mathbf{E}}_{X\mid Z}(X\mid Z=z)=\frac{e^{(z+{\sigma }^2{D}_z)}\left\{P_Z\right\}\left(z\right)}{P_Z\left(z\right)}.$$

By the Baker-Campbell-Hausdorff formula (Wilcox, 1967) we have that

$$\begin{array}{cc}\hfill e^{(z+{\sigma }^2{D}_z)}\left\{P_Z\right\}\left(z\right)=& e^{z+\frac{1}{2}{\sigma }^2}\left(e^{{\sigma }^2{D}_z}\left\{P_Z\right\}\left(z\right)\right)\hfill \\ \hfill =& e^{z+\frac{1}{2}{\sigma }^2}{P}_Z(z+{\sigma }^2),\hfill \end{array}$$

so that

$${\mathbf{E}}_{X\mid Z}(X\mid Z=z)=\frac{e^{z+\frac{1}{2}{\sigma }^2}{P}_Z(z+{\sigma }^2)}{P_Z\left(z\right)}.$$

Next, using the fact that ln(Y) = Z, we have by the change of variables formula

$$P_Z\left(\ln \right(y\left)\right)=y{P}_Y\left(y\right),$$

so that

$${\mathbf{E}}_{X\mid Y}(X\mid Y=y)=\frac{e^{\frac{3}{2}{\sigma }^2}{P}_Y\left(e^{{\sigma }^2}y\right)}{P_Y\left(y\right)}y.$$

Note that it would have been difficult to garner this result by simple inspection of the likelihood,

$$P_{Y\mid X}(y\mid x)=\frac{1}{y\sqrt{2\pi {\sigma }^2}}{e}^{-\frac{1}{2{\sigma }^2}{\left(\ln \right(y∕x\left)\right)}^2}.$$

The dual form is

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(y\right)=e^{-{\sigma }^2∕2}y\cdot f\left(e^{-{\sigma }^2}y\right).$$

B.5 Mixture of Uniform Noise

Consider the case when our observation is drawn from a uniform density, whose width is controlled by hidden variable X:

$$P_{Y\mid X}(y\mid x)=\{\begin{array}{cc}\frac{1}{2x},\hfill & \mid y\mid \le x\hfill \\ 0,\hfill & \mid y\mid >x\hfill \end{array}\phantom{\}},$$

where x ≥ 0. The density of Y is thus a mixture of uniform densities. We note that the (complement of the) cumulative distribution is

$$\begin{array}{cc}\hfill {\int }_{\mid y\mid }^{\infty }{P}_{Y\mid X}(\tilde{y}\mid x)d\tilde{y}=& \{\begin{array}{cc}\frac{1}{2x}(x-\mid y\mid ),\hfill & \mid y\mid \le x\hfill \\ 0,\hfill & \mid y\mid >x\hfill \end{array}\phantom{\}}\hfill \\ \hfill =& (x-\mid y\mid )P_{Y\mid X}(y\mid x),\hfill \end{array}$$

and thus, by inspection, an operator that has P_{Y | X} as an eigenfunction may be written

$$L\left\{P_Y\right\}\left(y\right)={\int }_{\mid y\mid }^{\infty }{P}_Y\left(\tilde{y}\right)d\tilde{y}+\mid y\mid P_Y\left(y\right),$$

giving

$$\begin{array}{cc}\hfill {\mathbf{E}}_{X\mid Y}(X\mid Y=y)=& \mid y\mid +\frac{{\int }_{\mid y\mid }^{\infty }{P}_Y\left(\tilde{y}\right)d\tilde{y}}{P_Y\left(y\right)}\hfill \\ \hfill =& \mid y\mid +\frac{\mathit{Pr}\{Y>\mid y\mid \}}{P_Y\left(y\right)}\hfill \\ \hfill =& \mid y\mid +\frac{1-\mathit{Pr}\{Y\le \mid y\mid \}}{P_Y\left(y\right)}.\hfill \end{array}$$

That is, the estimator adds to the observed value the complement of the cumulative distribution divided by the measurement density. The dual operator is

$${\mathbf{L}}^{\ast }\left\{f\right\}\left(y\right)=\{\begin{array}{cc}\mid y\mid f\left(y\right)+{\int }_{-y}^{y}f\left(\tilde{y}\right)d\tilde{y},\hfill & y\ge 0,\hfill \\ \mid y\mid f\left(y\right),\hfill & y<0.\hfill \end{array}\phantom{\}}$$