Toward reliable characterization of functional homogeneity in the human brain: Preprocessing, scan duration, imaging resolution and computational space

Abstract

While researchers have extensively characterized functional connectivity between brain regions, the characterization of functional homogeneity within a region of the brain connectome is in early stages of development. Several functional homogeneity measures were proposed previously, among which regional homogeneity (ReHo) was most widely used as a measure to characterize functional homogeneity of resting state fMRI (R-fMRI) signals within a small region (Zang et al., 2004). Despite a burgeoning literature on ReHo in the field of neuroimaging brain disorders, its test–retest (TRT) reliability remains unestablished. Using two sets of public R-fMRI TRT data, we systematically evaluated the ReHo’s TRT reliability and further investigated the various factors influencing its reliability and found: 1) nuisance (head motion, white matter, and cerebrospinal fluid) correction of R-fMRI time series can significantly improve the TRT reliability of ReHo while additional removal of global brain signal reduces its reliability, 2) spatial smoothing of R-fMRI time series artificially enhances ReHo intensity and influences its reliability, 3) surface-based R-fMRI computation largely improves the TRT reliability of ReHo, 4) a scan duration of 5 min can achieve reliable estimates of ReHo, and 5) fast sampling rates of R-fMRI dramatically increase the reliability of ReHo. Inspired by these findings and seeking a highly reliable approach to exploratory analysis of the human functional connectome, we established an R-fMRI pipeline to conduct ReHo computations in both 3-dimensions (volume) and 2-dimensions (surface).

Introduction

The human functional connectome is conceived as encompassing of brain functional networks (Biswal et al., 2010; Kelly et al., 2012; Milham, 2012; Zuo et al., 2012), and has been extensively explored by using resting state functional connectivity (RSFC) approaches (Biswal et al., 1995; Bullmore and Bassett, 2011; Fox and Raichle, 2007; Wang et al., 2010). While most studies focused on brain connectivity between different units of the functional connectome, the locally functional homogeneity of a region had rarely been examined directly. The cross-correlation coefficients of spontaneous low frequency (COSLOF) were originally proposed to examine functional synchrony alterations of the hippocampus in Alzheimer’s disease (Li et al., 2002). Zang et al. (2004) introduced the Kendall’s coefficient of concordance (KCC) or Kendall’s W (Kendall and Smith, 1939; Legendre, 2005) to measure the regional homogeneity of resting state time series between one voxel and its 26 neighbors (KCC-ReHo). KCC-ReHo has recently been revisited in the Fourier frequency domain by using a coherence measure (Liu et al., 2010), which is the frequency variant of COSLOF. Similarly, using the Pearson correlation, Deshpande et al. (2009) introduced integrated local correlation (ILC) to measure ReHo in fMRI data. More recently, Tomasi and Volkow (2010) proposed a novel metric – local functional connectivity density (lFCD) – to characterize regionally functional homogeneity in the human brain.

Among the ReHo measures mentioned above, KCC-ReHo has several advantages in both theory and application. First, unlike COSLOF, ILC and lFCD, it is a rank-based non-parametric data-driven approach, and thus allows for examining the temporally auto-correlated samples with non-normal distributions, and is more robust against noise in the data, which is useful for real R-fMRI time series (de Pasquale et al., 2010; Expert et al., 2011; Park et al., 2010; Zarahn et al., 1997), especially for recently developed fast imaging sequences (Feinberg et al., 2010; Moeller et al., 2010; Smith et al., 2012). Second, it is largely free of parametric settings (e.g., thresholds of connectivity and signal-to-noise ratio in lFCD) and requires no a priori knowledge regarding the structure or function of the brain. As such, it serves as a potentially promising data mining tool to study high spatial resolution images of the human brain. Finally, the computation of KCC-ReHo is relatively easy and has been implemented in software platforms with graphical user interfaces (Song et al., 2011). These benefits underlie the rich applications of KCC-ReHo for discovering brain function under both healthy and disease conditions as briefly introduced in the following paragraph.

KCC-ReHo of the functional connectome has been demonstrated to be associated with various phenotypic variables such as age, sex, intelligence and personality (e.g., Dai et al., 2012; Lopez-Larson et al., 2011; Wang et al., 2011b; Wei et al., 2011; Wu et al., 2007; Yan et al., 2011). Inter-individual variability in behavioral task performance was identified in the functional connectome as measured by the inter-individual variability of KCC-ReHo (e.g., Tian et al., 2012). Other work also suggests that ReHo measures differ between healthy and clinical populations, such as individuals with attention deficit hyperactivity disorder (Cao et al., 2006; Zhu et al., 2008), schizophrenia (Liu et al., 2006), depression (Guo et al., 2011a,b; Yao et al., 2009; Yuan et al., 2008), autism spectrum disorders (Paakki et al., 2010; Peng et al., 2011; Shukla et al., 2010), obsessive-compulsive disorders (Yang et al., 2010), mild cognitive impairment and Alzheimer’s disease (He et al., 2007; Liu et al., 2008; Zhang et al., 2012), epilepsy (Zhong et al., 2011), and Parkinson’s disease (Wu et al., 2009). Although the detection of within- and between-group differences in ReHo suggests that KCC-ReHo may reflect stable trait properties, there are several factors that could impact the measure. For example, the physiological and neural factors impacting other R-fMRI local measures (e.g., amplitudes) may also affect ReHo (Zang et al., 2007; Zou et al., 2008; Zuo et al., 2010a). Additionally, some preprocessing methods (e.g., spatial smoothing R-fMRI time series) may significantly change the ReHo magnitudes (Tian et al., 2012; Yan and Zang, 2010). Despite the wide application of KCC-ReHo, these factors raise concerns regarding the test–retest reliability of the measure and warrant its investigation.

In this study, we aim to provide a comprehensive investigation of the TRT reliability of the KCC-ReHo measure by 1) computing voxel-wise KCC-ReHo maps for a total 75 scans from 25 participants and estimating its intra- and inter-session TRT reliability, 2) building voxel-wise KCC-ReHo maps based on data with/without two specific preprocessing steps (i.e., smoothing and nuisance correction) to examine their influence on KCC-ReHo’s intensity and TRT reliability, 3) implementing KCC-ReHo on the cortical surface to evaluate the advantage of surface-based R-fMRI processing for ReHo (e.g., Two-dimensional functional homogeneity tends to measure local synchronization of gray matter signals while volume-based ReHo quantifies signal synchronization in both gray and white matter.), and 4) computing KCC-ReHo maps using 10 min TRT R-fMRI data acquired by multiband imaging sequences and systematically investigating the impact of temporal and spatial resolutions as well as scan durations on ReHo and their TRT reliability.

Materials and methods

TRT datasets

Two sets of TRT data (Table 1) were obtained from the International Neuroimaging Data-Sharing Initiative (INDI: http://fcon_1000.projects.nitrc.org/indi/indi_ack.html). Data were collected according to protocols approved by the institutional review boards of the NYU School of Medicine and Nathan Kline Institute, respectively. The first dataset (NYU TRT data) includes 25 individuals (http://www.nitrc.org/projects/nyu_trt). Three resting state scans were obtained with a standard echo planar imaging (EPI) sequence – R-fMRI_std_2000 – TR=2000 ms (3 mm isotropic voxels, 6.5 min) from each participant using a Siemens Allegra 3.0 Tesla scanner. For more information regarding data collection methods, please refer to Shehzad et al. (2009), Zuo et al. (2010a,b,c, 2012), Zuo and Xing (2011), Wang et al. (2011a). The second dataset was collected at the Nathan S. Kline Institute for Psychiatric Research (NKI). The enhanced NKI TRT (eNKI) data were acquired from 22 participants (http://fcon_1000.projects.nitrc.org/indi/pro/eNKI_RS_TRT/FrontPage.html), which excluded two participants from the original release (subject 0021001 had brain atrophy and subject 6471972 did not have a retest session). Each participant received three test–retest R-fMRI scans (at least one week apart) using a Siemens Trio 3.0 Tesla scanner. Two R-fMRI sequences of a recently developed multiband EPI (mEPI) (Moeller et al., 2010) are included: 1) R-fMRI_mx_645 – TR=645 ms (3 mm isotropic voxels, 10 min) to provide optimal temporal resolution and 2) R-fMRI_mx_1400 - TR=1400 ms (2 mm isotropic voxels, 10 min) to provide optimal spatial resolution. A standard EPI sequence – R-fMRI_std_2500 – TR=2500 ms, (3 mm isotropic voxels, 5 min) is included for reference. An MPRAGE structural image was obtained for each participant from both datasets. Informed consent was obtained prior to participation.

Table 1.

Two public TRT R-fMRI datasets.

ID	Sex	Age	TRT	Sequence	TR (s)	Voxel size	Duration
NYU	9 M, 16 F	30.7±8.8	45 min 11 months	EPI	2.0	3 mm	6.5 min
eNKI	16 M, 6 F	34.4±12.5	1 week	mEPI*	0.645	3 mm	10 min
				mEPI*	1.4	2 mm	10 min
				EPI	2.5	3 mm	5 min

^*Notes: mEPI = multiband EPI.

MRI image preprocessing

Image preprocessing was carried out using the Connectome Computation System (CCS: http://lfcd.psych.ac.cn/ccs.html), which provides a common platform for brain connectome analysis by integrating the functionality of afni, fsl, and freesurfer, extending the utility of FCP scripts (FCON_1000: http://www.nitrc.org/frs/downloadlink.php/2628) and by integrating the brain surface information reconstructed by freesurfer (version 5.1). The data preprocessing contained both anatomical and functional processing steps. CCS anatomical processing steps consisted of: 1) removal of MR image noise using a spatially adaptive non-local means filter (Xing et al., 2011; Zuo and Xing, 2011), 2) brain surface reconstruction via the recon-all command in freesurfer (Dale et al., 1999; Fischl et al., 1999a,b, 2001; Segonne et al., 2004, 2007), which has been demonstrated to show good test–retest reliability across scanner manufacturers and across field strengths (Han et al., 2006), 3) spatial normalization from an individual functional space to MNI152 standard brain space (FLIRT+FNIRT in fsl), and 4) boundary-based registration between individual structural and functional images (Greve and Fischl, 2009). CCS functional preprocessing steps include: 5) EPI volumes from the beginning of each scan were discarded to allow for signal equilibration (numbers of volumes discarded for R-fMRI_std_2000, R-fMRI_std_2500, R-fMRI_mx_1400 and R-fMRI_mx_645 are 0, 2, 4, and 8, respectively, corresponding to about 5 s exclusion), 6)slice timing correction, 7) 3D motion correction, 8) 4D global mean-based intensity normalization, 9) nuisance correction by regressing out 6 motion signals as well as individual white matter (WM) and cerebrospinal fluid (CSF) mean signals derived from the WM/CSF masks output by the segmentation routine of freesurfer (Jo et al., 2010), 10) band-pass temporal filtering (0.01–0.1 Hz), 11) removal of linear and quadratic trends, and 12) Gaussian (FWHM=6 mm) spatial smoothing. Of note, both volume- and surface-based brain registration (steps 3 and 4) were estimated for subsequent assessments on ReHo computational spaces. In step 5, no volumes were deleted for NYU TRT data because the scanner did so automatically. Slice timing(step 6) was not performed on mEPI data (R-fMRI_mx_1400 and R-fMRI_mx_645) because multiple slices were excited simultaneously for these sequences.

KCC-ReHo algorithm

We included the KCC-ReHo formula in (Zang et al., 2004) to reveal its intrinsic link to a spatial mean rank filter and provided a fast implementation in CCS. For a given voxel, R_i(i=1,…,n) was denoted as the ranks of its R-fMRI BOLD time series and n as the number of time points. KCC-ReHo is defined as

$$W=\frac{\sum _{i=1}^n{\left(R_i\right)}^2-n{\left(\stackrel{‒}{R}\right)}^2}{\frac{1}{12}{K}^2(n^3-n)}=12\frac{\sum _{i=1}^n{\left({\stackrel{‒}{R}}_i\right)}^2}{(n^3-n)}-3\frac{(n+1)}{(n-1)},$$ (1)

where K is the number of neighbors (including the voxel, e.g., a total 27 voxels used in this study) of the voxel, ${\stackrel{‒}{R}}_i$ is the mean rank across its neighbors at the i-th time point, and $\stackrel{‒}{R}$ is the overall mean rank across all neighboring voxels and time points. The operation of computing the mean rank is equivalent to a spatial mean filtering on the rank maps, which is a common image denoising operation (Gonzalez and Woods, 2006). Such a connection led to fast shell scripts of KCC-ReHo computation as detailed in CCS (http://lfcd.psych.ac.cn/ccs/lfcd_06_singlesubjectReHo.sh). All individual voxel-wise KCC-ReHo values were computed and standardized into KCC-ReHo z-values by subtracting the mean voxel-wise KCC-ReHo obtained for the entire brain (i.e., global KCC-ReHo), and then dividing by the standard deviation for subsequent analyses. This subject-wise ReHo normalization has been demonstrated to be able to improve both normality and reliability of amplitude measures across subjects in our previous work as described in Supplementary Materials from Zuo et al. (2010a).

Of note, there are two ways of introducing the smoothness in the above computation: 1) the intrinsic or natural smoothness of KCC-ReHo definition, and 2) the Gaussian smoothness of spatial smoothing BOLD time series or spatial KCC-ReHo maps as preprocessing steps. To make the findings comparable, we spatially smoothed the ReHo maps derived from unsmoothed BOLD time series and compared them to the KCC-ReHo maps from smoothed BOLD time series. Specifically, for the unsmoothed version of KCC-ReHo, we performed the same Gaussian spatial smoothing (6 mm FWHM) on KCC-ReHo z-maps as used to smooth R-fMRI data before any statistical evaluations.

TRT reliability

The TRT R-fMRI experiment is a typical longitudinal design. Similar to approaches in our previous study (Zuo and Xing, 2011), we employed linear mixed models (LMMs) to assess both intra- and inter-individual variability and further compute the reliability measured by the intra-class correlation coefficients (ICC). To calculate the ICC for each voxel, we considered a random sample of n subjects with d repeated measurements of a continuous variable Y characterizing the ReHo. We denoted Y_ij as the i-th measurement of the j-th subject (for i=1,…,d and j=1,…,n). In the current situation, Y_ij denotes the KCC-ReHo from the j-th participant’s i-th measurement occasions. We applied a two-level LMM to each voxel as the following decomposition of Y_ij,

$$Y_{\mathit{ij}}={\lambda }_{0j}+{\text{motion}}_{\mathit{ij}}+e_{\mathit{ij}},{\lambda }_{0j}={\mu }_{00}+p_{0j}+{\text{age}}_j+{\text{sex}}_j,$$ (2)

where μ₀₀ is a fixed parameter and p_0j and e_ij are independent random effects normally distributed with mean 0 and variances ${\sigma }_p^2$ and ${\sigma }_e^2$. The term p_0j is the participant effect and e_ij is the measurement error. Model (2) includes three types of covariates: scan-level covariates of motion_ij, and participant-level covariates of age_j and sex_j, all of which have been shown to have significant influence on R-fMRI metrics (Power et al., 2012; Satterthwaite et al., 2012; Van Dijk et al., 2012; Zuo et al., 2010c, 2012). Motion was quantified with the root mean square of frame-wise displacement (FD), which is similar to mean FD in Power et al. (2012). The voxel-wise whole brain KCC-ReHo statistical map can be built at the group-level by estimating the statistics of testing if μ₀₀ in the model (2) with all TRT scans from all participants significantly differs from 0. The ICC was defined as

$$\rho =\frac{{\sigma }_p^2}{{\sigma }_p^2+{\sigma }_e^2}.$$ (3)

ρ has the desired property to characterize the TRT reliability, i.e., decreasing as ${\sigma }_e^2$ increases and increasing as ${\sigma }_p^2$ increases. To avoid negative ICC and get a more accurate estimation of the sample ICC, the variance components in Model (2) were estimated with the restricted maximum likelihood (ReML) approach with the covariance structure of an unrestricted symmetrical matrix.

Using the NYU TRT R-fMRI data, we computed the intra-session (d=2) and inter-session (d=2) ICC to measure TRT reliability of KCC-ReHo. Specifically, the intra-session ICC was estimated based on Scan 2 and Scan 3, which were 45 min apart and conducted in a single scan session. The inter-session ICC was computed by using individual KCC-ReHo maps from Scan 1 and individual mean KCC-ReHo maps from Scan 2 and Scan 3 (Zuo et al., 2010b), which occurred 5–16 months after Scan 1. The ICC values were categorized into five common intervals (Landis and Koch, 1977): 0<ρ≤0.2 (slight), 0.2<ρ≤0.4 (fair), 0.4<ρ≤0.6 (moderate), 0.6<ρ≤0.8 (substantial), and 0.8<ρ<1.0 (almost perfect).

Influence of nuisance correction and spatial smoothing

Removal of white matter and CSF signals seems reasonable, as they do not likely correspond to neural activity. Similarly, head motion has been demonstrated to influence most connectivity measures, thus it likely affects ReHo. Global signal regression is more controversial due to potential introduction of negative correlations and potential to artifactually impact inter-individual differences in connectivity (Chai et al., 2012; Fox et al., 2009; Murphy et al., 2009; Saad et al., 2012). In the initial paper describing ReHo (Zang et al., 2004) and most applications published by using ReHo, preprocessing did not include removal of any nuisance signals although the functionality of removing head motion, white matter, CSF and global signal from BOLD time series is available in DPARSF (Yan and Zang, 2010) of REST software (Song et al., 2011), which is originally designed for seed-based functional connectivity (Fox et al., 2005, 2006). The effect of nuisance signal regression on the test–retest reliability of ReHo has not been previously evaluated, calling the need of a systematic investigation of the influence of these preprocessing on ReHo’s reliability to help the standardization on ReHo computation. Accordingly, we derived KCC-ReHo maps from data processed by 1) not regressing out any nuisance signals (RAW) and regressing out 2) head motion, white mater and CSF signals (MC+WM/CSF) as well as 3) head motion, white mater, CSF and global signals (MC+WM/CSF/GS). Subsequently, both intra- and inter-session ICC maps were computed based on all individual ReHo maps for each of the three preprocessing strategies based on NYU TRT R-fMRI data.

Given the recent concerns regarding the confounding influence of micromovements in intrinsic functional connectivity (iFC) analyses (Power et al., 2012; Satterthwaite et al., 2012; Van Dijk et al., 2012), we carried out a motion correction procedure by combining the scrubbing (Power et al., 2012) and interpolating (Carp, in press) approaches. Specifically, the time series of FD and DVARS per (Power et al., 2012) were computed. Before any preprocessing performed, the intensity at any time points with FD>0.5 mm or DVARS>5% will be replaced by an intensity interpolated from their neighbors’ intensities using trilinear methods. All individual ReHo maps were then derived from the corrected and preprocessed (i.e., SCB+WM/CSF) data and used to compute the ICC maps.

Spatially smoothing R-fMRI data was reported to introduce spurious increase in the amplitude (Tian et al., 2012; Yan and Zang, 2010) but not investigated if it can influence the test–retest reliability of ReHo. To systematically assess the impact of spatial smoothing on ReHo, we conducted ReHo and its TRT reliability analyses based on the data regressed out MC+WM/CSF and spatially smoothed (i.e., MC+WM/CSF+SM). Both amplitude and reliability of ReHo computed by using the two types of preprocessing (i.e., MC +WM/CSF+SM versus MC+WM/CSF) were compared.

The global KCC-ReHo was calculated for each of the 75 scans for KCC-ReHo maps. A two-way repeated measures ANOVA (i.e., two factors: scan of 3 levels and preprocessing of 2 levels) was adopted to test if there were any differences in the ReHo intensity between global KCC-ReHo derived from any two different preprocessing strategies. Intra- and inter-session ICC of global KCC-ReHo were estimated via the two implementations of Model (2), in which Y_ij denotes the global KCC-ReHo. We further compared the Fisher z-transformed ICCs obtained with the two different preprocessing strategies using the Z-statistic formula below (McGraw and Wong, 1996):

$$Z=\sqrt{\frac{(N-2)(d-1)}{2d}}\times \log \left[\frac{1+(d-1)({\rho }_{\text{with}}-{\rho }_{\text{without}})}{1-({\rho }_{\text{with}}-{\rho }_{\text{without}})}\right]$$ (4)

where N is the number of objects of measurement (i.e., participants) and d is the number of observations (i.e., repeated scans). The analytic procedure was also applied to voxel-wise KCC-ReHo maps. Given that the smoothness introduced by ReHo in nature is hard to estimate, all maps of statistical comparisons on voxel-wise ICC of KCC-ReHo were corrected for multiple comparisons using false discovery rate (FDR; http://www.fmrib.ox.ac.uk/fsl/randomise/fdr.html), implemented as in the script fsl_fdr.sh from Dr Thomas Nichols (http://www2.warwick.ac.uk/fac/sci/statistics/staff/academic-research/nichols/scripts/fsl/fsl_fdr.sh) (p<0.05, corrected). A non-parametric cluster-based statistic (e.g., permutation methods with threshold-free cluster enhancement correction, Smith and Nichols, 2009) should be another option to perform multiple corrections for statistical comparisons of ReHo.

Comparisons with integrated local correlation

Regarding the complexity of the real BOLD time series acquired during the resting state of the brain, we added relevant statistical tests to examine the normality and autocorrelation of the time series. We also examined the reliability of another measure of functional homogeneity, integrated local correlation (ILC), to add a reference of ReHo. Specifically, we performed the Durbin–Watson test (Bhargava et al., 1983) to examine the temporal autocorrelation in BOLD time series. The d statistic <2 means that the time series are positively autocorrelated. Meanwhile, Anderson–Darling test (BScholz and Stephens, 1987) was applied to test the normality of time series, higher AD-values indicate lower normality. For each voxel, the ILC was computed as the mean of the 26 correlation coefficients of the voxel’s time series and those from its 26 neighbors as described in Deshpande et al. (2009). All individual ILC maps were converted into their Fisher-Z version and submitted to the test–retest reliability analyses the same as for KCC-ReHo.

Surface-based ReHo

Surface-based fMRI processing has been demonstrated to achieve more accurate cross-subject matching of functional regions (Argall et al., 2006; Fischl et al., 1999b, 2008) and reflects the functional organization of the cortex more naturally. We thus transplanted the classic 3dReHo computation to its 2-dimensional variant (i.e., 2dReHo) by using cortical surface-based fMRI analysis. As in a recent study (Yeo et al., 2011), using the facility provided by the FsFast pipeline (http://surfer.nmr.mgh.harvard.edu/fswiki/FsFast) in freesurfer 5.1, we projected individual preprocessed (without smoothing) R-fMRI data into the fsaverage5 surface space, which contains a total 40,960 triangular faces and 20,484 vertices (see Fig. 1A for details of the cortical surface for one hemisphere). Specifically, for each pair of vertices in the pial and white matter surfaces generated by freesurfer, the mid-point of vertices is computed. The registration between the subject’s native fMRI volume and native anatomical volume was derived from the boundary-based co-registration algorithm (Greve and Fischl, 2009). The target surface of the projection was chosen as the fsaverage5 surface space used for projection and interpolation. For each vertex of fsaverage5 surface space, the corresponding (mid-point) coordinates in the subject’s native anatomical space were first computed and then the corresponding coordinates in subject’s native fMRI space. Finally, given these coordinates, trilinear interpolation was employed to interpolate the fMRI values. The distance between any pair of adjacent vertices is about 4 mm. The rationale of choosing the spatial resolution of the cortical surface model is to keep the numbers of units (i.e., voxel in volume space and vertex in surface space) as equal as possible across the two different computational spaces. The number of gray matter voxels in a gray matter mask (tissue probability ≥0.5) from the MNI152 3 mm standard volume space is around 33,059 including subcortical and cerebellar voxels. In freesurfer standard space of the cortical surface, the 4 mm resolution surface model (i.e., fsaverage5) has the closest numbers of units (20,484 vertices) to the number of voxels in the volume space. We thus chose the fsaverage5 as the target of our surface-based functional homogeneity analyses. Along with the same vein, given the spatial resolution (2 mm) of the R-fMRI_mx_1400 data, the above projection was conducted with the fsaverage6 surface including 2 mm-spaced 40,962 vertices.

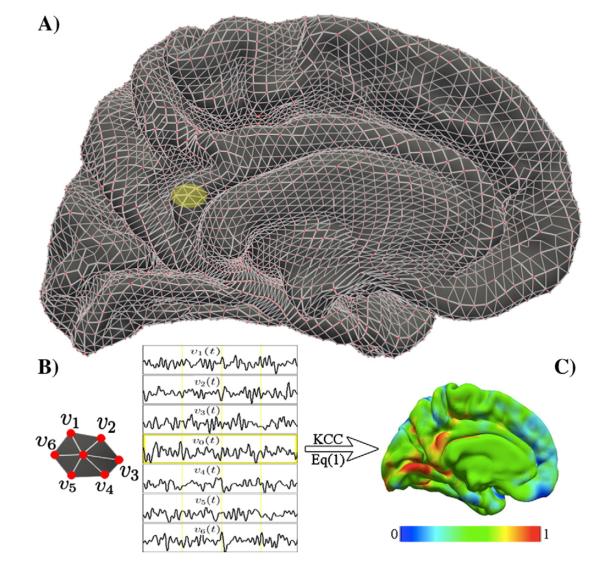
Fig. 1. KCC-ReHo computation on the cortical surface: 2dReHo.

The geometry of the cortical surface (e.g., here the medial cortical surface of the left hemisphere) is illustrated in (A). The preprocessed R-fMRI data are projected onto vertices of the cortical surface. For a given vertex v₀, its nearest neighbors are v₁, v₂, v₃, v₄, v₅, and v₆, which are indicated as the yellow patch (A) and are zoomed in (B). Based on R-fMRI time series from all the 7 vertices denoted by v_i(t), the Kendall’s coefficient of concordance (KCC) of the vertex v₀ is calculated. Such computation is repeated for all vertices in the surface to produce individual vertex-wise KCC-ReHo surface maps (C). The colormap indicates the KCC values.

To calculate 2dReHo, for a given vertex v₀, as illustrated in Fig. 1B, we denote v₁, v₂, v₃, v₄, v₅, and v₆ as its 6 neighbor vertices and v_i(t), i=0,1,…,6 as R-fMRI time series from all 7 vertices. The KCC of these 7 time series was computed as in Eq. (1) where K=7 to measure ReHo at vertex v₀. Such computational procedure was repeated for all vertices in surfaces of both left hemisphere (LH) and right hemisphere (RH) to produce vertex-wise KCC-ReHo surface maps – 2dReHo – (see Fig. 1C for the LH 2dReHo map from one participant). Of note, although the rationale of comparing 2dReHo to 3dReHo is keeping the same length of neighbors (i.e., length-one has 26 neighbors in the volume space but 6 neighbors in the surface space), regarding the different neighbor sizes for 3dReHo and 2dReHo, we also repeated reliability analyses for 2dReHo of a vertex and its 19 neighbors (i.e., length-two neighbors) and compared it with 3dReHo. Similar to 3dReHo, all individual vertex-wise KCC-ReHo values were standardized into z-values for subsequent analyses by subtracting the mean KCC-ReHo obtained for the entire brain surface and then dividing by the standard deviation.

Regional differences

For each R-fMRI scan, mean ReHo of gray matter (GM) was calculated across all GM voxels within a GM mask generated from a prior GM probability image (tissue probability≥25%). The mean ReHo of white matter (WM) was computed in the same way for all individuals and scans. Beyond this coarse-scale evaluation, the same analyses were also performed for several other anatomical and functional subdivisions of the brain. Specifically, the mean ReHo values were calculated for five common anatomical (frontal, parietal, occipital, temporal lobes and subcortical) subdivisions and six classic hierarchical (i.e., primary, unimodal, heteromodal, paralimbic, limbic and subcortical) subdivisions also employed to conduct the regional analysis (Mesulam, 1998). Finally, network-level regional analysis was carried out using a recently developed functional parcellation of the human cerebral cortex (Yeo et al., 2011) containing seven large-scale functional (i.e., visual, somatomotor, dorsal attention, ventral attention, limbic, frontoparietal, default) networks. The nonparametric Friedman’s test with three replications was used to test for any regional effects on KCC-ReHo’s spatial distribution. To demonstrate the regional differences of ReHo in TRT reliability, both mean and standard variation of intra-, inter- and multi-session ICC values were also computed for these subdivisions by averaging ICC values of their vertices.

Fast R-fMRI influence: Imaging resolution and scan duration

To study the effect of imaging resolution, we split both preprocessed (MC+WM/CSF) R-fMRI_mx_645 and R-fMRI_mx_1400 data into two equal parts (i.e., the first 5 min and the last 5 min of scans during the same session). This strategy permitted both computation of intra-session ICC and comparisons between fast and standard (i.e., R-fMRI_std_2500) sequences. The first 5 min data were employed to estimate both intra- and inter-session ICC for the three imaging sequences. Additionally, for seeking an assessment on the effect of scan duration on 2dReHo’s TRT reliability, the full length 10 min data was split into data with ten different durations from 1 min to 10 min with 1 min equal separation. For each duration, we calculated the inter-session ICC for the R-fMRI_mx_645 mEPI sequence.

Results

In the present work, we performed test–retest reliability analyses regarding multiple factors influencing the functional homogeneity measured by KCC-ReHo. We primarily report findings on test–retest reliability. Specifically, the influence of preprocessing on 3dReHo and its reliability was firstly reported. Based upon the optimization of preprocessing steps to produce more reliable 3dReHo, the TRT reliability of both 3dReHo and 2dReHo is presented and compared to each other. Finally, the impact of fast imaging sequences and scan durations on ReHo’s reliability is demonstrated on the cortical surface (i.e., 2dReHo).

We carefully monitored quality during brain surface reconstruction, registration and R-fMRI signal preprocessing to ensure no gross errors in brain extraction, segmentation, surface, registration as well as to ensure no gross head motion. Some examples of these quality controls can be found on the CCS website (http://lfcd.psych.ac.cn/ccs/QC.html).

Influence of preprocessing

Pair-wise comparisons from the two-way repeated measures ANOVA showed significant influence of nuisance correction and smoothing on global 3dReHo and its test–retest reliability. Specifically, nuisance correction slightly reduced the value of global 3dReHo (0.08609 vs. 0.09378: t=−12.2,p<0.0001) but increased its inter-session reliability (0.3402 vs. 0.0869: z=2.5,p<0.01). Additional preprocessing of spatial smoothing robustly strengthened the global 3dReHo (0.4805 vs. 0.08609: t=146.6,p<0.0001) while not significantly change its test–retest reliability.

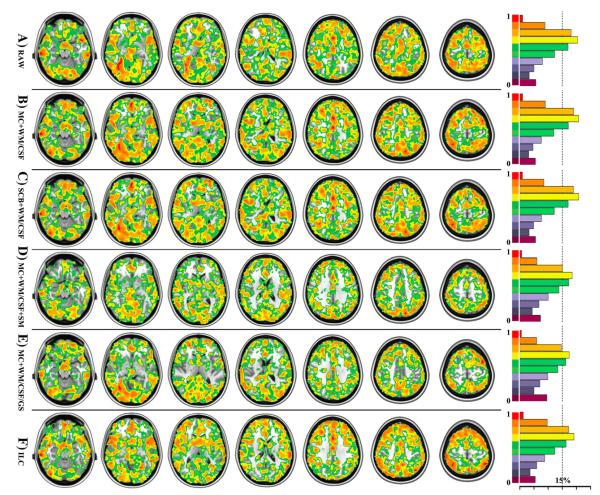
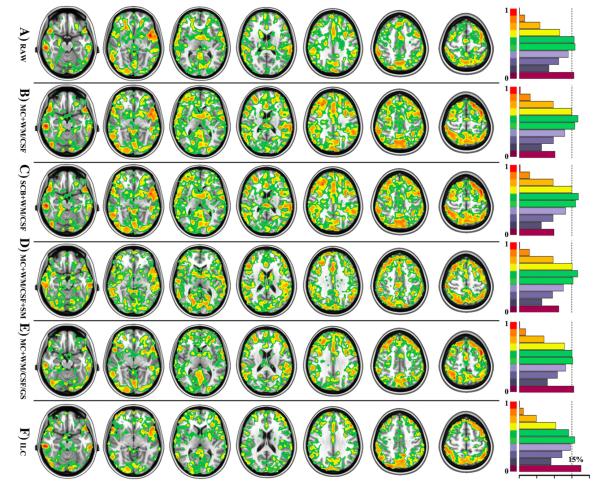
Voxel-wise reliability analyses detected robust ICC changes introduced by the two preprocessing steps. Nuisance correction for head motion and WM/CSF reshaped the distribution of ICC toward higher test–retest reliability as in Figs. 2 and 3. While this conclusion is not that obvious for intra-session reliability (Fig. 2B versus Fig. 2A), it is evident for inter-session (Fig. 3B versus Fig. 3A) test–retest reliability. As depicted in Figs. S1B and S2B, these significant improvements on ICC mainly occurred in the posterior cingulate cortex, precuneus, ventral medial prefrontal cortex, parahippocampal gyrus, lateral parietal cortex, dorsal lateral prefrontal cortex, posterior division of temporal cortex and putamen. However, inclusion of global signal in such preprocessing led to significant decreases of both intra- (Figs. 2E and S1E) and inter-session (Figs. 3E and S2E) reliability of ReHo. This could be a ceiling effect with local connections in the absence of GS adjustment, which could increase the variability of the local connections since GS regression tends to lower correlations. We thus strongly recommended regressing out head motion, white matter and CSF signals but not global signal in ReHo computation.

Fig. 2. Factors with influences on intra-session reliability of 3dReHo.

Six different factors of computing 3dReHo are investigated regarding their impacts on ICC, which are depicted as in six rows, respectively. Only voxels with ICC≥0.4 are displayed. All individual KCC-ReHo maps were derived from the data preprocessed by (A) the slice timing, realignment, temporal filtering, and removal of linear trends (RAW), (B) additional removal of six motion curves, mean white matter and cerebrospinal fluid signals (MC+WM/CSF), (C) additional motion scrubbing and interpolation (SCB+WM/CSF), (D) additional spatial smoothing (MC+WM/CSF+SM), and (E) additional removal of global mean signal without spatial smoothing (MC+WM/CSF/GS). Based on preprocessing (MC+WM/CSF), the functional homogeneity is also calculated by using the integrated local correlation (ILC). For each ICC map associated with the six factors, the ratio of gray matter voxels (tissue probability≥25%) exhibiting different levels of ICC or the normalized ICC histogram are visualized as in the right panel. The dash line indicates the position of 15% voxels.

Fig. 3. Factors with influences on inter-session reliability of 3dReHo.

Six different factors of computing 3dReHo are investigated regarding their impacts on ICC, which are depicted as in six rows, respectively. Only voxels with ICC≥0.4 are displayed. All individual KCC-ReHo maps were derived from the data preprocessed by (A) the slice timing, realignment, temporal filtering, and removal of linear trends (RAW), (B) additional removal of six motion curves, mean white matter and cerebrospinal fluid signals (MC+WM/CSF), (C) additional motion scrubbing and interpolation (SCB+WM/CSF), (D) additional spatial smoothing (MC+WM/CSF+SM), and (E) additional removal of global mean signal without spatial smoothing (MC+WM/CSF/GS). Based on preprocessing (MC+WM/CSF), the functional homogeneity is also calculated by using the integrated local correlation (ILC). For each ICC map associated with the six factors, the ratio of gray matter voxels (tissue probability≥25%) exhibiting different levels of ICC or the normalized ICC histogram are visualized as in the right panel. The dash line indicates the position of 15% voxels.

Figs. 2C (intra-session) and 3C (inter-session) showed highly similar ICC maps between (MC6+WM/CSF) and (SCB+WM/CSF) processing strategies. Figs. S1C (intra-session) and S2C (inter-session) further confirmed that there is no significant change of ICC introduced by performing SCB correction. We plotted the mean FD for both NYU and eNKI test–retest data (Fig. S13). These scatter plots indicated that there existed reasonable inter-individual variations in motion. At the group level, to show the effect of head motion on ReHo, we chose a subthreshold (p=0.1) regarding the small sample size to visualize the significance maps of ReHo-mean FD correlation (Fig. S11) for both 3dReHo (Fig. S11A) and 2dReHo (Figs. S11C and D). The positive correlation demonstrated highly similar spatial patterns in both volume and surface spaces while the negative correlation mainly lays in white matter for 3dReHo but in the default network for 2dReHo (although very weakly).

Figs. 2B and D demonstrated that spatial smoothing reduced the ratio of voxels exhibiting substantial intra-session reliability (i.e., ICC≥0.6), which was mainly distributed among anterior/posterior cingulate cortex, medial, dorsal and lateral prefrontal cortex, insular as well as occipital cortex (Fig. S1D). Regarding the inter-session reliability, the ratio of voxels exhibiting substantial ICC was almost identical for the two ICC maps derived from smoothed or non-smoothed data (Figs. 3B and D). Further statistical comparison between the two ICC maps showed that improvements from spatial smoothing mainly occurred in subcortical regions, dorsal prefrontal cortex and some cingulate cortex while it significantly reduced the reliability of ReHo in posterior cingulate cortex, precuneus, dorsal lateral prefrontal cortex and lateral occipital cortex (Fig. S2D).

TRT reliability of 3dReHo

The global 3dReHo demonstrated substantial intra-session test–retest reliability (0.6290), but only fair inter-session (0.3402) test–retest reliability. At the group level, this overall ReHo is positively correlated with the mean FD measure (p=0.0023) and negatively correlated with age (p=0.0069). The global ReHo did not show a significant gender effect (p=0.8736).

As illustrated in Figs. 2B and 3B, 3dReHo exhibited moderate to almost perfect test–retest reliability across a large portion of the gray matter in the brain. Specifically, the posterior cingulate cortex, precuneus, parahippocampal gyrus, lateral parietal cortex, dorsal lateral prefrontal cortex, anterior cingulate cortex, and posterior temporal cortex were among the highest test–retest reliable cortical regions.

To further explore the effect of frequency ranges in the temporal band-passing filtering, similar to our previous work (Zuo et al., 2010a), we re-analyzed the fast imaging data (RfMRI_mx_645) preprocessed by (MC+WM/CSF) and repeated the analyses to assess the test–retest reliability of ReHo across six different frequency bands (Buzsaki and Draguhn, 2004; Penttonen and Buzsaki, 2003): slow6 (0.004–0.01 Hz), slow5 (0.01–0.027 Hz), slow4 (0.027–0,073 Hz), slow3 (0.073–0.198 Hz), slow2 (0.198–0.538 Hz) and slow1 (0.538–0.775 Hz). Our results showed that ReHo was robust mainly in the low-frequency bands (Fig. S3C–F, slow3–6) while high frequency ReHo seems to be noisy (Figs. S3A and B). As depicted in Fig. S4, the frequency bands slow3 (Fig. S4C) and slow4 (Fig. S4D) produced the most reliable ReHo maps.

Comparisons with integrated local correlation

We provided analyses of the autocorrelation and normality of BOLD time series acquired with RfMRI_mx_645 imaging sequence. Fig. S12 (upper panel) demonstrated the mean d map across 44 scans from 22 subjects, indicating pretty strong positive autocorrelation of the time series in the whole brain, especially in the gray matter (the most robust d<0.05). Regarding the normality, Fig. S12 (lower panel) displayed that most signals resembled a normal distribution (AD<2.32, p<0.05). However, time series within bilateral frontal, occipital cortex as well as amygdala and parahippocampal regions showed non-normality.

The ILC measure was estimated and compared with KCC-ReHo in our test–retest reliability analysis. Based on the preprocessed data by regressing out head motion and WM/CSF nuisance signals (i.e., MC+WM/CSF), we calculated both ReHo and ILC maps for all 75 scans (3 scans/subject×25 subjects) to estimate both their intra- and inter-session reliability. As shown in Fig. 2, ILC exhibited fewer amounts of substantially reliable (ICC≥0.6) voxels for both intra-session (Fig. 2F) and inter-session (Fig. 3F) test–retest reliability than KCC-ReHo (Fig. 2B: intra-session; Fig. 3B: inter-session). Interestingly, further statistical comparisons on these ICC maps showed that some of these decreases of ICC were appearing within several (e.g., amygdala and dorsal lateral prefrontal) regions, which exhibited the most significant non-normality of their BOLD time series (Figs. S1F and S2F).

Cortical surface-based ReHo: 2dReHo

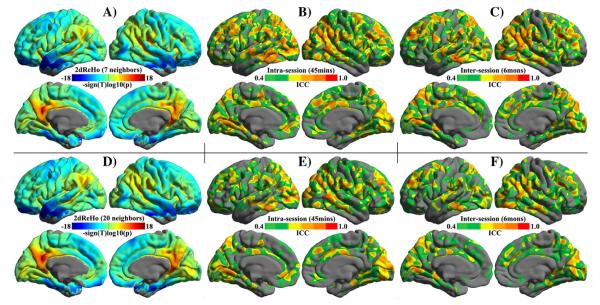
The surface-based KCC-ReHo (i.e., 2dReHo) computation significantly increased the overall intensity of functional homogeneity – the global 2dReHo (0.5125 vs. 0.08609: t=127.4,p<0.0001). Fig. 4A demonstrates the vertex-wise KCC-ReHo spatial maps across the cortical surfaces of the human brain at the group level as derived from model (2) based upon all 75 individual 2dReHo maps. Across the sheet of the cortex, posterior cingulate cortex/precuneus, lateral parietal cortex and posterior temporal cortex exhibited higher functional homogeneity than the prefrontal and anterior temporal cortex. The spatial pattern of length-two neighbors 2dReHo (Fig. 4D) is highly similar to length-one neighbors 2dReHoÕs pattern (Fig. 4A). Further analyses of regional differences indicated that: 1) parietal and insular lobes showed stable higher ReHo than frontal and temporal lobes across three scans and both hemispheres (Fig. S5); 2) paralimbic areas demonstrated the highest ReHo while heteromodal areas had the lowest ReHo as illustrated in Fig. S6; and 3) the limbic system was a network with the least functional homogeneity (Fig. S7). Additional Friedman’s tests indicated the existence of order effects on 2dReHo in regional differences across large-scale subdivisions of brain lobes, hierarchies and functional networks.

Fig. 4. Spatial pattern and test–retest reliability of 2dReHo.

Both group-level spatial maps of length-one neighboring (A) and length-two neighboring (B) 2dReHo are visualized. The linear mixed model based on all 75 individual 2dReHo maps (z-standardized) from 25 participants (each has 3 test–retest scans) generates vertex-wise 2dReHo surface maps. To show the spatial distribution of 2dReHo across the entire cortex, the value of —sign(t)log₁₀(p) (t is the t-value, and p is the p-value) at each vertex is depicted for both hemispheres. Warm colors for a vertex represent the significance of the vertex’s KCC-ReHo greater than the global mean ReHo across the entire cortex. Cool colors at a vertex denotes the significance of the vertex’s KCC-ReHo lower than the global mean at the group level. The ICC maps of intra-session (B, E) and inter-session (C, F) test–retest reliability of 2dReHo are depicted on the cortical surfaces. Only brain regions demonstrating at least moderate ICC (≥0.4) are colored. The colormap indicates ICC values.

TRT reliability of 2dReHo

A large portion of vertices on the cortex showed moderate to almost perfect intra-session (Fig. 4B) and inter-session (Fig. 4C) test–retest reliable KCC-ReHo. Most of these vertices with substantial to almost perfect reliability belonged to lateral parietal cortex, posterior cingulate cortex/precuneus, posterior temporal cortex as well as to the medial occipital and insular cortex. To compare the distribution of ICC between 2dReHo and 3dReHo, the volume ICC maps were projected onto the fsaverage5 surface and then the ratio of vertices showing ICC at 10 0.1-stepped intervals was computed for both 2dReHo and 3dReHo. This analysis clearly indicated that there is a gradient change on both intra-session (Figs. S9A/C) and inter-session (Figs. S9B/D) of ReHo measures. Specifically, length-one 2dReHo exhibited the highest inter-session reliability, followed by length-two 2dReHo and length-one 3dReHo, respectively. Regarding the intra-session reliability, length-one 3dReHo has the highest reliability among measures of functional homogeneity, followed by length-one 2dReHo and length-two 2dReHo. All large-scale subdivisions of brain lobes, hierarchies and functional networks demonstrated moderate to substantial reliability (Fig. S8). The global 2dReHo did not show significantly higher test–retest reliability than the global 3dReHo.

Influence of imaging resolution and scan duration

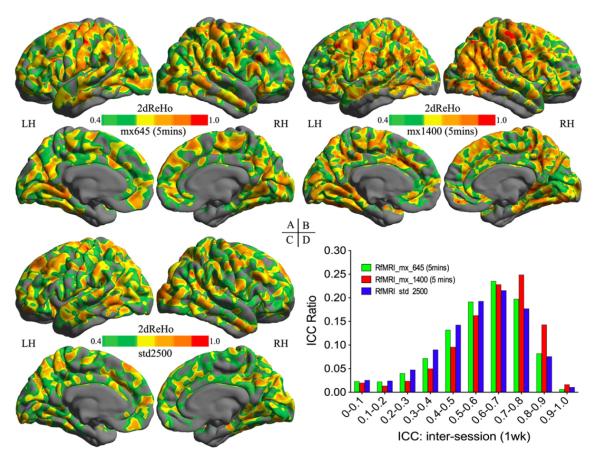
In keeping with our observations in the sections above, all individual 2dReHo maps were generated based upon nuisance corrected and not smoothed R-fMRI data acquired by the three different EPI sequences, respectively. Compared with the standard R-fMRI (std2500) sequence (Fig. 6C), two multi-band EPI (mx645: Fig. 6A, and mx1400: Fig. 6B) sequences demonstrated more spatially extended and robust cortical patterns of ICC. Among the two fast imaging sequences, increases in both temporal and spatial resolutions of the mx1400 sequence led to the best improvement in inter-session test–retest reliability (Fig. 6D).

Fig. 6. Influence of imaging resolution on test–retest reliability of 2dReHo.

The inter-session (one week apart) ICC maps of 2dReHo derived from mx_645 5-min (A), mx_1400 5-min (B), and std_2500 5-min (C) R-fMRI test–retest data. Only brain regions demonstrating at least moderate ICC (≥0.4) are colored. The colormap indicates ICC values. To access the influence of imaging sequences on the ICC distribution, the histogram of ICC values are plotted for these three ICC maps (D).

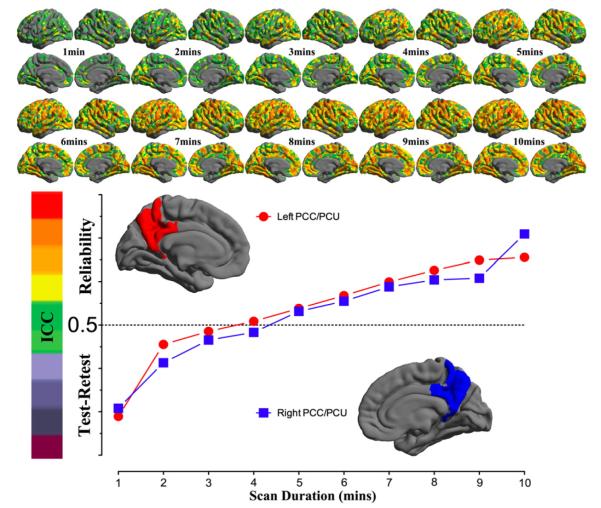
For each of the ten durations from 1 min to 10 min, the inter-session ICC map was estimated and shown as in Fig. 5. All these ICC maps were also integrated into a movie to demonstrate the temporal dynamics of test–retest reliability (Fig. S10). To gain more details on changes of reliability across time, we calculated the mean ICC values within the posterior and precuneus region for each of the ten scan durations and plotted them as a function of durations (the bottom panel in Fig. 5). For both hemispheres, the plot clearly showed that the 5 min scans already produced reliable (ICC>0.5) 2dReHo. Strikingly, as a measure of functional homogeneity, 2dReHo can achieve good inter-session reliability (ICC≥0.4) even with scan durations around 3 or 4 min. Interestingly, there seems to be a floor of 2dReHo reliability between 1 min and 2min scan duration.

Fig. 5. Influence of scan duration on test–retest reliability of 2dReHo.

Based on (MC+WM/CSF) preprocessed 10 min data, the one-week inter-session test–retest reliability was estimated as relevant ICC maps for each of ten scan durations from 1 min to 10 min (top panel). Only brain regions demonstrating at least moderate ICC (≥0.4) are colored. The colormap indicates ICC values. In the bottom panel, the mean ICC values within the posterior cingulate cortex and precuneus for both hemispheres are plotted as a function of scan duration. The dashed line indicates the level of 50% reliability. The posterior cingulate cortex and precuneus regions of interests are constructed by combining four parcels from the Destrieux Atlas (Destrieux et al., 2010) in freesurfer (G_cingul-Post-dorsal, G_cingul-Post-ventral, G_precuneus and S_subparietal).

Discussion

This study demonstrated high test–retest reliability for regional homogeneity (ReHo) in the functional connectome. We observed high test–retest reliability of ReHo within cortical regions including multiple default network and attention network regions. Moreover, test–retest reliability was significantly improved by utilization of a fast imaging sequence, use of nuisance correction and no spatial smoothing in data preprocessing, and representing the data with a surface-based computation. Accordingly, these factors were integrated into the Connectome Computation System (CCS) to provide a more efficient computation platform for reliably mapping the functional homogeneity of the human brain connectome.

Test–retest reliable functional homogeneity

At a micro-scale (e.g., the level of a single cell), neural homogeneity is considered an important and robust measure of brain activity (Fox and Norman, 1968). Our results demonstrate that at a macro-scale (i.e., voxel of several millimeters), such functional homogeneity as measured by Kendall’s correlation is a highly test–retest reliable characteristic of the human brain connectome (Bullmore and Sporns, 2009,2012). The high test–retest reliability thus allows ReHo to serve as a potential biomarker for tracing the changes of functional homogeneity while the brain develops, as well as in relation to behaviors and diseases. Meanwhile, the regions showing high test–retest reliability overlapped with the previously reported structural, functional and metabolic ‘backbones’ of the human brain connectome (Buckner et al., 2009; Gusnard and Raichle, 2001; Hagmann et al., 2008; Raichle et al., 2001). These observations may suggest that local synchronization of low-frequency spontaneous activity in the intrinsic brain architecture plays a fundamental role (Cabral et al., 2011; Singer, 1993).

Functional homogeneity on the cortical surface

Data analysis on the cortical surface offers an attractive approach for inter-subject matching and comparison (Clouchoux et al., 2005; Fischl et al., 1999b; Toro and Burnod, 2003; VanEssen and Drury, 1997). Surface-based resting-state functional connectivity (RSFC) analysis has been shown to be more robust and sensitive for mapping the default network (Seibert and Brewer, 2011; Seibert et al., 2012) and the entire brain connectome (Yeo et al., 2011). However, regional homogeneity and its test–retest reliability have not been investigated on the cortical surface. In this study, the functional homogeneity analysis was generalized onto the cortical surface, and such a change of computational space dramatically improved in long-term (5–16 months) test–retest reliability. The improvement may be attributed to: 1) the accurate estimate of the inter-subject variability in anatomy provided by vertex-wise analysis on the cortical surface (unlike voxels, which do not have any anatomical meaning and mix tissues of gray and white matters), 2) better inter-subject registration in both anatomical structure and functional organization by considering the cortical surface as a manifold with geodesic distances as the reference (unlike Euclidean distances, which neglect the intrinsic geometry of the highly folded human cortex), and 3) improved intra-subject alignment in functional processing by combining anatomical-informed function-structure co-registration (GM/WM boundary) and projection of functional data (local geometry), which involves additional spatial smoothing of interpolation guided by the gray matter tissue. These benefits may also translate to the TRT reliability of other RSFC approaches as well.

Functional homogeneity under fast imaging sequences

From the perspective of signal processing, higher sampling rates can benefit RSFC analysis by adequately sampling undesirable respiration and cardiac signals (Birn et al., 2008). Therefore, it has potential to further increase the test–retest reliability of functional homogeneity by increasing the acquisition resolutions in both time and space. Most recently, multi-band EPI sequences have been developed to accelerate R-fMRI data acquisition (Feinberg and Yacoub, 2012; Feinberg et al., 2010; Moeller et al., 2010) and show promise for advancing our understanding of human brain function (Smith et al., 2012). Our observations confirmed that improvements on both temporal and spatial resolutions significantly enhanced the long-term test–retest reliability of regional homogeneity, advancing applications of fast imaging of both healthy brain conditions and various brain disorders.

Uses of functional homogeneity

Our results indicated that 5 min of imaging scan duration is enough for getting test–retest reliable estimates of functional homogeneity. Van Dijk et al. (2010) observed the similar results for seed based intrinsic functional connectivity (iFC) analyses. This finding becomes more important for applications because data is lost through scrubbing to account for in-scanner motion (Power et al., 2012), especially in clinical populations like ADHD and autism, etc. In such cases, following scrubbing, a 10 min scan might be 5 min, or a 5 min scan might have 4 min of data. Fortunately, ReHo strengths still get good test–retest reliability even with acquisition times as brief as 4 min.

In the current work, we proposed reliable pipelines for ReHo computation in both volume and 6surface spaces. In practice, the 3dReHo analysis with nuisance corrected (i.e., MC6+WM/CSF) would be recommended for those who are interested in not only the cortex but also striatum and cerebellum, and do not want to take the extra time to run the reconstruction of cortical surfaces. However, 2dReHo would be extremely useful if researchers aim to integrate various measures of both structure and function on the cortical surface (i.e., a test–retest reliable multi-modal MRI integration).

Limitation and future direction

A recurring issue in the field of R-fMRI is head motion, which has complex relationships with age and various R-fMRI metrics at the group level (Power et al., 2012; Satterthwaite et al., 2012; Van Dijk et al., 2012). Such a relationship tends to be nonlinear with short-distance connectivity (Van Dijk et al., 2012), and thus makes carefully controlling the motion level crucial for ReHo computation. Meanwhile, motion-related artifactual modulations of BOLD signal are similar at nearby voxels (Friston et al., 1996), troubling the volume-based ReHo computation. Accordingly, we first regressed out motion at the individual level and took the mean motion into account at all group-level analyses. As complementary analysis, we further used the temporal scrubbing (Power et al., 2012) and the interpolating (Carp, in press) approach to correct the data for motion, and found no significant improvements on test–retest reliability induced by such a correction for motion. In our analyses, we did not regress out the temporal derivatives of the motion parameters. We also repeated the reliability analyses based on data preprocessed by regressing out motion parameters and their temporal differences, and did not observe significant improvements on ReHo’s reliability (data not shown). There are several other options of correcting the individual time series for head motion, including removal of high-order (Friston et al., 1996) and even voxel-wise motion related changes (Satterthwaite et al., 2013; Yan et al., 2012). The influence of these motion correction methods on functional homogeneity and its reliability will be explored in the future.

Previous studies have shown that numerous physiologic processes (e.g., cardiac and respiratory) can contribute artifactual signals to R-fMRI data (Bianciardi et al., 2009; Birn et al., 2006; Chang et al., 2009; Shmueli et al., 2007; Yan et al., 2009). In this study, we demonstrate that fast sampling rates improve test–retest reliability of functional homogeneity, indicating the advantage of uncoupling the cardiac/respiratory signals and the low frequencies of spontaneous resting state fluctuations. Brain structure shapes and couples its function (Honey et al., 2007), which makes uncoupling the structure and function of a local measure challenging. In this study, we took KCC-ReHo as a measure of functional homogeneity based on its temporal computation although some regional variability in local features of the brain structure could be introduced by variations in brain registration. A possible way of correcting ReHo for structural properties could be some forms of modulation based on the Jacobian (like in VBM, Ashburner and Friston, 2000).

Finally, the mean filtering based fast algorithm was only implemented for 3dReHo. In a future study, we will develop this filtering strategy for 2dReHo by using diffusion filters on the manifold of the cortical surface (Joshi et al., 2009).

Conclusion

We found that KCC-based functional homogeneity can be a highly test–retest reliable measure of brain activity after carefully optimizing data acquisition and preprocessing and computational implementation, both of which have been integrated into CCS. KCC-ReHo serves as a valuable candidate biomarker for exploring changes of brain function under normal development and pathological attack.