Abstract
Dispersal is a major life history trait of social organisms influencing the behavioral and genetic structure of their groups. Unfortunately, primate dispersal is difficult to quantify, because of the rarity of these events and our inability to ascertain if individuals dispersed or died when they disappear. Socioecological models have been partially developed to understand the ecological causes of different dispersal systems and their social consequences. However, these models have yielded confusing results when applied to folivores. The folivorous red colobus monkey (Procolobus rufomitratus) in Kibale National Park, Uganda is thought to exhibit female-biased dispersal, although both sexes have been observed to disperse and there remains considerable debate over the selective pressures favoring the transfers of males and females and the causes of variation in the proportion of each sex to leave the natal group. We circumvent this problem by using microsatellite DNA data to investigate the prediction that female dispersal will be more frequent in larger groups as compared to smaller ones. The rationale for this prediction is that red colobus exhibit increased within-group competition in bigger groups, which should favor higher female dispersal rates and ultimately lower female relatedness. Genetic data from two unequally sized neighboring groups of red colobus demonstrate increased female relatedness within the smaller group, suggesting females are less likely to disperse when there is less within-group competition. We suggest that the dispersal system is mediated to some degree by scramble competition and group size. Since red colobus group sizes have increased throughout Kibale by over 50% in the last decade, these changes may have major implications for the genetic structure and ultimately the population viability of this endangered primate.
Keywords: Procolobus rufomitratus, microsatellites, pedigree, group size, scramble competition, female dispersal
INTRODUCTION
Dispersal from the natal unit is one of the most important characteristics of an animal’s life history [Clobert et al., 2001] and males and females vary considerably in how often and far they disperse. Female-biased dispersal is common among mammals [Greenwood, 1980] and such sex-biased transfers influence the genetic relatedness in a group [Lawson Handley & Perrin, 2007]. For example, female-biased dispersal will result in a greater degree of relatedness among the males in a group. However, dispersal is difficult to study, because it is very rare and determining if individuals successfully dispersed or died when they disappear is very challenging [Di Fiore, 2003; Di Fiore et al., 2009]. Thus, the selective pressures favoring each sex to disperse and what causes variation in the proportion of females and males to leave the natal group remains controversial.
Efforts to understand dispersal have drawn insights from investigations of the ecology, behavior, and social systems of primates, which have all been formalized in socioecological models [Isbell & Young, 2002; Koenig, 2002; Snaith & Chapman, 2007; Sterck et al., 1997; Wrangham, 1980]. Genetic data have been very informative for testing these models [Di Fiore et al., 2009; Langergraber et al., 2007; Lukas et al., 2005; Morin et al., 1994; Strier et al., 2011]. These socioecological models have focused predominantly on how the distribution of females drives variation in social systems, behavior, and dispersal, with these patterns explained primarily by the variance of resources and predation [Koenig, 2002; Wrangham, 1980]. In situations where males are needed for group defense, or there are no advantages to form female coalitions to defend food resources [Isbell, 1991; Lukas et al., 2005; Wrangham, 1979], females are often the dispersing sex and males are philopatric. This creates a male-bonded social system, rather than a typical female-bonded one.
However, the forces shaping folivore dispersal are not clear, as there is often little in the way of male home range defense and because leaves are very abundant in tropical forests, it has been hypothesized that increased within-group competition for food resources (scramble competition) should be less intense or absent for folivorous primates [Isbell, 1991; Janson & Goldsmith, 1995; Oates, 1994; Struhsaker & Leland, 1987]. However, there is mounting evidence that folivores may exhibit significant scramble competition. Folivores have been demonstrated to exhibit increased day range as group size increases [Snaith & Chapman, 2008], are resource limited in larger groups [Koenig & Borries, 2002], exhibit patch depletion [Snaith & Chapman, 2005; Tombak, 2012], and their biomass is predicted by the quality of food resources [Chapman et al., 2004; Oates et al., 1990]. These findings suggest that resources are limiting to folivores and that scramble competition may be restricting group sizes [Borries et al., 2008; Snaith & Chapman, 2007, 2008]. If so, individuals living in larger groups would face increasing scramble competition for food resources [van Schaik, 1989; van Schaik & van Hooff, 1983], which would ultimately influence rates of dispersal and the genetic structure of a population [Di Fiore et al., 2009].
Female-biased dispersal characterizes the red colobus monkeys (P. rufomitratus) in Uganda’s Kibale National Park [Struhsaker, 2010], which is home to the largest viable population of the endangered P. r. tephrosceles [Chapman et al., 2010a; Struhsaker, 2005]. This subspecies numbers +17,000 individuals in the park and the population appears to be growing. While this population exhibits female-biased dispersal, both sexes have been observed to disperse and there remains considerable controversy over the causes and variance of these transfers [Oates 1994; Struhsaker, 2010; Struhsaker & Leland, 1985]. Average red colobus group sizes across the park have increased by 50% over the last 15 years [Gogarten et al., in review b] and these changes may have led to increased within-group competition [Chapman & Chapman, 2000; Snaith & Chapman, 2005]. Understanding the implications of these group size changes on dispersal and ultimately the genetic structure of this last stronghold of red colobus is imperative for their conservation and management [Hedrick & Kalinowski, 2000].
Following this logic, we hypothesized that there would be a relationship between group size and sex-biased dispersal patterns. We predicted that increases in group size among red colobus would lead to increased scramble competition for food, which would in-turn increase the frequency of female-biased natal dispersal (relative to smaller groups), and reduce female relatedness in larger groups. We tested this prediction that female dispersal will be more frequent in larger groups by analyzing microsatellite data from two neighboring red colobus groups of varying size [Allen et al., in press]. The degree of female relatedness within each group is used as an index of sex-biased dispersal patterns.
METHODS
Study Site and Groups
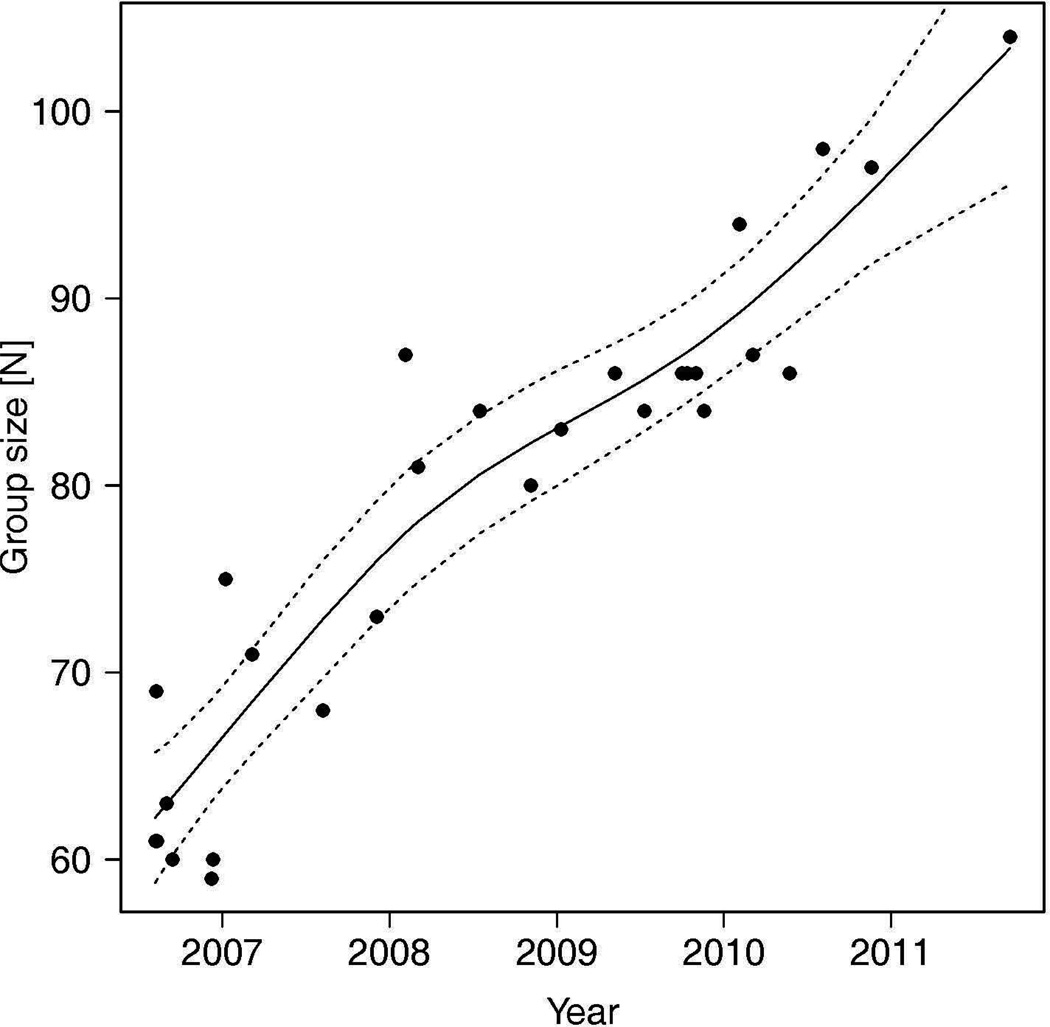
Kibale National Park is located in western Uganda at the foothills of the Rwenzori Mountains [Chapman & Lambert, 2000]. It is a 795 km2 park consisting of moist mid-altitude forest, home to some of the highest primate biomass documented anywhere on the globe [Chapman et al., 2010a; Oates et al., 1990]. Two groups of red colobus, called Large Mikana and Small Camp, range in the area adjacent to the Makerere University Biological Field Station, primarily in a region of old growth forests known as K30 [Chapman et al., 2010a; Snaith & Chapman, 2005]. Large Mikana is a big stable group of red colobus consisting of ~130 individuals, which was already well established in 2003 [Chapman et al., 2010a; Snaith & Chapman, 2005]. Small Camp is a newer group, which appeared to have formed just prior to 2003 and was initially displaced by Large Mikana and other bigger neighboring groups. The Small Camp group exhibited continuous growth between 2006 and 2011, during which it increased from 59 to 104 individuals (Fig. 1; Gogarten et al., in review: b). From 2006 to 2007, Small Camp consisted of 10 breeding males and 25 breeding females. Comparable counts of reproducing males and females are not available for Large Mikana, because of the greater difficulties of observing all individuals and breeding events in this big group. Female reproductive rate appears to be higher in smaller groups like Small Camp than in larger ones like Large Mikana (C.A. Chapman, unpublished data). Average group size was 48 animals for 16 groups of red colobus in the area of the Makerere University Biological Field Station and 43 individuals for 27 other groups from elsewhere throughout the park.
Fig. 1.
Group size of Small Camp since 2006. Counting arboreal primates (e.g., red colobus) in dense forest canopy is difficult, and thereby, is fraught with error (e.g., when animals sneak unnoticed by observers). However, the group counts of this graph (n = 27) are thought to be complete, because they were obtained opportunistically when the entire Small Camp was crossing en masse across open areas. The solid and dashed lines represent the predicted group size through time and its 95% confidence bands, respectively. These predictions were generated using a generalized additive model (GAM) with a smoothing spline on time since the first group count. This GAM does not assume a linear relationship between group size and time [Zuur et al., 2009] and was built with the R package “mgcv,” version 2.14.2 [R Development Core Team, 2012; Wood, 2011]. The model explains 88% of the variation in group size through time (R2 = 0.878, P < 0.001).
Group Samples and Microsatellite Data
Allen et al. [in press] collected blood and fecal samples for microsatellite DNA typing from 18 and 32 individuals of Large Mikana and Small Camp, respectively, over one year starting in 2006. Samples from 10 and four more individuals from each group, respectively, were then added in 2008. The 28 individuals of the Large Mikana sample consist of 12 adult females, 14 adult males, one juvenile male, and one male of unknown pre- or post-dispersal age. The 36 individuals of the Small Camp sample include 23 adult females, 12 adult males, and 1 juvenile male. The two juvenile and unknown males of Large Mikana and one juvenile male of Small Camp were included along with the adults in the calculations of within- and between-group genetic variation, but were excluded from the pairwise relatedness and pedigree analyses of the two groups (see below). These three males were included in the former, because they share no known a priori relationships with the other members of their groups. Thus, they constitute valid independent samples of their gene pools. Conversely, these three males were excluded from the latter, which were focused on the relationships of group members after dispersal. Thus, the pairwise relatedness and pedigree analyses were limited to the 61 post-dispersal adults.
Allen et al. [in press] also collected blood and fecal specimens for microsatellite DNA typing from 21 individuals of four other groups in Kibale. These authors performed three different tests with the total microsatellite data to verify that Large Mikana, Small Camp, and these four other groups (Dura, K-30, Mainaro, and Sebatoli) conform to a single panmictic population. On the basis of their results, these four additional groups were also included in the pairwise relatedness and pedigree analyses, specifically to estimate empirically the background allele frequencies of the red colobus population in Kibale.
The capture of individuals and the collection and handling of their blood and fecal samples followed Goldberg et al. [2009]. In brief, blood samples were stored on FTA cards, whereas fecal specimens were treated with the two-step procedure of Nsubuga et al. [2004]. Two to four fecal samples were collected from each individual. All 85 genotyped animals are individually named and are readily identifiable on the basis of their hair color, birthmarks, scars, broken tails, and other distinguishing features [Tombak et al., 2012]. Total genomic DNA was extracted from the blood and fecal specimens with the FTA protocol and Qiagen QIAamp Stool Mini Kit (catalogue number 51504) according to their manufacturers’ recommendations. To obtain adequate DNA for genotyping, DNA was extracted from two to four fecal specimens per individual.
The 85 individuals were genotyped for 11 microsatellite loci, which are known to be polymorphic in other colobines (A. Di Fiore, personal communication). These loci were amplified with a three-primer nested PCR approach [Schuelke, 2000], run on an AB3730xl automated sequencer (96 capillary), and scored with GeneMarker® (Softgenetics, State College, PA, USA). All loci were amplified three to four times from multiple extracts per individual to ensure the consistency and accuracy of the scored genotypes.
The resultant dataset of 11 microsatellite loci was checked for genotyping errors with MICRO-CHECKER, version 2.2.3 [van Oosterhout et al., 2004]. One locus (D17S1290) was subsequently removed from the dataset by Allen et al. [in press], because of its significant numbers of null alleles and scoring errors. Following these authors, the final dataset used in the current study consists of 10 microsatellite loci (D14S306, D3S1766, D2S1399, D7S1817, D20S206, D8S60, D8S165, D1S207, C2A, and D5S1457).
Standard Statistics
Estimates of within-group genetic diversity (na, ne, Ho, and He for observed and effective numbers of alleles and observed and expected heterozygosities, respectively) were calculated with POPGENE, version 1.3.2 [Yeh & Boyle, 1997]. Each locus of a group was tested against its Hardy-Weinberg expectations with the G-test of POPGENE. Wright’s FIS was estimated for each locus with FSTAT, version 2.9.3 [Goudet, 2002] and then across all loci with GDA, version 1.1 [Lewis & Zaykin, 2001]. The significance of each per-locus and total FIS was assessed with 10,000 randomizations of the genotypes and 10,000 bootstrap replications across loci, respectively. Each pair of loci within a group was tested for genotypic linkage disequilibrium with the G-test and 10,000 permutations of the genotypes in FSTAT. To correct for multiple comparisons, a sequential Bonferroni correction was applied in all group-wide series of tests [Rice, 1989].
A follow-up series of delete-1 jackknifing with GDA was performed for Large Mikana, in response to our finding of a significantly positive total FIS for this group (see below). In this delete-1 jackknifing, each locus of the Large Mikana dataset was sequentially removed and the resultant dropout matrix was then reanalyzed as before with GDA [Shao & Tu, 1995]. The removal of one locus at a time in the delete-1 jackknifing allowed us to identify which loci are responsible for the heterozygote deficit in Large Mikana, which is implicated by its significantly positive total FIS.
The above statistics and tests are for within-group variation: In turn, Wright’s FST was estimated with GDA to quantify the level of genetic divergence between Large Mikana and Small Camp. The significance of their FST was evaluated with 10,000 bootstrap replications across loci.
Pairwise Relatedness
The microsatellite datasets of Large Mikana and Small Camp were each analyzed with ML-RELATE [Kalinowski et al., 2006]. This approach uses maximum likelihood (ML) to estimate from co-dominant genetic markers (i.e., microsatellites) a coefficient of relatedness (r) and a relationship for every pair of individuals in a group [Wagner et al., 2006]. Thus, it relies on a traditional strategy, whereby the sampled individuals of a group are treated as independent pairs that span only one or two generations [Blouin, 2003; Jones et al., 2010].
In our ML-RELATE analyses of Large Mikana and Small Camp, the population-wide allele frequencies were set to the empirical estimates of the total microsatellite dataset for these two groups, Dura, K-30, Mainaro, and Sebatoli. A correction was made at each locus for typing errors due to null alleles [Kalinowski & Taper, 2006]. Ten thousand simulations were generated under each null hypothesis (i.e., possible relationship) to estimate a 95% confidence set of relationships for every pair of adults in the Large Mikana and Small Camp samples. Each pair of individuals was scored according to its 95% confidence set as either “related” (half sib, full sib, and/or parent/offspring), “unrelated” (unrelated only), or “ambiguous” (unrelated and half sib, full sib, and/or parent/offspring). These scores were then summarized for the males and/or females of Large Mikana and Small Camp.
Comparisons of the ML-RELATE frequencies of related, unrelated, and ambiguous pairs between Large Mikana and Small Camp are limited by a lack of independence (i.e., each individual is compared {n − 1} times to the other members of its group) and by the disproportionate sampling of the two groups at the time of their sample collections. In recognition of the first constraint, Fisher’s exact test was used in the frequency comparisons between groups for its heuristic value rather than to estimate a formal probability. In acknowledgment of the second limitation, delete-d jackknifing [Shao & Tu, 1995; Siddall, 1995] was performed with the 23 adult females of the Small Camp sample, given: (1) that the disproportionate sampling of the two groups is particularly acute for females and (2) that the females (but not the males) exhibit different levels of structure between the two groups (see below).
The ML-RELATE comparisons of the Large Mikana and Small Camp females are based on female/female pairs and not directly on individuals. The 12 sampled females of Large Mikana represent 66 female/female pairs. The number of breeding females in Large Mikana is estimated as ~50 assuming: (1) that this group was approximately twice as big as Small Camp at the time of their sample collections and (2) that the general sex ratio for red colobus is ~2.6 [Struhsaker, 2010; C.A. Chapman, unpublished data for these two groups and 52 others]. Thus, the proportion of sampled female/female pairs to breeding females is 1.32 (66/50) for Large Mikana. Conversely, the proportion of sampled female/female pairs to breeding females is 10.12 (253/25) for Small Camp at the time of its sample collections. By numerical evaluation, we find that a reduced subsample of eight adult females for Small Camp most closely approximates the proportion of female/female pairs to breeding females for Large Mikana (1.32). Specifically, eight subsampled females represent 28 female/female pairs for Small Camp, and thus, a proportion of female/female pairs to breeding females of 1.12 (28/25) for this group.
Correspondingly, delete-d jackknifing of the 23 Small Camp females was performed with subsamples of eight. Specifically, 15 of the 23 adult females in the Small Camp sample were randomly removed from their dataset to generate a subsample of eight retained females. Such subsampling was repeated 200 independent times. The 200 subsamples were reanalyzed as before with ML-RELATE and their numbers of related female/female pairs were summarized in a frequency histogram. The observed number of related female/female pairs in the Large Mikana sample was compared to this frequency histogram to test its significance after correcting for the disproportionate female sample sizes.
Pedigree Reconstructions
The microsatellite datasets of Large Mikana and Small Camp were also each analyzed with FRANz, version 2.0.0 [Riester et al., 2009, 2010]. This approach uses ML to estimate multi-generation pedigrees from co-dominant genetic markers [Almudevar, 2003]. FRANz differs from ML-RELATE and other related approaches in that it treats the sampled individuals of a group as a collective whole (rather than as pairs) that may span more than two generations.
In our FRANz analyses, the population-wide allele frequencies were fixed (as in ML-RELATE) to the empirical estimates for all six red colobus groups. The numbers of breeding males and females in Small Camp were set to 10 and 25, respectively, based on direct counts of identifiable individuals. Correspondingly, these numbers were doubled to 20 and 50 for Large Mikana as described above. Typing errors were accounted for by the model of Kalinowski et al. [2007] using the default rate of 0.01 [Pompanon et al., 2005]. As recommended by Riester et al. [2011], both microsatellite datasets were first tested for the presence of full sibs. As no significant full sib relationships were detected, all subsequent FRANz analyses were done without this search option.
The robustness of the ML pedigrees was evaluated with two different procedures. The first procedure involved Metropolis coupled Markov chain Monte Carlo (MCMCMC) sampling to estimate the posterior probabilities of each link in the ML pedigrees [Huelsenbeck & Ronquist, 2001]. These MCMCMC runs consisted of heating with three heated chains and one cold chain. Each chain was run for 100,000,000 total steps with samples taken every 2,500 generations from the cold chain after a burn-in of 10%. The second procedure involved a series of 11 tests to assess the stabilities of the ML pedigrees to changes in the numbers of breeding males and females and in the typing error rate (Table I). These 11 tests included varying the numbers of breeding males and females for Large Mikana from their original settings of {20, 50} to the alternative values of {10, 25}, {30, 75}, {40, 100}, {35, 35}, and {50, 20}. Similarly, the second procedure involved varying the typing error rate for both Large Mikana and Small Camp from its default setting of 0.01 to the alternative values of 0.05, 0.10, and 0.15.
TABLE I.
Stability Tests of the ML Pedigrees for Large Mikana and Small Camp
| Parameter settings | ML pedigrees | ||||||
|---|---|---|---|---|---|---|---|
| Group | Run conditions |
Breeding males |
Breeding females |
Typing error rate |
Links | Connection index |
Description |
| Large Mikana | Actual run (Fig. 3A) | 20 | 50 | 0.01 | 6 | 0.23 | Numbers of breeding males and females are less certain for Large Mikana |
| Test A | 10 | 25 | 0.01 | 7 | 0.27 | Numbers of breeding males and females are reset to those for Small Camp | |
| Test B | 30 | 75 | 0.01 | 4 | 0.15 | Numbers of breeding males and females are increased by 50% | |
| Test C | 40 | 100 | 0.01 | 4 | 0.15 | Numbers of breeding males and females are doubled | |
| Test D | 35 | 35 | 0.01 | 5 | 0.19 | While their total number is kept fixed, numbers of breeding males and females are set equal | |
| Test E | 50 | 20 | 0.01 | 5 | 0.19 | While their total number is kept fixed, numbers of breeding males and females are reversed | |
| Test F | 20 | 50 | 0.05 | 7 | 0.27 | Typing error rate is reset to an intermediate value ~33% in between its default setting and empirical maximum | |
| Test G | 20 | 50 | 0.10 | 8 | 0.31 | Typing error rate is reset to an intermediate value ~67% in between its default setting and empirical maximum | |
| Test H | 20 | 50 | 0.15 | 8 | 0.31 | Typing error rate is set to its empirical maximum | |
| Small Camp | Actual run (Fig. 3B) | 10 | 25 | 0.01 | 23 | 0.66 | Numbers of breeding males and females for Small Camp are well-established from the field data |
| Test I | 10 | 25 | 0.05 | 30 | 0.86 | See Test F | |
| Test J | 10 | 25 | 0.10 | 41 | 1.17 | See Test G | |
| Test K | 10 | 25 | 0.15 | 52 | 1.49 | See Test H | |
The default setting of 0.01 and the “empirical maximum” of 0.15 for the typing error rate represent values that are typical and are the largest for microsatellite datasets, respectively [Pompanon et al., 2005].
Initially, each ML pedigree was scored for its “connection index,” which is defined as the number of links in the genealogy divided by the sample size. This summary statistic offers a straightforward way to compare the level of structure (i.e., relatedness) among ML pedigrees (e.g., between those for Large Mikana and Small Camp). In turn, more formal statistical (probabilistic) comparisons of the ML pedigrees are complicated by the lack of independence among related individuals and the fact that parents can have multiple offspring. In light of these complications, we focused on the unlinked (i.e., fully unrelated) individuals of each pedigree, which are independent by definition, and relied on binomial testing to calculate the total probability of obtaining in Large Mikana ≥ “x” unlinked females and/or males by chance alone. The probabilities of unlinked females and/or males in these tests (“p”) were estimated from their empirical frequencies in the ML pedigree for Small Camp, which is represented by the larger of the two samples. In this way, the expected larger sampling error of the smaller Large Mikana dataset was directly accounted for in the calculations of the total binomial probabilities. At the same time, p was now parameterized with the larger Small Camp sample, which is expected to have greater statistical power.
Comparisons of the structure between the Large Mikana and Small Camp pedigrees are further constrained by the same problem of disproportionate sampling that limited the ML-RELATE analyses. As before, this disproportionate sampling was corrected by delete-d jackknifing of the 23 Small Camp females. By definition, a pedigree link refers to a connection between two individuals. The number of such possible connections for the Large Mikana females is 234 (i.e., 66 female/female plus 168 female/male arcs for the 12 females and 14 males of this sample). Thus, the proportion of possible female connections to breeding females is 4.68 (234/50) for Large Mikana. Conversely, the number of such possible connections for the Small Camp females is 529 (253 female/female plus 276 female/male arcs for the 23 females and 12 males of this sample). Thus, the proportion of possible female connections to breeding females is 21.16 (529/25) for Small Camp. By numerical evaluation, we again find that a reduced subsample of eight adult females for Small Camp most closely approximates the proportion of possible female connections to breeding females for Large Mikana (4.68). Specifically, eight subsampled females represent 28 female/female and 96 female/male pairs for Small Camp, and thus, a proportion of possible female connections to breeding females of 4.96 (124/25) for this group.
Correspondingly, delete-d jackknifing of the 23 Small Camp females was performed as before, except that the 200 jackknifed datasets were now each analyzed with FRANz. The observed proportion of unlinked females in the Large Mikana sample was compared to the frequency histogram for the 200 jackknifed datasets to test its significance after adjusting for the uneven female sample sizes.
Research Compliances
Permission to conduct this research was given by the Uganda Council for Science and Technology and the Ugandan Wildlife Authority. The Animal Care Committee of McGill University approved all procedures used in this study. All procedures followed the American Society of Primatologists’ Principles for the Ethical Treatment of Nonhuman Primates and Ugandan law. All animal care regulations and applicable national laws were followed.
RESULTS
Within- and Between-Group Genetic Variation
Large Mikana and Small Camp share similar levels of within-group diversity for the 10 microsatellite loci (Table II). Both groups share a mean ne of ~3.9 and an average He of ~0.71. After sequential Bonferroni correction, none of the 45 pairs of loci in either group is in significant genotypic linkage disequilibrium, none of the 10 loci in either Large Mikana or Small Camp differs significantly from its Hardy-Weinberg expectations, and none of the 10 loci in either sample is associated with a significantly positive or negative FIS. Total FIS is not significantly different from zero for Small Camp (−0.014, 95% bootstrap confidence interval of −0.071 to 0.041). Conversely, total FIS is significantly positive for Large Mikana (0.099, 0.015 to 0.173). This significantly positive total FIS is indicative of a heterozygote deficit and is primarily due to loci D14S306 and D3S1766. These two loci are the only ones of the Large Mikana dataset with P < 0.05 for their per-locus FIS (P = 0.011 and 0.016, respectively; nevertheless, these loci are non-significant after sequential Bonferroni correction). Importantly, the delete-1 jackknife removal of either D14S306 or D3S1766 results in a non-significant total FIS for Large Mikana. Conversely, the delete-1 jackknife removal of any one of the other eight loci does not change the result of a significantly positive total FIS for this group. The heterozygote deficit in Large Mikana is attributable to two particular loci and is thus not genome wide, which indicates that it may be due to locus-specific underdominant selection [Hedrick, 2011].
Table II.
Within-Group Standard Statistics of Genetic Diversity in Large Mikana and Small Camp
| Group | ||
|---|---|---|
| Standard statistic | Large Mikana | Small Camp |
| n (number of genotyped individuals) | 27.300 (24 – 28) | 34.800 (31 – 36) |
| na (observed number of alleles) | 5.700 (3 – 8) | 6.400 (3 – 11) |
| ne (effective number of alleles) | 3.931 (1.834 – 6.627) | 3.900 (1.877 – 6.028) |
| Ho (observed heterozygosity) | 0.641 (0.444 – 0.852) | 0.717 (0.528 – 0.917) |
| He (expected heterozygosity) | 0.710 (0.463 – 0.865) | 0.707 (0.474 – 0.846) |
| FIS (Wright’s fixation index) | 0.099 (0.015 – 0.173) | −0.014 (−0.071 – 0.041) |
The standard statistics for n, na, ne, Ho, and He correspond to their arithmetic means and ranges (in parentheses) for the 10 microsatellite loci of each group. Conversely, the standard statistics for FIS refer to their weighted means and 95% bootstrap confidence intervals across all loci.
Between groups, FST for Large Mikana and Small Camp (0.012) differs insignificantly from zero according to its 95% bootstrap confidence interval of −0.004 to 0.035. Thus, the two groups are implicated as evolving over evolutionary time as members of a single panmictic population [see also Allen et al., in press].
Pairwise Relatedness Differences
The frequencies of related, unrelated, and ambiguous pairs of adult females and/or males are summarized in Table III for Large Mikana and Small Camp. Between 71% and 80% of all individual pairs in the two groups are ambiguous as they cannot be resolved as either related or unrelated given the available microsatellite data. Nevertheless, the different frequencies of resolved female/female and male/male pairs document that a reduced level of female relatedness exists in Large Mikana. Thirty five percent of all resolved female/female pairs in Small Camp (18 out of 51) are related. Conversely, no related female/female pairs (0/13) are found in Large Mikana. This frequency difference would be significant (Fisher’s exact test, two-tailed) if not for the lack of independence among the multiple pairs of females. In turn, 40% of all resolved male/male pairs (6/15) are related in Small Camp. However, this frequency is not that much greater than that for Large Mikana males (35%, 9/26), and thereby, would not be significant (Fisher’s exact test, two-tailed). These different frequencies for the resolved pairs of females and males in the two groups support a pattern of less structure in Large Mikana, primarily because of less female relatedness.
Table III.
Frequencies of Related, Unrelated, and Ambiguous Pairs of Adult Females and/or Males in Large Mikana and Small Camp
| Group | Pairs | Related | Unrelated | Ambiguous | Totals |
|---|---|---|---|---|---|
| Large Mikana | Female/female | 0 (0.00)* | 13 (0.20)* | 53 (0.80) | 66 |
| Female/male | 8 (0.05) | 33 (0.20) | 127 (0.75) | 168 | |
| Male/male | 9 (0.10)** | 17 (0.19)** | 65 (0.71) | 91 | |
| Totals | 17 (0.05) | 63 (0.20) | 245 (0.75) | 325 | |
| Small Camp | Female/female | 18 (0.07)* | 33 (0.13)* | 202 (0.80) | 253 |
| Female/male | 19 (0.07) | 47 (0.17) | 210 (0.76) | 276 | |
| Male/male | 6 (0.09)** | 9 (0.14)** | 51 (0.77) | 66 | |
| Totals | 43 (0.07) | 89 (0.15) | 463 (0.78) | 595 |
Proportions are given for each row in parentheses.
The single and double asterisks mark the two sets of related and unrelated female/female and male/male frequencies, respectively, which are highlighted in the text.
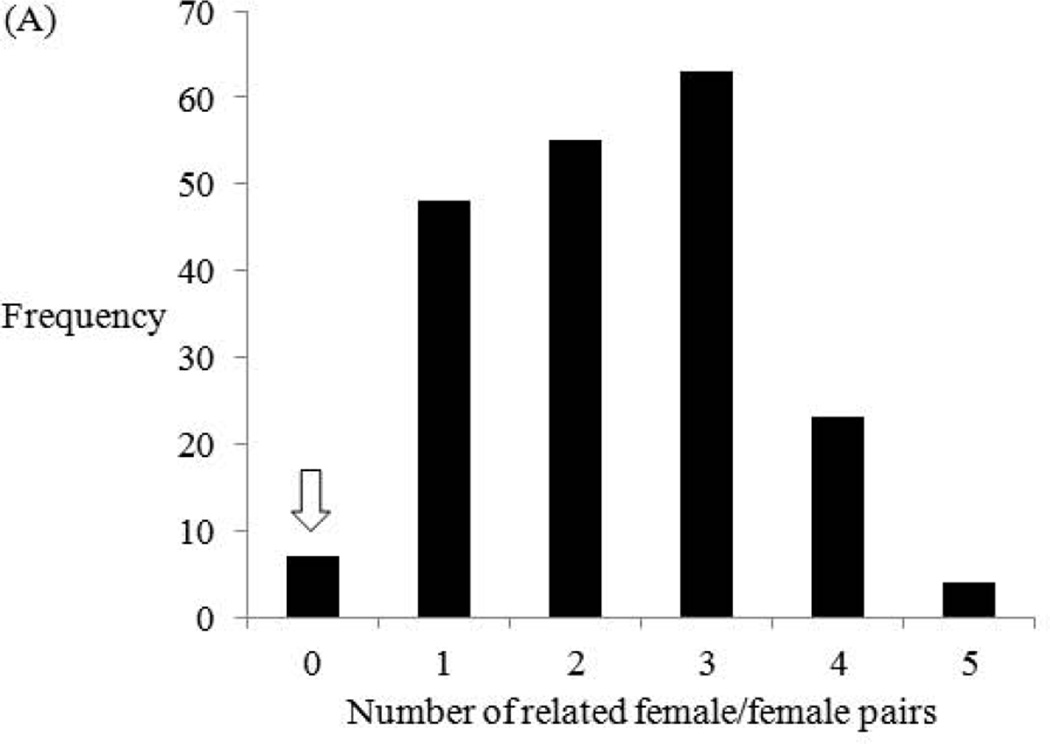
The frequency histogram for the delete-d jackknifing with ML-RELATE shows that the lowest recorded number of related female/female pairs among the Small Camp subsamples is zero (Fig. 2A). This minimum count is represented by seven (3.5%) of the 200 subsamples. The observed number of related female/female pairs in the full Large Mikana dataset is also zero (Table III). The lack of any related female/female pairs in the Large Mikana sample is significant at P = 0.035. This significance exists despite the subsampling of Small Camp females, which corrects for the disproportionate female sampling of the two groups at the time of their sample collections. It verifies that the ML-RELATE evidence for reduced female relatedness in Large Mikana is real and not an artifact of sampling bias.
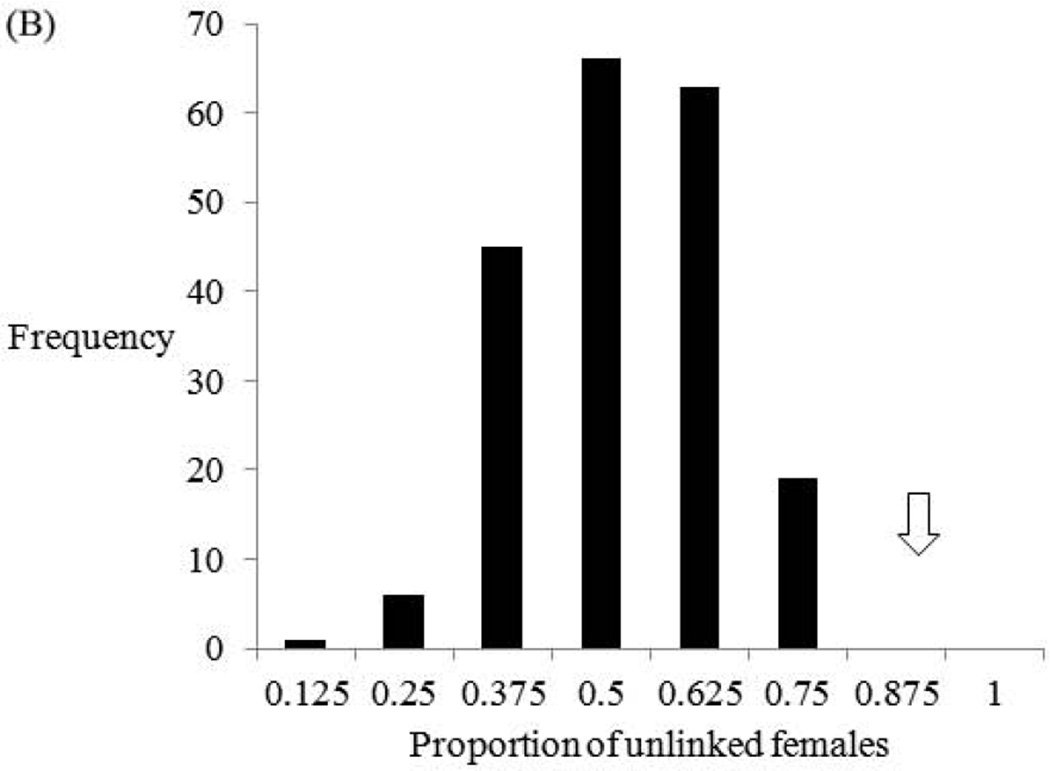
Fig. 2.
Frequency histograms summarizing the results of the delete-d jackknife tests with ML-RELATE (A) and FRANz (B). Each jackknife test is based on 200 random subsamples of the 23 adult females of Small Camp. Specifically, each subsample is derived from the random retention of eight of the 23 females in the complete Small Camp sample. In (A), the test statistic is the number of related female/female pairs for their matrix. In (B), it is the proportion of unlinked females in the ML pedigree for their dataset. Arrows mark the observed estimates of these two test statistics for the 12 adult females of the full Large Mikana sample (Fig. 3A, Tables III and IV).
Multi-generation Pedigree Differences
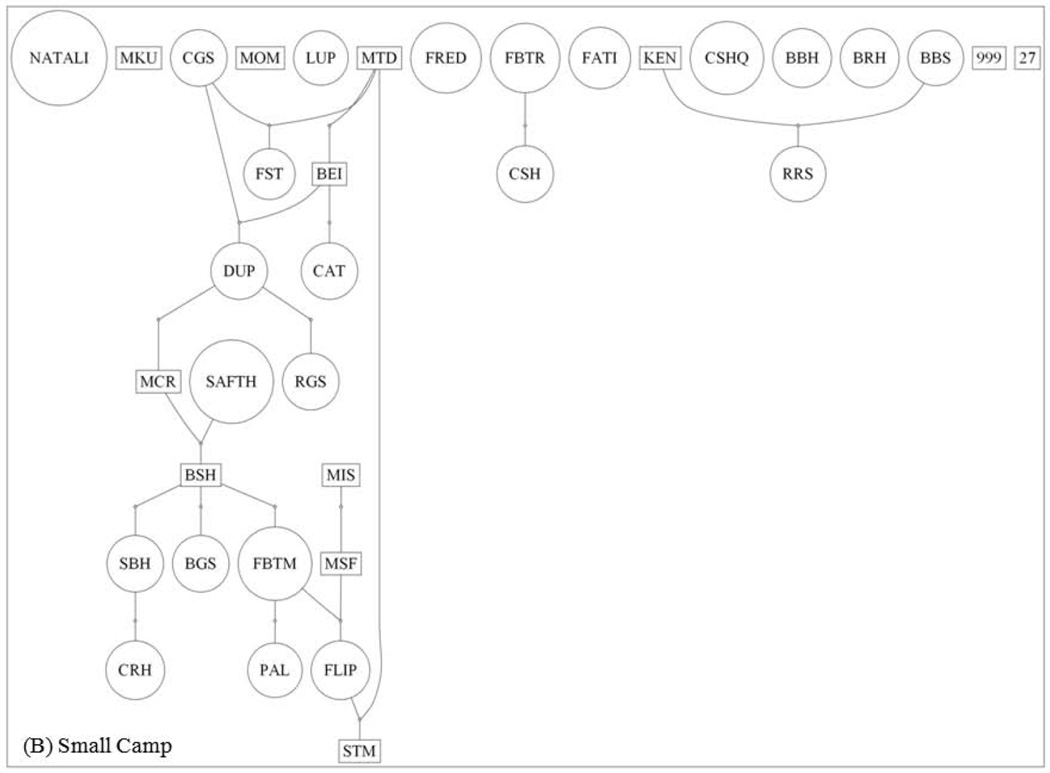
The ML pedigree for Large Mikana is less structured than that for Small Camp (Fig. 3). The Large Mikana pedigree extends up to five generations, includes six links, and is associated with a connection index of 0.23. Conversely, the Small Camp pedigree extends up to eight generations, contains 23 links, and is associated with a connection index of 0.66. More than twice as many individuals in the Large Mikana pedigree (69%) are unlinked as in that for Small Camp (31%; Table IV). The higher frequency of unlinked individuals in the Large Mikana pedigree is significant (binomial test, P < 0.001).
Fig. 3.
Maximum likelihood pedigrees for the adults of Large Mikana (A) and Small Camp (B). Males are represented by rectangles, whereas females are designated by circles. The numbers of breeding males and females are 20 and 50 for Large Mikana, respectively. These numbers are 10 and 25 for Small Camp.
Table IV.
Frequencies of Linked and Unlinked Adult Females and Males in the ML Pedigrees of Large Mikana and Small Camp (Fig. 3)
| Group | Sex | Linked individuals | Unlinked individuals | Totals |
|---|---|---|---|---|
| Large Mikana | Females | 1 (0.08) | 11 (0.92) | 12 |
| Males | 7 (0.50) | 7 (0.50) | 14 | |
| Both | 8 (0.31) | 18 (0.69) | 26 | |
| Small Camp | Females | 16 (0.70) | 7 (0.30) | 23 |
| Males | 8 (0.67) | 4 (0.33) | 12 | |
| Both | 24 (0.69) | 11 (0.31) | 35 |
Proportions are given for each row in parentheses.
The reduced structure of the Large Mikana pedigree is most evident for females (Table IV). The frequency of unlinked females in the Large Mikana pedigree (92%) is more than three times greater than that for Small Camp (30%). This higher frequency of unlinked Large Mikana females is significant (P < 0.001). Conversely, the frequency of unlinked males in the Large Mikana pedigree (50%) is not that much greater than that for Small Camp (33%). This higher frequency of unlinked Large Mikana males is not significant (P = 0.143).
None of the six and 23 links in the Large Mikana and Small Camp pedigrees is supported by a posterior probability of ≥0.95 (results not shown). Conversely, the 11 tests of stability and the delete-d jackknifing with FRANz indicate that the conclusion of a less structured pedigree for Large Mikana is robust. In the stability tests, the structure of the Large Mikana pedigrees decreases with an increase in the numbers of breeding males and females (tests A–C and the actual run; Table I). In turn, the structure of the ML pedigrees for both Large Mikana and Small Camp increases with the typing error rate (tests F–K and the two actual runs). Importantly, the tests with higher rates of typing errors for Small Camp (I–K) document that its ML pedigree for the actual run is conservative. In short, regardless of which conditions are used, the Large Mikana pedigrees remain less structured than that of the conservative actual run for Small Camp (Table I). The “worst case” scenario occurs when the typing error rate is set for Large Mikana to either 0.10 or 0.15. However, even then, the connection index for Large Mikana (0.31) remains less than half of that for the conservative actual estimate of 0.66 for Small Camp.
The frequency histogram for the delete-d jackknifing with FRANz shows that the highest recorded proportion of unlinked adult females among the 200 Small Camp subsamples is 0.750 (Fig. 2B). This highest estimate is represented by 19 (9.5%) of the 200 subsamples. Conversely, the observed proportion of unlinked females in Large Mikana (0.92) is greater than that for all 200 Small Camp subsamples (Fig. 3A, Table IV). The delete-d jackknifing test with FRANz is significant at P < 0.005. Once again, this significance documents that the FRANz support for reduced female relatedness in Large Mikana is real and not contingent on the original samples of the two groups.
DISCUSSION
Congruent Results for Reduced Genetic Structure in Large Mikana
The microsatellite data demonstrate that less genealogical structure exists in Large Mikana than in Small Camp, primarily because of reduced female relatedness in the bigger group. This conclusion in favor of lower relatedness in Large Mikana is corroborated by multiple lines of evidence including the ML-RELATE analyses (Table III), the actual FRANz runs (Fig. 3, Table IV), the FRANz stability tests (Table I), and the delete-d jackknifing of Small Camp females (Fig. 2).
The lack of formal statistical support from the FRANz posterior probabilities is attributable in large part to the absence of detailed age data, which are important for the assignment of parent/offspring directionality to the pedigree links [Riester et al., 2009]. It may also be due to the absence of significant full sibs, which help to narrow down the search for parentages [Wang, 2007]. In particular, the lack of formal statistical support due to the absence of specific age data may help to explain the unexpected deep depth of the ML pedigree for Small Camp, which spans eight generations (Fig. 3B). Given that the minimum breeding age for red colobus is four, the deep pedigree for Small Camp requires that male MTD of generation one is at least 32 years old, which would make him older than the known maximum age of ~30 years for this species [Struhsaker, 2010]. However, our age data for the individuals of the pedigree are limited to designations of “adult.” Thus, in the absence of more detailed age data, it remains possible that MTD is the son (rather than father) of male BEI, which would thereby reduce the depth of the Small Camp pedigree by one generation. An analogous (albeit more complicated) argument can also be made for male STM, who is the sole representative of generation eight. These possible reversals in link directionality and their corresponding reductions in pedigree depth serve as an important reminder that detailed age data are always of value for inferring relatedness.
FRANz remains a relatively new approach that has not been extensively tested with either simulated or real datasets [Riester et al., 2009, 2010]. Thus, its congruent results with those of ML-RELATE are important, because they offer support for its utility. Unlike other approaches that focus on individual pairs, FRANz collectively treats the sampled individuals of a group as potential members of a large extended family that can span three or more generations. This ability to treat the sampled individuals more broadly is of particular interest to species like the red colobus, which has overlapping generations, begins breeding between ages four and five, and can live upwards of 30 years [Struhsaker, 2010]. On the basis of its congruence with ML-RELATE and its more realistic handling of individuals, we recommend the use of FRANz for the estimation of relatedness. However, we also acknowledge that more testing of FRANz is now needed to verify its utility and present both analyses to facilitate comparisons with other studies.
Genetic Structure, Female Dispersal, and Group Size
Our microsatellite DNA data support a lower level of female (but not male) relatedness in Large Mikana, which may be attributed to a greater frequency of female-biased dispersal within this bigger group. Thus, our genetic results support previous field studies suggesting female-biased dispersal by red colobus that were based primarily on individual disappearances and immigration into study groups [Marsh, 1979; Struhsaker, 2010; C.A. Chapman, unpublished data]. Interestingly, the level of bias towards female dispersal seems to be dependent on group size, although further longitudinal investigations or studies of additional groups are needed to verify the generalizability of this finding. This may help explain the large variety of dispersal systems previously proposed for red colobus; much of this variation may have been due to studying groups of different sizes. This apparent plasticity in social systems is intriguing, and when coupled with decades of field research [Chapman et al., 2010a, b; Struhsaker, 2010], supports the hypothesis that group size and dispersal are inter-related, which suggests links between ecological processes and social systems. Sociological models previously proposed for primates [Isbell & Young, 2002; Koenig, 2002; Snaith & Chapman, 2007; Sterck et al., 1997; Wrangham, 1980] have generally viewed the social system of a species as a somewhat fixed characteristic that is shared by all individuals of the species or even genus and that is largely conserved among related evolutionary lineages (i.e., it exhibits phylogenetic inertia) [Chapman & Rothman, 2009; Struhsaker, 1969]. The current study suggests that at least one fundamental characteristic of social systems, which individuals disperse when they reach sexual maturity, is plastic and depends on the group size and possibly the nature of competition experienced within these groups [Chapman & Rothman, 2009]. This suggests that socioecological models that have been quite successful at explaining differences in social systems between species and genera will be applicable to understanding the sociological variation within species as well [Chapman & Rothman, 2009; Hohmann & Fruth, 2003; Nakagawa, 2008; Pochron & Wright, 2003; Sinha et al., 2005]. This may have major implications for understanding the evolution of primate social systems and incorporating within-species variation is becoming an increasingly important aspect of comparative analyses [Felsenstein, 2008; Ives et al., 2007; Stone et al., 2011].
Several studies have documented within-species variation in the behavior of red colobus. Snaith & Chapman [2008] observed several groups in Kibale and demonstrated that home ranges, daily travel distances, and group spread increase, while reproductive success decreases, with increasing group size. Similarly, a longitudinal analysis of the behavioral patterns of Small Camp demonstrated that as the group increased in size by over 70%, its dietary diversity and traveling duration increased, while time for feeding decreased [Gogarten et al., in review: a]. All of these trends indicate increasing levels of scramble competition with larger group size [Snaith & Chapman, 2005; Gogarten et al., in review: b]. In turn, other field studies of red colobus have suggested that male aggression towards females and their infants (including infanticide) can drive female dispersal [Lawson Handley & Perrin, 2007; Marsh, 1979; Struhsaker & Leland, 1987], but these are typically very rare events that are difficult to quantify. Our microsatellite DNA evidence suggests that females are more likely to disperse from their natal units at larger group sizes, thereby providing further support for a link among group size, competition, behavior, and the genetic structure of groups.
The rarity of dispersal events and the inability to exclude death as a possibility for individuals who disappear from a group makes studying these transfers extremely difficult. Our study joins several others [Di Fiore, 2003; Di Fiore et al., 2009; Hammond et al., 2006; Melnick & Hoelzer, 1992] in demonstrating the value of genetic approaches in understanding primate social systems. However, there are a number of other potential confounding factors that might influence differences in dispersal patterns between groups, such as the two studied here. For example, studying dispersal could be influenced by habituation, as unhabituated individuals may be less likely to join a group with human observers. We view this as an unlikely explanation for the observed results, because individuals who immigrated habituated rapidly in the presence of conspecifics that did not react to human observers and there was ample opportunity to immigrate while investigators were not with the study group. In addition, by studying the genetics of adult individuals in the group and the long lived nature of red colobus, we are able to observe the genetic legacy of immigration and dispersal that happened prior to habituation. We hope that future studies will be able to use these genetic methods to conclusively test the socioecological model and to compare rates of dispersal across a range of group sizes to examine plasticity in these vital demographic characteristics.
One excellent opportunity to test the generalizability of our result is the recent expansions of Small Camp, which has now grown to over 104 individuals (Fig. 1), thereby making it nearly as big as Large Mikana was in the current study. Future studies may benefit from the collection of new microsatellite data from the current members of both groups. We predict that updated microsatellite data will reveal a new level of relatedness in Small Camp, similar to that of Large Mikana, as the former is now much closer in size to that of this bigger group. Thus, we expect that its levels of scramble competition, male aggression, female dispersal, and relatedness will all have converged onto those of Large Mikana.
Given the recent increases in red colobus group sizes that have been documented throughout Kibale [Gogarten et al., in review: b], the current study suggests that there may be park-wide changes in the genetic structure of the groups. These changes may positively impact the population viability of this endangered species [Frankham et al., 2009; Ouborg et al., 2010]. Increases in female dispersal due to increased group size will result in the greater spread of alleles across groups, thereby enhancing the genetic diversity of the entire population. Such genetic variability has been implicated in the evolvability of populations, particularly in the face of changing environments, which are currently threatening primates globally [Chapman & Gogarten, 2012]. Increasing group sizes also lead to changes in behavior, which will have cascading effects on disease dynamics, diets, and more, thereby further necessitating standing genetic variation if this population is to survive and adapt [Gogarten et al., in review: a]. Understanding the interactions among changing group sizes, behavior, ecology, and genetics represents an important avenue of future research that will have major management and conservation implications.
ACKNOWLEDGMENTS
This research was partly supported by awards from the NSERC and CRC and by a grant from NIH (TW009237), which is part of the joint NIH-NSF Ecology of Infectious Disease Program and the UK Economic and Social Research Council. J.F.G. was supported by a Graduate Research Fellowship from NSF (Grant Number NSF 11-582) and the Canadian Institutes of Health Research’s Systems Biology Training Program. All procedures were approved by the McGill Animal Care Committee, Ugandan Wildlife Authority, and the Uganda Council of Science and Technology. We thank the Ugandan Field Assistants for their untiring work with the red colobus groups, T. Goldberg for his help with the darting program and individual identifications, M. Riester for his assistance with FRANz2.0.0, D. Reddig for his support with the computer analyses, and C.A. Baer, J.G. Burleigh, and M.R. Tennant for their helpful comments about our study.
Contract grant sponsors: NSERC; CRC; NIH; NSF; CIHR.
REFERENCES
- Allen JM, Miyamoto MM, Wu C-H, Carter T, Ungvari-Martin J, Magrini K, Chapman CA. Primate DNA suggests long-term stability of an African rainforest. Ecology and Evolution. doi: 10.1002/ece3.395. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almudevar A. A simulated annealing algorithm for maximum likelihood pedigree reconstruction. Theoretical Population Biology. 2003;63:63–75. doi: 10.1016/s0040-5809(02)00048-5. [DOI] [PubMed] [Google Scholar]
- Blouin MS. DNA-based methods for pedigree reconstruction and kinship analysis in natural populations. Trends in Ecology and Evolution. 2003;18:503–511. [Google Scholar]
- Borries C, Larney E, Lu A, Ossi K, Koenig A. Costs of group size: lower developmental and reproductive rates in larger groups of leaf monkeys. Behavioural Ecology. 2008;19:1186–1194. [Google Scholar]
- Chapman CA, Chapman LJ. Constraints on group size in redtail monkeys and red colobus: Testing the generality of the ecological constraints model. International Journal of Primatology. 2000;21:565–585. [Google Scholar]
- Chapman CA, Chapman LJ, Jacob AL, Rothman JM, Omeja P, Reyna-Hurtado R, Hartter J, Lawes MJ. Tropical tree community shifts: implications for wildlife conservation. Biological Conservation. 2010a;143:366–374. [Google Scholar]
- Chapman CA, Chapman LJ, Naughton-Treves L, Lawes MJ, McDowell LR. Predicting folivorous primate abundance: validation of a nutritional model. American Journal of Primatology. 2004;62:55–69. doi: 10.1002/ajp.20006. [DOI] [PubMed] [Google Scholar]
- Chapman CA, Gogarten JF. Primate conservation: Is the cup half empty or half full? Nature Education Knowledge. 2012;3:7. [Google Scholar]
- Chapman CA, Lambert JE. Habitat alteration and the conservation of African primates: A case study of Kibale National Park, Uganda. American Journal of Primatology. 2000;50:169–186. doi: 10.1002/(SICI)1098-2345(200003)50:3<169::AID-AJP1>3.0.CO;2-P. [DOI] [PubMed] [Google Scholar]
- Chapman CA, Rothman JM. Within-species differences in primate social structure: evolution of plasticity and phylogenetic constraints. Primates. 2009;50:12–22. doi: 10.1007/s10329-008-0123-0. [DOI] [PubMed] [Google Scholar]
- Chapman CA, Struhsaker TT, Skorupa JP, Snaith TV, Rothman JM. Understanding long-term primate community dynamics: implications of forest change. Ecological Applications. 2010b;20:179–191. doi: 10.1890/09-0128.1. [DOI] [PubMed] [Google Scholar]
- Clobert J, Danchin E, Dhondt AA, Nichols JD, editors. Dispersal. Oxford: Oxford University Press; 2001. p. 480. [Google Scholar]
- Di Fiore A. Molecular genetic approaches to the study of primate behavior, social organization, and reproduction. Yearbook of Physical Anthropology. 2003;46:62–99. doi: 10.1002/ajpa.10382. [DOI] [PubMed] [Google Scholar]
- Di Fiore A, Link A, Schmitt CA, Spehar SN. Dispersal patterns in sympatric woolly and spider monkeys: integrating molecular and observational data. Behaviour. 2009;146:437–470. [Google Scholar]
- Felsenstein J. Comparative methods with sampling error and within-species variation: contrasts revisited and revised. American Naturalist. 2008;171:713–725. doi: 10.1086/587525. [DOI] [PubMed] [Google Scholar]
- Frankham R, Ballou JD, Briscoe DA. Introduction to conservation genetics. 2nd edition. Cambridge: Cambridge University Press; 2009. p. 618. [Google Scholar]
- Gogarten JF, Bonnell TR, Campenni M, Wasserman MD, Chapman CA. Increasing group size alters behavior of a folivorous primate. Behavioral Ecology and Sociobiology. In review: a. [Google Scholar]
- Gogarten JF, Jacob AL, Ghai RR, Rothman JM, Twinomugisha D, Wasserman MD, Chapman CA. Causes and consequences of changing group sizes in a primate community over 15+ years: Implications of non-equilibrium states. Oecologia. In review: b. [Google Scholar]
- Goldberg TL, Sintasath DM, Chapman CA, Cameron KM, Karesh WB, Tang S, Wolfe ND, Rwego IB, Ting N, Switzer WM. Coinfection of Ugandan red colobus (Procolobus [Piliocolobus] rufomitratus tephrosceles) with novel, divergent delta-, lenti- and spumaretroviruses. Journal of Virology. 2009;83:11318–11329. doi: 10.1128/JVI.02616-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goudet J. FSTAT (version 1.2): a computer program to calculate F-statistics. Journal of Heredity. 2002;86:485–486. [Google Scholar]
- Greenwood PJ. Mating systems, philopatry and dispersal in birds and mammals. Animal Behaviour. 1980;28:1140–1162. [Google Scholar]
- Hammond RL, Handley LJL, Winney BJ, Bruford MW, Perrin N. Genetic evidence for female-biased dispersal and gene flow in a polygynous primate. Proceedings of the Royal Society B: Biological Sciences. 2006;273:479–484. doi: 10.1098/rspb.2005.3257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick PW. Genetics of populations. 4th edition. Sudbury: Jones and Bartlett Publishers; 2011. p. 675. [Google Scholar]
- Hedrick PW, Kalinowski ST. Inbreeding depression in conservation biology. Annual Review of Ecology and Systematics. 2000;31:139–162. [Google Scholar]
- Hohmann G, Fruth B. Culture in bonobos? Inter-specific similarities and intra-specific variation in behaviour. Current Anthropology. 2003;44:563–571. [Google Scholar]
- Huelsenbeck J, Ronquist F. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics. 2001;17:754–755. doi: 10.1093/bioinformatics/17.8.754. [DOI] [PubMed] [Google Scholar]
- Isbell LA. Contest and scramble competition: patterns of female aggression and ranging behaviour among primates. Behavioural Ecology. 1991;2:143–155. [Google Scholar]
- Isbell LA, Young TP. Ecological models of female social relationships in primates: similarities, disparities and some directions for future clarity. Behaviour. 2002;139:177–202. [Google Scholar]
- Ives RA, Midford PE, Garland T. Within-species variation and measurement error in phylogenetic comparative methods. Systematic Biology. 2007;56:252–270. doi: 10.1080/10635150701313830. [DOI] [PubMed] [Google Scholar]
- Janson CH, Goldsmith ML. Predicting group size in primates: foraging costs and predation risks. Behavioral Ecology. 1995;6:326–336. [Google Scholar]
- Jones AG, Small CM, Paczolt KA, Ratterman NL. A practical guide to methods of parentage analysis. Molecular Ecology Resources. 2010;10:6–30. doi: 10.1111/j.1755-0998.2009.02778.x. [DOI] [PubMed] [Google Scholar]
- Kalinowski ST, Taper ML. Maximum likelihood estimation of the frequency of null alleles at microsatellite loci. Conservation Genetics. 2006;7:991–995. [Google Scholar]
- Kalinowski ST, Taper ML, Marshall TC. Revising how the computer program CERVUS accommodates genotyping error increases success in paternity assignment. Molecular Ecology. 2007;16:1099–1106. doi: 10.1111/j.1365-294X.2007.03089.x. [DOI] [PubMed] [Google Scholar]
- Kalinowski ST, Wagner AP, Taper ML. ML-RELATE: a computer program for maximum likelihood estimation of relatedness and relationship. Molecular Ecology Notes. 2006;6:576–579. [Google Scholar]
- Koenig A. Competition for resources and its behavioral consequences among female primates. International Journal of Primatology. 2002;23:759–783. [Google Scholar]
- Koenig A, Borries C. Feeding competition and infanticide constrain group size in wild hanuman langurs. American Journal of Primatology. 2002;57(Supplement):33–34. [Google Scholar]
- Langergraber KE, Mitani JC, Vigilant L. The limited impact of kinship on cooperation in wild chimpanzees. Proceedings of the National Academy of Sciences USA. 2007;104:7786–7790. doi: 10.1073/pnas.0611449104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawson Handley LJ, Perrin N. Advances in our understanding of mammalian sex-biased dispersal. Molecular Ecology. 2007;16:1559–1578. doi: 10.1111/j.1365-294X.2006.03152.x. [DOI] [PubMed] [Google Scholar]
- Lewis PO, Zaykin D. Genetic Data Analysis: Computer program for the analysis of allelic data. Version 1.0 (d16c) 2001 Available from: http://lewis.eeb.uconn.edu/lewishome/software.html. [Google Scholar]
- Lukas D, Reynolds V, Boesch C, Vigilant L. To what extent does living in a group mean living with kin? Molecular Ecology. 2005;14:2181–2196. doi: 10.1111/j.1365-294X.2005.02560.x. [DOI] [PubMed] [Google Scholar]
- Marsh CW. Female transference and mate choice among Tana River red colobus. Nature. 1979;281:568–569. doi: 10.1038/281568a0. [DOI] [PubMed] [Google Scholar]
- Melnick D, Hoelzer G. Differences in male and female macaque dispersal lead to contrasting distributions of nuclear and mitochondrial DNA variation. International Journal of Primatology. 1992;13:379–393. [Google Scholar]
- Morin PA, Moore JJ, Chakraborty R, Jin L, Goodall J, Woodruff DS. Kin selection, social structure, gene flow, and the evolution of chimpanzees. Science. 1994;265:1193–1201. doi: 10.1126/science.7915048. [DOI] [PubMed] [Google Scholar]
- Nakagawa N. Despotic wild patas monkeys (Erythrocebus patas) in Kala Maloue, Cameroon. American Journal of Primatology. 2008;70:238–246. doi: 10.1002/ajp.20481. [DOI] [PubMed] [Google Scholar]
- Nsubuga AM, Robbins MM, Roeder AD, Morin PA, Boesch C, Vigilant L. Factors affecting the amount of genomic DNA extracted from ape faeces and the identification of an improved sample storage method. Molecular Ecology. 2004;13:2089–2094. doi: 10.1111/j.1365-294X.2004.02207.x. [DOI] [PubMed] [Google Scholar]
- Oates JF. The natural history of African colobines. In: Davies AG, Oates JF, editors. Colobine monkeys: their ecology, behaviour and evolution. Cambridge: Cambridge University Press; 1994. pp. 75–128. [Google Scholar]
- Oates JF, Whitesides GH, Davies AG, Waterman PG, DaSilva GL, Mole S. Determinants of variation in tropical forest primate biomass: New evidence from West Africa. Ecology. 1990;71:328–343. [Google Scholar]
- Ouborg NJ, Pertoldi C, Loeschcke V, Bijlsma R, Hedrick PW. Conservation genetics in transition to conservation genomics. Trends in Genetics. 2010;26:177–187. doi: 10.1016/j.tig.2010.01.001. [DOI] [PubMed] [Google Scholar]
- Pochron ST, Wright PC. Variability in adult group compositions of a prosimian primate. Behavioral Ecology and Sociobiology. 2003;54:285–293. [Google Scholar]
- Pompanon F, Bonin A, Bellemain E, Taberlet P. Genotyping errors: causes, consequences and solutions. Nature Reviews Genetics. 2005;6:847–859. doi: 10.1038/nrg1707. [DOI] [PubMed] [Google Scholar]
- R Development Core Team. R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. 2012 Available from: http://www.R-project.org/. [Google Scholar]
- Rice WR. Analyzing tables of statistical tests. Evolution. 1989;43:223–225. doi: 10.1111/j.1558-5646.1989.tb04220.x. [DOI] [PubMed] [Google Scholar]
- Riester M, Stadler PF, Klemm K. FRANz: reconstruction of wild multi-generation pedigrees. Bioinformatics. 2009;25:2134–2139. doi: 10.1093/bioinformatics/btp064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riester M, Stadler PF, Klemm K. Reconstruction of pedigrees in clonal plant populations. Theoretical Population Biology. 2010;78:109–117. doi: 10.1016/j.tpb.2010.05.002. [DOI] [PubMed] [Google Scholar]
- Riester M, Stadler PF, Klemm K, Cowell R. FRANz, version 2.0.0 documentation. Leipzig: University of Leipzig; 2011. Available from: https://github.com/lima1/franzpedigree/archives/master. [Google Scholar]
- Schuelke M. An economic method for the fluorescent labeling of PCR fragments. A poor man’s approach to genotyping for research and high-throughput diagnostics. Nature Biotechnology. 2000;18:233–234. doi: 10.1038/72708. [DOI] [PubMed] [Google Scholar]
- Shao J, Tu D. The jackknife and bootstrap. New York: Springer Verlag; 1995. p. 516. [Google Scholar]
- Siddall ME. Another monophyly index: Revisiting the jackknife. Cladistics. 1995;11:33–56. doi: 10.1111/j.1096-0031.1995.tb00003.x. [DOI] [PubMed] [Google Scholar]
- Sinha A, Mukhopadhyay K, Data-Roy A, Ram S. Ecology proposes, behaviour disposes: ecological variability in social organization and male behavioural strategies among wild bonnet macaques. Current Science. 2005;89:1166–1179. [Google Scholar]
- Snaith TV, Chapman CA. Towards an ecological solution to the folivore paradox: patch depletion as an indicator of within-group scramble competition in red colobus monkeys (Piliocolobus tephrosceles) Behavioral Ecology and Sociobiology. 2005;59:185–190. [Google Scholar]
- Snaith TV, Chapman CA. Primate group size and interpreting socioecological models: Do folivores really play by different rules? Evolutionary Anthropology. 2007;16:94–106. [Google Scholar]
- Snaith TV, Chapman CA. Red colobus monkeys display alternative behavioural responses to the costs of scramble competition. Behavioural Ecology. 2008;19:1289–1296. [Google Scholar]
- Sterck EHM, Watts DP, van Schaik CP. The evolution of female social relationships in nonhuman primates. Behavioral Ecology and Sociobiology. 1997;41:291–309. [Google Scholar]
- Stone GN, Nee S, Felsenstein J. Controlling for non-independence in comparative analysis of patterns across populations within species. Philosophical Transactions of the Royal Society B: Biological Sciences. 2011;366:1410–1424. doi: 10.1098/rstb.2010.0311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strier KB, Chaves PB, Mendes SL, Fagundes V, Di Fiore A. Low paternity skew and the influence of maternal kin in an equalitarian, patrilocal primate. Proceedings of the National Academy of Sciences USA. 2011;108:18915–18919. doi: 10.1073/pnas.1116737108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Struhsaker TT. Correlates of ecology and social organization among African cercopithecines. Folia Primatologica. 1969;11:80–118. doi: 10.1159/000155259. [DOI] [PubMed] [Google Scholar]
- Struhsaker TT. Conservation of red colobus and their habitats. International Journal of Primatology. 2005;26:525–538. [Google Scholar]
- Struhsaker TT. The red colobus monkey: variation in demography, behavior, and ecology of endangered species. Oxford: Oxford University Press; 2010. p. 376. [Google Scholar]
- Struhsaker TT, Leland L. Infanticide in a patrilineal society of red colobus monkeys. Zeitschrift fur Tierpsychologie. 1985;69:89–132. [Google Scholar]
- Struhsaker TT, Leland L. Colobines: infanticide by adult males. In: Smuts BB, Cheney DL, Seyfarth RM, Wrangham RW, Struhsaker TT, editors. Primate societies. Chicago: University of Chicago Press; 1987. pp. 83–97. [Google Scholar]
- Tombak KJ, Reid AJ, Chapman CA, Rothman JM, Johnson CA, Reyna-Hurtado R. Patch depletion behavior differs between sympatric folivorous primates. Primates. 2012;53:57–64. doi: 10.1007/s10329-011-0274-2. [DOI] [PubMed] [Google Scholar]
- van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P. MICRO-CHECKER: Software for identifying and correcting genotyping errors in microsatellite data. Molecular Ecology Notes. 2004;4:535–538. [Google Scholar]
- van Schaik CP. The ecology of social relationships amongst female primates. In: Standen V, Foley RA, editors. Comparative socioecology: The behavioural ecology of humans and other mammals. Boston: Blackwell Scientific Publications; 1989. pp. 195–218. [Google Scholar]
- van Schaik CP, van Hooff JARAM. On the ultimate causes of primate social systems. Behaviour. 1983;85:91–117. [Google Scholar]
- Wagner AP, Creel S, Kalinowski ST. Estimating relatedness and relationships using microsatellite loci with null alleles. Heredity. 2006;97:336–345. doi: 10.1038/sj.hdy.6800865. [DOI] [PubMed] [Google Scholar]
- Wang J. Parentage and sibship exclusions: higher statistical power with more family members. Heredity. 2007;99:205–217. doi: 10.1038/sj.hdy.6800984. [DOI] [PubMed] [Google Scholar]
- Wood SN. Fast stable restricted maximum likelihood and marginal likelihood estimation of semiparametric generalized linear models. Journal of the Royal Statistical Society B. 2011;73:3–36. [Google Scholar]
- Wrangham RW. On the evolution of ape social systems. Social Science Information. 1979;3:335–368. [Google Scholar]
- Wrangham RW. An ecological model of female-bonded primate groups. Behaviour. 1980;75:262–300. [Google Scholar]
- Yeh FC, Boyle TJB. Population genetic analysis of co-dominant and dominant markers and quantitative traits. Belgian Journal of Botany. 1997;129:157. [Google Scholar]
- Zuur AF, Ieno EN, Walker NJ, Saveliev AA, Smith GM. Mixed effects models and extensions in ecology with R. New York: Springer; 2009. p. 574. [Google Scholar]