Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2014 Feb 1.
Published in final edited form as: Clin Biomech (Bristol). 2012 Dec 6;28(2):157–163. doi: 10.1016/j.clinbiomech.2012.11.004

Changes in the Flexor Digitorum Profundus Tendon Geometry in the Carpal Tunnel Due to Force Production and Posture of Metacarpophalangeal Joint of the Index Finger: an MRI Study

Joel R Martin 1, Florent Paclet 1, Mark L Latash 1, Vladimir M Zatsiorsky 1
PMCID: PMC3609902  NIHMSID: NIHMS421503  PMID: 23219762

Abstract

Background

Carpal tunnel syndrome is a disorder caused by increased pressure in the carpal tunnel associated with repetitive, stereotypical finger actions. Little is known about in vivo geometrical changes in the carpal tunnel caused by motion at the finger joints and exerting a fingertip force.

Methods

The hands and forearms of five subjects were scanned using a 3.0T magnetic resonance imaging scanner. The metacarpophalangeal joint of the index finger was placed in: flexion, neutral and extension. For each joint posture subjects either produced no active force (passive condition) or exerted a flexion force to resist a load (~4.0 N) at the fingertip (active condition). Changes in the radii of curvature, position and transverse plane area of the flexor digitorum profundus tendons at the carpal tunnel level were measured.

Results

The radius of curvature of the flexor digitorum profundus tendons, at the carpal tunnel level, was significantly affected by posture of the index finger metacarpophalangeal joint (p<0.05) and the radii was significantly different between fingers (p<0.05). Actively producing force caused a significant shift (p<0.05) in the flexor digitorum profundus tendons in the ventral (palmar) direction. No significant change in the area of an ellipse containing the flexor digitorum profundus tendons was observed between conditions.

Interpretation

The results show that relatively small changes in the posture and force production of a single finger can lead to significant changes in the geometry of all the flexor digitorum profundus tendons in the carpal tunnel. Additionally, voluntary force production at the fingertip increases the moment arm of the FDP tendons about the wrist joint.

Keywords: MRI, carpal tunnel syndrome, moment arm, flexor digitorum profundus

1. Introduction

During finger actions like in grasping, typing or pressing tasks, fingertip forces result mainly from changes in the activation of the extrinsic muscles of the hand (Gonzalez et al., 2005; Goodman & Choueka, 2005). The extrinsic muscles are multi-joints muscles that span the distal interphalangeal (DIP), proximal interphalangeal (PIP), metacarpophalangeal (MCP) and wrist joints. A better understanding of the mechanics of the tendons at the wrist joint is important for understanding the hand and fingers functioning.

Several studies on the effects of joint position on the tendons geometry at the wrist joint have been performed without applying a force to the tendons (Brand & Hollister, 1999; Chao et al., 1989) and with artificial load or springs simulating active force (An et al., 1983; Armstrong & Chaffin, 1978; Brand et al., 1975; Youm et al., 1978). Very few authors have investigated the in-vivo tendon behavior under varying joint angles and muscle contractions (Keir & Wells, 1999; Martin et al, 2011). It was previously documented that the paths of the extrinsic flexor tendons about a joint change due to change in position of that joint and activation level of that muscle (Keir & Wells, 1999; Martin et al., 2011).

The purpose of this study has been to measure changes in the paths of the flexor digitorum profundus (FDP) at the carpal tunnel level due to changes in: (1) position of the MCP joint of the index finger and (2) force produced by the index finger. Based on the study by Keir & Wells (1999) we expect that we will observe changes in the tendon paths qualitatively similar to those reported in that study. Whether or not the magnitudes of the changes will be comparable is unknown.

2. Methods

2.1. Subjects

Five male subjects volunteered for the study. The subjects were young and reported no history of musculoskeletal injury or disease of the upper limbs. The average (standard deviation) age, mass, and height of the subjects were 21.8 (2.2) years, 71.7 (8.3) kg, and 179.9 (9.0) cm, respectively. None of the subjects had a history of long-term involvement in hand or finger activities such as professional typing or playing musical instruments. The subjects gave informed consent according to the procedures approved by the Institutional Review Board of the Pennsylvania State University.

2.2. Experimental Procedure

Prior to the MRI scan several anthropometric measures were taken from the subjects (Table 1). Hand length was measured from the most distal crease at the wrist to the tip of the longest finger. Hand breadth was measured on the palmar surface at the level of the MCP joints of fingers 2-5 with the fingers in a relaxed state of ab/adduction (i.e. subjects were instructed not to actively abduct or adduct their fingers). Measurements of the finger dimensions were taken on the dorsal surface. Phalanx lengths were measured from the approximate joint centers, based on visual inspection. Phalange circumferences were measured around the approximate midpoint of each phalange. Individual and four-finger flexion maximum voluntary contraction (MVC) forces were recorded. Subjects placed their four fingers on unidimensional force transducers (208C02, PCB Piezotronics, Depew, NY, USA) and were instructed to press as hard as they could for five seconds. During the MVC trials the MCP, proximal interphalangeal and distal interphalangeal joints were all in slight flexion (~10-20°). Although, this configuration is slightly different than that used in the MRI scans the force production capability of the fingers should not have been significantly altered. Pilot tests were performed to verify this (data not reported). The MVC was taken as the peak force produced during each trial. Two trials of each MVC were recorded and the average computed.

Table 1.

Anthropometric and maximum voluntary contraction (MVC) measurements taken on subjects. The values reported are: mean (standard deviation).

Hand Measurements
Hand Length (cm) 19.2 (1.0)
Hand Breadth (cm) 8.7 (0.7)
Wrist Circumference (cm) 16.7 (0.7)
Four-finger MVC (N) 67.0 (12.5)
Finger Measurements
I M R L
Total Length (cm) 9.9 (0.7) 10.9 (0.4) 10.2 (0.8) 8.2 (0.7)
Proximal Phalangeal Length (cm) 4.9 (0.4) 5.3 (0.2) 4.8 (0.6) 4.0 (0.5)
Middle Phalangeal Length (cm) 2.7 (0.2) 3.1 (0.3) 3.2 (0.5) 2.5 (0.4)
Distal Phalangeal Length (cm) 2.4 (0.2) 2.5 (0.2) 2.5 (0.2) 2.3 (0.3)
Proximal Phalangeal Circumference (cm) 6.5 (0.3) 6.4 (0.3) 6.2 (0.3) 5.4 (0.3)
Middle Phalangeal Circumference (cm) 5.7 (0.1) 5.8 (0.2) 5.5 (0.3) 4.8 (0.2)
Distal Phalangeal Circumference (cm) 5.2 (0.2) 5.3 (0.2) 4.9 (0.1) 4.5 (0.1)
MVC (N) 33.8 (7.9) 26.9 (5.1) 22.7 (8.3) 18.2 (4.9)
Open in a new tab

2.3. MRI Equipment and Scans

The MRI scans were performed using a 3.0 Tesla MRI scanner (Siemens Magnetom Trio 3T, Siemens Corporation, Germany) at the Social, Life, and Engineering Imaging Center (SLEIC) facility of the Pennsylvania State University by a trained MRI technician. Subjects were required to lay prone on the scanning table with their right arm extended above their head. Three index finger MCP joint positions and two force production conditions per position comprised the experimental conditions. The index finger was in the following MCP joint postures: 1) neutral (0°), 2) flexed (30° of flexion), and 3) extended (15° of extension). A custom-made device, consisting of a moveable platform to support the index finger and a flat platform support for the non-index fingers, was used to place the index finger in each of the positions (Fig. 1). The distal interphalangeal (DIP), proximal interphalangeal (PIP), and metacarpophalangeal (MCP) joint postures of the non-index fingers was neutral (0°) for all scans. There were six conditions in total: 1) passive-extension (PE), 2) passive-neutral (PN), 3) passive-flexion (PF), 4) active-extension (AE), 5) active-neutral (AN), and 6) active-flexion (AF). The middle, ring, and little fingers were lightly taped together so that their posture did not change during the scans.

Figure 1.

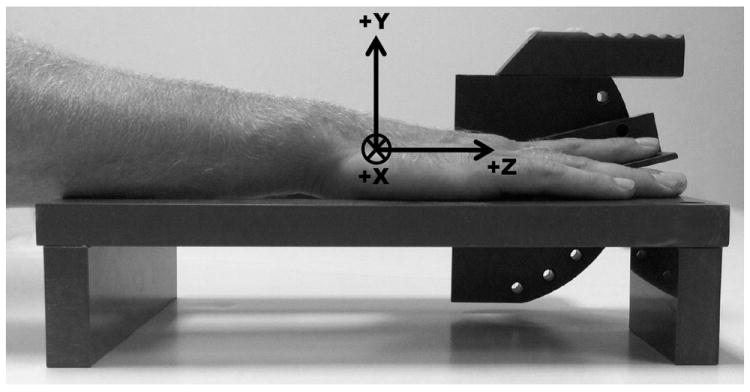
Figure 1

Open in a new tab

Schematic of device used to position index finger during MRI scans. Included is the coordinate system of the hand/forearm using the hook of hamate as the origin. The Z-axis was aligned with the longitudinal axis of the forearm with the proximal to distal direction being positive. The Y-axis was orientated in the anterior to posterior (positive) direction and the X-axis was oriented in the lateral to medial (positive) direction.

During the MRI scans the “passive” condition scan was performed first followed by the “active” condition scan for each index finger MCP joint position. After the passive scan subjects were removed from the scanner and a 400 g mass was hung from the apparatus then looped around their index fingertip. The suspended load generated a vertical force that produced an extension moment about the MCP joint. To resist the load, subjects had to produce a small active flexion force with their index finger. It was necessary to use a low amount of resistive force (10-15% MVC) since subjects were required to maintain the contraction for several minutes. This procedure was repeated until scans had been obtained for each of the three MCP postures (Fig. 2). The order of the scans was the following: 1) neutral, 2) flexion and 3) extension MCP postures. Two minutes of rest were given after completion of the active flexion force scans. The entire time to collect all of the scans was less than one hour.

Figure 2.

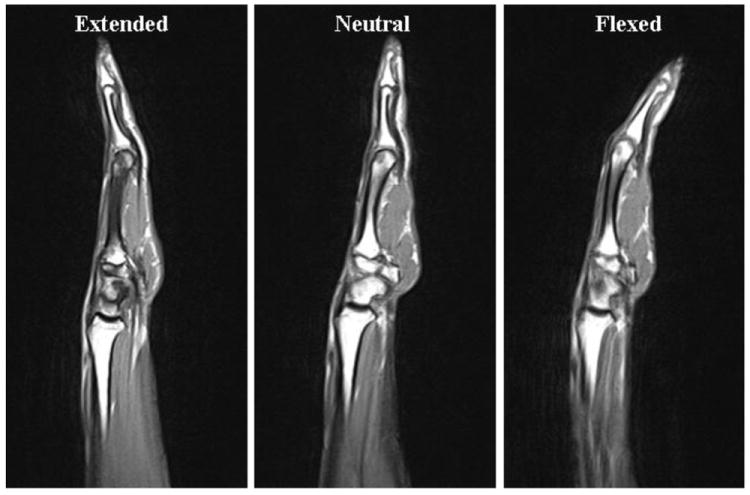
Figure 2

Open in a new tab

Sagittal plane scans from a single subject illustrating the index finger MCP configuration for the extended, neutral, and flexed positions.

For each combination of force level and index finger MCP posture, a localization and a T1 weighted 2D sagittal scans were taken (the localization scan is an initial scan in which the field of view of the MRI scanner is aligned with the anatomy of the subject). The time required for the localization and 2D axial scans was 0:51 and 1:16 min, respectively. The voxel size of these images was 0.8 × 0.8 × 7.0 mm (width × height × slice thickness). Using this slice thickness (7.0 mm), 45 slices were sufficient to scan the forearm and hand of all subjects. The TR (repetition time) and TE (echo time) values were 700 ms and 7.6 ms, respectively. The flip angle was 150°. Multiple pilot tests were performed to optimize the scan quality while minimizing the scan time. Reduction of scan time was important as longer times caused subjects to become fatigued during the active pressing scans and uncomfortable since they were instructed not to move during the scans. Fatigue and discomfort both could potentially lead to movements by the subjects, which would decreased the scan image quality.

2.4. Image Analysis

The paths of the tendons were obtained by manually digitizing the centroid of each finger’s tendon in the axial slices (transverse plane). A coordinate system was established in which the hook of hamate was the origin. The Z-axis was aligned with the longitudinal axis of the forearm with the proximal to distal direction being positive. The Y-axis was orientated in the anterior to posterior (positive) direction and the X-axis was oriented in the lateral to medial (positive) direction. The procedure was the following: (1) the slice in which the hook of hamate (HH) could be most clearly identified (Fig. 3A) was obtained and then (2) the image sequence was advanced six slices in the distal direction (42.0 mm = 6 slices × 7.0 mm/slice). At this level the FDP tendons of each finger were clearly identifiable. (3) A mouse cursor was placed over the centroid of each tendon and the X, Y, Z coordinates were recorded. (4) The image sequence was advanced one slice in the proximal direction and the X, Y, Z coordinates of the centroid of each tendon were recorded. (5) This was repeated until a total of ten slices were recorded (last slice was three slices proximal to the HH slice). (6) The X, Y, Z coordinates of the tip of the HH in the HH slice were recorded and used as the origin of the coordinate system of the hand (Fig. 3B). The steps 1-6 were repeated twice, by the same person, and the coordinates were averaged to minimize errors due to noise related to selecting the centroid of each tendon. The digitizing was performed using OsiriX software (Rosset et al. 2004).

Figure 3.

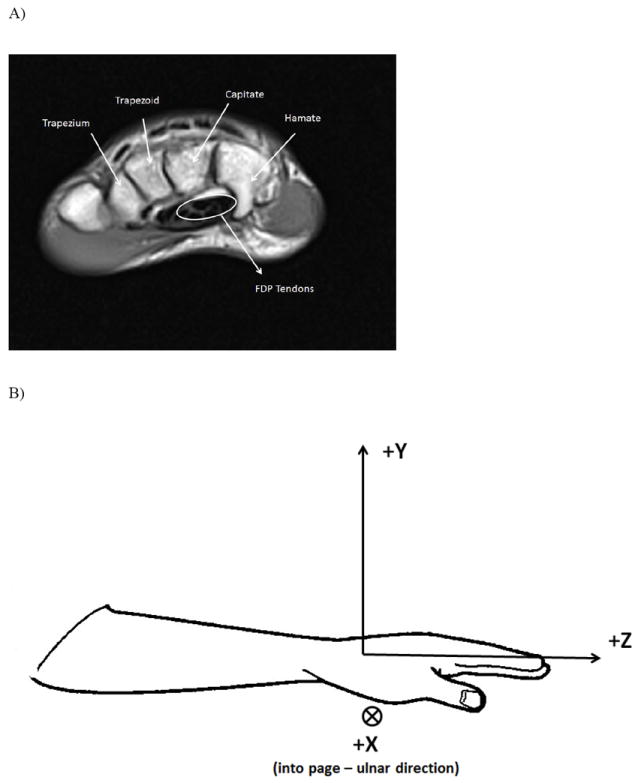
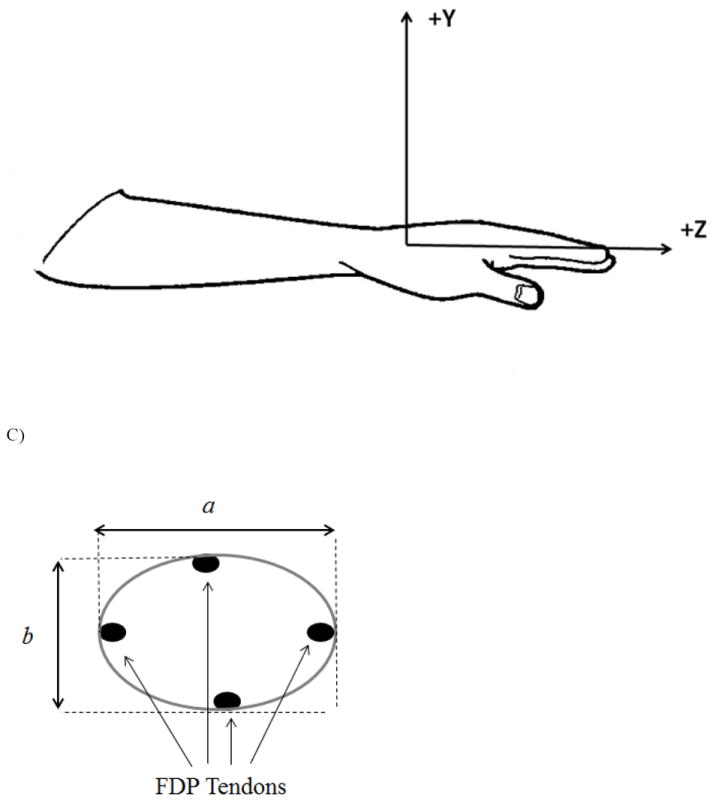
Figure 3

Figure 3

Open in a new tab

A) Slice at the hook of hamate level. The flexor digitorum profundus tendons are bundled close to the hamate and capitate bones. B) Coordinate system of the hand/forearm using the hook of hamate as the origin. The Z-axis was aligned with the longitudinal axis of the forearm with the proximal to distal direction being positive. The Y-axis was orientated in the anterior to posterior (positive) direction and the X-axis was oriented in the lateral to medial (positive) direction. C) Schematic of the computation of the ellipse area of the four FDP tendons. The major axis, a, corresponded to the maximum and minimum location of the tendons in the x-direction (medial-lateral). The minor axis, b, corresponded to the maximum and minimum location of the tendons in the y-direction (anterior-posterior).

2.5. Data Analysis

There were three measures of interest: (1) the area of a cross-sectional ellipse containing the four FDP tendons, (2) the radius of curvature of the FDP tendons in the Y-Z plane (i.e. sagittal plane) and (3) the Y-direction (i.e. ventral-dorsal direction) shift of the tendons relative to the PN condition. The ellipse area was computed using the following formula:

Area=π×(a2)×(b2) (1)

where a was the maximum X-coordinate minus the minimum X-coordinate of the four tendons and b was the maximum Y-coordinate minus the minimum Y-coordinate of the four tendons (Fig. 3C). The radius of curvature in the Y-Z plane was computed by using a least mean squares algorithm to fit a circle to data points. The Y- and Z-coordinates of each tendon for the middle eight slices (first and last slice were not used) of digitized tendon coordinates were used to fit the circle. The radius of curvature was equal to 1/radius of the circle. The shift in the Y-coordinate of the tendons for each of the conditions compared to the PN condition was computed by subtracting the Y-coordinate of the PN condition from each of the other conditions.

2.6. Statistical Analysis

Despite only obtaining data from five subjects statistical tests were performed. We ask that readers keep this fact in mind when interpreting p-values reported in the results section. Three repeated measure (RM) ANOVAs were performed. One was performed to examine the ellipse area (FORCE×POSTURE), another for the radius of tendon curvature (FORCE×POSTURE×FINGER) and the last one for the tendon shift (FORCE×POSTURE×FINGER). For each RM ANOVA the factor FORCE has two levels (active, passive), the factor POSTURE has three levels (flexion, neutral, extension) and the factor FINGER has four levels (index, middle, ring, little). Post hoc analysis was performed with Tukey post hoc. Repeated measure ANOVAs were performed using the statistical software SPSS (SPSS Inc., Chicago, IL, USA). Statistical significance was set at alpha = 0.05.

3. Results

3.1 Ellipse Area

The first result concerns the ellipse area. No significant difference (p>0.1) of the ellipse area due to any of the factors was found. The average ellipse area was 24.5 (9.5) mm2.

3.2 Radius of Curvature

The second result concerns the radius of curvature in the Y-Z plane (Fig. 4). There is a significant effect of the POSTURE (F2, 8=4.737, p<0.05): in extension the radius is larger, with a value of 191.0 (148.9) mm. There is also a significant effect of the FINGER (F3, 12=12.601, p<0.05). The general trend is that curvature decreases from the index to little finger. Another significant effect is the interaction of CONDITION × FINGER (F3, 12=4.91, p<0.05). The index finger tendon has a higher radius of curvature during the active condition than in passive one: 330.0 (156.0) mm and 166.0 (99.0) mm, respectively. Concerning the radius of curvature, the last significant effect is the triple interaction of CONDITION × POSTURE × FINGER (F6, 24=3.689, p<0.05). Tukey post-hoc shows that the radius of curvature is higher, i.e. the tendon path is becoming less curved or straighter: (1) for the index finger in active flexion (289.5 (156.7) mm) than in the passive flexion (156.4 (77.9) mm), and (2) in the active neutral position (366.1 (124.1) mm) than in the passive neutral position (108.8 (43.1) mm).

Figure 4.

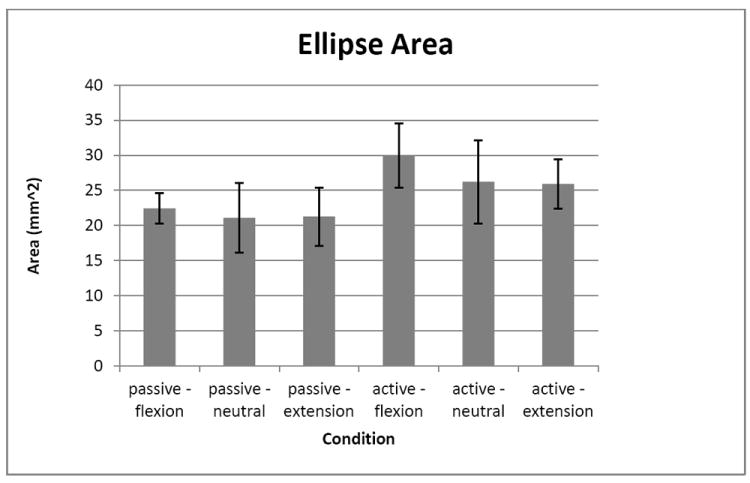
Figure 4

Open in a new tab

Ellipse area for each condition. Error bars are standard error.

3.3 Tendon Shift

The last result of this study is the tendon shift in the Y-direction (Fig. 5). It was found that during the active conditions (AF, AN, AE) the tendons shift closer towards the transverse carpal ligament (i.e. in the palmar direction) than in the passive conditions (PF, PN, PE). The shift is statistically higher during the active condition (1.7 (0.6) mm), than during the passive condition (0.7 (0.6) mm; F1, 4=11.046, p<0.05).

Figure 5.

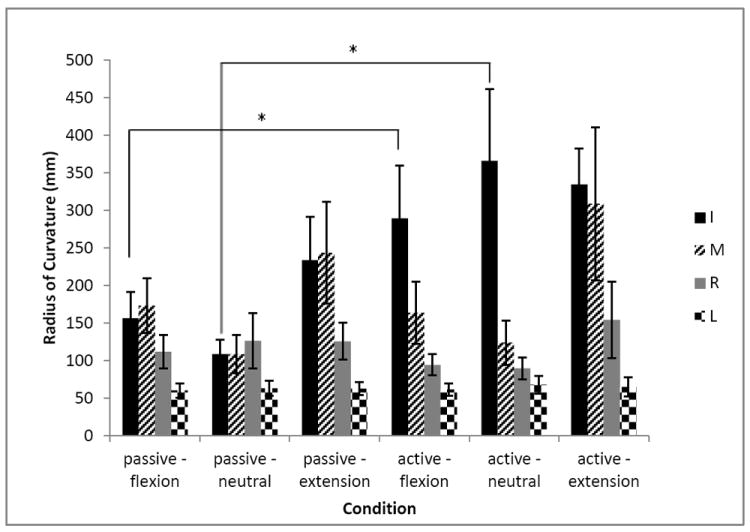
Figure 5

Open in a new tab

Radius of curvature in the Y-Z plane for the tendons of I, M, R and L fingers for each condition. Asterisk indicates a significant difference between the conditions. Error bars are standard errors.

4. Discussion

The major finding of this study was that changes in posture and force produced by a single finger can cause significant changes in the FDP tendon geometry within the carpal tunnel (Fig. 7). This finding is relevant to clinicians concerned with carpal tunnel syndrome: the change in tendon geometry can induce different levels of pressure on the median nerve (Lopes et al., 2011) or can affect the relative tendon movements after a carpal tunnel release surgery (Yoshii et al., 2008). Biomechanists would have an interest in the functional implications of the increased moment arms of the FDP tendons about the wrist joint due to the fairly small force production of a finger. We can expect that higher forces can induce higher moment arms, not only for the FDP, but for other tendons spanning the wrist joint. To the best of our knowledge the literature provides a change in the moment arms for the tendons at the wrist only for different wrist angle (Brand & Hollister, 1999) and not for different finger configurations, or different levels of forces in these tendons.

Figure 7.

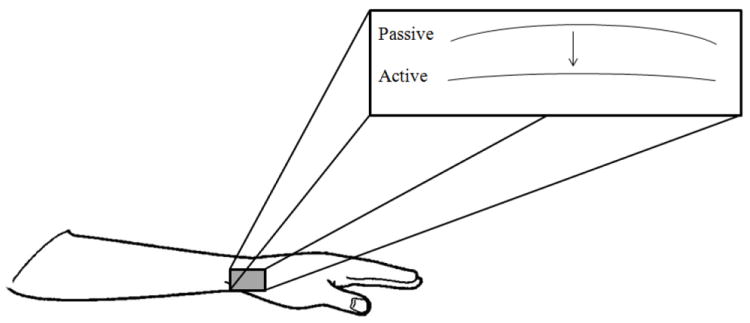
Figure 7

Open in a new tab

Schematic of geometric changes of tendons that occurred due to active force production. The tendons shifted ventrally towards the transverse carpal ligament and the radius of curvature increased (i.e. tendons straightened).

The ellipse area was calculated to be compared in vivo during active and passive conditions. The results demonstrate that this area doesn’t change, which suggests that all the tendons move in the same direction during a finger movement, in a passive or active condition, as demonstrated by Keir and Wells (1999). This finding is related to the shift of the tendons in the palmar direction. It should be noted that, although not statistically significant, the area of the tendons was larger for all active conditions than for the passive conditions (average active area was 21.1% larger than passive area). Additionally, the active condition required only about 10-15% MVC force production of a single finger. The difference in the area of the tendon cluster may have been found to be larger if the required force production had been higher. The anatomical limitation in the palmar direction is caused by the transverse carpal ligament which has a certain degree of compliance thus more force can induce a larger displacement (in the palmar direction) of the tendon due to the compliance of this ligament.

The second result concerns the tendon radius of curvature. Previous publications reported that the radius of curvature was highly dependent on the flexion of the wrist (Keir & Wells, 1999). Here we have found that the curvature of the tendons also depends on the fingers action and/or posture. Our findings are similar to those reported in a previous study (Keir & Wells, 1999) in which the wrist was placed in different postures with active and passive finger pressing conditions similar to ours. It was reported that flexion of the wrist causes movements of the flexor tendons towards the transverse carpal ligament, i.e. palmar direction. In that study the tendons were straighter (i.e. had larger radii of curvature) in the neutral and extended position of the wrist compared to the flexed position. Perhaps the next step in this line of research is to measure changes in the paths of tendons due to changes in position of the finger and wrist joints simultaneously. This will allow us to explore whether the tendon shift is greater when both joints are moved or if it is possible that the reported effects (current study and Keir & Wells, 1999) of movement at one joint can be canceled out by movement of another joint.

Tendon shift results show that the displacement of the tendon is higher during the active condition. That means that the moment arms of the finger tendons at the wrist joint increase during the activity of the fingers at different wrist angles. This result was observed also by Agee et al. (1998) on cadavers. The transverse carpal ligament seems to be highly compliant (Sucher et al., 2005) which allows for bowstringing of the flexor tendons at the wrist. Bowstringing is important for the hand biomechanics (Hume et al., 1998; Vigouroux et al., 2008; Zhao et al., 2000) because very small changes in the moments arms of the tendons can induce large changes in the tensions in the muscles involved at this joint (Valero-Cuevas et al., 1998), particularly for the wrist/finger muscles (Paclet & Quaine, 2012).

The results found in this study can be useful to help explain the mechanisms of carpal tunnel syndrome. Previous research has suggested that the main mechanism of carpal tunnel syndrome is increased pressure in the carpal tunnel (Gelberman et al., 1981; Luchetti et al., 1990; Okutsu et al., 1989; Rojviroj et al., 1990; Szabo & Chidgey, 1989). The ellipse area given by our results reflects the FDP tendons configuration inside the carpal tunnel and suggests that the increase of the FDP ellipse area means that the tendons exert more lateral force (i.e. a force in the palmar direction) on the anatomical adjacent tissue. This lateral force on the sides of the carpal tunnel induced by the tendon shift can be added to the pressure in the carpal tunnel during changes in finger posture and force production. The second result, the changes in the radius of curvature, reflects the bowstringing of the tendons and is congruent with the third observation that shows the tendons shift increase in the Y-direction (i.e. towards transverse carpal ligament) under activity of the fingers. These two results indicate that the tendons apply lateral forces on the transverse carpal ligament even during a small flexion force (10-15% of MVC) produced at the fingertip and in a neutral position. Therefore, the neutral MCP position is not necessarily a safe position in regards to the carpal tunnel syndrome. A previous study’s findings support this claim (Keir et al., 1998).

In order to validate our results and our assumption that the transverse carpal ligament is compliant, we have compared our results with the Xiu et al. (2005) study. These authors reported, for the X-axis, an elongation of 2.3 mm for the transverse carpal ligament under a 10 N load. After a basic calculation, based on Xiu et al. (2005) study, this elongation corresponds to a 5.6 mm possible increment along the Y-axis. Our results on the tendon shift show an average of 0.94 mm displacement (along the Y-axis) between active and passive conditions. Our results are clearly in the range of Xiu et al. (2005) results and agree with other previous studies (Fuss and Wagner, 1996; Sucher et al., 2005), which show similar results.

5. Conclusions

In conclusion, this study demonstrated that the tendon path in the carpal tunnel is very sensitive to the finger activity. The compliance of the carpal transverse ligament allows the tendons crossing this joint to be affected by a bowstringing phenomenon. A change in the moment arm (i.e. the tendon distance to joint center of rotation) occurs not only during wrist movements but also during finger movements and/or extrinsic finger muscles activity - even for small force values (~10-15% of MVC).

Figure 6.

Figure 6

Open in a new tab

Tendon shift in the Y-direction (towards transverse carpal ligament) for the tendons of I, M, R and L fingers for each condition. All condition values are compared to the passive-neutral position values. Asterisk indicates a significant difference between the conditions. Error bars are standard errors.

Acknowledgments

We would like to thank Dr. Susan Lemieux, Amanda Gearhart, Brian Johnson and Andrew Georgeson for their assistance with this project. This study was supported in part by NIH grants AG-018751, NS-035032, and AR-048563.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Agee JM, Maher TR, Thompson MS. Moment arms of the digital flexor tendons at the wrist: role of differential loading in stability of carpal tunnel tendons. J Hand Surg [Am] 1998;23(6):998–1003. doi: 10.1016/S0363-5023(98)80006-3. [DOI] [PubMed] [Google Scholar]
  2. An KN, Ueba Y, Chao EY, Cooney WP, Linscheid RL. Tendon excursion and MA of index finger muscles. J Biomech. 1983;16(6):419–425. doi: 10.1016/0021-9290(83)90074-x. [DOI] [PubMed] [Google Scholar]
  3. Armstrong TJ, Chaffin DB. An investigation of the relationship between displacements of the finger and wrist joints and the extrinsic finger flexor tendons. J Biomech. 1978;11:119–128. doi: 10.1016/0021-9290(78)90004-0. [DOI] [PubMed] [Google Scholar]
  4. Brand PW, Hollister AM. Clinical Mechanics of the Hand. 3. Mosby; Saint Louis: 1999. [Google Scholar]
  5. Chao EY, An KN, Cooney WP, Linscheid RL. Biomechanics of the hand. World scientific; Singapore: 1989. [Google Scholar]
  6. Fuss FK, Wagner TF. Biomechanical alterations in the carpal arch and hand muscles after carpal tunnel release: a further approach toward understanding the function of the flexor retinaculum and the cause of postoperative grip weakness. Clin Anat. 1996;9:100–108. doi: 10.1002/(SICI)1098-2353(1996)9:2<100::AID-CA2>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
  7. Gelberman RH, Hergenroeder PT, Hargens AR, Lundborg GN, Akeson WH. The carpal tunnel syndrome: a study of carpal tunnel pressures. J Bone Joint Surg. 1981;63A:380–381. [PubMed] [Google Scholar]
  8. Gonzalez MH, Mohan V, Elhassan B, Amirouche F. Biomechanics of the digit. J Am Soc Surg Hand. 2005;5(1):48–60. [Google Scholar]
  9. Goodman HJ, Choueka J. Biomechanics of the flexor tendons. Hand Clin. 2005;21:129–149. doi: 10.1016/j.hcl.2004.11.002. [DOI] [PubMed] [Google Scholar]
  10. Hume EL, Hutchinson DT, Jaeger SA, Hunter JM. Biomechanics of pulley reconstruction. J Hand Surg [Am] 1991;16:722–730. doi: 10.1016/0363-5023(91)90201-l. [DOI] [PubMed] [Google Scholar]
  11. Keir PJ, Bach JM, Rempel DM. Effects of finger posture on carpal tunnel pressure during wrist motion. J Hand Surg [Am] 1998;23A(6):1004–1009. doi: 10.1016/S0363-5023(98)80007-5. [DOI] [PubMed] [Google Scholar]
  12. Keir PJ, Wells RP. Changes in geometry of the finger flexor tendons in the carpal tunnel with wrist posture and tendon load: an MRI study on normal wrists. Clin Biomech. 1999;14:635–645. doi: 10.1016/s0268-0033(99)00012-1. [DOI] [PubMed] [Google Scholar]
  13. Lopes MM, Lawson W, Scott T, Keir PJ. Tendon and nerve excursion in the carpal tunnel in healthy and CTD wrists. Clin Biomech. 2011;26:930–936. doi: 10.1016/j.clinbiomech.2011.03.014. [DOI] [PubMed] [Google Scholar]
  14. Luchetti R, Schoenhuber R, Alfarano M, Deluca S, DeCicca G, Landi A. Carpal tunnel syndrome: correlations between pressure measurement and intraoperative electrophysiological nerve study. Muscle Nerve. 1990;13:1164–1168. doi: 10.1002/mus.880131211. [DOI] [PubMed] [Google Scholar]
  15. Martin JR, Latash ML, Zatsiorsky VM. Effects of the index finger position and force production on the flexor digitorum superficialis moment arms at the metacarpophalangeal joints – a magnetic resonance imaging study. Clin Biomech. 2012;27(5):453–459. doi: 10.1016/j.clinbiomech.2011.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Okutsu I, Ninomiya S, Hamanaka I, Kuroshima N, Inanami H. Measurement of pressure in the carpal canal before and after endoscopic management of carpal tunnel syndrome. J Bone Joint Surg. 1989;71A:679–683. [PubMed] [Google Scholar]
  17. Paclet F, Quaine F. Motor control theories improve biomechanical model of the hand for finger pressing tasks. J Biomech. 2012;45:1246–1251. doi: 10.1016/j.jbiomech.2012.01.038. [DOI] [PubMed] [Google Scholar]
  18. Rojviroj S, Sirirchativapee W, Kowsuwon W, Wongwiwattananon J, Tamnanthong N, Jeeravipoolvarn P. Pressures in the carpal tunnel. A comparison between patients with carpal tunnel syndrome and normal subjects. J Bone Joint Surg. 1990;71A:679–683. doi: 10.1302/0301-620X.72B3.2187880. [DOI] [PubMed] [Google Scholar]
  19. Rosset A, Spadola L, Ratib O. OsiriX: an open-source software for navigating in multidimensional DICOM images. J Digit Imaging. 2004;17(3):205–216. doi: 10.1007/s10278-004-1014-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Sucher BM, Hinrichs RN, Welcher RL, Quiroz LD, St Laurent BF, Morrison BJ. Manipulative treatment of carpal tunnel syndrome: biomechanical and osteopathic intervention to increase the length of the transverse carpal ligament: part 2. Effect of sex differences and manipulative “priming”. J Am Osteopath Assoc. 2005;105:135–143. [PubMed] [Google Scholar]
  21. Szabo RM, Chidgey LK. Stress carpal tunnel pressures in patients with carpal tunnel syndrome and normal patients. J Hand Surg. 1989;14A:624–627. doi: 10.1016/0363-5023(89)90178-0. [DOI] [PubMed] [Google Scholar]
  22. Valero-Cuevas FJ, Zajac FE, Burgar CG. Large index-fingertip forces are produced by subject-independent patterns of muscle excitation. J Biomech. 1998;31:693–703. doi: 10.1016/s0021-9290(98)00082-7. [DOI] [PubMed] [Google Scholar]
  23. Vigouroux L, Quaine F, Paclet F, Colloud F, Moutet F. Middle and ring fingers are more exposed to pulley rupture than index and little during sport-climbing: A biomechanical explanation. Clin Biomech. 2008;23(5):562–570. doi: 10.1016/j.clinbiomech.2007.12.009. [DOI] [PubMed] [Google Scholar]
  24. Xiu KH, Kim JH, Zong-Ming Li ZM. Biomechanics of the transverse carpal arch under carpal bone loading. Clin Biomech. 2010;25:776–780. doi: 10.1016/j.clinbiomech.2010.05.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Youm Y, Gillespie TE, Flatt AE, Sprague BL. Kinematic investigation of normal MCP joint. J Biomech. 1978;11:109–118. doi: 10.1016/0021-9290(78)90003-9. [DOI] [PubMed] [Google Scholar]
  26. Yoshii Y, Zhao CF, Henderson J, Zhao KD, Zobitz ME. Effects of carpal tunnel release on the relative motion of tendon, nerve, and subsynovial connective tissue in a human cadaver model. Clin Biomech. 2008;23:1121–1127. doi: 10.1016/j.clinbiomech.2008.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhao CF, Amadio PC, Berglund L, An KN. The A3 pulley. J Hand Surg. 2000;25:270–76. doi: 10.1053/jhsu.2000.jhsu25a0270. [DOI] [PubMed] [Google Scholar]
  28. Zatsiorsky VM, Li ZM, Latash ML. Coordinated force production in multi-finger tasks: finger interaction and neural network modeling. Biol Cybern. 1998;79:139–150. doi: 10.1007/s004220050466. [DOI] [PubMed] [Google Scholar]
  29. Zatsiorsky VM, Li ZM, Latash ML. Enslaving effects in multi-finger force production. Experimental Brain Research. 2000;131:187–195. doi: 10.1007/s002219900261. [DOI] [PubMed] [Google Scholar]

RESOURCES