Capturing Dynamic Patterns of Task-Based Functional Connectivity with EEG

Abstract

A new approach to trace the dynamic patterns of task-based functional connectivity, by combining signal segmentation, dynamic time warping (DTW), and Quality Threshold (QT) clustering techniques, is presented. Electroencephalography (EEG) signals of 5 healthy subjects were recorded as they performed an auditory oddball and a visual modified oddball tasks. To capture the dynamic patterns of functional connectivity during the execution of each task, EEG signals are segmented into durations that correspond to the temporal windows of previously well-studied event-related potentials (ERPs). For each temporal window, DTW is employed to measure the functional similarities among channels. Unlike commonly used temporal similarity measures, such as cross correlation, DTW compares time series by taking into consideration that their alignment properties may vary in time. QT clustering analysis is then used to automatically identify the functionally connected regions in each temporal window. For each task, the proposed approach was able to establish a unique sequence of dynamic pattern (observed in all 5 subjects) for brain functional connectivity.

Introduction

Studies of resting state and task-based functional connectivity aiming to identify similar functionally behaving regions in the brain have received increased attention over the past few years. Aside from healthy populations, different patient groups, including patients with Autism (Koshino et al. 2005; Koshino et al. 2008; Pollonini et al. 2010), traumatic brain injury (TBI) (Kasahara et al. 2010; Mayer et al. 2011), Alzheimer (Dauwels et al. 2010; Dauwels et al. 2010; Uhlhaas and Singer 2006) depression (Greicius et al. 2007; Sheline et al. 2010), have been the subject of functional connectivity studies. These studies have identified different connectivity networks in patient groups compared to healthy people. Different imaging modalities, each offering their own advantages and disadvantages, have been employed to investigate the brain’s functional connectivity (Biswal et al. 1995; Horwitz et al. 1998; Lowe et al. 1998; Lu et al. 2010; Stam 2004). Imaging modalities such as electroencephalography (EEG) and magnetoencephalography (MEG) are capable of measuring neuronal activity directly and offer high temporal resolutions (in the range of milliseconds) while their spatial resolution is usually in the order of centimeters. In contrast, functional Magnetic Resonance Imaging (fMRI), which basically measures the hemodynamic response, provides high spatial resolution, while its temporal resolution is in the range of seconds. In general, the imaging modality of choice is determined by the objective of the study.

It has been shown that the interactions between brain regions during the execution of a task are temporally dynamic (Büchel and Friston 1998; Kang et al. 2011; Kelly et al. 2008; Liu et al. 1999). These interactions generally happen within milliseconds intervals. EEG by providing high temporal resolution can therefore, be employed to capture these short-lasting events (Bhattacharya and Petsche 2005; Koenig et al. 2002; Kramer et al. 2008; Lehmann et al. 2012; Micheloyannis et al. 2006; Pijnenburg et al. 2008).

Assessing functional connectivity requires employing an appropriate measure of functional coupling among brain regions. Accordingly, several measures for detecting functional connectivity in either time domain or frequency domain have been proposed (Bhattacharya and Petsche 2005; Jalili and Knyazeva 2011; Kramer, van der Flier et al. 2008; Lehmann, Faber et al. 2012; Lithari et al. 2011; Micheloyannis, Pachou et al. 2006; Pijnenburg, Strijers et al. 2008). To trace the dynamic patterns of functional similarity among cortical regions during the execution of a task, analysis in the time domain would be appropriate.

Furthermore, as discussed above, stimulus-elicited brain responses are short-lasting events (John 1990; Koenig et al. 2005; Lehmann et al. 2005; Lehmann et al. 1998). Identifying the temporal windows corresponding to these events would be critical in studying task-based functional connectivity. Ignoring these variations can lead to dismissing the dynamic interactions of the brain regions (Kang, Wang et al. 2011). In the context of EEG, the event-related potentials (ERPs) consisting of a series of elicited components (ERP components) manifest these transient variations after a stimulus is presented. The ERP components are time-locked events that reveal several sensory, cognitive and motor processes (Alexander et al. 1995). Hence, part of our proposed method of identifying functionally connected regions during the execution of the task, is concerned with exploring EEG signals within the expected temporal windows of a number of previously studied ERP components.

In the present study, we attempt to establish a dynamic pattern for task-based functional connectivity, which will enable us to trace functionally connected regions during the execution of the tasks. To achieve this goal, first, EEG signals are divided into several segments. The temporal windows for EEG segmentation are set the same as the time intervals, where the occurrence of ERP components is expected. Second, we employed the dynamic time warping (DTW) algorithm to measure similarity among signals within each segment. DTW is a common practice in the field of speech processing (Sakoe and Chiba 1978) and is used to compare time series by taking into consideration that their alignment properties may vary in time. In other words, DTW measures similarity between two signals by compressing/expanding them and looking for their best nonlinear temporal alignment. With respect to the non-stationary behavior of the EEG signals (John 1990; Koenig, Studer et al. 2005; Lehmann, Faber et al. 2005; Lehmann, Strik et al. 1998), employing DTW seems to be more appropriate in comparison to the conventionally used methods like cross-correlation (Jalili and Knyazeva 2011; Lithari, Klados et al. 2011), which generally requires the assumption of stationarity. Therefore, to identify the functionally connected regions in each segment’s temporal window, a similarity matrix using DTW is constructed. It should be noted that the employed DTW technique is not the only approach that addresses the problem of nonlinearity quantification between time series, and there are other techniques (Dauwels et al. 2009; Dauwels et al. 2009; Dauwels et al. 2012; Quiroga et al. 2002; Victor and Purpura 1997) which have addressed this issue in different ways. Here we employed the DTW approach. Finally, the similarity matrix is used as an input to the Quality Threshold (QT) clustering (Heyer et al. 1999) algorithm. QT is a technique, which is used for unsupervised categorization of data sets. One of the advantages of using QT over other clustering methods such as k-means (Hartigan and Wong 1979) is that it does not require specifying the number of clusters apriori. Moreover, the outcome of the algorithm is not dependent on the order of the points to be clustered, and it always returns the same cluster outcomes.

The rest of the paper is organized as follows. First, experimental paradigms, data acquisition process, and analysis techniques are described. Next, results are presented and discussed.

Methods

Experimental Paradigms and Data acquisition

Five right handed subjects (aged 27.2 ± 5.1 years) participated in this study. All subjects provided written informed consents approved by the Georgetown University Institutional Review Board prior to the experiments. They had self-reported normal hearing and normal vision (corrected in one case).

For each participant, both tasks were completed in one session lasting about two hours. Two versions of the oddball paradigm, a modified visual (Wang et al. 1999) and an auditory (IRAGUI et al. 1993) were used. For the visual task, sequences of three different stimuli (shown in Figure 1) were presented. Each stimulus was presented for 50 ms, with inter-trial interval (ITI) of 1000–2000 ms. The plus sign image (Figure 1-a) was designated as a target stimulus with the appearance probability of 15%. Two other images appeared as frequent (Figure 1-b) and infrequent (Figure 1-c) non-target stimuli with the probability of 60% and 25%, respectively. Overall, 45 target and 250 non-target stimuli were presented. Subjects were asked to press a button when a target stimulus appeared on the screen.

Figure 1.

(a) Target (b) non target frequent (c) and non target infrequent stimuli

For the auditory oddball task, the auditory stimuli were presented for 50 ms in duration with an ITI of [1000–2000] ms. The stimuli were pure tones of 1000 Hz (non-target) and 2000 Hz (target) in frequency. The target stimulus was presented with probability of 15% with an overall of 45% targets versus 250 non-target stimuli.

EEG data acquisition and preprocessing

Brain potentials were recorded using 128-channel EEG system (Electrical Geodesic, Inc., Eugene, OR). The signals recorded from each channel were first visually examined for motion artifacts. Single trials impacted by motion were identified and removed from further analysis. The signal quality in few channels was found to be poor (possibly due to the dryness of the sensors during the recording). These channels were replaced by the average of their neighboring channels. For every participant, average ERP waveforms for target stimuli-related trials of both tasks (visual/auditory) were computed. To filter the physiological artifacts, the signals were high pass filtered at 1 Hz. Other major artifacts related to eye blink or muscle activities were then removed by employing the Independent Component Analysis (ICA) (Hyvärinen and Oja 2000) technique.

ICA aims at decomposing a linear mixture of measured EEG signals into the contributing sources, with the assumption that the sources are statistically independent. Since artifacts and signals of physiological sources are expected to be independent, the ICA algorithm can be used to separate them. If x is a set of n measured EEG signals, and element a_i,j in matrix A specifies the contribution of source s_j in matrix s to the signal x_i, one can write:

$$\mathbf{x}=\mathbf{As}.$$ (1)

To retrieve the source signals, the algorithm looks for maximum independency and estimates the unmixing matrix W, where W=A⁻¹. As a result, each signal source, s_i, can be defined as:

$$s_i=w_{i,1}{x}_1+w_{i,2}{x}_2+\dots +w_{i,n}{x}_n,$$ (2)

where w_i,j specifies the weighted contribution of x_i. To identify which of the estimated independent components are in fact the artifacts, an activity map localizing the contribution of each channel (w_i,j coefficients) was plotted for each source. For example, for the components corresponding to eye blinks, channels placed closer to the eye presented strong contributions. After identifying the artifacts’ components, they were removed, and the signal matrix was reconstructed. Signal preprocessing, including data visualization, filtering, and ICA analysis were performed in Matlab using the EEGLAB toolbox (Delorme and Makeig 2004).

ERP Segmentation

Both oddball tasks involved target and non-target stimuli. For this study, only epochs corresponding to the target stimuli were extracted and averaged. Epoch length was 1000 ms intervals (100 ms prestimulus and 900 ms poststimulus). To track possible changes in the functionally connected regions during the execution of each task, the ERP signals were segmented to a number of shorter temporal windows. Segments were obtained by extracting portions of the ERP signals where a number of well-studied ERP components were expected to be evoked. Selected temporal windows for the visual task were P100, N100, N200, and P300, with the expected latency windows of [50–190], [50–190], [150–300], [250–500] ms, respectively. For the auditory task, the same temporal windows were used except for the P100 and N100 intervals, which were shortened to [80–190] and [85–190] ms, respectively. All the above mentioned intervals were selected based on the previously reported time windows for the corresponding ERP components (Alexander, Porjesz et al. 1995; Brown et al. 2007; Folstein and Van Petten 2008; Itagaki et al. 2011; Kayser and Tenke 2006; Kayser et al. 1998).

Dynamic Time Warping

As previously stated, the majority of the functional connectivity studies performed in the time domain use cross-correlation to analyze the similarities among signals. The major limitation of this technique is that it fails to capture the similarities if the alignment properties of the signals vary in time. To address this issue and to assess brain functional connectivity during the execution of a task more accurately, we have employed dynamic time warping technique (Sakoe and Chiba 1978).

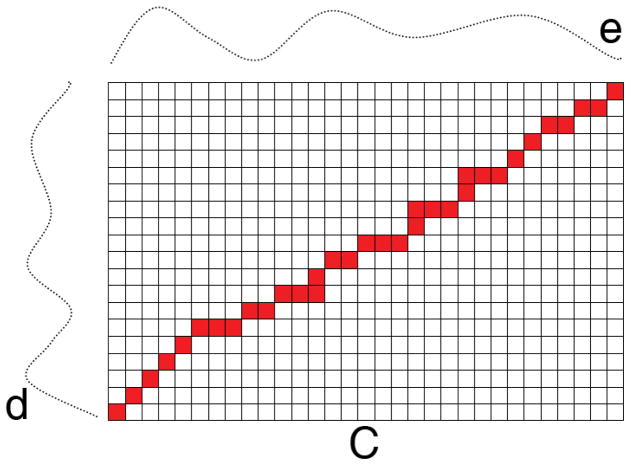
DTW technique finds the optimal alignment between two time series through a non-linear compression and extension of the time axes (as depicted in Figure 2). In fact, the basic problem that DTW attempts to solve is how to align the two time series in order to generate the most representative distance measure of their overall difference. Figure 3 illustrates how the analysis is done. Suppose, we are interested in computing the DTW distance between two EEG signals d=(d₁, d₂ … d_N) and e=(e₁, e₂, …, e_N) of length N. The first step is to calculate the distance between each point in signal d and all the points in signal e. Euclidean distance metric can be used for such distance computation. Therefore, for every point in signal d, N measured distance values are obtained, resulting in an N × N matrix (cost matrix) C ∈ ℝ^N×N (Figure 3). The signals are associated to this matrix such that the bottom-left and top-right corners of the matrix represent the distance between their beginning and the ending points, respectively.

Figure 2.

Two hypothetical time series with an overall similar shape but not well aligned along the time axis. To find the optimal alignment between two time series, one point from the first time series may be compared against a number of points from the second time series, after (Keogh and Ratanamahatana 2005).

Figure 3.

Two time series, which have similar pattern of activity but are not aligned in the time domain. Matrix C is the cost matrix in which the optimal warping path is shown as the sequence of solid squares (shown in red).

Once the cost matrix is formed, the second step is to find the best alignment between signals d and e. This alignment may be sought in a form of a warping path, p, consisting of a set of elements taken from matrix C (p=[p₁…p_L], where N≤L≤2N−1). A number of conditions can be enforced on this search, to reasonably limit the number of potential path candidates. For our analysis, only the paths satisfying the following conditions were considered:

• Boundary condition: start and end points of the warping path have to be the very first and last points of the given time signals, respectively

• Monotonicity condition: For any two consecutive points of the path, p_k = c_i,j and p_k-1 = c_m.n, (c_i,j and c_m,n ∈ C), the following condition should be satisfied: i-m ≥ 0, j-n ≥ 0. This condition guarantees that the path will not turn back on itself.

• Step size condition: restricts the path to advance only one step at a time

The optimal warping path (optimal alignment) is the one having the minimal total cost among all possible warping paths. Mathematically the optimal warping path (d_DTW) can be formulated as

$$d_{\mathit{DTW}}=min(\frac{{\sum }_{\text{L}=1}^{\text{L}}{\text{p}}_{\text{L}}}{\text{L}}).$$ (3)

To capture functional connectivity during the execution of both oddball tasks, for every segment of the 128 recorded EEG signals, DTW algorithm was applied and a 128×128 similarity matrix was constructed.

QT Clustering

Automatic identification of the most similar-behaving channels during various ERP components was carried out by employing a clustering algorithm called the Quality Threshold (QT). This algorithm was initially developed for the analysis of gene expression data (Heyer, Kruglyak et al. 1999). As explained in the previous section, for every segmented signal, a similarity matrix was computed through the DTW process. The QT algorithm begins with considering each of the 128 channels as a single cluster. In the next step, each cluster is expanded by adding channels with distance from the given cluster (taken from the similarity matrix) below a certain threshold set by the user. Once this is done for all clusters, the most populated cluster is retained and others are discarded. The same procedure is repeated for the discarded channels until either all channels are clustered, or the largest cluster does not pass the user-defined “minimum number of points” criteria. A more detailed description of the algorithm is provided in Appendix I.

Results

For each participant, applying the QT clustering algorithm on the segmented EEG signals resulted in the identification of the channels (brain regions) that, based on the DTW criteria, were functioning similarly during the corresponding time interval.

Figure 4-a illustrates the color-coded clustering results (on a 2D 128-sensor map) applied to the EEG signal within the time window [50–190] ms for one of the subjects. The representative temporal signals for each cluster are plotted in Figure 4-b. For each cluster, the solid line corresponds to the average value of the signals of all the channels in that cluster, and the dash lines represent the standard deviation of the signals. It can be seen that in this temporal window, the electrodes placed over the posterior region show a similar positive-going ERP component (shown in green), whereas the electrodes located at other regions exhibit different behavior (shown in red and black).

Figure 4.

(a) 2D map for functionally connected regions over the time interval of [50–190] ms shown by green, black, and red colors, (b) for each cluster, a cluster-representative signal obtained by averaging ERPs over all the channels (solid line), and its corresponding standard deviations (dash lines) are plotted.

As mentioned in the previous section, to cluster the data, QT clustering requires a user defined threshold value, which corresponds to the similarity level between the signals in each cluster. Setting a threshold value, which results in clusters with the most analogous activity pattern, can be a challenging task: a low threshold value may result in large clusters containing channels with distinct neuronal activities, while a high threshold value might result in a large number of smaller clusters. We tried several threshold values for each subject, and those values that resulted in clusters with a high intra-cluster similarity (a small standard variation for the cluster-average signal) and a low inter-cluster similarity (distinct activity patterns for cluster-average signals) were selected.

Another challenge in the group analysis was the variations in the head shape and size across subjects, as these variations resulted in slightly different electrode positions across subjects. In our analysis, we focused only on the activation regions, which were common in all the subjects, thus, ignoring the inter-subject variations in the spatial distribution of brain activity.

For each EEG segment, the group analysis involved finding the clusters that were spatially common across all the subjects. The clusters were selected if their corresponding ERP signals were consistent with the expected activity for the selected temporal window. As a result, the region identified as functionally connected was a subset of the corresponding ERP activity map for the given temporal window.

Figure 5 presents the group analysis results showing the 3D activation maps of functionally connected regions for multiple segments of both the auditory and the modified visual oddball tasks. The averaged and the standard deviation of the corresponding ERP waveforms (for one of the subjects as an example) are also plotted for each component. The red area on the scalp demonstrates the identified functionally connected regions whereas the yellow strip around this area determines the boundary of that region. Using the proposed technique for the auditory task, we identified functionally connected regions corresponding to all the four designated time intervals. For the visual task, the functionally connected regions were identified for three of four designated time intervals.

Figure 5.

ERP signal and its corresponding 3D map of the functionally connected regions distributed over the scalp for both auditory (left column) and visual (right column) tasks. The red region over the scalp demonstrates the identified functionally connected regions across all subjects whereas the surrounding yellow strip determines the boundary of the region.

Cluster Evaluation

In this section, we attempt to evaluate the performance of the clustering algorithm. Since there was no external information regarding the potential clustering structure, an unsupervised approach for measuring the performance of the clustering is being used. We determined the quality of the clustering algorithm by measuring the compactness of the clusters (cluster cohesion), as well as cluster separation (isolation). Cluster cohesion suggests how closely the ERP signals in a single cluster are, whereas cluster separation determines how well separated a cluster is from other clusters.

A commonly used method that takes into consideration both cluster cohesion and cluster separation is called silhouette coefficient (Tan et al. 2006). To calculate this coefficient, first the average DTW distance of the i^th ERP signal to all other ERP signals in its own cluster (w_i) is computed. Then, for the i^th ERP signal, the distance to the closest cluster (r_i) is determined. The silhouette coefficient for the i^th ERP signal is then computed by the following equation:

$${\mathit{silhouette}}_i=(r_i-w_i)/max(r_i,w_i).$$ (4)

The silhouette coefficient value for every ERP signal would vary between −1 and 1. Overall, a nonnegative value for the silhouette coefficient is desirable. This may be verified from (4), where the negative value corresponds to a case where the average distance of an ERP signal in a cluster from other members of the cluster is larger than its distance from members of other clusters. Furthermore, a positive silhouette coefficient value (r_i > w_i) suggests that the ERP signal is more similar to the members of its own cluster as opposed to the members of other clusters. In particular, values closer to 1 (r_i ≫ w_i), relate to improved performance for the clustering task.

The average silhouette coefficient of a single cluster (representing the functionally connected regions) for each subject, was determined by averaging over silhouette values of all the cluster members. Next, computed silhouette coefficient values for the selected cluster across subjects were determined by averaging the cluster’s silhouette coefficient of all subjects. The results are summarized in Table I.

Table I.

Average silhouette coefficient value corresponding to functionally connected regions of figure 5. Silhouette coefficient value varies between −1 and 1 whereas a positive silhouette coefficient value suggests that the ERP signal is more similar to its own cluster members as opposed to members of other clusters. Values closer to 1 correspond to improved performance for the clustering task.

Component	Silhouette coefficient/Auditory task	Silhouette coefficient/Visual task
N100	0.87
P100	0.90	0.92
N200	0.86	0.90
P300	0.91	0.89

It has been found in (Rousseeuw and Kaufman 1990), that an average silhouette coefficient greater than 0.5 indicates reasonable partitioning of data whereas values less than 0.2 suggest poor partitioning of the data. As can be seen in Table I, the silhouette coefficient for each cluster suggests that a precise partitioning of the data has been performed. In other words, the ERP signals corresponding to a functionally connected region have shown a pattern of activity that are strongly similar to each other, and are well distinct from the ERP signals belonging to other regions.

Discussion

Our proposed approach of segmenting the EEG signals into multiple temporal windows, followed by identifying the functionally connected regions (by employing DTW and clustering techniques), has enabled us to trace the brain interactions during the execution of both oddball tasks. We considered four temporal windows, ranged from early stages of the ERP (50–190 ms for visual and 80–190 ms for auditory tasks) to later intervals (250–500 ms). The early evoked potentials, such as the P100 and N100 components, are dependent on the stimulus type (auditory or visual), and are assumed to be generated in the primary auditory or visual cortices, respectively (Herrmann and Knight 2001). In contrast, the later ERP components, such as P300, are independent of the stimuli type and their sources are localized outside the primary sensory cortices (Katayama and Polich 1999; Polich 2007).

The scalp topography of the functionally connected regions obtained by our technique (Figure 5) in reference to the well-established ERP components complies with the aforementioned expected scalp distribution of brain activation. For the auditory task, the scalp topography of the functionally connected regions during N100 and P100 components within the bilateral temporal lobes suggests the involvement of the primary auditory cortex. The region of increased connectivity during the N200 component appeared to be within the frontocentral part of the scalp. This result is consistent with the previous reports for the N200 scalp topography (Alho 1995; Folstein and Van Petten 2008; Patel and Azzam 2005). The frontocentral contributed in forming the functionally connected regions during the P300 temporal window, which is in line with the previous studies (Bledowski et al. 2004; Brown, Clarke et al. 2007; Katayama and Polich 1999; Patel and Azzam 2005).

For the visual task, during the early P100 component ([50–190] ms), functionally connected bilateral regions were revealed over the visual cortex. The area of increased functional connectivity did not change significantly for the temporal window of the N200 component ([150–280] ms). Significant connectivity was observed over the occipital lobe along with a partial involvement of the parietal lobe. This is consistent with the previous reports, which have identified sources of the N200 component within the parietal and more posterior areas (Folstein and Van Petten 2008; Ogura et al. 1991). The scalp map of the functionally connected regions during the P300 component [250–500] ms shows a change from the posterior to the frontocentral distribution.

The functionally connected regions during the execution of the auditory task were revealed in two major areas: the temporal lobe (during the early ERP component) and the frontal-parietal observed with the involvement of occipital (during the early ERP component) and occipital-parietal and frontal lobes (the later ERP component). Overall, it seems that the functionally connected regions during the early poststimulus periods tend to vary systematically with the physical modality of the stimulus, whereas the later ERP components vary in relation to the higher-order processing mechanisms of the brain that become activated later in response to the stimulus.

The captured spatio-temporal dynamic changes in the functionally connected regions during the execution of the oddball tasks provide evidence that the task-related functional connectivity follows a dynamic pattern, and is not bounded to a static set of brain regions. We have been able to capture this temporal dynamic in the functional connectivity pattern at time intervals of 100 ms duration. Naturally, the method can work at shorter time intervals if it is of interest.

To compare our technique with the commonly used correlation technique, we analyzed functionally connected regions for the auditory task using both the DTW and the cross-correlation methods applied on the full length signal. We then applied QT clustering, and identified functionally connected regions that were common across all subjects.

Figure 6-a shows the functionally connected regions captured by DTW when applied to the full length signal. As it can be seen, the functionally connected regions corresponding to the N100 and P100 components (which were revealed by our segmentation approach as seen in Figure 5) were not detected with this approach. Full length signal analysis only identified the frontocentral part of the brain as the functionally connected region. Note that the analysis on the segmented signal for the P300 component had identified a comparable region (with a broader spatial distribution). Results for the cross-correlation analysis on the full length signal are shown in Figure 6-b. Similar to the DTW method, the cross-correlation technique also revealed the frontocentral part as the region of connectivity (slightly smaller in size compared to the DTW) and also was not able to capture the functionally connected regions corresponding to the P100 and N100 as was obtained when considering segmentation.

Figure 6.

3D maps of functionally connected regions obtained by two similarity techniques over the full length signal: (a) DTW and (b) cross-correlation.

As seen in Figure 6, compared to cross-correlation, DTW has identified a larger area for functionally connected regions. This can be explained by the fact that unlike cross-correlation, DTW also considers the nonlinear alignment of the signals. Therefore, the larger frontocentral area (revealed by the DTW) could be an indication of the brain regions with nonlinear similarity behavior.

It should be emphasized that in this paper, when looking for functionally connected regions, we were only interested in identifying the regions that were similarly “activated” (showing similar positive/negative ERP components). However, the technique is not bounded to activation signals, and can be used to reveal the functionally similar “behaving” regions in the broader sense. For example, the technique can be used to trace the regions of the brain where there are no activations during the execution of the task.

Our proposed approach enables tracing the task-based functional connectivity over the scalp, and has the potential to become a useful tool for research in the field of cognitive neuroscience. We showed that our technique can identify functional connectivity in a more accurate way compared to other existing techniques. It is expected that in healthy individuals, every task can have a unique dynamic functional connectivity pattern which might differ from that of patient population. Comparing such dynamic patterns between the two groups could further help clinical investigators to identify the underlying impairments of brain functional connections in the patient groups.

Highlights.

• A novel approach to capture dynamic patterns of functional connectivity using EEG is presented.

• Segmentation, Dynamic Time Warping, and Clustering techniques are employed.

• Functional connectivity patterns in response to two oddball tasks are successfully captured.