Optimal Sparse Segment Identification with Application in Copy Number Variation Analysis

Abstract

Motivated by DNA copy number variation (CNV) analysis based on high-density single nucleotide polymorphism (SNP) data, we consider the problem of detecting and identifying sparse short segments in a long one-dimensional sequence of data with additive Gaussian white noise, where the number, length and location of the segments are unknown. We present a statistical characterization of the identifiable region of a segment where it is possible to reliably separate the segment from noise. An efficient likelihood ratio selection (LRS) procedure for identifying the segments is developed, and the asymptotic optimality of this method is presented in the sense that the LRS can separate the signal segments from the noise as long as the signal segments are in the identifiable regions. The proposed method is demonstrated with simulations and analysis of a real data set on identification of copy number variants based on high-density SNP data. The results show that the LRS procedure can yield greater gain in power for detecting the true segments than some standard signal identification methods.

1 INTRODUCTION

In genetics, the study of DNA copy number variation (CNV) provides important insights on human inheritance and disease association (McCarroll and Altshuler 2007). CNV refers to duplication or deletion of a segment of DNA sequences compared to a reference genome assembly. Current high-throughput genotyping technology is able to generate genome-wide observations in kilobase resolution. In this type of ultrahigh-dimensional data, the number of CNV segments can be very small and the CNV segments can be very short, which impose major difficulties for detecting and identifying these segments. Note that changes in DNA copy number have also been highly implicated in tumor genomes, most are due to somatic mutations that occur during the clonal development of the tumor. The copy number changes in tumor genomes are often referred to as copy number aberrations (CNAs). In this paper, we focus on the CNVs from the germline constitutional genome. An important application is the detection and identification of CNVs based on data generated by genome-wide single nucleotide polymorphism (SNP) genotyping arrays for the germline DNA samples from normal tissues. There are about 500,000 to 1,000,000 numerical observations along the human genome of an individual; the number of CNV segments, however, is usually smaller than 100, and the CNV segments mostly range less than 20 SNPs (Zhang et al. 2009). In order to identify these CNVs for a given individual, it is important to first understand how the number of CNVs, the segment length and signal intensity affect the statistical power of CNV detection and identification. More discussion and background on CNV detection are given in Section 4.3. Similar problems arise in other fields including, for example, detecting moving objects (NRC 1995), detecting fissures in materials (Mahadevan and Casasent 2001), and identifying streams and roadbeds (Agouris et al. 2001). A common feature of these applications is that very sparse signals are hidden in a large amount of noise.

Motivated by the problem of CNV detection and other applications mentioned above, we consider in this paper the general problem of detecting sparse and short segments from a long sequence of noisy data. In particular, we assume that these signals are composed of several short linear segments, and our goals are to detect whether signal segments exist and identify the locations of these segments when they do exist. More specifically, we consider the following model where we observe {X_i, i = 1, …, n} with

$$X_i={\mu }_1{1}_{\{i\in I_1\}}+\dots +{\mu }_q{1}_{\{i\in I_q\}}+\sigma Z_{i,}1\le i\le n.$$ (1)

Here q = q_n is the unknown number of the signal segments, possibly increasing with n, I₁, … I_q are disjoint intervals representing signal segments with unknown locations, µ₁, … µ_q are unknown positive means, σ is an unknown noise level, and $Z_i\stackrel{iid}{~}N(0,1)$. Let 𝕀 = 𝕀_n be the collection of all signal segments. We formulate the detection and identification problem as the following testing problem

$$H_0:𝕀=\mathrm{\varnothing }{\text{against H}}_1:𝕀\ne \mathrm{\varnothing },$$

and if the alternative is true, identify the set of signal segments 𝕀.

The problem of detecting and identifying sparse and short signal segments pertains to statistical research in several areas. Without segment structure, it is closely related to large-scale multiple testing, which has motivated many novel procedures such as false discovery rate (FDR) (Benjamini and Hochberg 1995) and higher criticism thresholding (HCT) (Donoho and Jin 2008). Arias-Castro et al. (2005) considered the problem of detecting the existence of signals when there is only one signal segment. This is a special case of the detection part of our problem with q = 1. They showed that the detection boundary in this case is $\sqrt{2\log n}/\sqrt{|I|}$, i.e., the signal mean should be at least $\sqrt{2\log n}/\sqrt{|I|}$ in order for a signal with length |I| to be reliably detected and that the generalized likelihood ratio test (GLRT) can be used for detecting the segment. A closely related result in Section 6 of Hall and Jin (2010) demonstrates the detection boundary under a wide range of signal sparsity when signals appear in several clusters. Further, Arias-Castro et al. (2005) and Walther (2009) studied detection of geometric objects and spatial clusters in 2-dimensional space, respectively, and Arias-Castro et al. (2008) provides detection threshold for the existence of an unknown path in a 2-dimensional regular lattice or a binary tree.

The problem we consider here is also related to the problem of change-point detection, since it involves shifts in the characteristics of a sequence of data. Change-point detection in a single sequence has been extensively studied. See Zack (1983) and Bhattacharya (1994) for a review of the literature. Olshen et al. (2004) used the likelihood ratio based statistics for analysis of DNA copy number data, and Zhang and Siegmund (2007) proposed a BIC-based model selection criterion for estimating the number of change-points. Olshen et al. (2004) further developed an iterative circular binary segmentation procedure for segmentation of a single sequence and showed promising results in analysis of DNA copy number data, whereas Zhang et al. (2008) extended the problem of change-point detection from single sequence to multiple sequences in order to increase the power of detecting changes.

In this paper, we consider the challenging setting where the true signals are very sparse in the sense that both the number and the lengths of signal segments are very small. We present a statistical characterization of identifiable region of a signal segment, where it is possible to separate the segment from the noise. Furthermore, we propose a likelihood ratio selection (LRS) procedure to identify the signal segments, and show that the LRS provides consistent estimates for any signal segments in the identifiable region. In other words, the LRS procedure is an optimal procedure, which can reliably separate signal segments from noise as long as the signal segments can be estimated.

Our results show that, when the segment structure of signals is taken into account, much weaker signals can be identified, and the overall power is significantly improved. For unstructured sparse signals, it follows from Donoho and Jin (2004) and Jeng (2009) that the mean needs to be at least $\sqrt{2\log n}$ in order for the signals to be identifiable. On the other hand, for structured signals with one segment of length |I|, the detection threshold is $\sqrt{2\log n}/\sqrt{|I|}$ (Arias-Castro et al. 2005). Since identifying the locations of signals is more difficult than detecting their existence, the identification threshold for the structured signals should be at least $\sqrt{2\log n}/\sqrt{|I|}$. In this case, we find the identification threshold to be the same as the detection threshold in Arias-Castro et al. (2005) when signals are very sparse. However, the fundamental difference between our procedure and that of Arias-Castro et al. (2005) is that, in addition to detecting the existence of signals, our proposed LRS procedure accurately identifies the locations of the segments. In addition, we extend the setting of Arias-Castro et al. (2005) to more than one segment. Our study also provides a novel connection between recent developments in sparse signal detection and change-point problems.

The rest of the paper is organized as follows. We first introduce the LRS procedure for identifying the sparse linear segments in the data in Section 2. We then present the statistical characterization of the identifiable region and the asymptotic optimality results of the LRS in Section 3. Monte Carlo simulations are demonstrated in Section 4 to compare the performance of LRS with those of FDR and HCT. We also present real data results from applying the LRS procedure to analyzing a CNV data from a trio of three individuals. We conclude in Section 5 with some further discussions. The proofs are relegated to the Appendix.

2 LIKELIHOOD RATIO SELECTION

As mentioned in the introduction, our goal is to detect and identify the signal segments based on the sample {X₁, …, X_n} under the model (1). In this section we introduce a procedure that selects candidate intervals based on their likelihood ratio statistics. For any given interval Ĩ ⊆{1, 2, …, n}, define its likelihood ratio statistic as

$$X(\tilde{I})={\displaystyle \sum _{i\in \tilde{I}}{X}_i/\sqrt{|\tilde{I}|}}.$$

Under the null hypothesis, X(Ĩ) follows the standard normal distribution for any Ĩ. With sample size n, there are n² candidate intervals in total, and searching through all of them is computationally expensive if n is large as in many high-dimensional applications. Motivated by applications such as the CNV analysis and to reduce the computational complexity, we utilize the short-segment structure of signals and only consider candidate intervals with length less than or equal to L, where L is some number much smaller than n. We denote the set of such candidate intervals as 𝕁_n(L) with cardinality n × L. We argue that the selection of L should satisfy the following condition:

$$\overline{s}\le L<\underset{¯}{d},$$ (2)

where s̄ is the maximum signal length and d is the minimum gap between signals, i.e.,

$$\overline{s}=\underset{1\le j\le q}{\max }|I_j|,\mathit{\text{and}}\underset{¯}{d}=\underset{1\le j\le q-1}{\min }\{\text{distance between}{I}_j\text{and}{I}_{j+1}\}.$$

Condition (2) requires L to be larger than the maximum length of the signal segments, so that each signal segment is covered by some candidate intervals. On the other hand, L should be smaller than the shortest gap between signal segments, which ensure that no candidate reaches more than one signal segment. For applications such as the CNV analysis, L can be easily selected from a wide range since signals are very rare compared to the amount of noise. In CNV data, the lengths of signal segments are usually less than 20 SNPs, while the distances between deletion/amplification segments are rarely below 1000 SNPs. We show later in Section 4 that different choices of L only result in negligible differences in selection accuracy as long as condition (2) is satisfied. We mention that using smaller L involves less computational complexity and is, thus, preferred. On the other hand, if L is selected too small (< s̄) and some segments are estimated piece by piece, an easy remedy is to combine the estimates that are very close to each other into one piece.

Based on extreme value theory of normal random variables, we have

$$\underset{\tilde{I}\in {𝕁}_n(L)}{\max }X(\tilde{I})\le \sqrt{2\log (nL)}$$

with probability tending to 1 under the null hypothesis. So a reasonable threshold for significance testing is

$$t_n=\sqrt{2\log (nL).}$$ (3)

Our algorithm first finds all the candidate intervals with the likelihood ratio statistics greater than t_n. Intuitively, the proper estimates of signal segments should be the candidate intervals whose likelihood ratio statistics achieve the local maximums. Thus, the LRS procedure iteratively selects the interval from the candidate set with the largest likelihood ratio statistic, and then delete the selected interval and any other intervals overlapping with it from the candidate set. In the following, we present our procedure in detail for a chosen window size L.

• Step 1: Let 𝕁_n (L) be the collection of all possible subintervals in {1, …, n} with interval length less than or equal to L. Let j = 1. Define 1D540^(j) ={Ĩ ∈ 𝕁_n(L): X(Ĩ) > t_n}.

• Step 2: Let Î_j = arg max_{Ĩ∈𝕀^(j)}X(Ĩ).

• Step 3: Update 𝕀^(j+1)= 𝕀^(j)\{Ĩ ∈ 𝕀^(j):Ĩ ∩ Î_j ∅}.

• Step 4: Repeat Step 2–4 with j = j + 1 until 𝕀^(j) is empty.

Define the collection of selected intervals as 𝕀̂= {Î₁, Î₂, …}. If 𝕀̂ ≠ ∅, we reject the null hypothesis and identify the signal segments by all the elements in 𝕀̂.

Note that the above LRS procedure is designed for positive signal segments (µ_j > 0). When both positive and negative signal segments exist, a simple modification is to replace the X(Ĩ) in step 1 and 2 with |X(Ĩ)|.

3 ASYMPTOTIC OPTIMALITY OF LRS

In this section, we show that under certain conditions, LRS can reliably separate signal segments from noise whenever the signal segments can be estimated. This property is what we call the optimality of LRS.

To elucidate the exact meaning of optimality, we first introduce a quantity to measure the accuracy of an estimate of a signal segment. Recall that I is the collection of signal segments. Denote 𝕀̂ to be the collection of interval estimates. For any Î∈ 𝕀̂ and I ∈ 𝕀, define the dissimilarity between Î and I as

$$D(\widehat{I},I)-1-|\widehat{I}\cap I|\sqrt{|\widehat{I}||I|},$$ (4)

where | · | represents the cardinality of a set. Note that 0 ≤ D(Î, I) ≤ 1 with D(Î, I) = 1 indicating disjointness and D(Î, I) = 0 indicating complete identity. Similar quantity has been used in Arias-Castro et al. (2005) to measure the dissimilarity between intervals.

Definition 1

An identification procedure is consistent for a subset Ω ⊆ 𝕀 if its set of estimates 𝕀̂ satisfies

$$P_{H_0}(|\widehat{𝕀}|>0)+P_{H_1}(\underset{I_j\in \mathrm{\Omega }}{\max }\underset{{\widehat{I}}_j\in \widehat{𝕀}}{\min }D({\widehat{I}}_j,I_j)>{\delta }_n)\to 0,$$ (5)

for some δ_n = o(1). Obviously, the first term on the left measures the type I error. The second term, which is the probability that some signal segments in Ω are not ‘substantially matched’ by any of the estimates, essentially measures the type II error.

Definition 2

For any fixed I_j ∈ 𝕀, if there exists a threshold ${\rho }_j^{*}$ such that when ${\mu }_j>{\rho }_j^{*}$ there exists some identification procedure that is consistent for I_j, and when ${\mu }_j\le {\rho }_j^{*}$ no such procedure exists, we call the regions corresponding to ${\mu }_j>{\rho }_j^{*}$ and ${\mu }_j\le {\rho }_j^{*}$ the identifiable and unidentifiable regions of I_j, respectively.

We shall call procedure an optimal procedure if it is consistent for all the segments in their identifiable regions.

In this section, we demonstrate the optimality of LRS under condition (2) on L and additionally

$$\log L=o(\log n).$$ (6)

L that satisfies (6) can, for example, be of order log^a n, a > 1. Condition (2) and (6) can both hold in the situations that we are interested in, where signals are very sparse. We note that a consistent procedure also consistently estimates the true break points, which is usually of great interest in practical applications. This is because the dissimilarity measure D(Î, I) is closely related to the measure of distance between the estimated break points and the true break points. For two intervals I and Î with dissimilarity D(Î, I) < 1, define

$$BP(\widehat{I},I)=|\widehat{I}\backslash \widehat{I}\cap I|+|I\backslash \widehat{I}\cap I|.$$ (7)

Note that BP(Î, I) is the sum of distances between the lower and upper break points and their respective estimates. Then, it is easy to show that

$$BP(\widehat{I},I)\le 2D(\widehat{I},I)(|\widehat{I}|+|I|).$$

We also assume in this section that the variance σ² is known and, without loss of generality, is set to be 1. In real data analysis, σ can be easily estimated from the data since signals are sparse. More discussion on estimating σ is given in Section 5.

3.1 Optimality of the LRS when q = 1

In order to present all the basic theoretical elements in their simplest and cleanest form, we start with q = 1 and define I = I₁ and µ = µ₁. The following theorem provides the consistency result of LRS. The proof is given in the Appendix.

Theorem 1

Fix q = 1. Assume model (1), conditions (2) and (6). If

$$\mu \ge \sqrt{2(1+{\mathit{ϵ}}_n)\log n}/\sqrt{|I|}$$ (8)

for some ϵ_n such that ${ϵ}_n\gg 1/\sqrt{\log n}$, then the LRS is consistent for I, and the set of estimates𝕀̂ satisfies

$$P_{H_0}(|\widehat{𝕀}|>0)\le C/\sqrt{\log n}\to 0,$$ (9)

and

$$P_{H_1}(\underset{\widehat{I}\in \widehat{I}}{\min }D(\widehat{I},I)>{\delta }_n)\le C{n}^{-C{ϵ}_n^2}+C\overline{s}L{n}^{-C{\delta }_n^2}\to 0$$ (10)

for any δ_n such that $\sqrt{\log \overline{s}+\log L}/\sqrt{\log n}\ll {\delta }_n\ll 1$.

The result in Theorem 1 implies that the identification threshold ${\rho }^{*}(={\rho }_1^{*})$ is smaller than or equal to $\sqrt{2\log n}/\sqrt{|I|}$. In order to specify ρ*, we also need to derive a good lower bound for ρ*. By Theorem 2.3 in Arias-Castro et al. (2005), it follows that given log s̄ = o(log n), which is implied by (2) and (6), no method can reliably detect the existence of the signal segment when $\mu \le \sqrt{2\log n}/\sqrt{|I|}$. Since identifying the location of a signal segment is more difficult than detecting its existence, no identification procedure can be consistent when $\mu \le \sqrt{2\log n}/\sqrt{|I|}$. Therefore, ρ* should be larger than or equal to $\sqrt{2\log n}/\sqrt{|I|}$. By summarizing the above, we have the following corollary on the exact level of ρ* and the optimality of LRS.

Corollary 3.1

Fix q = 1. Consider model (1) and assume that the conditions (2) and (6) hold. Then the identification threshold ρ* is $\sqrt{2\log n}/\sqrt{|I|}$, and no identification procedure for I is consistent when $\mu \le \sqrt{2\log n}/\sqrt{|I|}$. On the other hand, the LRS is optimal in a sense that it is consistent for I when $\mu \ge \sqrt{2(1+{\in }_n)\log n}/\sqrt{|I|}$ for some ϵ_n such that $1/\sqrt{\log n}\ll {\in }_n\ll 1$.

The proof of Corollary 3.1 is straightforward and thus omitted.

3.2 Optimality of LRS when q > 1

We now consider the general case with q > 1 and assume

$$\log q=o(\log n),$$ (11)

which says that the number of signal segments is relatively very small. Define

$${\mathrm{\Omega }}^{+}=\{I_j\in \{I_1,\dots ,I_q\}:{\mu }_j\sqrt{|I_j|}\ge \sqrt{2(1+{\mathit{ϵ}}_n)\log n}\},q_1=|{\mathrm{\Omega }}^{+}|$$

for some ϵ_n such that ${\in }_n\gg \sqrt{\log q}/\sqrt{\log n}$ and

$${\mathrm{\Omega }}^{-}=\{I_j\in \{I_1,\dots ,I_q\}:{\mu }_j\sqrt{|I_j|}\le \sqrt{2\log n}\},q_2=|{\mathrm{\Omega }}^{-}|.$$

Note that Ω⁺∪Ω⁻ asymptotically equals to the whole set {I₁, …, I_q} when ϵ_n = o(1). We show that no procedure is consistent for Ω⁻. But it is possible for Ω⁺, and LRS is consistent for Ω⁺.

Theorem 2

Consider model (1) and assumes that the conditions (2), (6) and (11) hold. Then LRS is consistent for Ω⁺, and no procedure is consistent for Ω⁻.

In addition to being consistent for Ω⁺, LRS has a desirable property of estimating the segments in an order that reveals the relative signal strength of the segments. It is clear that the strength of a signal segment depends on its length and mean level. We can order the segments in Ω⁺ as I₍₁₎, …, I_(q1) such that ${\mu }_{(1)}\sqrt{|I_{(1)}|}\ge \dots \ge {\mu }_{(q_1)}\sqrt{|I_{(q_1)}|}$, and we show that under some mild conditions on the separation of signal strength, LRS first identify I₍₁₎, then I₍₂₎, and so on. This additional information can be important to practitioners and provides a rank order of the segments identified by the LRS procedure.

Theorem 3

Consider model (1) and assume that the conditions (2), (6) and (11) hold. In addition, assume

$${\mu }_{(j)}\sqrt{|I_{(j)}|}-{\mu }_{(j+1)}\sqrt{|I_{(j+1)}|}\ge {\delta }_n\sqrt{2\log n},{\forall }_j=1,\dots ,q_1-1$$ (12)

for some δ_n such that $\sqrt{\log q_1+\log \overline{s}+\log L}/\sqrt{\log n}\ll {\delta }_n\ll 1$. Then LRS is consistent for Ω⁺ and identifies the elements in Ω⁺ in the order of I₍₁₎, … , I_(q1).

Remark: Condition (12) requires that the signal strengths of segments are well separated. Otherwise, it is intuitively clear that the order of the segments being identified may change.

3.3 Comparison with identifying unstructured signals

When signals do not compose of segments or any other specific structures, we have the following standard model for a sequence of high-dimensional data:

$$\mathrm{X}~N(\theta ,{\mathrm{I}}_n),\theta \in {ℱ}_{s,\mu },$$ (13)

where I_n is an n×n identity matrix and ℱ_s,µ is the collection of n-dimensional vectors with at most s entries equal to µ > 0 and other entries equal to 0. The parameters s, µ, and the locations of the nonzero entries are unknown. Compared to model (1), the current model does not include any information on signal structure, so that consistent identification should be more difficult. This is shown in the following lemma.

Lemma 3.1

Assume model (13) with log s = o(log n), then when $\mu \le \sqrt{2\log n}$, no identification procedure is consistent for 𝕀 = {i : θ_i ≠ 0}.

Lemma 3.1 follows directly from Theorem 5 in Genovese et al. (2009) when log s = o(log n). The result implies that the identifiable regions for unstructured signals cannot be broader than $\mu >\sqrt{2\log n}$. Comparing this result with the identifiable regions in Corollary 3.1, which is $\mu >\sqrt{2\log n}/\sqrt{|I|}$, we see a clear advantage of the latter if signals have segment structure with |I| > 1. Note that similar to log s = o(log n) in Lemma 3.1, log s̄ = o(log n) is implied by conditions (2) and (6) in Corollary 3.1. So the comparison here is meaningful. By utilizing the segment structure, LRS is able to reliably identify much weaker signals than the popular methods such as the FDR. More comparisons are demonstrated in Section 4.

4 NUMERICAL STUDIES

4.1 Simulation Studies

In this section, we study numerical properties of the LRS via Monte Carlo Simulations. The sample size is set to be n = 5 ×10⁴, q = 5 locations of signal segments are chosen randomly, and the length of each signal segment is set to be s = 10. We set the signal mean µ = 1, 1.75, and 2. The data X_i, i = 1, …, n, is generated from N(A, 1), where A = µ if i is located on a signal segment and 0 otherwise. We repeat each simulation example 50 times.

For each simulated data set, we perform the LRS using L = 20, which satisfies the condition (2). Further, we set the threshold t_n at $\sqrt{2\log (nL)}\approx 5.26$. Note that the identifiable threshold for µ in Corollary 3.1 is $\sqrt{2\log (n)}/\sqrt{s}\approx 1.47$. We measure the estimation accuracy of LRS by three summary statistics: D_j and BP_j measure how well a signal segment and particularly its two endpoints are estimated, and #O measures the number of over-selections. Specifically, for a signal segment I_j, define

$$D_j=\underset{\widehat{I}\in \widehat{𝕀}}{\min }D(\widehat{I},I_j)\text{and}B{P}_j=\min \{\underset{\widehat{I}\in \widehat{𝕀}}{\min }BP(\widehat{I},I_j),s\},$$

where D(Î, I_j) and BP(Î, I_j) are defined as in (4) and (7). It is clear that smaller D_j and BP(Î, I_j) corresponds to better matching between I_j and some estimate Î ∈ 𝕀̂, and D_j = 0 if and only if I_j = Î. The summary statistic #O is defined as

$$\#O=\#\{\widehat{I}\in \widehat{𝕀}:\widehat{I}\cap I_j=\mathrm{\varnothing },{\forall }_j=1,\dots ,q\},$$

which is a non-negative integer, and #O = 0 if there is no over-selected intervals. We present in Table 1 the medians of D₁, … ,D_q, BP₁, …,BP_q, and #O over 50 replications. To estimate the standard error of the medians, we generate 500 bootstrap samples out of the 50 replication results, then calculate a median for each bootstrap sample. The estimated standard error is the standard deviation of the 500 bootstrap medians. The results indicate that the LRS quickly gains power after µ passes the threshold 1.47 and becomes more accurate as µ further increases. These results also indicate that the LRS can estimate the exact segmental breakpoints very well when µ passes the theoretical threshold, as reflected by the small values of the BP statistics.

Table 1.

Medians of the summary statistics D_j, BP_j, j = 1, …, 5 and #O over 50 replications for LRS. The estimated standard errors appear in parentheses in Tables 1–5.

	D1 BP1	D2 BP2	D3 BP3	D4 BP4	D5 BP5	#O
µ = 1	1.00(0.000)	1.00(0.000)	1.00(0.000)	1.00(0.000)	1.00(0.000)	0(0)
	10(0.00)	10(0.00)	10(0.00)	10(0.00)	10(0.00)
µ = 1.75	0.05(0.023)	0.05(0.026)	0.11(0.074)	0.12(0.075)	0.07(0.028)	0(0)
	1(0.47)	1(0.51)	2(0.99)	2.5(1.40)	1(0.54)
µ = 2	0.05(0.015)	0.05(0.014)	0.05(0.017)	0.05(0.009)	0.04(0.004)	0(0)
	1(0.29)	1(0.29)	1(0.35)	1(0.26)	1(0.02)

Next, we show the order of signal segments being estimated by LRS. We use the same setting as in the previous example, except that the signal mean of the 5 segments are set differently as µ₁ = 4, µ₂ = 3.5, µ₃ = 3, µ₄ = 2.5, µ₅ = 2, and the segment lengths s = 10, 15 are employed for each segment. According to Theorem 3, the order of the segments being estimated should be I₁, I₂, I₃, I₄, I₅. In Table 2, we show the median of the estimation orders for each segment in 50 replications and the number of times when all segments are estimated in the correct order. In detail, let A_j be the vector of estimation orders of I_j in 50 replications and N_j = median(A_j). We report N_j for j = 1, …, q and #OC, the number of times when I₁ is estimated first, then I₂, and so on.

Table 2.

Medians (N₁, …, N₅) of the estimation orders for segments and number of times all segments are estimated in the correct order over 50 replications.

	µ1= 4	µ2= 3.5	µ3= 3	µ4= 2.5	µ5= 2	#OC
s = 10	1(0)	2(0)	3(0)	4(0)	5(0)	28(3.67)
s = 15	1(0)	2(0)	3(0)	4(0)	5(0)	34(3.26)

The results in Table 2 clearly demonstrate that segments with stronger signal strength are estimated earlier, and the estimation order of each segment (represented by N_j) is very stable over 50 replications. On the other hand, the order consistency of all segments (represented by #OC) is harder to be achieved, and the result improves as the difference between signal strengths increases. The signal strength is a combination of effects of ${\mu }_j\text{and}\sqrt{|I_j|}$, so that, when s increases from 10 to 15, the difference between signal strengths is multiplied by $\sqrt{15}/\sqrt{10}$.

We now compare the LRS procedure with two other popular procedures for selecting significant signals, the FDR and the HCT procedures, both of which do not consider segment structure of the signals. The FDR procedure is carried out by first calculating the p-values of observations as p_i = P(N(0, 1) > X_i), 1 ≤ i ≤ n, and then performing the BH procedure in Benjamini and Hochberg (1995). Note that the unidentifiable region for unstructured signals is $\mu \le \sqrt{2\log n}$ as shown in Lemma 3.1. We conjecture that the successful region for FDR and HCT is $\mu >\sqrt{2\log n}\approx 4.65$. In order to compare these three procedures, we simulated data with signal mean set to be µ = 2, 4, and 6. Since FDR and HCT procedures do not provide interval estimates as LRS does, the measures of D_j and #O cannot be applied. Instead, we report the median of the true positives (TP), which counts the number of correctly identified signals, and that of the false positives (FP), which counts the number of incorrectly selected noises.

Table 3 presents results that clearly demonstrate the advantages of using the LRS procedure. When µ = 2, which is greater than the bound 1.36 for LRS and less than 4.65, FDR has no power, HCT has some power but severe over-selection, while LRS selects 39 out of 50 signals and controls the number of false positives to be less than 2. As µ increases, the performances of FDR and HCT improve, while LRS remains very accurate. The simulation results clearly verify the advantage of LRS achieved by utilizing segment structure of the signals.

Table 3.

Medians of TP and FP in 50 replications for FDR with false discovery rate = 0.05 and 0.1, HCT and LRS.

	FDR (0.05)		FDR (0.1)		HCT		LRS
	TP	FP	TP	FP	TP	FP	TP	FP
µ = 2	0(0.0)	0(0.0)	0(0.0)	0(0.0)	15(4.1)	391(677.5)	39(1.6)	2(0.5)
µ = 4	30(1.1)	1(0.3)	25(1.2)	3(0.4)	33(1.3)	14(2.4)	50(0.1)	0(0.0)
µ = 6	49(0.1)	2(0.3)	50(0.5)	5(0.5)	49(0.2)	2(0.5)	50(0)	0(0.0)

Our last set of simulations aim to evaluate the effect of possible spatial correlations on the LRS procedure by generating the noises from a multivariate normal distribution with the correlation matrix Σ specified by Σ_i,j = ρ^j−i, for ρ = 0.5, 0.7 and 0.9. All the other parameters are set to the same values as those in the first example with µ=2.0. Table 4 shows that the LRS procedure is not very sensitive to the spatial correlations of the noises, unless the correlations are very high. As we see in our analysis of real CNV data set in Section 4.3, the autocorrelations of the noises are very small, we therefore expect the spatial correlations should have no or little effect on the LRS procedure for real applications.

Table 4.

Medians of the summary statistics D_j, j = 1, …, 5, and #O over 50 replications for the LRS for Gaussian models with correlated noises, where ρ is the correlation between two nearby observations.

	D1	D2	D3	D4	D5	#O
ρ= 0.5	0.05(0.051)	0.09(0.026)	0.05(0.021)	0.11(0.028)	0.11(0.028)	2(0.24)
ρ = 0.7	0.09(0.036)	0.10(0.045)	0.09(0.044)	0.10(0.029)	0.09(0.040)	6(0.50)
ρ = 0.9	0.30(0.092)	0.15(0.060)	0.12(0.044)	0.23(0.096)	0.20(0.088)	11.5(0.51)

4.2 Sensitivity to Choice of L

The parameter L determines the computational complexity of LRS, so that smaller value of L is preferred as long as condition (2) is satisfied. We study the effect of L on estimation accuracy using the same simulation setup as in Section 4.1 with µ = 2. and present the results in Table 5.

Table 5.

Medians of D_j, j = 1, …, 5 and #O over 50 replications for LRS with different choices of L.

	D1	D2	D3	D4	D5	#O
L = 5	0.22(0.083)	0.26(0.049)	0.22(0.026)	0.26(0.152)	0.22(0.000)	0(0)
L = 10	0.05(0.010)	0.02(0.022)	0.05(0.019)	0.05(0.005)	0.02(0.022)	0(0)
L = 20	0.05(0.022)	0.09(0.022)	0.00(0.025)	0.05(0.014)	0.05(0.020)	0(0)
L = 100	0.05(0.019)	0.07(0.039)	0.09(0.024)	0.05(0.025)	0.05(0.028)	0(0)

Table 5 shows that the estimation result is robust with respect to the choice of L as long as condition (2) is satisfied. When L < s̄, estimation accuracy deteriorates as no candidates cover a whole segment and the LRS does not efficiently utilize the segment structure. A simple remedy is to increase the value of L, which will cost more computation complexity. Another simple remedy is to combine the identified intervals that are very close to each other. A more serious problem may occur when L > d. Then it is possible to have long interval estimates that cover more than one signal segments, and the adjacent signal segments cannot be distinguished. However, we note that in applications, such as CNV analysis, signal segments are rare and randomly located, and the value of d is usually large. In the simulation example with n = 5 × 10⁴, s = 10 and q = 5, d is observed to be above 1000 in all 50 replications.

Remark:We note that the variance σ² is pre-specified in theory and simulation analysis above. In practice, the noise level σ is often unknown and needs to be estimated. Under the sparse setting of the present paper, σ can be easily estimated. A simple robust estimator is the following median absolute deviation (MAD) estimator:

$$\widehat{\sigma }=\frac{\text{median}|X_j-\text{median(}{X}_j)|}{0.6745}.$$

Alternatively, other standard estimation procedures such as the MLE, can be applied. In particular, under the sparsity condition in Section 3, (log q +log s̄= o(log n)), the convergence rate of the MLE $\widehat{\sigma }\text{is}\sqrt{n}$, which is much faster than the convergence rates in Section 3 for segment identification with known σ. In numerical analysis, either the MAD estimator or the MLE can be used.

4.3 Application to CNV Identifications

Copy number variants refer to duplication or deletion of a segment of DNA sequences compared to a reference genome assembly. Availability of high-throughput genotyping technology such as the Illumina HumanHap550 BeadChip has greatly facilitated the identification of such genomic structural variations in kilo-base resolution (Feuk et al. (2006); Eichler et al. (2007)). Such CNVs are not so rare in the population and have been reported to be associated with several complex human diseases such as autism (Sebat et al. 2007), bipolar disorder (Lachman et al. 2007), cardiovascular disease (Pollex and Hegele 2007), and neuroblastoma (Diskin et al. 2009). It is therefore, very important to have computationally efficient statistical methods to detect such copy variants.

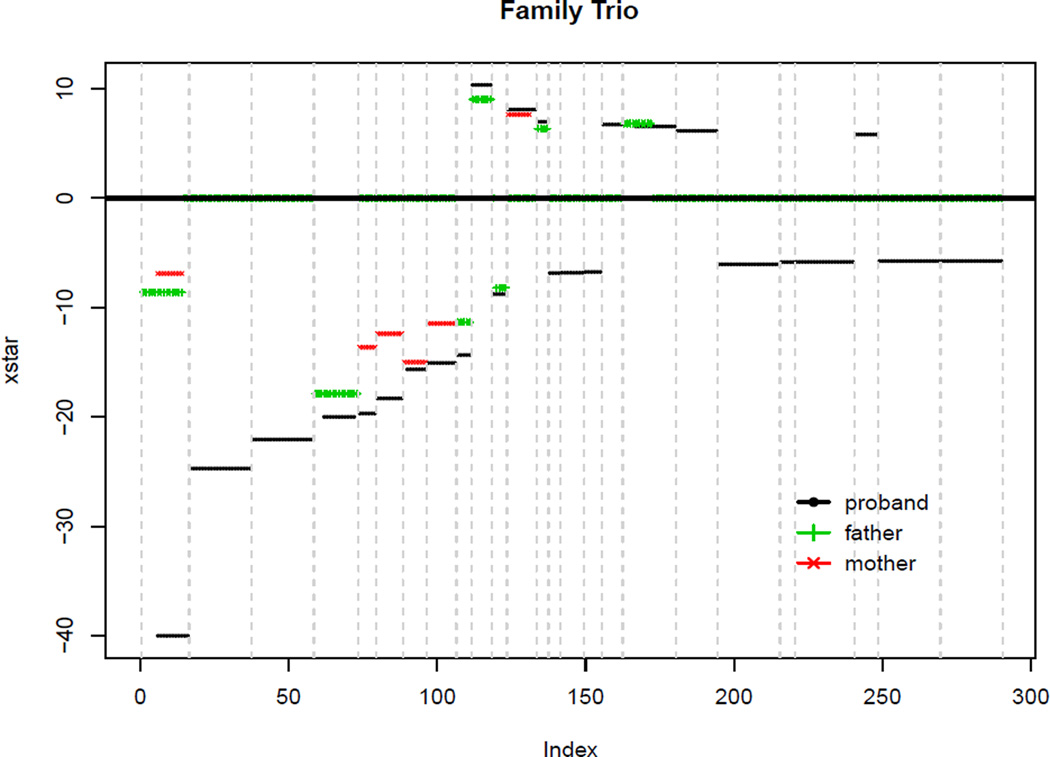
We demonstrate our proposed method using the genotyping data for a father-mother-child trio from the Autism Genetics Resource Exchange (AGRC) collection (Bucan et al. 2009), genotyped on the Illumina HumanHap550 array. For each individual and each SNP, our data is the measurement of normalized total signal intensity ratio called the Log R ratio (LRR), which is calculated as log₂(R_obs/R_exp) where R_obs is the observed total intensity of the two alleles for a given SNP, and R_exp is computed from linear interpolation of canonical genotype clusters (Peiffer et al. 2006). For each individual, we have a total of 547,458 SNPs over 22 autosomes, and the numbers of SNPs on each chromosome range from 8,251 on chromosome 21 to 45,432 on chromosome 2. To assess the levels of spatial correlations, we calculated the first- and second-order autocorrelations for the LRRs along the chromosomes and obtained the values of 0.095 and 0.085 for the child, 0.043 and 0.028 for the father, and 0.075 and 0.059 for the mother, respectively. This indicates that the spatial correlations among noises are indeed very weak. For each individual, our goal is to identify the CNVs based on the observed LRRs. We chose to use data from a trio in order to partially validate our results since we expect some CNVs are inherited from parents to child.

We first standardize the observed LRRs using MLE of mean and variance of the noise. Since both duplication and deletion can occur in a CNV region, a simple modification of taking absolute value of the likelihood ratio should be added in the LRS procedure, i.e. replace the X(Ĩ) in step 1 and 2 with |X(Ĩ)|. Also, because the numbers of SNPs in observed CNVs are usually smaller than 20 SNPs, we chose L = 20 in our LRS procedure. In addition, we only consider CNVs with 4 or more SNPs. The LRS procedure identified 18, 28 and 25 CNVs in father, mother and the child, respectively. The sizes of the identified CNV regions range from 4 to 20 for all three individuals, with most of them smaller than 20. Figure 1 shows the CNV segments with the likelihood ratio test scores (xstar) for the segments that the LRS algorithm selected for the child. We also plotted the CNV segments identified in the parents if they overlap with the CNV segments of the child. It is interesting to note that many of the CNV segments identified in the child were also observed in one of the parents, further indicating that some CNVs are inheritable and our LRS algorithm can effectively identify these CNVs. We examined the segments that were identified in the child only (i.e., the De novo CNVs) and noted that most of these segments are real. For example, plot (a) and (b) of Figure 2 presented the observed LRR values for the CNV regions that were identified in the child, but not in either of the parents. Plot (a) clearly indicates two CNVs identified by the LRS procedure. Further examination of this region indicates that there is in fact one longer CNV in this region, which is longer than 20. The LRS algorithm identified these two CNVs because L was set to 20 in order to save the computation time (see our discussion on the choice of L in Section 4.2), so that only intervals ≤ 20 were considered. As a common practice, one can always perform certain post-processing of the results to merge the close segments. The LRR values in plot (b) are not very large, however, most of the SNPs have negative LLR values. Comparing to the neighboring SNPs, it seems that there is indeed a change in LRR values.

Figure 1.

Summary of results of LRS for CNV detection for a trio: the LR test statistics for the CNV segments identified by the proposed LRS procedure for the child, sorted by the absolute values of the likelihood ratio statistics. One segment with large statistics (−116.70 for the child) is truncated as −40 for better view.

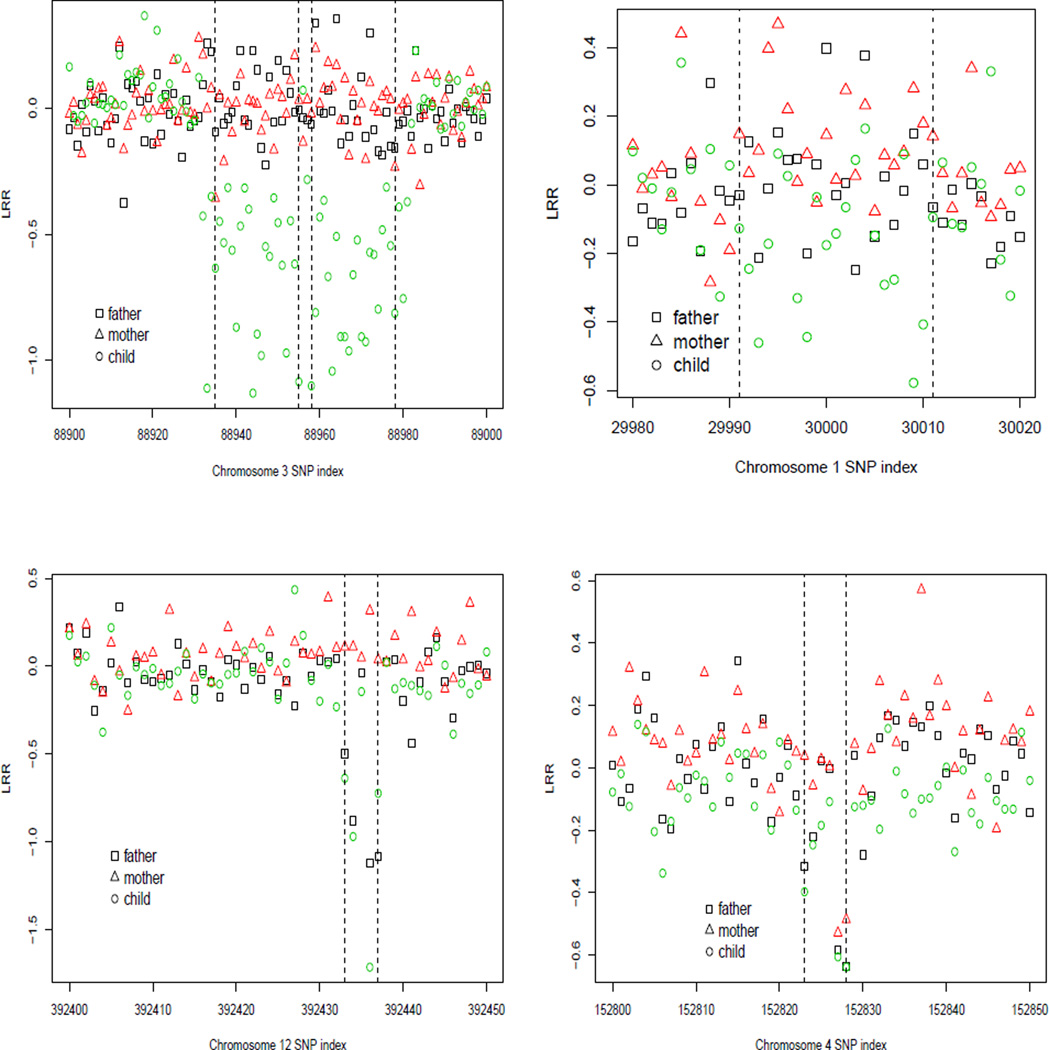
Figure 2.

LRR data for the CNV segments identified in the child. Top panel: CNV segments identified in the child, but not in either of the parents. (a) the two CNV segments on chromosome 3 and (b) the CNV segment on chromosome 1 that were identified in the child but not in either of the parents. Bottom panel: CNV segments identified by the LRS procedure but missed by the HHM method. (c) CNV segment on a chromosome 12 region and (d) CNV segment on a chromosome 4 region that were identified by LRS procedure but missed by the hidden Markov model. The CNV is marked by the two vertical dashed lines.

As a comparison, the hidden Markov model (HMM)-based method as implemented in PennCNV package (Wang et al. 2007) identified 16, 18 and 17 CNVs in father, mother and the child, respectively. If the trios are considered together and the familial transmission of the CNVs is also considered, the PennCNV identified 21, 21 and 20 CNVs in the father, mother and the child, respectively. Overall, we see that the LRS procedure identified almost all the CNVs that were identified by the HMM-based procedure. However, the LRS identified a few more CNVs that are missed by the hidden Markov model-based method. As an example, the LRS procedure identified an identical deletion CNV of 5 SNPs in both the father and the child on chromosome 12, but the HMM method failed to identify this CNV. The plot (c) of Figure 2 shows the observed LLR for the SNPs in this CNV region, clearly indicating that the existence of a CNV in this region. Another example includes a deletion CNV with 6 SNPs that was not identified in the child by the HMM approach (see plot (d) of Figure 2). Note that the LLR of all these 6 SNPs are negative in this CNV region, further indicating that this CNV is likely to be true. However, this of course needs further biological validation.

5 Discussion

We have studied the problem of detecting and identifying sparse short segments in a long one dimensional sequence of data with Gaussian noise. The conditions for the existence of a consistent identification procedure were given. The LRS procedure was developed and shown to be optimal in selecting the true segments. The simulation results have clearly demonstrated that the proposed procedure can greatly outperform other popular methods such as the FDR or HCT when the segmental features of the signals are present. We demonstrated the LRS procedure in an application that identifies CNVs based on high-density SNP data, showing that our procedure can be more powerful than other popular methods such as the HMM-based methods.

The optimality of LRS is essentially guaranteed by its close relationship to generalized likelihood ratio test (GLRT), which can be computationally very expensive when dealing with high-dimensional data. The LRS procedure utilizes the short-segment structure of the data by only considering short intervals as candidates, which reduces the order of computation complexity from n² to n × L. This large reduction makes LRS an efficient method for handling ultrahigh-dimensional signal detection problem.

In the present paper we focused on the optimal segment identification with Gaussian noise. Another important topic is the development of efficient procedures and theoretical results for segment identification with general noise. Moreover, an interesting problem for future research is to develop a similar framework for segment identifications using data from multiple sequences when one can assume that the segment starts at the same location at least over a subset of these sequences (Zhang et al. 2008). This can potentially increase the power of detecting the true segments that are shared across multiple samples.

APPENDIX: PROOFS

In this section, we provide the proofs for the theorems and lemma presented in this paper. Denote P_A(B) as the probability of B given A.

Proof of Theorem 1

We show (9) first. Recall that for any interval Ĩ,

$$X(\tilde{I})={\displaystyle \sum _{i\in \tilde{I}}{X}_i/\sqrt{|\tilde{I}|}}.$$

The construction of 𝕀̂ by LRS implies that

$$P_{H_0}(|\widehat{𝕀}|>0)\le P_{H_0}(\underset{\tilde{I}\in 𝕁n(L)}{\max }X(\widehat{I})>t_n)\le n\cdot L\cdot P(N(0,1)>t_n)\le \frac{C}{\sqrt{\log n}}.$$

.

Next, we show (10). Recall 𝕀⁽¹⁾ = {Ĩ ∈ 𝕁_n(L) : X(Ĩ) > t_n}. Define the following events:

$$A=\{{𝕀}^{(1)}\ne \mathrm{\varnothing }\}\text{and}B=\{D({\widehat{I}}_1,I)\le \delta n\}.$$

It is easy to see that

$$P_{H_1}(\underset{\widehat{I}\in \widehat{𝕀}}{\min }D(\widehat{I},I)>{\delta }_n)=1-P_{H_1}(A\cap B)=1-P_{H_1}(A)(1-P_{H_1}(B^c|A))\le P_{H_1}(A^c)+P_{H_1}(B^c|A).$$ (14)

Now we calculate the above two terms respectively. By definition of 𝕀⁽¹⁾,

$$P_{H_1}(A^c)=P_{H_1}(\underset{\tilde{I}\in {𝕁}_n(L)}{\max }X(\tilde{I})\le t_n)\le P_{H_1}(X(I)\le t_n)=P_{H_1}(N(0,1)\le t_n-\mu \sqrt{I})\le n^{-C{\mathit{ϵ}}_n^2}$$ (15)

under condition (8). For the second term, define

$${𝕂}_n(L)=\{\tilde{I}\in {𝕀}^{(1)}:D(\tilde{I},I)>{\delta }_n\}.$$

Then given A, B^c implies Î₁ ∈ 𝕂_n(L), which, by the definition of Î₁, implies the existence of some Î ∈ 𝕂_n(L) such that X(Ĩ) ≥ X(I). Denote

$${𝕂}_0=\{\tilde{I}\in {𝕂}_n(L):\tilde{I}\cap I=\mathrm{\varnothing }\},{𝕂}_1=\{\tilde{I}\in {𝕂}_n(L):\tilde{I}\cap I=\mathrm{\varnothing }\}.$$

So we have

$$P_{H_1}(B^c|A)\le P_{H_1}(\exists \tilde{I}\in {𝕂}_n(L):X(\tilde{I})\ge X(I))\le {\displaystyle \sum _{\tilde{I}\in {𝕂}_0}{P}_{H_1}(X(\tilde{I})-X(I)\ge 0)+}{\displaystyle \sum _{\tilde{I}\in {𝕂}_1}{P}_{H_1}(X(\tilde{I})-X(I)\ge 0).}$$ (16)

Since both X(Ĩ) and X(I) are normal random variables, we can write

$$X(\tilde{I})-X(I)=L{R}_1+L{R}_2+L{R}_3,$$

Where

$$L{R}_1=(\frac{1}{\sqrt{|\tilde{I}|}}-\frac{1}{\sqrt{|I|}}){\displaystyle \sum _{i\in \tilde{I}\cap I}{X}_i~N({\nu }_1,{\tau }_1),}$$

$$L{R}_2=\frac{1}{\sqrt{|\tilde{I}|}}{\displaystyle \sum _{i\in \tilde{I}\backslash \tilde{I}\cap I}{X}_i~N({\nu }_2,{\tau }_2),}$$

$$L{R}_3=-\frac{1}{\sqrt{|\tilde{I}|}}{\displaystyle \sum _{i\in I\backslash \tilde{I}\cap I}{X}_i~N(-{\nu }_3,{\tau }_3),}$$

$${\nu }_1=(\frac{1}{\sqrt{|\tilde{I}|}}-\frac{1}{\sqrt{|I|}})|\tilde{I}\cap I|\mu ,{\nu }_2=0,{\nu }_3=\frac{|I\backslash \tilde{I}\cap I|}{\sqrt{|I|}}\mu ,$$

$${\tau }_1={(\frac{1}{\sqrt{|\tilde{I}|}}-\frac{1}{\sqrt{|I|}})}^2|\tilde{I}\cap I|,{\tau }_2=\frac{|\tilde{I}\backslash \tilde{I}\cap I|}{|\tilde{I}|},{\tau }_3=\frac{|I\backslash \tilde{I}\cap I|}{|I|}.$$

Note that LR₁, LR₂ and LR₃ are independent, then

$$L{R}_1+L{R}_2+L{R}_3~N(\nu ,\tau ),$$

Where

$$\nu ={\nu }_1+{\nu }_2-{\nu }_3\le (\frac{|\tilde{I}\cap I|}{\sqrt{|\tilde{I}|}}-\sqrt{|I|})\mu ,\tau ={\tau }_1+{\tau }_2+{\tau }_3\in \left[0,3\right].$$

Since M(Ĩ, I) < 1 − δ_n implies

$$(\frac{|\tilde{I}\cap I|}{\sqrt{|\tilde{I}|}}-\sqrt{|I|})\mu <-{\delta }_n\sqrt{|I|}\mu ,$$

then for any Ĩ ∈ 𝕂_n(L),

$$\nu \le -\mu \sqrt{|I|}{1}_{\{\tilde{I}\cap I=\mathrm{\varnothing }\}}-{\delta }_n\mu \sqrt{|I|}{1}_{\{\tilde{I}\cap I=\mathrm{\varnothing }\}}.$$

On the other hand, the cardinality of 𝕂₀ is bounded by Σ_{Ĩ∈𝕁n(L):Ĩ∩I=∅} 1{X(Ĩ) > t_n}, which converges to Σ_{Ĩ∈𝕁n(L):Ĩ∩I=∅}P(X(Ĩ)>t_n) exponentially fast. Therefore, under condition (8), we have

$${\displaystyle \sum _{\tilde{I}\in {𝕂}_0}{P}_{H_1}(X(\tilde{I})\ge X(I))\le C\cdot L\cdot P}(N(0,\tau )\ge \mu \sqrt{|I|})\le C{n}^{-C}$$ (17)

and

$${\displaystyle \sum _{\tilde{I}\in {𝕂}_1}{P}_{H_1}(X(\tilde{I})\ge X(I))\ge |I|\cdot L\cdot P}(N(0,\tau )\ge {\delta }_n\mu \sqrt{|I|})\le C|I|L{n}^{-C{\delta }_n^2},$$ (18)

where $|I|L{n}^{-{\delta }_n^2}\to 0$ by the range of δ_n. Combine (16), (17), and (18), we have

$$P_{H_1}(B^c|A)\le C{n}^{-C\mathit{ϵ}n}+C|I|L{n}^{-C{\delta }_n^2}.$$ (19)

.

Finally, (10) follows by summing up (14), (15), (19) and the range of ϵ_n.

Proof of Theorem 2

For the result in set Ω⁻, we apply a similar regrouping idea as in Arias-Castro et al. (2005). Assume (A) only segments in Ω⁻ exist, and they are in {k_js̄+1, …, (k_j+1) s̄} for some k₁, … k_q1 . We show that no procedure is consistent under this situation. This is enough to show that no procedure is consistent in Ω⁻ without assuming (A). Let

$$W_k=(X_{k\overline{s}+1}+\dots +X_{(k+1)\overline{s}})/\sqrt{\overline{s}}={\theta }_k+Z_k^{\text{'}},k=0,\dots ,n/\overline{s}-1,$$

where $Z_k^{\text{'}}{~}^{iid}N(0,1)$. Note that θ_k = 0 at all but q₂ randomly chosen locations. Since log q₂ = o(log n) is implied by condition (11), then result follows by Lemma 3.1.

For the result in set Ω⁺, it is enough to show

$$P_{{\mathrm{\Omega }}^{+}=\mathrm{\varnothing }}(|\widetilde{𝕀}|>0)\le \frac{C}{\sqrt{\log n}}\to 0,$$ (20)

and

$$P_{{\mathrm{\Omega }}^{+}=\mathrm{\varnothing }}(\underset{I_j\in {\mathrm{\Omega }}^{+}}{\max }\underset{{\tilde{I}}_j\in \widehat{𝕀}}{\min }D({\widehat{I}}_j,I_j)>{\delta }_n)\le C{q}_1{n}^{-C{ϵ}_n^2}+C{q}_1\overline{s}L{n}^{-C{\delta }_n^2}\to 0$$ (21)

for ϵ_n and δ_n such that

$${\mathit{ϵ}}_n\gg \frac{\sqrt{\log q}}{\sqrt{\log n}},\frac{\sqrt{\log q_1+\log \overline{s}+\log L}}{\sqrt{\log n}}\ll {\delta }_n\ll 1.$$

We extend the proof of Theorem 1 to the case q₁ > 1. Obviously, (20) can be derived by the same argument for (9). Now we consider (21). Note that all the elements in 𝕁_n(L) can not reach more than one signal segments. Therefore, the construction of 𝕀̂ implies that the accuracy of estimating any I_j ∈ Ω⁺ is not influenced by the estimation of other elements in Ω⁺. (Other elements can only influences the order of I_j being estimated.) This means that the accuracy of estimating any I_j ∈ Ω⁺ is equivalent to the case when only one segment I_j exists. Define the following events:

$$A_j=\{I^{(1)}\ne \mathrm{\varnothing }\text{and only}{I}_j\text{exists}\},B_j=\{D({\widehat{I}}_{1,}{I}_j)\le {\delta }_n\},j=1,\dots ,q_1.$$

Then we have

$$P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(\underset{I_j\in {\mathrm{\Omega }}^{+}}{\max }\underset{{\widehat{I}}_j\in \widehat{𝕀}}{\min }D({\widehat{I}}_j,I_j)>{\delta }_n)\le P(\exists I_j\in {\mathrm{\Omega }}^{+}:I_j\in A_j^c\cup (A_j\cap B_j^c))\le {\displaystyle \sum _{j=1}^{q_1}P(A_j^c)}+{\displaystyle \sum _{j=1}^{q_1}P}(B_j^c|A_j).$$ (22)

By similar arguments leading to (15) and (19) in proof of Theorem 1, we have

$$P(A_j^c)\le n^{-C{\mathit{ϵ}}_n^2},P(B_j^c|A_j)\le C{n}^{-C{\mathit{ϵ}}_n}+C|I_j|L_n{}^{-C{\delta }_n^2},j\in \{1,\dots ,q_1\}.$$ (23)

Then (21) follows after combining (22) and (23).

Proof of Theorem 3

For the result of LRS in set Ω⁺, it is enough to show

$$P_{{\mathrm{\Omega }}^{+}=\mathrm{\varnothing }}(|\widehat{𝕀}|>0)\le \frac{C}{\sqrt{\log n}}\to 0,$$ (24)

and

$$P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(\underset{1\le j\le q_2}{\max }D({\widehat{I}}_j,I_{(j)})>{\delta }_n)\le C{q}_1{n}^{-C{\mathit{ϵ}}_n^2}+C{q}_1^2\overline{s}L{n}^{-C{\delta }_n^2}\to 0$$ (25)

for ϵ_n and δ_n such that

$${\mathit{ϵ}}_n\gg \frac{\sqrt{\log q}}{\sqrt{\log n}},\frac{\sqrt{\log q_1+\log \overline{s}+\log L}}{\sqrt{\log n}}\ll {\delta }_n\ll 1.$$

Note that the order of segments being estimated is fixed in (25).

Obviously, (24) can be derived by the same argument for (9). Now consider (25). Define the following events:

$$A_j=\{{𝕀}^{(j)}\ne \mathrm{\varnothing }\},B_i=\{D({\widehat{I}}_j,I_{(j)})\le {\delta }_n[2\log n/({\mu }_{(j)}^2{I}_{(j)})]\},j=1,\dots ,q_1.$$

Then we have

$$P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(\underset{1\le j\le q_1}{\max }D({\widehat{I}}_j,I_{(j)})>{\delta }_n)\le 1-P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(A_1\cap B_1\cap \dots \cap A_{q_1}\cap B_{q_1})\le P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(A_1^c)+P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(B_1^c|A_1)+\dots +P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(B_{q_1}^c|A_1,B_1,\dots ,A_{q_1}).$$ (26)

.

Since the signal segments are not too close to each other, by the choice of L in (2), none of the candidates in 𝕀⁽¹⁾ reaches more than one signal segments. This means that given A₁,B₁, …,A_j−1,B_j−1, I_(j) has not been deleted in the first j −1 loops. So by similar argument leading to (15), we have

$$P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(A_j^c|A_1,B_1,\dots ,A_{j-1},B_{j-1})\le P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(X(I_{(j)})\le t_n)\le n^{-C{\mathit{ϵ}}_n^2},j=1,\dots ,q_1.$$ (27)

.

Some modifications are needed to derive a similar result as (19). Given A_j, we have X(Î_j) ≥ X(I_(j)) since I_(j) is not deleted in the first j − 1 loops. Define

$${𝕂}_n^{(j)}(L)=\{\widehat{I}\in {𝕀}^{(1)}:D(\widehat{I},I_{(j)})>{\delta }_n[2\log n/({\mu }_{(j)}^2{I}_{(j)})]\},j=1,\dots ,q_1.$$

Then given $A_j,B_j^c\text{implies}{\widehat{I}}_j\in {𝕂}_n^{(j)}(L)$, which further implies the existence of some $\widehat{I}\in {𝕂}_n^{(j)}(L)$ such that X(Ĩ) ≥ X(I_(j)). Denote

$${𝕂}_0^{(j)}=\{\tilde{I}\in {𝕂}_n^{(j)}(L):\tilde{I}\cap I_{(k)}=\mathrm{\varnothing },k=1,\dots ,q_1\},$$

$${𝕂}_1^{(j)}=\{\tilde{I}\in {𝕂}_n^{(j)}(L):\tilde{I}\cap I_{(k)}\ne \mathrm{\varnothing },k\in \{1,\dots ,q_1\}\}.$$

So we have

$$P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(B_j^c|A_1,\dots ,B_{j-1},A_j)\le {\displaystyle \sum _{\tilde{I}\in {𝕂}_0^{(j)}}P(X(\tilde{I})-X(I_{(j)})\ge 0)}+{\displaystyle \sum _{\tilde{I}\in {𝕂}_1^{(j)}}P(X(\tilde{I})-X(I_{(j)})\ge 0)}.$$ (28)

Rewrite X(Ĩ) − X(I) = LR₁ + LR₂ + LR₃ the same way as in the proof of Theorem 1. Consider the set Ĩ\Ĩ ∩ I_(j). Unlike in the q = 1 case, where this set includes only noise, here it can overlap with other signal segments, which are I_(j+1), …, I_(q1) and I₍₁₎\(Ĩ₁ ∩ I₍₁₎), …, I_(j−1)\(Ĩ_j−1 ∩ I_(j−1)). Note that for any k ∈ {1, …, j − 1},

$$B_k\Rightarrow \frac{\sqrt{|{\widehat{I}}_k\cap I_{(k)}|}}{\sqrt{|I_{(k)}|}}\ge 1-{\delta }_n\frac{2\log n}{{\mu }_{(k)}^2|I_{(k)}|}\Rightarrow |{\widehat{I}}_k\cap I_{(k)}|\ge {(1-{\delta }_n\frac{2\log n}{{\mu }_{(k)}^2|I_{(k)}|})}^2|I_{(k)}|$$

$$\Rightarrow \sqrt{|I_{(k)}\backslash {\widehat{I}}_{(k)}\cap I_{(k)}|}\le 2\sqrt{{\delta }_n\frac{\log n}{{\mu }_{(k)}^2}}\Rightarrow {\mu }_{(k)}\sqrt{|I_{(k)}\backslash ({\widehat{I}}_{(k)}\cap I_{(k)})|}\le 2\sqrt{{\delta }_n\log n}.$$

Then, given A₁, …, B_j−1, A_j, LR₂ has mean value

$${\nu }_2\le \max \{{\mu }_{(j+1)}\sqrt{|I_{(j+1)}|},2\sqrt{{\delta }_n\log n}\}={\mu }_{(j+1)}\sqrt{|I_{(j+1)}|}$$

when Ĩ∩I_(k) ≠ ∅ for k ≠ j, and ν₂ = 0 otherwise. Correspondingly, given $A_1,\dots ,B_{j-1},A_j,B_j^c$ implies that LR₁ + LR₂ + LR₃ has mean value

$$\nu \le (\frac{|\tilde{I}\cap I_{(j)}|}{\sqrt{\tilde{I}}}-\sqrt{|I_{(j)}|}){\mu }_{(j)}+{\mu }_{(j+1)}\sqrt{|I_{(j+1)}|}{1}_{\{\tilde{I}\cap I_{(k)}\ne \mathrm{\varnothing },k\ne j\}}\le -{\mu }_{(j)}\sqrt{|I_{(j)}|}{1}_{\{\tilde{I}\cap (I_{(1)}\cup \dots \cup I_{(q_1)})=\mathrm{\varnothing }\}}-{\delta }_n{\mu }_{(j)}\sqrt{|I_{(j)}|}{1}_{\{\tilde{I}\cap I_{(j)}\ne \mathrm{\varnothing }\}}-({\mu }_{(j)}\sqrt{|I_{(j)}|}-{\mu }_{(j+1)}\sqrt{|I_{(j+1)}|})1_{\{\tilde{I}\cap I_{(k)}\ne \mathrm{\varnothing },k\ne j\}}.$$

By the fact that ${\mu }_{(j)}\sqrt{|I_{(j)}|}\ge \sqrt{2(1+{ϵ}_n)\log n}$ in Ω⁺ and condition (12), we further get

$$\nu \le -{\sqrt{2(1+{\mathit{ϵ}}_n)\log n1}}_{\{\tilde{I}\cap (I_{(1)}\cup \dots \cup I_{(q_1)})=\mathrm{\varnothing }\}}-{\delta }_n\sqrt{2\log n}{1}_{\{\tilde{I}\cap I_{(k)}\ne \mathrm{\varnothing },k\in \{1,\dots ,q_1\}\}}.$$

So, in set Ω⁺, we have

$${\displaystyle \sum _{\tilde{I}\in {𝕂}_0^{(j)}}P(X(\tilde{I})-X(I_{(j)})\ge 0)}\le CLP(N(0,\tau )\ge \sqrt{2(1+{\mathit{ϵ}}_n)\log n})\le C{n}^{-C}$$ (29)

and

$${\displaystyle \sum _{\tilde{I}\in {𝕂}_1^{(j)}}P(X(\tilde{I})-X(I_{(j)})\ge 0)}\le q_1\overline{s}LP(N(0,\tau )\ge {\delta }_n\sqrt{2\log n})\le C{q}_1\overline{s}L{n}^{-C{\delta }_n^2}.$$ (30)

Combine (28), (29), and (30), we have

$$P_{{\mathrm{\Omega }}^{+}\ne \mathrm{\varnothing }}(B_j^c|A_1,\dots ,B_{j-1},A_j)\le C{n}^{-C{\mathit{ϵ}}_n}+C{q}_1\overline{s}L{n}^{-C{\delta }_n^2}.$$ (31)

.

Finally, (25) follows by summing up (26), (27), and (31).