A New Perceptual Difference Model for Diagnostically Relevant Quantitative Image Quality Evaluation: A Preliminary Study

Abstract

Purpose

Most objective image quality metrics average over a wide range of image degradations. However, human clinicians demonstrate bias toward different types of artifacts. Here, we aim to create a perceptual difference model based on Case-PDM that mimics the bias of human observers towards different artifacts.

Method

We measured artifact disturbance to observers and calibrated the novel PDM. To tune the new model, which we call Artifact-PDM, degradations were synthetically added to three healthy brain MR data sets. Four types of artifacts (noise, blur, aliasing, or “oil-painting” which shows up as flattened, over-smoothened regions) of standard Compressed Sensing (CS) reconstruction, within a reasonable range of artifact severity, as measured by both PDM and visual inspection, were considered. After the model parameters were tuned by each synthetic image, we used a Functional Measurement Theory pair-comparison experiment to measure the disturbance of each artifact to human observers and determine the weights of each artifact’s PDM score. To validate Artifact-PDM, human ratings obtained from a Double Stimulus Continuous Quality Scale experiment were compared to the model for noise, blur, aliasing, oil-painting and overall qualities using a large set of CS reconstructed MR images of varying quality. Finally, we used this new approach to compare CS to GRAPPA, a parallel MRI reconstruction algorithm.

Results

We found that for the same Artifact-PDM score, the human observer found incoherent aliasing to be the most disturbing and noise the least. Artifact-PDM results were highly correlated to human observers in both experiments. Optimized CS reconstruction quality compared favorably to GRAPPA’s for the same sampling ratio.

Conclusions

We conclude our novel metric can faithfully represent human observer artifact evaluation and can be useful in evaluating CS and GRAPPA reconstruction algorithms, especially in studying artifact trade-offs.

1. INTRODUCTION

Magnetic Resonance Imaging (MRI) provides soft tissue contrast superior to other imaging modalities, but also typically requires longer acquisition time, which limits its applications in many scenarios such as diagnosis and management of acute ischemic stroke³³. One way to reduce acquisition time is by reducing the amount of acquired data, and applying complicated reconstruction algorithms to recover full FOV images from the partially acquired data. However, the challenge is to retain as much diagnostic information as possible, relative to an ideal image reconstructed from fully sampled data.

In Partially Parallel Imaging (PPI), the incomplete data can be reconstructed using knowledge of coil sensitivity patterns and/or reference data¹⁹. However, noise and aliasing artifacts are commonly seen in PPI³². As a result, many regularization techniques have been applied to PPI reconstruction to improve or trade-off these degradation patterns. For instance, Tikhonov regularization, when applied to Generalized Autocalibrating Partially Parallel Acquisition (GRAPPA), trades off noise and blur artifacts³⁴. Since these regularization techniques require optimization of reconstruction parameters, it is possible to create thousands of test images. It is impractical to evaluate all of these images by hand, so there is a great need for computer evaluation of image quality, a need that has been emphasized in recent scientific meetings^1–3.

Current popular assessment methods are insufficient. Signal to Noise Ratio (SNR) and Root Mean Square Error (RMSE) are the standard measurements, but they can be diagnostically misleading³⁵. For example, an image with higher SNR but lower spatial resolution does not necessarily provide more diagnostic information than an image with lower SNR but higher spatial resolution³⁶. In fact, radiologists are more accustomed to images with a certain level of white noise than to noise-free images^36,37. When a reference image is available, a minimum error energy criterion, RMSE, is often employed. However, the minimum error may not be the most diagnostically accurate image either, especially after trading-off different types of artifacts that happen when regularization is employed. Regularization also has the potential to create structured image features that do not exist in the true image. This kind of image features like ghosting artifact may show up as a small RMSE, but could lead to misdiagnosis^4–6, especially when these new features have similar structure to local anatomy. This prevents the using of blind expert reviewers to assess comparative image quality, because those erroneous “features” will not necessarily be recognized as incorrect.

A perceptual difference model (e.g., Case-PDM) is superior to other automatic evaluation metrics, including detection models, for evaluation of MR image quality⁷. However, current models do not differentiate between different artifacts, each of which interferes with diagnostic information in different ways. For example, Hunold et al.⁸ found that aliasing artifacts impair diagnostic value of the cardiac images more severely than noise in cardiac cine MRI. Krishnam et al.⁹ found that flow-related artifacts and cardiac motion artifacts degrade diagnostic content of steady-state free precession (SSFP) magnetic resonance angiography (MRA) images more than noise and blurring effects. In 7T brain imaging, aliasing artifacts are more dangerous than other artifacts. For instance, they can obscure Hippocampal structures to create a significant disturbance during brain disease diagnosis¹⁰. Radiographic interpretation training documents¹¹ state that structured noise, as opposed to random noise, can contribute to visual search errors that are common and most often result from incomplete evaluation of a medical image. Although many observers learn to recognize artifacts, the need to negotiate around numerous artifacts leads to reduced observer confidence in decision making¹². Therefore, to create an image quality metric that is diagnostically relevant, one has to quantify the relative disturbance of those different image artifacts to the observer.

To assess MR image reconstruction algorithms in the past, we have used a perceptual difference model (Case-PDM), which models the functional anatomy of the visual pathway, including the optics of the eye, the sensitivity of the retina, the spatial contrast sensitivity, and the channels of spatial frequency found in the visual cortex^7,20. The two inputs are a test image (acquired quickly and therefore likely to be degraded) and a reference image (acquired more slowly and therefore with higher quality). The output is a spatial map of the likelihood of a perceptible difference, which can be averaged over a region-of-interest (ROI) to yield a scalar image quality metric. Case-PDM has been shown in a variety of MR experiments (including parallel MR imaging) to correlate with human observers^7,20–22. It has been used for comparing competing MR reconstruction methods and for optimizing algorithmic free parameters^20–22.

Compressed Sensing (CS) allows the reconstruction of sparse images or signals from very few samples^13–14. It has recently been applied to MRI for reconstruction with partially acquired data^15–18. There are at least two advantages to CS over PPI. First, although PPI reduces acquisition time at the cost of reduced SNR, CS typically has higher SNR than the reference image, whereas PPI does not, because CS typically does not use as much regularization as PPI due to its highly incoherent sampling¹⁵. Second, CS does not require expensive multi-channel receiver systems. However, current CS reconstructions also trade off artifact removal and preservation of sharp edges and fine structures. This can be caused by improper regularization of the sparsifying transforms and/or improper balance of sparsity and data fidelity^38,39. The damaged information and unpredictable residual artifacts could be mistaken for pathology³⁶.

In this paper, we develop a novel model (Artifact-PDM) that is able to quantify the severity of different degradations. We calibrated and compared the results of this model to experimentally measured CS and PPI reconstruction image quality using two kinds of experiments: FMT (Functional Measurement Theory) experiments to calibrate the relative severity of different typical MRI reconstruction artifacts, and DSCQS (Double-Stimulus Continuous-Quality Scale) experiments to determine the correlation between the automatic and human observer image quality.

2. METHODS

Case-PDM mimics the human visual system to capture the perceptual difference between input reference and test images. In the Case-PDM, the visual cortex filter has 31 channels: 6 different orientations with 6 different spatial frequencies and the baseband (zero spatial frequency). Each of these channels is equally weighted, which means that Case-PDM averages image quality over a wide range of image artifacts. We extended Case-PDM to include the severity of disturbance of different reconstruction artifacts. Then, we calibrated the relative severity among artifact evaluations and validated this new metric using human observer experiments.

2.1 Development of Artifact-PDM

To selectively evaluate different image artifacts, the 31 channels of the cortex filter should be weighted differently, according to the characteristic spatial frequency and orientation of each specific artifact. To do this, synthetic images were created from each input reference image by adding one type of distortion like noise, blur, aliasing, or oil-painting artifact, and then normalized between 0 and 255. Responses of these 31 cortex channels for each synthetic image were summarized to be 31 scalar scores and then normalized between zero and one. Thus, there are 4 sets of normalized values, or channel weights, corresponding to each type of artifact. In order to evaluate one specific artifact of a MR image reconstruction, which has multiple types of artifact in it, a corresponding set of channel weights multiplied PDM to weight the 31 cortex channels for the selective evaluation. The whole image region was used as a ROI in this paper. Thus, the new algorithm can give multiple artifact-specific assessments. However, these selective-artifact PDM scores may not be comparable due to their unknown relative importance. To make the selective evaluations comparable, we must calibrate them to the disturbance of each type of artifact, which was determined by human observers. We term this algorithm “Artifact-PDM”.

2.2 Raw Data and Reconstruction Algorithms Used in Experiments

A Total Variation (TV) and Wavelet Transform (WT) sparsification based CS reconstruction algorithm¹⁵, and the GRAPPA parallel MRI k-space reconstruction algorithm²⁷ were evaluated and compared in this paper. Three high resolution raw parallel MRI brain data sets (T₂-weighted, flip angle = 90°, TR/TE = 3000/85 ms, matrix size 512×512, slice thickness = 20mm, FOV = 205mm×205mm, resolution 0.4mm×0.4mm) were acquired from a healthy volunteer. Three planes were acquired (Sagittal, Coronal, and Transverse) on a Philips Achieva 3T scanner (Best, Netherlands) with an 8-channel head coil (Invivo Corporation, Gainesville, Florida, United State). Data for GRAPPA reconstruction²⁷ was synthetically generated by decimating the original full-sampled k-space data by the reduction factor, which is an integer number f_R (i.e. one of every f_R k-space lines in phase encoding direction is omitted). The calibration region of k-space was fully sampled, and the missing k-space data were estimated with GRAPPA. Finally, the reconstructed image was obtained by sum-of-squares of the multi-channel data. The reference images were obtained from the raw data sets by using sum-of-squares.

Data for CS reconstruction was generated synthetically by randomly under-sampling the two-dimensional reference k-space data, which was obtained from the reference image through Fourier transform, in the phase encoding direction. Then, the CS algorithm was used to recover a full-FOV image¹⁵. The sampling pattern was created according to predesigned probability density function (PDF) with a sampling ratio r_S (r_S = 1/f_R) ¹⁵. We used a set of optimal regularization parameters reported previously³⁹.

We compared both algorithms to the naive zero-filling method (i.e. zero-filling the non-sampled k-space), or “ZF”, and to each other. For GRAPPA reconstruction, a kernel of regular size 4×5 was used for each channel. A wide range of r_S was used in the MRI reconstructions. All three reconstruction methods can produce noise, blur and aliasing artifacts. Only CS reconstruction can have oil-painting artifact.

2.3 Measuring Artifact Disturbance: FMT (Functional Measurement Theory) Experiment

We used a FMT experiment to measure artifact disturbance to human observer. In image quality research, it is known that if scenes have to be judged by direct rating, subjects may use a separate internal quality scale for each distortion observed. The Functional Measurement Theory (FMT) experiment is adopted from Anderson’s functional measurement theory^23–24. In this approach, image qualities are compared rather than separately evaluated, in order to force subjects to link the quality ratings for both images that have degradation patterns. Thus, it is possible to measure artifact disturbance to observer by rating different degradation patterns through FMT experiment.

Three raw brain images (“Sagittal”, “Coronal”, and “Transverse” in Fig. 1a–c) of size 512×512 were used to generate test images. Each image was directly degraded by adding four types of artifacts respectively: noise, blur, aliasing and oil-painting artifacts. Gaussian white noise with zero mean and different standard deviations (σ=1–30) was added to the real and imaginary channels of complex k-space data, obtained from the original image through Fourier transform, to create the noisy datasets. Blurred datasets were created by convolving the original image with a circular averaging filter (i.e. a pillbox filter) of radius 0.5 to 0.7. Aliased datasets were created by variable density random sampling patterns. Here, randomly selected phase encode lines are inverse Fourier transformed after zero-filling the unsampled k-space data. Oil-painting artifacts were created by CS reconstruction with a relatively high TV weight. We ensured the range of severity for each artifact was reasonable and comparable by using both Case-PDM and visual inspection. Hence, three datasets were generated, where each dataset had one reference image (Sagittal, Coronal, or Transverse) and 20 degraded images (four degradation patterns with 5 levels of degradation each). Within each dataset, every test image was compared to every other test image, including a comparison to itself, giving a total 231 comparisons. Each pair of images was shown twice at random, giving 441 evaluations.

Fig. 1.

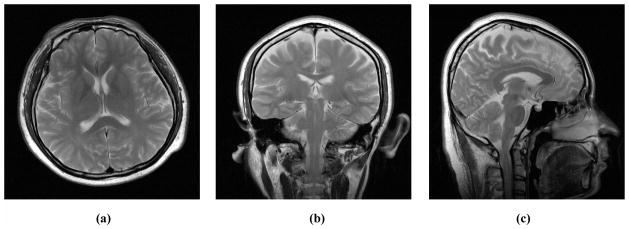
Raw images used for human observer experiments. (a) is Transverse, (b) Coronal, and (c) Sagittal. Their MR raw data were used for both CS and PPI reconstruction.

During the experiment, each evaluation was displayed with the images side by side on the screen, and human subject was asked to rate the quality difference between them (subjects were asked: “how much Left image is better than Right image”) using a scale from −10 to +10. The plus and the minus signs were used to indicate whether the left or the right image was preferred. A training session of 60 randomly selected images pairs, which were not included in the test datasets but were similar to them, was presented to each subject before the start of the actual experiment. There was 18 seconds time limit for each trial.

FMT data analysis was done on subjective rating matrices. For each subject, one 21×21-element matrix was obtained (one row and one column per image) for each part of the experiment, with element (i, j) representing the score given by the subject for the difference in quality between the pair of images, images i and j being displayed on the left and the right hand sides of the GUI, respectively. To apply the FMT method, one needs to observe parallelism for the scores within the different rows and columns, or to calculate the interaction between rows and columns by means of two-way analysis of variance method²⁴. If parallelism was observed or no significant interaction was found, according to FMT, a quality score on an interval scale for each stimulus can be determined by averaging (with opposite signs) the row and column means of the matrix that correspond to that stimulus. A general quality score for all subjects was obtained by averaging the individual quality scores, after normalizing the individual scores using a z-score transform²⁴,

$$z_i=\frac{x_i-\overline{x}}{\sigma }$$ (1)

where x̄ and σ are mean and standard deviation for score x, to minimize the variation in the individual score, which is caused by the fact that not all subjects used the full range of the numerical scale in comparing image qualities.

We calibrated Artifact-PDM to the subjective data. First, Artifact PDM was used to calculate artifact-selective PDM scores for the test images. Then, for each degradation pattern, we fit Artifact-PDM scores and their corresponding z-scores obtained from FMT experiment to a curve modeled by y = ax^b using a least squares approach. a and b are scalar values, y represents z-scores shifted by an offset value equal to the reference z-score and x represents for the Artifact-PDM predictions. An origin is added representing the reference image, which has the best image quality, to optimize the regression line. This allows Artifact-PDM to be comparable across different degradation patterns, with a calibrated score of zero representing best image quality. The fitting accuracy was examined by calculating the correlation coefficient of the model transformation log(y) = log(a) + b log(x).

Once the Artifact-PDM has been calibrated by FMT, it can be used to evaluate images degraded by multiple types of artifacts. Assessment of each artifact can be quantified by converted z-score (or, “artifact score”) from Artifact-PDM score. Overall image quality, which considers the observer’s bias over different degradation patterns, can thus be obtained by averaging all the artifact scores (we call it “comprehensive score” hereafter). A score value of zero always indicates the best image quality.

2.4 Human Subject Correlation: Double-Stimulus Continuous-Quality Scale (DSCQS) Experiment

We used DSCQS experiment to validate the new artifact assessment metric on CS reconstructions corrupted by four types of artifacts. Test images were created by the CS reconstruction algorithm¹⁵. The same raw brain images (Fig 1a–c) were used. DSCQS is a human subject rating method recommended by International Telecommunication Union²⁵ It has been applied to MRI previously^20,26. Here, we used a previously described method^{7, 21} to test the full range of image quality in our images. For each experiment, we selected 40 test reconstructions with Case-PDM scores spread uniformly from the best to the worst. Each human subject presentation consisted of a two-panel display, with the high-quality reference image and a randomly selected test image on the left and right, respectively. Observers were instructed to score the quality of the test image on a scale of 100 to 0, with 0 being the best quality and 100 being the worst quality. Observers were aware that we considered the reference image to be “best” and that they should consider it to have a score of zero⁷. A training session consisted of 30 test images was supplied for each subject before the experiment. The training dataset was independent of experimental datasets but was similar to one of them. In both the training and the experimental sessions, subjects were asked to rate five image quality aspects (noise, blur, aliasing, oil-painting and overall) in each image presentation. The score was entered using either the mouse or keyboard. To account for intra-observer differences, each of the 40 test images was displayed and evaluated twice in each session. The experiment was carried out in a darkened room and normally took 1 hour. A perceptually linearized, high quality monitor was used. There was no time limitation, and subjects were allowed to revise any of their results at any time.

We studied correlation between artifact scores and subjective ratings. First, the two scores for the same test image and subject were averaged to reduce intra-observer variability. Observer data from each subject were fitted to model y = ax + b, where x is Artifact-PDM score and y is z-score. The x-intercepts of these fitted lines were calculated, and these intercepts actually corresponded to the data points where Artifact-PDM found the difference but human subjects did not. Therefore, the x-intercept could be regarded as a measurement of the “non-perceptible” threshold. To test the model prediction accuracy, linear correlation coefficients (i.e. Perason’s product-moment coefficients) between artifact scores and corresponding human ratings were calculated.

2.5. Experimental Conditions

We used a display software running on a conventional Dell Precision T5400 Mini Tower, Quad Core Xeon Processor 3.0-GHz personal computer (Dell Inc., Round Rock, TX) with a NVIDIA NVS 290 256MB RAM display adapter. We used a standard Dell UltraSharp 24-inch widescreen flat panel LCD display color monitor (model 2408WFP) with a 6ms pixel refresh rate and a display resolution of 1920 × 1200 pixels. The display had an 8-bit dynamic range and pixel size on the screen was 0.3 mm. The minimum and maximum luminances were 0.01 Cd/m² (black) and 99.9 Cd/m² (white) at gray-levels of 0 and 255, respectively. All experiments were performed in a dark room. The viewing was binocular and the viewing distance was loosely enforced at 0.3 meter. To maintain constant display conditions across observers, subjects were not allowed to adjust window or level settings or to use the zoom function. The same display and viewing conditions were also applied to Artifact-PDM.

Four engineers and one radiologist, aged between 19 and 33 years, participated in the FMT (Eng_1-4 and Rad) and DSCQS (Eng_1-2) experiments as observers. All observers had normal or corrected-to-normal visions, and their acuities were measures using a Snellen eye chart at a distance of 10 ft (3.05 m) and a reading card at 14 in (0.356 m).

3. RESULTS

3.1 Artifact Disturbance Calibration for Artifact-PDM (FMT)

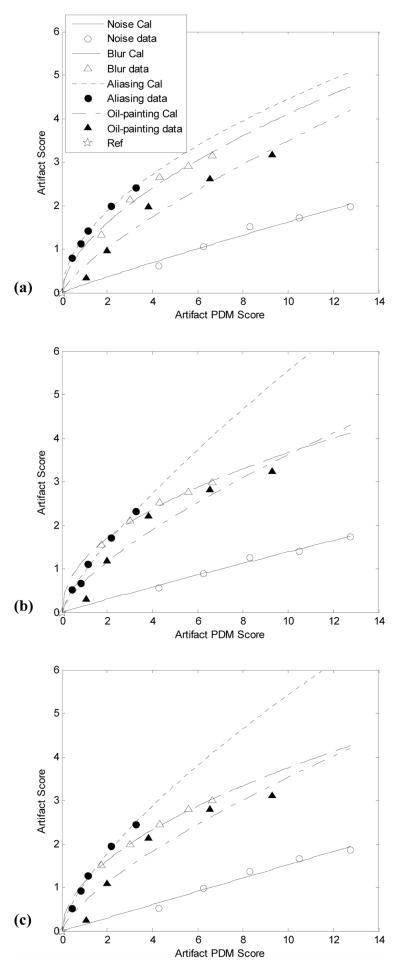
Parallelism was observed and no significant interaction was found within every subject’s raw 21×21-element matrix data, confirming a good FMT experiment. For each data set, the subjective rating matrix was transformed into 21 z-scores for the 21 test images including the reference image, and then averaged over all four subjects. The averaged z-score for each reference image is listed in Table 1. With an origin at the z-score of reference image, the averaged human subject data were plotted against corresponding artifact PDM scores in Fig. 2, and data from four different degradation patterns (i.e. noise, blur, aliasing and oil-painting) were fitted to a non-linear model, to form four FMT curves (or, “calibration lines”). The Artifact-PDM predictions agreed an average correlation coefficient of 0.98 with subjects’ ratings for all different artifacts, subjects and data sets. All four calibration lines were separate, indicating that not all artifacts have the same ranking according to human observers. Within a reasonably wide range of artifact, which we found to be approximately from 0 to 12 in terms of PDM score⁷, only calibration lines of blur can interact with aliasing. Noise is the least disturbing artifact among the four types of artifacts. We found the variation of calibration lines across three brain data sets was about 0.11 of the ratio of standard deviation to mean, which implies little variability between data sets.

Table 1.

Reference image’s z-score (origin of calibration line)

		Transverse	Coronal	Sagittal
Reference Z-Score	mean	−1.7983	−1.6644	−1.7501
	std	0.2279	0.2788	0.1818

Fig. 2.

Artifact disturbance calibration lines obtained from FMT experiment for the Transverse (a), Coronal (b) and Sagittal (c) data sets. For the same artifact severity of noise, blur, aliasing, or oil-painting degradation pattern, as measured by Artifact-PDM, their disturbances to human observer distribute differently, with noise being the least disturbing. One could observe that the Artifact-PDM shows good correlation to artifact scores, but the relationship is not linear except for the noise.

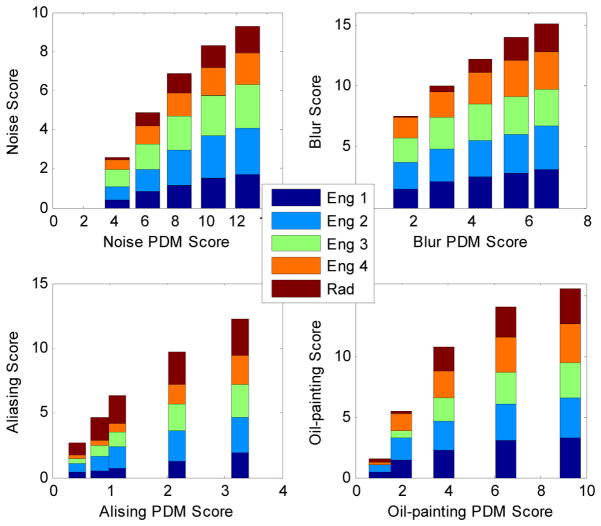
The radiologist performed similarly to the other engineers. Fig. 3 shows individual ratings against PDM predictions for one brain data set during the FMT experiment.

Fig. 3.

Individual ratings from one radiologist and four engineers against Aliasing-PDM predictions when they evaluated Transverse brain data set during the FMT experiment.

3.2 Human Subject Correlation (DSCQS)

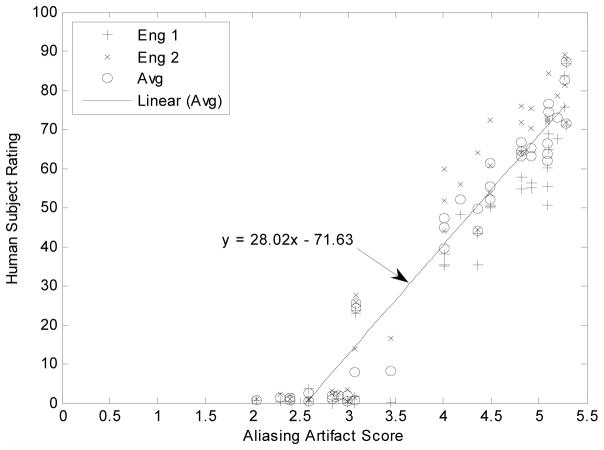
The human rating results were plotted as the function of artifact scores and Fig. 4 shows results from the DSCQS aliasing artifact experiment for the Sagittal data set. A highest linear correlation coefficient, r²=97%, was observed between the human subject ratings and aliasing scores. Correlations with different artifact scores and x-intercepts for all three data sets are summarized in Table 2.

Fig. 4.

Linear correlation between Artifact-PDM and observers when evaluating aliasing artifact. Data are from CS reconstructions of Sagittal image in the DSCQS experiment. Cross points represent responses from subject Eng-1, “x” points represent responses from subject Eng-2, and open circle points represent average responses. The average human subject data (open circle) were fitted to y = ax + b, and the functions were represented by the straight lines in the figure.

Table 2.

Data analysis for DSCQS experiment

	Transverse		Coronal		Sagittal
	Correlation	Intercept	Correlation	Intercept	Correlation	Intercept
Noise Score	0.8046	2.1474	0.8332	2.0345	0.8711	2.1898
Blur Score	0.9504	2.9226	0.9231	2.9346	0.8472	3.1908
Aliasing Score	0.9517	2.7485	0.9664	2.2989	0.9706	2.5560
Oil-Painting Score	0.9308	1.8402	0.8878	1.6373	0.8999	1.1914
Comprehensive Score	0.9509	1.6582	0.9461	1.5035	0.9563	1.9642

3.3 Comparison of MRI Reconstruction Algorithms

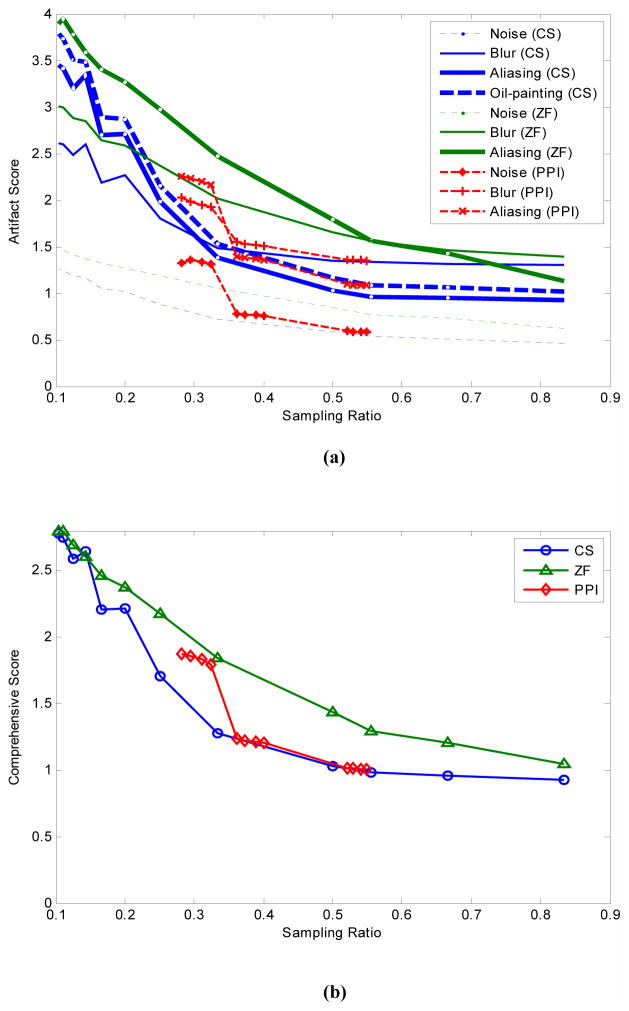
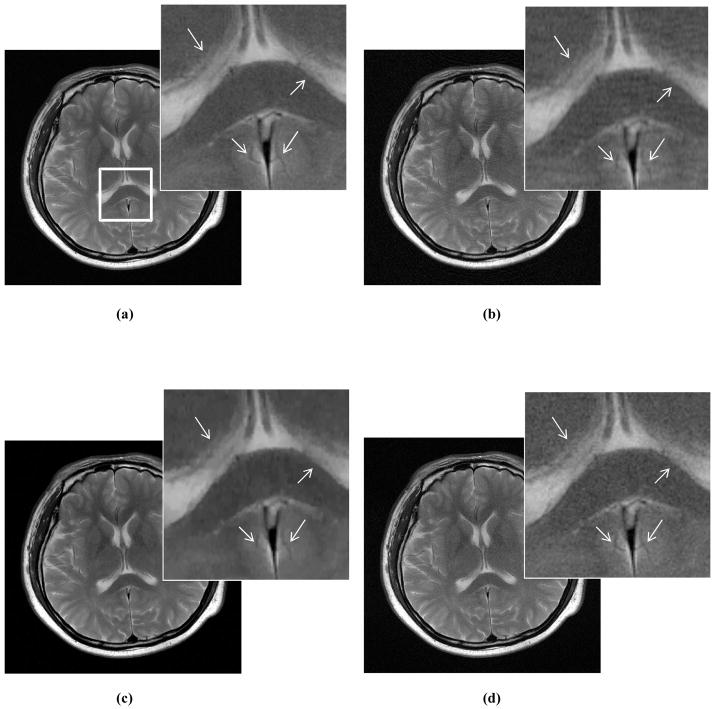
To compare reconstruction algorithms, we averaged calibration lines (Fig. 2) across three training data sets since their variations were relatively small. Fig. 5 contains plots of the reconstruction image quality (artifact score and overall quality, or comprehensive score) as a function of sampling rate r_S for the Transverse data set. Out of the averaged artifact scores for the three algorithms, ZF’s aliasing had the highest score and CS’s noise the lowest (Fig. 5a). In terms of overall image quality (Fig. 5b), CS outperformed GRAPPA at low sampling rate (r_S <0.33) but both performed very closely above that. Both algorithms were better than ZF. Fig. 6 shows images reconstructed by each of the three algorithms with a 50% sampling rate. Similar results were also observed for the Coronal and Sagittal data sets.

Fig. 5.

Comparison of MR reconstruction algorithms for the Transverse data set. (a) shows different artifact scores for CS, ZP and PPI reconstructions at different sampling rate. (b) shows comprehensive score for the three methods. CS was ranked the best by both selective artifact evaluation and overall quality evaluation.

Fig. 6.

Algorithm comparison for MR reconstructions using only 50% data. (a) is a reference image. (b)–(d) correspond to images reconstructed by ZF, CS and GRAPPA, respectively.

4. DISCUSSION

In this preliminary study of diagnostically relevant image quality, we measured human observer bias towards individual artifacts, and correlated this to our novel perceptual model, Artifact-PDM. For a comparable severity of image degradation, as measured by Case-PDM, observers rated images degraded with different artifacts differently. For our brain data sets, within a relevant, but wide, range of severity, as measure by Artifact-PDM, disturbances due the four tested artifacts were ranked as: aliasing>oil-painting>noise, with blur ranked either before or after aliasing (depending on its severity). The high ranking of aliasing might be because subjects’ eyes are more sensitive to middle spatial frequencies as compared to both low and high spatial frequencies⁴⁰. Among the four artifacts, disturbance due to noise is almost linear with severity (i.e. fitting coefficient b ≈ 1 in the model y = ax^b), while all others are nonlinear (Fig. 2). This is likely because the frequency spectrum of white noise is very stable^28,41.

The observer and artifact scores were highly correlated in both the FMT and DSCQS experiments. The FMT experiment showed a correlation of r²=0.97 between observer ratings and Artifact-PDM scores, which indicates that calibrated Artifact-PDM can faithfully represent the observer bias. The DSCQS experiment validated the ability of this new metric to discriminate between different artifacts in images corrupted by a mixture of degradations. In this experiment, calibrated Artifact-PDM showed high correlation (r² up to 96%) with both selective artifact ratings and overall quality ratings (Table 2). The Artifact-PDM’s overall quality assessment, or comprehensive score, was obtained by averaging the artifact scores. The x-intercepts in Fig. 4 provide one method to determine the “non-perceptible difference” threshold. As shown in Table 2, these intercepts varied for different artifacts and different images. This implies that human perceptual sensitivity varies to different artifact⁴². However, this is not a very robust method to calculate the threshold, because significant extrapolation is required. To precisely measure the non-perceptible difference threshold, one needs to perform an alternative forced choice (AFC) experiment⁷. However, this result was not needed for this demonstrative study, so we did not determine the thresholds in this paper.

Artifact-PDM can characterize image artifacts by their spatial frequencies and orientations. Similarly, findings in both physiology and psychophysics²⁸ show that human visual system is a linear system and neurons in the striate cortex are tuned to specific spatial frequencies and orientations. Here, we used a cortex filter with 6 orientation channels and 6 spatial frequency channels to mimic the human visual cortex. By weighting these different channels, Artifact-PDM was able to discriminate different types of image artifacts, as validated by DSCQS experiment. This is because each image artifact can be characterized by specific frequencies and orientations. For example, aliasing artifact due to under-sampling demonstrates certain repetitive spatial pattern, which is often seen in MR image reconstruction. However, a calibration procedure might be needed when evaluating a new type of artifact and/or a different organ/anatomy. In this preliminary study, we only showed brain data sets. We will use other organs/image contents to validate this new metric. As the current study did not include pathological data, we will continue to study the performance of Artifact-PDM for evaluation of clinical images.

We used the entire image region as a ROI for assessing different types of artifacts including aliasing. To evaluate aliasing better, one can apply a binary mask, which corresponds to the repetitive image parts, to the spatial map of Artifact-PDM output. Such masks may be determined through edge detection on both reference and test images, and/or Fourier analysis of sampling pattern. We will study this topic further in the future.

Artifact-PDM was useful for evaluating reconstruction algorithms. The proposed image quality evaluation metric was able to quantify the relative severity of different artifacts in the same image. For the same sampling ratio, Artifact-PDM showed that CS reconstruction quality compared favorably to that of GRAPPA, having less noise, blur and aliasing artifact. Our metric was especially helpful in quantifying image artifact trade-offs, which can allow the optimization of free parameters to yield reconstructions with the lowest possible perceptual disturbance.