Dental CT metal artefact reduction based on sequential substitution

Abstract

Objective: Metal artefacts can seriously degrade the visual quality and interpretability of dental CT images. Existing image processing algorithms for metal artefact reduction (MAR) are either too computationally expensive to be used in clinical scanners or effective only in correcting mild artefacts. The aim of the present study was to investigate whether it is possible to improve the efficacy of the computationally efficient projection-correction approach to MAR by exploiting the spatial dependency or autocorrelation between adjacent CT slices.

Methods: A new projection-correction algorithm [MAR by sequential substitution (MARSS)] was developed based on the idea that the corrupted portions of the projection data can be substituted with the corresponding portions from an unaffected adjacent slice. The performance of MARSS was evaluated relative to the projection-correction method of Watzke and Kalendar using a two-alternative forced choice (2AFC) visual trial involving 20 observers and 20 clinical CT data sets.¹⁶

Results: The Cochran Q test revealed no significant difference in the responses across all observers. The data were then pooled and analysed using a one-tailed exact binomial test. This revealed that the proportion of responses in favour of MARSS was significant (P < 2.2 × 10⁻¹⁶). A second Cochran Q test revealed no significant difference in the responses across all images.

Conclusions: It is possible to improve the efficacy of projection correction by exploiting spatial autocorrelation. The 2AFC results suggest that the proposed MARSS algorithm outperforms competing computationally efficient algorithms in terms of reducing metal artefacts whilst at the same time preserving/revealing anatomic detail.

Introduction

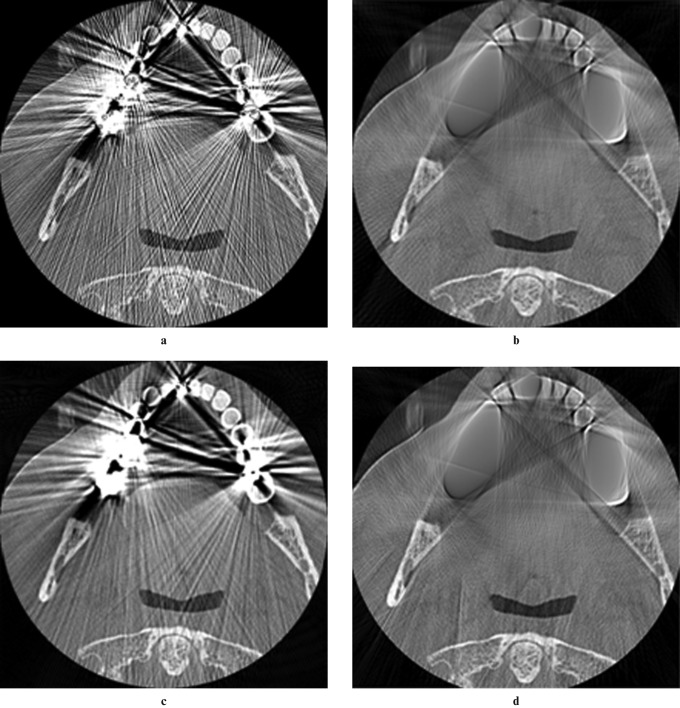
CT is an attractive modality for dental imaging because the resulting image data reveal the true three dimensional (3D) relationships between teeth and their supporting tissues. Applications of dental CT include the investigation of disease in deep bony tissues, the assessment of injury/fractures in the maxillofacial region, pre-operative assessment for implants and forensic identification.^1,2 Nevertheless, the interpretation of CT images can be problematic because they can contain geometric and intensity artefacts or distortions which seriously degrade the image quality.³ In dental CT the most significant sources of artefacts are metallic restorations. These metal artefacts present as pronounced dark and light streaks in the CT images reconstructed using the filtered back-projection method commonly used in commercial CT scanners (Figure 1a). Although the filtered back-projection method is an explicit and computationally efficient way of reconstructing a CT slice image from its sinogram or projection data, it is not optimal when the object being scanned contains metal parts. This is because the X-rays that pass through them are much more attenuated than those that pass through soft tissues and bone. Reconstruction of the resulting incomplete/corrupted sinogram data using filtered back projection then yields images with dark and light streaks. The greater the number of metal objects present, the worse the degree of metal artefact corruption.

Figure 1.

Visual comparison of the efficacy of several metal artefact-reduction algorithms. (a) Original dental CT image containing metal artefacts originating from several metal restorations. (b) Method of Kalender et al.⁹ (c) Method of Takahashi et al.¹² (d) Method of Watzke and Kalender¹⁶

A number of practical steps can be taken to avoid or minimize metal artefacts, including having the patient remove metal objects (e.g. jewellery) and adjusting the gantry angulation. Whilst the adjustment of gantry angulation can eliminate or significantly diminish the occurrence of metal artefacts in adjacent slices (called interplane artefacts), it cannot effectively diminish metal artefacts within a slice (called inplane artefacts). For this reason, a variety of image-processing algorithms have been developed to reduce metal artefacts in CT images post acquisition. They can be broadly classified into four groups: (i) iterative reconstruction methods; (ii) projection-correction methods; (iii) reconstruction-correction methods; and (iv) combinations of i–iii.

Iterative reconstruction methods are specifically designed to reconstruct images from incomplete projections.^4-6 They permit flexible modelling of the sinogram formation process and of the statistics of projection uncertainty.⁷ Although these methods can effectively reduce the appearance of metal artefacts in the reconstructed images, they are computationally much more expensive than filtered back projection and thus impractical for clinical use in CT scanners.⁸

Projection-correction methods are designed to correct those portions of the projection data corrupted by the presence of metal parts.^9-12 The effectiveness of these methods depends on both the accuracy with which the corrupted portions of the sinogram are identified and the quality of the correction performed. The fact that metal artefacts are a mixture of beam hardening, partial volume and aliasing artefacts in particular makes the accurate determination of the metal-related corruption in the projection data difficult.¹³ Consequently, whilst such methods can significantly attenuate metal artefacts originating from a single metal object, they are much less effective when multiple metal objects are involved.

Reconstruction correction methods are designed to correct metal artefacts in the images reconstructed from the corrupted projection data.^14,15 The main advantage of this class of methods is that they are computationally efficient because they operate on the reconstructed images without the requirement of forward and backward projection. Their disadvantage is that they are effective only for correcting mild artefacts.

Finally, hybrid methods are combinations of the above approaches. An example is the method of Watzke and Kalender,¹⁶ which yields a single corrected image from a weighted combination of the results of a projection-correction and a reconstruction-correction method.

In summary, none of the existing metal artefact reduction methods are suitable for use in clinical dental CT scanners because they are either computationally too expensive or effective only in correcting mild artefacts. Of the computationally efficient metal artefact reduction algorithms that have been published, only a small number are designed/claimed to be effective for metal artefacts induced by multiple metal parts. These include the projection-correction methods of Kalender et al⁹ and Takahashi et al¹² and the hybrid method of Watze and Kalender.¹⁶ Figure 1 illustrates that although the hybrid method yields the best result, none of these methods are entirely satisfactory.

The aim of the present study was to investigate whether it is possible to improve the efficacy of projection correction whilst preserving its computational efficiency by exploiting the spatial dependency or autocorrelation between adjacent CT slices. The question was motivated by our previously reported investigation into the feasibility of using radiograph-like images reconstructed from post-mortem dental CT data for forensic identification.¹⁷ More specifically we investigated the feasibility of matching these radiograph-like images to ante-mortem conventional radiographs (periapical, bitewing and panoramic) on the basis of tooth/restoration contours. Therein we reported on the need for metal artefact reduction to improve both the visual quality of the reconstructions and their interpretability, particularly in relation to tooth contours. To this end we present a new metal artefact reduction algorithm. We also present the results of an empirical evaluation of the efficacy of the algorithm vs the method of Watzke and Kalender.¹⁶

Materials and methods

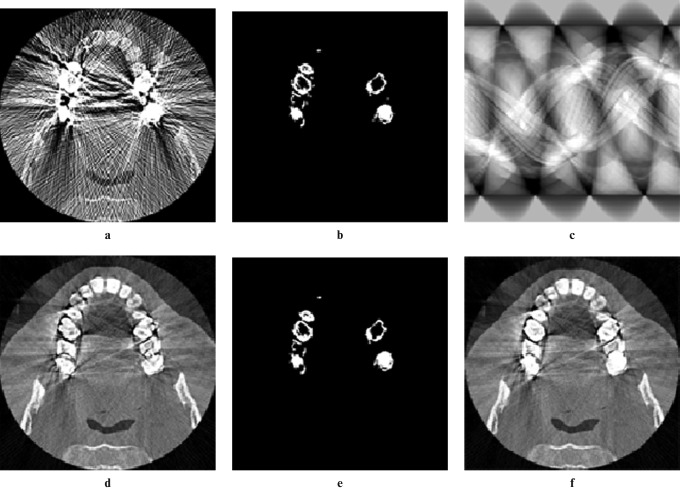
The proposed algorithm, which we call metal artefact reduction by sequential substitution (MARSS), is based on the idea that the corrupted portions of the projection data can be substituted with the corresponding portions of the projection data from an unaffected adjacent slice. The rationale is that in reconstructed CT data there exists spatial dependence or autocorrelation such that voxels in close proximity will have similar values. In the case of dental CT, if the data are acquired so that the axial slices are parallel to the occlusal plane then metal artefacts will be predominantly intraplane and not interplane. This means that reconstructed axial slices containing the roots of the teeth will be free from metal artefacts. Thus, proceeding sequentially from the roots to the crown, when a slice with metal artefacts is encountered, its sinogram is corrected using data from the sinogram or corrected sinogram of the preceding slice. A formal description of the MARSS method for dental CT data is presented in Table 1. The algorithm takes as input a set of axial slice images through the maxilla or mandible, acquired parallel to the occlusal plane, that have been reconstructed by the CT scanner. It also takes as input a threshold value (T) and a radius (r). The threshold is used to obtain a binary mask of the metal restorations in each slice. The connected components in this mask corresponding to the metal restorations are likely to have linear protuberances from the streak artefacts. Furthermore the mask may contain additional narrow and isolated connected components. The radius defines the size of a disc-structuring element used to filter these unwanted elements from the mask. The disc should be sufficiently large that it will not fit into any of these elements. The values of T and r can be determined either interactively or automatically. In the former case, for example, this can be implemented in a graphical user interface using two sliders: one for T and one for r. As the slider indicators are moved the mask of the current slice image is updated. A scrollbar can be used to scroll through individual slices. In the latter case, values for T and r can be defined based on values determined from several sample data sets. Selected steps of the algorithm are illustrated in Figure 2.

Table 1. Proposed method for metal artefact reduction in dental CT data.

Inputs: 1. Set of axial CT slice images through the maxilla or mandible, acquired parallel to the occlusal plane

2. Threshold value T

3. Radius r

Output: Set of reconstructed, metal artefact reduced, axial CT slice images (the algorithm is in place; i.e. after execution the input images will have been overwritten with the output images)

Steps:

1. for each slice image (SI) in turn (proceeding sequentially from the roots to the crown) (see Figure 2a)

2. obtain a binary mask (BM) of the metal restorations by thresholding the SI with respect to T (see Figure 2b)

3. if the BM is not empty

4. forward project the SI to obtain the target projection data (TPD);

5. forward project the preceding slice image to obtain the source projection data (SPD);

6. forward project the BM to obtain the mask projection data (MPD);

7. for each non-zero pixel in the MPD

8. replace the corresponding pixel in the TPD with its counterpart in the SPD (see Figure 2c);

9. end for

10. back project the corrected TPD to obtain the corrected slice image (CSI) (see Figure 2d);

11. perform a morphological opening on the BM using a disk of radius r (see Figure 2e);

12. for each pixel in the complement of the BM

13. replace the corresponding pixel in the SI with its counterpart in the CSI (see Figure 2f)

14. end for

15. end if

16. end for

Figure 2.

Illustration of selected steps in the proposed algorithm. (a) Original axial slice image. (b) Binary mask of the metal restorations and streaks. (c) Corrected sinogram. (d) Image reconstructed from (c). (e) Morphological opening of (b) by a disk. (f) Final result

To evaluate the effectiveness of the MARSS algorithm for attenuating metal artefacts originating from multiple metal parts we elected to compare its performance to that of the Watzke and Kalender method (WK method) using a two-alternative forced choice visual experiment.¹⁶

20 human observers with good or corrected vision were recruited for the experiment from among the postgraduate research students, academic staff and general staff in the School of Information Technology and Electrical Engineering at the University of Queensland: 15 with formal training in image/signal processing and 5 without. 20 dental CT data sets, corresponding to 20 different subjects each with 2 or more metal restorations, were randomly selected from the archives of 2 local diagnostic dental imaging practices. 16 were acquired using a Toshiba Aquilion CT scanner (Toshiba Medical Systems, Inc, Tustin, CA) and 4 were acquired using an i-CAT CT scanner (Xoran Technologies, Inc, Ann Arbor, MI). Each of the 16 spiral CT data sets comprised reconstructed axial slices, acquired parallel to the occlusal plane, through either the mandible or the maxilla. Similarly each of the four cone beam CT (CBCT) data sets comprised reconstructed axial slices orientated parallel to the occlusal plane. Given that metal artefacts also present as streak artefacts in CBCT data (albeit not just predominantly intraplane) it was decided to use the additional data to increase the sample size beyond the recommendation by Myers et al that it be at least 16 for subsequent analysis using the Cochran Q test (see Results).¹⁸ Collectively, axial slice thicknesses ranged from 0.3 mm to 0.5 mm. Inplane pixel (square) sizes ranged from 0.17 mm to 0.4 mm. Approval from the Human Research Ethics Committee of the University of Queensland was obtained for this study.

For each data set in turn, the axial slice images were visually reviewed and the slice most affected by metal artefacts selected for the experiment. The 20 selected images were independently processed using MARSS and the WK method. T used in the MARSS algorithm was defined as one-third of the maximum pixel intensity value found in the input CT data set. r (of the disc-structuring element) used in the algorithm was defined as 1.

A MATLAB® (MathWorks Inc., Natick, MA) program was written to present to the user 1 of the 20 sets of 3 images (original image, MARSS result, WK result) at a time and to allow the user to select either the MARSS result or the WK result in response to the question: “Which image is the best? In making this decision you will need to consider how well the artefacts have been reduced/removed and how well the anatomic detail has been preserved/revealed”. The program initially presents the user with two example images (from two additional CT data sets) to acquaint them with what an image with metal artefacts looks like compared with one without. Each invocation of the program yields the 20 sets of images in a random order, and for each set of images the MARSS result and the WK result are presented in a random order.

Each of the 20 observers performed the experiment under the same lighting and viewing conditions. In particular a 30-inch thin film transistor liquid crystal display (TFT-LCD) was used under regular office ambient lighting with a one-to-one mapping of image pixels to screen pixels. Each observer was told to make his/her own decision about the relative importance of each of the quality factors raised by the “Which image is the best?” question. Each observer completed this task in isolation from the other observers and was blind to the results of the other observers.

Results

A Cochran Q test was performed in R (R development core team, Vienna, Austria) to determine whether there is a difference in the responses (Table 2) of the 20 observers. The null hypothesis was that the proportion of responses in favour of MARSS is the same for each observer vs the alternate hypothesis that it is not. The test was performed at the α = 0.01 level of significance. The P-value for the test was 0.02797 and so the null hypothesis could not be rejected. The conclusion, therefore, is that the proportion of observer responses in favour of MARSS is the same for all observers.

Table 2. Results collated by observer and by image.

By observer	MARSS:WK	Count
	18:2	1
	19:1	6
	20:0	13
By image	MARSS:WK	Count
	17:3	1
	18:2	1
	19:1	3
	20:0	15

MARSS (metal artefact reduction by sequential substitution) is the proposed method and WK is the method of Watzke and Kalender.¹⁶

Next the data were pooled, i.e. the data were considered to be 400 independent Bernoulli trials, and an exact binomial test was performed in R to determine whether the observers preferred MARSS to the WK method. The null hypothesis was that the proportion of responses in favour of MARSS is π = 0.5 vs the alternate hypothesis that π > 0.5. The test was again performed at the α = 0.01 level of significance. The P-value for the test was less than 2.2 × 10⁻¹⁶ and so the null hypothesis was rejected. The conclusion, therefore, is that the observers deemed MARSS to be more effective than the WK method.

Finally, a Cochran Q test was performed to determine whether the observer responses (Table 2) differed among the 20 different images. The null hypothesis was that the proportion of responses in favour of MARSS is the same for each image vs the alternate hypothesis that it is not. Again, the test was performed at the α = 0.01 level of significance. The P-value for the test was 0.5262 and so the null hypothesis could not be rejected. The conclusion, therefore, is that the proportion of responses in favour of MARSS is the same for the 20 different images.

Discussion

The results of the two-alternative forced choice visual trial show that the proposed method (MARSS) performs better than the hybrid method of WK,¹⁶ which is itself the best of a handful of computationally efficient algorithms claimed/designed to be effective for metal artefacts induced by multiple metal parts. The results, as Figure 2 demonstrates, suggest that MARSS is able to effectively remove the streak-like artefacts and to restore/preserve the underlying dental structures. It must be acknowledged, however, that the visual trial is a subjective evaluation and that the results do not provide data on diagnostic accuracy or performance. For example, the 20 observers had to make a subjective judgement about image quality and given that they were predominantly signal/image processing experts they were possibly not the best judges of whether or not anatomical detail had been preserved/restored. In future work we intend to quantitatively evaluate the performance of MARSS, albeit indirectly, in the context of forensic identification. In particular we are interested in matching radiograph-like images reconstructed from post-mortem dental CT data to ante-mortem conventional radiographs on the basis of tooth/restoration contours.¹⁷ Two such reconstructions of a CT data set are shown in Figure 3: one from the raw CT data and the other from a MARSS-processed version of this data.

Figure 3.

Application of the proposed method to the reconstruction of a panoramic radiograph-like image from dental CT data for forensic identification. (a) Panoramic reconstruction from dental CT data corrupted by metal artefacts. (b) Panoramic reconstruction using the same CT data as in (a) but after the application of the metal artefact reduction by sequential substitution (MARSS) algorithm

The efficacy of MARSS is afforded by its ability to correct the corrupt portions of the projection data of an individual slice by substituting values from the non-corrupted (or possibly corrected) projection data in an adjacent slice. MARSS is effective when the metal corruption can be constrained to be largely intraslice. This is possible in dental CT imaging, for example, by acquiring axial slices that are parallel to the occlusal plane.

In conclusion, MARSS is conceptually simple, easy to implement and can effectively remove metal artefacts originating from multiple metal restorations in dental CT images. Moreover, because it is a projection-correction method, it is also very fast. In our experience MARSS is able to render severely degraded images useful for oral diagnosis, pre-operative assessment of implants and forensic identification.¹⁷ In principle, MARSS can be applied to CT data acquired for other parts of the body containing small and/or numerous metallic objects such as clips and prostheses.