The first observation of Carbon-13 spin noise spectra

Graphical abstract

Highlights

► We report the first observation of Carbon-13 spin noise spectra. ► Non-linear amplitude response at high concentration indicates the influence of radiation damping. ► The proton decoupled noise spectra show absence of heteronuclear NOE enhancement.

Abstract

We demonstrate the first ¹³C NMR spin noise spectra obtained without any pulse excitation by direct detection of the randomly fluctuating noise from samples in a cryogenically cooled probe. Noise power spectra were obtained from ¹³C enriched methanol and glycerol samples at 176 MHz without and with ¹H decoupling, which increases the sensitivity without introducing radio frequency interference with the weak spin noise. The multiplet amplitude ratios in ¹H coupled spectra indicate that, although pure spin noise prevails in these spectra, the influence of absorbed circuit noise is still significant at the high concentrations used. In accordance with the theory heteronuclear Overhauser enhancements are absent from the ¹H-decoupled ¹³C spin noise spectra.

1. Introduction

NMR noise spectra, i.e. spectra obtained without rf-excitation of the observed nuclear spins, have recently attracted renewed interest both because of their fundamental aspects (e.g. for their capability to observe unperturbed equilibrium states and their independence of longitudinal relaxation) and due to their potential to yield superior sensitivity at very low spin concentrations as well as excitation free imaging [1–5].

For the first time nuclear spin noise was observed experimentally by detecting nuclear quadrupole resonance (NQR) noise arising from ³⁵Cl nuclei in a solid NaClO₃ sample using a SQUID detector at low temperature (1.5 K) [6]. Disregarding noise originating from instrument imperfections, NMR noise has been shown to consist of entangled positive (i.e. more than thermal circuit noise) and negative (i.e. less than thermal circuit noise) components, which can be attributed to “pure spin noise” and “absorbed circuit noise” (ACN), respectively [7]. Pure spin noise originates from the tiny fluctuating nuclear magnetic moments and their incomplete cancellation as predicted by Bloch [8], while ACN is a consequence of radiation damping, which has a major impact under the conditions used for most spin noise experiments to date. NMR noise, actually mostly the ACN-component has been used recently as an indicator for optimized reception tuning of NMR probes [9–12].

While pure ¹H spin noise can be observed in true equilibrium on liquid samples under imaging conditions [5] as well as in solids [12], noise spectra of ¹²⁹Xe [13] were observed under hyperpolarization conditions, where ACN prevails. So, to the best of our knowledge, as of to date only ¹H and ¹²⁹Xe nuclear spin noise and ³⁵Cl quadrupolar noise have been reported experimentally. In the present communication we report the first ¹³C spin noise spectra and discuss their implications with respect to spin noise detection in general.

According to the derivation of McCoy and Ernst [14] at perfect tuning, i.e. at the spin noise tuning optimum (SNTO) [9,11], where the circuit tuning frequency ω_c is equal to the Larmor frequency ω, the deviation of the power spectral density conditions for on-resonance signals from the thermal noise level depends on the radiation damping rate λ_r and the transverse relaxation rate λ₂ as given by:

$$W(\omega )-W(\infty )=\left[\frac{{\lambda }_2({\lambda }_2+{\lambda }_r^0)}{{\left({\lambda }_2+{\lambda }_r\right)}^2}-1\right]W_c$$ (1)

with W_c being the noise spectral density of the rf-coil, which together with the preamplifier noise defines the thermal noise level. The amplitudes and the signs of the NMR noise signals (negative ones indicating “less than thermal noise”, i.e. absorbed circuit noise) are determined by the term in square brackets in Eq. (1), which depends on λ₂, λ_r, and ${\lambda }_r^0$, the radiation damping rate in thermal equilibrium between coil and sample. For a cryogenically cooled probe λ_r is defined as

$${\lambda }_r=\frac{{\mu }_0\gamma \eta {\mathit{QM}}_z}{2}=\frac{{\lambda }_r^0}{\vartheta }$$ (2)

where μ₀ is the permeability of free space, γ the gyromagnetic ratio of the observed nucleus, η the filling factor; Q is the frequency dependent [15] quality factor of the probe rf-circuit, ϑ the temperature ratio between the sample and the coil (with high relevance with respect to cryogenically cooled probe circuits), and M_z is the longitudinal magnetization, which in thermal equilibrium is equal to M₀:

$$M_0=\frac{1000{\mathit{cN}}_A{\gamma }^2{\hslash }^2{B}_0}{4\mathit{kT}}$$ (3)

with the spin concentration c [mol L⁻¹] at the respective Larmor frequency (the signal multiplet structure has to be taken into account here, if present), the Avogadro number N_A, the reduced Planck’s constant $\hslash$ and the Boltzmann constant k.

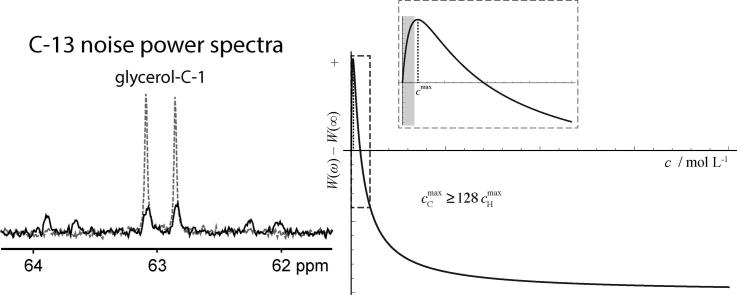
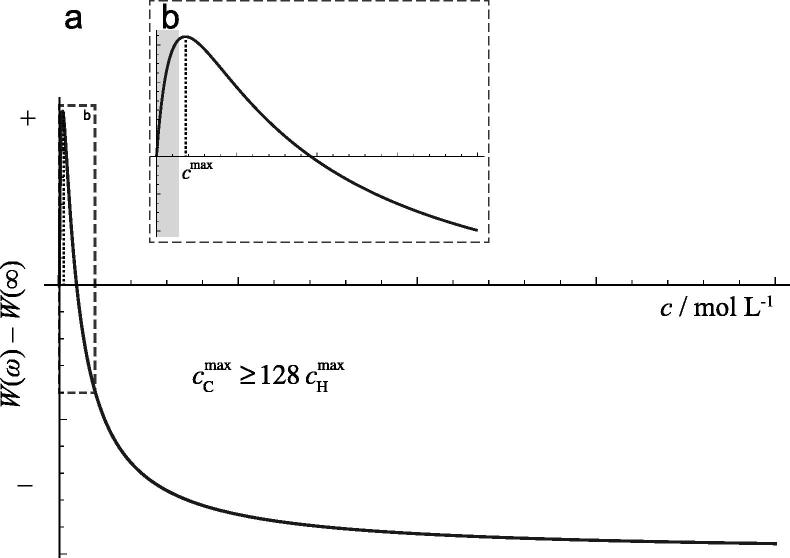
Fig. 1 shows computed graphs illustrating the general spin concentration dependence of the NMR noise signal amplitude according to the term in square brackets in Eq. (1).

Fig. 1.

(a) Theoretical relative peak amplitude of NMR noise at ω₀ = ω_c as a function of the spin concentration according to Eq. (1). (b) Zoomed the region of lower concentrations as indicated by the dashed box in (a), denoting the expected regime relevant for ¹³C by the inset grey rectangle. The width of the initial “peak” in the curve, and the concentration at which the intensity of the spin noise signal has a maximum, strongly vary for different nuclei due to changes of their specific properties.

It has already been shown by Hoult and Ginsberg that spin noise can be detected with probe circuits of low quality factors Q [16]. In the case of the detection of ¹³C NMR noise, the main challenge derives from the low gyromagnetic ratio leading to a much lower M₀. Together with Q being smaller due to its dependence on the Larmor frequency [15] this has the consequence that the concentration, where the NMR noise signal has an intensity maximum, varies according to

$$c^{\text{max}}=\frac{(\vartheta -2)4\mathit{kT}{\lambda }_2}{1000\pi N_A{\gamma }^3{B}_0{\mu }_0\eta Q\vartheta }$$ (4)

Assuming equal spin concentrations (which is difficult to achieve in practice), the maximum for ¹³C is encountered at a more than 128 times lower concentration than for ¹H:

$$c_{{}^{13}\text{C}}^{\text{max}}⩾128c_{{}^1\text{H}}^{\text{max}}$$ (5)

Since the influence of radiation damping on the NMR noise signal is very much reduced under these conditions, the contribution of absorbed circuit noise to the detected signal is expected to be much smaller than for ¹H. In the limiting case of Eq. (1), i.e. ${\lambda }_r^0\gg {\lambda }_r\text{,}{\lambda }_r\ll {\lambda }_2$ the noise power signal amplitudes depend linearly on the spin concentration,

$${\displaystyle \underset{{\lambda }_r^0\gg {\lambda }_r\text{,}{\lambda }_2\gg {\lambda }_r}{\lim }}\left[\frac{{\lambda }_2({\lambda }_2+{\lambda }_r^0)}{{\left({\lambda }_2+{\lambda }_r\right)}^2}-1\right]=\frac{{\lambda }_r^0}{{\lambda }_2}$$ (6)

since ${\lambda }_r^0$ as of Eq. (2), is also linearly dependent on the spin concentration. Thus this represents the limiting case of pure spin noise, arising from the statistical fluctuations of the magnetic moments [8] without “self-quenching” by radiation damping, as represented by the denominator in Eq. (1). Therefore, although the radiation damping rate has a major influence on the NMR noise signal for narrow lines and high magnetization, giving rise to the phenomenon of absorbed circuit noise (ACN) [7], with the pertinent setup (low γ and lower η) the contribution of ACN to the detected total NMR noise signal is very small and the signal intensities should be nearly linearly dependent on the spin concentration. A similar linear dependence is also found under gradient conditions [5], in paramagnetic solutions [11] and in static solid powders [12].

The range of concentrations and NMR noise signal amplitudes that can be covered for ¹³C in our experimental setup is indicated by the area shaded in grey in Fig. 1b.

It has to be noted, that for inverse detection probes the ¹³C spin noise amplitude is expected to be even smaller than this rough estimate due to the lower filling factor η deriving from the coil geometry. Also the “spin noise to thermal noise” ratio is subject to noise arising from the different “auxiliary” electronic components for multiple tuning, filters and traps, which also depend on ω.

Although the above considerations predict that the ¹³C noise power is reduced by a factor of more than 128 with respect to ¹H, we deemed it possible to obtain a ¹³C NMR spectrum in the absence of any r.f. irradiation by exploiting a combination of state-of-the-art hardware (a latest generation, i.e. 2011, cryogenically cooled probe, highly stable low-noise electronics), high concentrations and isotopic enrichment.

2. Results and discussion

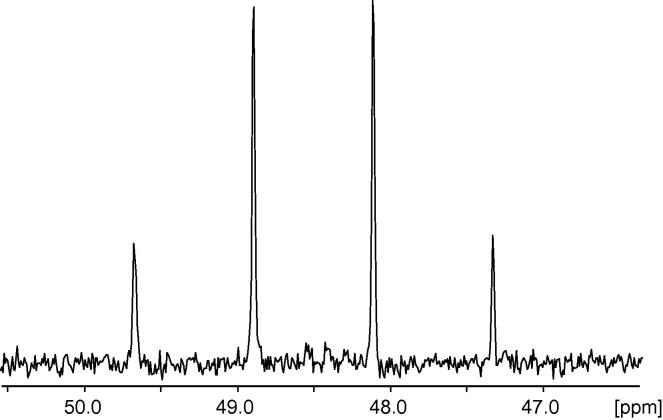
Fig. 2 shows a directly ¹³C detected spin noise spectrum of isotopically enriched methanol obtained after 8 h of acquisition without decoupling. The proton spin density for the CH₃ group of this sample (99.5% ¹³C methanol with 5% DMSO-d₆ to provide for field-frequency locking) is 70 mol L⁻¹ while the ¹³C spin density is ∼23 mol L⁻¹. The quartet splitting (1:3:3:1) reduces the component spin densities to 2.9 and 8.7 mol L⁻¹ for the lower and higher components, respectively. For such high concentrations the observed line shape of the ¹³C noise signal is always positive. In contrast to that, the ¹H NMR noise spectrum (not shown) of this sample shows a dip line shape for all signals. However the deviation of the measured multiplet component amplitude ratios (1:2.5:2.5:1) from the ideal (1:3:3:1) indicates the existence of radiation damping through absorbed circuit noise, which decreases the observed noise signal amplitudes significantly. Comparison of ¹³C λ₂ and λ_r values for this sample show that even at this high concentration the radiation damping rate (0.2π Hz, as estimated from the ¹³C spin density and the known probe parameters), although by an order of magnitude lower than the transverse relaxation rate (2.2π Hz, as estimated from the line width), are already high enough to cause detectable non-linear effects.

Fig. 2.

¹³C detected NMR noise spectrum of ¹³C labelled methanol (99% ¹³C, Aldrich, with 5% DMSO-d6 added as a lock substance) obtained at 176 MHz (Bruker Avance III 700 MHz system equipped with an Ascend magnet, a cryogenically cooled TCI probe (with rf-coils at 17 K and a cold ¹³C preamplifier at 77 K), a HPLNA preamplifier and a digital receiver (DRU) after acquiring 8 h of ¹³C NMR raw noise using a pseudo 2D acquisition sequence [11]. A total of 600 noise blocks with 49.6 s acquisition time were recorded at a total spectral width of 15 ppm. Power averaging [13] was carried out in Scilab (version 5.3.3, http://www.scilab.org) setting the final digital resolution to 1.5 Hz and using a sliding window with 1/7 overlap, leading to the accumulation of a total of 309,000 power spectra. The resulting spectrum contained an artefact arising from the spectrometer electronics at 48.4 ppm. This spike was removed by subtracting a noise spectrum acquired without sample. The ¹³C chemical shift is identical to the one observed in a pulse spectrum referenced to external TSP in D₂O.

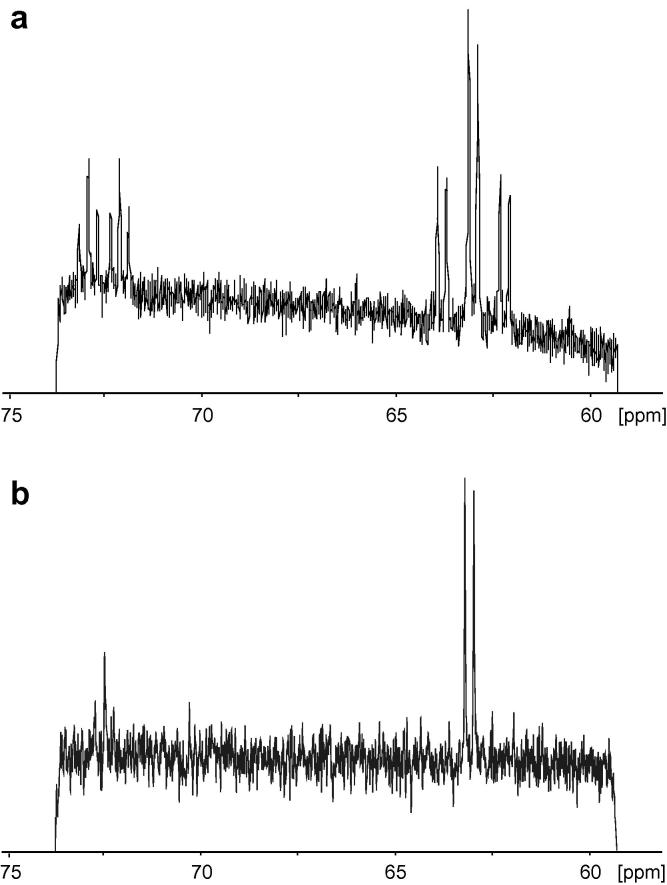
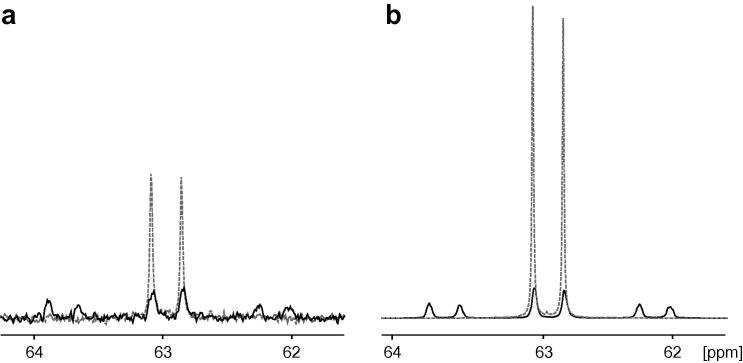
In Fig. 3a the more complex NMR noise spectrum of ¹³C glycerol (8.22 mol L⁻¹), obtained after 14 h acquisition without decoupling, is shown. For the most intense resonances a signal-to-thermal-noise ratio of 4 could be achieved already after 5 h. In this case the amplitude ratios correspond closely to the ideal values, since the individual ¹³C spin isochromat concentrations are 1.03 mol L⁻¹ and 2.05 mol L⁻¹ for the signal at 72.5 ppm and 2.06 mol L⁻¹ and 4.11 mol L⁻¹ for the different intensities of the multiplet at 63 ppm and thus lower than in the methanol sample. Therefore the glycerol case corresponds more closely to a situation of pure spin noise.

Fig. 3.

(a) Carbon-13 detected NMR noise power spectrum of ¹³C labelled glycerol (300 μl glycerol (99% ¹³C enriched, Aldrich) and 200 μl D₂O (Euriso-top, for field-frequency lock and to allow for adjusting the sample filling height) recorded at 176 MHz ¹³C frequency on the same hardware as in Fig. 2. A total of 1024 noise blocks with 49.6 s acquisition time were recorded at a spectral width of 15 ppm in totally 14 h. Noise power averaging [13] was carried out in Scilab as described in Fig. 2, resulting in the addition of a total of 527,360 power spectra. (b) Proton decoupled (17 mW, 200 μs 90° decoupling pulse length for WALTZ16) ¹³C detected NMR noise spectrum after 2.5 h of acquisition. 10,240 noise data blocks of 0.77 s were acquired in a pseudo-2D mode. Processing was applied as described in Ref. [11]. Note that the noise baselines in these spectra corresponds to the thermal noise levels without spin noise or absorbed circuit noise, the cutoff at the edges being caused by the processing. Carbon-13 chemical shifts are identical to the ones observed in a pulse spectrum referenced to external TSP in D₂O.

¹³C NMR spectra are usually acquired with ¹H spin decoupling. To avoid sample heating and hardware damage in the special situation of continuous noise detection the minimum required power for CW and WALTZ decoupling was determined by pulse spectra. As expected, decoupling causes collapse of the splittings from the coupling to protons, allowing for a reduced acquisition time. A WALTZ decoupled ¹³C noise spectrum is shown in Fig. 3b. In this case a reasonable signal-to-thermal-noise ratio was already achieved after 2.5 h with decoupling. In spite of the weak spin noise signal we did not observe any indications of rf-cross talk or interference on the carbon channel.

The integral ratios of the multiplet components in the coupled spectra in Fig. 3 correspond to the number of carbon atoms and to the multiplicities due to homo- and heteronuclear couplings. This indicates that the concentration is low enough to observe pure spin noise in a situation corresponding to the initial near-linear part of the intensity curve of Fig. 1b. In contrast to that analysis of the quartet components in Fig. 2 shows that the signal intensities deviate from the ratios given by Pascal’s triangle. These deviations from the expected multiplet ratios, while interfering with traditional chemical analytical applications, can offer new cues to intrinsic probe and sample characteristics relating to radiation damping.

To evaluate the influence of the heteronuclear Overhauser effect ¹H-decoupled and coupled noise and pulse spectra of the same ¹³C-glycerol sample, acquired with identical decoupling times and duty cycles and processed identically are compared in Fig. 4.

Fig. 4.

(a) Noise acquired and (b) pulse excitation-FID acquired Carbon-13 multiplets of glycerol-C-1. The full traces are fully coupled spectra and dashed traces correspond to proton decoupled spectra (0.17 W power with 65 μs 90° decoupling pulse duration with a decoupling duty cycle of 84%). 64 k noise data blocks of 0.39 s were acquired in a pseudo-2D mode, further acquisition parameters were as given in Fig. 2. Processing was applied as described in Ref. [11]. In case of the proton decoupled noise spectrum (dashed trace) 0.17 W decoupling with 65 μs 90° decoupling pulse length for WALTZ16 were used. For better comparison the peak areas of the coupled multiplets were normalized to 1 in both cases as discussed in the text.

From the ¹³CH₂ multiplets in these spectra the proton-decoupled/coupled integral ratios were determined as 1.35 ± 0.35 from the spin noise spectra and 2.05 ± 0.02 from the pulsed spectra. The large error margin derives mostly from the low spin-noise-to-thermal-noise ratio of the coupled noise spectrum. The decoupled/coupled integral ratios corroborate that within the error margin of these experiments there is no NOE in the spin noise spectra, since pure spin noise is polarization independent. Any change in the ¹³C population levels only affects the radiation damping rate and thus the ACN component according to Eq. (2) and is thus too small to be detected under the conditions of these experiments. Increasing the population difference would actually decrease the noise peak amplitudes.

So, while coupled ¹³C-noise spectra are very time consuming, NMR noise spectroscopy bears the potential of obtaining completely NOE-free spectra in presence of heteronuclear decoupling.

3. Conclusions

We have shown that with state-of-the-art NMR cryogenically cooled probes ¹³C spin noise spectra can be directly detected with and without decoupling of the protons. Contrary to ¹H noise spectra recorded under similar conditions these ¹³C noise spectra consist of only positive signals, indicating the prevalence of pure spin noise. For the highest accessible ¹³C spin concentrations analysis of the multiplet amplitudes in the ¹H coupled ¹³C noise spectrum of methanol reveals that the influence of absorbed circuit noise caused by ¹³C radiation damping is small but detectable as a less than linear response to the spin concentration. At lower concentration, in the absence of ¹³C radiation damping, ¹H decoupled ¹³C noise spectra are devoid of any influence of the heteronuclear Overhauser effect.