Feasibility of EMG-Based Neural Network Controller for an Upper Extremity Neuroprosthesis

Abstract

The overarching goal of this project is to provide shoulder and elbow function to individuals with C5/C6 Spinal Cord Injury (SCI) using functional electrical stimulation (FES), increasing the functional outcomes currently provided by a hand neuroprosthesis. The specific goal of this study was to design a controller based on an artificial neural network (ANN) that extracts information from the activity of muscles that remain under voluntary control sufficient to predict appropriate stimulation levels for several paralyzed muscles in the upper extremity. The ANN was trained with activation data obtained from simulations using a musculoskeletal model of the arm that was modified to reflect C5 SCI and FES capabilities. Several arm movements were recorded from able-bodied subjects and these kinematics served as the inputs to inverse dynamic simulations that predicted muscle activation patterns corresponding to the movements recorded. A system identification procedure was used to identify an optimal reduced set of voluntary input muscles from the larger set that are typically under voluntary control in C5 SCI. These voluntary activations were used as the inputs to the ANN and muscles that are typically paralyzed in C5 SCI were the outputs to be predicted. The neural network controller was able to predict the needed FES paralyzed muscle activations from “voluntary” activations with less than a 3.6% RMS prediction error.

I. INTRODUCTION

A complete spinal cord injury (SCI) at the C5/C6 level is a devastating condition that leaves a person with complete paralysis of their lower extremities, trunk and hands. The shoulder and elbow retain some voluntary function but typically the arm is weak due to paralysis of several key muscles (e.g., triceps, pectoralis major, lattisimus dorsi or pronators), reducing the arm’s workspace and impairing the ability to perform some basic activities of daily living. Functional Electrical Stimulation (FES) is a technology that can restore function in individuals with SCI [1] by delivering small electrical impulses to activate the nerves that remain intact even though they do not receive commands from the central nervous system due to the injury. Determining the timing and levels of stimulation remains a challenge due to the complexity and redundancy present in the musculoskeletal system, and the non-linear response of the muscles to electrical stimulation [2]. Because of this, attempts to restore proximal function (i.e., shoulder and elbow) have been limited [3–5], especially due to the challenge of controlling the stimulation automatically and in a natural manner. Since this SCI population retains function in some of their proximal arm muscles, this study was focused on exploring a control alternative that uses signals from the muscles with voluntary function to identify the movement intention and provide appropriate stimulation levels to the paralyzed muscles, providing effortless, synergistic control.

Upper extremity neuroprostheses for hand paralysis are currently programmed with activity-specific patterns and controlled proportionally using one of several input signals such as EMG from voluntary muscles, wrist angle or using contralateral shoulder movement [6]. A controller that interacts seamlessly with the natural function remaining after C5/C6 SCI must be capable of dealing with the nonlinearities and complex dynamics observed in the neuromuscular system. Artificial intelligence approaches such as neural networks have been shown to be capable of dealing with this type of complexity, and several attempts to use them for FES control can be found in the literature [7–9]. Crago and his colleagues used artificial neural networks (ANN) to demonstrate control of stimulation and stiffness for a single joint system [10] and a wrist and hand coupled joint system [11], initially based on musculoskeletal modeling results. Later, they implemented this type of controller to control multiple degrees of freedom in the thumb [12]. These studies demonstrated that an ANN-based controller is capable of generating the appropriate levels of stimulation for muscles to coordinate movement in coupled joints. Popovic and colleagues also studied the possibility of using neural networks and other artificial intelligence techniques to learn the synergies between shoulder and the elbow and control the stimulation for elbow extensors [13]. The relevance of this work was to identify the kinematic relationships between the proximal upper extremity joints. Neural networks have also been used for FES control in lower extremity systems, where the controller is capable of learning the pattern of activations necessary to produce cycling-type movements. Abbas and his colleagues proposed a neural network to control stimulation in the lower extremities while performing a cycling task [7]. In later work, the controller was tested experimentally by training it to track a periodic torque trajectory signal [14, 15]. The system successfully generated stimulation patterns, but it learned to perform only a few specific motor tasks and lacked the ability to generalize to a broader range of movements.

Using voluntary controlled EMG signals to extract command signals is an appealing alternative for controlling artificial devices whether they are a neuroprosthesis [16–20], a robot [21, 22], a virtual arm [23] or a prosthetic arm [24–28]. Our previous studies have shown that retained voluntary function can potentially be used to control a neuroprosthesis. A time-delayed artificial neural network (TDANN) was used to predict shoulder and elbow joint angles from EMG signals recorded from proximal arm muscles [16], demonstrating that EMG signals contain relevant information about the arm’s movement intention. In subsequent work a musculoskeletal model of the arm, modified to reflect SCI, was used to obtain the muscle activations required to hold the arm in certain postures [29]. A static neural network was trained with these data to predict “FES paralyzed” muscle activations using “voluntary” muscle activations as inputs. The prediction errors using four “voluntary” muscles as inputs (trapezius, rhomboids, infraspinatus and biceps) and four “paralyzed” muscles as outputs (serratus anterior, coracobrachialis, latissimus dorsi, and pectoralis major) averaged 10% of maximum activation level, indicating that it is possible to estimate the muscle activity of FES muscles from retained voluntary activity. Later, Giuffrida and Crago used a neural network to predict triceps stimulation levels for elbow extension using the EMG activity from several shoulder muscles as inputs [17]. They implemented it in a subject who was able to do high reaching tasks with automatic control of the triceps stimulation generated by the neural network controller.

The long term goal of this project is to determine which of the available muscles to stimulate and how to appropriately control and coordinate this stimulation with retained voluntary function, thus improving shoulder and elbow function in individuals with C5/C6 SCI. The proposed approach exploits retained voluntary function by extracting the movement intention from the activity of muscles under voluntary control and using this information to determine the levels of stimulation required. Based on this principle, positioning the arm and maintaining shoulder joint stability become a synergistic cooperation between the remaining nervous system and the actions of the artificial FES controller. The work reported here extends previous work by including the dynamic characteristics of the arm during movements rather than just postures and by obtaining an approximation to the muscle activation patterns using inverse dynamic simulations from a musculoskeletal model.

II. METHODS

A. General Approach

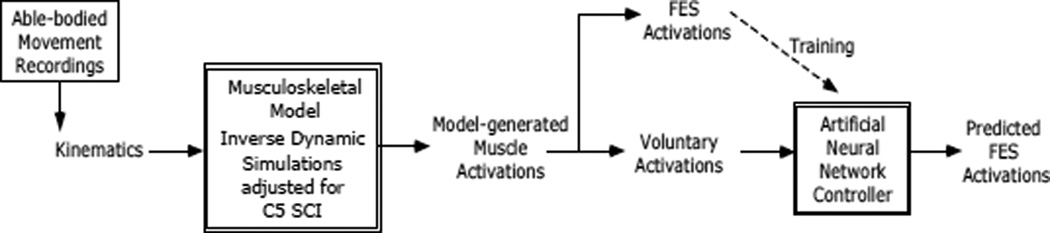
Fig 1 summarizes the overall approach used in this study. Muscle activation patterns where estimated for a series of arm movements using a musculoskeletal model of the shoulder and elbow. The movements (inputs to the model) were recorded from able-bodied subjects, but the model was adjusted to reflect the condition of a C5 SCI individual, including the potential of using FES in some paralyzed muscles. Inverse dynamic simulations were run to estimate the muscle activation patterns, both for “voluntary” and “FES paralyzed” muscles, necessary to drive the movements recorded. An artificial neural network was then trained to predict “FES paralyzed” muscle activations from “voluntary” muscle activations, mimicking the real situation where EMG signals from voluntarily controlled muscles will be processed by a controller and used to automatically determine the appropriate levels of stimulation for paralyzed muscles.

Fig 1.

Block diagram summarizing the approach taken for this study. Able-bodied movement kinematics were recorded and used as inputs to an inverse simulation with a musculoskeletal model of the arm that was modified to reflect C5 SCI plus the actions of FES on several muscles. Muscle activations required to perform the recorded movements were used as a training data for a artificial neural network controller that learns the relationship between "voluntary" and "FES" muscle activations.

B. Generation of muscle activation patterns

Arm movements from three able-bodied subjects were recorded using an Optotrak motion analysis system (Northern Digital Inc.). Dynamic trials were recorded during which the subjects performed different arm motions that included reaching motions at different heights and a set of activities of daily living (ADL) that included feeding, drinking, hair brushing, dressing and lifting objects. Data were processed to obtain the orientations of the clavicle, scapula, humerus and forearm with respect to the thorax. Definitions of the bony landmarks, coordinate systems, and the order of rotation to obtain Euler angles were done following the International Shoulder Group recommendations for reporting upper extremity human joint motions [30]. The kinematics were recorded at 30Hz.

Inverse dynamic simulations were run with a musculoskeletal model of the shoulder and elbow [31] to estimate muscle activation patterns required to execute the recorded movements. During inverse simulations, the inputs to the model are the kinematics of the recorded movements (i.e., Euler angles with orientations of each bone segment) and the outputs are the muscle forces required to perform these movements. Relative force (i.e., muscle force divided by the maximal force of that muscle at its current length) was used in this study as an estimate of muscle activation. Muscle dynamics were not included in this model. In our experience, lack of adequate available force has been the primary factor limiting upper extremity FES system performance. Therefore, the conditions of a C5 SCI subject were approximated in the model by decreasing the maximum relative forces that could be generated by each muscle [32]. This approximation did not consider other physiological effects such as spasticity or co-contraction that are sometimes present after SCI. However, the reduction in maximum forces adequately reflects the main effect of C5 SCI. Estimates of the maximum muscle relative forces in a C5 SCI individual were obtained by considering the anatomical innervation levels of each muscle relative to the location of the SCI, as well as the averaged results of manual muscle tests from our C5/C6 SCI subject database. Paralyzed muscles were given essentially zero maximum forces. Some paralyzed muscles that are available to be stimulated were included in the simulations with a 50% maximum relative force. For these paralyzed (but “stimulated”) muscles, an additional optimization constraint was imposed to require all of the various contractile elements representing a given muscle to have the same activation level, simulating the gross effect of electrical stimulation. A muscle selection procedure described previously [32] was performed to select an optimal set of candidate paralyzed muscles for FES, which served here as the target outputs for the proposed controller. It was found that infraspinatus, serratus anterior and triceps were paralyzed muscles that when stimulated will provide enough strength to restore several specific activities of daily living mainly involving reaching motions. Robustness of this result was investigated by evaluating different kinematic strategies used by different able-bodied subjects and obtaining a similar muscle selection outcome. Furthermore, adjusting the model to reflect a complete C5 SCI is the worst case in terms of pure muscle power available. The same muscle selection process could be used to explore individuals with lower level injuries or incomplete injuries, and the resulting muscle set would likely be different. These selected “FES paralyzed” muscles were used as controller outputs. For the model simulations, kinematic data were resampled at 12.5Hz, typical frequency used for FES applications in the upper extremity.

C. Selection of voluntary muscles (controller input)

In the C5/C6 SCI population, there are several voluntary muscles whose activation levels could potentially serve as inputs to this proposed controller, so a multi-input multi-output (MIMO) system identification technique was used to analyze the potential of candidate “voluntary” muscles to predict the activations for the “FES paralyzed” muscles. The candidate input muscles considered were trapezius (clavicular and scapular portions), deltoid (clavicular and scapular portions), levator scapulae, rhomboids, teres minor, supraspinatus, subscapularis, biceps (short and long heads), brachioradialis, brachialis and supinator. A frequency domain (f-MIMO) and a time domain (t-MIMO) analysis were done to obtain the frequency responses and the impulse responses respectively between each of the candidate input muscles and each of the output muscles. The f-MIMO procedure generates a value of coherence (Equation 1) that describes the relationship between each input and each output at each frequency. Coherence has a value between 0 and 1, with a value closer to 0 indicating a very weak relationship between an input and an output and a value closer to 1 indicating there is a stronger relation between a particular input and a particular output. In our application, a high partial coherence between a particular “voluntary” muscle activation and the desired “stimulation” muscle activation suggests that the particular “voluntary” muscle would be a useful input to the ANN analysis described below. The t-MIMO procedure generates an impulse response function (IRF) that indicates the strength and time interval (i.e., the system memory) over which the various “voluntary” muscle activations signals are related to the “stimulated” muscle activations. This information was used to guide the selection of the architecture for the controller by suggesting the duration of past values of the input signal that should be used for the prediction. This analysis was also used as a preliminary linearized version of the more general artificial neural network approach to be described below. The magnitude of the integrated IRF’s provided a measure of the strength of the relationship between a “voluntary” muscle activation input and a “stimulated” muscle activation output, providing an additional indication of which input muscles were likely to be the most effective in predicting needed output activations. We focused on using four input muscles since a realistic neuroprosthesis implementation currently limits us to four channels for EMG recordings.

$$\mathit{\text{Coherence}}:\frac{|P_{xy}(f){|}^2}{P_{xx}(f)P_{yy}(f)}$$ EQUATION 1

Where Pxy is the cross-spectrum between the input signal x and the output signal y, and Pxx and Pyy is the auto-spectrum for signals x and y respectively.

D. Training data

Training data must represent adequately the space of possible input-output relationships for the controller to generalize to a wide range of movements of interest. We recorded the various movements in several different able-bodied subjects. The amount of data and the specific movements used for training the controller vary within each subject. This was done purposefully to include a range of kinematic strategies and to assure realistic variability in the training data. Table I summarizes the types of movements and amount of data simulated for each subject. The movements included activities of daily living like reaching for an object or pushing a button, eating, drinking and personal care activities such as combing hair, dressing with a shirt, washing your trunk and arms and tooth brushing. In general, these activities require accurate positioning of the arm in space but do not require significant force generation.

TABLE I.

Types of Movements Recorded From Three Subjects (S1, S2, S3) and Amount of Data (In Seconds) Used for Neural Network Training, Validation and Testing

Movements	S1	S2	S3
Reaching high	60	15	15
Reaching med	0	75	15
Drinking	78	45	15
Eating	60	60	30
Personal care (combing hair, washing, dressing, tooth brushing)	155	60	45
	353	255	120

E. Controller

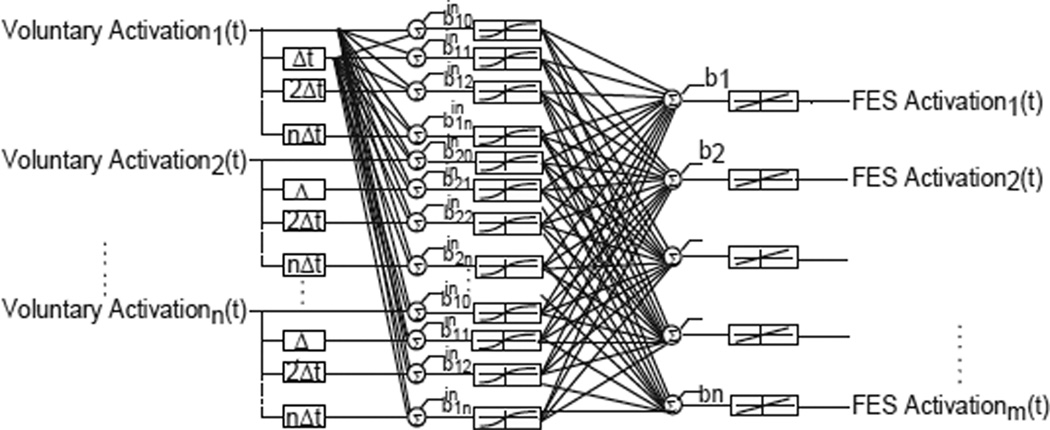
In this study, we evaluated the use of an artificial neural network (ANN) to map the dynamic and nonlinear relationship between the input and output muscle activations. We selected a two-layer feed forward ANN with a non-linear tangent-sigmoidal activation function for the hidden layer and a linear output layer. Both static ANN (i.e. current values of muscle activations as the only inputs) and time-delayed ANN (i.e. current and past muscle activations as inputs) were evaluated. Time-delayed inputs were considered to capture the spatio-temporal properties of the muscle activations. Fig 2 shows the typical architecture of the ANN. All ANNs were trained using MATLAB’s Neural Network Toolbox (The Math Works, Inc.).

Fig 2.

Neural network controller architecture. The inputs are the voluntary muscle activations, including both current and past values depending on the architecture. The hidden layer is comprised of neurons with tangential-sigmoidal activation functions and the output layer has linear activation functions. The outputs are the needed FES paralyzed muscle activations.

A neural network based controller must be robust enough to account for possible variations in the muscle activation patterns due to different kinematic strategies, fatigue, external loads, etc. Several strategies were used to achieve good generalization. First, the data was split into training, validation and testing data sets using approximately 60%, 20% and 20% of the full data set respectively. The training data set was used for training the network, and the validation set was used during the training itself to monitor the performance of the ANN to novel inputs. Increases in the validation error indicate that the ANN is losing its ability to generalize and is specializing by mapping only the specific training examples. Thus, training was stopped when the validation error did not improve or increased for 50 consecutive training iterations. The weights of the network with the minimum validation error were saved as the final network structure. Finally, the testing data set was used to evaluate the predictive ability of the trained network as explained below.

All the ANN were trained in batch mode using a Bayesian regularization algorithm [33] because this technique improves the generalization capacity of the network by including a term with the sum of squared weights in the minimization function. Having smaller weights helps prevent the memorization of the training data and thus allows for better generalization. In addition, this algorithm provides a measure of how many weights are being used effectively by the network, providing important information on the size of the ANN trained [34]. Other algorithms whose weights were adjusted using Levenberg-Marquardt and conjugate gradient strategies were also evaluated, but with no meaningful improvement in training time or performance.

The number of neurons used in the hidden layer was varied systematically between 3 and 30 hidden neurons while the prediction error was monitored. The goal was to find the smallest architecture that was capable of providing good prediction results. An architecture with fewer neurons will generalize and perform better with data not used during training and could potentially used in a real-time implementation for a neuroprosthetic user. The use of a variable number of past values of the input signals was also investigated and compared to a static architecture that only uses current values for the prediction. The number of delays determines how many past values of the input signals should be used as an input to the ANN and determines how much history of the signal is required to accurately predict the output activations. Based on the results from the t-MIMO procedure described above, this delay was varied from 0 to 0.96s (0 to 12 past values at 12.5Hz). The maximum number of iterations and minimum error goal where chosen heuristically based on the performance observed during training. Each network architecture was trained three different times to account for different initialization weights. Analysis of variance (ANOVA) was use to verify if there were significant differences between the architectures trained.

The performance of all the trained networks was measured as the ability to predict data from the testing data set. The goodness of fit of the ANN was quantified as the root mean square (RMSE, see Equation 2) between the musculoskeletal model-generated target activations for the FES paralyzed muscles and the corresponding activations predicted by the ANN. The muscle activation levels are naturally confined to a range of 0–1, so the RMSE inherently provides a measure of error relative to maximum activation. All RMSE in the results will be presented as a percentage of maximum muscle activation.

$$\mathit{\text{RMSE}}:\sqrt{\frac{{\sum }_{i=1}^N{(y_i^{\mathit{\text{predicted}}}-y_i^{\mathit{\text{target}}})}^2}{N}}$$ EQUATION 2

III. RESULTS

A. Muscle selection

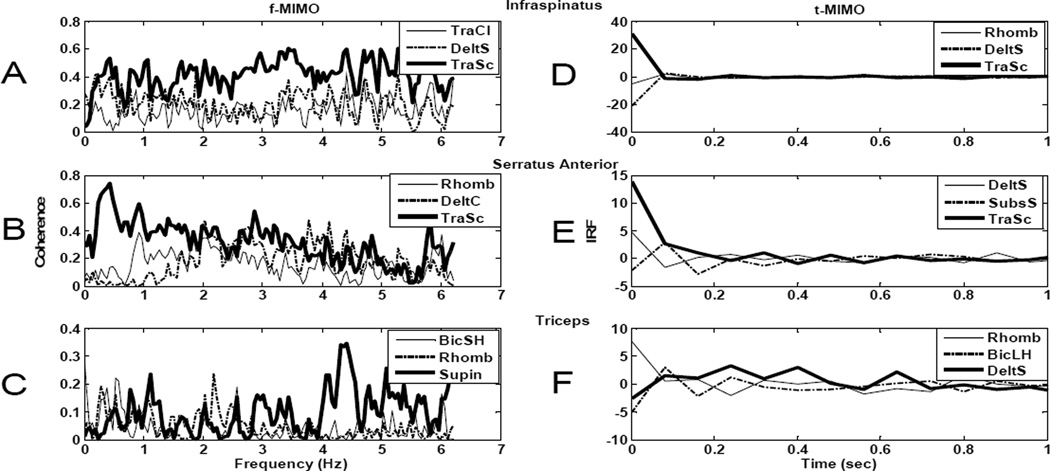
Fourteen upper extremity muscles that are likely to have some voluntary function (and hence EMG signals) in individuals with C5 SCI were chosen as potential “voluntary” input muscles to predict the needed activations of FES paralyzed muscles. We used two criteria for evaluating the four of these fourteen muscles that were most likely to provide the best prediction of the needed activations. The first approach was based on the frequency domain partial coherence between each input muscle and each output muscle. The multi-input (14 voluntary muscles), multi-output (the needed activations of infraspinatus, serratus anterior, and triceps) linear system identification procedure was performed, and the voluntary muscles with the greatest ability to predict the needed activations were determined by the magnitude of the partial coherence between each input and each output. Each panel in the left column of Fig 3 shows the frequency domain partial coherence functions between 0 and 6.25 Hz for the three input muscles with the largest partial coherence for infraspinatus (panel A), serratus anterior (panel B), and triceps (panel C). Note that a coherence value of 1.0 indicates that a given input can perfectly predict a given output, while a value of 0 indicates no relationship between the input and output. All other muscle inputs resulted in lower coherence than those illustrated. Across the three output muscles, the partial coherence functions indicate that trapezius, deltoids, rhomboids, biceps and supinator contain the most relevant information for predicting the needed activations of the infraspinatus, serratus anterior, and triceps.

Fig 3.

Frequency domain partial coherence functions and impulse response functions (IRFs) for input muscle selection. Frequency domain partial coherence functions (A,B, and C) and impulse response functions (D,E, and F) between the most relevant input muscles (highest partial coherence for the frequency domain and highest integrated IRF magnitude for the IRF) and the three output FES paralyzed muscles: infraspinatus (A,D), serratus anterior (B,E) and triceps (C,F). Muscle key: TraCl: trapezius clavicular portion, TraSc: trapezius scapular portion, DeltS: deltoid scapular portion, DeltC: deltoid clavicular portion, Rhomb: rhomboids, BicSH: biceps short head, BicLH: biceps long head and Supin: supinator.

The second approach for selecting the input muscles with the best predictive ability for the needed activations of the output muscles was the magnitude of the time domain relationships (via impulse response functions) between each input and each output muscle. The right column of Fig 3 shows examples of several of these impulse response functions over a range of 0–1s. The IRFs relating the 14 input muscles to the 3 output muscles were integrated over a 1s interval as another indication of the strength of the relationship between each input and each output muscle. For each panel in the right column of Fig 3, the IRFs from the 3 input muscles with the greatest integrated magnitudes for a given output muscle (infraspinatus in panel D, serratus anterior in panel E, and triceps in panel F) are illustrated. Across all three panels, the IRFs show rhomboids, deltoids (scapular portion), trapezius (scapular portion), subscapularis and biceps (long head) as the muscles with the most relevant information to predict the output activations.

The final set of four input muscles (the scapular portion of the trapezius, the scapular portion of the deltoids, the rhomboids, and the biceps) were determined based on these frequency and time domain analyses. Three of these input muscles (the scapular portion of the trapezius, the scapular portion of the deltoids, and the rhomboids) act at the shoulder and were each found to be strong predictors of needed activation for at least two of the three output muscles. The fourth input muscle (biceps) was chosen because the prediction of triceps activation was not as good as for the infraspinatus and serratus anterior (note the lower partial coherence magnitudes in Fig 3C, relative to 3A and 3B), and biceps (either long head or short head) was found by both the frequency and time domain analyses to be a strong contributor to the prediction of needed triceps activation.

B. Dynamics between activations of input and output muscles

The shapes of the IRFs illustrated in the right column of Fig 3 also suggest that the activations of the input and output muscles are, the majority of the time, strongly related for IRF lags equal to zero. This result implies that the relationships between most input muscles and most output muscles is largely instantaneous and does not contain significant dynamics.

C. Optimization of ANN architecture

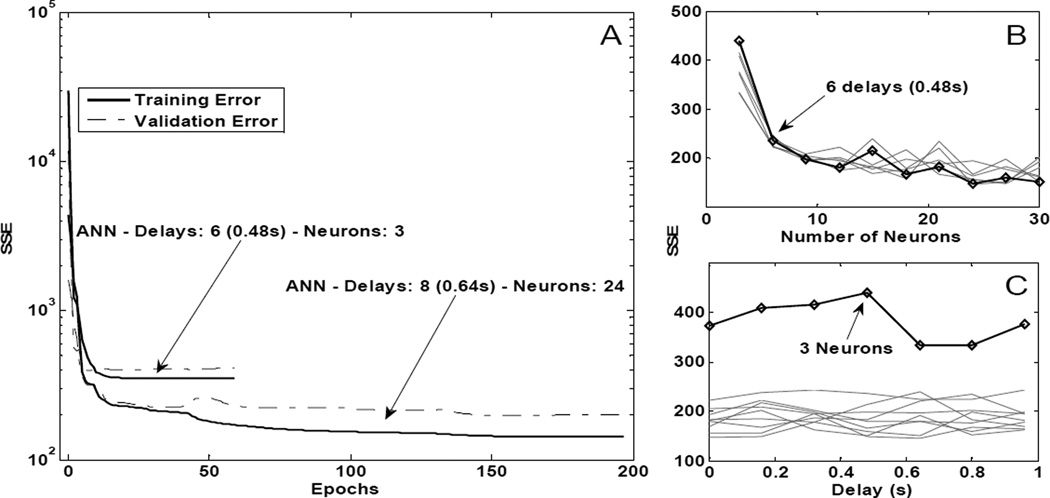
As described in the Methods, we varied a number of architectural parameters of the ANN to determine an optimal structure for predicting needed activations for paralyzed but stimulated muscles from the activations of muscles under voluntary control. Fig 4 summarizes these results. Panel 4A shows the typical decrease in the sum of squared errors between the target (paralyzed but stimulated) activations and those predicted by the input (voluntary) activations being processed by the current network weights as a function of training epoch number. Both the training (solid lines) and validation error (dotted lines) are shown for two representative architectures, one with six delays (0.48s) and three hidden neurons and one with eight delays (0.64s) and 24 hidden neurons. Training was terminated when the validation error either remained the same or slightly increased for the last 50 epochs of training. Both architectures required relatively few epochs (59 and 197 respectively) to meet this termination criteria. Also shown in Fig 4 are effects on the training sum squared error (SSE) when varying the number of hidden neurons (panel 4B) and when varying the number of time delayed inputs used (panel 4C). Training error decreased as the number of hidden neurons increased from 3 to 6 (panel 4B), but then remained approximately constant as additional neurons were added. A statistically significant difference (p<0.05) was found between using 3 neurons and using more than 3, but there was no significant (p>0.05) improvement seen if the number of hidden layer neurons increased from 6 to 30. As shown in Fig 4C, the sum of squared error did not decrease when the number of past values of the muscle activation signals included as ANN inputs was increased. Indeed, an ANOVA showed no significant difference (p=0.3013) between any of the different delays used for training, a result that was consistent with the time-domain system identification approach used to select optimal input muscles.

Fig 4.

Typical training sessions for different neural network architectures and training performance for architectures with different parameters. A: Training and validation sum squared error (SSE) vs. the number of epochs for two representative architectures with six delays (0.48s) and three hidden neurons and with eight delays (0.64s) and 24 hidden neurons. B: Training SSE for various architectures as a function of number of hidden neurons. The bold trace highlights architectures with 6 delays (0.48s) and varying number of neurons. The light traces correspond to architectures trained with other number of delays while varying the number of neurons. C: Training SSE as a function of the number of time delays. The bold line highlights architectures with 3 neurons and varying number of delays. The light traces correspond to architectures trained with other number of neurons while varying the number of delays.

D. ANN predictions of needed muscle activations

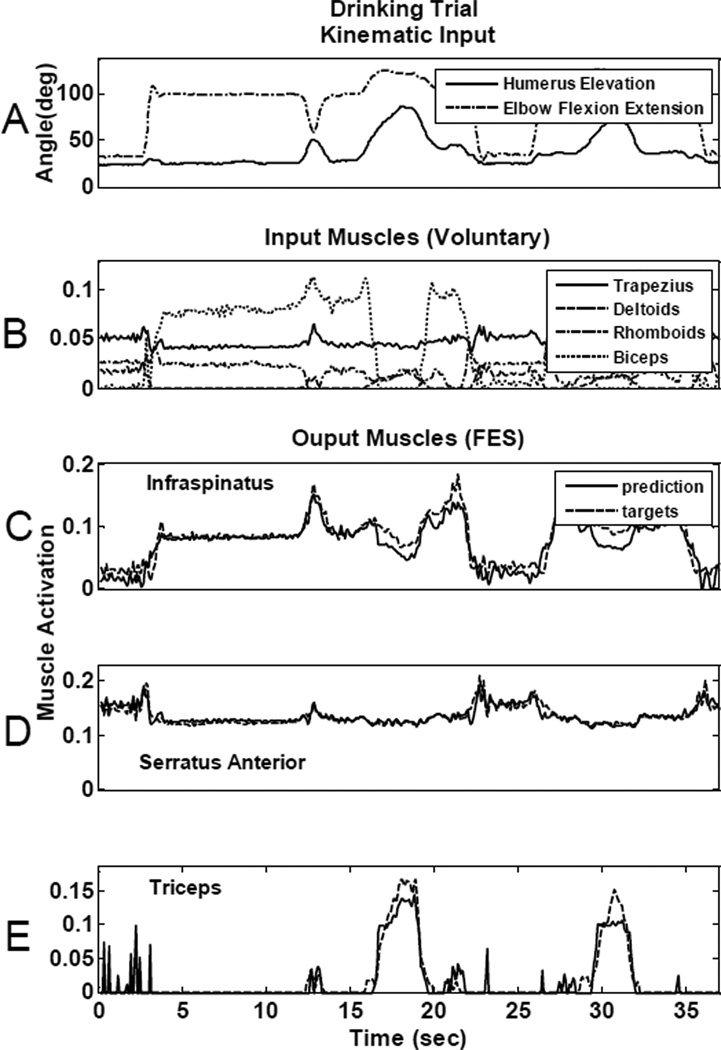
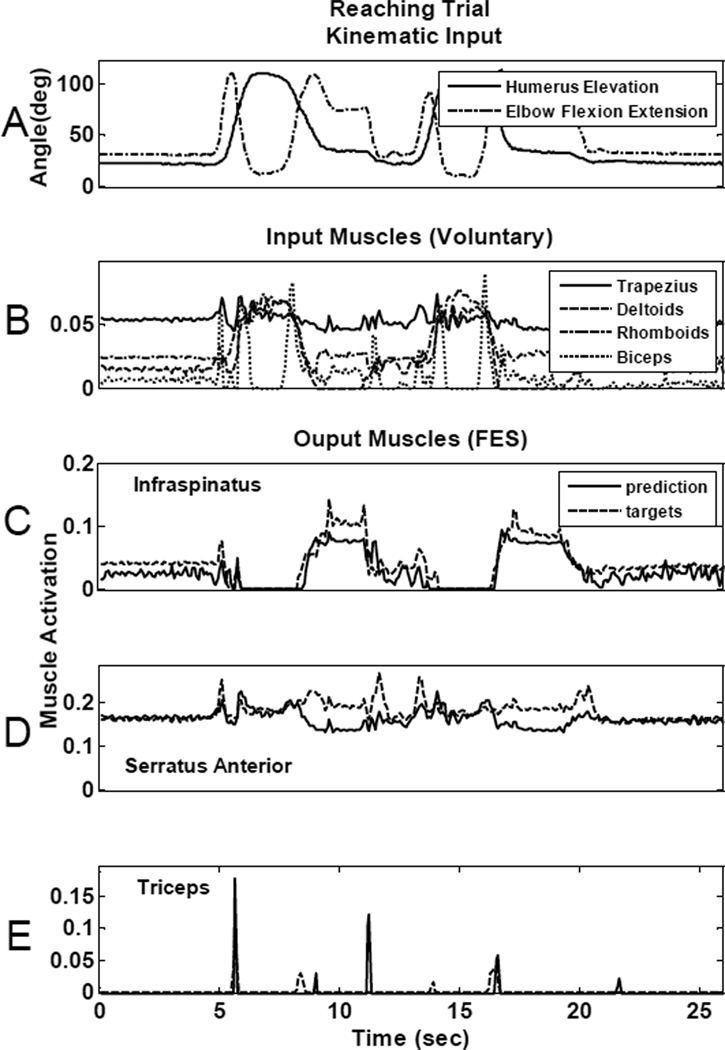
Once the optimal set of four muscles was chosen and the appropriate ANN parameters determined, the four input muscles were then used as inputs to a nonlinear, time-delayed artificial neural network (Fig 2) to determine their overall ability to predict the needed activations of the most important “paralyzed” muscles. Fig 5 and Fig 6 show the prediction ability of the neural network for two different movements that were not used in the training of the ANN. Fig 5, illustrates results from a drinking movement and Fig 6 shows results from a reaching motion, for one representative ANN architecture with twelve delays (0.96s) and 6 hidden neurons. In both figures, panel A plots the humeral elevation angle and elbow flexion/extension angle recorded from an able-bodied subject performing the respective movements. Panel B in each figure shows the “voluntary” muscle activations that were used as ANN inputs to predict the FES muscle activations. Panels C, D, and E show the ANN-generated FES muscle activation predictions (solid lines) overlaid on the target activations derived from the inverse musculoskeletal model simulations (dotted lines) for infraspinatus (panel C), serratus anterior (panel D), and triceps (panel E). Table II summarizes the RMSE for each movement type for each muscle. RMSE was calculated independently for each movement from the testing data set using the same representative architecture (12 delays, 6 neurons) from Figs 5 and 6. The first and third rows correspond to the errors for the predictions shown in Figs 5 and 6. Performance varied across movement types and muscles. For example, serratus anterior prediction was better for the drinking trial (RMSE: 0.74%) than for the high reaching motion (RMSE: 2.99%). Even though there were variations in accuracy across movements and muscles, the overall muscle activation predictions were quite accurate. Prediction errors averaged across the three muscles were always under 2.58% for the representative architecture shown (see Table II) and under 3.6% RMSE for all different neural network architectures trained.

Fig 5.

Neural network controller prediction ability for a drinking movement. A: Representative kinematics for the movement: humerus elevation and elbow flexion/extension angles. B: Controller input voluntary muscle activations for trapezius, deltoids, rhomboids and biceps. ANN prediction for infraspinatus (C), serratus anterior (D) and triceps (E). Dotted lines show the target muscle activations obtained from the model inverse simulations and the solid lines show the predictions obtained from the neural network controller.

Fig 6.

Neural network controller prediction ability for a reaching movement. A: Representative kinematics for the movement: humerus elevation and elbow flexion/extension angles. B: Controller input voluntary muscle activations for trapezius, deltoids, rhomboids and biceps. ANN prediction for infraspinatus (C), serratus anterior (D) and triceps (E). Dotted lines show the target muscle activations obtained from the model inverse simulations and the solid lines show the predictions obtained from the neural network controller.

TABLE II.

Summary of Rms Prediction Errors (% Activation) Per Movement Recorded

Muscles Movements	Infraspinatus	Serratus Anterior	Triceps	Average
Reaching high	1.82	2.99	1.21	2.01
Reaching med	4.19	1.43	1.30	2.31
Drinking	1.56	0.74	1.50	1.27
Eating	2.06	1.41	1.12	1.53
Personal care	2.56	1.20	3.99	2.58

Finally, we investigated if the input muscle selection had an effect on the network performance. Specifically, we selected four alternative combinations of input muscles that included one or more of the muscles f muscles that the linear system identification indicated might contribute to the prediction. We trained a neural network with the previously shown architecture of twelve delays (0.96s) and 6 hidden neurons. Table III shows the RMSE for these different input sets. The first row (shaded) corresponds to set described previously in detail. The average RMSE was indeed lower, although only slightly, than the other sets. For all five muscle sets illustrated in Table III, the average RSME values were also always lower (3.09%) than the 3.6% average RSME encountered across all other ANN architectures (i.e., different number of delayed inputs, different number of hidden layer neurons) trained.

TABLE III.

RMSE (% Activation) for Different Input Sets Using a Representative Neural Network Architecture With 12 Delays (0.96s) And 6 Neurons.

Muscles Muscle Input Sets	Infraspinatus	Serratus Anterior	Triceps	Average
Trapezius (clavicular), Deltoid (scapular), Subscapularis, Supinator	3.16	2.27	3.84	3.09
Trapezius (clavicular), Deltoid (scapular), Rhomboids, Biceps	2.7	2.22	2.9	2.61
Trapezius (clavicular and scapular), Deltoid (clavicular and scapular)	2.99	1.82	3.48	2.76
Trapezius (clavicular and scapular), Rhomboids, Subscapularis	2.69	1.53	4.07	2.76
Trapezius (scapular), Deltoid (scapular), Rhomboids, Biceps	2.73	1.57	3.12	2.47

IV. DISCUSSION

Our long term goal is to design a neuroprosthesis controller for individuals with C5/C6 SCI that uses EMG recordings from muscles with retained voluntary function to automatically predict electrical stimulation levels for paralyzed muscles that allow the user to make movements in a natural, almost effortless manner. The initial results presented here have focused on establishing the feasibility of this approach using activation signals obtained via inverse simulations of a musculoskeletal model. After recording arm movements in able-bodied subjects and estimating muscle activation patterns from inverse dynamic simulations using a musculoskeletal model of the arm, an artificial neural network was successfully trained to predict FES muscle activations using voluntary muscle activations as inputs. RMS prediction errors were always under 3.6% of maximum muscle activation, suggesting that remaining activity in voluntary function can indeed be used effectively to predict required (FES-based) activation levels for paralyzed muscles.

A. Musculoskeletal Model

We used a musculoskeletal model of the shoulder and elbow to approximate the muscle activation patterns required for an individual with C5 SCI to perform simple activities of daily living using their retained voluntary function augmented by a realistic FES system. The model was therefore adjusted to replicate a C5 SCI by reducing the maximum forces that each voluntary muscle available could generate. In addition, muscles that would be activated with FES were given a maximum force of 50% of able-bodied maximum. FES muscles that had been divided into multiple elements to represent their range of mechanical actions were constrained so the activation of all elements were identical, reflecting the likely effects of FES. These adjustments represent the main mechanical limitations of SCI and FES, presumably leading to activations patterns that are meaningfully representative of the available voluntary and paralyzed FES muscles. For this study, we used kinematic data recorded from able-bodied subjects as inputs to the inverse simulations of the musculoskeletal model. The outputs of these inverse simulations (the muscle activations) were then used as both inputs (the “voluntary” muscles) and outputs (the “FES” muscles) for training the ANN controller. Several assumptions were made for the model simulations. The optimization criteria used in the inverse simulations distributed the required joint torques across muscles by minimizing the amount of energy needed to execute tasks [35]. Although reasonable, energy consumption might not be the most prominent or the only goal following SCI [36]. The model does not take into account the particular physiological properties of a single subject (e.g., denervation of specific muscles or compensatory kinematic strategies to achieve movements after SCI), but rather used generic average maximum force values and able-bodied movement trajectories. Our approach is certainly capable of specifying an effective ANN controller for a single subject (with specific muscle strength patterns) and for other (non-able-bodied) kinematic strategies, but we felt that it was more important to demonstrate the overall concept of this new approach using “typical” physiological parameters and using “ideal” (i.e., able-bodied) movement trajectories. Future work will certainly pursue such approaches. For this initial study, we are very encouraged by the ability to automatically predict needed FES patterns. We further feel that the results provide an initial estimate of the ANN structure needed to provide such performance for any C5 subject.

B. Input Muscle Selection

We used a linear multi-input, multi-output (MIMO) system identification technique to obtain both impulse response functions and frequency domain coherences to identify an optimal set of voluntary muscles to use for predicting needed FES patterns. We selected a particular group of four input muscles based on their high coherence and large integrated IRF magnitudes, and the performance of these choices was borne out by the excellent results obtained using the ANN. However, an equally important result was that there are many other sets of input muscles that had remarkably similar predictive abilities. This could provide significant flexibility to provide specific users with a range of different voluntary muscles and a range of desired restored functions with effective automatic control of FES. For example, if the individual has good control of his shoulder and prefers to enhance function in the elbow for fine positioning of the hand (flexion/extension and pronation/supination), the input muscles could consist of the biceps and supinator muscles which are under voluntary control and are antagonistic to the paralyzed triceps and pronator muscles. Our analyses suggest that the muscle selection will be task specific. Since we considered mostly kinematic oriented tasks that involve reaching movements throughout the workspace, the input muscles selected by our approach all actively participated in such tasks. Focusing on more isometric-type tasks such as transfers or wheelchair propulsion will almost certainly result in a different set of optimal input muscles. The basic approach demonstrated here should be applicable to such situations.

C. ANN Controller

An artificial neural network (ANN) was the core component of the proposed controller. This approach is essentially a pattern recognition system that relates patterns in the “input” muscle activations to the activations needed for “FES” muscles. We were successful in training the ANN to learn the relationship between voluntary and paralyzed muscle activations for dynamic movements performed across the workspace, moving a step ahead in our goal of designing a EMG-based controller that activates paralyzed muscles in a more natural and automatic manner. Other non-linear function approximation techniques such as system identification [37] or optimal control [38] are likely equally capable of capturing the dynamic properties of the muscle activations. However, we adopted this neural network approach because it has shown robust convergence and fast training for this type of application [34]. Furthermore, these ANN’s can be implemented with modest processing and real-time speed performance.

Overall, the prediction errors achieved with the trained neural network controller were universally low (less than 3.6% RMSE). This result suggests that the neural network architecture is able to learn the relationship between muscle activations rather well without the need for other inputs (such as the location of the arm in space) that might require additional (implantable) sensors. This is an important finding that supports the idea that activations in muscles across the upper extremity are related through synergistic patterns controlled by the nervous system [39]. Furthermore, our results indicate that this relationship can be predicted using mathematical algorithms and function approximation techniques such as neural networks. Even though the RMSE were low, we did find variations in prediction accuracy across movements and muscles. What our results thus far do not indicate, however, are the mechanical consequences of the small (<3.6% RSME) activation errors on movement performance. A proper model-based evaluation of this question would use the voluntary and predicted FES activations as inputs to forward simulation using our musculoskeletal model, and the resulting predicted movements could be compared to those originally recorded from the able-bodied subjects. Unfortunately, current forward simulations run into numerical stability problems within several hundred ms and thus cannot provide the needed movement predictions. Work continues towards solving this challenge with forward simulations [40].

We trained the ANN using a specific set of movements that were considered high priority functional activities for individuals with C5 SCI, and the ANN was able to predict activations for similar motions quite accurately. Activations for motions that are significantly different than those used to train the ANN are not likely to be well-predicted. However, including additional motions in the training set would address this issue.

We also plan to implement this ANN-based controller in human subjects with C5 SCI. As previously discussed, there are likely to be challenges related to user-specific muscle parameters, individual movement patterns, and physiological changes (e.g., fatigue). However, there is the real possibility that the user will adapt to the small errors in the predicted activations by subtle changes in the activation of the input muscles, thus significantly reducing the mechanical impact of the ANN prediction errors. Our hypothesis is that the ANN approach will come very close to activating the muscles in appropriate patterns and that adaptation by the retained voluntary neural control mechanisms of the user will result in a very effective controller.

Our results showed that a rather simple artificial neural network is capable of providing excellent predictions of needed muscle activations. We found a basically instantaneous relationship between the activations of input and output muscles, meaning that a simple static network should be sufficient. We also found that a very small number of hidden layer neurons were capable of providing a good prediction, suggesting that a modest-sized ANN is sufficient to achieve convergence and good prediction capability. This is an important finding for future implementation in a human subject because (i) the controller can be trained very fast, (ii) modifications and parameter adjustment to the controller can be done online with minimal computational burden and most importantly (iii) the implemented ANN controller can be given to the user in a small, power-efficient portable system for daily home use.

D. Implications

This feasibility study showed that a simple neural network-based controller should be able to predict the stimulation levels for paralyzed muscles based on the activations levels from muscles under voluntary control. Furthermore, we used a model in lieu of a human subject to evaluate many different conditions and found that this approach was a useful tool for replicating SCI and predicting the outcome of an implanted neuroprosthesis.

In a real situation, we expect EMG signals to replace the model-predicted muscle activations levels, allowing a rather direct translation of our simulation-based approach to human users with C5 SCI by using EMG signals recorded from voluntarily controlled muscles. In a similar way, muscle activation levels for paralyzed muscles can be mapped to levels of stimulation by measuring muscle recruitment curves and determining the maximum level of activation that can be achieved with electrical stimulation. We believe the controller designed in this study can be implemented to drive a real neuroprosthesis for a subject with SCI after a few adjustments and user-specific customization of the controller through online training.

Incorporating retained voluntary control mechanisms exploits the immense adaptive ability of the human nervous system. A long-term hypothesis of this work is that intact portions of the nervous system can readapt to the use of the neuroprosthesis and learn to interact with it. We expect that the proposed controller will successfully interact with remaining motor function in a continuous adaptation process, creating a synergistic relation between the nervous system and the neuroprosthesis that will restore function in an automatic and more natural manner.

Biographies

Juan Gabriel Hincapie, Ph.D. received his B.Sc degree in Electronics Engineering from Universidad de los Andes, Bogotá, Colombia in 2002 and his M.Sc and Ph.D. in Biomedical Engineering from Case Western Reserve University, Cleveland, USA in 2005 and 2008 respectively. His research focuses in the use of electrical stimulation of the nervous system to restore function in individuals with neurological disorders and provide therapies for autonomic and cardiovascular disorders and his interests include EMG-based control of neuroprostheses, neuromuscular control, biomechanics and musculoskeletal modeling. He is currently a scientist for Boston Scientific Corporation.

Robert F. Kirsch, Ph.D. obtained his B.S. in Electrical Engineering from the University of Cincinnati (1982), and M.S. (1986) and Ph.D. (1990) in Biomedical Engineering from Northwestern University. He was a post-doctoral fellow in the Dept. of Biomedical Engineering at McGill University in Montréal from 1990–1993. Dr. Kirsch is currently an Associate Professor of Biomedical Engineering at Case Western Reserve University and Associate Director for Research in the Cleveland VA FES Center. Dr. Kirsch’s research focuses on restoring movement to disabled individuals using functional electrical stimulation (FES) and controlling FES actions via natural neural commands. Computer-based models of the human upper extremity are used to develop new FES approaches. FES user interfaces, including ones based on brain recordings, are being developed to provide FES users with the ability to command movements of their own arm.